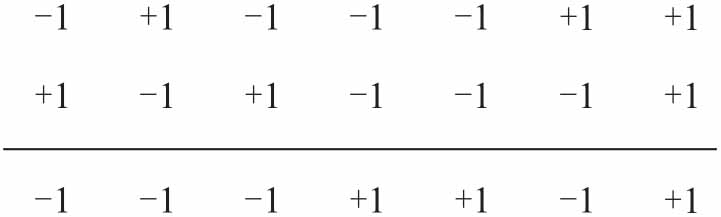GPS定位技术 - 李理的博客

本文介绍GPS定位技术。

概述
原理
坐标系
地图投影
时间系统
位置计算方法
GPS系统
计算GPS卫星的位置
计算行程时间
- 确定行程时间的具体方法
误差分析与精度因子
- 误差主要原因
- DOP
减小误差
A-GPS
参考文献

概述

本节内容主要参考了[1 ][2 ][3 ][4 ]。

不管是无人驾驶还是V2X通信，感知车辆当前的位置都是一个最基本的要求。对于V2X应用来说，我们不但要知道车辆在哪条马路上，而且还需要更准确的知道在哪个车道上。因为美国90%的车道(lane)宽度大于3米，所以如果定位精度在1.5米之内就可以判断车辆在哪个车道上。最常见的定位信息来自于全球导航卫星系统(Global Navigation Satellite System, GNSS)。GNSS可以提供较精确的定位信息，但是通常还达不到1.5米的要求，而且在市内或者有建筑物遮挡卫星信号的时候误差更大。最常用的GNSS是美国的GPS(Global Positioning System)，此外还有欧洲的Galileo、俄罗斯的GLONASS和中国的北斗。当然目前最常用的还是美国的GPS，我们下面都以GPS为例来介绍。

卫星导航是一种通过全球导航卫星系统(GNSS)精确测定地球上任何一点的位置和时间的方法。目前，卫星导航接收机可供个人定位、商业定位、导航、勘测和测定精确时间之用，用作个人、休闲和商业方面的用途也日渐增多。使用GNSS可在地球表面上的任何一点精确测定以下数值，如果下图所示：

图：卫星导航的基本功能来自[4]

精确位置(经度、纬度和高度坐标)，精度范围在20m到约1mm之间。
精确时间(协调世界时，即UTC)，精度范围在60ns到约5ns之间。

可由上述数值推导出行程(路径)的速度和方向，这些数值由围绕地球运行的卫星提供。行程的速度也可通过多普勒频移测量直接确定。

GPS系统的全称为：授时与测距导航系统/全球定位系统(NAVSTAR-GPS)，设计为军民两用。我们通常认为GPS是用来定位的，但其实它还可以来进行时钟的准确同步，在后面的计算过程中会发现怎么用它来同步GPS接收器和UTC(GPS原子钟)的时间。GPS由由美国空军第50航空联队负责运营[5 ]，最初目的是是军用，但是后来逐渐民用。我们现在用的手机或者各种导航设备都可能使用GPS，虽然没有直接给美国国防部授权费，但是(正规)GPS芯片生产商都已经交过授权费了。

原理

GPS定位的原理是三边测量术(Trilateration)，一些资料误认为是三角测量(Triangulation)，这是不对的[6 ]。GPS定位的原理如下图：

图：卫星导航的基本功能来自[5]

如果我们知道一个物体离三个已知位置的物体(卫星)的距离，那么我们就能计算出这个物体的位置。具体来说，我们通过这三个卫星画三个球，那么这三个球必定相交于空间里的一个点。如果读者和我一样没有空间想象力，那么可以看公式：

\[dist_1 = \sqrt{(x-x_1)^2+(y-y_1)^2+(z-z_1)^2} \\ dist_2 = \sqrt{(x-x_2)^2+(y-y_2)^2+(z-z_2)^2} \\ dist_3 = \sqrt{(x-x_3)^2+(y-y_3)^2+(z-z_3)^2} \\\]

其中x,y,z是要定位的物体的三维笛卡尔坐标，$(x_i,y_i,z_i)$是第i个卫星的坐标，$dist_i$是物体到第i个卫星的距离。三个方程，三个未知数，那么应该可以求出唯一解(没证明过，但应该是这样的，而且好像没有解析解)。

卫星在每一个时刻的精确位置叫做星历，而粗略的位置叫年历，这些信息卫星会用广播的方式定期发送。因此GPS接收器可以通过收听这些广播获得没依靠卫星的精确位置，那现在的问题就是怎么确定每一个卫星到接收器的距离。如果我们能够让GPS接收器的时钟完全和GPS卫星同步，那么我们可以通过接受的信号和实际(通过星历)的信号的时延来得到电磁波从卫星到GPS接收器的行程时间，如果再假设电磁波的速度是固定光速$c=3 \times 10^8m/s$，则可以计算出卫星到接收器的距离。

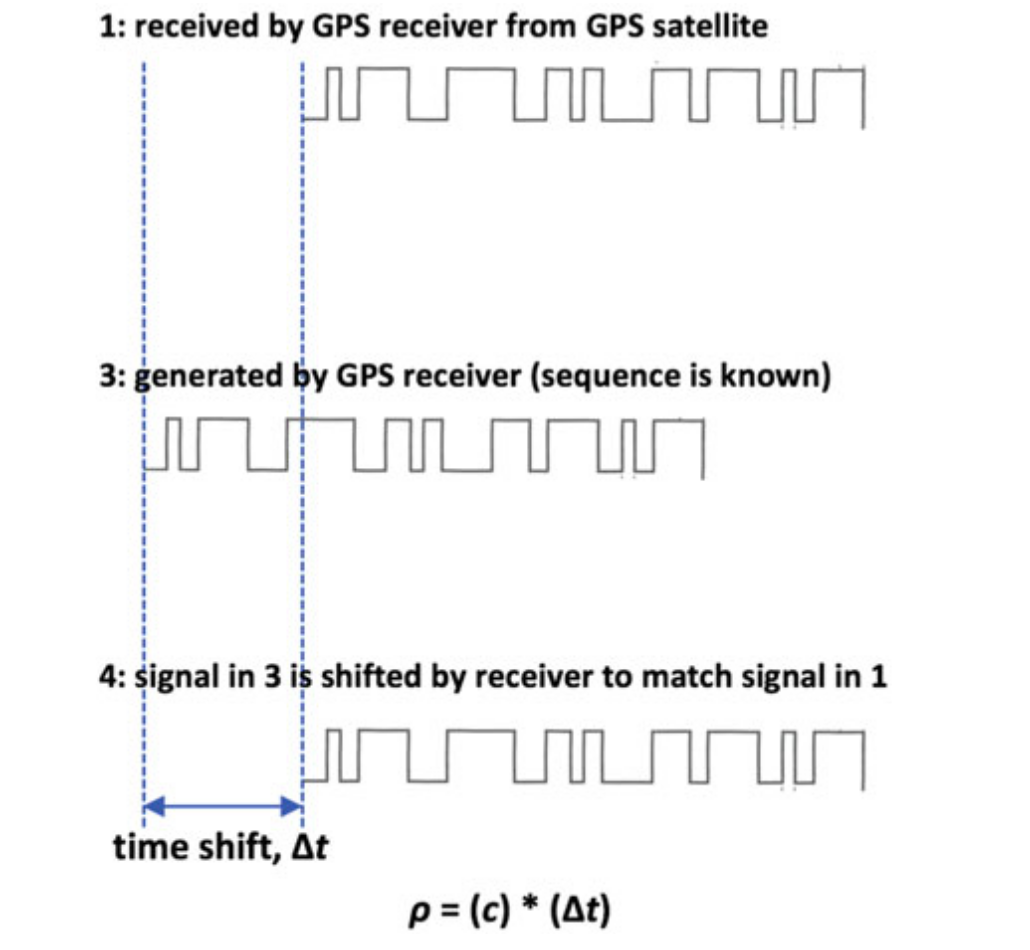
因为光速很快，即使1μs的时差也会带来300m的位置误差，但是我们不可能花费高额度代价个GPS接收器配备昂贵的原子钟。实际我们会把GPS接收器和GPS卫星的时差$\Delta t$也当成一个未知量，这个时候我们需要4个方程才能解出4个未知量，所以我们需要4颗GPS卫星的信号才能进行定位。

图：计算伪距(pseudorange)

计算距离的方法如上图所示，通过星历，我们可以”生成”GPS卫星目前的信号，如图中3所示。而实际接受到的信号是图中1，通过相关的计算我们可以得到这两个信号的时移$\Delta t$，然后乘以光速c就得到伪距。为什么叫”伪”距呢？因为GPS接收器和卫星的时钟差异，这不是卫星到真实的距离，所以叫伪距。

坐标系

前面我们在介绍GPS原理时使用的是三维的笛卡尔坐标系统，但是我们平时是在地球这个球体表面运动。在小的尺度上看可以认为是直线运动，但是在大一点的尺度看我们都是沿着球面进行曲线的运动，这个时候使用经度和维度这样的表示方法会更加简单。

我们都知道地球是圆的，往往把它想象成一个理想的球体。但实际上地球并不圆，而且形状经常改变，要界定它的边界都不容易。比如我们在北京建造一幢摩天大楼，则地球的形状就变了。甚至我们跺跺脚，地球都可能发生极其轻微的变形。另外地球周围的大气等是否也算作地球的一部分，这也不是那么能简单说的清楚的事情。但地球究竟有多圆？描述我们这个蓝色星球的外形一直是一项充满挑战的科学工作。数百年来，提出了若干个不同的模型以尽可能真实地表述地球的近似真实外形。

我们用(定义)地球体为这样的形体：平均海平面的零点即为其表面。该表面由地球重力所决定，因而其几何描述极其复杂。研究人员借用了希腊文中的地球一词，将该表面的几何外形称为大地水准面(Geoid)，由此得到的假想球体叫做地球体。

图：大地水准面(Geoid)是地球表面的近似外形

大地水准面是一个非常接近海平面并且具有相同重力势能的表面，如果一个人能够挖掘一条切断陆地、连接起海洋的运河的话，那么这个运河的水面也就是大致的大地水准面。大地水准面是波动的，有的地区高些，有的地区低些，差别甚至可以达到1000公里距离相差100米(注：美国新墨西哥州的Carlsbad就是这样的)[8 ]。为什么要定义这么一个不规则，无法用一个公式精确描述的”假想”模型呢？由于重力矢量(vector)总是垂直于大地水准面的，铅垂线(plumb lines)和水准仪(spirit levels)的工作会受到大地水准面的直接影响。所以我们在测量高度的时候使用测量地点的大地水准面作为基点是很方便的，比如我们盖一个房子，我们的地可能不平，那么怎么测量房子的高度呢？我们首先需要一个方向，而使用重力相反的方向显然是比较合适的。那这个方向(轴)的起点呢？显然使用海平面作为起点是比较合适的，这也是我们通常用海拔来描述一个地球表面物体的高度的原因。我国1987年规定将青岛验潮站1952年1月1日~1979年12月31日所测定的黄海平均海水面作为全国高程的起算面。并推测得青岛观象山上国家水准原点高程为72.260m。根据该高程起算面建立起来的高程系统，称为1985国家高程基准。我国各地面点的海拔，均指由黄海平均海平面起算的高度[9 ]。

图：水准仪：来自百度百科

上图是水准仪，如果要测量两点的高度差(当然别太远了)，则分别在两点放置水准仪，水准仪会提供一条垂直于重力加速度方向的视线，然后利用水准尺读取两点的高程差。那么我首先测量离高程基准近的点A，得到A的高程，然后再测A附近的B和A的差距得到B的高程。但是前面也提到大地水准面是不规则的，不同高程的水准面(重力势能相等的面)是不平行的，所以沿不同路线测得的两点间高差将有差异。比如我不测A，而是测附近的A’，然后再测A’和B的高程差，这样两种方法得到的B的高程可能是不同的。

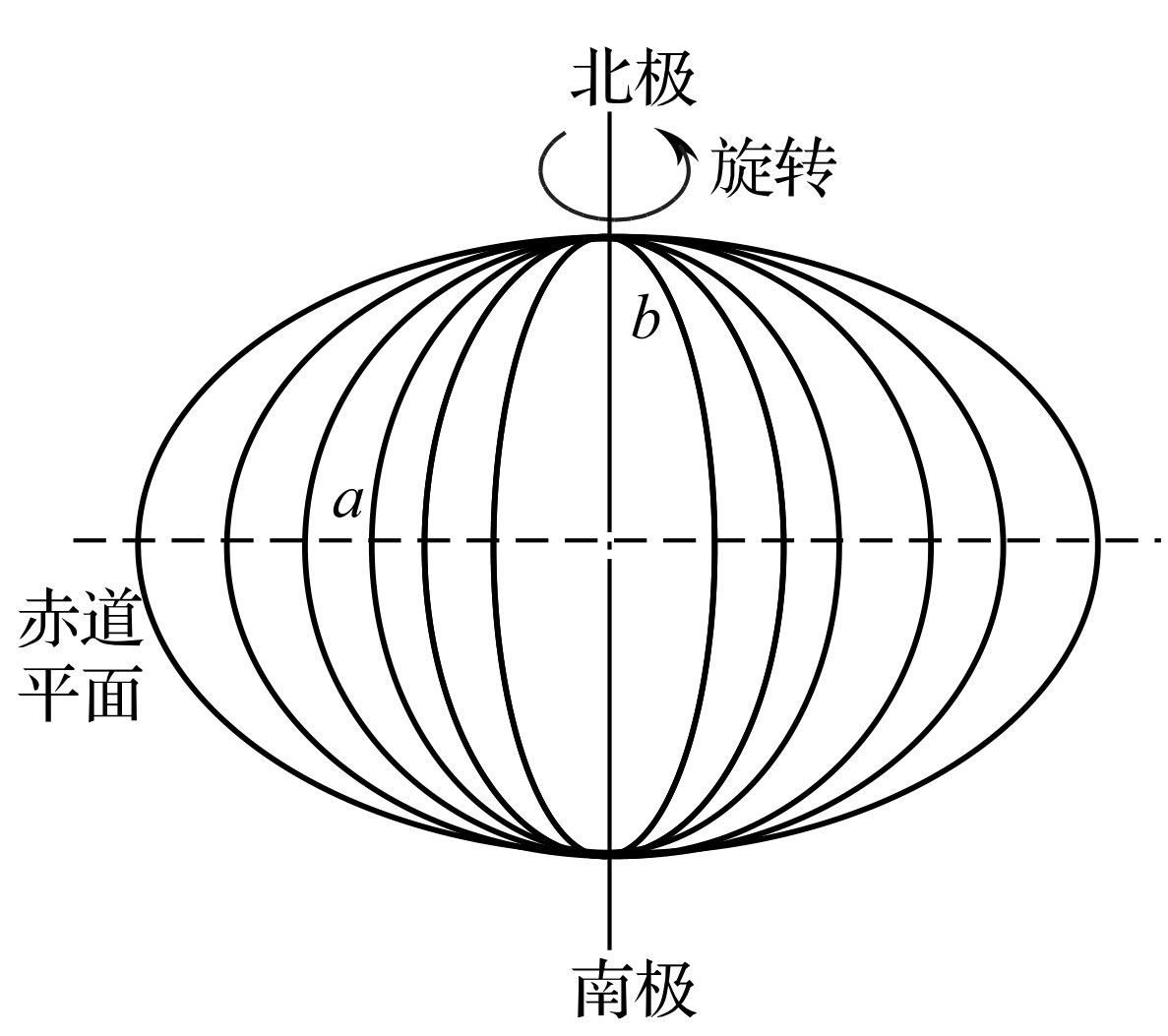
在进行计算时，Geoid是难以处理的形体。因此在进行日常的测量工作时需要一种简单、便于定义的外形。这种用作替代的表面就是椭球。如果一个椭圆的表面绕其对称的南北极轴线旋转，就会得到一个椭球体。

图：椭球体

椭球由两个参数确定：长半轴a(位于赤道面)；短半轴b(位于南北极轴)。椭球与理想球体的外形偏差成为扁率(f)：

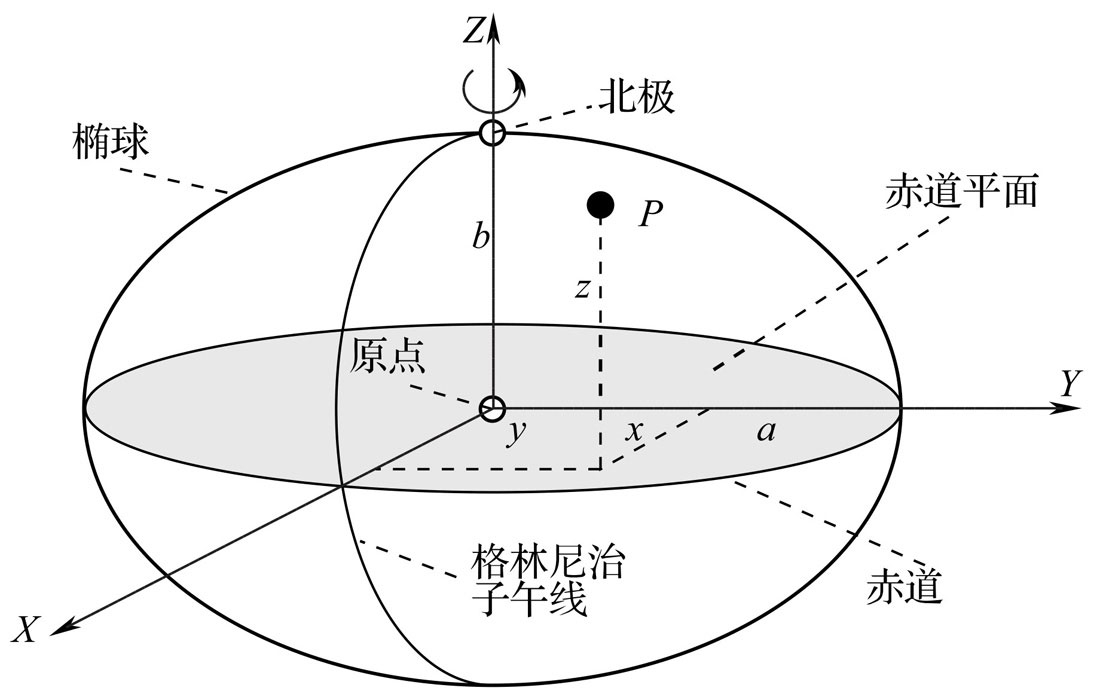
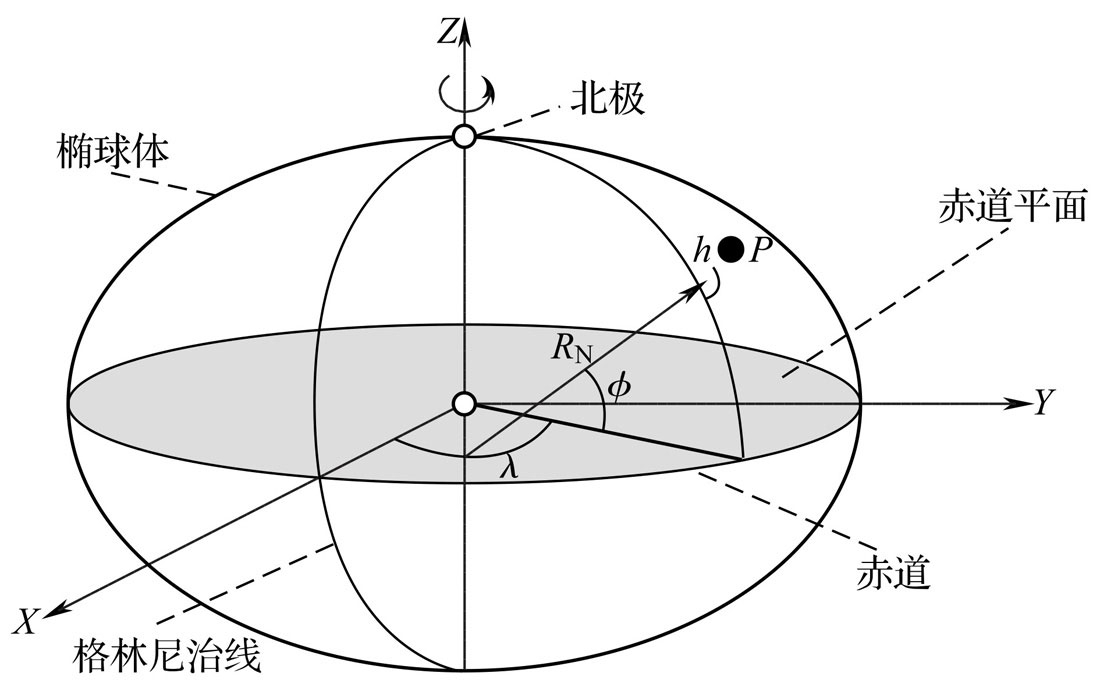
\[f=\frac{a-b}{a}\]

现在我们要用一个椭球体来近似地球体，那么这个椭球体的长半轴和短半轴分别是多少呢？另外这个椭球的中心位于哪个位置呢？这当然也是一个定义的问题。用地球的质心来作为椭球的中心是很自然的选择，当然随着地球的自转，这个位置会发生变化。接下来我们需要定义这个椭球体的摆放位置，在这之前我们首先定义笛卡尔坐标系统。这个坐标系统的原点就是质心，Z坐标就是质心指向北极的方向，XY轴的平面就是赤道平面，把赤道和格林尼治子午线(本初子午线)与赤道平面相交的点作为X轴，根据右手法则可以确定Y轴的方向，如下图所示：

那么这个椭球体的长半轴a和短半轴b分别是多少呢？为了更好的”拟合”的地球体，科学家进行了测算(怎么算出来的我没搞明白，感兴趣的读者可以参考[10 ])，得到如下的值：

这个参考系统是1984年搞出来的，所以就叫做WGS-84(World Geodetic System, 世界大地测量系统)，目前的GPS就使用这个坐标系统，因此我们的GPS定位设备得到就是WGS-84的坐标值。为了计算和使用方便，我们通常使用经度、维度和高度的方法来描述地球表面的一个点，如下图所示：

图：椭球坐标系示意图

对于点P，朝着椭球体做一条垂线，垂线与椭球相交与P’。因为对称性，直线PP’一定包含在某个扇面里。这个扇面与零度经线的夹角就是经度$\Phi$。同时PP’延长后会投射到赤道上某一点，从原点到这个点的直线与PP’的夹角就是维度$\lambda$，而PP’的长度就是高度h。

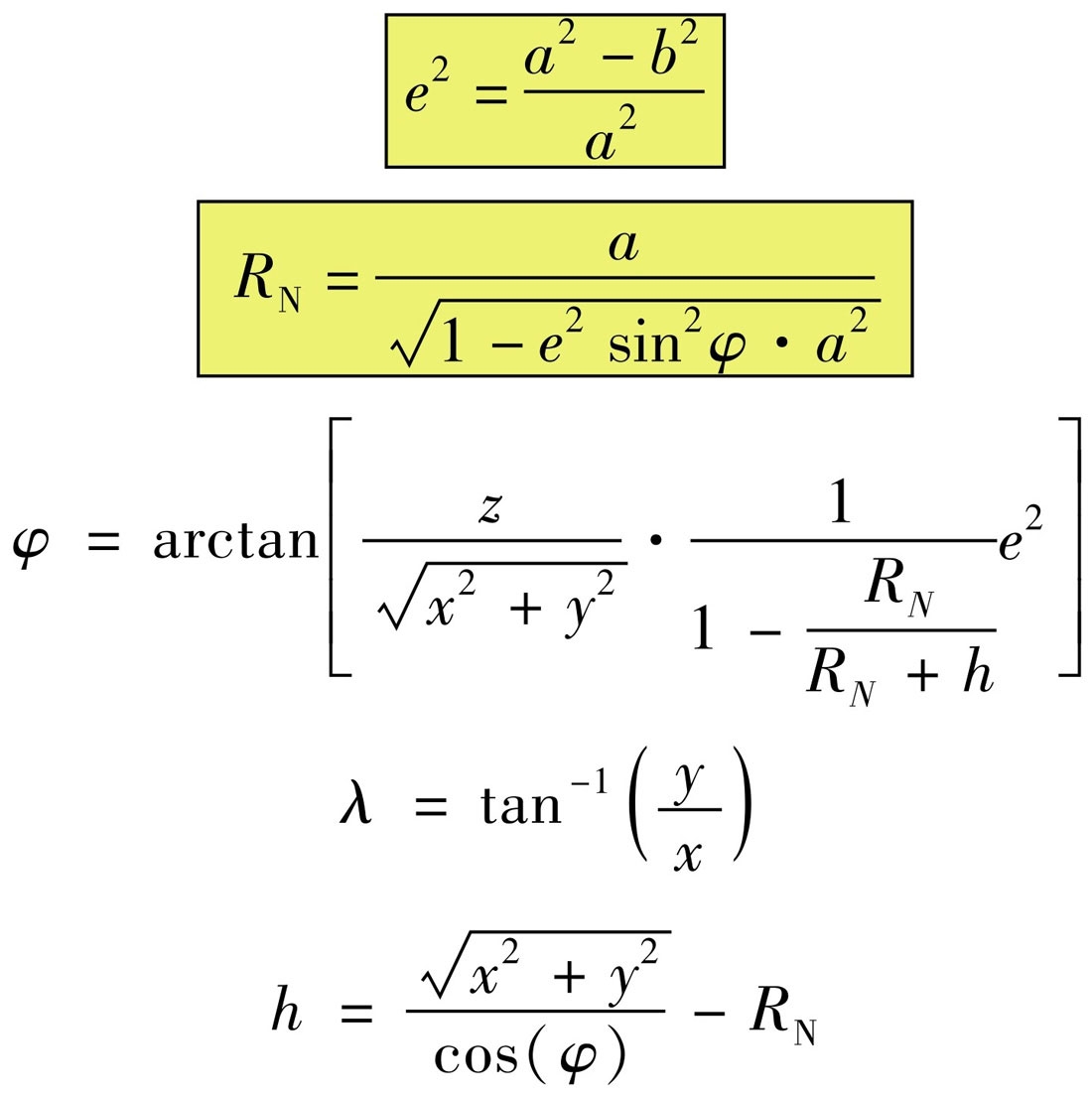
笛卡尔坐标和椭球坐标可以相互转化，比如下面的公式可以实现把笛卡尔坐标转化成椭球坐标：

不过上面的公式里，$R_N$是依赖$\phi$的，所以需要迭代才能求解。而把椭球坐标转化成笛卡尔坐标就很简单了：

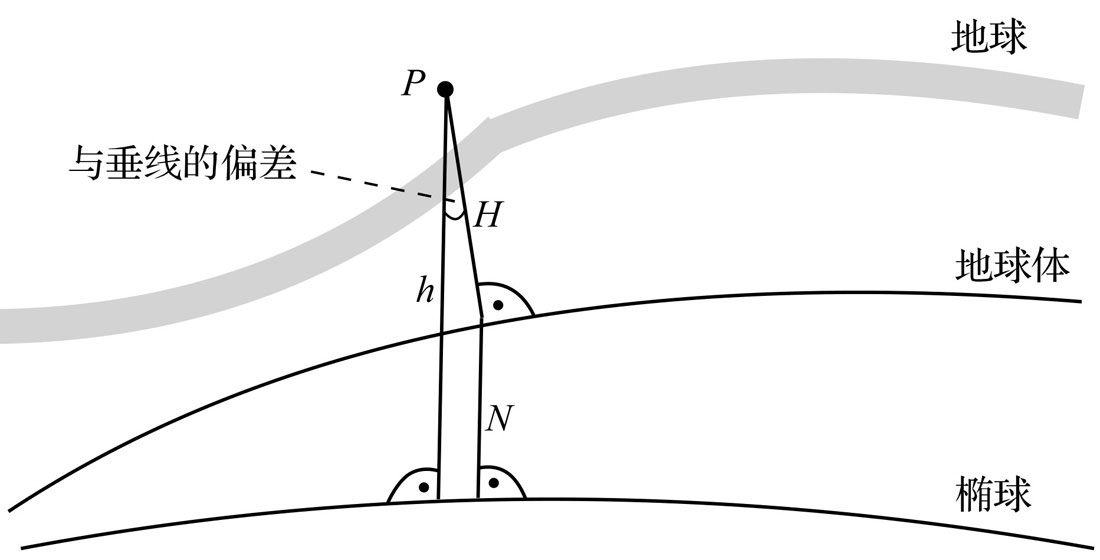
\[x = [R_N+h] cos \phi cos \lambda \\ y = [R_N+h] cos \phi sin \lambda \\ z = [R_N [1 - e^2]+h]sin \phi\]

椭球非常适合描述经度和维度表示的点的位置。高程要么基于地球体(大地水准面)要么基于参考椭球。它们之间的关系如下图：

图：地球体与椭球之间的差异

\[h=H+N\]

其中，h是到参考椭球的高度，H是到地球体的高度，而N称为大地水准面起伏。我们从某些测绘地图得到的海拔高度就是H，而从GPS拿到的是h，这一点要注意。

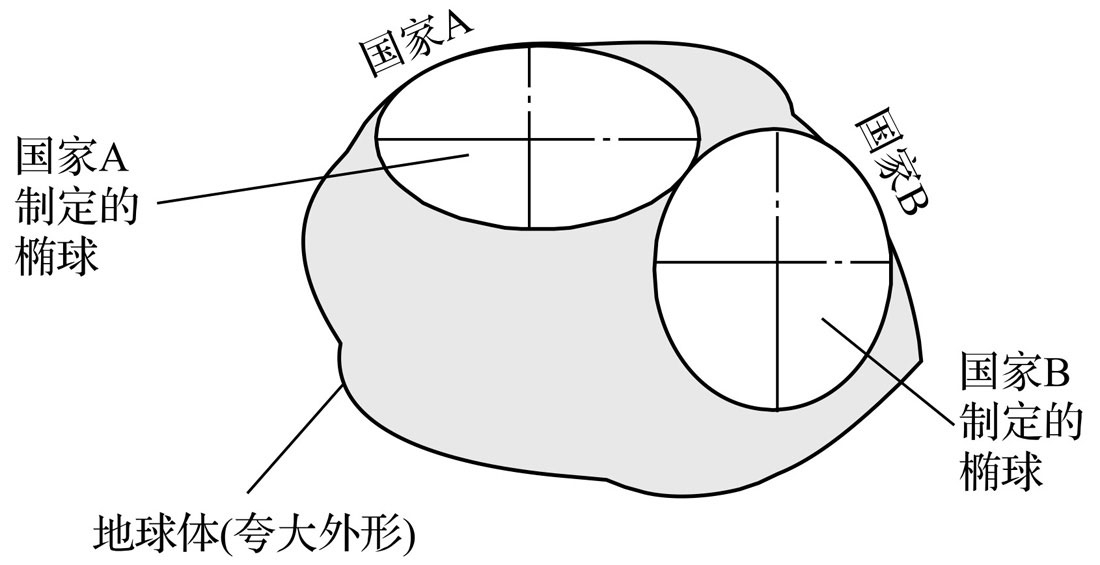
WGS-84是为了拟合整个地球体而定义出来的一种大地测量系统，但是不见得是对某个国家或者地区最优的方式。比如下图：

图：本地(local)参考椭球体

我们完全可以定义原点不在地球质心，而且长短半轴比WGS-84小但是拟合的更好的参考椭球体。比如国家A，我们可能定义一种大地测量系统；对于国家B，则使用另外一种。中国于上世纪50年代和80年代分别建立了1954年北京坐标系和1980西安坐标系[11 ]，最新的规范是2000国家大地坐标系[12 ]，不过最新的规范在2018年7月1日才开始全面使用[13 ]。这些坐标系统和WGS-84不同，因此使用时可能需要在它们之间进行转换。

另外如果我们在中国大陆使用地图服务的话，我们可能会看到GCJ-02这个坐标系统，这又是什么东西呢？GCJ-02是国家测绘局(国测局，GCJ，这样的缩写比较罕见)02号标准的意思。它是一种对经纬度数据的加密算法，即加入随机的偏差。国内出版的各种地图系统(包括电子形式)，必须至少采用GCJ-02对地理位置进行首次加密[14 ]。由于最开始的时候一些国外地图服务商没搞明白这点，直接使用了GCJ-02加密的坐标来显示POI，从而把这些POI移到太平洋上去了，所以网友也戏称火星坐标。根据[15 ]，据说为了避免泄露国家机密，国家测绘局的专家设计了一种地形图非线性保密处理技术。其实就是对原始坐标(比如WSG-84)进行一个非线性的变换，这个变换会导致POI的经纬度相对于原来发生一定偏移，但是还是会尽量保证POI之间的相对位置关系(否则把北京变到南京南边就坏了)。从数学上来说这是一个不可逆的过程，我们不能求这个变换函数的反函数，因此无法精确的根据加密后(GCJ-02)的坐标得到原始的坐标。但是这个算法是公开的(在任何地图相关的终端你都必须实现这个算法，当然就很容易泄露出去了)，因此可以用迭代的方法求近似解。网上有一些算法能够近似的把GCJ-02坐标系统转换成原始坐标的经纬度，感兴趣的读者可以参考[16 ][18 ]。百度地图的坐标在GCJ-02的基础上又做了一次非线性变化，得到的坐标叫做BD-09坐标[17 ]。根据[18]，简单的解密能够到达米级别的精度，如果使用更多次的迭代还可以得到更高精度的解，所以当初专家们的设计安全目标并没有达成。但这并不妨碍这个算法仍然不知疲倦的在各种设备里运行大量无意义的计算(增加碳排量)并且他们通过授权插件使用权获得大量收入。

地图投影

虽然用椭球坐标的经度、维度和高程来描述地球表面的一个点很方便，但是我们不能成天捧个地球仪出门，日常生活中我们更习惯把各种地标信息绘制在一张平面的纸上，这样方便携带。把三维椭球体表面附近的点映射到二维平面上的方法就叫做地图投影。把一个高维的数据投影成低维的空间总会损失一些信息，当然也会保留一些信息，根据我们希望保留哪些信息就能找到不同的投影方法。为什么地图都是错的是一个很有意思的视频，感兴趣的读者可以看看。下面我们介绍几种常见的地图投影方法。

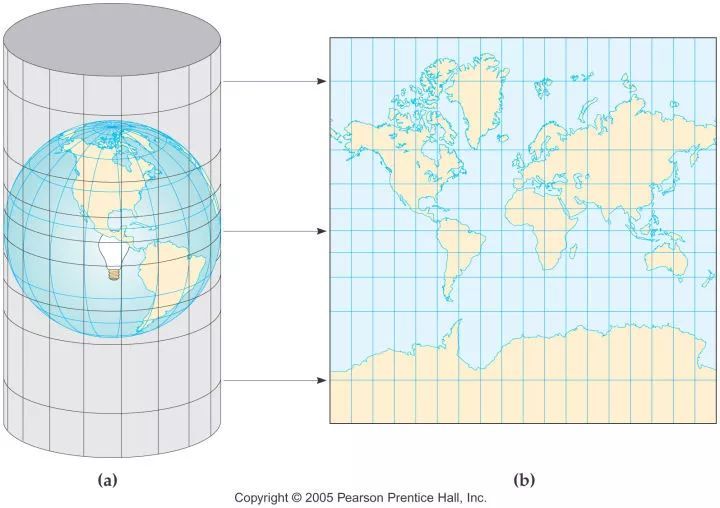
墨卡托投影(Mercator Projection)

根据[19 ][20 ]，墨卡托投影的原理如下图所示：

图：墨卡托投影

假设地球是一个椭球体，我们用很大的一张纸卷成一个圆柱体把地球包起来。然后对于地球表面的每一个点P，我们都可以从地心发出一条经过改点的射线，然后与圆柱体(纸卷)相交于点P’，P’就是P在地图上的投影。通过把所有(当然理论上是无穷的，但是我们可以采样足够多就行)点都进行这样的投影，就可以把地球表面的每一个点都投射到纸卷上。最后我们把这个纸卷展开，就得到了地球的墨卡托投影。北极和南极附近的点会投影到Y轴方向很大的值(极点会投影到Y为无穷大的地方)，我们没有那么大的纸，而且南极和北极除了企鹅和北极熊也没有太多人类，没有太大看地图的需求，所以通常我们只是投影到最高维度为正负85.05度就行。另外我们需要定义平面笛卡尔坐标的原点和XY轴方向，墨卡托投影的原点就是经纬度都是0度的点的投影(本初子午线和赤道的交点)，赤道的投影为X轴，本初子午线的投影为Y轴。从西往东为X的正方向，从南往北为Y的正方向。这样的结果使得整个地图以本初子午线(欧洲)为中心，它的东西方向对于地图的右边和左边，而南北极位于它的下方和上方。

墨卡托投影特点如下：

原来的经线(子午线)都汇聚于极点，纬度愈高经线的间距愈小，而在墨卡托投影上，经线全部画成与赤道上间隔相等的平行直线
- 我们把地球想象成一个西瓜，然后两条经线就是从上往下切西瓜，切出来一瓣一瓣的西瓜。原来的西瓜的两条经线会相交于南北极，但是展开后就变成了一个长方形。
地球表面上假想的各纬线间隔基本是相等的，而在墨卡托投影上纬线间隔由赤道向两极逐渐扩大，而且经纬线以同一倍数扩大
- 因为这个特性，维度越高的地方南北方向的放大效应越大
墨卡托投影上经、纬线均为平行直线而且经纬线之间互相正交
- 这个就是前面说的一瓣被掰扯成一个长方形。
地球上的等角航线在地图上均表现为直线
- 这个后面详细解释
图上能正确表示航线与子午线的夹角，例如航线在地球上与子午线的夹角为15°，图上也表示为15°
- 同上
比例尺随纬度而变化，在一张地图上纬度不同，同一距离的比例尺也不同，不能比较面积

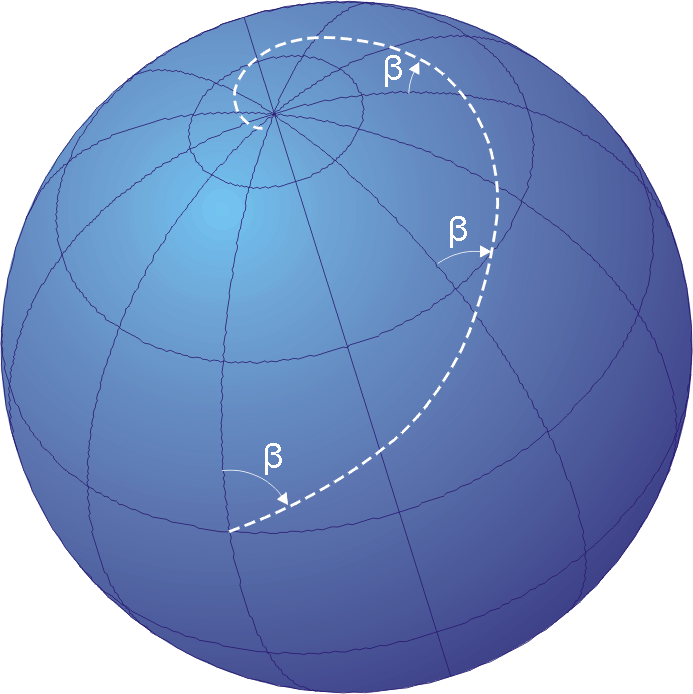
下面我们来解释一下什么是等角航线。根据[21 ][22 ]，等角航线是指地球面上一条与所有经线相交成等方位角的曲线，又名恒向线、斜航线。在地球表面上除经线和纬线以外的等角航线，都是以极点为渐近点的螺旋曲线，如下图所示：

图：等角航线，来自维基百科

我们先来看两个特殊情况，如果我们沿着与经线(与真北方向平行的方向)运动，显然我们走的是圆形(地球这个球体上的一个圆)的弧线。类似如果我们沿着纬线(与赤道平行)运动，我们也是走一个圆形的轨迹。否则，如果我们从地球上任意一个点沿着与经线(真北方向)保持一个固定的夹角运动，我们会沿着一条螺旋曲线运动，并且最终的极限点是极点(上图是北极)。在没有GPS等精确定位的大航海年代，我们通常会沿着等角航线来进行航海。为什么要用这种方法呢？因为测量船只与经线的角度是比较容易的，我们有罗盘，我们在墨卡托投影的地图上找到起点和终点，然后画出一条直线，这条直线与真北方向的夹角就是我们航线的角度。我们只要保持船只的方向不变，经过螺旋的曲线就能达到目的地。能够实现这个目标的关键就是墨卡托投影能够正确表示航线与子午线的夹角，从而使得等角航线在地图上表现为直线。

等角航线不是球面上最短的曲线，最短的曲线是经过这两点的大圆的一段劣(短)弧，这就是所谓的大圆航线[23 ][24 ]。但是这段圆弧与经线的夹角显然不会不变(除非起点和终点的经度或者维度相同)，这需要航行的时候经常修正航线，这对大航海时代的船长来说难度就很大。现代有了GPS等更加先进定位技术之后，长途飞机和船只就能走更短的大圆航线了，不过实际由于领空/领海等政治因素的限制，大部分航班并不是走的最短的路线。

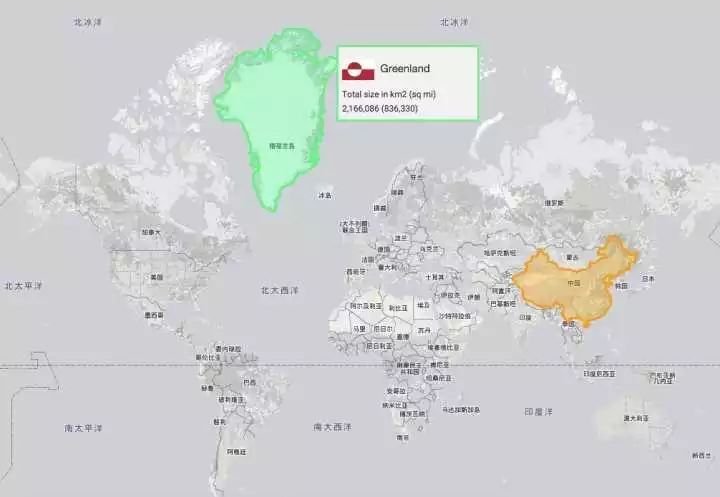
但是墨卡托投影对于高纬度的几何体的放大作用是大于低纬度的形体的，因此如果在墨卡托投影的地图上测量中国和格陵兰岛，会发现格陵兰岛的面积会比中国大。如下图所示：

图：格陵兰岛和中国

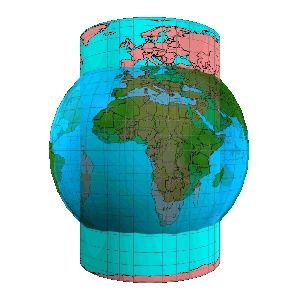
注意：上面的墨卡托投影选择的是使用一个圆柱体来包(切)住椭球体。但是也可以用别的的圆柱体，这个圆柱体不一定能恰好”包”住椭球体，它可能把椭球体割开，所以叫做割圆柱投影。比如下图：

图：正轴等角(割)圆柱投影

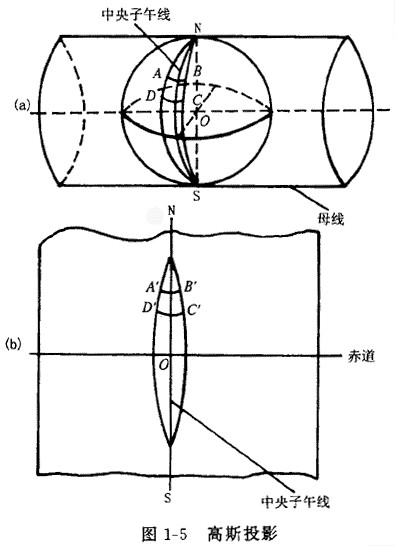
高斯-克吕格投影

高斯-克吕格投影又称为横轴墨卡托投影，西方喜欢用这个名字，中国喜欢叫高斯-克吕格投影或者高斯投影。它是由德国数学家、物理学家、天文学家高斯于19世纪20年代拟定，后经德国大地测量学家克吕格于1912年对投影公式加以补充，故称为高斯-克吕格投影。根据[25 ][26 ][27 ]，高斯-克吕格投影的方法如下：

和墨卡托投影类似，我们用一个椭圆柱把椭球体包起来，只不过是横过来，这就是横轴墨卡托这个名字的来由。为什么墨卡托用一个圆柱来包，而横轴墨卡托用椭圆柱来包呢？原因是我们把椭圆绕南北极旋转得到假想的地球体，因此用一个与赤道平行的平面去切这个椭球得到的是一个圆，但是从垂直于赤道的方向去切的话得到的是椭球，所以横轴墨卡托要用椭圆柱去包。

图：高斯-克吕格投影

如上图所示，如果我们选定一根子午线(经线)作为中心子午线，然后左右各选择相邻的3度经线来切西瓜，就可以得到一瓣西瓜，用前面墨卡托投影类似的方法我们可以把这一瓣西瓜投影成一根长方形。然后我们再转到地球6度，又切出一瓣西瓜，……，最终我们把地球切成60个6度的西瓜，把60个正方形拼接起来就得到全球的地图。当然通常高斯-克吕格投影只是用来绘制一根国家的地图，所以只需要切少量数量的西瓜就行，而且西瓜的中心子午线和西瓜跨越的经度是可以根据需要来调整的。中国的经度范围西起73°东至135°，可分成六度带十一个，各带中央经线依次为75°、81°、87°、……、117°、123°、129°、135°，或三度带二十二个。六度带可用于中小比例尺(如 1:250000)测图，三度带可用于大比例尺(如 1:10000)测图，城建坐标多采用三度带的高斯投影。

高斯-克吕格投影是按分带方法各自进行投影，故各带坐标成独立系统。以中央经线投影为纵轴(x), 赤道投影为横轴(y),两轴交点即为各带的坐标原点。纵坐标以赤道为零起算，赤道以北为正，以南为负。我国位于北半球，纵坐标均为正值。横坐标如以中央经线为零起算，中央经线以东为正，以西为负，横坐标出现负值，使用不便，故规定将坐标纵轴西移500公里当作起始轴，凡是带内的横坐标值均加500公里。由于高斯-克吕格投影每一个投影带的坐标都是对本带坐标原点的相对值，所以各带的坐标完全相同，为了区别某一坐标系统属于哪一带，在横轴坐标前加上带号，如(4231898m,21655933m)，其中21即为带号。

UTM投影

UTM是通用横轴墨卡托投影(Universal Transverse Mercator)的缩写[28 ]。因为横轴墨卡托投影不同国家用不同的分带方法，这样无法统一，因此定义通用(Universal)的切西瓜方式如下：将地球划分为60个投影带，每带经差为6度。另外与横轴墨卡托投影不同，这里不是用一个椭圆柱横着把地球完整包(相切)起来，而是用一个小一点圆柱”包”(割)住北纬84度和南纬80度直接的这部分地球。UTM投影与高斯投影的主要区别在南北格网线的比例系数上，高斯-克吕格投影的中央经线投影后保持长度不变，即比例系数为1，而UTM投影的比例系数为0.9996。UTM投影沿每一条南北格网线比例系数为常数，在东西方向则为变数，中心格网线的比例系数为0.9996，在南北纵行最宽部分的边缘上距离中心点大约363公里，比例系数为1.00158。高斯-克吕格投影与UTM投影可近似采用 $X_{utm}=0.9996 * X_{高斯}$，$Y_{utm}=0.9996 * Y_{高斯}$进行坐标转换。

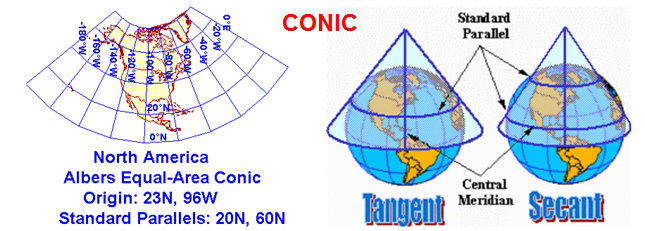
兰勃特投影

中国的基本比例尺地形图(1：100万、1：50万、1：25万、1：10万、1：5万、1：2.5万、1：1万、1：5000)除1：100万以外均采用高斯-克吕格为地理基础。而1：100万地形图采用兰勃特投影，所以我们也介绍一下这个投影。兰勃特投影是由德国数学家兰勃特(J.H.Lambert)设计的正形圆锥投影[29 ][30 ]。如下图所示：

图片来自The World is Flat

可以用一个圆锥体正向(从上往下)去切或者割这个椭球体，然后地心发出射线进行投影。

兰勃特投影的特点是：

角度没有变形，即投影前后对应的微分面积保持图形相似，故亦可称为正形投影。
等变形线和纬线一致，即同一条纬线上的变形处处相等。
两条标准纬线上没有任何变形。
在同一经线上，两标准纬线外侧为正变形(长度比大于1)，而两标准纬线之间为负变形(长度比小于1)。因此，变形比较均匀，变形绝对值也比较小。
同一纬线上等经差的线段长度相等，两条纬线间的经纬线长度处处相等。

我国1：100万地形图采用了兰勃特投影，其分幅原则与国际地理学会规定的全球统一使用的国际百万分之一地图投影一致。纬度按纬差4°分带，从南到北共分成15个投影带，每个投影带单独计算坐标，每带两条标准纬线，第一标准纬线为图幅南端纬度加30′的纬线，第二标准纬线为图幅北端纬度减30′的纬线，这样处于同一投影带中的各图幅的坐标成果完全相同，不同带的图幅变形值接近相等，因此每投影带只需计算其中一幅图(纬差4°，经差6°)的投影成果即可。由于是纬差4°分带投影的，所以当沿着纬线方向拼接地图时，不论多少图幅，均不会产生裂隙；但是，当沿着经线方向拼接时，因拼接线分别处于上下不同的投影带，投影后的曲率不同，致使拼接时产生裂隙。

时间系统

因为GPS使用电磁波的行程时间来计算距离(伪距)，而电磁波以光速前进，细微的时间误差都会导致很大的空间误差。虽然GPS接收器可以通过多余的一颗卫星来消除本身和GPS卫星的时间差，但是GPS卫星本身(GPS卫星之间)的时钟必须非常精确的同步。下面我们来介绍一下GPS涉及到的5个重要时间系统。

国际原子时(TAI)

国际原子时标(国际原子时，TAI)是为了形成统一的”绝对”时标而建立的，它可同时满足各种用途的不同物理要求。其中的用途之一是GPS定位，时标在里面起到非常重要的作用。自1967年起，秒被定义为原子物理常数。非放射性元素铯(133 Cs)被选作基准。铯原子选定能级之间的谐振频率被规定为9192631770Hz。以此定义的时间成为SI计量系统(国际单位制)的一部分。原子时的起点被设定为1958年1月1日0时0分。

协调世界时(UTC)

引入协调世界时(UTC)是为了提供以原子时为基础可用于地球现实世界时间的时标。协调世界时以前称为格林尼治标准时间(GMT)或世界时。协调世界时与国际原子时的差别在于秒的计数上，即UTC＝TAI-n，其中n等于所有累加的秒数，可在每年12月31日和6月30日结束时增加一个闰秒。闰秒因其反映了地球自转变缓趋势而非常必要，并能对时钟进行修正以保持时间的统一和精确。

原子钟时是一种非常精确的定义，那么为什么要搞一个闰秒让大家的生活变得如此艰难呢？因为地球绕太阳的运动并不规律，按照现在的定义每天86400秒太阳会在早上升起，但是时间长了也许到了我们几百代子孙之后早上八点可能变成了太阳落山(即使太阳晚升起半个小时也让人类不习惯)，所以需要定期修正。但是地球的精确位置很难计算，只能定期通过测量来决定在哪年的12月31日和6月30日结束时增加一个闰秒。

GPS时

通常GPS系统时间被表述为星期数及该星期已消逝的秒数。其起始日期为1980年1月6日星期日0时0分(UTC)。每个GPS星期开始于星期六与星期日之间的午夜，此时由主控站的母钟提供连续时标。GPS时与协调世界时之间的时差被连续处理并包含在导航信息中。GPS时与协调世界时的区别在于所有累加的秒数(2009年GPS时间与协调世界时相差15s)以及对秒的划分。GPS控制站保持GPS时的秒标记与协调世界时相差不超过1μs。GPS时与协调世界时的时差和GPS导航信息在子帧(后面会介绍)中一同发送。

因为GPS的目的主要是同步时间而不是要我们知道早上八点该起床了，所以它使用的其实是原子时钟。也就是当前时刻与起始时间的时差，但是为了便于理解，才转换成年月日时分秒。但是前面说了UTC的闰秒很麻烦，时不时要调整卫星的原子钟。GPS系统不想揽这个活，把这个任务留个GPS的用户，反正从定位的角度来说只要每个卫星的时间同步就行，快个半秒一秒的不影响定位。

卫星时

由于GPS卫星所载原子钟固有的和不规则的频率误差，各卫星的时间会与GPS系统时间存在偏差。控制站对卫星时钟进行监控，并通知任何观察到的时差。在进行本地GPS测量时应考虑时间偏差。

地方时

地方时是指特定地区或区域所使用的时间。地方时与协调世界时的关系由时区及有关标准和夏令时的规定确定。更多历法时间的内容可以参考日历相关的算法。

以下时间值在2009年内有效：

国际原子时-协调世界时＝+34s
GPS时-协调世界时＝+15s
国际原子时-GPS时＝+19s

位置计算方法

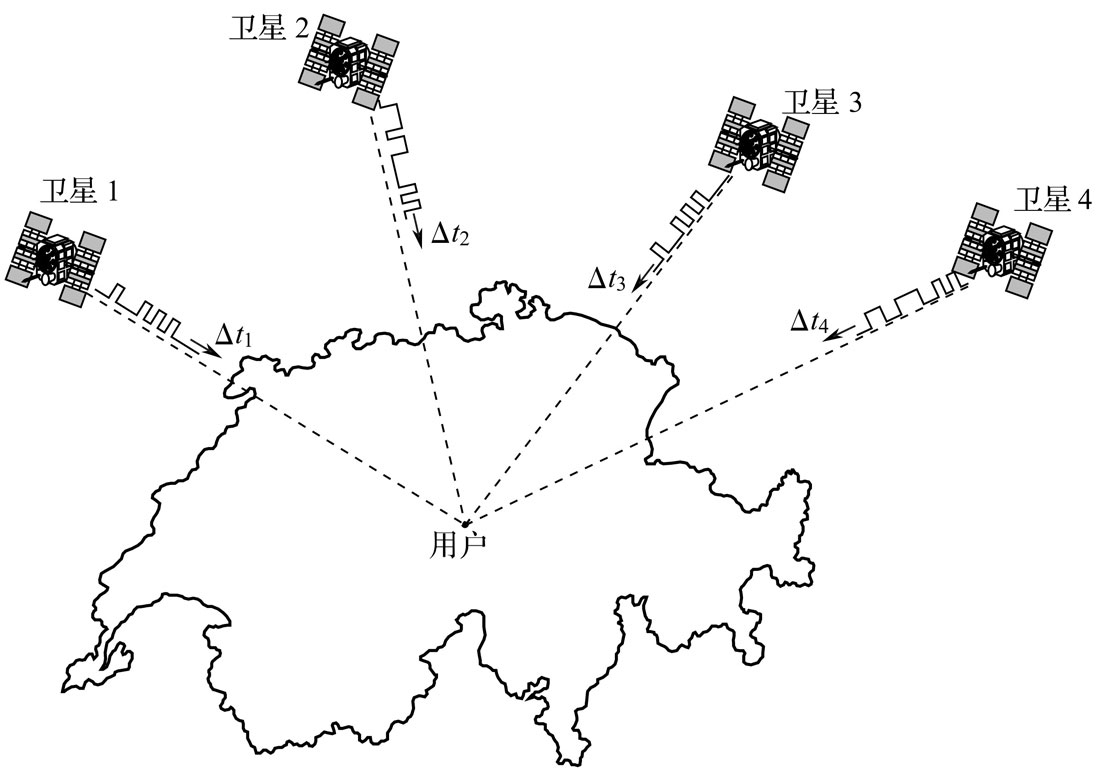
前面我们介绍过GPS定位的原理，如果GPS接收器能够严格与GPS卫星时间进行同步，理论上只需要接收到3颗卫星的行程时间从而乘以光速就得到距离，再根据发生时间(收到时间-行程时间)可以知道卫星在发射时的精确位置，从而可以定位GPS接收器。但是由于GPS接收器很难保持与GPS卫星的时间严格同步，所以我们需要把GPS接收器与GPS卫星的时间差也当成一个未知变量，因此需要4颗卫星才能定位。如下图所示：

图：实际定位需要4颗卫星

通过接收到的信号，我们可以获得4颗信号的行程时间$\Delta t_1, \Delta t_2, \Delta t_3, \Delta t_4$，也就是接收时间-发送时间。注意：GPS接收器某一时刻收到的4颗GPS卫星发来的信号的发送时间是不同的，因为4颗卫星的位置是不同的，但是肯定都是同一个时刻(瞬间)被GPS接收器接收到。我们收到信号后根据信号的内容就能”解码”出这个信号的发送时间(后面会介绍怎么实现解码)，而且我们认为GPS卫星的时间是同步于UTC的(严格来说是GPS时间，和UTC有固定的秒数差异，前面介绍过，GPS接收器可以校正)。我们假设GPS接收器与GPS卫星的时间差是$\Delta t_0$，如果$\Delta t_0>0$表明接收器的时间快了，如果$\Delta t_0<0$则表示慢了那么多秒。我们可以测量到的行程时间并不是”真正”的行程时间，而是行程时间加$\Delta t_0$。因此我们用测量的行程时间乘以光速得到不是”真实”的距离，而是”伪”距(pseudo range, PSR)：

\[\Delta t_{measured} = \Delta t + \Delta t_0 \\ PSR = \Delta t_{measured} \cdot c = \Delta t + \Delta t_0 \cdot c \\ PSR = R + \Delta t_0 \cdot c\]

上式中R是卫星和接收器的真实距离，但是未知；c是光速常量；$\Delta t$是卫星到接收器的”真正”行程时间，未知；$\Delta t_0$是卫星时钟和接收器时钟的差；PSR是伪距。根据距离计算公式：

\[R = \sqrt{(X_{sat}-X_{user})^2 + (Y_{sat}-Y_{user})^2 + (Z_{sat}-Z_{user})^2}\]

把这个公式代入上面PSR那个公式得到：

\[PSR = \sqrt{(X_{sat}-X_{user})^2 + (Y_{sat}-Y_{user})^2 + (Z_{sat}-Z_{user})^2} + \Delta t_0 \cdot c\]

这是一颗卫星得到的公式，我们用4颗卫星就可以得到4个公式：

\[PSR_i = \sqrt{(X_{sat_i}-X_{user})^2 + (Y_{sat_i}-Y_{user})^2 + (Z_{sat_i}-Z_{user})^2} + \Delta t_0 \cdot c\]

上式对于i=1~4成立，$PSR_i$是已知的(测量行程时间乘以光速)，4颗卫星位置$(X_{sat_i},Y_{sat_i},Z_{sat_i})$也是已知的，未知的是$(X_{user}, Y_{user}, Z_{user})$和时差$\Delta t_0$。四个方程四个未知数，因此有唯一解。

有很多方法来求解上面的方程组，感兴趣的读者可以参考[31 ][32 ][33 ][34 ][35 ]。

上面除了可以解出GPS接收器的位置$(X_{user}, Y_{user}, Z_{user})$，还能计算GPS接收器和GPS卫星的时差，从而可以对GPS接收器的时钟进行校对。所以GPS全称是授时与测距导航系统/全球定位系统。

接下来的问题是怎么计算行程时间。但是在这之前，我们要先介绍一下GPS系统相关的一些知识。

GPS系统

全系统描述

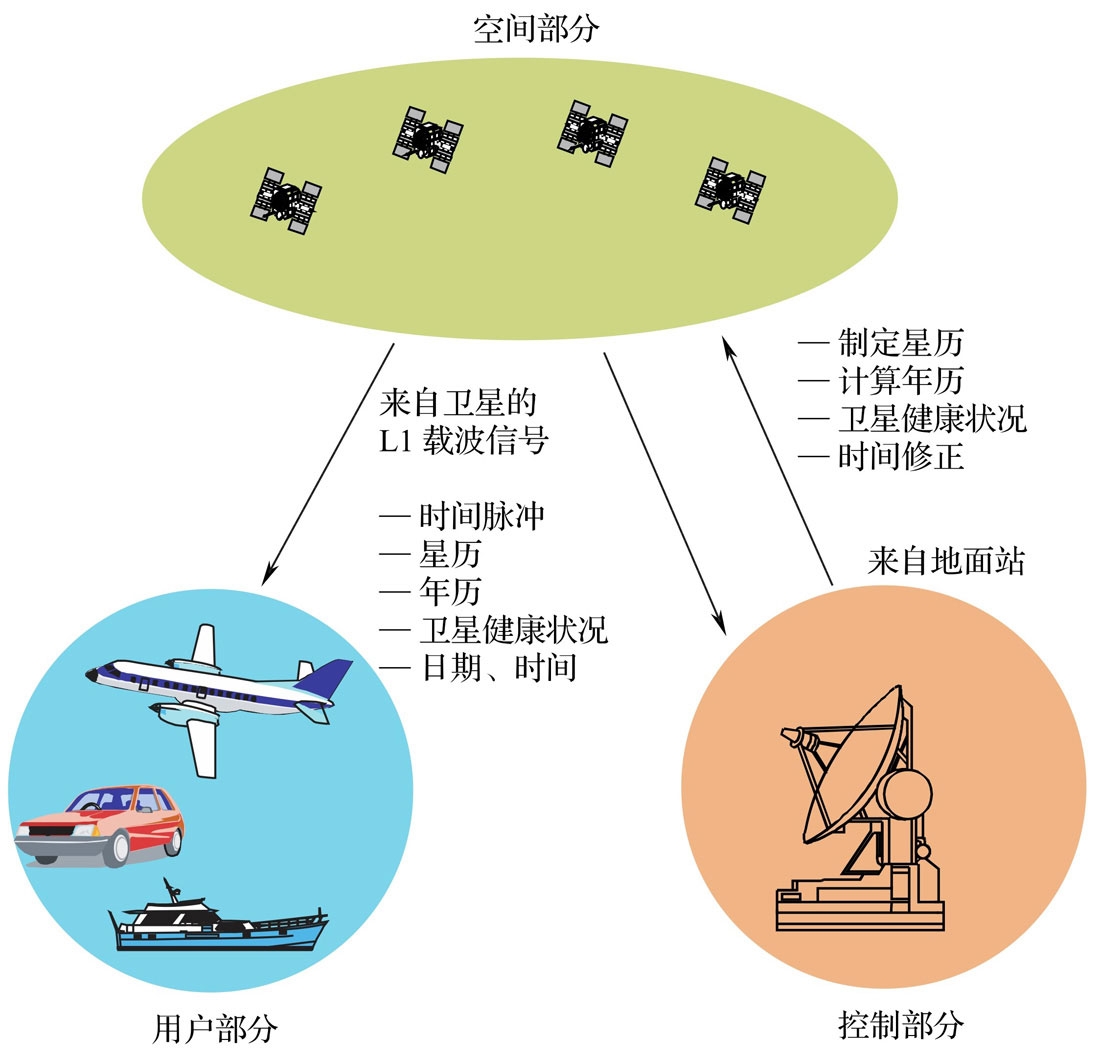
GPS由三个部分组成，如下图所示：

图：GPS的三个组成部分

空间部分
- 包括所以在轨工作的卫星
控制部分
- 所有与系统监控有关的地面站：主控站、监控站和地面控制站
用户部分
- 所有民用和军用用户

空间部分与用户部分的通信是单向的。地面控制站与卫星的通信是双向的。GPS是一种无源定位技术，GPS接收器并不需要(也不能，除非你破解了控制部分)往GPS卫星发送信号，所以网上有些北斗的支持者说使用GPS会泄露用户的信息是完全没有道理的。但GPS卫星确实可以给GPS接收器发送错误的定位信息，因此非美国的盟友把GPS用于军事目的会很危险。下面分别介绍这三个部分。

空间部分

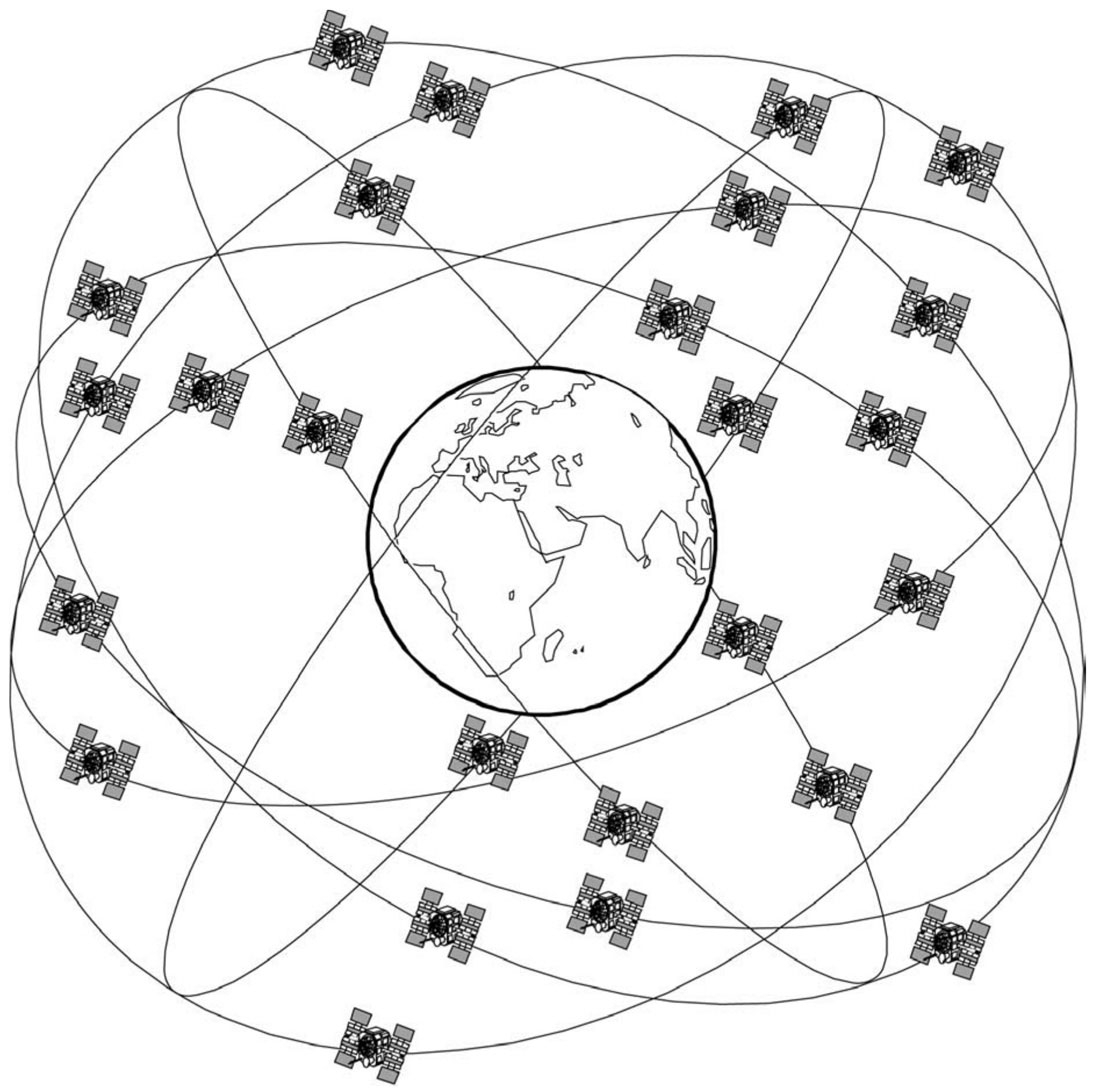
GPS的空间部分由多达32颗工作卫星组成，这些卫星在6个不同的轨道平面上围绕地球运转，如下图所示。这些卫星的轨道高度距地面20180km，与赤道的夹角为55°。任何一颗卫星均在12h内绕行一周。由于地球也在运转，卫星会在约24h(准确时间为23h 56min)后重返其地面上空的出发位置。

图：GPS卫星在6个轨道平面上绕地球运转

通过精巧的安排这些卫星的位置，GPS系统可以保证在全球任何地方的和任何时候，GPS接收器至少可以收到4颗卫星的信号。当然不能是有信号遮挡的地方，比如隧道这些地方。

所有的GPS卫星均使用星载原子钟来保持同步信号，这些信号以相同的频率(1575.42MHz)发送。地面上接收到的最小信号强度为-158～-160dBW。根据规定，最大信号强度约为-153dBW。

卫星以50bit/s的速率发送以下信息(导航电文)

卫星时和同步信号
精确轨道数据(星历)
用于确定精确卫星时的时间修正信息
所有卫星的近似轨道数据(年历)
用于计算信号发送时间的校正信号
电离层数据
卫星的工作状态(健康状况)信息

发送完所有上述信息所需的时间为12.5min。通过使用导航电文，接收机能够确定每个卫星信号的发送时间以及在发送时卫星的精确位置。每颗GPS卫星都会发送为其分配的唯一签名。签名由1023个0和1组成的伪随机噪声(PRN)码，广播历时1ms并连续重发，如下图所示：

图：伪随机噪声(PRN)

该签名码供接收机用于以下两方面：

通过唯一的签名模式可识别出信号是由哪颗卫星发送的
信号行程时间测量

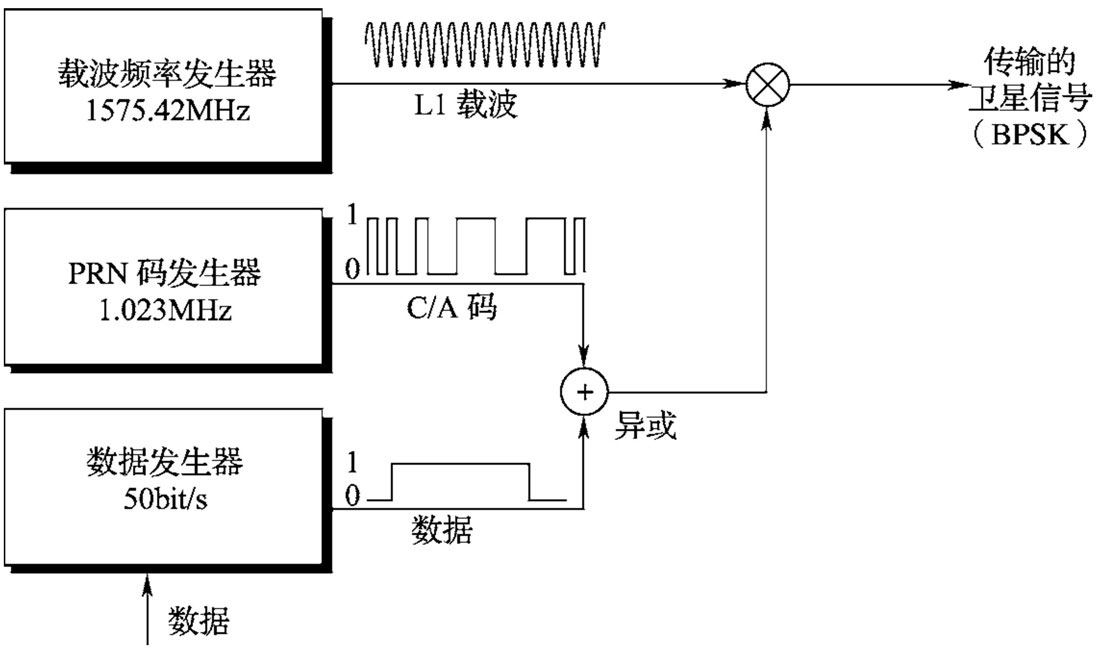
在每颗卫星上均载有4台高精度原子钟，由其中一台原子钟的共振频率生成以下工作所需的时间脉冲和频率：

50Hz数据脉冲
C/A(粗捕获)码(频率为1.023MHz的PRN码广播)，该码采用异或操作调制数据并2MHz带宽发送数据
民用L1载波频率(1575.42MHz)

图：简化的卫星框图

图：GPS信号的数据结构

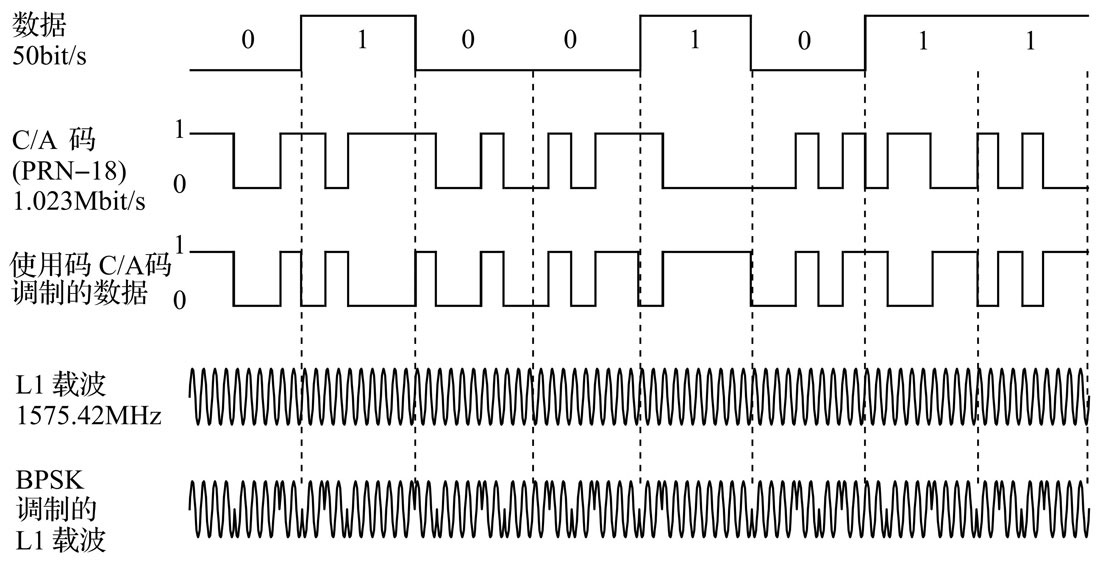
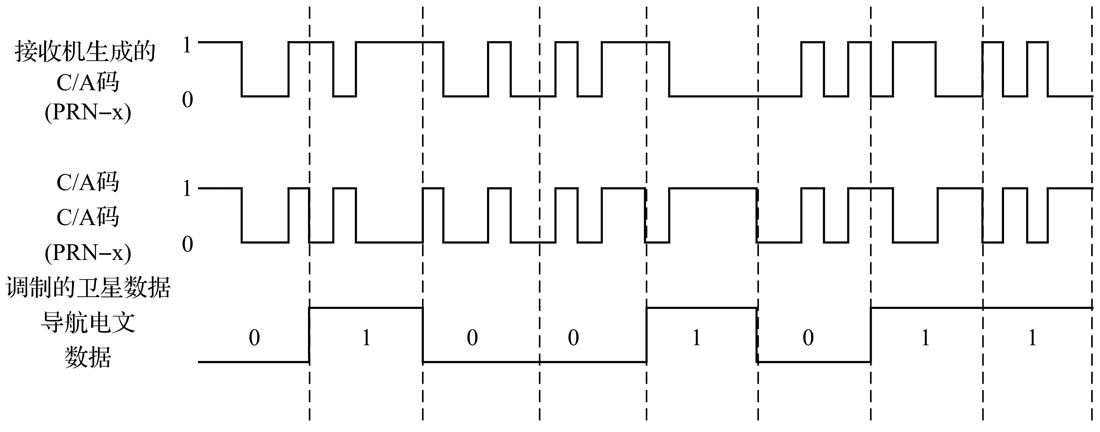
上图最上面是50bit/s的导航电文，包含了用于定位的重要信息。第二行是第18颗卫星的PRN，不同卫星的PRN是不相同的，我们后面会用这个信息来识别信号是哪个卫星发过来的，而且导航电文部分有时间信息，因此我们可以精确的知道PRN的每一个高低电平位置的时间。知道时间很重要因为这是计算行程时间的关键，后面还会讲具体怎么计算行程时间。第三行是把上面两个信号用异或操作得到的结果，用专业词汇上来讲这是一种”扩频”技术，如果没有相关知识我们可以这样的简单理解：第三行的信号如果用第二行的信号再异或就可以”解扩”得到原始的第一行的50bit/s的导航电文。第四行是用于发送信号的L1载波，第五行就是使用二进制相移键控(BPSK)调制的技术把第三行的数字信号”搬到”1575.42MHz的L1载波上。

而GPS接收器收到第五行的信号后首先会解调，得到第三行的信号，然后通过相关性搜索(或者频域的搜索)得到这个信号是哪个卫星发过来的，然后用这个卫星的PRN(相关性搜索还能”对齐”，其实就知道了信号的发送时间)异或(解扩)这个信号得到导航电文。相关性搜索会用到PRN码一个很重要的特性：同一个卫星的PRN码自相关性最好，但是不同卫星的码和码之间的互相关性就会很差。

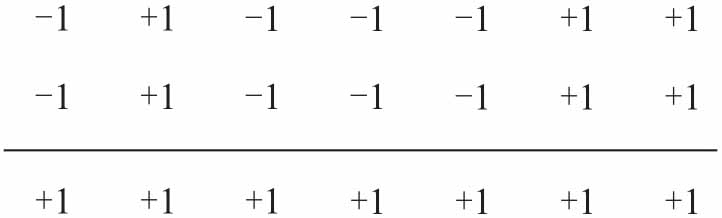
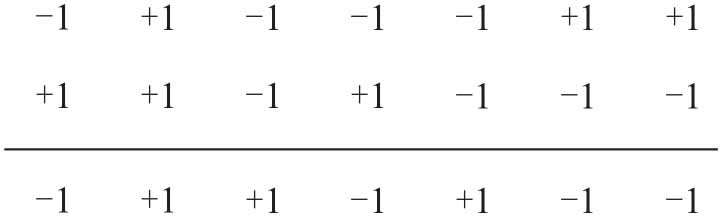
假设有个1023码片的序列，随机序列，每个码片采样一个点，本地复现一个一摸一样的码片，点和点之间去做乘，然后做累加，如果完全对准的情况下 11=1，-1-1=1，累加之后就是1023，这是最大的值。你尝试移动它，本地从第二个码片开始，输入的码片从第一个开始，在做点对点相乘，再做累加，因为序列是随机的，所以累积出来的值趋于0，这样互相关性就趋于0，就能区分不同的卫星。

扩频和CDMA

不了解通信原理的读者可能无法明白上面说的是什么，这里简单的介绍一下扩频和CDMA的知识，更多内容请参考[36 ][37 ]。如果对这些内容不感兴趣，可以跳过。

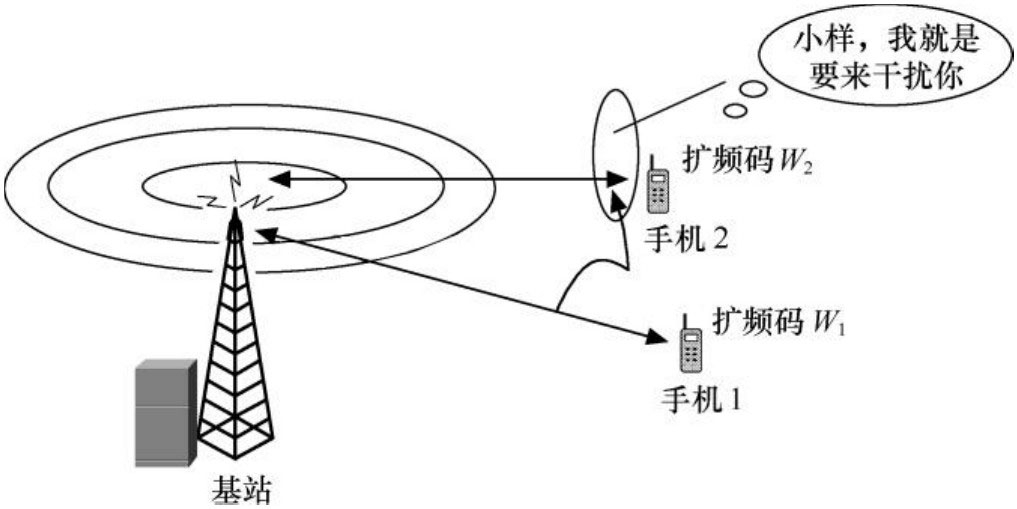
CDMA更像是鸡尾酒宴会，大家可以在一个大房间里进行交谈。既然都是在一个屋子里，如果都是用中文说话，那麻烦就大了，你会不断地被与你无关的人说的话所干扰，甚至搞得你无法和你想交流的对象进行正常的交流。这时候如果大家所采用的编码方式不同，比如你用中文，张三用英语，李四用意大利语，王五用西班牙语，情况就会好得多。你的对家用中文作为”扩频码”和你说话，尽管背景噪声很嘈杂，但是你还是可以很好地分辨出他的声音，OK，咱可以正常交流。这时候张三说的英语的声波过来干扰了，怎么办呢，这时候你的大脑就相当于处理机，它就会这么反应：”对不起，哥们，英语咱一窍不通，您的扩频码咱不认识，咱只当是背景噪声直接过滤了。”

请注意，扩频码有一个特点，那就是必须正交。正交在数学里的概念就是完完全全不相关，也即两个信号的乘积在某个区间内积分为零。换句话说，就是你这编码和编码之间要没啥相关性，英语和汉语就适合做扩频码，因为英语和汉语没啥相关性，很容易就可以区分开来(其实这句话并不完全正确，汉语里有很多舶来品，比如沙发——sofa，好莱坞——Hollywood)。但是湖北话和湖南话做扩频码就不合适了，重叠部分太多了，一起说会干扰得一塌糊涂。

说到这里，相信大家也明白扩频码大致是怎么回事了。但是估计很快就有人会有疑问，在”鸡尾酒宴会”中，要找到两两正交的扩频码是很简单的事情，英语和汉语、韩语与日语，差别都非常大，几乎可以理解为完全没有什么相关性。而我们机器所使用的都是”0”和”1”(按习惯分别用电平值”+1”和”-1”表示)，你果真能找到那么多没有交集、完全不相关的序列吗？

在这里，我们得首先搞清楚对于两个序列，什么叫做不相关，定义很简单，两个序列乘的结果加起来等于0就叫做不相关。比如说{+1, -1}和{+1, +1}两个序列，相乘的结果就是1×1+1×(-1)=0，等于0就说明你们俩没关系，不来电，换成数学的话来说就叫做不相关。

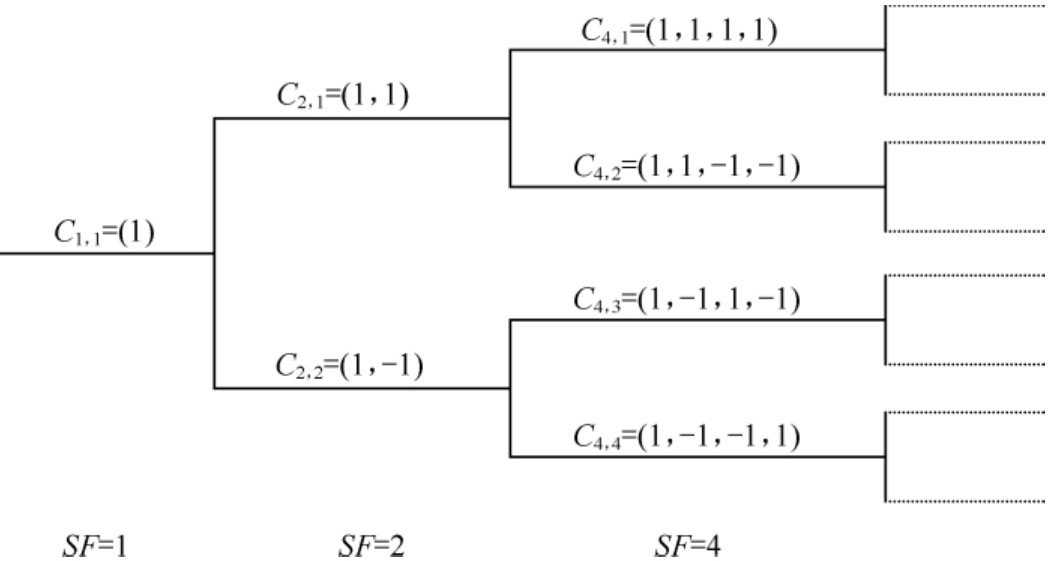
我们很容易就能推出一大堆这样的序列，比如{+1, +1, +1, +1}和{+1, +1, -1, -1}，乃至可以按下图所示的码树一直推演下去。大家不难得出，每个纵列的码序列相乘的结果都是0，也就是说是完全不相关的。我们可以把每个序列当成一门语言，序列和序列之间是相互正交的，就好比语言和语言之间是正交的一样。那么只要把原始数据用这个序列来编码，就可以让不同人的原始数据进行正交。我们把用这个序列来对原始数据进行编码的过程叫做扩频，而这个序列就叫做扩频码。

图：扩频码的生成

3大3G标准的扩频码都产自Walsh序列，上图就是Walsh序列生成的一简单的演示。在cdma2000中，扩频码也称为Walsh码，而在WCDMA和TD-SCDMA中则称为OVSF(Orthogonal Variable Spreading Factor，正交可变扩频因子)码，其实两者来源都一样，只是生成方式略有不同而已。

其实到这里，我们只是说明了存在这样一系列的序列，它们之间就像英语和中文一样，没有什么相关性，那么不同的用户采用不同的序列来编码，就可以互相不干扰。跟”扩频”两个字好像没有关系，一个”扩”字，一个”频”字，在本节中暂时还没有看到。另外，对于一个原始的话音信号，到底是怎样和这些序列进行运算，从而能实现和其他用户的话音信号互不干扰的过程，也没有举例，没有举例的话，大家的印象也就不可能很深刻。别急，以上两个问题，我们马上就要讲到。

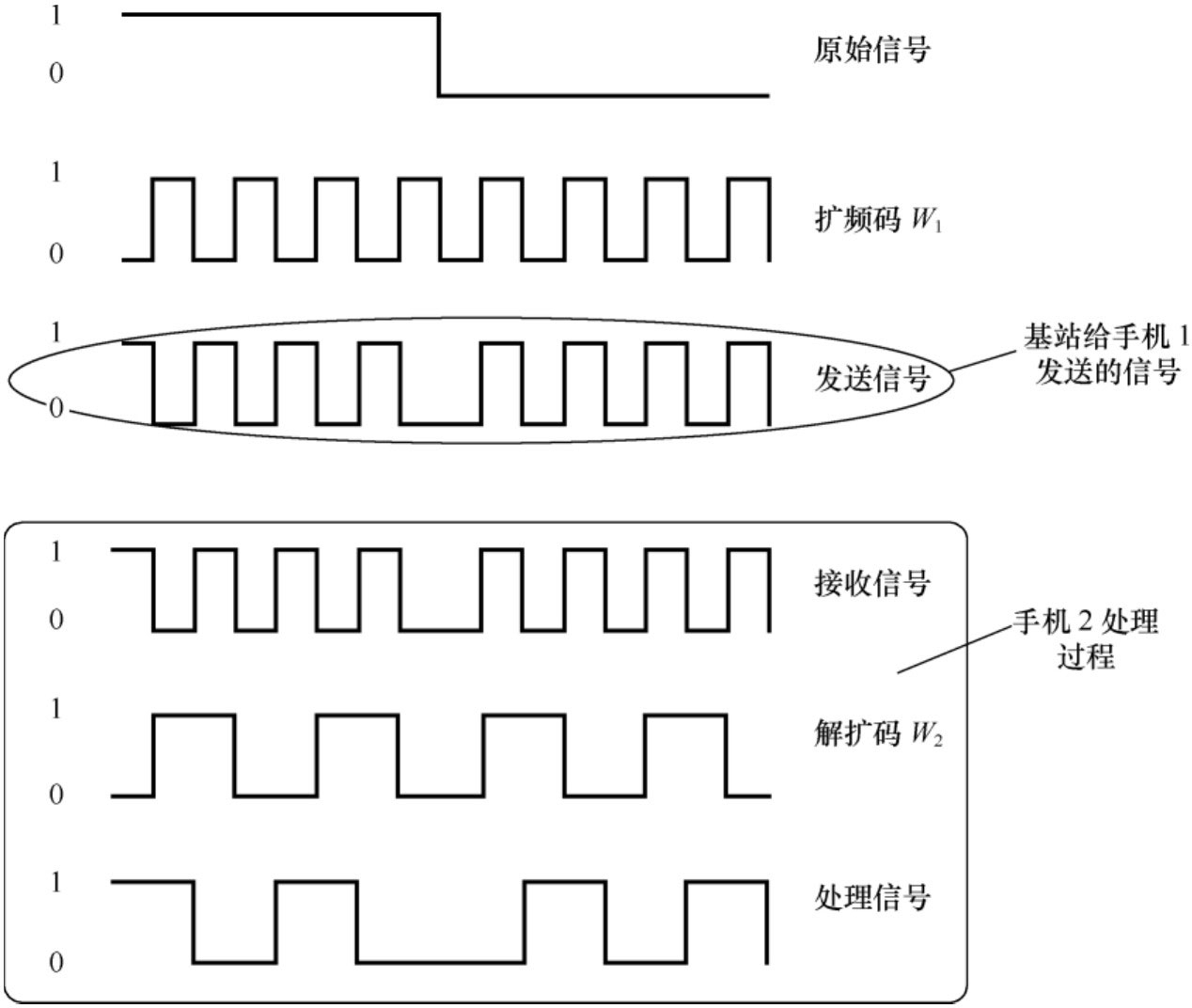
所谓”扩频”，就是让话音信号序列和比它速率高得多的扩频序列相乘，从而延展它的频带。我们举一个例子来说明这个问题。假设我原来的话音信号是”10”，那么它和一串”1101100110100011”的码在发送端手机进行扩频，然后在接收端手机进行解扩，这个过程是怎样的？在这里说明一下，下图中的运算是模二加运算。

图：扩频与解扩的过程

上图很好地说明了一个信号从发送端扩频到接收端解扩还原信号的过程，假设原始话音信号速率是R，那么它扩频后的速率就达到了8R，也就是频率是原来的8倍，这个就叫做”扩频”。扩频完成了，信号也开始在空中发送了，然而一个基站下是不止一个手机的，手机1的信号跑去干扰手机2是很正常的，如下图所示。由于手机1和手机2使用的频率是完全相同的，如果扩频码不能有效区分两个信号，那么同频干扰的威力是十分可怕的。

图：手机1的信号去干扰手机2

我们在上面把不同的扩频码比喻成不同的语言，信誓旦旦说它们是不会互相干扰的，是不是真的是这样，有待我们来验证。我们把上图中接收端的解扩码换成W2，发送信号还是用上图所示圆圈中的那个发送信号，这样就变成了手机2接收了基站发给手机1的信号，看看手机2是怎么把它过滤掉的，如图所示：

图：手机2处理干扰的过程

从上图看好像干扰还没有消掉，形成了一串”1100110000110011”的序列，其实这种理解有误。解扩之后，信号又变成了低频信号，只应该有两个码元，同一个码元内高低电平的变化会进行积分，积分的值才是最终的值。在第一个周期内，信号为”11001100”，换算成高低电平也就是”-1, -1, +1, +1, -1, -1, +1, +1”，把这8个值加起来等于多少？0！也就是说，其他手机发过来的信号，由于扩频码正交的特性，都可以过滤掉。

上述就是CDMA的工作原理。用扩频码对原来的低频信号进行扩频，使之在整个频段上工作，由于扩频码的正交性，不同的用户可以用不同的扩频码来进行区分，这就是CDMA(Code Division Multiple Access，码分多址)这个词的来历。

Walsh码的正交性有个前提：码必须是同步的，否则正交性无从谈起。如何实现码同步呢？一般使用PN码来实现。

PN码简介

PN码，即伪随机码。

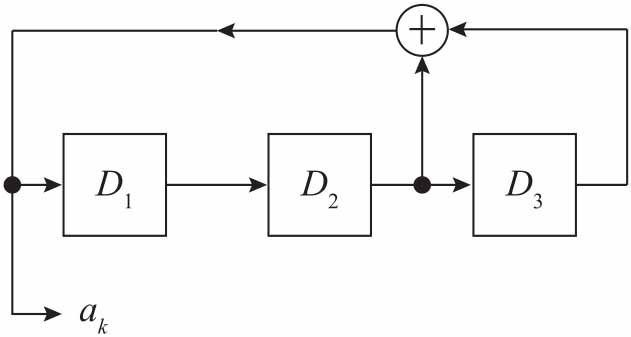
m序列是由n级线性移位寄存器产生的周期为2n−1的码序列，是最长线性移位寄存器序列的简称。m序列具有很好的自相关性，一般使用m序列作为PN码。以n=3为例，m序列的产生电路如下图所示。

图：m序列产生电路

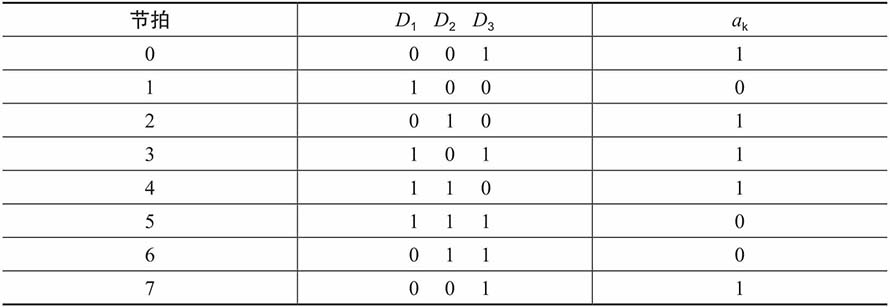
假定寄存器的初始状态为：D1=0，D2=0，D3=1，输出a1=1。第1个时钟脉冲到来后，状态演变为：D1=1，D2=0，D3=0，输出a2=0。第2个时钟脉冲到来后，状态演变为：D1=0，D2=1，D3=0，输出a3=1。依次节拍状态如下表所示。

表：寄存器状态

第7个状态又回到移位寄存器的初始状态，并不断循环。

很明显，该m序列的周期为23−1=7，一个周期的序列为：1011100。

同步原理

m序列具有很好的自相关特性，可以用来实现同步。自相关运算过程如下：

本地产生一个m序列。
移动1位，与接收到的m序列逐位相乘再求和。
移动2位，与接收到的m序列逐位相乘再求和。
依此类推，即可得到自相关运算结果。

注：计算之前要将0映射为+1，将1映射为-1。

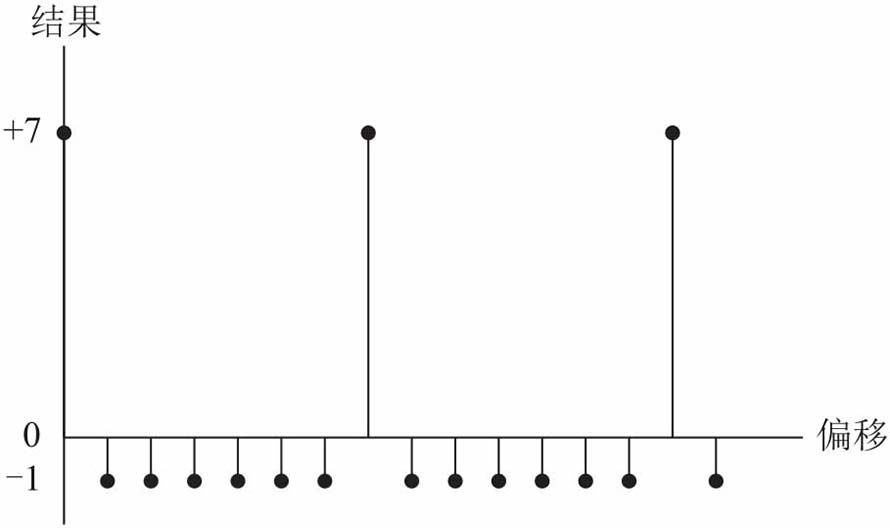
接着n=3的m序列的例子。如果本地产生的序列与接收序列刚好对齐，逐位相乘再求和的结果为7，如下图所示。

图：本地序列与接收序列对齐

如果本地产生的序列与接收序列错开1位，逐位相乘再求和结果为-1，如下图所示：

图：本地序列与接收序列错开1位

如果本地产生的序列与接收序列错开2位，逐位相乘再求和结果为-1，如下图所示：

图：本地序列与接收序列错开2位

依此类推。将所有的计算结果画到一张图中，如下图所示：

图：自相关计算结果

可以发现如下规律：

如果本地产生的序列与接收到的序列刚好对齐，逐位相乘再求和的结果为：7。
如果本地产生的序列与接收到的序列没有对齐，逐位相乘再求和的结果为：-1。
根据m序列的自相关性，很容易实现m序列的同步，有了这个做基础，Walsh码的同步就不成问题了。

控制部分

GPS卫星控制部分(操作控制系统，OCS)由位于科罗拉多州的主控站、5个监控站(每个站均配备原子钟并分布在全球赤道附近)和3个向卫星发送信息的地面控制站组成。控制部分最重要的任务有：

观测卫星运动并计算轨道数据(星历)
监视卫星时钟并预测其运行情况
对星上时间进行同步
转发收自卫星的精确轨道数据
转发所有卫星的近似轨道数据(年历)
转发其他信息，其中包括卫星健康状况、时钟误差等

控制部分还负责监视人为信号失真(选择可用性，SA)，以降低供民用使用时的系统定位精度。在2000年5月之前，美国国防部出于政治和战略考虑故意降低系统精度。其中包括使用随机误差信号调制部分卫星的时间信号，或者伪造星历。2000年5月初，SA系统失效，为此定位精度从100m左右猛然提高到13m。

在2000年5月2日之后，只在必要时才激活地区性或全球性人为失真(SA)。这一原则既保留了在特定重点地区降级或限制GPS使用的可能性，又使在这些地区以外的系统精度不受限制。实际上还未曾听说有重新激活SA系统的事例。

美国国防部于2007年9月18日宣布，下一代GPS卫星(GPSⅢ)的卫星导航信号将不再做人工失真处理。这一代卫星也不再考虑信号失真的技术可行性。由于美国政府未向GPSⅢ卫星加入信号失真功能，并克制实行现有的SA措施，这将确保GPS对于民用用户的可靠性。

用户部分

GPS卫星发送的无线电信号到达地面上的接收机约需67ms。由于信号以恒定速度(光速C)行进，其行程时间可确定卫星与用户之间的准确距离。

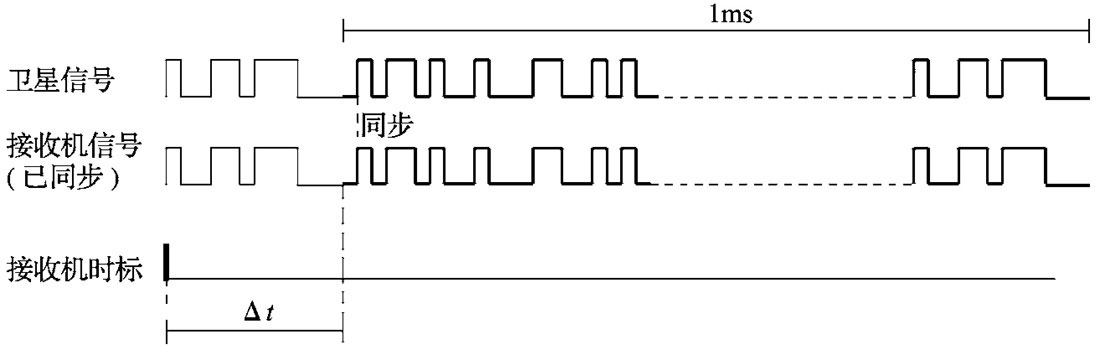
接收机会收到4个不同的信号，这些信号来自4颗卫星，每个信号都具有相同的结构。使接收机生成的信号与收自卫星的信号同步，将测得的4颗卫星的信号时间偏移Δt作为时标，如下图所示。然后将测得的所有4颗卫星信号的时间偏移Δt用来确定精确的信号行程时间。这些时间偏移乘以光速得到的距离称为伪距。

图：测量信号行程时间

为确定用户的位置，需要与4颗卫星进行无线电通信。与这些卫星之间的距离通过信号的行程时间确定。然后接收机根据伪距和这4颗卫星的已知位置计算出用户的经度λ、纬度φ、高程h和时间t。这个过程前面已经介绍过了(只是求出WGS-84笛卡尔坐标，但是转化成经纬度也很容易)。

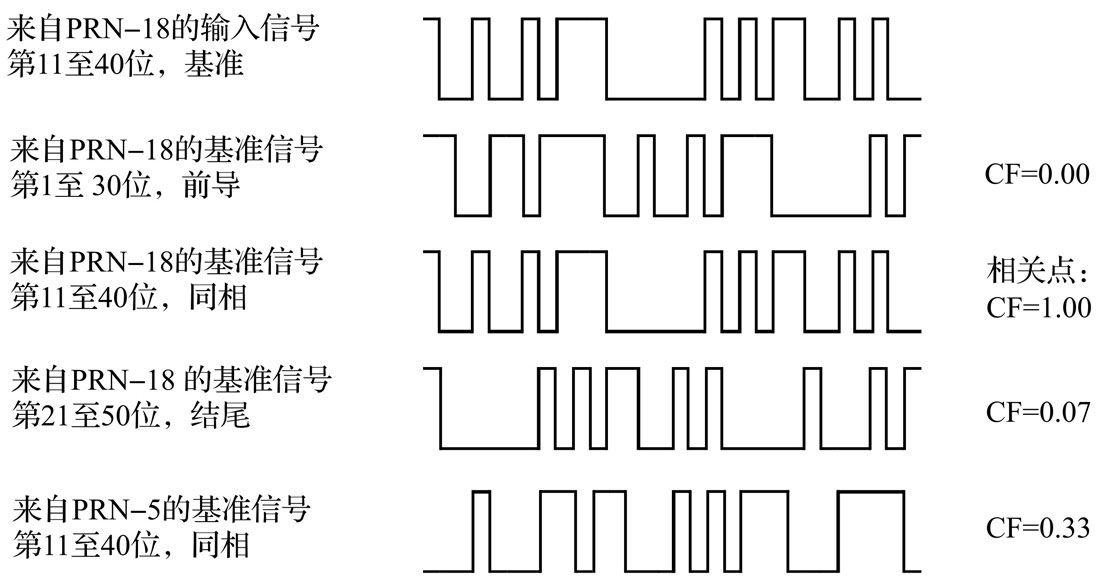
上文提到，所有的GPS卫星以相同的频率发送信号，但使用不同的C/A码。通过相关性来进行卫星辨识和信号恢复。由于接收机能够识别所有目前使用的C/A码，通过将所有已知编码与所有接收到的卫星信号进行系统的移位和比较，最终会找到完全匹配者(也就是说，相关因子CF为1)，并得到相关点(见下图)。相关点用于测量实际的信号行程时间以及辨识卫星。

图：30位校准处理图示

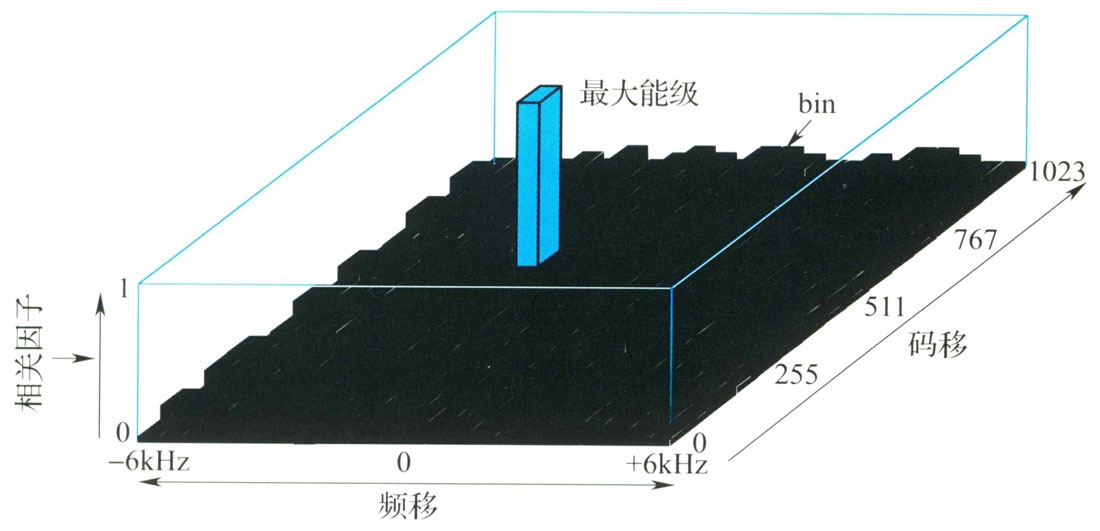
由于多普勒效应(卫星和接收机处于相对运动状态)的影响，发送的信号在接收点的频移可能会达到±5000Hz。因此，信号行程时间的确定和数据恢复不仅要与所有可能相移的所有编码相关，还要辨识正确的相位载波频率。此外，本地基准频率可能也有偏差，这就加大了需要搜索的频率宽度。本地振荡器1ppm的频率误差相当于1.575kHz的多普勒频移。下图表示多普勒频移在±6kHz范围内时的本地振荡器偏差情况。通过将所有编码和载波频率与收到的卫星信号进行系统的移位和比较，就会找到一个完全吻合的点(即相关因子为1)。

图：在编码和载波频率域内搜索最大相关点

GPS导航电文

本节内容描述GPS导航电文的结构，不感兴趣的读者可以跳过。

GPS导航电文是以50bit/s发送的连续数据流。每颗卫星都向地球转发以下信息：

系统时间和时钟修正值
卫星自身的高精度轨道数据(星历)
所有其他卫星的近似轨道数据(年历)
系统健康状况等

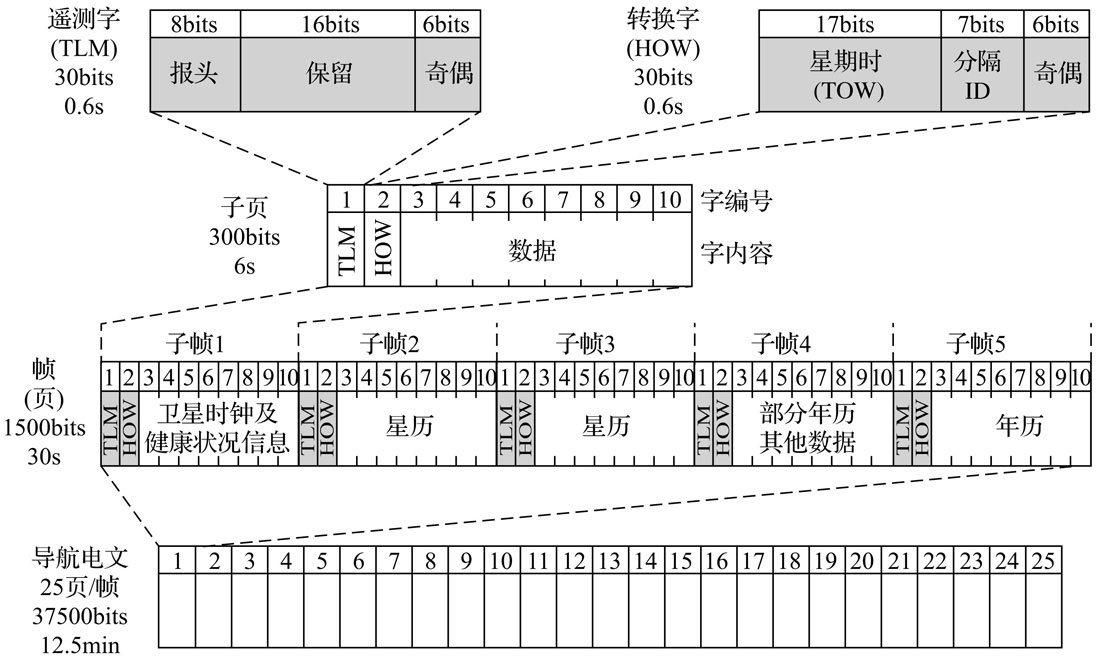
导航电文对于计算卫星的当前位置以及确定信号行程时间是必不可少的。数据流被调制成各卫星的HF载波。数据按照称为帧或页的逻辑分组单元发送。各帧的长度为1500bits，发送需要花费30s。一帧又被分为5个子帧。各子帧的长度为300bits，发送需要花费6s。发送一个完整的年历需要25个不同的帧。因此整个年历的发送时间为12.5min。除非配有GPS增强器(参见后文)，否则GPS接收机必须收集到至少一个完整的年历才能计算初始位置。

导航电文的结构

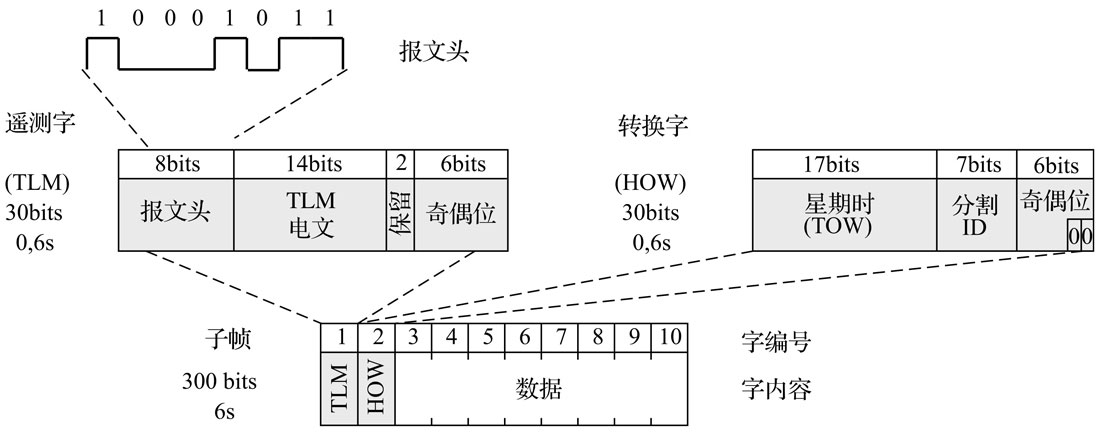
一帧的长度为1500bits，发送需要花费30s。这1500bits的信息被分为5个子帧，每个子帧300bits(发送需花费6s)。每个子帧由10个字(word)组成，每个字含30bits。子帧以一个遥测字(TLM)和一个转换字(HOW)开头。一个完整的导航电文由25帧(页)组成。下图给出了导航电文结构的图示。

图：导航电文的结构

子帧包含的信息

每一帧被分为5个子帧，每个子帧用于传送不同的信息。

子帧1包含了发送信号的卫星的时间值，其中包括用于修正信号传输延迟和星载时钟时间的参数，以及卫星健康状况信息和卫星位置精度的估算值。子帧1还用于提供传送10bits GPS星期数(10bits可表示从0至1023的数值)。GPS时始于1980年1月6日星期日0时0分0秒。每经过1024个星期后，星期数重新从0开始。该事件称为“星期归零”。

子帧2和3包含了发送信号的卫星的星历数据。这些数据提供了非常精确的卫星轨道信息。

子帧4包含了编号为25～32的卫星的年历数据(注意：每个子帧只能用于发送一颗卫星的数据)、GPS时与协调世界时之间的差异(即：闰秒或UTC偏差)以及与电离层导致的测量误差有关的信息。

子帧5包含了编号为1～24的卫星的星历数据(注意：每个子帧只能用于发送一颗卫星的数据)。所有的25页信息与编号为1～24的卫星的健康状况信息一同发送。

遥测字(TLM)与转换字(HOW)

每个单帧的首字是遥测字(TLM)，它包含了一个8bits长的前置序列(10001011)用于同步，接下来是为授权用户保留的16bits。与所有的字一样，遥测字的最后6bits为奇偶校验位。

转换字(HOW)紧跟在每个子帧的遥测字后面。转换字长度为17bits(17bits可表示从0至131071的数值)，其中包含了下一子帧的起始时间，以星期时(TOW)发送。星期时从GPS星期的起点数值0开始(过渡期为星期六23时59分59秒至星期日0时0分0秒)，并且该数值每6s加1，由于每周有604800s，计数在归零之前从0累加至100799。每隔6s将一个标志加入到数据流中与转换字一同发送，以便与P码同步。第20～第22bit用于转换字，以标识刚发送完的子帧。

25页的细分

完整的导航电文需要25页，发送至少需要12.5min。一页或一帧分为5个子帧。所有25页的子帧1～3的信息内容均相同。这意味着接收机每30s就能获得发送卫星的完整时钟值和星历数据。子帧4与子帧5之间的差异仅在于发送信息的组织方式。

对于子帧4，第2、3、4、5、7、8、9和10页转发编号为25～32的卫星的年历数据。在所有情况下，每页只用来传送一颗卫星的年历数据。第18页用来传送对电离层闪烁的修正测量值，以及协调世界时与GPS时之间的差异。第25页包含了所有32颗卫星的配置信息(即分区关系)以及编号为25～32的卫星的健康状况。

对于子帧5，第1至第24页转发编号为1～24的卫星的年历数据。在所有情况下，每页只用来传送一颗卫星的年历数据。第25页用来传输编号为1～24的卫星的健康状况信息以及初始年历时间。

GPS现代化

自1978年GPS投入使用以来，所有的卫星都向地面发送以下三种信号：

在L1频率(1575.42MHz)上
- 一路民用信号(使用C/A信号、BPSK(1)调制的SPS服务)，一路军用信号(使用P(Y)信号、BPSK(10)调制的PPS服务)；
在L2频率(1227.60MHz)上
- 第二路军用P(Y)信号。

美国国防部计划逐步改进GPS信号结构。对于民用而言，引入第二个和第三个频率是非常重要的，如果在定位时可以使用更多的频率，就能补偿甚至消除电离层对信号行程时间的影响。由于在电离层中的传输速度C取决于频率，因此实现这种补偿是可能的。除了两路新信号，GPS现代化还增强了民用用户的信号强度并提高了军事应用能力。因此后来陆续出现了L3、L4和L5的频率信号，其中L5是民用的。下面是目前为止GPS的信号频率汇总：

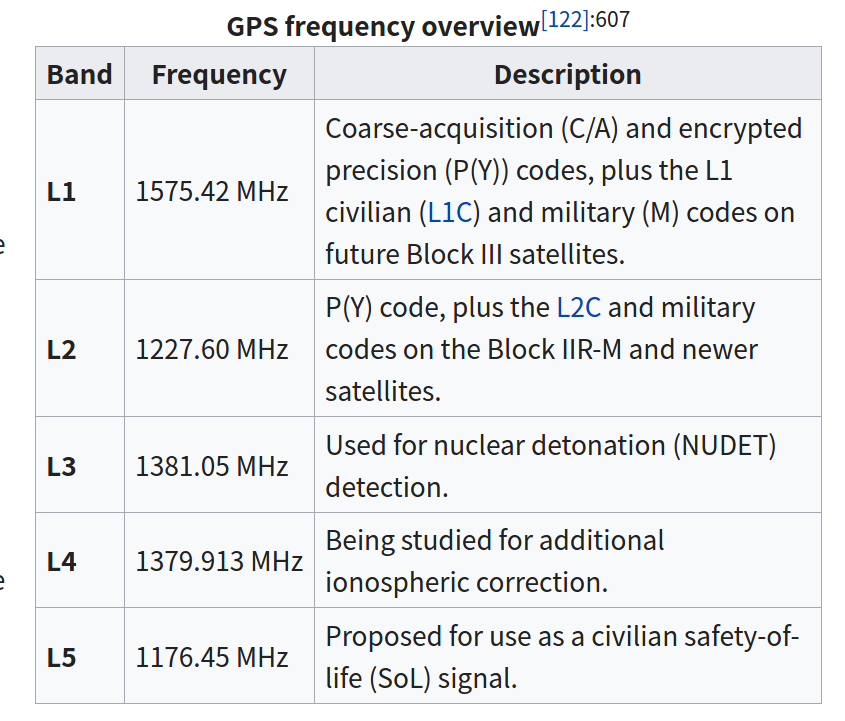图：GPS frequency overview 来自wikipedia

计算GPS卫星的位置

前面我们在求解GPS接收器的位置时假设我们知道发射信号时的GPS卫星的准确位置，但是这个位置又是怎么知道的呢？根据前面GPS导航电文的介绍，读者可能也会猜测出来这个位置信息就在星历里。没错，星历里包含了这颗卫星最近4个小时的准确轨道信息。那么具体怎么通过星历计算GPS在WGS-84笛卡尔坐标系统的位置呢？我们这里就不介绍了，感兴趣的读者可以参考[38 ]或者[34 ]。

计算行程时间

现在我们回到计算行程时间这个问题，解决这个问题之后整个GPS定位的过程就比较完整了。我们再来回顾一下重要的几个时钟系统。

UTC，协调世界时。
GPS时，用于GPS系统的时间系统。
- GPS时与协调世界时的差别在于所有累计的秒数(2008年相差14s)以及低于1μs的误差。GPS时与协调世界时之差以及该差值的当前特性通过导航电文(子帧4，第18页)发送。
星时，每颗卫星的星上时间。
- 卫星时与GPS时的具体差值以及该差值的当前特性通过导航电文(子帧1，第1至25页)发送。
接收机时，GPS接收机的内部时间。
- 该时间通常由内部的石英晶体振荡器确定，有别于GPS时和/或协调世界时。该差值$t_0$在GPS接收机开始工作时未知，但经过数次测量后可以降低。

确定行程时间的具体方法

以下部分讨论了确定信号行程时间所需的方法。为了保留该方法的全貌，对该过程的描述做了大量简化。行程时间用于计算自卫星至接收机的距离(R)。

第1步：通过相关性确定信号到达时间

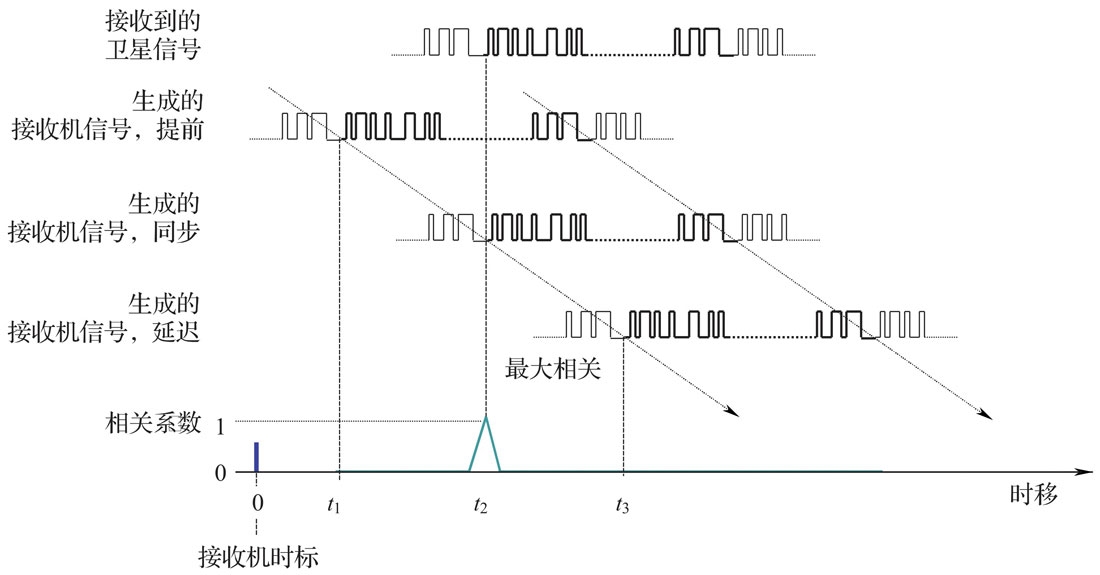
GPS接收机会接收到来自1颗或多颗卫星的信号。每个信号都具有相关性。在此描述的相关处理是针对单个信号的，但所有的卫星信号都必须进行同样处理。由于接收机在接收信号时发射信号的卫星数量(x)是未知的，接收机会生成各种PRN码(x＝1～32)。将这些编码按时间平移，直至某个PRN码与卫星信号x的时间和信号形式达到最大相关所需的时间平移和接收机时标(如毫秒间隔)确定了所观测卫星信号的到达时间(时间以接收机时给出)。

图：搜索最大相关

图：确定卫星信号到达时间

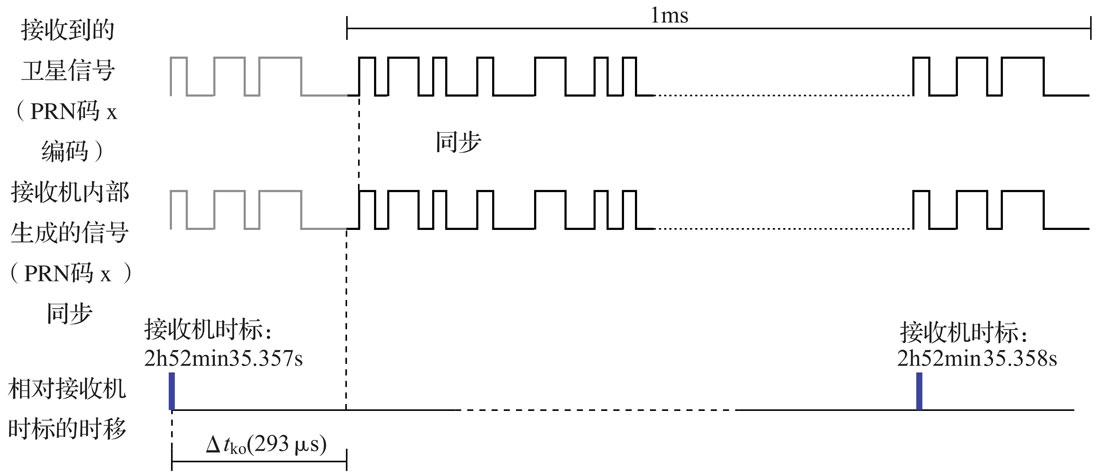
注意：我们的GPS接收机接受到的信号是连续的。我们把到达时间”定”为收到信号的第一个PRN的开始时刻，因为PRN是1ms发送1023个bit(1.023MHz)，我们收到的第一个bit可能是这1023个中的任何一个，如果我们收到的不是第一个而是第i个，那么我们要往后走(1023-i)个bit。这样我们的”收到”时间就是PRN的第1个bit，这样便于计算其发送时间。所以上图中信号的到达时间的精确值为2h25min35.7293s。

第2步：对数据和/或导航电文进行重构

搜索并保持最大相关，即卫星信号与接收机生成的PRN序列连续同步。将时移的PRN序列(C/A码)与卫星信号关联，由此可重构导航电文，如下图所示：

图：重构导航电文

第3步：确定发送时间

导航电文的每个子帧以8bits的报文头开始。遥测字(TLM)报文头的结构定义为10001011的模式，该比特序列每6s重复一次。在导航电文带有17bits星期时(TOW)电文的首个子帧的转换字(HOW)中，包含有该报文头的发送时间(以卫星时表示)。

图：重构导航电文的遥测字(TLM)和转换字(HOW)

此时GPS接收机开始在导航电文中搜索10001011模式。由于该模式也可能在导航电文的其他部分出现，因此还必须符合其他参数条件：

两个逻辑0必须出现在假定的报文头之后第51比特和第52比特(转换字的最后两个奇偶校验位设为0)。
从假定的报文头之后第16比特开始的奇偶校验位(遥测字的奇偶校验位)必须正确。
假定的报文头之前的两比特必须为0(子帧结束位置的每个字最后的奇偶校验位设为0)。
从假定的报文头之后第22比特开始的遥测字电文(17bits)中给出的时间必须大致正确。由于每6s反复提供时间信息，因此对接收机的时间测量精度要求不必太高。
下一个子帧的报文头必须正好在假定的报文头之后第300比特开始。

如果系统确认达到上述条件之一，则不必再比较所有的约束条件。报文头第一比特的发送时间位于上一帧导航电文的遥测字中。该时间以卫星时给出，但由于该信息包含在导航电文中，可将其转换为GPS时。

上面的描述比较细节，但是核心就是怎么找到信号的发送时间。通过前面两步之后，我们可以保持接收到的信号与接收机生成的PRN序列连续同步，从而持续把50bit/s的导航电文解码出来。而且导航电文每过6s会出现10001011开头的遥测字(TLM)，所以我们在同步后一直往后搜索在6s内总能找到一个时刻，这个时刻有信号的GPS发送时间，当然我们也有接收器的当前时间，从而可以计算出行程时间。

误差分析与精度因子

误差主要原因

到目前为止，尚未考虑计算中的误差量。在GNSS技术中，总误差可能会由各种原因造成：

卫星时钟：尽管每颗GPS卫星都配有4台高精度原子钟，但10ns的时间误差足以产生相当于3m的定位误差。
卫星轨道：一般来说，卫星位置的真实值只能做到1～5m的精度。
光速：信号以光速从卫星出发。
- 它们在穿越电离层和对流层时会减慢，因此不能将其视为常数。这种与标准光速的偏差会给计算位置带来误差。
信号行程时间误差测量
- 全球卫星导航系统接收机只能以有限的精度确定输入的卫星信号时间。
多径效应：由于接收到被反射的信号，误差量会进一步加大。
卫星几何形态
- 如果用于测量的4颗参考卫星较为接近，确定位置会更加困难。卫星几何形态对测量精度的影响被称为DOP(精度因子，Dilution Of Precision的缩写)。

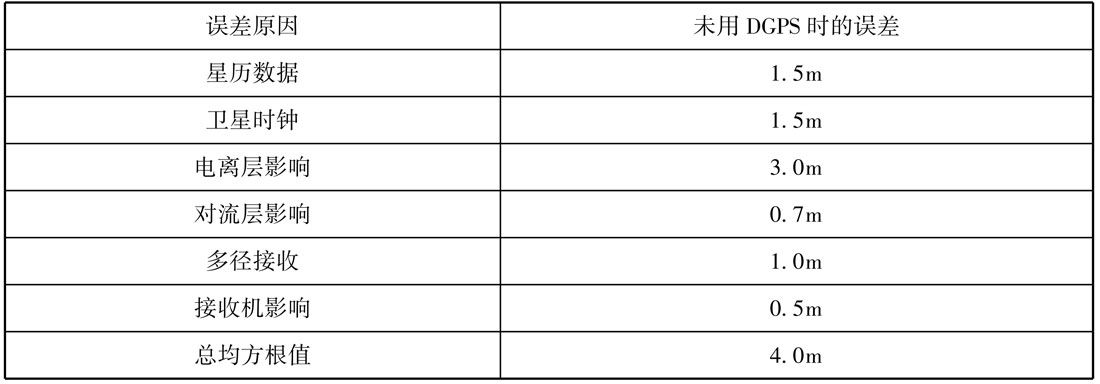
测量误差的成因有多种。下表给出了不同误差源所导致的水平位置误差范围。

图：误差原因

DOP

GPS导航的定位精度一方面取决于各个伪距测量，另一方面取决于所用卫星的几何构型。该构型可用一个标量来表示，在导航领域中称为DOP(精度因子)。DOP值描述了对精度的削弱程度，因而它是星座与不精确度之间相关性的因子或度量。如果DOP值较高(例如，所有可见的卫星彼此之间比较接近)，则预期的不精确度也会升高。

卫星几何形态对不精确度的影响如下图所示。当两颗卫星之间的间距较大时(左图)，定位误差(红色区域)较小。如果它们彼此较为接近(右图)，则误差区域较大。这一原理适用于需确定的位置存在不确定性时，称为距离误差(R－E：黄色和蓝色区域)，对两颗卫星同样起作用。R(R1和R2)代表测得的从卫星到用户的距离(伪距)。

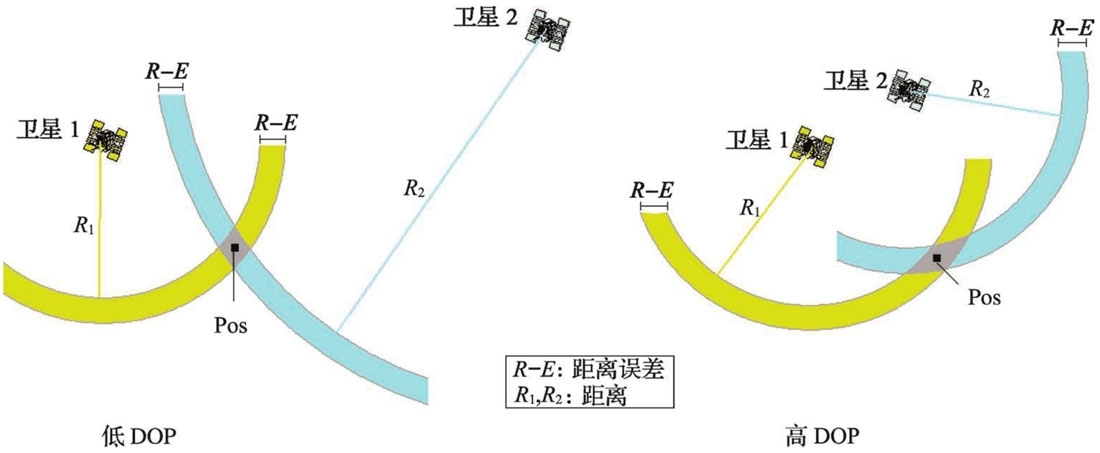图：以距离R1和R2为半径作圆，交点处的夹角越平坦，DOP值越高

减小误差

前面我们介绍GPS定位的原理，但是普通的GPS定位的精度一般是10米左右，不能满足V2X到车道(1.5米)的需求。

GPS误差的原因

星历数据
- 在发送信号时卫星位置精度一般只能达到1～5m。
卫星时钟
- 尽管每颗卫星都携带了4台原子钟，但时基会有偏差。对于稳定性为10- 13的振荡器，其时间误差可达10ns。10ns的时间误差产生的距离误差约为3m。
电离层影响
- 电离层是位于距地面60～1000km之间的大气层。电离层中的气体分子被严重电离。电离主要是由于太阳辐射所致(仅发生在白天！)。信号以光速从卫星发出穿越真空。在电离层内，这些信号的速度减慢，因此不能再被视为常数。电离的程度取决于时间和地点，在白天及赤道地区最为严重。如果电离强度已知，可在一定程度上通过地理修正模型进行补偿。此外，如果信号速度的改变与频率相关，还可通过使用双频GPS接收机进行额外修正。
对流层影响
- 对流层是位于距地面0～15km之间的大气层。其误差成因是气体分子密度和空气湿度的变化。密度随着高度的增加而下降。密度或湿度的增加减缓了卫星信号的速度。
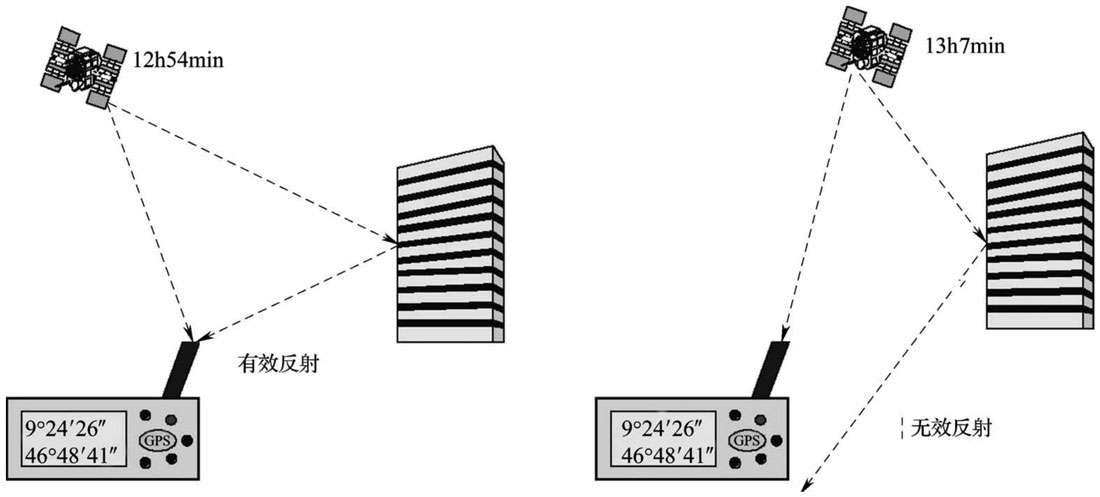
多径效应
- GPS信号会被建筑物、丛林、山峰等反射，在到达接收机之前形成回波。信号会因干涉而失真。多径效应可通过选择测量位置(避免反射)、测量时间和使用好天线等方法获得一定程度的补偿。

图：发射对测量时间的影响

接收机影响
- 还有一些误差是由于GPS接收机测量噪声和接收机内的时间延迟造成的，可使用更先进的技术来削弱这一影响。
DOP的影响

减小误差的方法

通过双频测量补偿电离层影响

电离层对测量误差的影响最大。如果发射的无线电信号穿越电离层，低频信号受减缓影响更为严重。通过使用两种不同的信号频率，可以在很大程度上补偿电离层的影响。GPS有L1和L5两个频率发送民用信号，所以可以会采用这一补偿原理。具体原理不做详细介绍，读者可以参考[39 ]。根据[40 ]，双频GPS能到3-5米的定位精度。

地理修正模型

该模型主要用来补偿电离层和对流层的影响。修正因子仅在应用于特定或有限区域时才有效。下面我们重点介绍一下D-GPS，因为这些技术可以让定位精度达到1-3厘米。

D-GPS

D-GPS是差分GPS(Differential GPS)的缩写[41 ]。我们将一台GPS接收机安置在基准站上进行观测。基准站已知精密坐标，计算出基准站到卫星的距离改正数，并由基准站实时将这一数据发送出去。用户接收机在进行GPS观测的同时，也接收到基准站发出的改正数，并对其定位结果进行改正，从而提高定位精度。差分GPS分为两大类：伪距差分和载波相位差分。

伪距差分原理

这是应用最广的一种差分。在基准站上，观测所有卫星，根据基准站已知坐标和各卫星的坐标，求出每颗卫星每一时刻到基准站的真实距离。再与测得的伪距比较，得出伪距改正数，将其传输至用户接收机，提高定位精度。这种差分，能得到米级定位精度。

载波相位差分原理

载波相位差分技术又称RTK(Real Time Kinematic)技术，是实时处理两个测站载波相位观测量的差分方法。即是将基准站采集的载波相位发给用户接收机，进行求差解算坐标。载波相位差分可使定位精度达到厘米级。大量应用于动态需要高精度位置的领域。

具体的计算原理这里不做介绍，感兴趣的读者可以参考[42 ]。

A-GPS

最后我们简单的介绍一下A-GPS，了解一下加快GPS接收器启动速度的方法。

市场上结合了移动无线功能和卫星导航功能(如GPS)的设备数量在不断增加。这种组合通常用于基于位置的服务(LBS)。可以说这些设备并非总处于工作状态，尤其是定位通过GPS完成时更是如此，原因在于GPS接收机的功耗限制了电池工作时间。

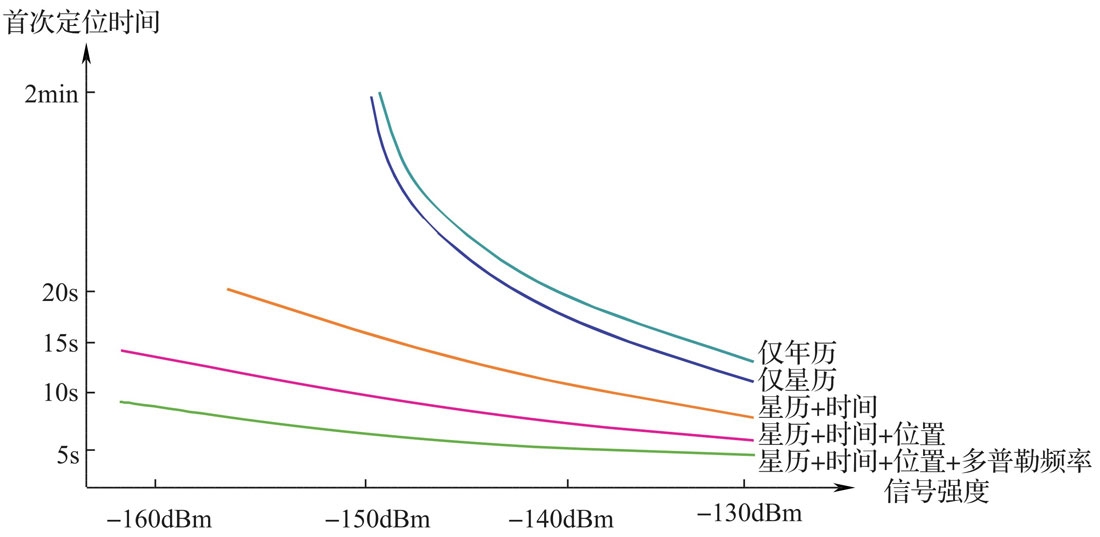
由于GPS设备很少工作，它有可能没有关于卫星位置的信息。在停用2h或更长的时间后，为能开始工作它必须首先下载卫星的轨道数据。GPS接收机获取轨道数据并计算出首次位置一般至少需要18～36s的时间(该时间称为首次定位时间：TTFF)。在不利的接收条件下(例如，城区高层建筑妨碍了对天空的直视时)，可能需要数分钟才能完成首次位置的计算。启动慢是GPS固有的限制，无法通过改进接收机技术来克服。

当缺少轨道数据时，GPS接收机必须执行一次完整的搜索过程，以便找到可用的卫星、下载数据和计算位置。在编码－频率域内对大约30颗GPS卫星进行搜索非常耗时，编码－频率域每级的积分时间通常至少需要1ms(1个C/A码周期)。如果将频率范围按50Hz的步长划分(即频率间隔为2×6000/50Hz＝240Hz)，则需要对多达1023×50＝51150个位置(bins)进行搜索(需要51s)。

在信号较弱时可通过提供额外的卫星轨道数据和其他GPS信息来快速定位和测量。这些信息可通过其他信道获得，例如通过GSM、GPRS、CDMA或UMTS。这一应用称作辅助服务，并用于辅助GPS(A-GPS或AGPS)。A-GPS是一种使用辅助数据来加速定位的功能或服务。GPS接收机通过移动通信网络或直接经互联网获得辅助数据。辅助数据中包含以下信息：

卫星星座(星历)；
精确轨道数据(星历、轨道)；
时间信息；
GPS接收机的多普勒频率和频移(误差)。

通过使用这些辅助数据，即便在不利的信号条件下GPS接收机也能够迅速定位。在弱信号条件下，这通常是获取定位的唯一途径。取决于辅助数据的复杂性和完整性，启动时间可能会显著缩短。剩余的启动时间取决于GPS信号的强度。通常辅助信息的可用性和精度越高，启动时间就越短。

图：各种辅助数据时近似的启动时间

集成了GPS设备的移动台仍需至少能看到4颗卫星。使用A-GPS时，GPS接收机需要一个用于接收辅助数据的接口。通过减少轨道数据的接收时间从而最大程度节省了启动时间。因为我们的手机通常会同时有无线网络和GPS，因此它的启动速度比纯GPS设备快[43 ]。

概述

原理

坐标系