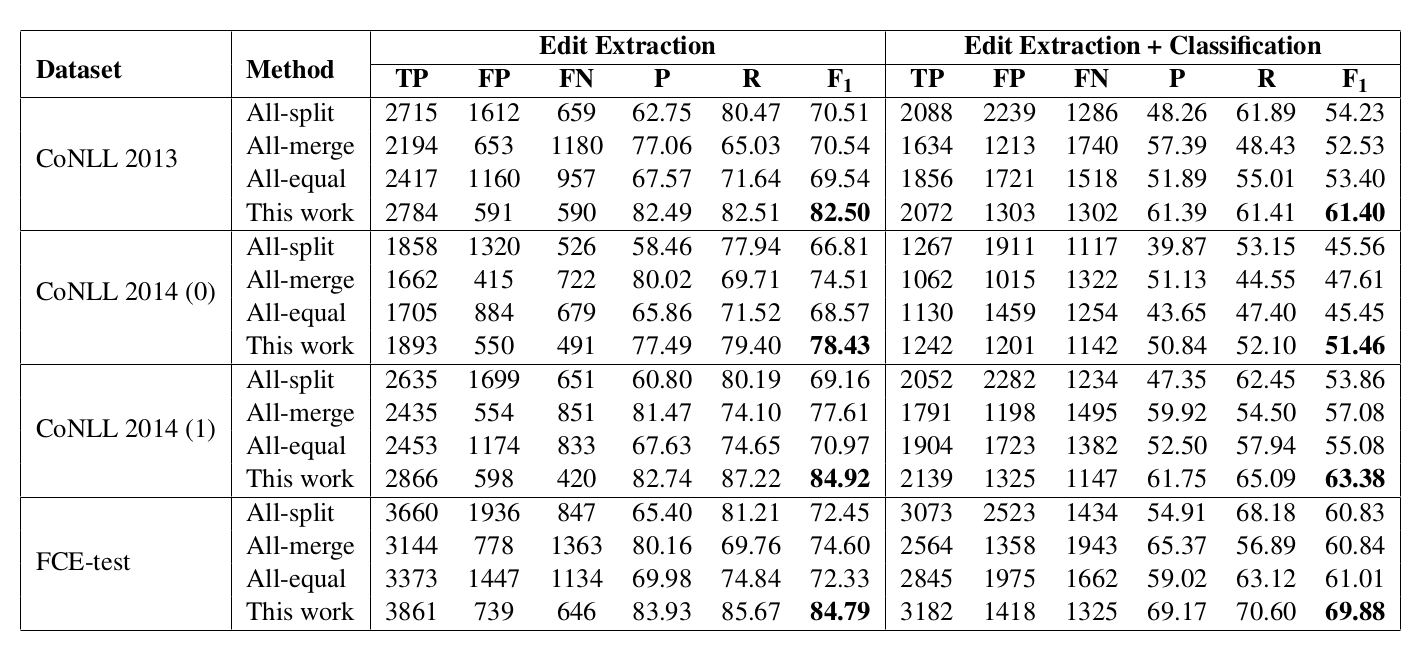
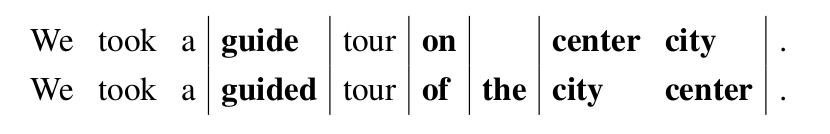errant是一个工具,当给定语法纠错的英语平行句对时它能自动抽取错误并且对错误进行分类。
目录
安装和使用
安装
python3 -m venv errant_env
source errant_env/bin/activate
pip3 install errant==2.1.0
python3 -m spacy download en
errant_parallel
我们创建两个文件:
echo "It a bok ." > 1.txt
echo "It is a book ." > 2.txt
$ errant_parallel -orig 1.txt -cor 2.txt -out diff
Loading resources...
Processing parallel files...
我们来看一下结果:
$ cat diff
S It a bok .
A 1 1|||M:VERB|||is|||REQUIRED|||-NONE-|||0
A 2 3|||R:SPELL|||book|||REQUIRED|||-NONE-|||0
输出是M2格式,第一行以S开头,后面是原始的(错误的)句子;A开头的是需要进行的编辑操作。所以的编辑操作都是”替换”。
比如”A 1 1”表示在第2(下标0开始)个位置插入”is”。这可能难以理解,但是如果我们用编程语言来表示就是把words[1:1]替换成”is”,大家可以试试这段python代码:
>>> words=['It', 'a', 'bok']
>>> words[1:1]=['is']
>>> words
['It', 'is', 'a', 'bok']
“A 2 3”表示把第3个词(bok)替换成”book”:
>>> words=['It', 'a', 'bok']
>>> words[2:3]=['book']
>>> words
['It', 'a', 'book']
注意:所有的下标都是基于原始句子,因此我们不能认为第一个编辑把它变成了”It is a bok”,所以bok的下标是3。我们还是要用原始的下标位置2。
“M:VERB”的意思是缺了(Missing)一个动词(Verb),而”R:SPELL”表示替换,而且是一个拼写错误。
errant_compare
我们可以用这个命令来比较算法产生的M2文件的效果,它的用法为:
errant_compare -hyp <hyp_m2> -ref <ref_m2>
论文简介
Automatic extraction of learner errors in ESL sentences using linguistically enhanced alignments
本文提出了一种方法来自动的从非母语学者(English as a Second Language, ESL)的对齐句对中自动抽取错误的方法。具体来说,给定一个有错误的句子和纠正后的句子,本文的算法首先使用语言学增强的对齐算法来对齐两个句子的词(Token),然后使用规则来合并可能的对齐。
Introduction
在机器翻译里,把源语言和目标语言的句子进行词对齐是传统方法的必要步骤。人工来标注成本很高,因此有了很多工具比如GIZA++来自动对齐。
对于语法纠错(Grammatical Error Correction, GEC),我们也希望把错误的句子和正确的句子对齐,从而知道哪些地方有错误。但是GEC和机器翻译不同,它的平行句对是同一个语言的句子,其中一个有语法错误而另外一个是正确的。因为一个句子错误的地方不会太多,所以GEC的对齐会简单很多。GEC领域常见的First Certificate in English(FCE)和National University of Singapore Corpus of Learner English(NUCLE)这两个语料库都是手工标注每一个错误的。比如下面是一个对齐的示例:
但是手工标注每一处错误还是成本很高,而且可能存在不一致。比如”has eating”有的时候被标注为[has → was],有时候又是[has eating → was eating]。类似的,[has eating → was eaten]有时候被拆成两个编辑:[has → was]和[eating → eaten]。另外也有研究表明,如果要求标注者进行细粒度的标注,可能会约束标注者的思维,从而产生不自然的句子。而且如果只是要求标注者标注正确的句子(而不是标注每一处错误),标注的速度也会提高很多。因此,有工具能够自动对齐平行的纠错句对,是非常重要的。
背景介绍
最早的尝试是使用Levenshtein距离进行对齐,然后使用最大熵分类器判断没对齐的都是什么类型的错误。但是这种方法处理不了两个词交换顺序的情况,比如[only can → can only]。也无法处理短语的情况,比如[look at → watch]。原因是Levenshtein距离基于单个Token(大致就是词)的插入、删除和修改操作来计算的。为了处理多个Token的情况,需要判断什么时候把两个或多个操作合并成一个。当时使用了最简单的合并全部相邻的未对齐Token。但是这种策略的错误率很高,所以又单独训练了一个模型来判断两个操作是否应该合并。
但是这种用模型的方法依赖于特定的数据集,换一个数据集就不是特别好使。
自动对齐
Damerau-Levenshtein距离
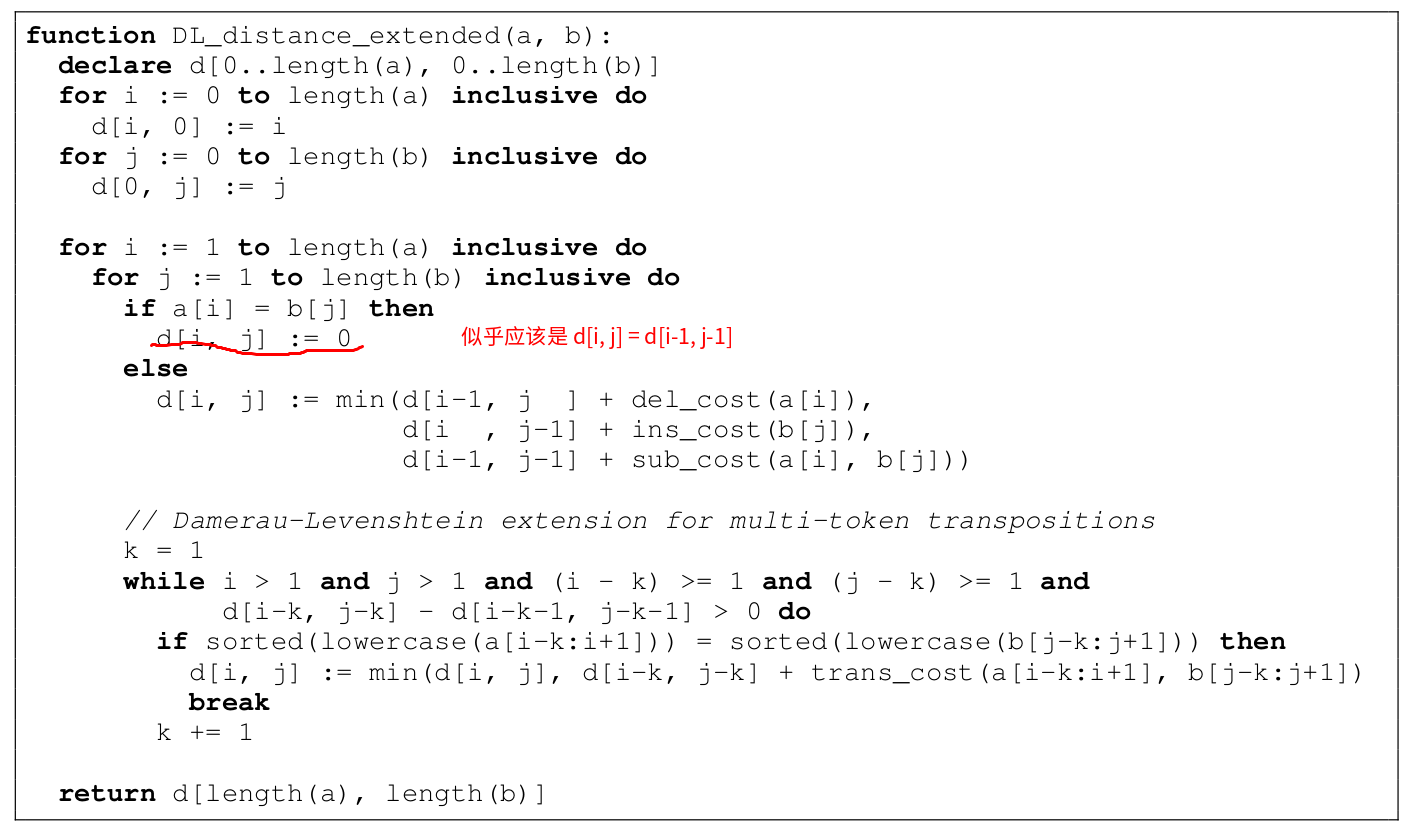
如果使用最基本的Levenshtein距离,[only can → can only]会变成三个操作:[only → Ø]、[can → can]和[Ø → only]。也就是删掉only,can和can对齐,以及插入only。为了解决交互顺序的问题,本文使用了扩展的Damerau-Levenshtein算法,如下图所示:
标准的Damerau-Levenshtein算法只能除了两个词的交换,为了处理多个词的交换,上面的代码进行了扩展。n个词的交互的cost是n-1,这和标准的Damerau-Levenshtein算法是一致的。
基于语言学启发的对齐
为了引入语言学的信息,我们修改了替换(replace)操作的cost函数:
-
如果两个词只是大小写不同,比如[the → The],则cost为0;
-
如果两个词的词干(lemma)相同,比如”met”和”meeting”,则cost为0.499;
-
如果两个词的词性(POS)相同,如果是实词(动词、名词、形容词和副词),cost为0.5;非实词为0.25。
上面这些值的目的是为了使替换的cost范围为[0,2),这样的对齐倾向于替换而不是先删除后插入,因为这两个操作的cost加起来是2。
通过融入上面的语言学信息后的对齐算法会比单纯的使用Levenshtein好很多,因为这种对齐方式也是符合人类纠错常识的。
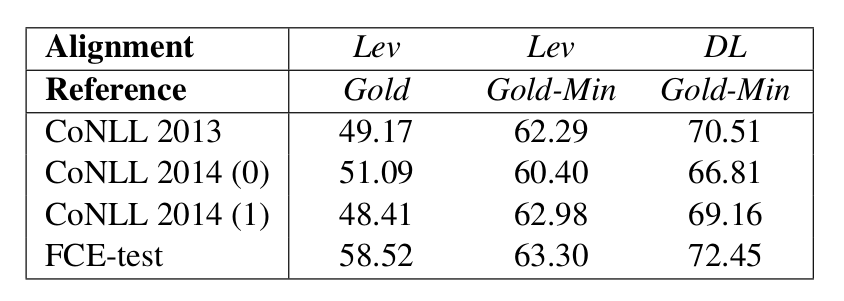
对齐的实验
下图是对齐算法的对比实验,Lev表示标准的Levenshtein算法,DL表示使用了语言学信息来定义cost的Damerau-Levenshtein算法。从中可以看出,DL算法会好不少。
合并
合并算法使用了如下的规则:
-
通过M(匹配)把对齐分成若干段,各段独立的进行合并操作。
-
标点再加上后面相同Token的进行合并。比如[, → .] + [we → We]会合并成[, we → . We]。
-
词的位置交互不合并,比如[only can → can only]保留原样。
-
所有格的情况合并,比如[freinds → friend] + [Ø → ’s]合并成[freinds → friend ’s]。
-
两个词去掉空格等于纠正后的词,那么合并。比如[sub → subway] + [way → Ø] = [sub way → subway]
-
如果替换的两个词比较像(字符级的重合度超过75%),则作为一个独立的对齐不参与合并。比如[writting → writing],但是如果这个词的词性与前一个相同,则还是可能会合并。这主要是为了处理[eated → have eaten],因为按照前面的规则,eated和eaten比较像,所以不能合并have eaten,但是实际应该合并。
-
如果某个替换的前面也是一个替换操作,则这个替换单独作为对齐不参与合并。
-
如果组合操作最多(原文为最少,我感觉应该是最多)包含一个实词,则合并。比如[On → In] + [the → Ø] + [other → Ø] + [hand → addition] = [On the other hand → In addition]。
-
连续的相同的词性的Token需要合并,比如[because → Ø] + [of → for] = [because of → for]。
-
一个序列最后一个定冠词(the)不能合并(很奇怪的规则!)。
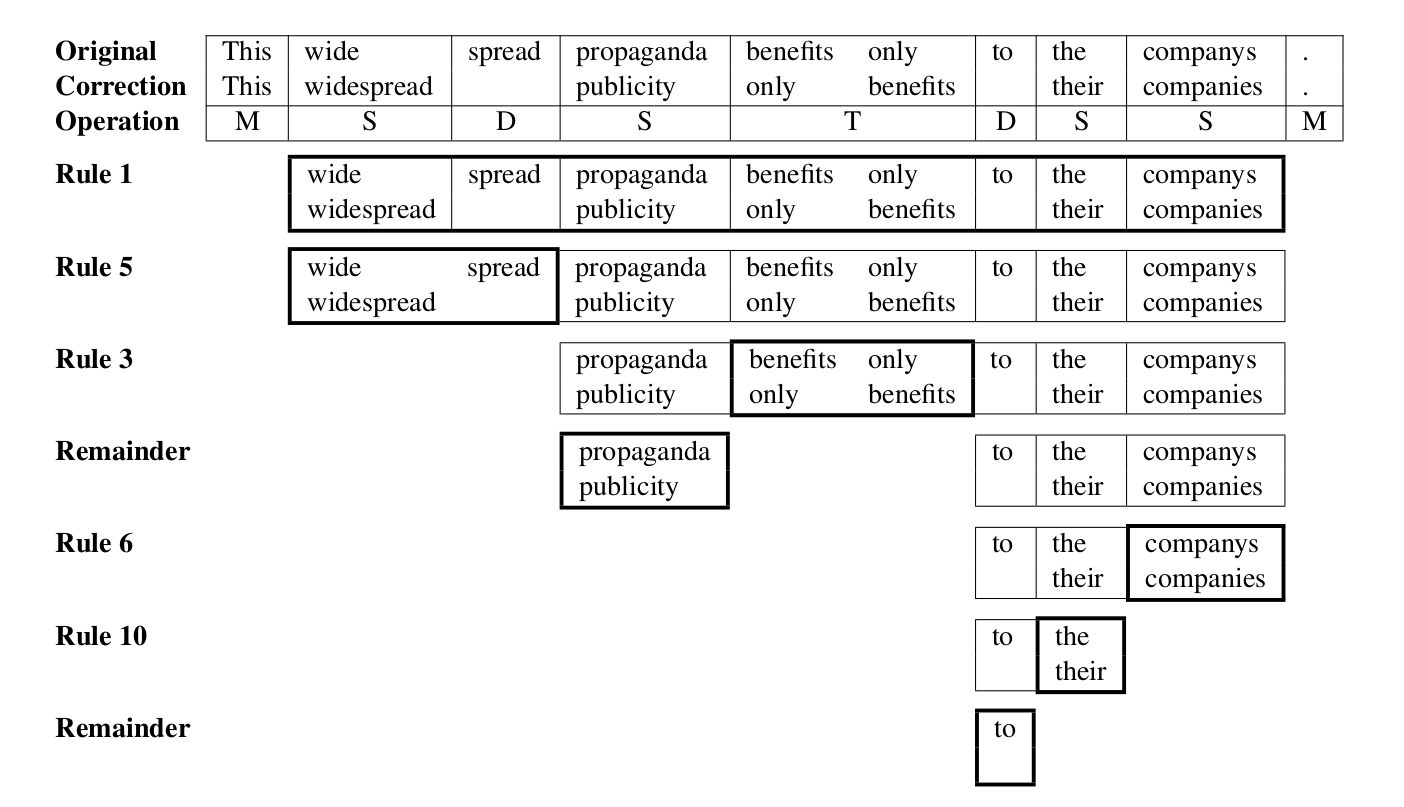
规则很多,我们来看一个例子。
-
根据规则1,首先开始的This和最后的”.”是匹配(M)的,所以需要合并的是中间的部分。
-
接着根据规则5, wide和spread两个合并成”widespread”。
-
根据规则3,交换的”benifits only”不参与合并。
-
propaganda左右都定了,所以它也就不能在参与合并了。
-
根据规则6,companys和companies很像,所以不参与合并。
-
根据规则10,最后一个The不参与合并。
-
to的左右都固定了,所以不用再合并。
合并的实验结果如下:
可以看出本文的结果都比base好。
Automatic annotation and evaluation of error types for grammatical error correction
前面的文章根据两个对齐的纠错句对,可以实现对齐并且合并连续的对齐。接下来要解决的问题就是判断没有对齐的到底是什么语法错误,这就是本篇文章的内容。
基于规则的错误类型分类
在本文之前,通常会训练分类器,但是在一个数据集上得到的模型在另外一个数据集上效果不行。本文提出了一种规则的方法,效果好而且不用训练模型,因而不存在数据集差异的问题。
根据经验,大部分错误类型都和词性相关,因此本文首先设计了一些规则根据词性来判断错误类型。如果词性判断不了,再根据缺失(插入)、不需要(删除)和错误(替换)来判断错误类型。最后再编写了一些规则来处理拼写错误和交互顺序的问题。总共有50条规则,虽然很多,但是非常直白。
这里最重要的就是动词的错误,它会非常细微。比如下图的例子,虽然正确的句子都是相同的,但是错误的句子的错误类型完全不同:
为了处理上图的错误,我们需要如下的规则:
-
如果两个词转换成小写后完全相同,则是正字法(orthography)的问题。
-
如果错误的词根本不是一个词(需要词典来判断?),则是拼写错误。
-
如果两个词的词干(lemma)相同,则是动词(Verb)的错误。
-
一个是动名词(gerund, VBG)或者分词(participle),则判断为词形(form)的问题。
-
一个是过去式(VBD),则判断为时态问题。
-
一个是第三人称,则判断为单复数问题。
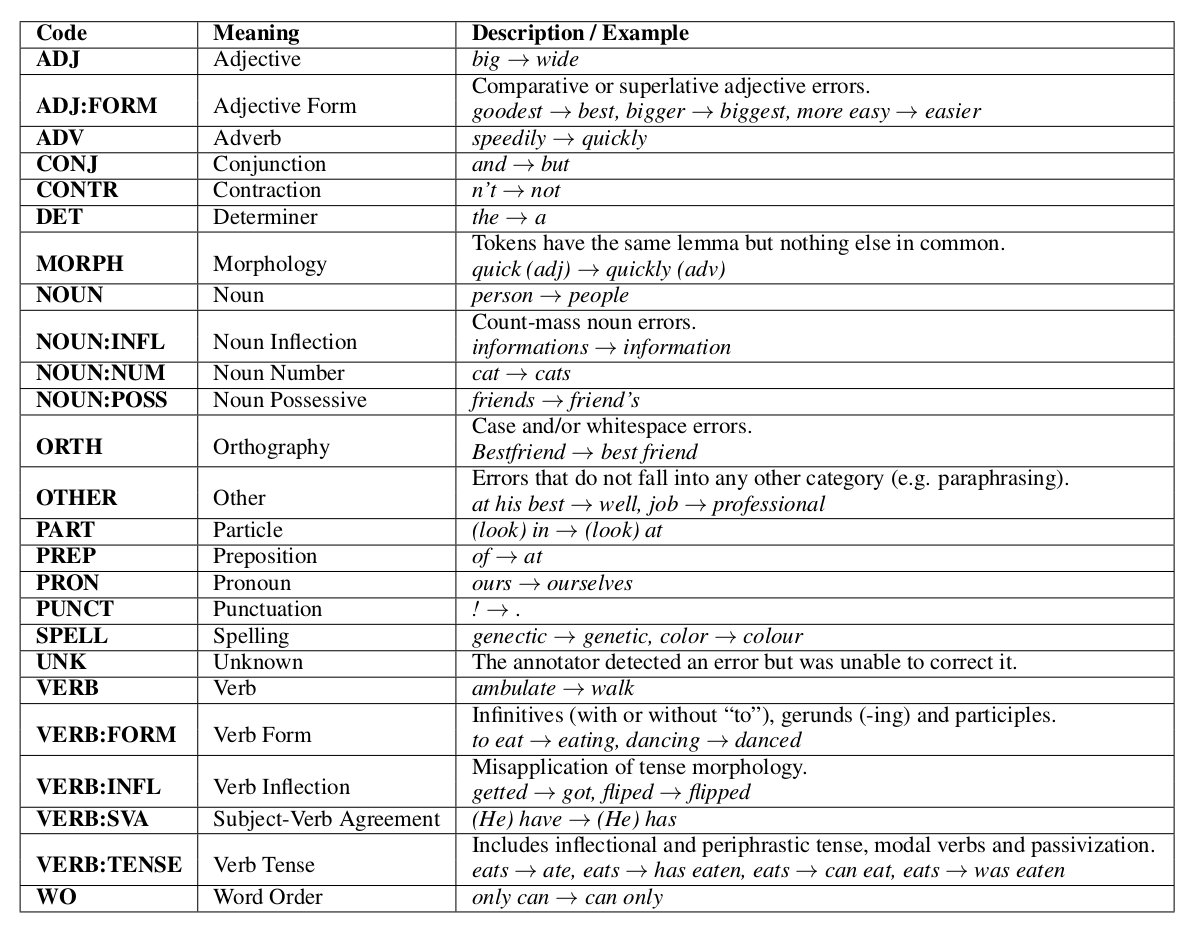
下面是25种常见的错误类型和示例:
更多错误类型的规则可以参考源代码。
代码分析
API
快速上手
import errant
annotator = errant.load('en')
orig = annotator.parse('This are gramamtical sentence .')
cor = annotator.parse('This is a grammatical sentence .')
edits = annotator.annotate(orig, cor)
for e in edits:
print(e.o_start, e.o_end, e.o_str, e.c_start, e.c_end, e.c_str, e.type)
代码比较简单,首先load spacy的英语(en)模型,然后用得到的annotator(spacy)对错误句子和正确句子进行parse,最后用annotate方法得到它们之间的差异,也就是需要进行的编辑操作。其中,e.o_start是本次编辑操作在original(错误句子)的开始下标。注意:这里parse函数有一个默认的tokenise参数,默认值为False,如果tokenise为False,则它假设我们的句子已经分好词了,所以直接用空格分词。如果我们希望它用spacy分词,则可以传入True。
上面代码的输出为:
1 2 are 1 2 is R:VERB:SVA
2 2 2 3 a M:DET
2 3 gramamtical 3 4 grammatical R:SPELL
Loading
import errant
import spacy
nlp = spacy.load('en')
annotator = errant.load('en', nlp)
errant.load()函数会创建一个annotator对象,必要的参数是lang,目前只能是”en”。第二个参数是spacy模型,如果为None则会创建spacy模型:
nlp = nlp or spacy.load(lang, disable=["ner"])
Annotator对象的方法
annotator.parse(string, tokenise=False)
使用spacy做词干还原(Lemmatise),词性标注,以及句法分析。tokenise为True时会用spacy分词。返回spacy的Doc对象。
annotator.align(orig, cor, lev=False)
把spacy处理后的两个对象进行对齐。默认使用Damerau-Levenshtein算法,如果设置lev为True则使用标准的Levenshtein算法。返回一个Alignment对象。
annotator.merge(alignment, merging=’rules’)
对齐的操作进行合并。merging有4种可能值:
- rules: 默认值,使用论文里提到的规则方法合并
- all-split: 不合并: MSSDI -> M, S, S, D, I
- all-merge: 除了match(M)都合并: MSSDI -> M, SSDI
- all-equal: 相同类型的操作合并: MSSDI -> M, SS, D, I
函数返回Edit对象的列表。
annotator.classify(edit)
对一次编辑操作判断其错误类型。该函数返回输入的edit,并且直接修改edit.type属性。
annotator.annotate(orig, cor, lev=False, merging=’rules’)
对输入的两个句子进行处理。它等价于依次调用annotator.align、annotator.merge和annotator.classify。返回Edit对象的列表。
因此这个函数等价于:
import errant
annotator = errant.load('en')
orig = annotator.parse('This are gramamtical sentence .')
cor = annotator.parse('This is a grammatical sentence .')
alignment = annotator.align(orig, cor)
edits = annotator.merge(alignment)
for e in edits:
e = annotator.classify(e)
annotator.import_edit(orig, cor, edit, min=True, old_cat=False)
给定spacy的orig和cor两个Doc对象,以及一个表示edit的list——[o_start, o_end, c_start, c_end(, type)],返回对应的Edit对象。如果min为True,则会去掉Edit相同的词,比如[a b -> a c] = [b -> c]。old_cat如果为True,则不调用错误类型的分类函数,从而保留原始的错误分类。示例:
import errant
annotator = errant.load('en')
orig = annotator.parse('This are gramamtical sentence .')
cor = annotator.parse('This is a grammatical sentence .')
edit = [1, 2, 1, 2, 'SVA'] # are -> is
edit = annotator.import_edit(orig, cor, edit)
print(edit.to_m2())
输出:
A 1 2|||R:VERB:SVA|||is|||REQUIRED|||-NONE-|||0
Alignment对象
Alignment对象包括如下属性:
- alignment.orig和alignment.cor
- spacy的Doc对象,表示parse后需要对齐的两个句子。
- alignment.cost_matrix和alignment.op_matrix
- 对齐产生的cost矩阵和opration矩阵。
- alignment.align_seq
- 两个序列的最佳对齐方式。
比如’This are gramamtical sentence .’和’This is a grammatical sentence .’的Alignment对象为:
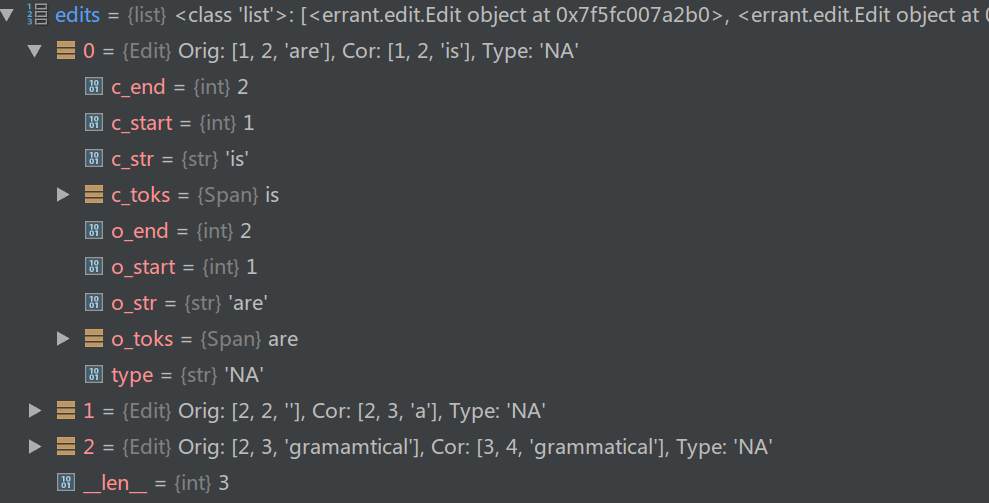
Edit对象
Edit对象有如下属性:
- edit.o_start,edit.o_end,edit.o_toks和edit.o_str
- 一个编辑操作对应的original(错误)的Token的开始和结束offset。
- edit.c_start,edit.c_end,edit.c_toks和edit.c_str
- 一个编辑操作对应的正确的Token的开始和结束offset。
- edit.type
- 错误类型
比如’This are gramamtical sentence .’和’This is a grammatical sentence .’的Edit的list为:
代码简析
我们用如下的代码来分析errant的主要代码:
import errant
annotator = errant.load('en')
orig = annotator.parse('This are gramamtical sentence .')
cor = annotator.parse('This is a grammatical sentence .')
alignment = annotator.align(orig, cor)
edits = annotator.merge(alignment)
for e in edits:
e = annotator.classify(e)
errant.load(‘en’)
def load(lang, nlp=None):
# Make sure the language is supported
supported = {"en"}
if lang not in supported:
raise Exception("%s is an unsupported or unknown language" % lang)
# Load spacy
nlp = nlp or spacy.load(lang, disable=["ner"])
# Load language edit merger
merger = import_module("errant.%s.merger" % lang)
# Load language edit classifier
classifier = import_module("errant.%s.classifier" % lang)
# The English classifier needs spacy
if lang == "en": classifier.nlp = nlp
# Return a configured ERRANT annotator
return Annotator(lang, nlp, merger, classifier)
load就是用spacy.load加载其模型,然后导入errant.en.merger和errant.en.classifier这两个对象,分别用于对齐的合并以及错误分类。
parse
def parse(self, text, tokenise=False):
if tokenise:
text = self.nlp(text)
else:
text = self.nlp.tokenizer.tokens_from_list(text.split())
self.nlp.tagger(text)
self.nlp.parser(text)
return text
parse主要就是调用spacy进行词性标注和句法分析。如果tokenize是True,则用self.nlp做分词、词性标注和句法分析;如果tokenize是False,则假设text是空格切分的,就直接使用text.split()。然后再调用nlp.tagger和nlp.parser。
align
align函数是最重要的对齐函数,不过它并没干真正的活。
def align(self, orig, cor, lev=False):
return Alignment(orig, cor, lev)
Alignment的构造函数
class Alignment:
# Input 1: An original text string parsed by spacy
# Input 2: A corrected text string parsed by spacy
# Input 3: A flag for standard Levenshtein alignment
def __init__(self, orig, cor, lev=False):
# Set orig and cor
self.orig = orig
self.cor = cor
# Align orig and cor and get the cost and op matrices
self.cost_matrix, self.op_matrix = self.align(lev)
# Get the cheapest align sequence from the op matrix
self.align_seq = self.get_cheapest_align_seq()
真正的对齐是Alignment的align函数。
Alignment.align
代码很长,可以对照这里阅读。
def align(self, lev):
# Sentence lengths
o_len = len(self.orig)
c_len = len(self.cor)
# Lower case token IDs (for transpositions)
o_low = [o.lower for o in self.orig]
c_low = [c.lower for c in self.cor]
# Create the cost_matrix and the op_matrix
cost_matrix = [[0.0 for j in range(c_len+1)] for i in range(o_len+1)]
op_matrix = [["O" for j in range(c_len+1)] for i in range(o_len+1)]
# Fill in the edges
for i in range(1, o_len+1):
cost_matrix[i][0] = cost_matrix[i-1][0] + 1
op_matrix[i][0] = "D"
for j in range(1, c_len+1):
cost_matrix[0][j] = cost_matrix[0][j-1] + 1
op_matrix[0][j] = "I"
# Loop through the cost_matrix
for i in range(o_len):
for j in range(c_len):
# Matches
if self.orig[i].orth == self.cor[j].orth:
cost_matrix[i+1][j+1] = cost_matrix[i][j]
op_matrix[i+1][j+1] = "M"
# Non-matches
else:
del_cost = cost_matrix[i][j+1] + 1
ins_cost = cost_matrix[i+1][j] + 1
trans_cost = float("inf")
# Standard Levenshtein (S = 1)
if lev: sub_cost = cost_matrix[i][j] + 1
# Linguistic Damerau-Levenshtein
else:
# Custom substitution
sub_cost = cost_matrix[i][j] + \
self.get_sub_cost(self.orig[i], self.cor[j])
# Transpositions require >=2 tokens
# Traverse the diagonal while there is not a Match.
k = 1
while i-k >= 0 and j-k >= 0 and \
cost_matrix[i-k+1][j-k+1] != cost_matrix[i-k][j-k]:
if sorted(o_low[i-k:i+1]) == sorted(c_low[j-k:j+1]):
trans_cost = cost_matrix[i-k][j-k] + k
break
k += 1
# Costs
costs = [trans_cost, sub_cost, ins_cost, del_cost]
# Get the index of the cheapest (first cheapest if tied)
l = costs.index(min(costs))
# Save the cost and the op in the matrices
cost_matrix[i+1][j+1] = costs[l]
if l == 0: op_matrix[i+1][j+1] = "T"+str(k+1)
elif l == 1: op_matrix[i+1][j+1] = "S"
elif l == 2: op_matrix[i+1][j+1] = "I"
else: op_matrix[i+1][j+1] = "D"
# Return the matrices
return cost_matrix, op_matrix
对于插入、删除和交换(transpose)操作来说,操作的cost分别是1、1和n-1(n是交换的词个数),而替换的操作需要按照论文的语言学信息计算,其代码为:
def get_sub_cost(self, o, c):
# Short circuit if the only difference is case
if o.lower == c.lower: return 0
# Lemma cost
if o.lemma == c.lemma: lemma_cost = 0
else: lemma_cost = 0.499
# POS cost
if o.pos == c.pos: pos_cost = 0
elif o.pos in self._open_pos and c.pos in self._open_pos: pos_cost = 0.25
else: pos_cost = 0.5
# Char cost
char_cost = 1-Levenshtein.ratio(o.text, c.text)
# Combine the costs
return lemma_cost + pos_cost + char_cost
另外除了cost_matrix,还需要用op_matrix记录对应的操作是插入、删除、交换还是替换。最后得到cost_matrix和cost_matrix之后需要通过回溯找到最优的对齐路径,这就需要下面函数。
Alignment.get_cheapest_align_seq
def get_cheapest_align_seq(self):
i = len(self.op_matrix)-1
j = len(self.op_matrix[0])-1
align_seq = []
# Work backwards from bottom right until we hit top left
while i + j != 0:
# Get the edit operation in the current cell
op = self.op_matrix[i][j]
# Matches and substitutions
if op in {"M", "S"}:
align_seq.append((op, i-1, i, j-1, j))
i -= 1
j -= 1
# Deletions
elif op == "D":
align_seq.append((op, i-1, i, j, j))
i -= 1
# Insertions
elif op == "I":
align_seq.append((op, i, i, j-1, j))
j -= 1
# Transpositions
else:
# Get the size of the transposition
k = int(op[1:])
align_seq.append((op, i-k, i, j-k, j))
i -= k
j -= k
# Reverse the list to go from left to right and return
align_seq.reverse()
return align_seq
这个函数从op_matrix最后的元素(op_matrix[len(self.op_matrix)-1, len(self.op_matrix[0])-1])开始回溯。然后根据op_matrix进行回溯。比如操作是”M”(匹配)或者”S”(替换),那么i和j的下标都往回走一个。如果是”D”(删除),则i减一而j不变。如果是”I”(插入),则j减一i不变。如果是交换(Transposition),则op_matrix记录的是交换的词的个数-1,则i和j都减掉这个数。
Annotator.merge
def merge(self, alignment, merging="rules"):
# rules: Rule-based merging
if merging == "rules":
edits = self.merger.get_rule_edits(alignment)
# all-split: Don't merge anything
elif merging == "all-split":
edits = alignment.get_all_split_edits()
# all-merge: Merge all adjacent non-match ops
elif merging == "all-merge":
edits = alignment.get_all_merge_edits()
# all-equal: Merge all edits of the same operation type
elif merging == "all-equal":
edits = alignment.get_all_equal_edits()
# Unknown
else:
raise Exception("Unknown merging strategy. Choose from: "
"rules, all-split, all-merge, all-equal.")
return edits
我们只看基于规则的合并,也就是self.merger.get_rule_edits(alignment)
merger.get_rule_edits
def get_rule_edits(alignment):
edits = []
# Split alignment into groups of M, T and rest. (T has a number after it)
for op, group in groupby(alignment.align_seq,
lambda x: x[0][0] if x[0][0] in {"M", "T"} else False):
group = list(group)
# Ignore M
if op == "M": continue
# T is always split
elif op == "T":
for seq in group:
edits.append(Edit(alignment.orig, alignment.cor, seq[1:]))
# Process D, I and S subsequence
else:
processed = process_seq(group, alignment)
# Turn the processed sequence into edits
for seq in processed:
edits.append(Edit(alignment.orig, alignment.cor, seq[1:]))
return edits
如果是M则不合并,如果是T(交换)也不合并,其它情况调用process_seq。process_seq的代码比较繁琐,这里就不介绍了。
classifier.classify
def classify(edit):
# Nothing to nothing is a detected but not corrected edit
if not edit.o_toks and not edit.c_toks:
edit.type = "UNK"
# Missing
elif not edit.o_toks and edit.c_toks:
op = "M:"
cat = get_one_sided_type(edit.c_toks)
edit.type = op+cat
# Unnecessary
elif edit.o_toks and not edit.c_toks:
op = "U:"
cat = get_one_sided_type(edit.o_toks)
edit.type = op+cat
# Replacement and special cases
else:
# Same to same is a detected but not corrected edit
if edit.o_str == edit.c_str:
edit.type = "UNK"
# Special: Ignore case change at the end of multi token edits
# E.g. [Doctor -> The doctor], [, since -> . Since]
# Classify the edit as if the last token wasn't there
elif edit.o_toks[-1].lower == edit.c_toks[-1].lower and \
(len(edit.o_toks) > 1 or len(edit.c_toks) > 1):
# Store a copy of the full orig and cor toks
all_o_toks = edit.o_toks[:]
all_c_toks = edit.c_toks[:]
# Truncate the instance toks for classification
edit.o_toks = edit.o_toks[:-1]
edit.c_toks = edit.c_toks[:-1]
# Classify the truncated edit
edit = classify(edit)
# Restore the full orig and cor toks
edit.o_toks = all_o_toks
edit.c_toks = all_c_toks
# Replacement
else:
op = "R:"
cat = get_two_sided_type(edit.o_toks, edit.c_toks)
edit.type = op+cat
return edit
这个函数就是规则的错误分类。首先判断Edit的两个c_tokens和o_tokens。如果只有一个不空,则说明是缺失(Missing,插入操作)或者多余(Unnecessary,删除操作)。否则先处理最后一个词相同的情况,比如[Doctor -> The doctor], [, since -> . Since]。最后处理Replacement,调用的是get_two_sided_type函数。这个函数就是那50多种规则,这里就不介绍了,感兴趣的读者可以阅读其代码。
- 显示Disqus评论(需要科学上网)