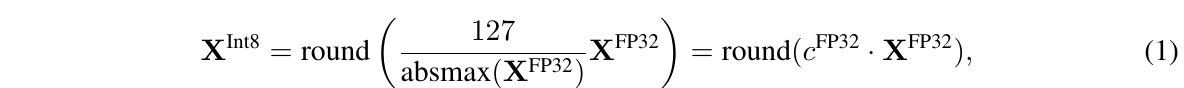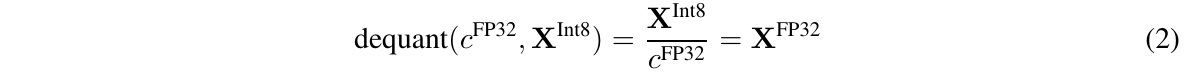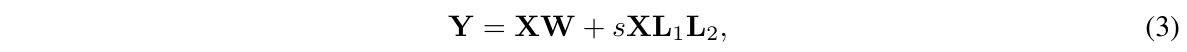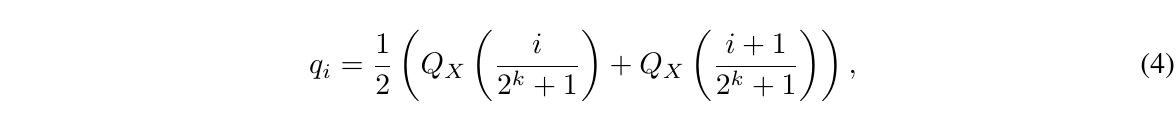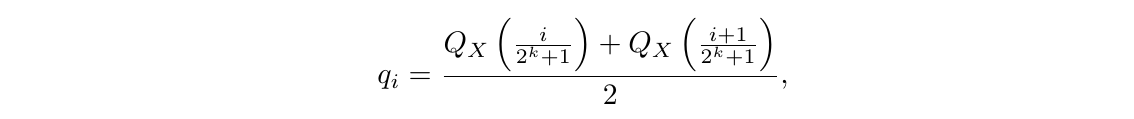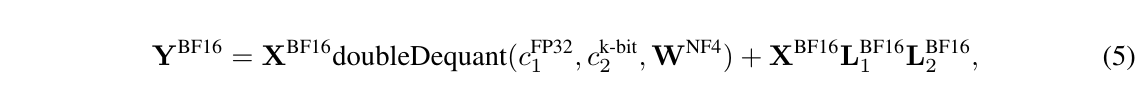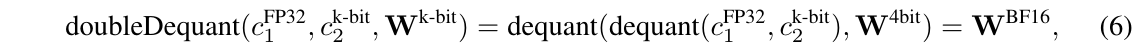本文是论文QLoRA: Efficient Finetuning of Quantized LLMs的解读。
目录
Abstract
本文介绍QLoRA,这是一种高效的微调方法,可以在单个48GB GPU上进行微调,从而减少内存使用量足以微调一个650亿参数的模型,同时保持完整的 16位微调任务性能。QLoRA通过一个冻结的、4位量化的预训练语言模型反向传播梯度到低秩适配器 (LoRA)。我们最好的模型系列,名为Guanaco,在Vicuna基准测试上表现优于所有以前公开发布的模型,达到了ChatGPT性能水平的 99.3%,仅需要在单个GPU 上进行24小时的微调。QLoRA引入了一系列创新,以在不牺牲性能的前提下节省内存:(a) 4 位NormalFloat(NF4),这是一种对于正态分布权重信息理论上最优的新数据类型;(b) 重量化,通过量化量化常数来减少平均内存占用;和 (c) 分页优化器,用于管理内存波动。我们使用QLoRA对1000多个模型进行微调,并对8个指令数据集、多个模型类型 (LLaMA、T5) 以及通常无法运行的模型规模 (例如,330亿和650亿参数模型) 进行了详细的指令追踪和聊天机器人性能分析。我们的结果表明,在小而高质量的数据集上进行QLoRA微调可以取得最先进的结果,即使使用比先前的最先进模型更小的模型也是如此。我们基于人工和 GPT-4评估提供了对聊天机器人性能的详细分析,显示GPT-4评估是与人工评估的一种廉价且合理的替代方案。此外,我们发现当前的聊天机器人基准测试不能信任,无法准确评估聊天机器人的性能水平。一个例外的分析演示了Guanaco在某些方面与ChatGPT相比的不足之处。我们发布了我们所有的模型和代码,包括用于4位训练的CUDA内核。
1. Introduction
微调大型语言模型(LLMs)是改善其性能的一种非常有效的方法。然而,对非常大的模型进行细调成本过高;对 LLaMA 65B 参数模型的常规 16 位微调需要超过780GB的GPU内存。尽管最近的量化方法可以减少LLMs的内存占用,但是这些技术仅适用于推理,而在训练过程中会出现问题。
我们首次展示了可以在不降低性能的情况下对经过量化的4位模型进行微调的可能性。我们的方法,QLoRA,使用一种新颖的高精度技术将预训练模型量化为4位,然后通过通过模型反向传播梯度来调整一小组可学习的低秩适配器权重。
QLoRA将65B参数模型进行微调的平均内存要求从超过780GB 的GPU 内存减少到小于48GB,而且与16位完全微调的基线相比,不降低运行时或预测性能。这标志着LLM微调的可访问性发生了重大变化:现在可以在单个 GPU 上进行微调最大的公开可用模型。使用QLoRA,我们训练了Guanaco模型系列,第二好的模型在Vicuna基准测试上达到了ChatGPT性能水平的 97.8%,而且可以在单个消费级GPU上进行微调,时间不到12小时;使用单个专业 GPU 超过24小时,我们的最大模型实现了99.3%,基本上缩小了在 Vicuna 基准测试上与 ChatGPT 之间的差距。在部署时,我们最小的Guanaco 模型(7B 参数仅需要5GB的内存,在Vicuna基准测试上的表现超过了26GB Alpaca模型超过20百分点)。
 表1:对模型之间的一场比赛的Elo评分,平均计算了10,000次随机的初始排序。比赛的胜者由GPT-4决定,它声明对于Vicuna基准测试的给定提示哪个响应更好。显示了95%的置信区间(±)。在GPT-4之后,Guanaco 33B和65B赢得了最多的比赛,而Guanaco 13B的得分超过了Bard。
表1:对模型之间的一场比赛的Elo评分,平均计算了10,000次随机的初始排序。比赛的胜者由GPT-4决定,它声明对于Vicuna基准测试的给定提示哪个响应更好。显示了95%的置信区间(±)。在GPT-4之后,Guanaco 33B和65B赢得了最多的比赛,而Guanaco 13B的得分超过了Bard。
QLORA引入了多项创新,在不牺牲性能的前提下减少内存使用:(1) 4位NormalFloat,这是一种对于正态分布数据而言在信息论上最优的量化数据类型,其实际效果比4位整数和4位浮点数更好。(2) 重量化,一种量化量化常数的方法,平均每个参数节省约0.37位(对于65B模型约为3GB)。(3) 分页优化器,使用NVIDIA统一内存来避免在处理具有较长序列长度的小批量时发生的梯度检查点内存峰值。我们将这些贡献结合到一个更好调优的LoRA方法中,该方法在每个网络层都包含适配器,因此几乎避免了在先前工作中看到的所有准确性折衷。
QLORA的效率使我们能够对指令微调和聊天机器人性能进行深入研究,这是使用常规微调由于内存开销而不可能的模型规模。因此,我们在多个指令微调数据集、模型体系结构和大小(从80M到65B参数)之间训练了超过1,000个模型。除了展示QLORA恢复了16位性能并训练了一流的聊天机器人Guanaco之外,我们还分析了训练模型的趋势。首先,我们发现数据质量比数据集大小更为重要,例如,在聊天机器人性能方面,一个9k样本的数据集(OASST1)胜过了一个450k样本的数据集(FLAN v2,子采样),即使两者都旨在支持指令跟随泛化。其次,我们表明,强大的大规模多任务语言理解(MMLU)基准性能并不意味着强大的Vicuna聊天机器人基准性能,反之亦然——换句话说,对于特定任务而言,数据集的适用性比大小更为重要。
此外,我们还提供了对聊天机器人性能的广泛分析,该分析既使用人类评估者又使用GPT-4进行评估。我们使用锦标赛风格的基准测试,其中模型在比赛中相互竞争,以生成给定提示的最佳响应。比赛的胜者由GPT-4或人类注释者判断。锦标赛结果被聚合成Elo分数,以确定聊天机器人性能的排名。我们发现GPT-4和人类在锦标赛中对于模型性能的排名大致一致,但我们还发现存在强烈分歧的情况。因此,我们强调,基于模型的评估虽然提供了一种廉价的替代人工注释的方法,但也存在不确定性。
我们通过对Guanaco模型进行定性分析,进一步补充了聊天机器人基准结果。我们的分析突显了定量基准未捕捉到的成功和失败案例。我们发布所有带有人类和GPT-4注释的模型生成,以促进进一步研究。我们开源我们的代码库和CUDA内核,并将我们的方法集成到Hugging Face transformers堆栈中,使其易于访问。我们发布了7/13/33/65B大小模型的适配器集合,这些模型在8个不同的指令跟随数据集上进行了训练,总共有32个不同的开源微调模型。
2. Background
Block-wise k-bit Quantization
量化是将输入从包含更多信息的表示离散化为包含更少信息的表示的过程。通常,这意味着将具有更多位的数据类型转换为更少位,例如从32位浮点数转换为8位整数。为了确保低位数据类型的整个范围被使用,输入数据类型通常通过对输入元素的绝对最大值进行归一化而被重新缩放到目标数据类型范围内,这些元素通常结构化为张量。例如,将32位浮点(FP32)张量量化为具有范围[-127, 127]的Int8张量:
其中c是量化常量或者量化缩放因子。反量化正好相反:
这种方法的问题在于,如果输入张量中出现大幅度的值(即异常值),则量化区间——即某些比特组合——在某些区间中很少或没有数字被量化,导致利用不充分。为了防止异常值问题,一个常见的方法是将输入张量分块,每个块都独立进行量化,每个块都有自己的量化常数 c。这可以形式化为:我们将输入张量 $X \in R^{b \times h}$划分为大小为 B 的 n 个连续块,通过将输入张量展平并将线性段切片成 n=(b × h)/B 个块。我们使用公式 (1)独立地对这些块进行量化,从而创建一个量化张量和n个量化常数$c_i$。
补充内容
本部分内容来自Road to Efficient LLMs 2: QLoRA
我们来自己实现简单的量化:
import torch
tensor = torch.tensor([0.32, -1.76, 0.025, -1.22])
下面是float32到int8的量化函数:
def quantize(X_FP32):
# Get the absolute maximun value in tensor X_FP32
abs_max = torch.max(torch.abs(X_FP32))
# Define the quantization constant C
c_FP32 = 127 / abs_max
# Round the multiplication result to nearest value
X_Int8 = torch.round(c_FP32 * X_FP32)
return X_Int8, c_FP32
这个函数求出float32向量X_FP32中绝对值最大值abs_max,这样我们用X_FP32除以abs_max就可以把它归一化到[-1,1],然后再乘以127就可以把它们缩放到[-127,127]之间,这样就可以用int8来保存float32,当然需要round函数把浮点数转换成整数。为了后面能够反量化(dequantize),我们这个函数除了返回量化后的int8向量,还会返回缩放因子c_FP32。
我们来测试一下量化函数:
quantized_tensor, c = quantize(tensor)
print("Original Tensor:", tensor)
print("Quantized Tensor:", quantized_tensor)
# Output
Original Tensor: tensor([ 0.3200, -1.7600, 0.0250, -1.2200])
Quantized Tensor: tensor([ 23., -127., 2., -88.])
从上面我们可以看到,原来的0.32被转换成了23,因此在推理或者训练时我们肯定不能用量化后的值。为了计算,我们需要反量化,也就是把int8转换成float32,这当然会带来误差(quantize的round函数带来),我们希望这个误差越小越好。下面我们来实现dequantize函数:
def dequantize(c_FP32, X_Int8):
X_FP32_dequant = X_Int8 / c_FP32
return X_FP32_dequant
和前面的qunatize一起,我们看看量化的误差:
tensor = torch.tensor([0.32, -1.76, 0.025, -1.22])
quantized_tensor, c = quantize(tensor)
dequantized_tensor = dequantize(c, quantized_tensor)
print("Original Tensor:", tensor)
print("Quantized Tensor:", quantized_tensor)
print("Dequantized Tensor:", dequantized_tensor)
print("c:", c)
# Output
Original Tensor: tensor([ 0.3200, -1.7600, 0.0250, -1.2200])
Quantized Tensor: tensor([ 23., -127., 2., -88.])
Dequantized Tensor: tensor([ 0.3187, -1.7600, 0.0277, -1.2195])
c: tensor(72.1591)
看起来还不错,原来的0.32通过量化和反量化变成了0.3187;0.025变成了0.0277。
不过如果输入的向量存在野点(outlier,也就是和大部分数的范围不一致的数),结果就没有那么好了。下面我们看一个例子:
tensor = torch.tensor([0.32, -1.76, 0.025, -1.22,100.1])
quantized_tensor, c = quantize(tensor)
dequantized_tensor = dequantize(c, quantized_tensor)
print("Original Tensor:", tensor)
print("Quantized Tensor:", quantized_tensor)
print("Dequantized Tensor:", dequantized_tensor)
print("c:", c)
# Output
Original Tensor: tensor([ 3.2000e-01, -1.7600e+00, 2.5000e-02, -1.2200e+00, 1.0010e+02])
Quantized Tensor: tensor([ 0., -2., 0., -2., 127.])
Dequantized Tensor: tensor([ 0.0000, -1.5764, 0.0000, -1.5764, 100.1000])
c: tensor(1.2687)
输入的tensor中有一个100.1,它明显和其它数的范围不一样,比那些数大了一个数量级。为了让它可以存放在[-127,127]之间,就会让其它的数变得很小。我们看到,0.32和0.025都被量化成了0,这样反量化回去也是0。这样的误差是不可接受的。
那怎么办呢?有些方法是尝试检测这些野点,然后把它们排除在量化范围之外。另外一种本文采样的方法就是减少野点造成的问题的范围,也就就是Blockwise-quantization。也就是把一个很长的向量切分成B个块(block),这样一个野点最多就影响相同block的那些数。【译注:看起来这个方法也不太完美】
Low-rank Adapters
低秩适配器(LoRA)微调是一种通过使用一小组可训练参数(通常称为适配器)来减少内存需求的方法,同时不更新保持固定的完整模型参数。在随机梯度下降过程中,梯度通过保持固定的预训练模型权重传递到适配器,适配器被更新以优化损失函数。LoRA通过额外的分解投影增强了线性投影。给定一个投影 $XW = Y$,其中 $X \in R^{b \times h},W \in R^{h \times o}$,LoRA计算:
其中$L_1 \in R^{h \times r}, L_2 \in R^{r \times o}$,s是一个标量。
Memory Requirement of Parameter-Efficient Finetuning
由于LoRA的内存占用非常小,我们可以使用更多的适配器来提高性能,而不显著增加总内存使用量。虽然LoRA 被设计为参数高效的微调(PEFT)方法,但大多数LLM微调的内存占用来自激活梯度,而不是学到的LoRA参数。对于在FLAN v2上以批量大小1训练的7B LLaMA 模型,LoRA 权重相当于原始模型权重的常用 0.2%,LoRA输入梯度的内存占用为567MB,而 LoRA 参数仅占用26MB。使用梯度检查点,输入梯度平均减少到每个序列18MB,使其比所有LoRA 权重加在一起更占内存。相比之下,4位基础模型的内存占用为5,048MB。这突显了梯度检查点的重要性,但也表明过于激进地减少LoRA参数量只会带来轻微的内存优势。这意味着我们可以使用更多适配器,而不显著增加整体训练内存占用。正如后文所讨论的,这对于恢复完整的16位精度性能至关重要。
3. QLoRA Finetuning
QLoRA 通过我们提出的两种技术——4位NormalFloat(NF4)量化和双重量化,实现了高保真度的4位微调。此外,我们引入了分页优化器,以防止梯度检查点期间的内存波动导致传统上使得在单台机器上对大型模型进行微调变得困难的内存不足错误。
QLoRA具有一种低精度存储数据类型,通常为4位,在我们的情况下通常为BFloat16,以及一种计算数据类型,通常为BFloat16。实际上,这意味着每当使用QLoRA权重张量时,我们将张量反量化为BFloat16,然后以16位执行矩阵乘法。
接下来,我们讨论QLoRA的组成部分,然后给出QLoRA的正式定义。
4-bit NormalFloat Quantization
NormalFloat(NF)数据类型建立在分位数量化的基础上,分位数量化是一种在信息理论上最优的数据类型,确保每个量化区间从输入张量中获得相等数量的值。分位数量化通过估计输入张量的经验累积分布函数来工作。
分位数量化的主要局限性在于分位数估计的过程昂贵。因此,通常使用快速分位数近似算法(例如 SRAM 分位数)来估计它们。由于这些分位数估计算法的近似性质,该数据类型对于异常值(通常是最重要的值)具有较大的量化误差。
当输入张量来自一个固定到一个量化常数的分布时,可以避免昂贵的分位数估计和近似误差。在这种情况下,输入张量具有相同的分位数,使得精确的分位数估计在计算上可行。
由于预训练神经网络权重通常具有零中心的正态分布,标准差为σ(见附录 F),我们可以通过缩放σ以使分布正好适应到我们数据类型的范围,将所有权重转换为一个固定的分布。对于我们的数据类型,我们设置了任意的范围为[-1, 1]。因此,数据类型和神经网络权重的分位数都需要归一化到这个范围内。
对于零均值正态分布,标准差σ在范围[-1, 1]内的信息理论上最优的数据类型计算如下:(1)估计理论上N(0, 1)分布的2k + 1分位数,以获得正态分布的k位量化数据类型,(2)取此数据类型并将其值归一化到[-1, 1]范围内,(3)通过绝对最大重新缩放将输入权重张量量化为[-1, 1]范围内。
一旦权重范围和数据类型范围匹配,我们就可以像通常一样进行量化。步骤(3)相当于将权重张量的标准差重新缩放以匹配k位数据类型的标准差。更正式地说,我们估计数据类型的$2^k$个值$q_i$如下:
其中 $Q_X (·)$ 是标准正态分布 N(0, 1)的分位函数。对于对称的k位量化,一个问题是这种方法没有对零的精确表示,而零是将padding和其他零值元素进行量化时的重要属性,这样可以避免误差。为了确保离散零点为0,并且为了使用k位数据类型的所有$2^k$位,我们通过估计两个范围 $q_i: 2^{k−1}$(负部分)和 $2^{k−1} + 1$(正部分)的分位数$q_i$,然后合并这些$q_i$集合并删除在两个集合中都出现的两个零之一,从而创建了一个非对称的数据类型。我们将得到的数据类型称为k位NormalFloat(NFk),因为该数据类型对于零中心正态分布的数据是信息理论上最优的。该数据类型的确切值可在附录E中找到。
补充材料
上面一节没看到?没看懂就对了,否则你就不需要阅读本文了。请要相信这一点:我们没看懂不是因为自己太笨,而是因为作者没有写好或者遗漏了一些背景知识。学习中会碰到很多问题,有一句话对我帮助很大:“如果一本书读不懂不要责备自己,要么是这本书写得不好,要么是自己缺少了作者假设我们知道的一些背景知识。” 所以一本书或者一篇文章仔细阅读后还是理解不了的话就赶紧扔掉去找更好更适合自己的资料。
NF4的量化和反量化过程
我们先不看理论,而是看看实际是怎么量化的,也就是怎么把一个float32的向量(block)变成4个bit的数([0,15]),然后又是怎么反量化回去的。这个过程如下图所示:
输入向量是X=[0.32, -1.76, 0.025, -1.22],我们首先找到absmax(X)=1.76,然后X/absmax(X)归一化成[0.1818, -1, 0.0142, -0.6932]。然后根据NF4=[-1.0000, -0.6962, -0.5251, -0.3949, -0.2844, -0.1848, -0.0911, 0.0796, 0.1609, 0.2461, 0.3379, 0.4407, 0.5626, 0.7230, 1.0000]进行舍入。这个NF4数组是16个数字,它是怎么来的我们后文再讲。
比如0.1818在0.1609和0.2461之间,最接近的就是0.1609,因此我们把它舍入到0.1609。这里有一个需要注意:0.0142在0和0.0796之间,按理应该舍入到0,但是我们看到它舍入到0.0796了。这是为什么呢?因为在神经网络里,0通常代表padding,我们为了区分padding和较小的数,所以不能把0.0142舍入到0。
舍入后我们保存的时候就保存这个数的下标就行,比如0.1609,它的下标就是8(下标9开始)。
反量化就是根据下标从NF4数组里获取值,然后乘以absmax就可以了。图中的最后一步是有问题的,比如0.1609*1.76=0.283184。它这里反量化回去完全没有误差,这是不太可能的。
非线性量化
量化通过降低精度来压缩数值表示以节省空间。量化是将k位整数映射到域D中的实数元素,即 \(Q^{\text{map}}:[0, 2^k − 1] \mapsto D\)。例如,IEEE 32位浮点数据类型将索引 $0…2^{32} − 1$ 映射到域 [-3.4e38, +3.4e38]。我们使用以下符号:$Q^{\text{map}}(i) = Q_i^{\text{map}} = q_i$,例如 $Q^{\text{map}}(2^{31} + 131072) = 2.03125$,这是IEEE32位浮点数据类型的映射方式。
要将一种数据类型量化为另一种,我们需要三个步骤。 (1)计算一个归一化常数 N,将输入张量T转换为目标量化数据类型$Q^{\text{map}}$ 的域 D 的范围, (2)对于 T/N 的每个元素,找到域 D 中最接近的相应值 $q_i$, (3)存储与$q_i$对应的索引 i 在量化输出张量 $T^Q$ 中。 要获得反量化张量$T^D$,我们查找索引并进行反标准化:$TDi = Q^{\text{map}}(T_i^Q) · N$。
要执行动态量化的这个过程,我们首先通过除以绝对最大值进行归一化为范围[-1, 1]:N = max(|T|)。 然后,我们通过二分搜索找到最接近的值:
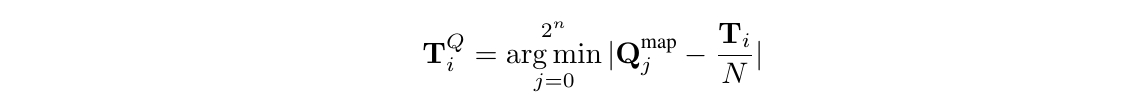
分位数量化(Quantile Quantization)
前面在野点的例子可以看出,它带来的问题是大部分数都集中在很小的区域里。比较”理想”的情况是4bit(或者8bit)的每一个”数”都是相同的概率被用到的。比如对于符合某个分布(比如正态分布)的数据的N(比如N=1600)个采样,16个数(索引)都被量化过N/16=100次。
实现对任意概率分布X满足这一特性的一种方法是将概率分布函数$f_X$划分为 $2^k$个区间,其中每个区间具有相等的面积,并且这些区间的中点是量化映射$Q^{\text{map}}$的值q。在经验上,这相当于一个包含$2^k$个bin的直方图,其中每个区间包含相等数量的值。
我们如何找到每个直方图区间的中点?这等同于找到具有相等概率质量的累积分布函数$F_X$的$2^k$个不重叠值x。这些值可以通过使用其反函数,即分位函数 $Q_X = F_X^{-1}$的方法最容易找到。我们可以通过使用概率范围 [0, 1] 上等间隔的$2^{k+1}$个分位数之间的中点来找到每个直方图区间的中点:
为了根据经验分布找到q,我们可以通过找到张量T的经验累积分布函数的$2^k$个等间距样本分位数来估计具有未知分布X的的样本分位数。我们将这种量化称为分位数量化。
为了有效地估计样本分位数,通常需要专门的近似分位数估计算法,比如SRAM-Quantiles。因为与本文关系不大,这里就不介绍了,感兴趣的读者可以参考8-bit Optimizers via Block-wise Quantization。【在附录里,正文中没有,^_^】
分位数(quantile)简介。概率论还给老师的读者可以搜索一下网上的资料。比如知乎:如何通俗地理解分位数?和Math is Fun: Percentiles。
NF4的原理
在我们先前关于 INT-8 的讨论中,我们强调了如何在范围 [-127, 127](Int8)内表示高精度数据。相比之下,使用 NF4受限于 $2^4=16$个不同的值。这明显比我们在INT-8中获得的256个值要少得多。一个自然的问题是:我们如何确定这16个值中的哪一个能最好地表示模型的无数潜在权重值?
根据论文:
由于预训练的神经网络权重通常具有以标准差σ为中心的正态分布,我们可以通过调整σ的比例尺度,使分布完全适应我们数据类型的范围,从而将所有权重转换为单一的固定分布。对于我们的数据类型,我们设置了任意的范围为 [−1, 1]。因此,数据类型和神经网络权重的分位数都需要被归一化到这个范围内。
论文在附录里详细验证了常见的LLM如LLaMA的权重确实符合正态分布,感兴趣的读者可以参考论文。
考虑到大多数预训练神经网络权重都符合这个分布,我们可以将正态分布划分为16个不同的水平(或值)。为了实现这一点,我们可以使用与正态分布相关联的分位数函数来找到这16个确切的分位数。让我们深入了解如何从正态分布中导出这16个值,以更有效地表示我们模型的权重。
在某些情况下,输入数据或特征通常会用零进行padding,以保持特定的空间维度或确保数据的对齐。对零的精确表示确保了这些填充能够准确地表示,并且不会在计算中引入人为的瑕疵。如果没有对零的精确表示,接近零的值在量化过程中可能会被舍入为小的非零值。这可能在计算中引入不准确,特别是当这些小值与其他大值相乘的时候。
对称的k位量化意味着对于值零没有精确的表示。为了解决这个问题并确保零的精确表示,本文引入了一种非对称的数据类型。这是通过分别考虑正值和负值的分位数,然后合并它们来实现的,确保只有一个零值。我们为负的部分创建$2^{k-1}$ 个值,为正的部分创建$2^{k-1}+1$个值,并删除重叠的值。下面来看具体的做法。这里参考了NF4 Isn’t Information Theoretically Optimal (and that’s Good)。
1.选择一个比较小的$\delta = \frac{1}{2}(\frac{1}{32} + \frac{1}{30})$。我们可以计算出$1-\delta=0.9677083333333334$。
2.计算均匀pacing的8个数,$p_1,…,p_8$,其中$p_1=\delta, p_8=1/2$。
3.找到它们高斯CDF函数$\Phi$的逆,也就是计算$\hat{q_i}=\Phi^{-1}(p_i)$。
这几步用代码来描述就是:
delta = 1/2*(1/32+1/30)
print(torch.linspace(delta, 0.5, 8))
print(norm.ppf(torch.linspace(delta, 0.5, 8)))
输出:
tensor([0.0323, 0.0991, 0.1659, 0.2327, 0.2996, 0.3664, 0.4332, 0.5000])
[-1.84813142 -1.28665578 -0.97040379 -0.72985929 -0.52568489 -0.34148556
-0.16827238 0. ]
为什么这么做呢?因为我们希望找到左边一半(更准确的说是$7=2^4-1$)分位数。也就是[0.0323, 0.0991, 0.1659, 0.2327, 0.2996, 0.3664, 0.4332, 0.5000]值的分位点。为什么选择delta呢?我也不是特别理解,感觉选择它之后,每个点作为中心点的话,左右的宽度都是0.06左右,比如0.0323代表的bin是0~(0.0323+0.0991)/2=0~0.0657,0.0991代表的bin是0.0657~0.1325,…,这样每个bin的宽度也就是采样落在其中的概率是相同的。
QLoRA的官方代码实现稍有不同,但是结果稍有不同:
offset = 0.9677083
v3 = (-norm.ppf(torch.linspace(offset, 0.5, 8)[:-1])).tolist()
结果:
[-1.8481308221817017, -1.2866554260253906, -0.9704037308692932, -0.7298591732978821, -0.5256848931312561, -0.34148547053337097, -0.16827237606048584]
其中offset = 1 - delta。从数学上感觉它们应该是等价的(我们没有详细研究证明过),但是我不知道为什么要这么实现。
4.计算9个均匀paced概率值$r_8,…,r_{16}$,其中$r_8=1/2, r_{16}=1-\delta$。
5.计算$\hat{q_i}=\Phi^{-1}(r_i)$。
这个和上面类似,只不过这里的$r_8$不需要了,因为前面的1/2分位数就是零了。
代码:
print(torch.linspace(0.5, 1-delta, 9))
print(norm.ppf(torch.linspace(0.5, 1-delta, 9)))
结果:
tensor([0.5000, 0.5585, 0.6169, 0.6754, 0.7339, 0.7923, 0.8508, 0.9092, 0.9677])
[0. 0.14707497 0.29742005 0.45484772 0.6245116 0.81448966
1.03979003 1.33611882 1.84813166]
前面产生了7个负数和零,这一步产生8个正数(去掉零),总共得到16个数,这就是前面NF4数组的计算过程。
Double Quantization
我们引入了二次量化(DQ),即对额外节省内存的量化常数进行量化的过程。为了实现精确的4位量化,我们通常需要把块切的很细,从而避免野点的问题,但这也会需要存储很多小块的常数absmax,从而带来相当大的内存开销。例如,当块大小是64并且我们使用32位来存储常数时,量化常数平均每个参数增加 32/64 =0.5位。二次量化有助于减小量化常数的内存占用。
具体而言,二次量化将第一次量化的量化常数$c^{\text{FP32}}_2$视为第二次量化的输入。这第二步产生了量化的量化常数$c_2^{\text{FP8}}$和第二级量化常数 $c^{\text{FP32}}_1$。我们在第二次量化中使用8位浮点数和块大小为256,因为观察到了8位量化没有性能下降,这与 Dettmers 和 Zettlemoyer 的研究结果一致。由于$c_2^{\text{FP8}}$为正值,我们在量化之前从$c_2$中减去平均值,以使值围绕零居中,并利用对称量化。平均而言,对于块大小为64,这种量化将每个参数的内存占用从32/64 =0.5位减少到 8/64 + 32/(64 · 256) = 0.127位,每个参数减少了0.373位。
这个方法比较易懂,我再用自己的话复述一遍(前面是ChatGPT翻译)。对于每一个块B(64个浮点数),我们需要存储absmax(B),如果用fp32存储,那么相当于每一个参数平均额外增加了32/64=0.5个bit,因此每个参数是4.5bit。而每个块的absmax本身就是fp32,也可以用分块的方法进行fp8压缩(不能再用NF4压缩了,否则效果就不行了),假设我们对256个块的absmax进行压缩,那么就可以把这256个fp32变成256个fp8,当然还需要存储这一次压缩的absmax,还需要一个fp32。这样对于每个块来说平均从32/64减少到8/64,当然还有额外的开销,那就是每256个absmax需要一个fp32,因此均摊下来就是32/(64*256)。
Paged Optimizers
我们使用 NVIDIA 统一内存特性,该特性在CPU和GPU之间进行自动页面传输,以确保在GPU偶尔内存不足的情况下进行无误的GPU处理。该特性类似于CPU RAM和磁盘之间的常规内存分页。我们利用此特性为优化器状态分配分页内存,当GPU内存不足时,这些状态会自动转移到CPU RAM 中,并在优化器更新步骤需要内存时分页回到GPU内存中。
这一部分需要阅读代码才能明白,更多是工程优化,我没有花时间去研究。
QLoRA
利用上述三个优化技术,我们为具有单个LoRA 适配器的量化基础模型中的单个线性层定义QLoRA如下:
也就是QLoRA进行前向计算时首先通过doubleDequant函数把原始模型的参数反量化成fp16,然后在加上LoRA适配层,LoRA的参数是不量化的,因为它们需要反向传播优化。而原始模型的参数是freeze的,因此可以量化。其中doubleDequant(·)定义为:
上式的意思是先用$c^{\text{FP32}}_1$反量化得到每个块的absmax常量,然后再用这个常量反量化NF4参数。参数W是NF4,absmax常量$c_2$被量化成fp8。
对于参数更新,只需要适配器权重对误差的梯度$\frac{\partial E}{\partial L_i}$,而不需要4位权重的梯度$\frac{\partial E}{\partial W}$。然而,计算$\frac{\partial E}{\partial L_i}$需要通过方程(5)进行,这里通过链式法则会隐含使用$\frac{\partial E}{\partial W}$,这就需要把$W^{\text{NF4}}$反量化成$W^{\text{BF16}}$。
总的来说,QLoRA有一个存储数据类型(通常是4位NormalFloat)和一个计算数据类型(16位BrainFloat)。我们将存储数据类型去量化为计算数据类型以执行前向和反向传播,但我们仅计算使用16位BrainFloat的LoRA参数的权重梯度。
其它
其它内容包括实验和更多分析,当然是说这个方法很好了,我这里就不赘述了。不过补充一下,NF4 Isn’t Information Theoretically Optimal (and that’s Good)认为NF4并不是信息论最优的量化方法,感兴趣的读者可以看看。
- 显示Disqus评论(需要科学上网)