翻译：DeepSeek-V3 Explained 2: DeepSeekMoE

本文翻译DeepSeek-V3 Explained 2: DeepSeekMoE。

这是 DeepSeek-V3 系列的第二篇文章，我们将解释 DeepSeek [1, 2, 3] 模型中的另一项关键架构创新：DeepSeekMoE [4]。

具体来说，我们将解释专家混合（Mixture-of-Experts，MoE）的工作原理、它为何在大型语言模型（LLM）中如此受欢迎以及它所面临的挑战。我们还将讨论专家专长与知识共享之间的权衡，以及 DeepSeekMoE 如何设计以实现更好的权衡。

最棒的是：为了让这些概念更直观，我们将通过一个餐厅的比喻来分解所有内容，通过厨房中厨师的角色来阐明 MoE 中的每个元素。

背景
DeepSeekMoE 架构
- 细粒度专家分割 (Fine-Grained Expert Segmentation)
- 共享专家隔离 (Shared Expert Isolation)
评估
总结
参考文献

背景

LLM 中的 MoE（专家混合）

在大型语言模型（LLM）的背景下，MoE 通常指的是用 MoE 层替换 Transformer 模型中的前馈网络（FFN）层，如下图所示：

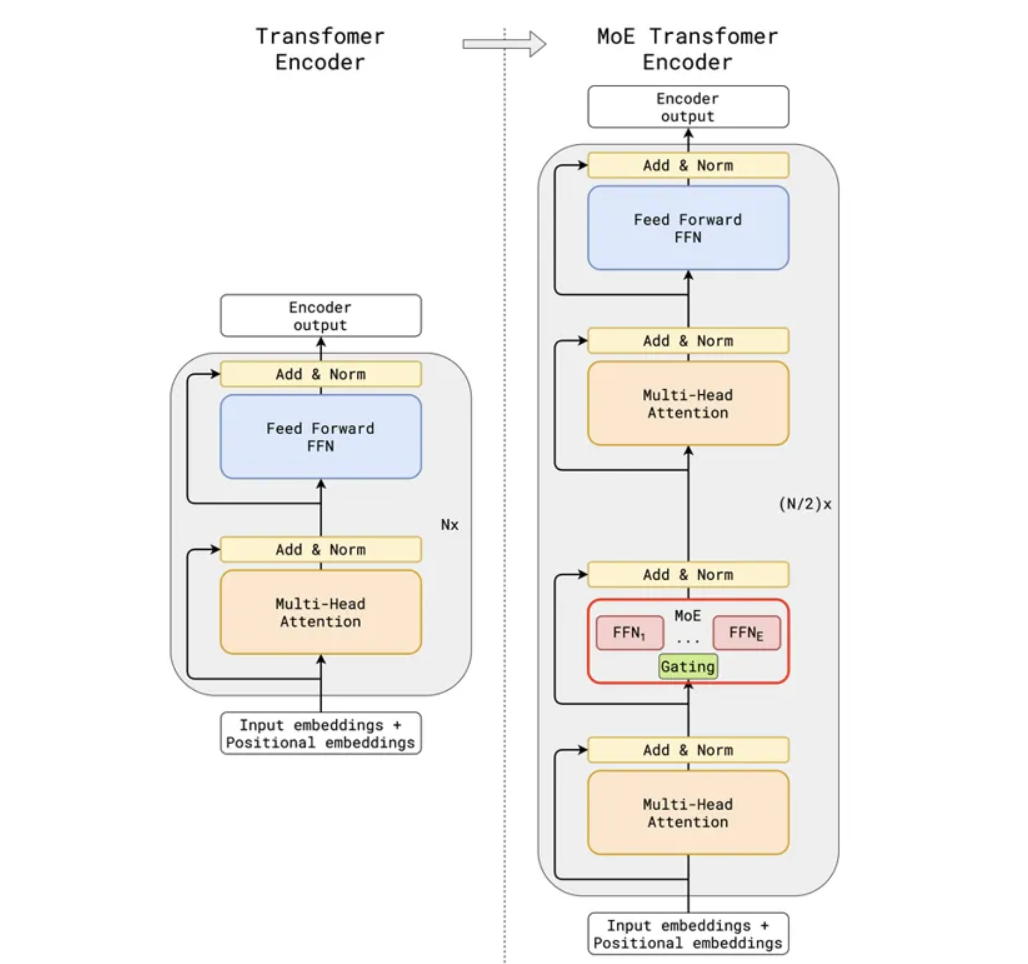图1：MoE 层的示意图。图片来自 GShard 论文 [5]。

更具体地说，左侧展示了 N 个 Transformer 层的堆叠，每个层都包含一个 MHA（多头注意力）子层和一个 FFN（前馈网络）子层。相比之下，右侧展示了 N/2 个 Transformer 层的堆叠，其中较低 Transformer 层中的 FFN 子层已被 MoE 层取代。换句话说，每隔一个 Transformer 层的 FFN 子层都将被 MoE 层替换。在实践中，我们可以在指定的 Transformer 层间隔处用 MoE 替换 FFN。

如果我们进一步探究 MoE 层，会发现它包含一个门控（Gating）操作，后跟一系列 FFN。每个 FFN 都与标准 FFN 子层具有相同的架构。这些 FFN 层在 MoE 中被称为“专家（experts）”，而门控操作则经过训练，用于选择哪个专家应该被激活来处理特定的输入。

MoE 的通用架构可以用以下更正式的方式描述（公式编号沿用 [4]）：

其中：

$u^l_t$ 和 $h^l_t$ 分别是第 $l$ 个 Transformer 层中第 $t$ 个 token 的输入和输出隐藏状态。
$\text{FFN}_i$ 是总共 $N$ 个专家中的第 $i$ 个专家。
$g_{i, t}$ 是通过对 softmax 输出应用 TopK 操作，为给定 token $t$ 和专家 $i$ 获得的门控值。
方程 (5) 中的 $e^l_i$ 通常被称为第 $i$ 个专家的质心（centroid），它可以通过聚合过去所有被路由到第 $i$ 个专家的输入 token 来计算：

\[e_i^l = \frac{\sum_{t \in S_i} g_{i,t} u_t^l}{\sum_{t \in S_i} g_{i,t}}\]

现在我们从 (5) 到 (3) 逆序逐步解释上述方程：

在方程 (5) 中，$u^l_t$ 和 $e^l_i$ 之间的内积衡量了当前输入 token 与过去被路由到第 $i$ 个专家的平均输入 token 的接近程度。直观地讲，如果专家 $i$ 已经处理了大量与当前 token 相似的输入，那么它也应该更擅长处理当前的 token。接着，对这个内积应用 Softmax，将其转换为一个分布。由于我们有 $N$ 个专家，因此每个 token 也会有 $N$ 个 $s_{i, t}$ 值。

在方程 (4) 中，我们对所有的 $s_{i, t}$ 值应用 TopK 操作，生成稀疏的 $g_{i, t}$ 值。

在方程 (3) 中，稀疏的 $g_{i, t}$ 值被用来选择 $K$ 个专家，以计算输出隐藏状态。

换句话说，对于第 $t$ 个 token，总共 $N$ 个专家中只有 $K$ 个会被激活，这导致 $g_{i, t}$ 值是稀疏的，因为 $K$ 通常非常小。通过这种设计，模型中的总可训练参数量会因为额外的 FFN 而增加，但在前向传播过程中，只有一小部分参数会被激活。

这就是为什么我们经常看到带有 MoE 的大型语言模型会将其模型大小描述为“总参数 XX，其中每个 token 激活 YY 参数”，其中 YY 远小于 XX，就像 DeepSeek-V3 的例子：

“它包含 2360 亿总参数，其中每个 token 激活 210 亿参数……”

那么，如果 MoE 会引入更多参数，它的好处是什么呢？

MoE 的优点与挑战

MoE 的一个巨大优势在于它反映了许多具有相似原理的现实场景，因此我们可以利用这些例子来更直观地理解它。

现在想象一下，我们正在为一家中餐和意大利菜都供应的餐厅招聘厨师，我们有两种选择：

方案一： 雇佣一位精通中餐和意大利菜的厨师，让他或她能独立处理每道菜。这类似于一个标准的 Transformer 模型，其中一个单独的 FFN 子层将处理所有输入 token。

方案二： 雇佣多位厨师，每位厨师专门擅长中餐或意大利菜，外加一名主厨，根据厨师的专长将订单分配给他们。这类似于 MoE 方法，其中每位厨师都扮演着专家的角色，而主厨则充当门控机制来选择专家。

通过上述类比，很明显，方案二不仅使招聘更容易，而且可以确保两种菜肴都以更高的质量准备。相比之下，找到一位精通多种菜肴的厨师要困难得多——如果不是不可能的话——而且我们可能不得不牺牲菜肴的质量。

回到我们的 LLM 场景，MoE 的动机部分与规模化假设（scaling hypothesis）有关，即当在大量数据上扩展 LLM 时，会出现涌现能力，这就是为什么我们现在看到 LLM 变得越来越大，例如 GPT 模型已经从 1.17 亿参数扩展到 1750 亿参数。

如果你对 GPT 模型的规模化感兴趣，可以查阅我之前的文章：《理解 ChatGPT 的演变：第二部分 — GPT-2 和 GPT-3》。

然而，并非所有人都有特权以如此规模训练 LLM，而 MoE 提供了一种折衷方案：它允许我们扩大模型规模以增加模型容量，同时通过仅激活每个输入 token 总参数的一小部分来保持训练和推理成本可控。

如 [4] 所示，你可以训练一个 20 亿参数的模型，但只激活 3 亿参数；一个 160 亿参数的模型只激活 28 亿参数；甚至一个 1450 亿参数的模型也只激活 222 亿参数。在每种情况下，一次只有大约 1/7 的总参数被使用，这显著提高了训练和推理效率。

然而，每种设计都有其自身的局限性并带来新的挑战。对于 MoE 而言，其性能严重依赖于门控机制的有效性，因为不能保证它总是将每个输入 token 路由到最优专家，并且可能出现少数专家频繁被激活以处理大多数输入 token，而其他专家则“闲置”，没有接触到足够的训练 token。这通常被称为“专家崩溃（expert collapse）”问题。

这还会导致其他问题，如负载不平衡（load imbalance）（因为大多数输入 token 被路由到一小部分专家）和不稳定性（instability）（当输入 token 被路由到未获得足够任务训练的专家时，结果不佳）。

这就是为什么在 MoE 架构中，我们经常会看到关于负载均衡（load balancing）的大量讨论。

DeepSeekMoE 也提出了一些负载均衡策略，但我们将在本文中重点关注其关键创新，并在下一篇文章中深入探讨负载均衡策略，解释无辅助损失负载均衡（auxiliary-loss-free load balancing）[8]。

知识专长与知识共享

在上述餐厅招聘的例子中，当我们做出招聘决定时，实际上也在权衡知识专长与知识共享：方案一优先选择通才但可能牺牲深度，而方案二则优先选择专长。这种权衡存在于许多现实生活中的组织形式中，比如公司、团队等。

在 MoE 中也存在这种权衡，但方式更为隐性。理论上，每个专家都应该专注于特定的方面，因为只有一部分输入 token 会被路由到每个专家，并且所有专家仍然共享一些共同知识，因为它们共享许多参数。与真实组织的情况不同，很难确定每个单独的专家有多么专业化，以及他们共享知识的程度。

权衡专长和知识共享是 MoE 架构的一个关键设计考量，因为无论是过度专业化还是过度冗余都不是理想的。

在前一种情况下，拥有过度专业化的专家可能导致训练和推理的不稳定性，并且任何次优的路由都可能导致性能不佳。同时，这通常会导致容量利用不足，因为高度专业化的专家只能处理一小部分 token。

在后一种情况下，如果专家变得过于相似，MoE 引入的额外参数将不会带来容量上的成比例增长，这无疑是对有限计算资源的浪费。

在下一节中，我们将看到 DeepSeekMoE 是如何设计来在这两者之间实现更好的权衡的。

DeepSeekMoE 架构

DeepSeekMoE 利用两项关键创新来平衡 MoE 中的知识专长与知识共享，即细粒度专家分割（fine-grained expert segmentation）和共享专家隔离（shared expert isolation）。

图3：DeepSeekMoE 示意图。图片来自 [4]。

细粒度专家分割 (Fine-Grained Expert Segmentation)

DeepSeekMoE 中提出了细粒度专家分割，以促进专家专长化，其背后的直觉非常简单：对于一个输入 token，激活的专家越多，处理该 token 所需的知识就越有可能被分解并由不同的专家获取。

在我们之前的餐厅例子中，这类似于将每位厨师细分为专业的技能，如下图所示。最初，我们有一位厨师负责准备所有中餐，另一位厨师负责所有意大利菜。应用细粒度专家分割后，每种菜肴所需的技能被划分为多个专家，这样我们就会有一组厨师负责中餐，另一组厨师负责意大利菜，每位厨师只需掌握该菜系中的某项特定技能。

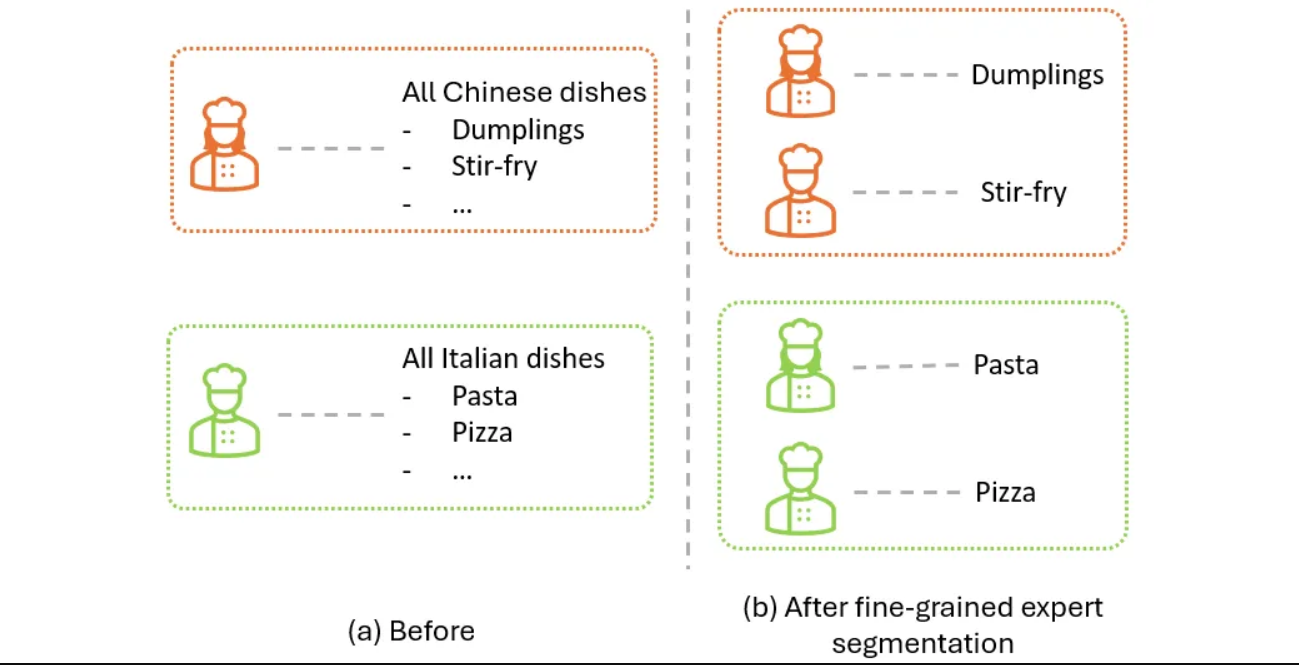图 4：使用餐厅示例说明应用细粒度专家分割前 (a) 和后 (b) 的情况。图片由作者提供。

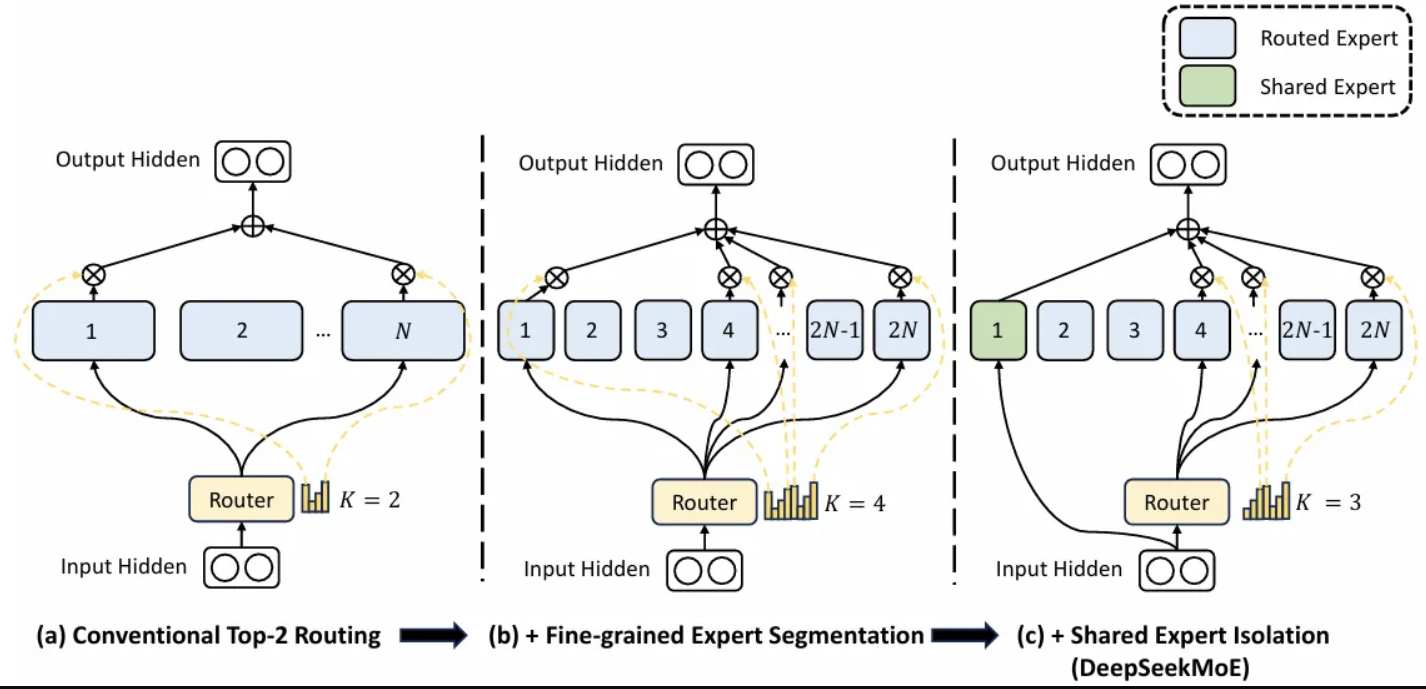
这也在图 3 中得到了说明，其中子图 (a) 中每个输入 token 被路由到 N 个专家中的 2 个，而在 (b) 中，每个 token 将被路由到 2N 个专家中的 4 个。在更一般的情况下，我们可以将专家数量从 N 增加到 mN，同时将每个专家 FFN 的中间隐藏维度减少到 1/m，并为每个输入 token 激活 m 倍的专家。这样，(a) 和 (b) 的总体计算成本将大致保持不变。

尽管作者没有为该策略的有效性提供任何理论证明，但他们确实设计了实验来验证他们的想法，我们将在“评估”部分介绍这些实验。

共享专家隔离 (Shared Expert Isolation)

DeepSeekMoE 提出的另一项技术是隔离一部分共享专家以减少冗余。其背后的直觉是：如果我们保留一些共享专家来学习跨不同任务的通用知识，这可能会让其他专家有更多自由摆脱此类通用知识的束缚，从而减少这些非共享专家之间的冗余。

在我们的餐厅示例中，这类似于将所有厨师进一步分成两组，如下图所示。其中，上半部分所示的第一组厨师负责处理通用的烹饪技能，例如基本的刀工、烹饪技术和调味原则，而第二组的厨师则更专注于他们各自的特色菜肴。

例如，饺子厨师可以只专注于饺子的包法和蒸煮，而无需担心摆盘技巧；意面厨师可以只专注于制作更好的意面，而无需学习切菜技巧。结果是，厨师之间的知识冗余可以减少。

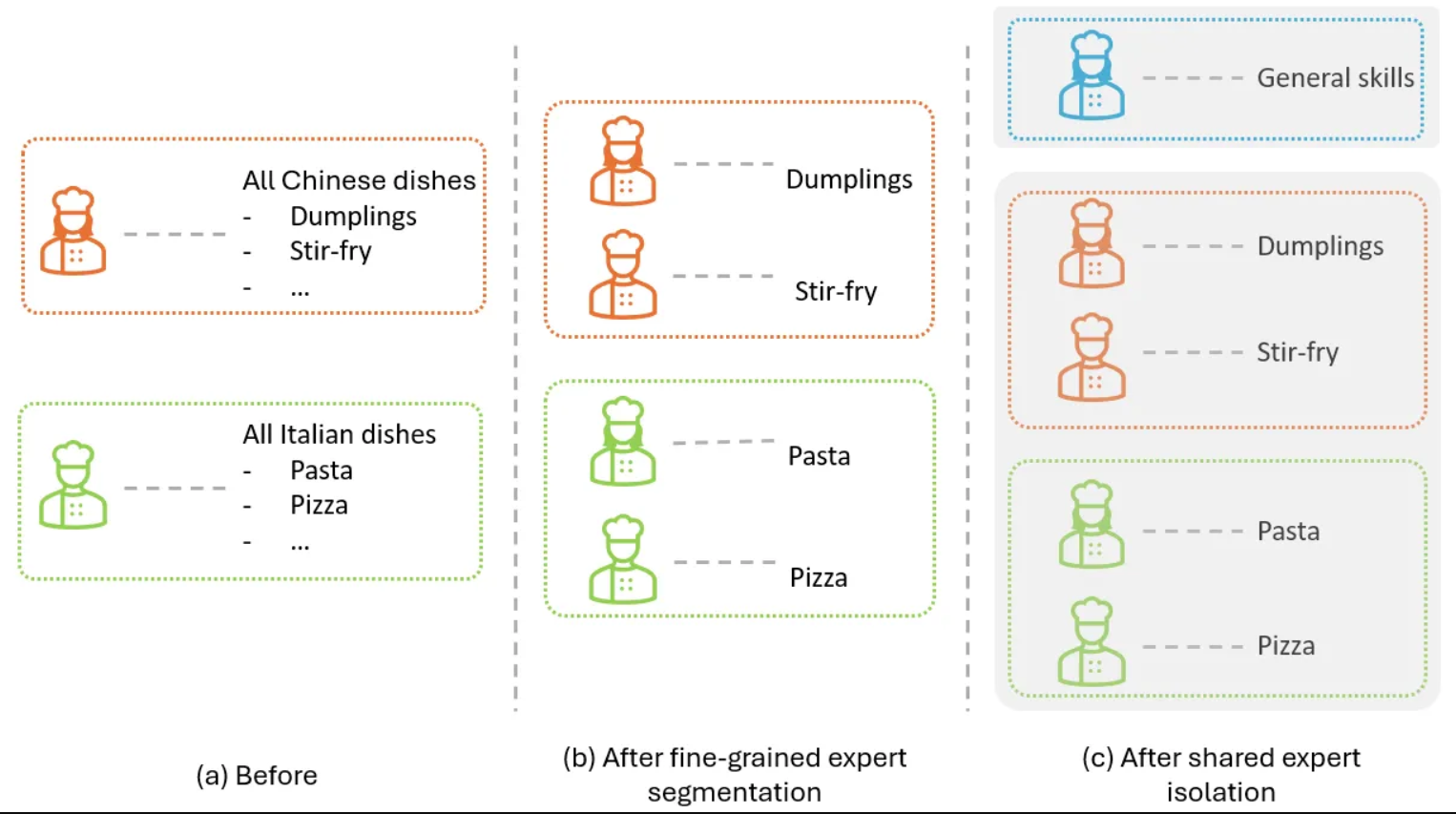图 5：在餐厅示例中，在图 4 的基础上增加共享专家隔离。图片由作者提供。

图 3 (c) 也展示了 DeepSeekMoE 如何实现这一策略：其中一个专家被选定为共享专家（用绿色突出显示），因此所有输入 token 都将直接路由到该专家，而无需经过路由器。同时，激活的专用专家数量从 4 个减少到 3 个，从而使激活的专家总数与图 3 (b) 中的数量保持一致。

综上所述，DeepSeekMoE 架构可以用下图右侧的形式更正式地阐述，我们将其与之前的通用 MoE 进行比较，以突出其区别：

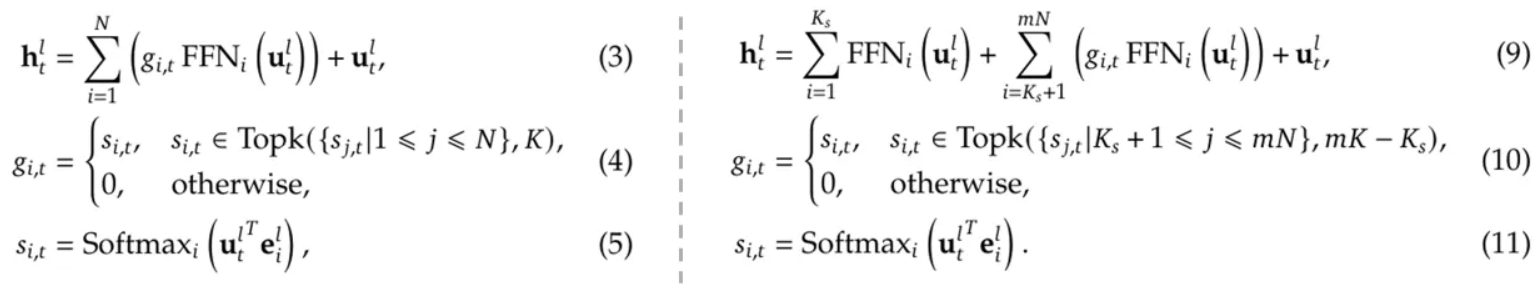图 6：（左）通用 MoE 与（右）DeepSeekMoE。图片由作者根据 [4] 中的公式创建。

其中：

方程 (11) 与之前的方程 (5) 相同。
方程 (10) 类似于方程 (4)，但在这里我们应用 TopK 来从 $(mN - K_s)$ 个专家中选择 $(mK - K_s)$ 个专家，其中 $K_s$ 表示共享专家的数量。
方程 (9) 将方程 (3) 中的第一项拆分为两个子项，分别对应共享专家和路由专家。

同样，原始论文中没有对所提出策略的有效性提供理论证明，但正如我们将在下一节中看到的那样，评估结果确实表明添加共享专家可以提升性能并减少知识冗余。

评估

正如我们之前提到的，尽管这两种策略背后的直觉听起来合理，但作者并未提供任何理论证明来证实它们，这使得我们不清楚它们是否确实能帮助解决专业化与知识共享之间的矛盾，以及它们能帮助到何种程度。

基本上，我们想了解三个核心问题：

DeepSeekMoE 能否取得更好的结果？
细粒度专家分割能否以及在多大程度上促进专业化？
共享专家隔离能否以及在多大程度上减少冗余？

为了理解这些问题，作者精心设计了一系列实验，在此提及它们至关重要。

DeepSeekMoE 能否取得更好的结果？

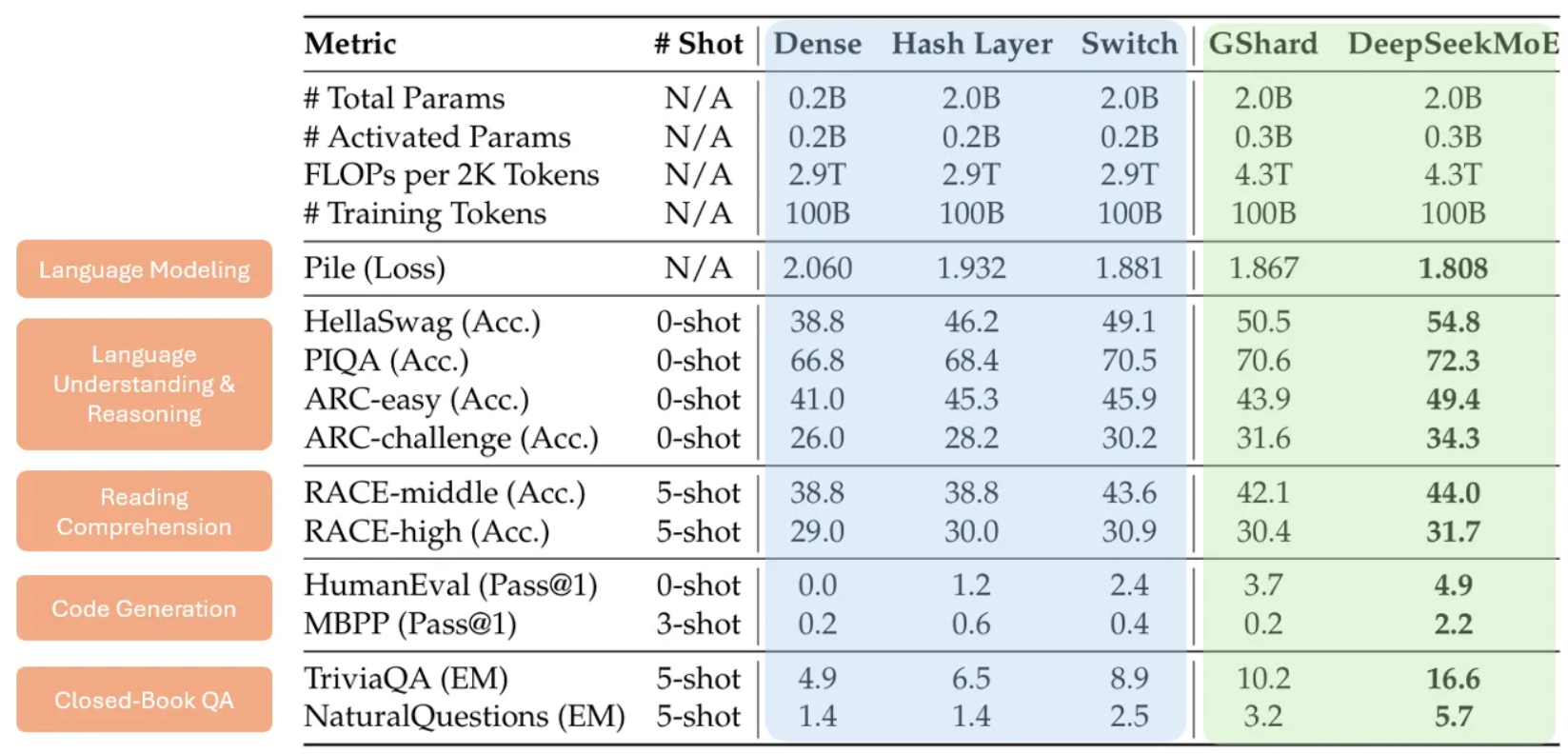
首先，作者考察了他们的方法是否能带来更好的整体性能。为了验证这一点，他们训练了一系列具有可比的总参数/激活参数的模型，并在不同任务上进行评估。他们的主要结果总结在下表中，最佳指标已加粗显示。

图 7：整体性能。图片由作者根据 [4] 中表 1 创建。

有几点值得注意：

蓝色高亮列比较了标准 Transformer (Dense) 与两种 MoE 架构（Hash Layer [6] 和 Switch Transformer [7]），表明在激活参数相当的情况下，MoE 架构可以实现显著更好的性能。
绿色高亮列进一步比较了 DeepSeekMoE 与另一种 MoE 方法 GShard [5]，表明在激活参数相当的情况下，DeepSeekMoE 取得了显著更好的性能。
然而，取得更好的性能并不一定意味着在专业化与知识共享之间取得了更好的权衡，因此我们仍然需要其他实验。

DeepSeekMoE 是否有利于专业化？

直接衡量专家的专业化程度很困难，相反，作者从一个相反的方向设计了一个有趣的实验：禁用一些路由靠前的专家，看看会发生什么。

直观地讲，当专家越专业化时，它们的可替代性就越低，因此，禁用路由靠前的专家应该会对性能产生更大的影响。

更具体地说，他们在 DeepSeekMoE 和 GShard x 1.5 中都进行了禁用路由靠前专家的实验，其中后者作为基线，因为这两种方法在没有专家被禁用时具有可比的 Pile loss（见下图中对应于比例 0 的最左侧点）：

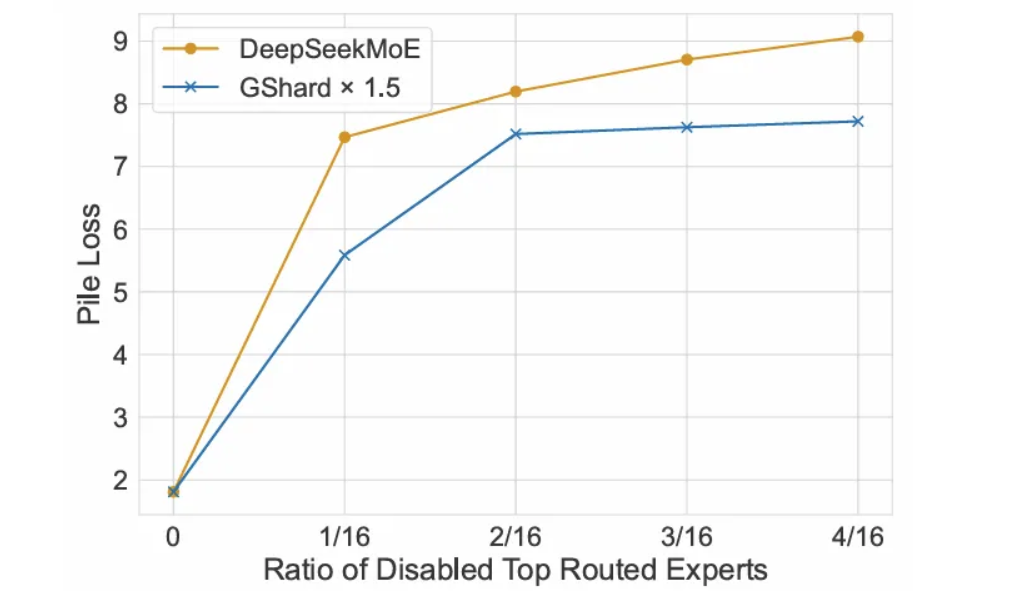图 8：DeepSeekMoE 和 GShard x 1.5 在禁用路由靠前的专家后的 Pile loss。图片来自 [4]。

随着被禁用的路由专家比例的增加，DeepSeekMoE 的 Pile loss 持续升高，这表明 DeepSeekMoE 中的路由专家更加专业化，因此更难被其他专家取代。

DeepSeekMoE 是否减少了知识冗余？

秉持类似的想法，作者还禁用了共享专家并激活了另一个路由专家，以观察共享专家是否可以通过添加额外的路由专家来替代。

结果，他们观察到“Pile loss 显著增加，从 1.808 上升到 2.414”，这证实了共享专家所获得的知识在某种程度上是独一无二的，并且路由专家没有得到充分训练来覆盖那部分知识。换句话说，路由专家更专业化，冗余度更低。

总结

在本文中，我们通过餐厅的例子类比，解释了 DeepSeekMoE，这是 DeepSeek-V2 和 DeepSeek-V3 等 DeepSeek 模型中采用的一项主要架构创新。

更具体地说，我们介绍了 MoE 的通用工作原理、其优点和挑战，以及专家专业化与知识共享之间的权衡。接着，我们解释了 DeepSeekMoE 中的两个关键要素：细粒度专家分割和共享专家隔离。我们还在评估部分讨论了其性能。

我们的主要结论是，DeepSeekMoE 通过促进专家专业化，可以在与通用 MoE 架构相当的计算成本下，取得更好的结果，从而提高计算效率。