负对数似然和交叉熵

目录

• 负对数似然损失
  • 概率视角看模型
  • 负对数似然(Negative Log Likelihood)损失
    • 最大似然准则（Maximum Likelihood Criterion）
    • 最大化对数似然 (Maximizing Log-Likelihood)
    • 最小化负对数似然 (Minimizing Negative Log-Likelihood)
    • 推断 (Inference)
  • 构建损失函数的流程
  • 例子：二分类的负对数似然损失
  • 例子：多类别分类 (Multiclass Classification)
• 交叉熵损失以及它与负对数似然损失的等价关系
• Pytorch里的loss
  • NLLLoss
  • CrossEntropyLoss
    • 参数
    • 形状
    • NLLLoss和CrossEntropyLoss的关系
  • BCELoss
    • 参数
    • 形状
  • BCEWithLogitsLoss
  • BCELoss和两分类的CrossEntropyLoss的关系
    • 区别
    • 等价性
  • 实际使用中的选择建议
  • BCELoss应用与多标签分类
    • 理解多标签分类
    • BCELoss 在多标签分类中的应用
    • 多标签分类例子：电影类型预测
    • 代码示例 (PyTorch)
    • 输出结果解释

负对数似然损失

概率视角看模型

在机器学习里，我们通常认为模型直接根据输入$x$计算一个预测值 $y$。现在我们转换视角，将模型视为计算一个给定输入 $x$ 时，针对所有可能输出 $y$ 的条件概率分布 $P_r(y|x)$。损失函数鼓励每个训练输出 $y_i$ 在由相应输入 $x_i$ 计算得到的分布 $P_r(y_i|x_i)$ 下具有高概率。

比如在下图，我们预测输出的分布。 其中：

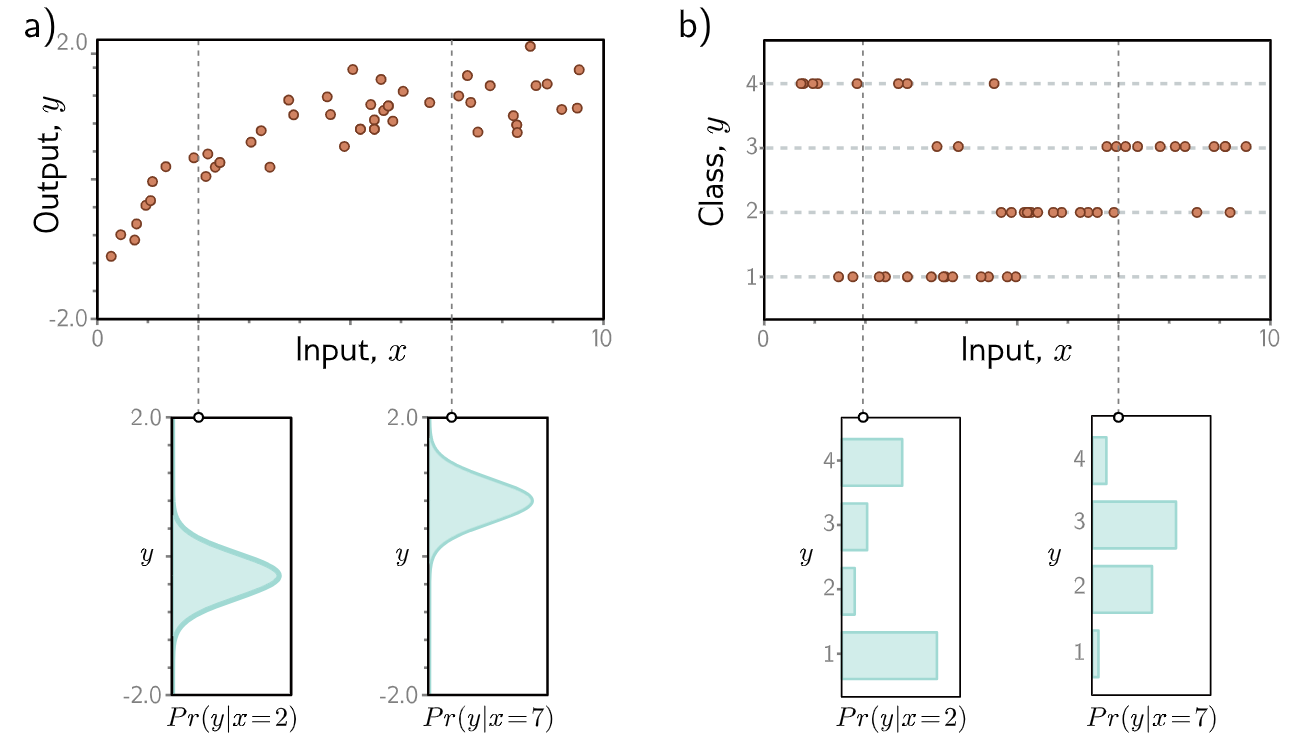
a) 回归任务，目标是根据训练数据 ${x_i, y_i}$（橙色点）从输入 $x$ 预测一个实数值输出 $y$。对于每个输入值 $x$，机器学习模型预测一个关于输出 $y \in \mathbb{R}$ 的概率分布 $P_r(y|x)$（青色曲线显示了 $x = 2.0$ 和 $x = 7.0$ 时的分布）。最小化损失函数对应于最大化训练输出 $y_i$ 在由相应输入 $x_i$ 预测的分布下的概率。

b) 在分类任务中预测离散类别 $y \in {1, 2, 3, 4}$ 时，我们使用离散概率分布，因此模型为 $x_i$ 的每个值预测一个关于 $y_i$ 的四种可能值的不同直方图。

图片来自Understanding Deep Learning

这种视角的转变引出了一个问题：模型 $f[x, \phi]$ 究竟如何适应以计算概率分布？解决方案很简单。首先，我们选择一个在输出域 $y$ 上定义的参数化分布 $P_r(y|\theta)$。然后，我们使用网络来计算该分布的一个或多个参数 $\theta$。

例如，假设预测域是实数集，即 $y \in \mathbb{R}$。在这里，我们可以选择定义在 $\mathbb{R}$ 上的单变量正态分布。该分布由均值 $\mu$ 和方差 $\sigma^2$ 定义，因此 \(\theta = \{\mu, \sigma^2\}\)。机器学习模型可以预测均值 $\mu$，而方差 $\sigma^2$ 则可以被视为一个未知常数。如果二分类或者多分类问题，那么我们可以使用伯努利分布或者分类分布；然后用模型来预测伯努利分布或者分类分布的参数。

负对数似然(Negative Log Likelihood)损失

最大似然准则（Maximum Likelihood Criterion）

模型现在针对每个训练输入 $x_i$ 计算不同的分布参数 $\theta_i = f[x_i, \phi]$。每个观测到的训练输出 $y_i$ 在其对应的分布 $P_r(y_i|\theta_i)$ 下应该具有高概率。因此，我们选择模型参数 $\phi$ 以最大化所有 $I$ 个训练样本的组合概率：

这个组合概率项是参数的似然（likelihood），因此方程1 被称为最大似然准则（maximum likelihood criterion）。

这里我们隐含地做了两个假设。首先，我们假设数据是独立同分布的（identically distributed）（输出 $y_i$ 的概率分布形式对于每个数据点都是相同的）。其次，我们假设给定输入的输出的条件分布 $P_r(y_i|x_i)$ 是独立的（independent），因此训练数据的总似然分解为：

换句话说，我们假设数据是独立同分布（i.i.d.）的。

最大化对数似然 (Maximizing Log-Likelihood)

最大似然准则（方程 5.1）并不是非常实用。每个项 $P_r(y_i|f[x_i, \phi])$ 都可能很小，因此许多这些项的乘积会变得非常微小。用有限精度的算术表示这个量可能会很困难。幸运的是，我们可以等价地最大化似然的对数：

这个对数似然准则之所以等价，是因为对数是一个单调递增函数：如果 $z > z’$，那么 $\log[z] > \log[z’]$，反之亦然（图2）。因此，当我们改变模型参数 $\phi$ 以提高对数似然准则时，我们也同时提高了原始的最大似然准则。这还意味着两个准则的整体最大值必须在同一个位置，所以在这两种情况下，最佳模型参数 $\hat{\phi}$ 是相同的。然而，对数似然准则的实际优势在于它使用项的和而非乘积，因此用有限精度表示它没有问题。

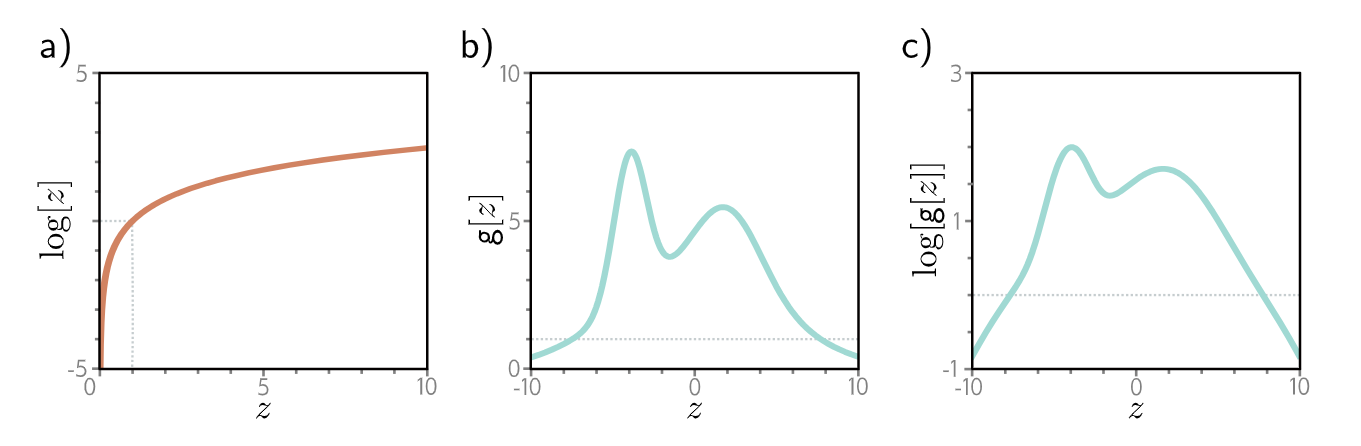图2：a) 对数函数是单调递增的。如果 $z > z’$，那么 $\log[z] > \log[z’]$。因此，任何函数 $g[z]$ 的最大值将与 $\log[g[z]]$ 的最大值处于相同的位置。 b) 函数 $g[z]$。 c) 该函数的对数 $\log[g[z]]$。在对数变换后，$g[z]$ 上所有具有正斜率的位置仍然保持正斜率，而那些具有负斜率的位置仍然保持负斜率。最大值的位置保持不变。

最小化负对数似然 (Minimizing Negative Log-Likelihood)

最后，我们注意到，按照惯例，模型拟合问题通常被框定为最小化损失。为了将最大对数似然准则转换为最小化问题，我们将其乘以负一，从而得到负对数似然准则：

这构成了最终的损失函数 $L[\phi]$。

推断 (Inference)

网络不再直接预测输出 $y$，而是确定 $y$ 的概率分布。当我们进行推断时，通常需要一个点估计而不是一个分布，因此我们返回分布的最大值：

通常可以根据模型预测的分布参数 $\theta$ 找到此表达式。例如，在单变量正态分布中，最大值出现在均值 $\mu$ 处。

构建损失函数的流程

使用最大似然方法为训练数据 ${x_i, y_i}$ 构建损失函数的秘诀如下：

1. 选择一个合适的概率分布 $P_r(y|\theta)$，该分布定义在预测值 $y$ 的域上，并具有分布参数 $\theta$。
2. 设置机器学习模型 $f[x, \phi]$ 来预测这些参数中的一个或多个，因此 $\theta = f[x, \phi]$ 且 $P_r(y|\theta) = P_r(y|f[x, \phi])$。

3. 为了训练模型，找到最小化训练数据集对 ${x_i, y_i}$ 上的负对数似然损失函数（negative log-likelihood loss function）的网络参数 $\hat{\phi}$：

   \[\hat{\phi} = \underset{\phi}{\operatorname{argmin}} \left[ L[\phi] \right] = \underset{\phi}{\operatorname{argmin}} \left[ - \sum_{i=1}^{I} \log \left[ P_r(y_i|f[x_i, \phi]) \right] \right]. \quad (6)\]
4. 为了对新的测试样本 $x$ 执行推断，返回完整的分布 $P_r(y|f[x, \hat{\phi}])$ 或该分布最大值所对应的值。

例子：二分类的负对数似然损失

在二元分类中，目标是将数据 $x$ 分配到两个离散类别中的一个 $y \in \{0, 1\}$。在这种情况下，我们将 $y$ 称为标签。二元分类的例子包括 (i) 从文本数据 $x$ 预测餐厅评论是积极的 ($y = 1$) 还是消极的 ($y = 0$)，以及 (ii) 从 MRI 扫描 $x$ 预测是否存在肿瘤 ($y = 1$) 还是不存在肿瘤 ($y = 0$)。

我们再次遵循第 5.2 节的流程来构建损失函数。首先，我们选择一个定义在输出空间 $y \in \{0, 1\}$ 上的概率分布。一个合适的选择是伯努利分布，它定义在域 $\{0, 1\}$ 上。它有一个单一参数 $\lambda \in [0, 1]$，表示 $y$ 取值为 1 的概率（图 5.6）：

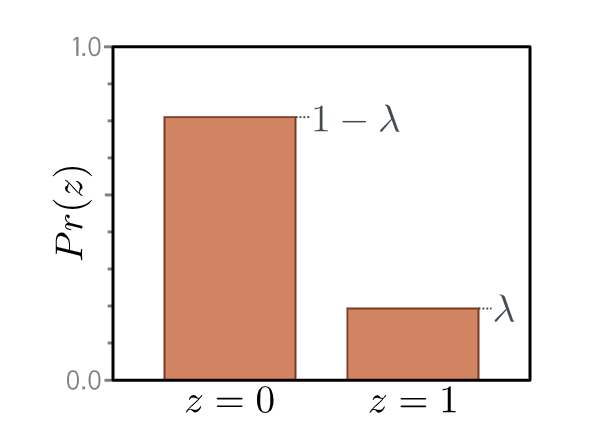伯努利分布定义在域 $z \in {0, 1}$ 上，并且只有一个参数 $\lambda$，该参数表示观测到 $z = 1$ 的概率。因此，观测到 $z = 0$ 的概率是 $1 - \lambda$。

这可以等价地写为：

其次，我们将机器学习模型 $f[x, \phi]$ 设置为预测单个分布参数 $\lambda$。然而，$\lambda$ 只能取值范围在 $[0, 1]$ 内，我们无法保证网络输出会落在这个范围。因此，我们将网络输出通过一个将实数 $\mathbb{R}$ 映射到 $[0, 1]$ 的函数。一个合适的函数是逻辑 S 型函数（logistic sigmoid）（图 5.7）：

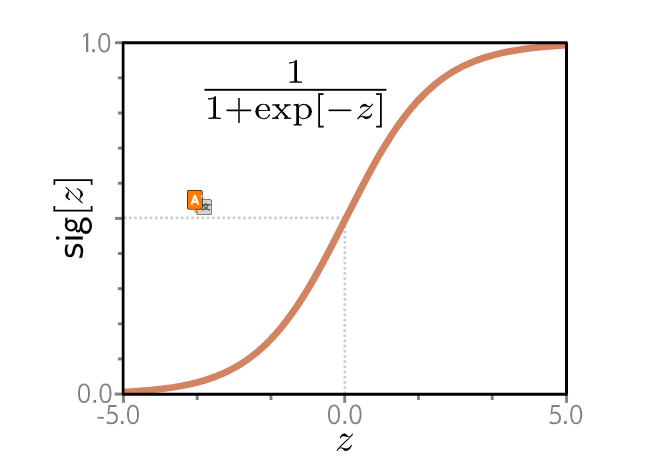逻辑S型函数 (Logistic sigmoid function)。此函数将实数线 $z \in \mathbb{R}$ 映射到 0 到 1 之间的数字，即 $sig[z] \in [0, 1]$。输入为 0 时被映射到 0.5。负数输入被映射到小于 0.5 的数字，正数输入则被映射到大于 0.5 的数字。

因此，我们预测分布参数为 $\lambda = sig[f[x, \phi]]$。现在的似然是：

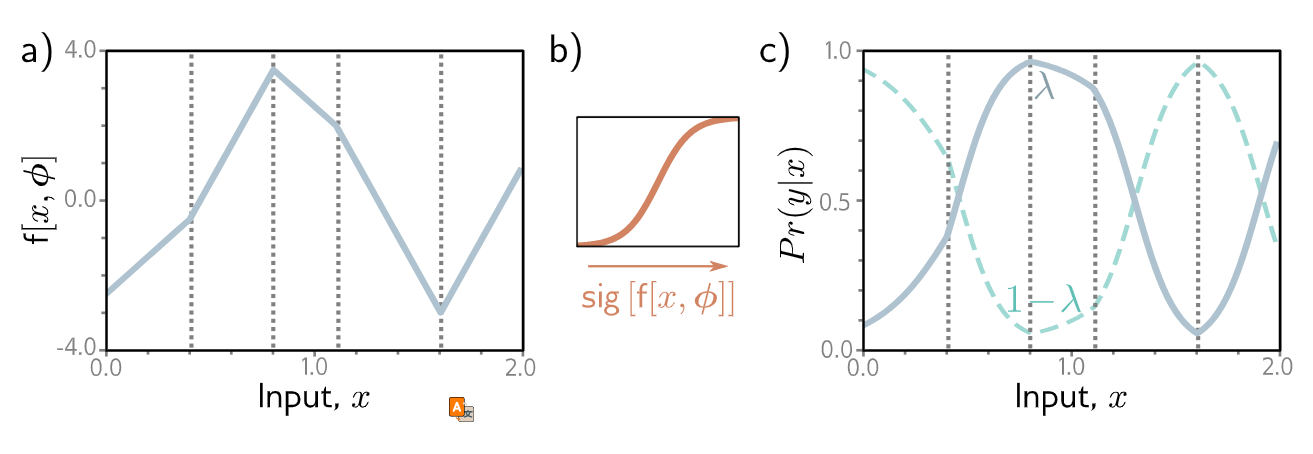二元分类模型。a) 网络输出是一个分段线性函数，它可以取任意实数值。b) 这经过逻辑S型函数转换，将这些值压缩到 [0, 1] 的范围。c) 转换后的输出预测了 $y = 1$ 的概率 $\lambda$（实线）。因此，$y = 0$ 的概率是 $1 - \lambda$（虚线）。对于任意固定的 $x$（垂直切片），我们得到一个类似图 5.6 所示的伯努利分布的两个值。损失函数倾向于那些在与正例 $y_i = 1$ 关联的位置 $x_i$ 产生大 $\lambda$ 值，并在与负例 $y_i = 0$ 关联的位置产生小 $\lambda$ 值的模型参数。

这在图 5.8 中用一个浅层神经网络模型进行了描绘。损失函数是训练集的负对数似然：

由于将在第 5.7 节中解释的原因，这被称为二元交叉熵损失（binary cross-entropy loss）。

经过变换后的模型输出 $sig[f[x, \phi]]$ 预测伯努利分布的参数 $\lambda$。这表示 $y = 1$ 的概率，因此 $1 - \lambda$ 表示 $y = 0$ 的概率。当我们执行推断时，可能需要 $y$ 的点估计，因此如果 $\lambda > 0.5$ 则设置 $y = 1$，否则设置 $y = 0$。

例子：多类别分类 (Multiclass Classification)

多类别分类的目标是将输入数据样本 $x$ 分配到 $K > 2$ 个类别中的一个，即 $y \in \{1, 2, \ldots, K\}$。实际例子包括 (i) 预测手写数字图像 $x$ 中是 $K = 10$ 个数字 $y$ 中的哪一个，以及 (ii) 预测不完整句子 $x$ 后面是 $K$ 个可能单词 $y$ 中的哪一个。

我们再次遵循第 5.2 节的秘诀。首先，我们选择一个定义在预测空间 $y$ 上的分布。在这种情况下，$y \in \{1, 2, \ldots, K\}$，所以我们选择分类分布（categorical distribution） (图 5.9)，它定义在这个域上。它有 $K$ 个参数 $\lambda_1, \lambda_2, \ldots, \lambda_K$，这些参数决定了每个类别的概率：$P_r(y = k) = \lambda_k$。(21) 这些参数被限制在零和一之间，并且它们必须共同和为一，以确保是一个有效的概率分布。

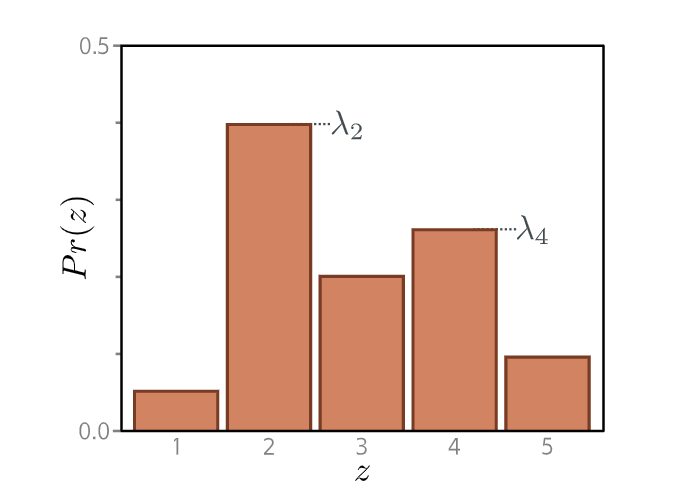分类分布（Categorical distribution）。分类分布将概率分配给 $K > 2$ 个类别，并带有相关的概率 $\lambda_1, \lambda_2, \ldots, \lambda_K$。这里有五个类别，所以 $K=5$。为了确保这是一个有效的概率分布，每个参数 $\lambda_k$ 必须在 $[0, 1]$ 的范围内，并且所有 $K$ 个参数的和必须为一。

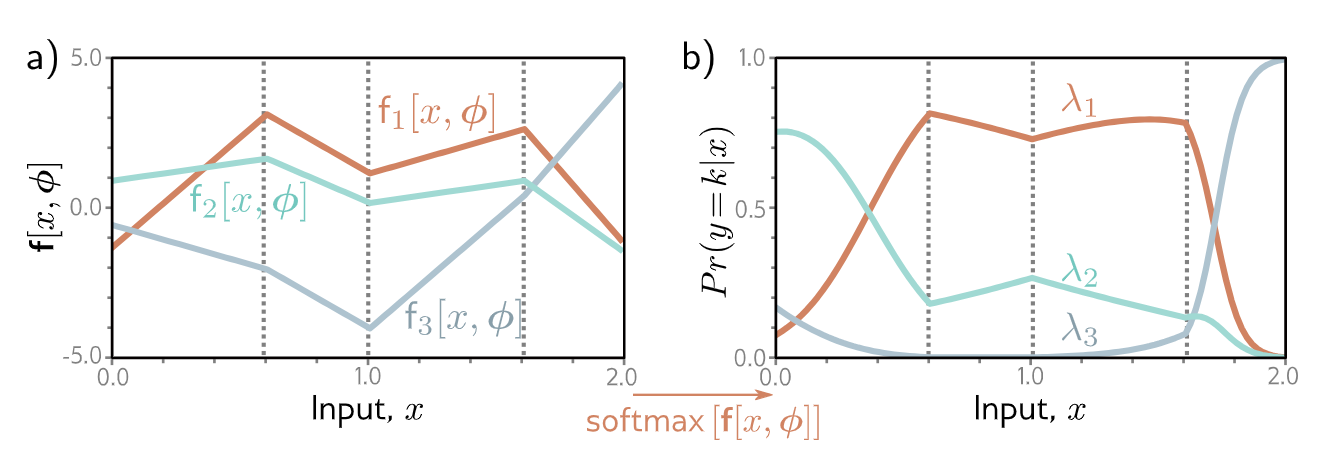$K=3$ 类别的多类别分类。a) 网络有三个分段线性输出，它们可以取任意值。b) 经过 Softmax 函数后，这些输出被约束为非负且和为一。因此，对于给定的输入 $x$，我们计算得到分类分布的有效参数：该图的任何垂直切片都会产生三个和为一的值，这些值将构成类似于图 5.9 中分类分布的柱高。

然后，我们使用一个具有 $K$ 个输出的网络 $f[x, \phi]$ 来从输入 $x$ 计算这些 $K$ 个参数。不幸的是，网络输出不一定会服从上述约束。因此，我们将网络的 $K$ 个输出通过一个函数，该函数确保这些约束得到遵守。一个合适的选择是 Softmax 函数 (图 5.10)。它接收一个长度为 $K$ 的任意向量，并返回一个相同长度的向量，但其中的元素现在在 $[0, 1]$ 范围内且和为一。Softmax 函数的第 $k$ 个输出是：

其中指数函数确保了非负性，分母中的和确保了 $K$ 个数字的和为一。

因此，输入 $x$ 具有标签 $y = k$ 的似然（图 5.10）是：

损失函数是训练数据的负对数似然：

其中 $f_{y_i}[x_i, \phi]$ 和 $f_{k’}[x_i, \phi]$ 分别表示网络的第 $y_i$ 和第 $k’$ 个输出。由于将在第 5.7 节中解释的原因，这被称为多类别交叉熵损失（multiclass cross-entropy loss）。

经过变换后的模型输出代表了一个关于可能类别 $y \in {1, 2, \ldots, K}$ 的分类分布。对于点估计，我们取概率最大的类别 $\hat{y} = \underset{k}{\operatorname{argmax}} \left[ P_r(y = k | f[x, \hat{\phi}]) \right]$。这对应于图 5.10 中对于该 $x$ 值哪条曲线最高。

交叉熵损失以及它与负对数似然损失的等价关系

在本章中，我们开发了最小化负对数似然的损失函数。然而，交叉熵损失（cross-entropy loss）这个术语也普遍存在。在本节中，我们将描述交叉熵损失，并证明它与使用负对数似然是等价的。

注意：这里说的交叉熵损失指的是经验分布(target)是one-hot的情况，也就是说target是一个分类标签的情况。否则如果经验分布是正常的分布，两者是不等价的，在这种情况下，只能使用交叉熵损失。比如在模型蒸馏的时候，我们的target是另外一个模型的概率分布，那么我们只能使用交叉熵损失而无法使用负对数似然损失。

交叉熵损失基于这样的思想：找到参数 $\theta$，以最小化观测数据 $y$ 的经验分布（empirical distribution） $q(y)$ 与模型分布（model distribution） $P_r(y|\theta)$ 之间的距离（图 5.12）。两个概率分布 $q(z)$ 和 $p(z)$ 之间的距离可以使用 Kullback-Leibler (KL) 散度来评估：

现在考虑我们观测到在点集 ${y_i}_{i=1}^I$ 上的经验数据分布。我们可以将其描述为点质量的加权和：

其中 $\delta[\cdot]$ 是狄拉克 delta 函数。我们希望最小化模型分布 $P_r(y|\theta)$ 与该经验分布之间的 KL 散度：

其中第一项消失了，因为它不依赖于 $\theta$。剩余的第二项被称为交叉熵（cross-entropy）。它可以被解释为在考虑到我们已经从另一个分布中了解到的信息后，一个分布中仍然存在的不确定性量。现在，我们代入方程 5.28 中 $q(y)$ 的定义：

第一行中两项的乘积对应于将图 5.12a 中的点质量与图 5.12b 中的分布的对数进行逐点相乘。我们得到的是以数据点为中心的一组有限的加权概率质量。在最后一行中，我们消除了常数缩放因子 $1/I$，因为它不影响最小化的位置。

在机器学习中，分布参数 $\theta$ 由模型 $f[x_i, \phi]$ 计算得出，因此我们有：

这正是第 5.2 节中秘诀的负对数似然准则。

因此，负对数似然准则（源于最大化数据似然）和交叉熵准则（源于最小化模型与经验数据分布之间的距离）是等价的。

Pytorch里的loss

前面介绍了交叉熵损失以及负对数似然损失，下面介绍一下Pytorch里的实现，以及它们各自的适用场景。

NLLLoss

根据文档，NLLLoss用于多类别分类 (Multiclass Classification)，二分类可以看成是一种特殊的多类别分类。

它的构造函数为：

torch.nn.NLLLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean')

它对于训练具有 $C$ 个类别的分类问题非常有用。

如果提供了可选参数 weight，它应该是一个一维张量，为每个类别分配权重。当训练集不平衡时，这尤其有用。

通过前向调用提供的 input 预期包含每个类别的对数概率。input 必须是一个大小为 (minibatch, C) 或 (minibatch, C, d1, d2, ..., dK) 的张量，其中 $K \ge 1$ 适用于 $K$ 维情况。后者对于更高维度的输入很有用，例如计算 2D 图像的逐像素 NLL 损失。

在神经网络中，通过在网络的最后一层添加一个 LogSoftmax 层，可以轻松获得对数概率。如果您不想添加额外的层，可以使用 CrossEntropyLoss 代替。

此损失函数期望的 target 应该是一个介于 $[0, C-1]$ 范围内的类别索引，其中 $C$ 是类别数量；如果指定了 ignore_index，此损失也接受该类别索引（该索引可能不一定在类别范围内）。

未降维（即 reduction 设置为 'none'）的损失可以描述为：

其中 $\mathbf{x}$ 是输入，$\mathbf{y}$ 是目标，$\mathbf{w}$ 是权重，而 $N$ 是批量大小。如果 reduction 不是 'none'（默认为 'mean'），则：

参数

• weight (Tensor, 可选)：赋予每个类别的手动重新缩放权重。如果提供，它必须是一个大小为 $C$ 的张量。否则，它将被视为所有元素均为 1。

• size_average (bool, 可选)：已弃用（请参阅 reduction）。默认情况下，损失在批次中的每个损失元素上进行平均。请注意，对于某些损失，每个样本有多个元素。如果 size_average 字段设置为 False，则损失将改为对每个小批量求和。当 reduce 为 False 时，此参数被忽略。默认值：None。

• ignore_index (int, 可选)：指定一个被忽略且不参与输入梯度的目标值。当 size_average 为 True 时，损失会在非忽略目标上进行平均。

• reduce (bool, 可选)：已弃用（请参阅 reduction）。默认情况下，损失根据 size_average 对每个小批量的观测值进行平均或求和。当 reduce 为 False 时，改为返回每个批次元素的损失，并忽略 size_average。默认值：None。

• reduction (str, 可选)：指定应用于输出的降维方式：'none' | 'mean' | 'sum'。'none'：不应用任何降维；'mean'：取输出的加权平均值；'sum'：对输出求和。注意：size_average 和 reduce 正在被弃用，在此期间，指定这两个参数中的任何一个都将覆盖 reduction。默认值：'mean'。

上面的文档看起来很复杂，我们来看一个例子就清楚了：

>logprobs = torch.tensor([[-0.1, -0.3, 0.2], [-0.1, -0.1, 0.5]])

>loss_fn = nn.NLLLoss(reduction="none")

>loss_fn(logprobs, torch.tensor([1, 2]))
tensor([ 0.3000, -0.5000])

我们假设这是一个三分类的例子，batch_size=2，因此NLLLoss的期望输入是(2,3)。并且每一行表示一个概率分布的对数。注意：这只是它的期望，但是上面的例子我们故意没有达到这个期望。比如第一行的三个值求指数后加起来不等于1，而且第二行还有正值，但是概率最大是1，取log后最大是0。不过NLLLoss并不会检查这些。另外为了便于查看结果，我们设置了reduction为”none”。我们的target是1和2，也就是说第一个样本的标签(Label)是1(代表第二个分类)；第二个样板的标签是2。我们看到NLLLoss最终的结果等价于[-probs[0, 1], -probs[1, 2]]。如果我们看它的代码，它确实就是这样实现的：

loss = -input[torch.arange(batch_size), target] * current_weight

CrossEntropyLoss

根据文档，这个Loss的构造函数是：

CrossEntropyLoss(weight=None, size_average=None, ignore_index=-100, reduce=None, reduction='mean', label_smoothing=0.0)

这个判别准则计算输入 logits 和目标之间的交叉熵损失 (cross entropy loss)。

它在训练 C 类分类问题时非常有用。如果提供可选参数 weight，它应该是一个 1D 的 Tensor，用于为每个类别分配权重。这在训练集不平衡时特别有用。

input 预期包含每个类别的未归一化 logits（通常不需要为正或和为 1）。对于未批量输入，input 必须是大小为 (C) 的 Tensor；对于批量输入，可以是 (minibatch, C) 或 (minibatch, C, d1, d2, …, dK)，其中 K ≥ 1 用于 K 维情况。后一种形式对于更高维度的输入（例如计算 2D 图像的逐像素交叉熵损失）非常有用。

此判别准则预期的 target 应包含以下两种情况之一：

• 类别索引，范围为 [0, C)，其中 C 是类别的数量；如果指定了 ignore_index，此损失也接受此类别索引（此索引不一定在类别范围内）。在这种情况下，未进行归约（即 reduction 设置为 'none'）的损失可以描述为：

  \[\ell(\mathbf{x}, \mathbf{y}) = \mathbf{L} = \{l_1, \ldots, l_N\}^\top, \quad l_n = -w_{y_n} \log \frac{\exp(\mathbf{x}_{n, y_n})}{\sum_{c=1}^C \exp(\mathbf{x}_{n, c})} \cdot \mathbf{1}\{y_n \neq \text{ignore\_index}\}\]

  其中 $\mathbf{x}$ 是输入，$\mathbf{y}$ 是目标，$w$ 是权重，$C$ 是类别数量，$N$ 跨越了 minibatch 维度以及 K 维情况下的 $d_1, \ldots, d_K$。如果 reduction 不是 'none' (默认为 'mean')，则：

  \[\ell(\mathbf{x}, \mathbf{y}) = \begin{cases} \frac{1}{\sum_{n=1}^N w_{y_n} \cdot \mathbf{1}\{y_n \neq \text{ignore\_index}\}} \sum_{n=1}^N l_n, & \text{if reduction}=\text{`mean'}; \\ \sum_{n=1}^N l_n, & \text{if reduction}=\text{`sum'}. \end{cases}\]

  请注意，这种情况等同于对输入应用 LogSoftmax，然后是 NLLLoss。

• 每个类别的概率；当每个 minibatch 项需要多个类别标签时（例如用于混合标签、标签平滑等），这很有用。在这种情况下，未进行归约（即 reduction 设置为 'none'）的损失可以描述为：

  \[\ell(\mathbf{x}, \mathbf{y}) = \mathbf{L} = \{l_1, \ldots, l_N\}^\top, \quad l_n = - \sum_{c=1}^C w_c \log \frac{\exp(\mathbf{x}_{n, c})}{\sum_{i=1}^C \exp(\mathbf{x}_{n, i})} \mathbf{y}_{n, c}\]

  其中 $\mathbf{x}$ 是输入，$\mathbf{y}$ 是目标，$w$ 是权重，$C$ 是类别数量，$N$ 跨越了 minibatch 维度以及 K 维情况下的 $d_1, \ldots, d_K$。如果 reduction 不是 'none' (默认为 'mean')，则：

  \[\ell(\mathbf{x}, \mathbf{y}) = \begin{cases} \frac{1}{N} \sum_{n=1}^N l_n, & \text{if reduction}=\text{`mean'}; \\ \sum_{n=1}^N l_n, & \text{if reduction}=\text{`sum'}. \end{cases}\]

注意

当 target 包含类别索引时，此判别准则的性能通常更好，因为这允许进行优化计算。仅当每个 minibatch 项的单个类别标签限制性过大时，才考虑将 target 作为类别概率提供。

参数

• weight (Tensor, 可选)：分配给每个类别的手动重新缩放权重。如果给出，必须是大小为 C 的 Tensor，并且数据类型为浮点型。
• size_average (bool, 可选)：已废弃（参见 reduction）。默认情况下，损失在批次中的每个损失元素上取平均值。请注意，对于某些损失，每个样本有多个元素。如果字段 size_average 设置为 False，则损失改为对每个 minibatch 求和。当 reduce 为 False 时被忽略。默认值：True。
• ignore_index (int, 可选)：指定一个将被忽略且不计入输入梯度的目标值。当 size_average 为 True 时，损失对未被忽略的目标取平均值。请注意，ignore_index 仅适用于目标包含类别索引的情况。
• reduce (bool, 可选)：已废弃（参见 reduction）。默认情况下，损失根据 size_average 对每个 minibatch 的观测值进行平均或求和。当 reduce 为 False 时，返回每个批次元素的损失，并忽略 size_average。默认值：True。

• reduction (str, 可选)：指定应用于输出的归约方式：'none'

  'mean'

  'sum'。

  • 'none'：不应用任何归约。
  • 'mean'：取输出的加权平均值。
  • 'sum'：对输出求和。 注意：size_average 和 reduce 正在被废弃，同时，指定这两个参数中的任何一个都将覆盖 reduction。默认值：'mean'。
• label_smoothing (float, 可选)：一个介于 [0.0, 1.0] 之间的浮点数。指定计算损失时的平滑量，其中 0.0 表示不进行平滑。目标将成为原始真实值和均匀分布的混合，如《Rethinking the Inception Architecture for Computer Vision》中所述。默认值：0.0。

形状

• Input：形状为 (C)、(N, C) 或 (N, C, d1, d2, …, dK)，其中 K ≥ 1 用于 K 维损失的情况。
• Target：
  • 如果包含类别索引，形状为 ()、(N) 或 (N, d1, d2, …, dK)，其中 K ≥ 1 用于 K 维损失的情况，每个值应介于 [0, C) 之间。使用类别索引时，目标数据类型必须为 long。
  • 如果包含类别概率，目标必须与输入形状相同，并且每个值应介于 [0, 1] 之间。这意味着使用类别概率时，目标数据类型必须为 float。
• Output：如果 reduction 为 'none'，形状为 ()、(N) 或 (N, d1, d2, …, dK)，其中 K ≥ 1 用于 K 维损失的情况，具体取决于输入的形状。否则，为标量。

其中：

• C = 类别数量
• N = 批次大小

例子：

# Example of target with class indices
loss = nn.CrossEntropyLoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5)
output = loss(input, target)
output.backward()
# Example of target with class probabilities
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5).softmax(dim=1)
output = loss(input, target)
output.backward()

NLLLoss和CrossEntropyLoss的关系

前面已经说过，如果target是分类的索引，也就是one-hot的概率分布，那么CrossEntropyLoss等价于对logits应用LogSoftmax变成对数概率后，然后应用NLLLoss。

如果target是正常的概率分布，比如上面的例子中target是一个普通的概率分布(torch.randn(3, 5).softmax(dim=1))，那么就无法用NLLLoss来实现。

用一句话概括：nn.CrossEntropyLoss 等价于 nn.LogSoftmax 加上 nn.NLLLoss。

由于 CrossEntropyLoss 已经包含了 LogSoftmax 这一步，所以在大多数标准的分类任务中，你通常不需要单独使用 NLLLoss。直接使用 CrossEntropyLoss 更方便，也更推荐，因为它能更好地处理数值稳定性问题。

然而，在以下特定情况下，你可能需要单独使用 NLLLoss：

1. 你的模型输出已经经过 LogSoftmax 处理：

   • 如果你在模型设计的最后一层明确地使用了 nn.LogSoftmax（或者 torch.log_softmax 函数），那么你的模型的输出已经是对数概率了。
   • 在这种情况下，为了避免重复应用 LogSoftmax（这会导致错误或不必要的操作），你应该直接使用 nn.NLLLoss 来计算损失。
   • 例子：

     import torch
     import torch.nn as nn
     import torch.nn.functional as F
     
     # 假设模型的输出是原始 logits
     logits = torch.randn(4, 10) # batch_size=4, num_classes=10
     targets = torch.randint(0, 10, (4,)) # 真实标签
     
     # 情况1：使用 CrossEntropyLoss (推荐，直接处理 logits)
     criterion_ce = nn.CrossEntropyLoss()
     loss_ce = criterion_ce(logits, targets)
     print(f"CrossEntropyLoss: {loss_ce.item()}")
     
     # 情况2：手动应用 LogSoftmax，然后使用 NLLLoss (等价于情况1)
     log_probs = F.log_softmax(logits, dim=1) # 手动应用LogSoftmax
     criterion_nll = nn.NLLLoss()
     loss_nll = criterion_nll(log_probs, targets)
     print(f"NLLLoss after manual LogSoftmax: {loss_nll.item()}")
     
     # 结果会非常接近或相同（浮点误差可能导致微小差异）
     

2. 你需要对 LogSoftmax 和 NLLLoss 之间的过程进行干预或自定义：

   • 如果你需要在计算对数概率之后、计算损失之前，对这些对数概率进行一些额外的处理（例如，某些复杂的注意力机制，或者需要访问对数概率本身以进行其他计算），那么你可能需要分别使用 LogSoftmax 和 NLLLoss。

另外前面也说过，NLLLoss的target只能是label，而不能是概率分布。如果我们需要target也是一个分布，比如模型蒸馏的时候，target是来自teacher的概率分布，而不是hard的label，那么就只能用CrossEntropyLoss，比如：

# 教师模型输出的概率分布（非one-hot）
teacher_probs = torch.tensor([[0.1, 0.7, 0.2], [0.3, 0.2, 0.5]])

logits = torch.tensor([[1.0, 2.0, 3.0],[1.0, 1.2, 1.3]])
# 学生模型的log概率输出
student_log_probs = nn.LogSoftmax(dim=1)(logits)

# 用KL散度等价形式：
loss = -torch.sum(teacher_probs * student_log_probs) / teacher_probs.size(0)

loss_ce = nn.CrossEntropyLoss()(logits, teacher_probs)  

#loss_nll = nn.NLLLoss()(student_log_probs, teacher_probs)# 报错！

BCELoss

根据文档，BCELoss的构造函数为：

torch.nn.BCELoss(weight=None, size_average=None, reduce=None, reduction='mean')

此准则用于衡量目标值和输入概率之间的二元交叉熵 (Binary Cross Entropy)。

未进行归约（即 reduction 设置为 'none'）的损失可描述为：

其中 $N$ 是批次大小。如果 reduction 不是 'none'（默认为 'mean'），则：

这常用于衡量例如自编码器中重构误差。请注意，目标值 $y$ 应该是介于 0 和 1 之间的数字。

需要注意的是，如果 $x_n$ 为 0 或 1，上述损失方程中的一个对数项在数学上将是未定义的。PyTorch 选择将 $\log(0)$ 设为 $-\infty$，因为 $\lim_{x \to 0} \log(x) = -\infty$。然而，损失方程中存在无限项会带来一些不良后果。

首先，如果 $y_n=0$ 或 $(1-y_n)=0$，我们就会出现 0 乘以无穷大的情况。其次，如果损失值为无穷大，我们的梯度中也会出现无穷大项，因为 $\lim_{x \to 0} \frac{d}{dx} \log(x) = \infty$。这将导致 BCELoss 的反向传播方法对 $x_n$ 而言是非线性的，并且将其用于线性回归等任务将不再直接。

我们的解决方案是 BCELoss 会将其对数函数的输出限制在大于或等于 -100。这样，我们总能得到有限的损失值和线性的反向传播方法。

参数

• weight (Tensor, 可选)：一个手动缩放的权重，应用于每个批次元素的损失。如果给定，必须是大小为 nbatch 的 Tensor。
• size_average (bool, 可选)：已弃用（请参阅 reduction）。默认情况下，损失在批次中的每个损失元素上取平均值。请注意，对于某些损失，每个样本有多个元素。如果 size_average 字段设置为 False，则损失将改为对每个小批量求和。当 reduce 为 False 时忽略。默认值：True。
• reduce (bool, 可选)：已弃用（请参阅 reduction）。默认情况下，损失根据 size_average 对每个小批量的观察值进行平均或求和。当 reduce 为 False 时，将返回每个批次元素的损失，并忽略 size_average。默认值：True。
• reduction (str, 可选)：指定应用于输出的归约方式：'none' | 'mean' | 'sum'。
  • 'none'：不应用任何归约。
  • 'mean'：输出的总和将除以输出中的元素数量。
  • 'sum'：输出将被求和。 注意：size_average 和 reduce 正在弃用中，在此期间，指定这两个参数中的任何一个都将覆盖 reduction。默认值：'mean'。

形状

• Input：(∗)，其中 ∗ 表示任意数量的维度。
• Target：(∗)，与输入具有相同的形状。
• Output：标量。如果 reduction 为 'none'，则为 (∗)，与输入具有相同的形状。

例子：

m = nn.Sigmoid()
loss = nn.BCELoss()
input = torch.randn(3, 2, requires_grad=True)
target = torch.rand(3, 2, requires_grad=False)
output = loss(m(input), target)
output.backward()

注意：如果input是0或者1，那么会出现$\log -\infty$，pytorch的做法是把它变成-100。比如下面的例子：

loss = nn.BCELoss()
loss(torch.tensor([1.0]), torch.tensor([0.5]))
tensor(50.)

BCEWithLogitsLoss

BCEWithLogitsLoss和BECLoss的区别在于：BECLoss的输入已经是概率了，而BCEWithLogitsLoss的输入是没有经过sigmoid的logits。所以BCEWithLogitsLoss逻辑上等价于先对输入进行sigmoid，然后再计算log概率。但是在实现的时候这个损失函数在内部集成了 Sigmoid 激活函数，直接接收模型的原始 logits（即未经过 Sigmoid 的输出）。这样做的好处是数值更稳定，并且可以利用 “log-sum-exp trick” 进行优化计算。

BCELoss和两分类的CrossEntropyLoss的关系

对于二分类问题，BCELoss和CrossEntropyLoss都可以使用，从数学上它们是等价的。但是使用它们时有一些区别。

区别

BCELoss期望的模型的输出(它的输入)是经过 Sigmoid 激活函数处理后的概率值，介于 0 到 1 之间。通常，模型最后一层会是一个单一神经元，输出一个值，然后通过 Sigmoid 转换为概率。

CrossEntropyLoss期望的模型输出 (它的输入)是未经 Softmax 激活函数处理的原始 logits。如果用于二分类，模型最后一层通常输出两个值，分别代表两个类别的得分。

等价性

从数学上讲，当 CrossEntropyLoss 应用于只有两个类别的问题时，它的计算方式与 BCELoss (结合 Sigmoid) 是等价的。

具体来说：

• BCELoss + Sigmoid: * 模型输出一个 logit $z$。
  • 通过 Sigmoid 转换为概率 $p = \sigma(z) = \frac{1}{1 + e^{-z}}$。
  • 然后使用 BCELoss 计算 $-(y \log p + (1-y) \log (1-p))$。
• CrossEntropyLoss + Softmax (2类):
  • 模型输出两个 logits $z_0, z_1$。
  • 通过 Softmax 转换为概率 $p_0 = \frac{e^{z_0}}{e^{z_0} + e^{z_1}}$, $p_1 = \frac{e^{z_1}}{e^{z_0} + e^{z_1}}$。
  • 假设真实标签是 $y \in \{0, 1\}$，损失计算为 $- (y \log p_1 + (1-y) \log p_0)$（这里为了与 BCELoss 形式对应，将 $p_0$ 视为 $1-p_1$）。
  • 如果你将 $z_0 = 0$（通常通过将一个 logits 值固定为 0 来实现，或者理解为相对值），那么 $p_1 = \frac{e^{z_1}}{e^0 + e^{z_1}} = \frac{e^{z_1}}{1 + e^{z_1}} = \sigma(z_1)$。此时，CrossEntropyLoss 的形式就等价于 BCELoss。

实际使用中的选择建议

尽管两者在数学上可以等价，但在实践中，通常会根据模型输出的形状和预期来选择：

1. 推荐使用 nn.BCEWithLogitsLoss 用于二分类。
   • 当你的模型最后一层输出一个值（代表正类的 logit）时，这是最直接、数值最稳定的选择。
   • 它内部处理了 Sigmoid 转换，所以你直接传入原始 logits 即可。
2. 使用 nn.CrossEntropyLoss 用于二分类也可以，但需要注意模型输出的形状。
   • 你的模型最后一层需要输出两个值（对应两个类别）。
   • 它内部处理了 Softmax 转换，所以你也直接传入原始 logits。
   • 尽管可以用于二分类，但通常认为它更适合于多分类问题。

BCELoss应用与多标签分类

理解多标签分类

首先，我们需要区分多分类 (Multi-class Classification) 和多标签分类 (Multi-label Classification)：

• 多分类： 每个样本只属于一个类别。例如，一张图片是猫、狗或鸟，但绝不可能是猫又是狗。这种问题通常用 CrossEntropyLoss。
• 多标签分类： 每个样本可以同时属于多个类别。例如，一部电影可以同时被标记为“动作片”、“科幻片”和“冒险片”。一张图片中可能同时包含“猫”和“狗”。

在多标签分类中，对于每个样本，我们模型需要对每个可能的标签独立地进行二元判断（是/否）。

BCELoss 在多标签分类中的应用

由于每个标签的预测都是一个独立的二元分类问题，因此 BCELoss 非常适合处理多标签分类任务。

具体来说，如果一个样本有 $L$ 个可能的标签，那么模型会为这个样本生成 $L$ 个预测值，每个值对应一个标签的“存在”概率。BCELoss 会独立地计算每个标签的二元交叉熵损失，然后将这些损失加起来（或平均）作为总损失。

通常，我们不会直接使用 nn.BCELoss，而是使用其更稳定和方便的变体：nn.BCEWithLogitsLoss。

多标签分类例子：电影类型预测

假设我们要构建一个模型，根据电影的某些特征（例如剧情描述、演员等）来预测它所属的类型标签。一部电影可能同时属于多个类型（如动作、科幻、喜剧）。

场景设定：

• 电影数量 (Batch Size)： 4 部电影
• 电影类型数量 (Number of Labels)： 5 种类型，分别是：
  • 0: 动作 (Action)
  • 1: 科幻 (Sci-Fi)
  • 2: 喜剧 (Comedy)
  • 3: 恐怖 (Horror)
  • 4: 爱情 (Romance)

模型输出 (Input Logits)：

模型的最后一层会有 5 个神经元（对应 5 种电影类型），输出原始的 logits。每个 logit 代表模型对该类型存在的信心。

例如，对于第一部电影，模型可能会输出 [2.5, -1.0, 0.8, -3.0, 1.5]。这些是原始分数，不是概率。

真实标签 (Target)：

由于是多标签分类，每部电影的真实标签是一个多热 (multi-hot) 编码向量。向量的长度与类型数量相同，如果某个类型存在，则对应位置为 1，否则为 0。

例如：

• 电影 A：动作片，科幻片 –> [1, 1, 0, 0, 0]
• 电影 B：喜剧片，爱情片 –> [0, 0, 1, 0, 1]
• 电影 C：动作片，恐怖片 –> [1, 0, 0, 1, 0]
• 电影 D：只有科幻片 –> [0, 1, 0, 0, 0]

代码示例 (PyTorch)

import torch
import torch.nn as nn
import torch.nn.functional as F

# 1. 定义模型输出 (Logits) 和真实标签 (Multi-hot)

# 假设这是一个神经网络模型的最后一层输出，未经过Sigmoid激活
# 形状: (batch_size, num_labels)
# 这些是原始的 logits，代表模型对每个标签存在的“信心分数”
model_output_logits = torch.tensor([
    [ 2.5, -1.0,  0.8, -3.0,  1.5],  # 电影 A 的 logits
    [-0.5,  1.2,  2.0, -0.8,  1.8],  # 电影 B 的 logits
    [ 1.0, -2.0, -1.5,  2.5, -0.3],  # 电影 C 的 logits
    [-1.2,  3.0, -0.7, -1.0, -2.5]   # 电影 D 的 logits
], dtype=torch.float32)

# 真实标签，使用 multi-hot 编码
# 形状: (batch_size, num_labels)
# 1表示该标签存在，0表示不存在
true_labels = torch.tensor([
    [1., 1., 0., 0., 0.],  # 电影 A: 动作, 科幻
    [0., 0., 1., 0., 1.],  # 电影 B: 喜剧, 爱情
    [1., 0., 0., 1., 0.],  # 电影 C: 动作, 恐怖
    [0., 1., 0., 0., 0.]   # 电影 D: 科幻
], dtype=torch.float32)

# 2. 创建 BCEWithLogitsLoss 损失函数
# BCEWithLogitsLoss 会在内部应用 Sigmoid
loss_criterion = nn.BCEWithLogitsLoss()

# 3. 计算损失
loss = loss_criterion(model_output_logits, true_labels)

print(f"计算出的 BCELoss (均值): {loss.item()}")

# 4. 理解内部机制（可选，BCEWithLogitsLoss 已自动处理）

# a. 手动将 logits 转换为概率 (Sigmoid)
predicted_probabilities = torch.sigmoid(model_output_logits)
print("\n模型预测的概率 (Sigmoid 激活后):")
print(predicted_probabilities)

# b. 手动计算每个标签的二元交叉熵损失，并求平均
# 这是一个概念性演示，实际使用 BceWithLogitsLoss 即可
manual_bce_loss_elements = - (true_labels * torch.log(predicted_probabilities) +
                              (1 - true_labels) * torch.log(1 - predicted_probabilities))

print("\n每个样本每个标签的单独BCELoss贡献:")
print(manual_bce_loss_elements)

# 将所有损失贡献求平均 (BCEWithLogitsLoss默认reduction='mean')
mean_manual_bce_loss = torch.mean(manual_bce_loss_elements)
print(f"\n手动计算的平均 BCELoss: {mean_manual_bce_loss.item()}")

# 可以看到 loss.item() 和 mean_manual_bce_loss.item() 非常接近
# 因为 BCEWithLogitsLoss 在内部做了更稳定的 log-sigmoid 计算

输出结果解释

计算出的 BCELoss (均值): ... 将是所有电影所有标签的平均损失。

在幕后，BCEWithLogitsLoss 对 model_output_logits 中的每个元素（即每个电影的每个类型预测）和 true_labels 中对应的每个元素独立地应用二元交叉熵计算。然后，如果 reduction 参数为 'mean'（默认值），它将所有这些独立计算的损失加起来并求平均值。

这个例子清晰地展示了 BCELoss (或更常用的 BCEWithLogitsLoss) 如何通过将多标签分类问题分解为多个独立的二元分类问题，并为每个问题计算损失，从而有效处理多标签分类任务。

• ← Previous Post
• Next Post →