本文介绍AlphaGoZero的原理。更多文章请点击深度学习理论与实战:提高篇。
目录
之前介绍的AlphaGo虽然能够战胜人类世界冠军,但是会使用人类职业棋手的棋谱来训练Policy Network,而且在MCTS的rollout时的Rollout Policy和Tree Policy都使用了大量启发式的规则,这些规则是和游戏相关的。而AlphaGo Zero可以完全不使用任何人类的棋谱,完全通过自对弈(self play)的强化学习就可以达到超过AlphaGo的水平。它唯一利用的知识就是围棋的规则,并且抛弃了AlphaGo里MCTS的Rollout,直接用神经网络来预测一个叶子节点的Value,并且把Policy Network和Value Network合二为一,使得模型更加简单。令人惊奇的是,完全自对弈学到的模型只是训练了3天(当然借助了Google TPU集群的超强计算力)就超过了AlphaGo Master(战胜李世石的版本之后的另一个更强版本),战绩是100比0!
AlphaGo Zero的意义在于它是一种通用的(至少对于完全信息(Perfect Information)的博弈)方法,从而理论上可以推广到任意的博弈游戏里。事实也确实如此!后面我们会介绍AlphaZero,它把这种方法推广到象棋等其它棋类游戏。
基本原理
AlphaGo Zero只有一个网络$f_\theta$,它的参数是$\theta$。它的输入是当前局面和之前历史局面的原始表示s,它的输出是模型预测的可能走法的概率和这个局面的Value(可以认为当前局面的胜率)。$(\textbf{p},v)=f_\theta(s)$。其中向量$\textbf{p}$表示当前局面每个合法走法的概率,$p_a=Pr(a \vert s)$。而v是一个数值,范围是[-1,1],表示当前玩家的胜率。和AlphaGo的网络结构不同,AlphaGo Zero使用了更先进的残差网络结构、Batch Norm和ReLU激活函数,更详细的网络结构后面我们会介绍。
这个网络没有任何监督数据,完全是通过自博弈学习出来的。一开始是随机的参数,从而是随机的策略,然后用这个策略去自对弈,然后用对弈的结果来训练新的模型从而得到更好的策略。
在自对弈的过程中,对于每一个局面s,AlphaGo Zero都会用当前网络$f_\theta$来指导MCTS的搜索。MCTS会输出每种走法的概率$\pi$,和模型预测的走法相比,经过MCTS搜索得到的走法概率更加准确,因为它往前看了很多步。MCTS得到的概率会用来重新训练网络,使得它能够更好的预测$Pr(a \vert s)$。这可以看成是一种Policy Improvement。同时在搜索的过程中使用这个策略来指导,然后用游戏结束的得分z来计算每个走法(action)的Q(s,a),这可以看成是Policy Evaluation。
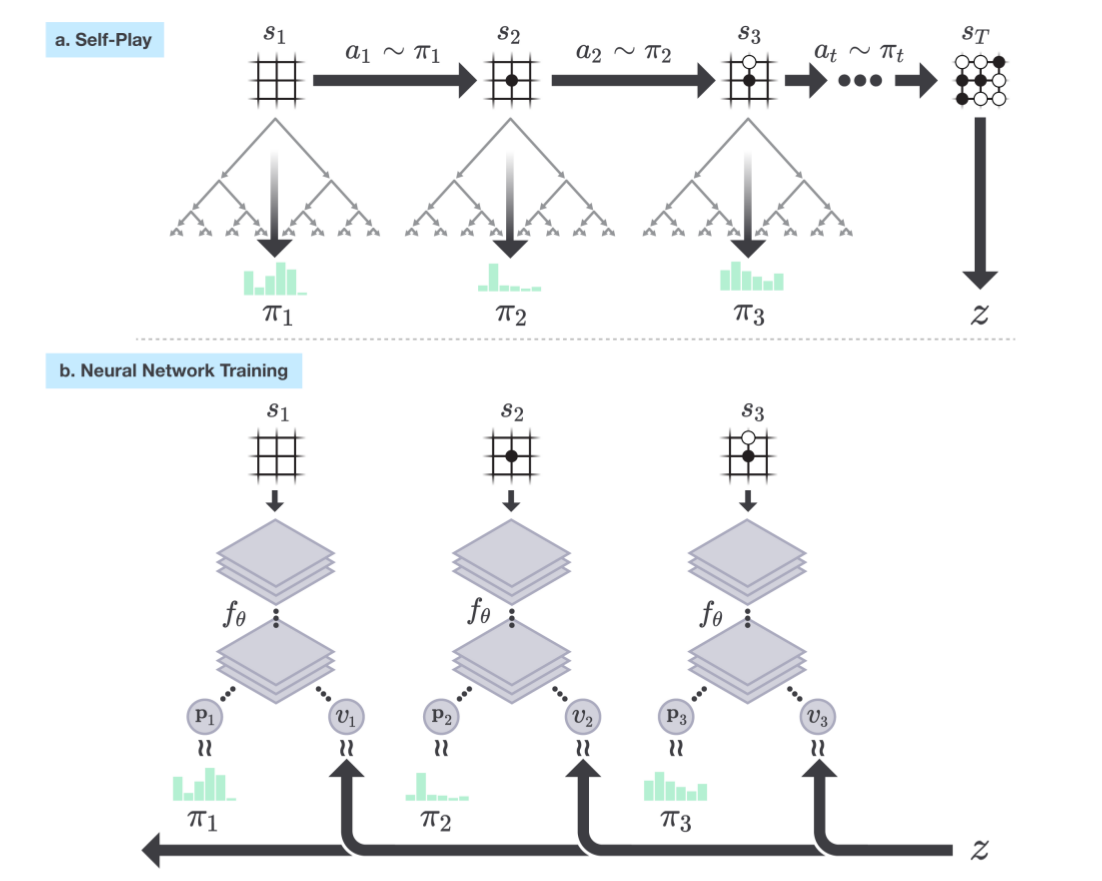
一局(或者更多局)自对弈结束之后,我们就可以把最终的得分z赋给这个对局的每一个状态得到$(a, \pi, z)$,用这个来训练新的$f_\theta$从而得到更强的策略。过程下图所示。图a中我们用当前网络来知道MCTS的搜索,同时估计出比网络预测的$\textbf{p}$更准确的$\pi$,训练的时候按照概率分布$\pi$来随机选择一种走法。
当一局自对弈结束之后我们就可以根据游戏规则得到最终的胜负z。图b里我们把这个z赋给对局中的每一个状态(如果是对手走的局面就变成-z)。然后用$(a,\pi,z)$作为训练数据重新训练网络$f_\theta$来得到更强的策略(模型),然后用更强的策略再自对弈下去。。。
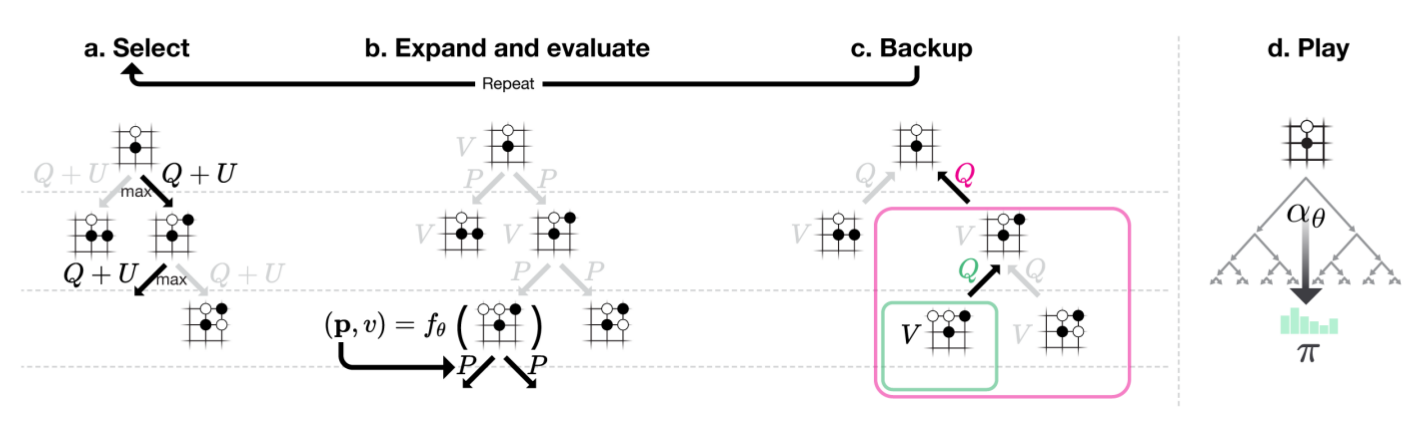
接下来我们来看AlphaGo Zero的MCTS过程,如下图所示。 和AlphaGo相比,AlphaGo Zero的MCTS更加简单。AlphaGo的MCTS在到底叶子节点之前会选择UCT最大的action a,到了叶子节点除了用Value Network计算其Value,也进行rollout policy模拟游戏到结束来看胜率,最终把这两个值加权起来看做这个节点的Value,并用这个Value来更新Q(s,a)。而AlphaGo Zero不会进行rollout,直接用网络的预测v来计算这个叶子节点的value从而更新Q(s,a)。
比如在下图中,图a我们选择UCT最大的action一直到叶子节点,图b我们用$f_\theta$计算这个节点的$(\textbf{p},v)$。图c我们用这个v来更新从根到叶子路径上所有边对应的N(s,a)和Q(s,a)。多次MCTS之后我们可以得到跟节点每个走法(边)的N(s,a),根据这个N(s,a)我们可以计算出当前状态(根)下不同走法的概率分布$\pi$,然后根据这个概率分布来随机走一步棋。具体怎么用N(s,a)来计算$\pi$后面我们会介绍。
我们首先来看UCT也就是MCTS选择不同走法的概率,它的计算公式为:
\[\begin{split} UCT=Q(s,a)+U(s,a) \\ U(s,a) = c_{puct}P(s,a)\frac{\sqrt{\sum_bN(s,b)}}{1+N(s,a)} \end{split}\]Q(s,a)是状态s和走法a的Q值函数,初始值是零,每一次MCTS的搜索都会更新它,后面我们会讲到怎么更新它。而U(s,a)和网络预测的P(s,a)成正比,和它的访问次数N(s,a)成反比。我们可以这样解读U(s,a):一种走法探索的越少,我们就要尽量多的探索(explore)它,当然如果神经网络告诉我们这种走法比较好(P(s,a)大),那么我们也应该尽可能多的尝试它。而Q(s,a)是根据搜索的结果得出的值,它代表根据实际搜索结果,在s状态下走a的好坏,因此Q(s,a)代表exploit项——我们尽量尝试已经被证明过的好的走法。
当一次MCTS走到一个叶子节点s’的时候,我们会用当前的网络来预测$(\textbf{p},v)=f_\theta(s’)$。因此我们可以展开s’的边,同时得到s’的Value,我们用下面的公式来更新这条路径上的所有边的Q(s,a):
\[Q(s,a)=\frac{1}{N(s,a)}\sum_{s'|s,a \rightarrow s'}^{V(s')}\]这个公式的意思是:对于路径上的某条边,比如(s,a),因为这条边最终是走到了s’,并且我们知道了网络估计的s’的大致价值,那么取平均值就可以认为是Q(s,a)。比如,我们进行了100次MCTS搜索,那么某条边(s,a)可能被访问了2次,这两次访问最终到底叶子节点的价值是0.5和0.4,那么我们就认为Q(s,a)=0.45。注意:如果某个叶子节点是游戏结束,那么就不需要用网络计算它的价值了,而是直接根据游戏规则计算这个叶子节点的得分,胜负分别是+1和-1。
一个根节点s经过100词MCTS搜索之后,我们可以得到所有走法的N(s,a),那么我们就可以根据N(s,a)计算更加准确的$Pr(a \vert s)$,从而可以根据它来选择一个走法(另外它也是用于训练$\textbf{p}$的目标)。
\[\pi \propto N(s,a)^{1/\tau}\]这里$\tau$是temperature parameter。因此N(s,a)越大,说明算法认为$Pr(a \vert s)$也越大。前面描述了自对弈走一步的过程,我们不断重复这个过程直到游戏结束,这样我们就知道最终的胜负z。对于自对弈的每一个局面s,假设对弈走了N步,我们都可以得到N个训练数据$(s, \pi, z)$,我们通过多次自对弈就很多训练数据,然后用这些训练数据重新调整模型参数得到更强的模型。我们调整参数的损失函数为:
\[l=(v-z)^2 - \pi^Tlog \textbf{p} +c \left \vert \theta \right \vert^2\]我们期望模型预测的v和实际游戏的结果z尽量解决,同时我们计算模型预测的走法概率分布$\textbf{p}$和“真实”分布$\pi$的交叉熵。而最后一项是为了防止过拟合的正则项。
实验分析
论文从零开始训练AlphaGo Zero三天,共进行了490万局自对弈,每个局面进行1600次MCTS搜索。模型共进行了700,000次minibatch的更新,每个minibatch的局面数为1024。这个网络共有20个残差block,后文会介绍网络结构。
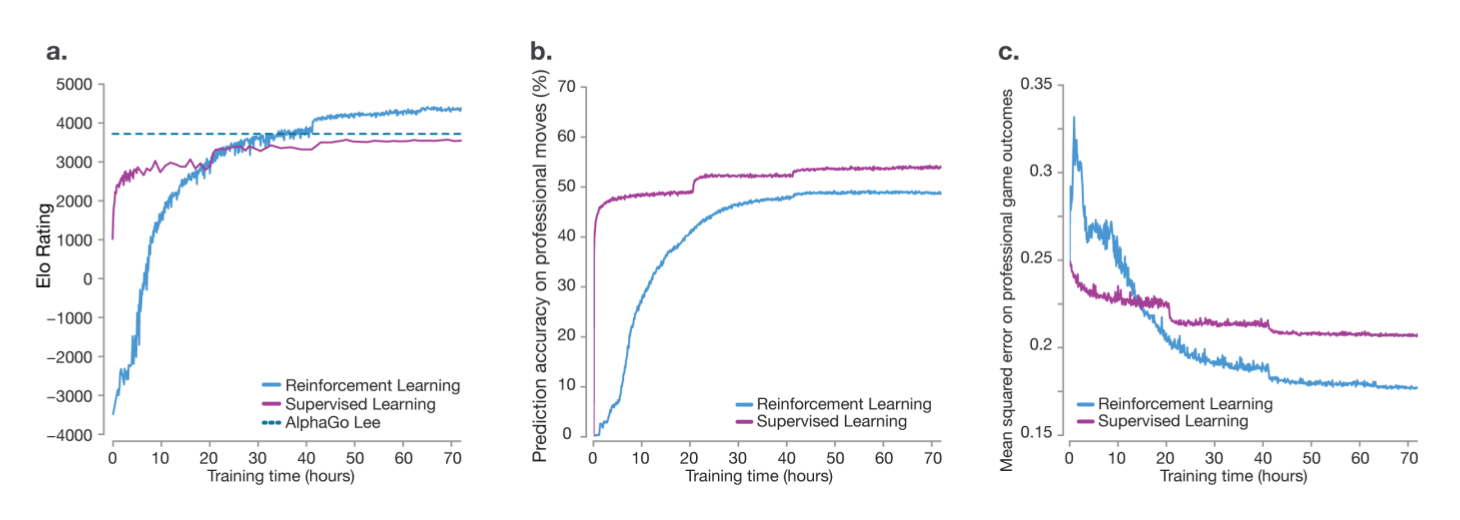
为了对比,论文也用人类职业棋手的棋谱来进行监督学习的训练(但是网络结构是一样的)。结果如下图所示。图a中的直线是AlphaGo-Lee(和李世石对局的AlphaGo),经过36个小时的训练之后,AlphaGo Zero已经超过了AlphaGo-Lee的水平。而监督学习的水平开始会比较高,但是最终进步比较慢。图b是用监督学习和强化学习用于预测人类职业棋手走子策略的对比,可以看成监督学习能够更加准确的预测(学习)人类职业棋手的走子策略。图c是对比两种方法预测职业棋手最终比赛结果,可以看成强化学习方法预测的更加准确。
从上面的分析我们可以看出,监督学习更多的是学习人类棋手的走法,而强化学习它能探索更多人类棋手没有尝试过(人类棋手认为不好但其实很好)的走法。
AlphaGo Zero训练72个小时之后和AlphaGo Lee进行了100局比赛,结果是100比0!
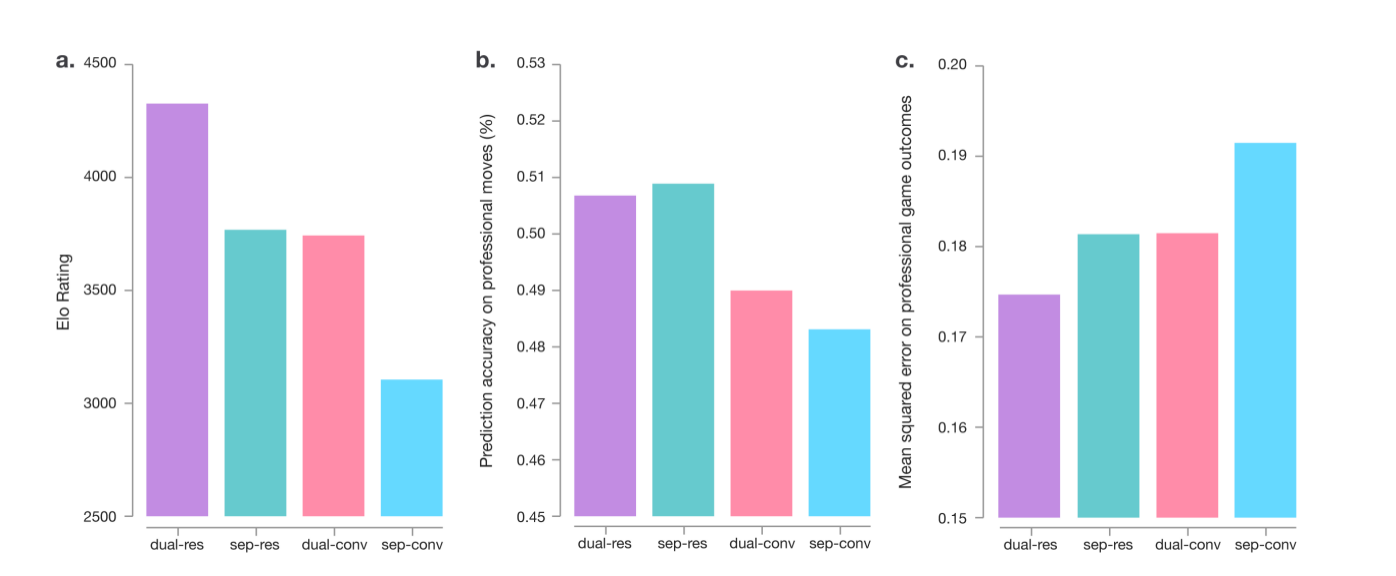
因为AlphaGo Zero的神经网络结构和AlphaGo相比除了使用了更新的残差网络之外还把后者的Policy Network和Value Network合二为一了。为了分析两者各自的贡献,论文也做了如下实验:用相同的数据分别训练4个网络,分别使用残差(AlphaGo Zero)和普通的卷积网络(AlphaGo)、合并和不合并两个网络。实验结果如下图所示。从棋力上看(图a),使用残差并且合并的网络最强,使用残差网络的非合并网络第二,使用普通卷积的合并网络第三,使用卷积的非合并网络最差,而第二和第三差别不大,因此两者对于最终的改进贡献都挺大。
从图b来看,使用残差的非合并网络预测职业棋手最准,而AlphaGo Zero使用残差合并网络稍低于它排第二。从图c来看,使用残差合并网络的预测对局结果最准确,因此它的棋力最强。图b说明合并的网络能更好的学到人类之外的一下对局策略(人类棋手认为并不好,但是AlphaGo Zero认为好,而最准从上帝的视角来看也是好的策略)
AlphaGo Zero学到的围棋知识
AlphaGo Zero能够通过自对弈学到很多人类发现的定式(joseki),也会发现新的定式,甚至发现很多人类没有发现的知识。作者对围棋并不熟悉就跳过了,有兴趣的读者可以参考原始论文。
AlphaGo Zero的最终棋力
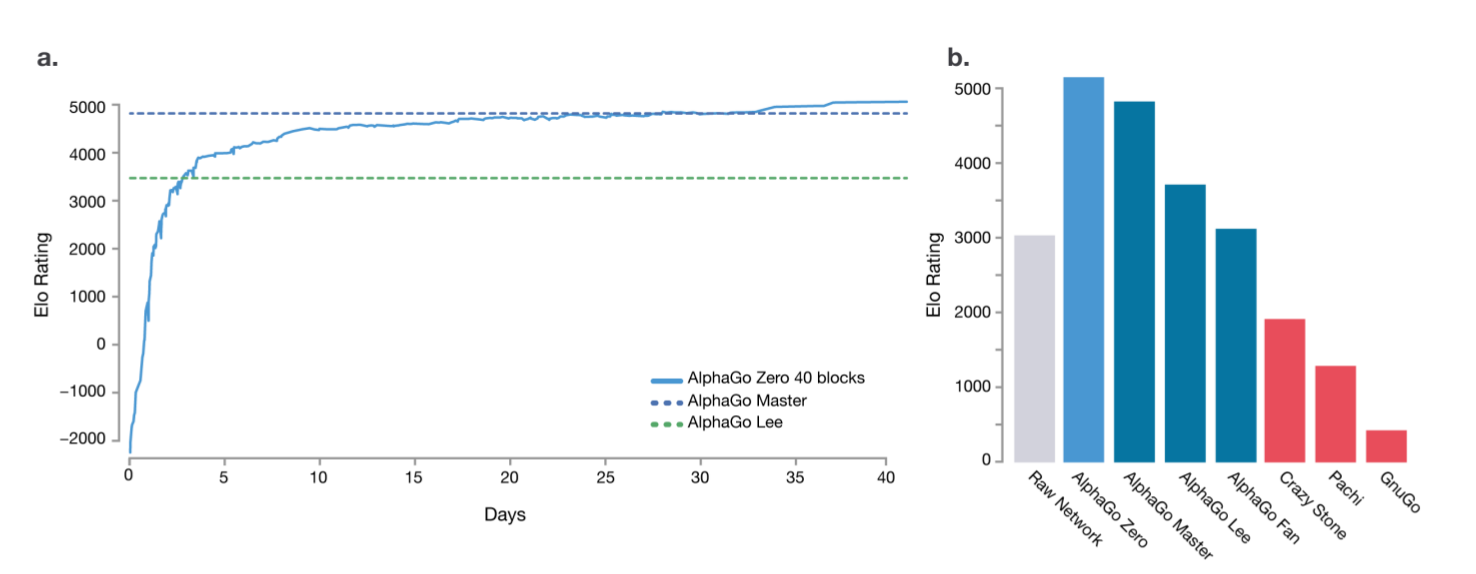
最终的AlphaGo Zero版本训练了40天,它进行了2900万次自对弈,进行了3100万次minibatch的参数更新,minibatch大小是2048。网络结果也从之前的20个残差块变成了40个。它的棋力随训练时间的变化如下图a所示,它最终的elo分超过5000,而击败李世石的AlphaGo不到4000分。图b是它和其它版本的软件的对比,其中AlphaGo-Lee就是击败李世石的版本,而AlphaGo-Fan是击败樊麾的版本,而AlphaGo-Master是AlphaGo-Lee的改进版,2017年在弈城等网络对战平台连胜60名人类高手(包括中国的柯洁)的版本。
实现细节
AlphaGo的不同版本
- AlphaGo Fan
这是2015年10月和樊麾对弈的版本,它使用了176个GPU来进行分布式的计算。前面介绍AlphaGo的发表在Nature上的论文描述的就是这个版本的AlphaGo。
- AlphaGo Lee
这是2016年3月4-1击败李世石的版本,当时并没有公开的论文描述它的细节。和AlphaGo Fan的区别有两点:Value Network的训练数据是来自AlphaGo的自对弈(有MCTS和rollout)而不是使用Policy Network的自对弈(没有MCTS);AlphaGo Lee的网络结构比AlphaGo Fan要复杂,它使用了12个卷积层,对弈的时候使用了48个TPU进行搜索。
- AlphaGo Master
这是2017年1月在弈城等网络对战平台连续战胜60位人类高手的版本。它的实现和AlphaGo Lee基本相同,但是它训练的更好,棋力更强。
- AlphaGo Zero
这是本节介绍的版本,它完全不用人类的棋谱,从零开始通过自对弈来学习。它只有一个网络实现Policy和Value Network的功能,MCTS的时候没有Rollout,对弈时它只使用了4个TPU进行搜索。
围棋知识
AlphaGo Zero只使用了基本的围棋规则而没有任何的人类启发规则或者特征。具体内容为:
-
围棋的基本规则 基本规则包括走子规则和游戏胜负的判定规则。如果双方都pass或者总共超过19x19x2 = 722步,则认为游戏结束
-
MCTS和自对弈结束是使用Tromp-Taylor方法计算胜负。
-
神经网络的输入是19x19的“图像”
-
围棋棋盘旋转或者对称变换后是一样的, AlphaGo Zero使用了这个知识。
除了上面的列表,AlphaGo没有使用任何其它的围棋知识。
自对弈的Pipeline
AlphaGo Zero的三个主要部分是并行异步执行的:神经网络参数$\theta_i$会持续的用最近的自对弈数据进行训练;Player $\alpha_{\theta_i}$的棋力会持续被评估;当前最好的Player用于产生新的自对弈数据。
优化
网络$f_{\theta_i}$会使用Google Cloud的Tensorflow进行训练,使用了64个GPU和19个CPU的参数服务器(Parameter Server)。每个worker的batch大小是32,因此每个minibatch总共是64x32=2048。数据是从最近的500,000个对局中随机采样。训练是冲量的方法,冲量为0.9。并且learning rate会衰减,如下图所示。
 图:AlphaGo Zero训练时的Learning rate schedule
图:AlphaGo Zero训练时的Learning rate schedule
L2正则项词参数$c=10^{-4}$。训练每1000次会产生一个新的checkpoint文件,用于模型评估。
评估
为了保证产生高质量的自对弈数据,每个新模型的模型都会和当前最好的模型进行400场比赛,如果新的模型胜率超过55\%,那么就把新模型作为当前最好模型,用它来进行自对弈。
自对弈
当前最强的Player $\alpha_{\theta_*}$通过自对弈来产生训练数据。每次迭代,它会产生25,000次对局,每一步使用1600次MCTS模拟。前30步,$\tau$为1,这样它会按照N(s,a)的比例来寻找走法a(从而有一定的Explore);而之后$\tau \to 0$,从而每次选择最可能的走法。为了在$\tau \to 0$的时候有一定的Explore,MCTS的根节点的P(s,a)会增加Dirichlet的噪声。$P(s, a) = (1 − \epsilon)p_a +\eta_a$,其中$\epsilon=0.25$,$\eta \sim Dir(0.03)$。
监督学习
为了对比,论文也训练了监督的网络模型$f_{\theta_{SL}}$,使用的是KGS的人类对局数据,某个局面s下人类棋手走了a,那么就设置target $\pi_a=1, \pi_{\ne a}=0$。
搜索算法
在MCTS里每个局面s都是树中的一个点,s局面下所有可能的走法a都是它下面的一条边,边我们用(s,a)来标识。每条边(s,a)都包含如下统计信息:
\[\{N(s,a), W(s,a), Q(s,a), P(s,a)\}\]其中N(s,a)是这条边的访问次数,W(s,a)是累加的Value,而$Q(s,a)=W(s,a)/N(s,a)$,而P(s,a)是模型预测的选择这条边的先验概率$p(a \vert s)$。
Selection
MCTS的Selection阶段从根$s_0$开始,应用上式选择孩子节点一直到叶子节点(孩子节点没有展开的或者说没有边的叫作叶子)为止。
我们这里再来仔细的分析一些U(s,a):
\[U(s,a) = c_{puct}P(s,a)\frac{\sqrt{\sum_bN(s,b)}}{1+N(s,a)}\]参数$c_{puct}$用于控制U(s,a)和Q(s,a)的权重,P(s,a)是模型预测的$Pr(a|s)$。而分母是1+N(s,a),它说明我们应该尽量 探索之前没有探索过局面。那分子什么意思呢?如果不看开根号,它就是局面a的访问总次数。因为不同子树的访问次数不同,如果没有这一项,有的子树访问次数较多,那么U(s,a)总体就会偏低。有了这一项,就可以看成N(s,a)与s的其它走法N(s,a’)的相对数值,从而与它们的绝对数量无关。否则可能出现s对应的U(s,a),U(s,b)都很大,而s’对应的U(s’,a),U(s’,b)都很小,从而使得U(s,a)的取值范围有很大的变化。
Expand和Evaluation
上面的步骤遇到叶子节点$s_L$后停止,然后把它的所有走法$(s_L,a)$都加到树中,并使用网络$f_\theta$计算$(\textbf{p}, v)$。新加的边$(s_L,a)$对应的N(s,a),W(s,a),Q(s,a)都是零,而$P(s,a)=\textbf{p}_a$。
Backup
有了叶子节点的Value(来自$f_\theta(s_L)$的v),我们就可以更新从根到$s_L$的所有边上的信息,从而计算新的Q(s,a):
\[N(s_t,a_t)=N(s_t,a_t)+1, W(s_t,a_t)=W(s_t,a_t)+v, Q(s_t,a_t)=\frac{W(s_t,a_t)}{N(s_t,a_t)}\]更新了之后,下一次MCTS时的Selection就可能发生变化,因为Q(s,a)已经变化了(当然U(s,a)也会变化)。
Play
经过一定次数的MCTS之后,我们需要在根节点$s_0$选择一条边a来下一步棋。我们使用如下公式来选择:
\[\pi(a|s_0)=\frac{N(s_0,a)^{1\tau}}{\sum_b N(s_0,b)^{1\tau}}\]同一局自对弈走完一步棋后又需要再次进行MCTS,这里会复用之前的MCTS产生的树(因此这棵树只会在一局比赛的第一步创建),比如之前树的根是$s_0$,我们选择了走法a,得到新的树根$s_1$,那么我们会把$s_1$对应的子树当成下一步MCTS的树,而$s_0$的其它子树都可以丢弃掉。
AlphaGo Zero和AlphaGo的主要区别是:不使用rollout因此也就不需要Tree Policy,只有一个网络代替AlphaGo的Policy Network和Value Network。另外AlphaGo Zero的叶子节点总是会被Expand,而AlphaGo会动态的决定是否Expand。另外叶子节点的Evaluation是同步的,也就是所有线程会等到其结果,而不是异步的。
网络结构
AlphaGo Zero的输入是19x19x17的“图像”,17个特征平面(feature plane)都是二值的。其中8个平面表示我方最近8个时刻的棋子,而另外8个表示对手的。
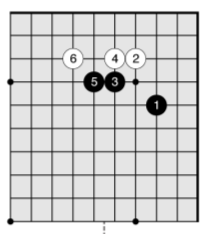
我们通过一个具体的例子来说明输入,比如上图是10x10的棋盘,共走了6步棋。那怎么表示当前的状态s呢?为了简化,我们把最近的8个时刻变成最近的3个时刻。
那么当前时刻我(黑)方的棋子为,注意值为1的位置:
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 0 0 0 0
0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
前一个时刻我方的棋子为:
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
再前一个时刻为:
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
对手的也类似,这样我们就可以得到10x10x6(对应论文为19x19x16)个,另外我们需要表示当前局面轮到谁走棋,这本来只需要一个数字就行了,但是为了使用卷积网络,我们用一个plane来表示,比如接着上面的例子,黑方走子为1,那么特征平面就是:
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
如果当前只走了1步棋,那么上一个时刻和上上一个时刻呢?论文里简单的用全零的plane表示。
得到了输入$s_t$之后会把它输入网络里。神经网络第一层是卷积层,然后后面是19个或者39个残差块(Residual Block)。
卷积层的结构为:
-
256个3x3的卷积核,stride是1
-
Batch Normalization
-
ReLU
每个残差块的结构为:
-
256个3x3的卷积核,stride是1
-
Batch Normalization
-
ReLU
-
256个3x3的卷积核,stride是1
-
Batch Normalization
-
输入和5的输出相加(skip connection)
-
ReLU
最后一个残差块的输出会连接两个”Head”分别用于计算$\textbf{p}$和v。我们把它们叫作policy head和value head。
policy head的结构为:
-
2个1x1的卷积核,stride是1
-
Batch Normalization
-
ReLU
-
线性全连接层,输出是19x19+1=362的logits。除了361个点可以走之外,还有一种选择就是pass
value head的结构为:
-
1个1x1的卷积和,stride是1
-
Batch Normalization
-
ReLU
-
线性全连接层,输出256
-
ReLU
-
线性全连接层,输出1
-
tanh激活
- 显示Disqus评论(需要科学上网)