本文介绍AlphaZero的原理。更多文章请点击深度学习理论与实战：提高篇。
目录
简介
前面的AlphaGo Zero没有使用任何人类棋谱和人类经验就可以通过自对弈学习达到远超人类冠军的水平。而(国际)象棋等在棋类游戏虽然已经被“解决”了，比如国际象棋，自从Deep Blue战胜卡斯帕罗夫之后，软件的棋力不断在提高。但是这些软件使用的还是类似Deep Blue的技术——AlphaBeta搜索+人工特征+开局残局库等等，这些技术使用了大量棋类知识和人类经验。那能不能把AlphaGo Zero就技术移植到其它的棋类游戏呢？这就是AlphaZero要解决的问题。
AlphaZero和前面的AlphaGo Zero基本一样，只不过把它用于了象棋等其它棋类游戏（当然也可以用于围棋）。下面我们来看它和AlphaGo Zero的区别。
- 对于围棋，结果只有胜负，但是象棋有平局(z=0)
- 对于围棋，AlphaGo Zero利用了对称性，而AlphaZero不使用它来增强数据
- AlphaGo Zero得到新的模型之后会和当前最优的比赛，胜率超过55%才替换当前模型，而AlphaZero没有这个步骤，直接更新模型，用新的模型来自对弈
- AlphaGo Zero的超参数使用贝叶斯优化来选择，而AlphaZero重用AlphaGo Zero的超参数，对于象棋也使用围棋的超参数
图解
为了更加了解AlphaZero的实现细节，我们用图来说明MTCS的过程，本节内容参考了AlphaGo Zero - How and Why it Works。
为了简化，这里图示的例子是简单的井字棋(tic-tac-toe)游戏。这是一种在3*3格子上进行的连珠游戏，和五子棋类似，由于棋盘一般不画边框，格线排成井字故得名。游戏需要的工具仅为纸和笔，然后由分别代表O和X的两个游戏者轮流在格子里留下标记（一般来说先手者为X），任意三个标记形成一条直线，则为获胜。当然这是一个很简单的游戏，我们用minimax就能搜索最优解，但是这里我们的目的是通过它来介绍AlphaZero的实现细节。
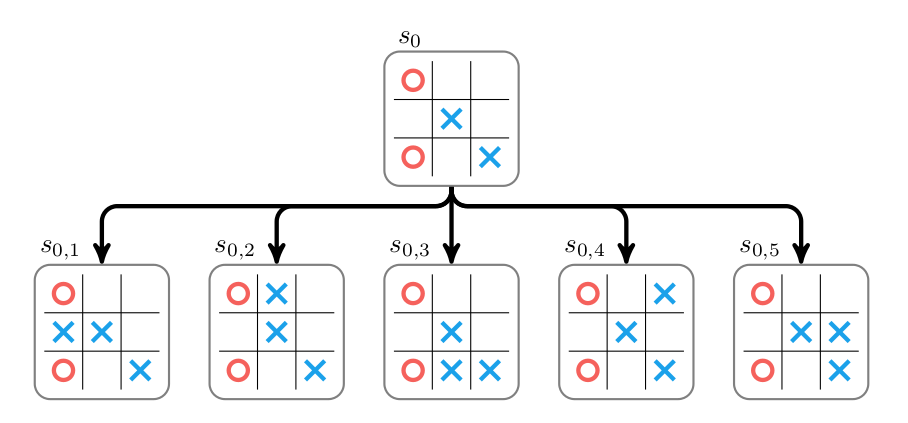
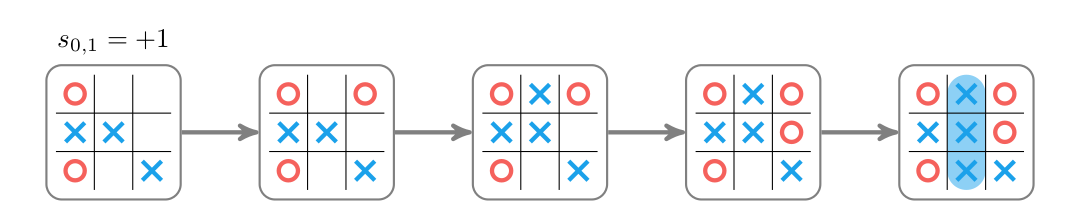
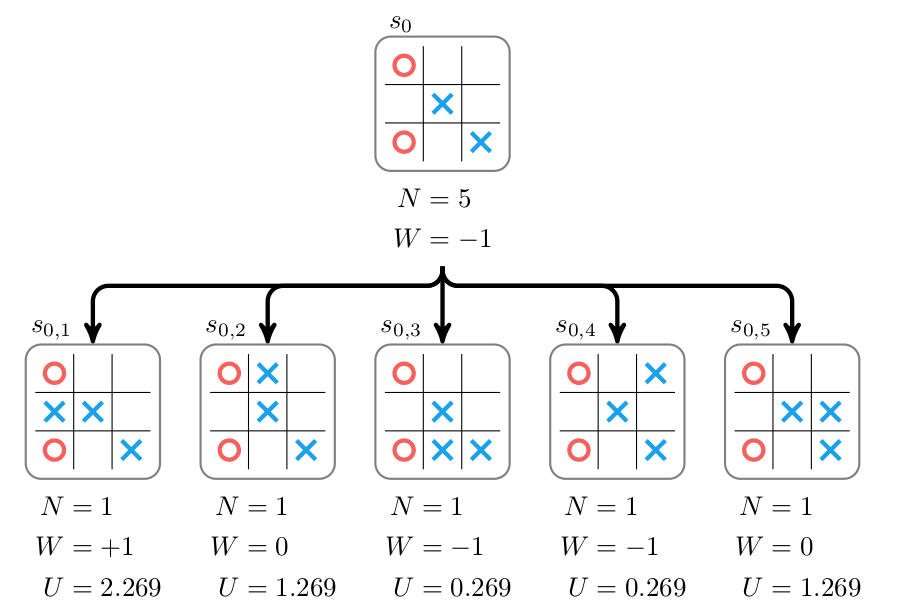
我们首先介绍AlphaGo里的有rollout的MCTS。游戏的初始状态是$s_0$，假设现在轮到AlphaZero走棋，它的所有action(走法)的集合为$\mathcal{A}$。MCTS搜索开始的时候搜索树只有一个根节点$s_0$，同时它也是一个叶子节点（没有任何边被展开）。根据前面介绍的MCTS过程，它的Selection直接就到叶子节点了，因此Expand这个叶子节点，如下图所示。在这个局面下有5种走法，也就是5条边，走完每种走法后得到5个新的节点(局面)。我们现在需要知道这些节点(状态)的Value，怎么求这些节点的Value呢？我们可以使用rollout，也就是模拟对局到游戏结束，通常我们会模拟很多次rollout，然后平均其Value，这里为了简单，我们只rollout一次。比如节点$s_{01}$的一次rollout过程如下图所示。这次模拟我方(走X的)获胜，因此Value是+1。这里的rollout使用了随机的策略，这通常不是很好的模拟。更好的模拟是用一个rollout policy或者直接用一个网络来计算$s_{01}$的Value，前者是AlphaGo使用的方法而后者是AlphaZero使用的方法，我们这里先用随机的模拟。这样我们就访问了$s_{01}$了一次，累计的W是+1。
图：Expand示例
图：Rollout示例
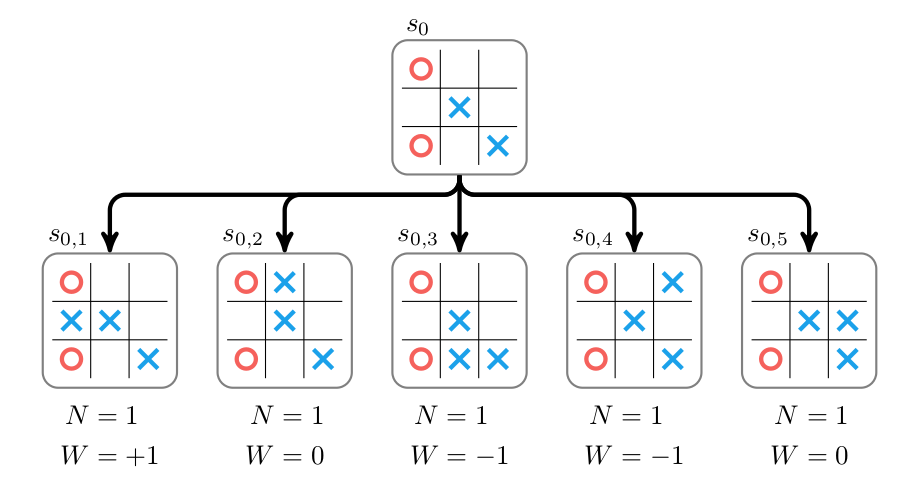
类似的，我们可以对其它4个状态进行rollout，结果如下图所示。
图：Rollout其它叶子节点
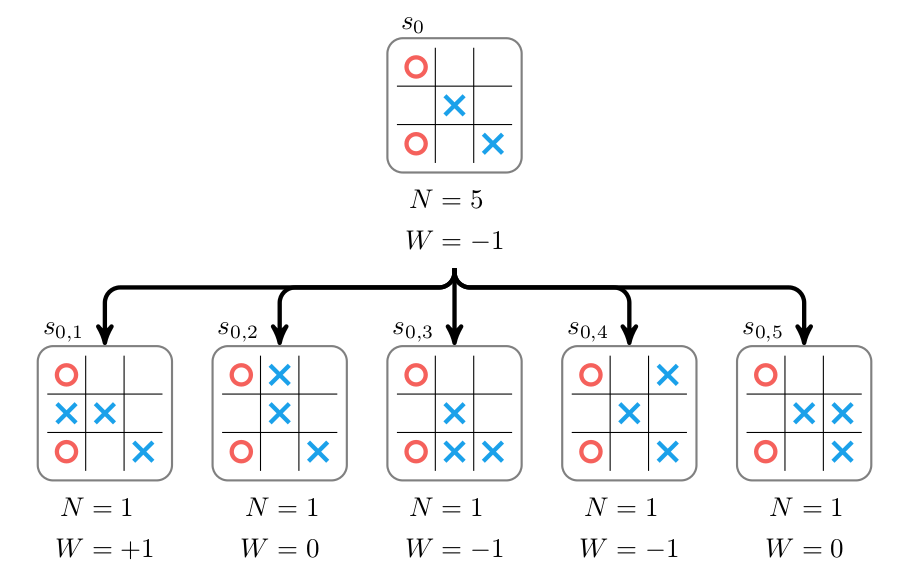
接下来我们进行Backup，把叶子节点得到的Value累加到根节点，结果如下图所示。根节点的访问次数是5，W是-1。
图：Backup
到此为止，一次MCTS的搜索就完成了。原始的AlphaGo遇到叶子节点不一定展开，而且计算叶子的Value时会综合考虑它的rollout分和Value Network的打分。我们这里把所有的叶子都展开，并且把Value Network省略掉了。
接着我们会继续重复这个过程，在没有到叶子节点之前会使用UCT选择走法(子节点)，到了叶子节点就展开并且用rollout估计它的Value，然后往上更新路径中所有节点的N(s,a)和W(s,a)，它们计算得到新的Q(s,a)，而新的Q(s,a)会影响下一次MCTS的选择。比如UCT的选择公式：
\[U_i = \frac{W_i}{N_i} + c\sqrt{\frac{\ln N_p}{N_i}}\]这个公式的$W_i$是第i个子节点的累加Value，$N_i$是它的访问次数，$N_p$是它父亲节点的访问次数。因此它会优先选择(探索)Q(s,a)比较大的走法，这和人类下棋类似的——我们优先尝试更可能的走法(Exploit)。当然第二项也让我们偶尔尝试一些很少尝试的走法(Explore)因此，第二次MCTS首先会计算根节点$s_0$所有孩子的UCT，如下图所示。
图：第二次MCTS的Selection
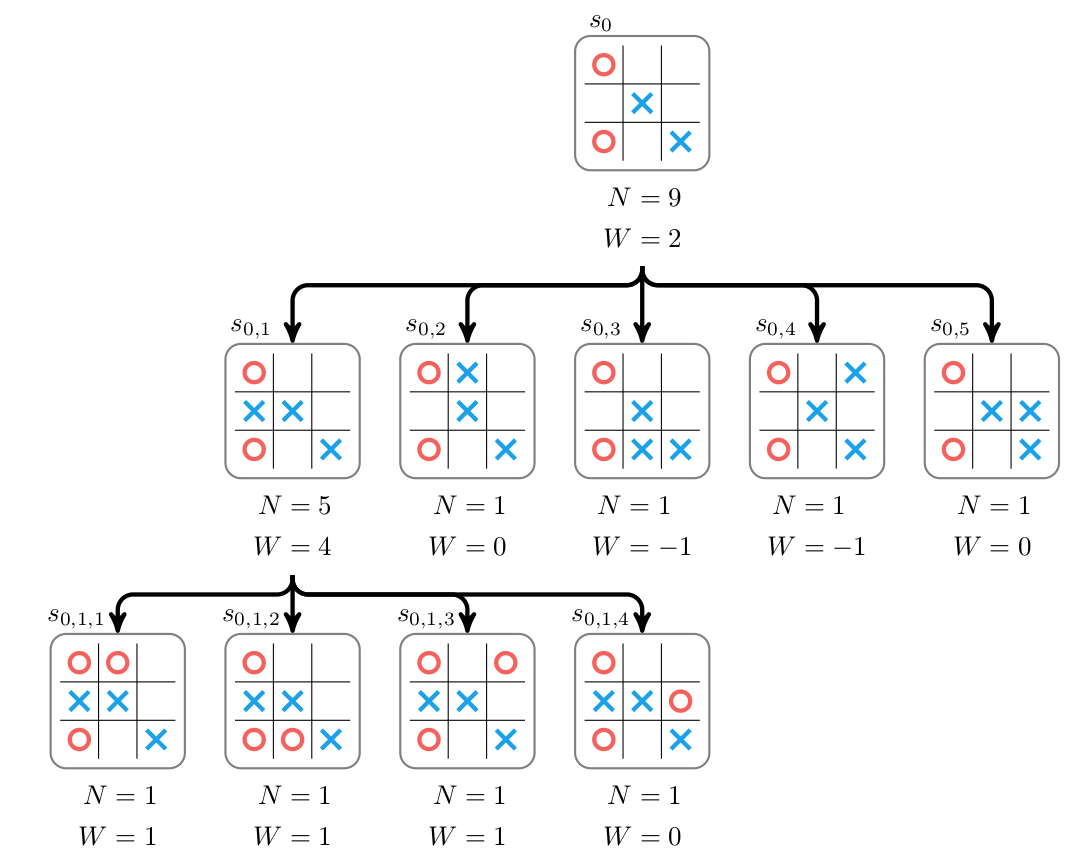
这里孩子$s_{01}$的得分最高，因此我们接着选择它。因为它是个叶子节点，因此Selection的过程就结束了。接着我们展开$s_{01}$并且对它的还在用rollout估计其Value，然后更新路径中$s_{01},s_0$的N和W，如图\ref{fig:az-how-6}所示。展开后$s_{01}$有4个孩子$s_{011},s_{012},s_{013},s_{014}$，rollout后的Value是1,1,1和0，因此我们可以backup，更新$s_{01}$的N为5，W为4；更新$s_0$的N为9，W为2。注意W是相对于玩家X来说的，如果当前玩家是O，那么它的Value需要取反。比如最终rollout的结果是X赢了，而当前节点的玩家是O，那么它的Value是-1，因此节点的Value总是相对于当前走棋的玩家来说的。
图：第二次MCTS的Expand和Evaluation
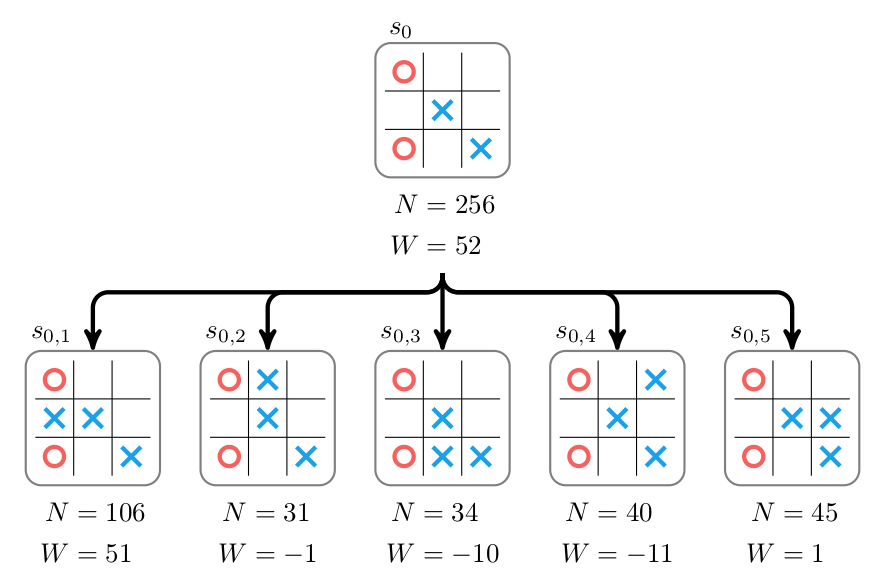
我们可以不断的进行多次MCTS搜索，那么它就会不断的展开和更新节点的Value。MCTS到了一定次数或者超过一定时间我们就可以停止。然后我们可以根据根节点孩子的访问次数N的多少来选择走棋，如果是对弈，那么就选择N最大的走法。如果是强化学习，那么可以按照N的比例来走棋。图\ref{fig:az-how-7}是进行了256次MTCS后的结果，我们应该走$s_{01}$，因为它的N最大。
图：256次MCTS的结果
围棋或者象棋的状态空间非常大，我们通过rollout得到的Q(s,a)来指导它更多的Exploit是比较困难的，这是我们可以用一个Policy Network来指导它，新的UCT公式为：
\[U_i = \frac{W_i}{N_i} + c P_i\sqrt{\frac{\ln N_p}{1 + N_i}}\]其中$P_i$是Policy Network预测当前局面下走$a_i$的概率$p(a_i \vert s_0)$。如下图所示。
图：加入Policy Network去掉rollout
另外一个改进(AlphaZero)就是去掉费时并且复杂的rollout，直接用Value Network估计叶子状态的值，如下图所示。
图：用Value Network去rollout
然后我们把Policy Network和Value Network合并成一个网络$f(s) \rightarrow [\boldsymbol{\mathbf{p}}, W]$就可以得到AlphaZero。
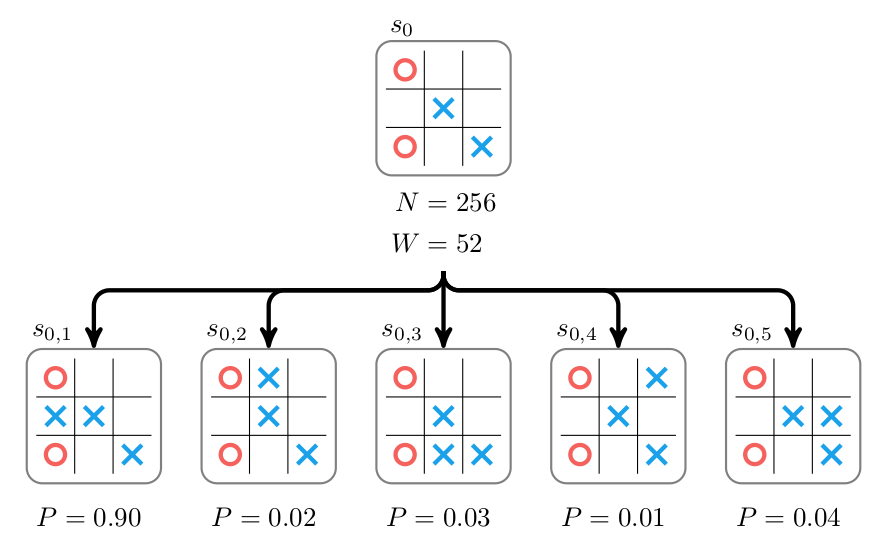
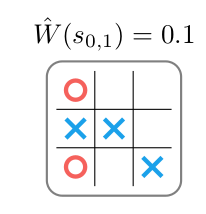
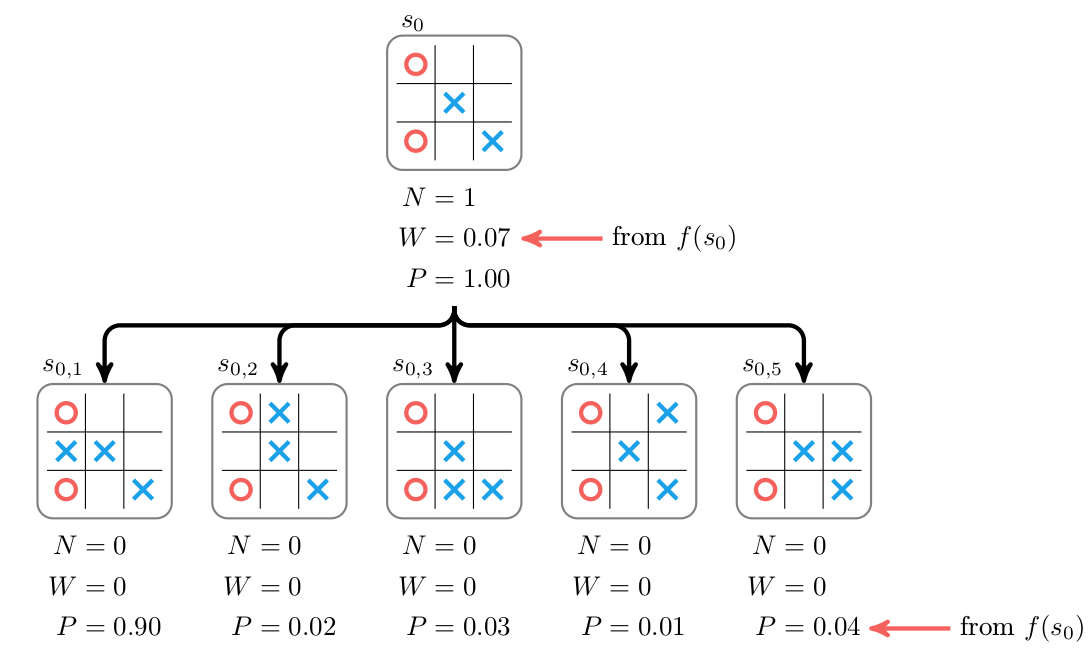
比如第一次MCTS时，搜索树只有一个节点$s_0$，selection直接遇到叶子节点$s_0$结束。然后展开$s_0$得到5个孩子节点，然后用网络估计$s_0$的Value和$p(a \vert s_0)$，如下图所示，注意里面红色箭头的标注。$s_0$的N是1，W是网络预测的1，它的P没有什么意义。然后它的5个孩子的N都是0，W也是0，P就是$p(a_i \vert s_0)$。然后是backup，因为是根节点，没有什么可以backup的。
图：AlphaZero的Expand和Evaluation
注意：这里的图是把N(s,a),W(s,a)和P(s,a)存在孩子节点上的，另外一种=实现是把它们存在边上，后面的代码我们使用的是这种方法，请读者注意。
接着进行第二次MCTS搜索，首先是Selection，这次遇到的$s_0$就不是叶子节点了，因此根据UCT选择，因为这些孩子的Q都是0，因此P(s,a)决定了我们应该选择第一个孩子$s_{01}$。因为$s_{01}$是叶子，所以Selection结束。
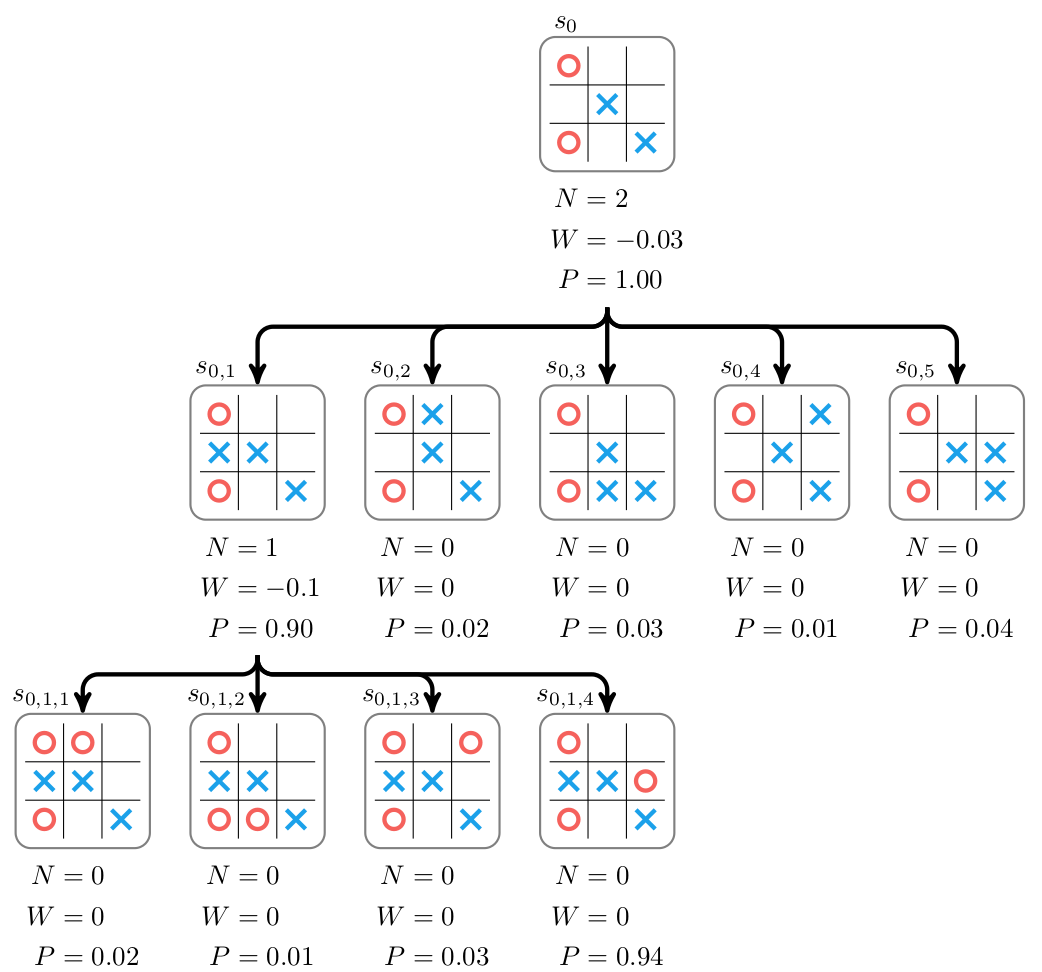
接着我们把$s_{01}$展开，并且用网络计算它的Value和$p(a \vert s_{01})$。然后把这个Value往上bakcup到$s_0$，更新$s_0$的W和N。如下图所示。
图：AlphaZero的Expand和Evaluation
通过多次MTCS之后，我们就可以用N计算根节点$s_0$的走子概率：
\[\pi_i=N(s,a_i)^{1/\tau}\]这样AlphaZero就走了一步棋。然后我们可以重复过程让AlphaZero不停的用MTCS接着往下走棋直到游戏结束，这个时候我们可以根据游戏规则得到最终的value z。然后对于这个对局的每一个局面我们都可以得到一个训练数据$(s_t, \pi_t, z_t)$，我们可以让它自对弈很多局，生成很多训练数据，然后再用这些训练数据来训练新的网络从而得到新的更强的Player。然后再用新的Player又自对弈，从而不断的进行强化学习的训练。我们训练网络的损失函数为：
\[(W - Z)^2 + {\boldsymbol{\mathbf{\pi}}}^\top \ln\boldsymbol{\mathbf{p}} + \lambda \|\boldsymbol{\mathbf{\theta}}\|_2^2\]公式中$(W - Z)^2$是Value的损失，交叉熵$\pi^\top \ln\boldsymbol{\mathbf{p}}$是Policy的损失，而$\lambda |\theta|_2^2$是正则项，参数$\lambda \geq 0$控制正则的强弱。AlphaZero完全是不需要任何人类知识的，它从随机的策略开始(随机的网络参数)，然后通过自对弈不断的提高自己的水平。
实验结果
论文用AlphaZero分别训练了围棋、象棋和将棋(日本象棋)的模型，都从零开始训练了700,000次minibatch，每个minibatch有4096个局面。然后和当前最好的软件进行了对比，围棋是和AlphaGo Zero对弈，而象棋是和Stockfish对弈，将棋是和Elmo对弈。其中Stockfish是一个开源的象棋软件，它获得过2016 TCEC的世界冠军，棋力是最顶级的软件，Elmo也是最强的将棋软件之一。它们都采用了前面介绍的类似Deep Blue的技术，需要花费大量的人类来提取领域特征，调整模型权重，加入海量开局库和残局库，使用更好的剪枝方法来提升AlphaBeta搜索的速度。。。
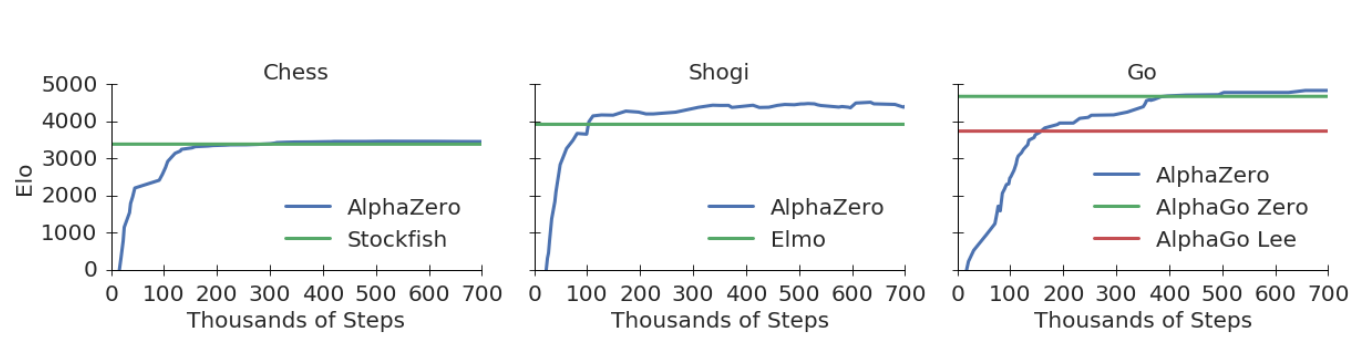
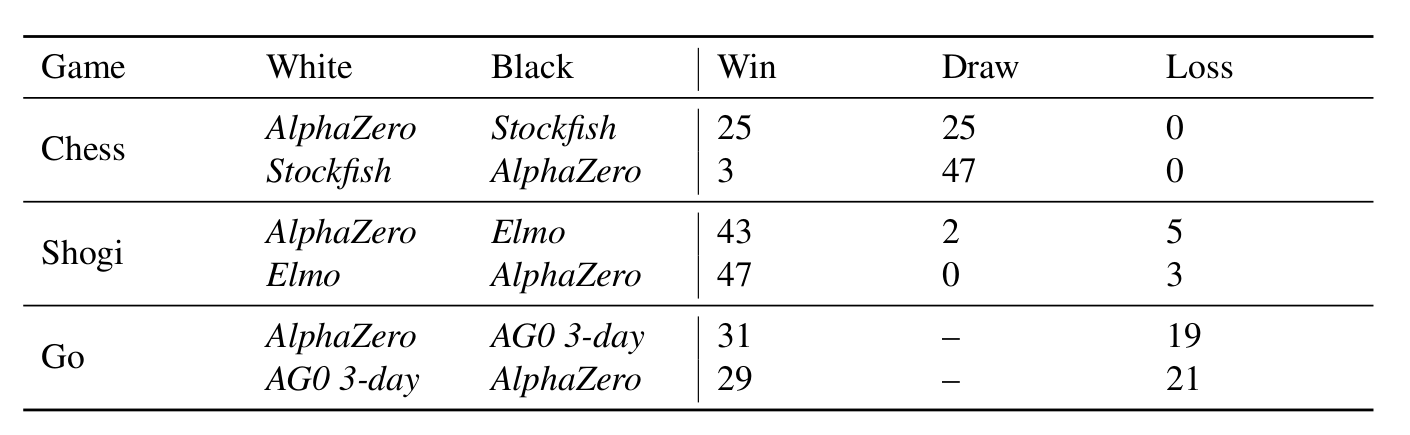
而AlphaZero完全不需要这些就可以轻松的达到甚至超过它们！下图是棋力随训练的迭代次数的变化，而下图是AlphaZero和这些软件的对弈结果。
图：棋力随训练的迭代次数的变化
图：AlphaZero和顶尖软件的比赛
可以看出，AlphaZero的棋力明显超出了AlphaGo Zero和Elmo，而稍微超出Stockfish。这也许可以说明象棋软件的水平离最优解已经不远了？不过网上也有争议，说论文实验的Elmo没有使用开局库和残局库。
实现细节
状态表示
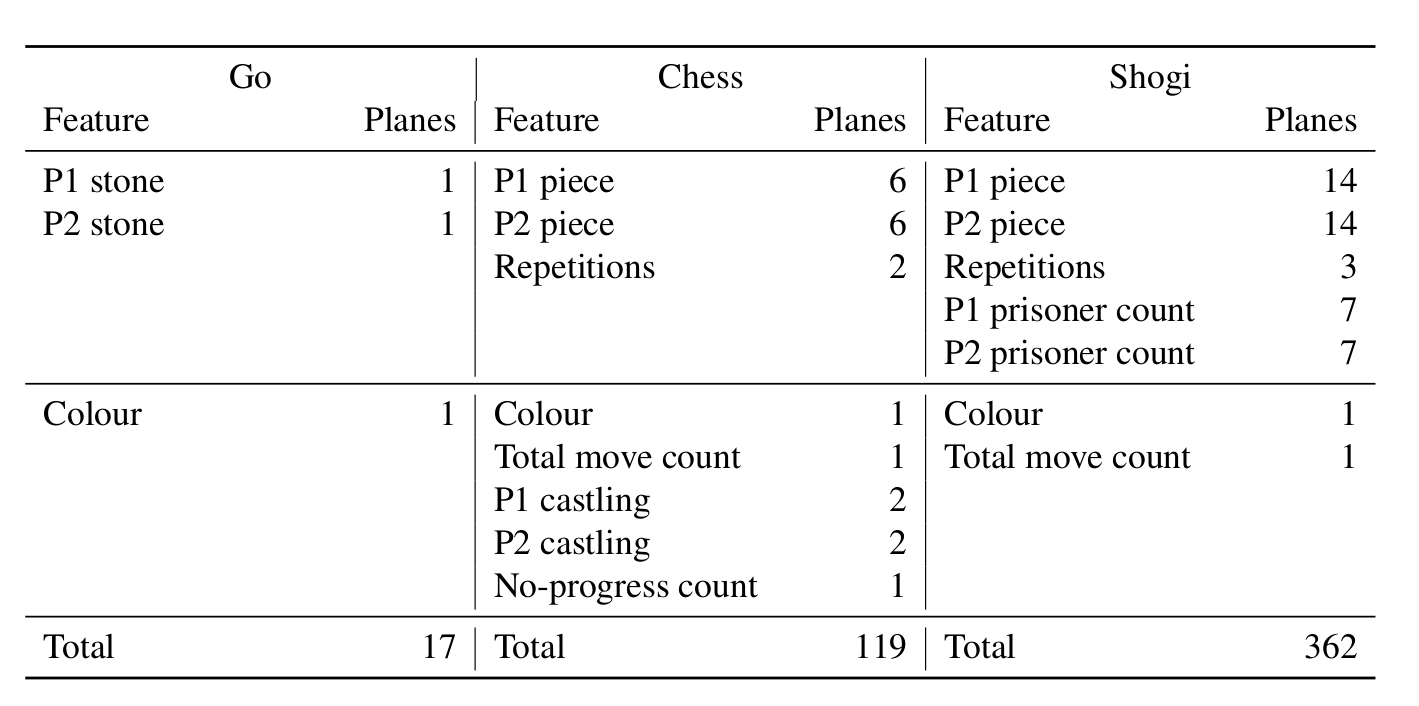
AlphaZero的状态表示如下图所示。其中围棋和前面的AlphaGo Zero完全一样。
图：AlphaZero的状态表示
将棋笔者不了解，我们这里分析一下象棋的状态(局面)表示。围棋的棋子只分黑白，因此使用N(19)xNx2来表示一个时刻黑棋和白棋，然后共有8个时刻(当前时刻之前的八个局面)。而象棋除了分颜色之外还分棋子——皇、后、车、马、相和兵卒共6种，因此需要N(8)xNx(Tx12)，另外象棋如果连续出现两次重复局面会判和，因此还需要NxNx(Tx2)来表示黑白双方是否出现重复局面。和围棋的走子plane类似，是否重复也是常量plane。和围棋一样，我们也需要一个plane来表示当前局面轮到谁走。另外象棋增加了一个plane，用于表示走到目前局面总共花了多少步(total move count)。象棋还有特殊的王车易位（castling），可以分为短易位和长易位，黑白双方都需要因此总共4个plane。另外象棋规则连续50步没有吃子(no progress)就是和棋，因此需要一个plane来表示当前局面有多少步没有progress了。这样总的plane数为8x8x(8x(6+6+2)+1+1+4+1)=8x8x119。
走法表示
围棋的走法很简单，理论上361个点中没有棋子的地方都可以走。而象棋就不同，象棋的走法需要选择一个棋子，然后根据不同棋子的规则走到一个新的位置，如果新位置有对方的棋子，可能还要“吃掉”对方的棋子。另外想王车易位和兵升变都有特殊复杂的规则。
但总结一下，象棋的走子首先选择一个要走的棋子，然后根据规则选择一个合法的位置。我们用8x8x73的plane来表示$p(a \vert s)$。其中8x8表示选择棋盘中的哪个棋子，而73是不同走法的总数，当然并不是每个棋子都有73种走法，有些组合是不合棋规的。73种走法中56种表示后的走法（类似中国象棋车的走法，但是可以走对角线）。56种走法可以分为8个方向(N, NE, E, SE, S, SW, W, NW)，比如N表示往北(向上)走，NE表示东北(45度对角线往右上)。。。每个方向最多能走7步（当然如果在中间，可能实际只能走4步），那么8x7=56。皇、兵、相和车都包含在这56种走法中，而马的走法(走日字)比较特殊，需要另外8种走法。还有9种走法是兵的特殊走法。
- 显示Disqus评论(需要科学上网)