用AlphaZero来玩Connect4游戏

本文通过一个简单的Connect4游戏介绍AlphaZero的实现。更多文章请点击深度学习理论与实战：提高篇。

转载请联系作者(fancyerii at gmail dot com)！

Connect4规则简介
获取代码
代码阅读
测试代码

接下来我们通过一个简单的Connect4游戏来介绍AlphaZero的代码，读者通过代码能够更加深入的了解怎么实现AlphaZero。

Connect4规则简介

Connect4的棋盘是一个6x7的格子，我们可以把它想象成7个“管子”。每次走棋时选择一个“管子”把球放进去，在重力的作用下小球会掉到相应的格子里。因此刚开始我们放进去的小球都会在最低层。双方轮流走子，如果一方出现连续水平、垂直或者对角线的小球就算赢了。如果42个格子都放满了还没有分出胜负就算平局。这个游戏非常简单，用Alpha-Beta搜索很快就可以找到最优解——这是一个先手必胜的一个游戏。

读者可以在这里试玩一下。另外这个网站也一个教程介绍怎么用Alpha-beta搜索解决Connect4的问题，这是网址，源代码在这里，有兴趣的读者可以去看看。当然我们的目的不是为了解决这个简单的游戏，而是通过它来介绍AlphaZero的实现。

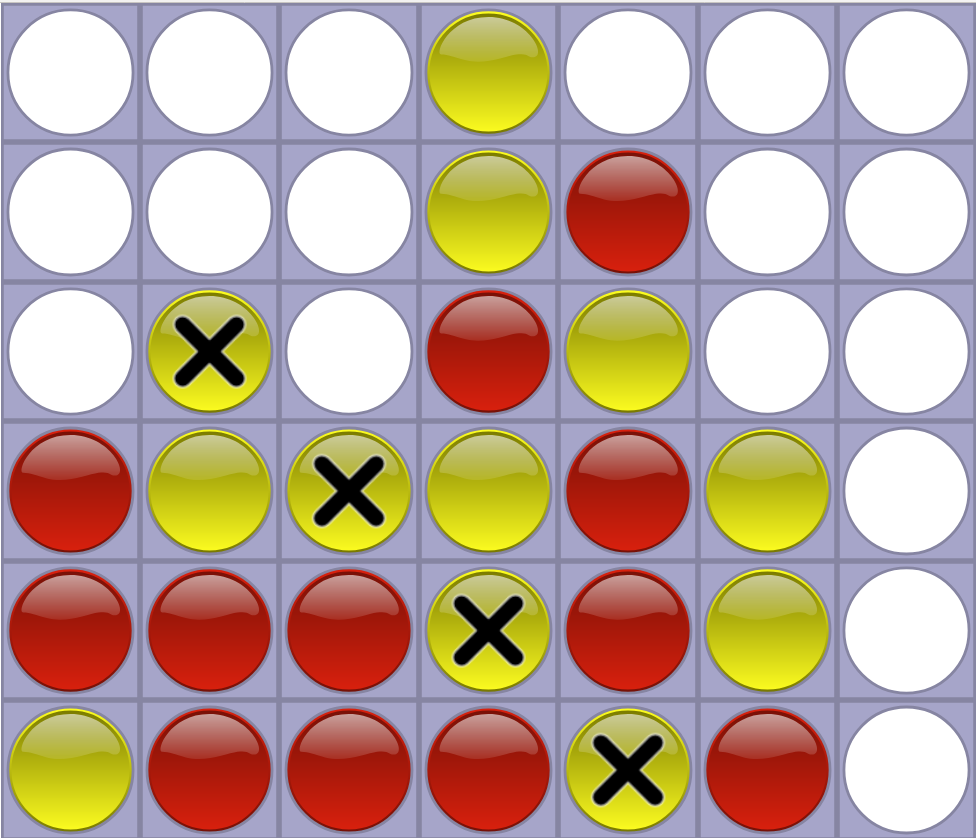
比如下图所示，黄球方获胜。

图：Connect4获胜局面

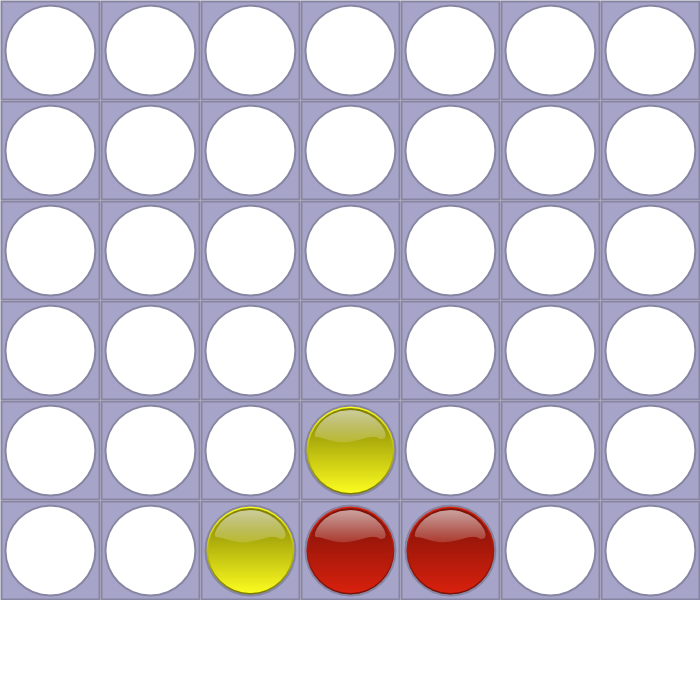
常见的棋类游戏都需要“记谱法”，对于connect4来说非常简单，记录每一步选择了哪个管子即可。比如棋谱”4453”对于的是下图所示的局面。它的意思是红方首先走在第4列，然后黄方也走第4列(堆在上面)，然后红方走第5列，黄方走第3列。当然不是所有的数字组合都是合法的，比如”44444434”，因为前6步双方以及把第4列放满了，因此第8步是不能在放第4列了。

图：棋谱”4453”对应的Connect4局面

获取代码

读者可以从这里或者作者的fork版本获取代码。这个实现使用了Keras，读者先需要安装好，运行jupyter notebook后就可以开始训练和测试。

代码阅读

游戏规则

在介绍AlphaZero的算法之前我们首先看怎么实现Connect4游戏规则，完整代码在game.py里。这个文件包含两个类，Game和GameState。Game代表一次对局，而GameState表示对局中的一个局面。

Game类的构造函数

class Game:

	def __init__(self):
		self.currentPlayer = 1
		self.gameState = GameState(np.array([0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], dtype=np.int), 1)
		self.actionSpace = np.array([0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], dtype=np.int)
		self.pieces = {'1':'X', '0': '-', '-1':'O'}
		self.grid_shape = (6,7)
		self.input_shape = (2,6,7)
		self.name = 'connect4'
		self.state_size = len(self.gameState.binary) # 84
		self.action_size = len(self.actionSpace) # 42

currentPlayer表示当前玩家是红方(先手)还是黄方(后手)，分别用1和-1表示。GameState就是当前的局面，具体代码后面会介绍，这里的初始局面就是所有位置(6x7=42)都是零。actionSpace表示可以走棋的位置，所有可能的走法是42个位置，但是在每个局面下最多可以有7种走法（每个管子一种，如果某个管子填满了，那么就少一种走法）

pieces用于在终端绘图，先手(1)用X表示，后手(-1)用O表示，没有走的地方(0)用-表示。state_size是gameState.binary的个数，它等于84。GameState.binary后面会讲到。

Game.reset函数

这个函数把Game恢复到初始状态。

	def reset(self):
		self.gameState = GameState(np.array([0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0], dtype=np.int), 1)
		self.currentPlayer = 1
		return self.gameState

Game.step函数

它实现走一步棋的逻辑。

	def step(self, action):
		next_state, value, done = self.gameState.takeAction(action)
		self.gameState = next_state
		self.currentPlayer = -self.currentPlayer
		info = None
		return ((next_state, value, done, info))

这个函数的输入是走法action，然后调用gameState(GameState类的实例)的takeAction函数，这个函数生成一个新的状态next_state、新状态的值value和游戏是否结束done。然后把当前游戏状态gameState设置成next_state。接着更换下一步走棋的玩家。

identities函数

它会返回一个状态(局面)的对称的局面。因为Connect4游戏是关于第4个列对称的，所以我们训练模型的时候可以把一个局面和它对称的局面都进行训练。这个函数的输入是一个局面和这个局面下所有action的Value，输出一个list(长度为2)，第一个元素就是输入本身，而第二个元素是它的对称(状态对称，action的Value也对称)。

比如输入是局面：

['-', '-', '-', 'O', '-', '-', '-']
['-', '-', '-', 'X', '-', '-', '-']
['-', '-', '-', 'O', '-', '-', '-']
['-', '-', '-', 'X', '-', '-', '-']
['-', 'X', '-', 'O', '-', '-', '-']
['-', 'X', 'O', 'X', '-', '-', '-']

那么对称的局面就是：

['-', '-', '-', 'O', '-', '-', '-']
['-', '-', '-', 'X', '-', '-', '-']
['-', '-', '-', 'O', '-', '-', '-']
['-', '-', '-', 'X', '-', '-', '-']
['-', '-', '-', 'O', '-', 'X', '-']
['-', '-', '-', 'X', 'O', 'X', '-']

接下来我们介绍GameState类，它表示游戏中的一个状态(局面)。在介绍这个类的代码之前我们首先简单的介绍一些棋盘表示(Board Representation)的问题。棋谱表示就是用什么样的数据结构来表示棋盘(状态/局面)。

比如对于围棋，我们可以用一个19x19的二维数组表示棋谱，如果某个点上是黑棋，那么对应的值就是1；如果是白棋就是-1；如果是空白就是0。对于Connect4，我们也可以用类似的方法，用6x7的数组表示。因为每个位置的值只有3中情况，为了压缩空间和提高计算速度，有很多更加“紧凑”的表示方法，比如可以使用BitBoard的方法，有兴趣的读者可以阅读这篇文章。里面有很多很tricky的位运算，是一个很好的锻炼数据结构的问题，有兴趣的读者可以仔细阅读。理解了之后读者也可以尝试修改GameState的实现，从而加快程序的速度。

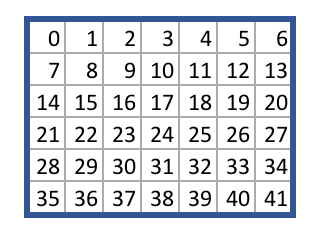
这里使用如下图所示的表示方法，用一个一维数组表示，下标的顺序是从上到下从左到右。

图：棋盘表示

GameState的构造函数：

class GameState():
	def __init__(self, board, playerTurn):
		self.board = board
		self.pieces = {'1':'X', '0': '-', '-1':'O'}
		self.winners = [
			[0,1,2,3],
			[1,2,3,4],
			# 其它水平4连珠....
			
			[0,7,14,21],
			[7,14,21,28],
			# 其它垂直4连珠....
			
			[3,9,15,21],
			[4,10,16,22],
			# 其它左下对角线4连珠
			
			[3,11,19,27],
			[2,10,18,26],
			# 其它右下对角线4连珠
		]
		self.playerTurn = playerTurn
		self.binary = self._binary()
		self.id = self._convertStateToId()
		self.allowedActions = self._allowedActions()
		self.isEndGame = self._checkForEndGame()
		self.value = self._getValue()
		self.score = self._getScore()

其中winners用于判断是否某个玩家4子连成直线。

_binary函数

这个函数的作用是把一个局面变成一个长度为84的二值(binary)向量，原来的长度为42的向量的取值是3中可能(-1,0,1)。我们可以用两个42的向量分别表示红方和黄方在每个局面是否有棋子。比如：

['-', '-', '-', 'O', '-', '-', '-']
['-', '-', '-', 'X', '-', '-', '-']
['-', '-', '-', 'O', '-', '-', '-']
['-', '-', '-', 'X', '-', '-', '-']
['-', 'X', '-', 'O', '-', '-', '-']
['-', 'X', 'O', 'X', '-', '-', '-']

我们最原始的表示方法为：

[0, 0, 0,-1, 0, 0, 0,
 0, 0, 0, 1, 0, 0, 0,
 0, 0, 0,-1, 0, 0, 0,
 0, 0, 0, 1, 0, 0, 0,
 0, 1, 0,-1, 0, 0, 0,
 0, 1,-1, 1, 0, 0, 0,
]

二值化之后变成两个长度为42的数组，第一个数组用来表示红方，如果只为1，表示这个位置是红旗，否则不是红旗（可能是空或者黄棋）。类似的，第二个数组用来表示黄方。最后把这两个长度为42的数组拼接成一个84的数组，这就是_binary()的输出。它的完整代码为：

	def _binary(self):
		currentplayer_position = np.zeros(len(self.board), dtype=np.int)
		currentplayer_position[self.board==self.playerTurn] = 1
		
		other_position = np.zeros(len(self.board), dtype=np.int)
		other_position[self.board==-self.playerTurn] = 1
		
		position = np.append(currentplayer_position,other_position)
		
		return (position)

_convertStateToId函数

这个函数和上面的_binary类似，它把得到的84个bit变成一个字符串，这样就可以唯一的表示一个局面。代码为：

	def _convertStateToId(self):
		player1_position = np.zeros(len(self.board), dtype=np.int)
		player1_position[self.board==1] = 1
		
		other_position = np.zeros(len(self.board), dtype=np.int)
		other_position[self.board==-1] = 1
		
		position = np.append(player1_position,other_position)
		
		id = ''.join(map(str,position))
		
		return id

_allowedActions函数

这个函数计算当前局面下合法的走法。参考图\ref{fig:az-connect4-3}，它是从位置0一直遍历到41，然后做如下判断：如果它是最后一行(i >= len(self.board) - 7)，那么只有它是空的(0)就可以走；否则要看它所在的列的下一行是否有棋子(不等于0)。

def _allowedActions(self):
	allowed = []
	for i in range(len(self.board)):
		if i >= len(self.board) - 7: # 如果是最后一行
			if self.board[i]==0: # 如果没被走过
				allowed.append(i)
		else:
			if self.board[i] == 0 and self.board[i+7] != 0: #i没棋子并且下一行i+7有棋子
				allowed.append(i)
	
	return allowed

这个实现并不是很高效，它的循环次数是42，更好的办法应该从每一列的最下往上走，遇到第一个非空的就加入到allowed里，有兴趣的读者可以自己修改一下看看训练速度是否有提高。它最好的情况循环7次，最坏42次。

当然更快的办法是“记下”每一列下一个走子位置，然后每走一步其就更新这一步对应的列的下一个走子位置。比如一上来7列的走子位置是[35,36,37,38,39,40,41]，接着如果红方走38，那么这个数组就更新为[35,36,37,38-7=31,39,40,41]。这个“增量”的算法不需要循环。

_checkForEndGame函数

这个函数用来判断游戏是否结束，有两种结束条件：42个格子都走满了；对手赢了(因为当前是“我”方走，所以只能是对方赢；如果“我”方走了一步制胜棋，那么这个时候轮到对手走棋，然后判断为“对手”也就是“我”方赢)。

def _checkForEndGame(self):
	if np.count_nonzero(self.board) == 42: # 走满
		return 1
	
	for x,y,z,a in self.winners:
		if (self.board[x] + self.board[y] + self.board[z] + self.board[a]
			 == 4 * -self.playerTurn):
			# 对手获胜
			return 1
	# 没结束
	return 0

当然，我们也可以使用“增量”的方式来实现更快的判断。我们需要记下当前局面走了步棋，如果走了42步就结束。另外判断对手获胜不要判断所有的可能，而只需要判断上一步棋“可能”连接成4子的那些winners。上面判断用了个小技巧，最直觉的判断应该是：

if self.board[x] == -self.playerTurn && self.board[y] == -self.playerTurn 
	&& self.board[z] == -self.playerTurn && self.board[a] == -self.playerTurn 

但是加法比多个逻辑判断要满，因为条件判断会使得CPU流水线失效。原来是4个条件，现在变成4个加法和一个条件，这样会快一些。当然如果使用bitboard表示，加法可以直接用位运算替代，速度更快。

_getValue函数

这个函数会返回当前局面的得分，返回的是3-tuple，第一个元素是这个局面“真实”的Value，如果对手获胜，那么值为-1，否则(没有结束或者平局结束)为0。第二个元素表示这个局面对于当前玩家来说的得分，第三个元素表示对于对手来说的得分。

	def _getValue(self):
		# This is the value of the state for the current player
		# i.e. if the previous player played a winning move, you lose
		for x,y,z,a in self.winners:
			if (self.board[x] + self.board[y] + self.board[z] + self.board[a]
				 == 4 * -self.playerTurn):
				return (-1, -1, 1)
		return (0, 0, 0)

如果对手获胜，那么返回(-1, -1, 1)；否则返回(0, 0, 0)。

_getScore函数

这个函数读取前面函数的第2和第3个元素，表示当前玩家的得分以及对手的得分。

	def _getScore(self):
		tmp = self.value
		return (tmp[1], tmp[2])

takeAction函数

走一步棋，返回新的状态，新状态的得分以及是否游戏结束。

def takeAction(self, action):
	newBoard = np.array(self.board)
	newBoard[action]=self.playerTurn
	
	newState = GameState(newBoard, -self.playerTurn)
	
	value = 0
	done = 0
	
	if newState.isEndGame:
		value = newState.value[0]
		done = 1
	
	return (newState, value, done) 

代码很简单，首先复制当前局面board到newBoard，然后在newBoard里加入当前棋子”newBoard[action]=self.playerTurn”。接着用这个newBoard构造一个新的GameState，需要把playerTurn反转。然后在判断是否游戏结束并且返回这个局面的Value。

训练主要代码

接下来我们看训练的主流程，代码为：

env = Game()

import config

######## LOAD MEMORIES IF NECESSARY ########

if initialise.INITIAL_MEMORY_VERSION == None:
	memory = Memory(config.MEMORY_SIZE)
else:
	memory = pickle.load(...)

######## LOAD MODEL IF NECESSARY ########

# create an untrained neural network objects from the config file
current_NN = Residual_CNN(config.REG_CONST, config.LEARNING_RATE, (2,) + env.grid_shape, 
	env.action_size, config.HIDDEN_CNN_LAYERS)
best_NN = Residual_CNN(config.REG_CONST, config.LEARNING_RATE, (2,) + env.grid_shape, 	
	env.action_size, config.HIDDEN_CNN_LAYERS)

# If loading an existing neural netwrok, set the weights from that model
if initialise.INITIAL_MODEL_VERSION != None:
	best_player_version = initialise.INITIAL_MODEL_VERSION
	print('LOADING MODEL VERSION ' + str(initialise.INITIAL_MODEL_VERSION) + '...')
	m_tmp = best_NN.read(env.name, initialise.INITIAL_RUN_NUMBER, best_player_version)
	current_NN.model.set_weights(m_tmp.get_weights())
	best_NN.model.set_weights(m_tmp.get_weights())
# otherwise just ensure the weights on the two players are the same
else:
	best_player_version = 0
	best_NN.model.set_weights(current_NN.model.get_weights())


######## CREATE THE PLAYERS ########

current_player = Agent('current_player', env.state_size, env.action_size, config.MCTS_SIMS, 
	config.CPUCT, current_NN)
best_player = Agent('best_player', env.state_size, env.action_size, config.MCTS_SIMS, 
	config.CPUCT, best_NN)

iteration = 0

while 1:

	iteration += 1
	
	print('ITERATION NUMBER ' + str(iteration))
	
	######## SELF PLAY ########
	print('SELF PLAYING ' + str(config.EPISODES) + ' EPISODES...')
	_, memory, _, _ = playMatches(best_player, best_player, config.EPISODES, 
		lg.logger_main,
		turns_until_tau0=config.TURNS_UNTIL_TAU0, memory=memory)
	print('\n')
	
	memory.clear_stmemory()
	
	if len(memory.ltmemory) >= config.MEMORY_SIZE:
	
		######## RETRAINING ########
		print('RETRAINING...')
		current_player.replay(memory.ltmemory)
		print('')
		
		if iteration % 5 == 0:
			pickle.dump(memory, open(run_folder + "memory/memory" + 	
				str(iteration).zfill(4) + ".p", "wb"))
		
		lg.logger_memory.info('====================')
		lg.logger_memory.info('NEW MEMORIES')
		lg.logger_memory.info('====================')
		
		memory_samp = random.sample(memory.ltmemory, min(1000, len(memory.ltmemory)))
		
		
		######## TOURNAMENT ########
		print('TOURNAMENT...')
		scores, _, points, sp_scores = playMatches(best_player, current_player, 	
			config.EVAL_EPISODES, lg.logger_tourney,
			turns_until_tau0=0, memory=None)
		print('\nSCORES')
		print(scores)
		print('\nSTARTING PLAYER / NON-STARTING PLAYER SCORES')
		print(sp_scores)
		# print(points)
		
		print('\n\n')
		
		if scores['current_player'] > scores['best_player'] * config.SCORING_THRESHOLD:
			best_player_version = best_player_version + 1
			best_NN.model.set_weights(current_NN.model.get_weights())
			best_NN.write(env.name, best_player_version)
	
	else:
		print('MEMORY SIZE: ' + str(len(memory.ltmemory)))

首先我们构造一个Game对象env，然后构造或者加载一个Memory对象。Memory对象用于存储自对弈的$(s, \pi, z)$，用于训练新的网络，后面我们会详细分析其代码。

接着构造current_NN和best_NN两个Residual_CNN，这是AlphaZero的神经网络。然后用这两个网络构造两个Agent：current_player和best_player。best_player是当前最佳的玩家，我们会用它来自对弈产生训练数据，然后用这些数据来训练current_player。定期它们俩会进行比赛，如果current_player战胜了best_player，那么就用current_player来替代best_player。

接下来的大循环”while 1”就是强化学习的过程。

这个循环首先继续自对弈：

_, memory, _, _ = playMatches(best_player, best_player, config.EPISODES, 
    lg.logger_main,
    turns_until_tau0=config.TURNS_UNTIL_TAU0, memory=memory)
    
if len(memory.ltmemory) >= config.MEMORY_SIZE:
    current_player.replay(memory.ltmemory)
	scores, _, points, sp_scores = playMatches(best_player, current_player, 
		config.EVAL_EPISODES, lg.logger_tourney,
		turns_until_tau0=0, memory=None) 
    if scores['current_player'] > scores['best_player'] * config.SCORING_THRESHOLD:
	    best_player_version = best_player_version + 1
	    best_NN.model.set_weights(current_NN.model.get_weights())
	    best_NN.write(env.name, best_player_version) 

这里调用playMatches让best_player自对弈，然后产生训练数据，放到memory里。接着用训练数据来训练current_player(前提是memory有足够数量的数据)。最后让current_player来“挑战”best_player。如果current_player获胜次数/best_player > 1.3，那么就认为挑战成功，用当前的模型替代最佳的模型，用新的模型来自对弈。否则还是保留老的best_player。

这就是AlphaZero的主训练流程，下面我们来分析里面的一些重要对象和函数。

Memory类

这个类存放用于训练current_player的数据。

构造函数

class Memory:
	def __init__(self, MEMORY_SIZE):
		self.MEMORY_SIZE = config.MEMORY_SIZE
		self.ltmemory = deque(maxlen=config.MEMORY_SIZE)
		self.stmemory = deque(maxlen=config.MEMORY_SIZE)

Memory对象有两个队列(deque)：ltmeory(long term?)和stmemory(short term?)。其中stmemory用于自对弈没有结束时存放的临时的$(s,\pi,z)$，因为在自对弈结束前我们是不知道对弈结果z的。当一次自对弈结束后，我们就可以把z回填进去，然后就把临时的训练数据放到ltmemory里，接着把stmemory清空，而ltmemory是不清空的（除非满了把老的挤出去）。

commit_stmemory

def commit_stmemory(self, identities, state, actionValues):
	for r in identities(state, actionValues):
		self.stmemory.append({
			'board': r[0].board
			, 'state': r[0]
			, 'id': r[0].id
			, 'AV': r[1]
			, 'playerTurn': r[0].playerTurn
			})

这个函数用于把一个状态state和它的Q(s,a)保存到临时的stmemory里。这里首先用identities函数进行对称的处理（实际传入的是Game.identities函数）,然后把它加入到stmemory里。它会存储GameState对象state，这个状态的棋盘表示board——这是长度为42的数组，id以及playerTurn，最后会存储Q(s,a)即actionValues。这里actionValues是一个长度42的数组，用于存储每个action的Value。注意虽然理论上有42种可能的action，但是每一步最多只有7种可能的值，也就是说长度42的数组最多7个非零。

commit_ltmemory

def commit_ltmemory(self):
	for i in self.stmemory:
		self.ltmemory.append(i)
	self.clear_stmemory()

这个函数的作用就是把临时内存stmemory里的训练数据放到训练内存ltmemory。然后调用函数clear_stmemory把stmemory清空。

clear_stmemory

def clear_stmemory(self):
	self.stmemory = deque(maxlen=config.MEMORY_SIZE)

清空stmemory(构造一个新的deque对象)。

Residual_CNN

这个类就是AlphaZero的网络$f_\theta(s)=[\textbf{p},v]$。

构造函数

class Residual_CNN(Gen_Model):
	def __init__(self, reg_const, learning_rate, input_dim,  output_dim, hidden_layers):
		Gen_Model.__init__(self, reg_const, learning_rate, input_dim, output_dim)
		self.hidden_layers = hidden_layers
		self.num_layers = len(hidden_layers)
		self.model = self._build_model()

Residual_CNN继承了Gen_Model，输入参数为：

reg_count 正则项权重，这里的值是0.0001
learning_rate 0.1
input_dim (2, 6, 7)
output_dim 42
hidden_layers 残差块的配置，这里为5个残差块，每个是残差块的有75个4x4的卷积核。

神经网络的输入是(2, 6, 7)，它是把输入局面(状态)按照红黄两方进行二值化后的特征，和之前介绍的MemoryState._binary类似，只不过输出是个3维的Tensor。具体实现是下面的convertToModelInput函数。

convertToModelInput

def convertToModelInput(self, state):
	inputToModel = state.binary
	inputToModel = np.reshape(inputToModel, self.input_dim) 
	return (inputToModel)

这个函数把状态state变成(2,6,7)的Tensor，它直接得到state.binary(84,)，然后reshape成(2,6,7)。

_build_model

构造函数的最后会调用这个函数来构造网络结构。

def _build_model(self):	
	main_input = Input(shape = self.input_dim, name = 'main_input')
	
	x = self.conv_layer(main_input, self.hidden_layers[0]['filters'], 
			self.hidden_layers[0]['kernel_size'])
	
	if len(self.hidden_layers) > 1:
		for h in self.hidden_layers[1:]:
			x = self.residual_layer(x, h['filters'], h['kernel_size'])
	
	vh = self.value_head(x)
	ph = self.policy_head(x)
	
	model = Model(inputs=[main_input], outputs=[vh, ph])
	model.compile(loss={'value_head': 'mean_squared_error', 'policy_head':	
						softmax_cross_entropy_with_logits},
		optimizer=SGD(lr=self.learning_rate, momentum = config.MOMENTUM),	
		loss_weights={'value_head': 0.5, 'policy_head': 0.5}	
	)
	
	return model

这里使用Keras来构造网络，首先是定义Input，然后第一层是卷积层(调用conv_layer)，接下来的4层是残差层(调用residual_layer)。然后调用value_head构造Value Head，调用policy_head构造Policy Head。定义模型Model，输入是main_input，输出是vh和ph。最后调用Model.compile进行编译，其中损失有两个：value_head是最小均方误差损失；policy_head是交叉熵损失。它们的权重都是0.5，优化器是带冲量的SGD。

conv_layer

这个函数构造卷积块，它又一个卷积层，Batch Normalization层和一个LeakyReLU组成，代码如下：

def conv_layer(self, x, filters, kernel_size):
	
	x = Conv2D(
		filters = filters
		, kernel_size = kernel_size
		, data_format="channels_first"
		, padding = 'same'
		, use_bias=False
		, activation='linear'
		, kernel_regularizer = regularizers.l2(self.reg_const)
		)(x)
	
	x = BatchNormalization(axis=1)(x)
	x = LeakyReLU()(x)
	
	return (x)

residual_layer

def residual_layer(self, input_block, filters, kernel_size):
	
	x = self.conv_layer(input_block, filters, kernel_size)
	
	x = Conv2D(
		filters = filters
		, kernel_size = kernel_size
		, data_format="channels_first"
		, padding = 'same'
		, use_bias=False
		, activation='linear'
		, kernel_regularizer = regularizers.l2(self.reg_const)
		)(x)
	
	x = BatchNormalization(axis=1)(x)
	
	x = add([input_block, x])
	
	x = LeakyReLU()(x)
	
	return (x)

残差层首先是一个卷积层(conv_layer)，然后是卷积，batch norm和skip connection，最后是激活函数。

value_head

def value_head(self, x):
	x = Conv2D(
		filters = 1
		, kernel_size = (1,1)
		, data_format="channels_first"
		, padding = 'same'
		, use_bias=False
		, activation='linear'
		, kernel_regularizer = regularizers.l2(self.reg_const)
		)(x)
	
	x = BatchNormalization(axis=1)(x)
	x = LeakyReLU()(x)
	
	x = Flatten()(x)
	
	x = Dense(
		20
		, use_bias=False
		, activation='linear'
		, kernel_regularizer=regularizers.l2(self.reg_const)
		)(x)
	
	x = LeakyReLU()(x)
	
	x = Dense(
		1
		, use_bias=False
		, activation='tanh'
		, kernel_regularizer=regularizers.l2(self.reg_const)
		, name = 'value_head'
		)(x)

	return (x)

Value Head的输入是(batch, 75, 6, 7)，首先经过一个1x1的卷积变成(batch, 1, 6, 7)。然后经过batch norm和激活，大小仍然是(batch, 1, 6, 7)，然后使用Flatten展开成(batch, 42)，接着是一个Dense层变成(batch, 20)，再来一个LeakyReLu，最后使用一个Dense变成(batch, 1)，并且把最后的输出命名为”value_head”，这个名字在前面compile使用到了。

policy_head

def policy_head(self, x):	
	x = Conv2D(
		filters = 2
		, kernel_size = (1,1)
		, data_format="channels_first"
		, padding = 'same'
		, use_bias=False
		, activation='linear'
		, kernel_regularizer = regularizers.l2(self.reg_const)
		)(x)
	
	x = BatchNormalization(axis=1)(x)
	x = LeakyReLU()(x)
	
	x = Flatten()(x)
	
	x = Dense(
		self.output_dim
		, use_bias=False
		, activation='linear'
		, kernel_regularizer=regularizers.l2(self.reg_const)
		, name = 'policy_head'
		)(x)
	
	return (x)

它的输入也是(batch, 75, 6, 7)，经过卷积变成(batch, 2, 6, 7)，batch norm，LeakyReLu大小不变，然后Flattern变成(batch, 84)，然后接一个全连接层变成(batch, 42)，它就是42个可能action的logits。

Gen_Model

基类Gen_Model里封装了用Keras进行训练预测的一些代码，代码比较简单直观：

def predict(self, x):
	return self.model.predict(x)

def fit(self, states, targets, epochs, verbose, validation_split, batch_size):
	return self.model.fit(states, targets, epochs=epochs, verbose=verbose, 
		validation_split = validation_split, batch_size = batch_size)

def write(self, game, version):
	self.model.save(run_folder + 'models/version' + "{0:0>4}".format(version) + '.h5')
 
def read(self, game, run_number, version):
	return load_model( run_archive_folder + game + '/run' + str(run_number).zfill(4) + 
		"/models/version" + "{0:0>4}".format(version) + '.h5', 
		custom_objects={'softmax_cross_entropy_with_logits': 
				 softmax_cross_entropy_with_logits})

Agent

核心代码都在Agent类里，但是为了便于理解，我们不直接阅读它的代码，而是分析训练的代码，再需要的地方我们“跳到”Agent相应的函数去阅读。我们再来看一些自对弈while循环里的代码：

_, memory, _, _ = playMatches(best_player, best_player, config.EPISODES, 
	lg.logger_main,
	turns_until_tau0=config.TURNS_UNTIL_TAU0, memory=memory)

if len(memory.ltmemory) >= config.MEMORY_SIZE:
	current_player.replay(memory.ltmemory)
	scores, _, points, sp_scores = playMatches(best_player, current_player, 
	config.EVAL_EPISODES, lg.logger_tourney,
	turns_until_tau0=0, memory=None) 
	if scores['current_player'] > scores['best_player'] * config.SCORING_THRESHOLD:
		best_player_version = best_player_version + 1
		best_NN.model.set_weights(current_NN.model.get_weights())
		best_NN.write(env.name, best_player_version)   

首先是调用funcs.py文件里的playMatches函数进行自对弈产生训练数据。然后是调用Agent(current_player).replay进行学习，最后再调用playMatches进行PK。因此最重要的两个函数就是playMatches和replay，我们下面逐个来分析。

playMatches函数

完整的代码较长，为了易读，这里把一些不太重要的代码去掉了。

def playMatches(player1, player2, EPISODES, logger, turns_until_tau0, memory = 
		None, 	goes_first = 0):

	env = Game()
	
	for e in range(EPISODES):
		state = env.reset()
		
		done = 0
		turn = 0
		player1.mcts = None
		player2.mcts = None
		
		
		while done == 0:
			turn = turn + 1
			
			#### Run the MCTS algo and return an action
			if turn < turns_until_tau0:
				action, pi, MCTS_value, NN_value = 
					players[state.playerTurn]['agent'].act(state, 1)
			else:
				action, pi, MCTS_value, NN_value = 
					players[state.playerTurn]['agent'].act(state, 0)
			
			if memory != None:
				####Commit the move to memory
				memory.commit_stmemory(env.identities, state, pi)
			
			
			### Do the action
			state, value, done, _ = env.step(action)
		 
			if done == 1: 
				if memory != None:
					#### 游戏结束时把最终的z写会到临时内存的所有走法里。
					for move in memory.stmemory:
						if move['playerTurn'] == state.playerTurn:
							move['value'] = value
						else:
							move['value'] = -value
					
					memory.commit_ltmemory()
				## 省略了一些统计对局胜负的统计信息。
	
	return (scores, memory, points, sp_scores)

上面的代码主要有两个大的for循环，第一个”for e in range(EPISODES)”是产生EPISODES(30)局自对弈；而第二个”while done == 0”是产生一局自对弈的每一个走法。我们来看第二个循环的核心代码：

if turn < turns_until_tau0:
	action, pi, MCTS_value, NN_value = players[state.playerTurn]['agent'].act(state, 1)
else:
	action, pi, MCTS_value, NN_value = players[state.playerTurn]['agent'].act(state, 0)

memory.commit_stmemory(env.identities, state, pi)

state, value, done, _ = env.step(action)

if done == 1:
	#### 游戏结束时把最终的z写会到临时内存的所有走法里。
	for move in memory.stmemory:
		if move['playerTurn'] == state.playerTurn:
			move['value'] = value
		else:
			move['value'] = -value
	memory.commit_ltmemory()	

首先是调用Agent的act来进行MCTS搜索然后选择一个action，这里有一个参数turns_until_tau0(10)，如果当前棋局总的走子次数小于它，那么选择action的时候按照概率$\pi(a|s)$随机选择；如果大于，则选择概率最大的走法。它的意思是开局阶段多探索，到后期就少探索了。

MCTS也会产生$\pi$，接着把state和pi存到临时内存stmemory里(这个时候还没有对弈结果z)。

然后调用Game(env).step(action)走一步棋。

如果游戏结束了，那么把step返回的value就是最终的结果，把它写到临时内存的每一个训练数据里。最好把临时内存的训练数据放到ltmemory并且情况stmemory。

Agent.act

这个函数会涉及最最核心的MCTS的代码，请读者仔细阅读，必要的时候可以往前参考论文。

def act(self, state, tau):
	
	if self.mcts == None or state.id not in self.mcts.tree:
		self.buildMCTS(state)
	else:
		self.changeRootMCTS(state)
	
	#### run the simulation
	for sim in range(self.MCTSsimulations):
		self.simulate()
	
	#### get action values
	pi, values = self.getAV(1)
	
	####pick the action
	action, value = self.chooseAction(pi, values, tau)
	
	nextState, _, _ = state.takeAction(action)
	
	NN_value = -self.get_preds(nextState)[0]

	return (action, pi, value, NN_value)

我们在一局自对弈中之后构造一次MCTS搜索树，之后会复用这棵树，这就是前面4行代码。这里除了”self.mcts == None”还有一个条件”state.id not in self.mcts.tree”，因为代码除了可以自对弈，也可以有人来和机器对弈，如果前一步是人走的，那么有可能之前的MCTS搜索树是没有这个节点的，这个时候也需要buildMCTS。

buildMCTS

def buildMCTS(self, state):
	self.root = mc.Node(state)
	self.mcts = mc.MCTS(self.root, self.cpuct)

它会创建一个Node对象和一个MCTS对象。

Node类

class Node():
	def __init__(self, state):
		self.state = state
		self.playerTurn = state.playerTurn
		self.id = state.id
		self.edges = []
	
	def isLeaf(self):
		if len(self.edges) > 0:
			return False
		else:
			return True

Node对应搜索树里的节点，表示一个状态，它的edges代表这个状态可能的走法。如果一个Node的edges是空，那么说明它没有被Expand，那么它就是叶子节点。

Edge类

class Edge():
	def __init__(self, inNode, outNode, prior, action):
		self.id = inNode.state.id + '|' + outNode.state.id
		self.inNode = inNode
		self.outNode = outNode
		self.playerTurn = inNode.state.playerTurn
		self.action = action
		
		self.stats =  {
			'N': 0,
			'W': 0,
			'Q': 0,
			'P': prior,
			}

Edge代表树中的边，代表一种走法，一个action，它有一个inNode和outNode，分别表示走之前和走之后的局面。它的id是起点的id和终点的id拼起来，中间加了一个’|‘。另外我们会在边上存储N(s,a),W(s,a),Q(s,a),P(s,a)

changeRootMCTS

def changeRootMCTS(self, state):
	self.mcts.root = self.mcts.tree[state.id]

如果某个节点之前以及MCTS搜索过了(在MCTS树里)，那么就可以复用它。这里只需要修改root就行了，这棵子树里的信息比如N(s,a),W(s,a)等还可以复用，从而加快后面MCTS的速度。

for sim in range(self.MCTSsimulations):
	self.simulate()

这就是最重要的MCTS的模拟过程，这是通过函数simulate来实现的。这里的代码是模拟50次。

simulate

def simulate(self):
	##### MOVE THE LEAF NODE
	leaf, value, done, breadcrumbs = self.mcts.moveToLeaf()
	leaf.state.render(lg.logger_mcts)
	
	##### EVALUATE THE LEAF NODE
	value, breadcrumbs = self.evaluateLeaf(leaf, value, done, breadcrumbs)
	
	##### BACKFILL THE VALUE THROUGH THE TREE
	self.mcts.backFill(leaf, value, breadcrumbs)

每次MCTS模拟首先根据UCT选择走法一直到叶子节点，这是通过mcts(MCTS类)的moveToLeaf函数实现。接着Expand和Evalute叶子节点，最后用叶子节点的Value更新这条路径上的所有边的统计信息。下面我们逐个来看。

MCTS

这个类封装一个MCTS树，它的构造函数是：

class MCTS():
	
	def __init__(self, root, cpuct):
		self.root = root
		self.tree = {}
		self.cpuct = cpuct
		self.addNode(root)

root记录MCTS的树根(当前要走棋的局面), tree是一个dict，key是Node.id，value是Node，这个dict的目的是快速根据Node的id找到Node。addNode代码就是往这个dict加Node：

def addNode(self, node):
	self.tree[node.id] = node

MCTS类最重要的函数就是moveToLeaf和backFill，前面的simulate会调用这两个函数。

def moveToLeaf(self):
	breadcrumbs = []
	currentNode = self.root
	
	done = 0
	value = 0
	
	while not currentNode.isLeaf():
		maxQU = -99999
		
		if currentNode == self.root:
			epsilon = config.EPSILON
			nu = np.random.dirichlet([config.ALPHA] * len(currentNode.edges))
		else:
			epsilon = 0
			nu = [0] * len(currentNode.edges)
		
		Nb = 0
		for action, edge in currentNode.edges:
			Nb = Nb + edge.stats['N']
		
		for idx, (action, edge) in enumerate(currentNode.edges):
		
			U = self.cpuct * \
				((1-epsilon) * edge.stats['P'] + epsilon * nu[idx] )  * \
				np.sqrt(Nb) / (1 + edge.stats['N'])
			
			Q = edge.stats['Q']
	 
			if Q + U > maxQU:
				maxQU = Q + U
				simulationAction = action
				simulationEdge = edge
		 
		newState, value, done = currentNode.state.takeAction(simulationAction)
		currentNode = simulationEdge.outNode
		breadcrumbs.append(simulationEdge)
		
	return currentNode, value, done, breadcrumbs

breadcrumbs用于存放从根到叶子节点经过的所有边，当backFill时会使用叶子节点的Value更新这些边上的Q(s,a),W(s,a)等统计信息。

接着就是一个大的while循环，根据UCT算法找当前节点最合适的走法(边)。

这里有epsilon和nu两个变量，用于UCT的计算。我们再来回顾一下UCT的公式：

\[\begin{split} a_t &= \underset{a}{argmax}(Q(s_t,a)+u(s_t,a)) \\ u(s,a) &= c_{puct}P(s,a)\frac{\sqrt{\sum_bN_r(s,b)}}{1+N_r(s,a)} \end{split}\]

$q(s,a)$直接就存在边上——edge.stats[‘Q’]，而u(s,a)比较复杂，我们一个一个来看。首先是分子里根号里的$\sum_bN_r(s,b)$，这是通过下面的代码来实现的：

for action, edge in currentNode.edges:
	Nb = Nb + edge.stats['N']

因此u(s,a)应该这样计算：

U = self.cpuct * edge.stats['P']  * np.sqrt(Nb) / (1 + edge.stats['N'])

但这里实际的代码却是：

U = self.cpuct * ((1-epsilon) * edge.stats['P'] + epsilon * nu[idx] )
	 * np.sqrt(Nb) / (1 + edge.stats['N'])

把$P(s,a)$变成了$(1-\epsilon)P(s,a)+\epsilon\nu(i)$。如果不是树根，那么$\epsilon=0$，两者是相同的，如果是树根$\epsilon$不是零(这里是0.2)，而nu是从dirichlet分布抽样的值。这样做的目的是让根节点的孩子有更多的探索机会，因为即使某个孩子的P(s,a)是零，U仍然可能大于零。

最终把Q+U就是当前走法的UCT，我们记录最大的UCT对于的走法(边)和孩子。

找到最大的UCT之后，我们就模拟执行这个action进入新的状态，同时把这个action(边)加到breadcrumbs里：

newState, value, done = currentNode.state.takeAction(simulationAction)
currentNode = simulationEdge.outNode
breadcrumbs.append(simulationEdge)

这个过程一直进行，直到叶子节点，最后返回的是4-tuple：(叶子节点、叶子节点的Value、游戏是否结束和breadcrumbs)。

MCTS类另外一个重要的函数就是backFill，用于更新breadcrumbs里边的统计信息。

def backFill(self, leaf, value, breadcrumbs):	
	currentPlayer = leaf.state.playerTurn
	
	for edge in breadcrumbs:
		playerTurn = edge.playerTurn
		if playerTurn == currentPlayer:
			direction = 1
		else:
			direction = -1
	
		edge.stats['N'] = edge.stats['N'] + 1
		edge.stats['W'] = edge.stats['W'] + value * direction
		edge.stats['Q'] = edge.stats['W'] / edge.stats['N']

注意叶子节点的得分value是相对于leaf.state.playerTurn来说的，比如叶子节点的玩家是红方，并且游戏结束，获胜的是黄方，因此value是-1。那么breadcrumbs的边如果playerTurn和叶子相同，那么它的得分是-1，否则是1。所以这里会计算breadcrumbs里边的direction，如果和叶子的playerTurn相同是1，否则是-1。接着更新N(s,a)和W(s,a)，最后根据它们计算Q(s,a)。

为什么要处理playerTurn呢？我们回顾一些网络的输入。它是一个(2, 6, 7)的Tensor，其一个(6, 7)代表当前玩家的棋子的信息；而后一个代表对手的信息。因此网络学习到的特征是不分先后手的，这和AlphaZero里的方法稍有不同。AlphaZero的P1永远代表先手，P2永远代表后手，然后有一个plane表示当前玩家是先手还是后手。这样我们可以认为它为P1学习了一个模型，为P2学习了另外一个模型(虽然它们会共享很多与先后手无关的知识)。而这里学到的知识是和先后手无关的。

simulate的另外一个重要函数是计算叶子节点的Value以及展开叶子节点。

def evaluateLeaf(self, leaf, value, done, breadcrumbs):
	
	if done == 0:
		value, probs, allowedActions = self.get_preds(leaf.state)
		
		probs = probs[allowedActions]
		
		for idx, action in enumerate(allowedActions):
			newState, _, _ = leaf.state.takeAction(action)
			if newState.id not in self.mcts.tree:
				node = mc.Node(newState)
				self.mcts.addNode(node) 
			else:
				node = self.mcts.tree[newState.id] 
			
			newEdge = mc.Edge(leaf, node, probs[idx], action)
			leaf.edges.append((action, newEdge))
		
	return ((value, breadcrumbs))

这个函数首先调用get_preds(leaf.state)计算V(s)和$P(a \vert s)$，返回值value就是V(s)，而probs和allowedActions就是$P(a \vert s)$，probs返回长度为42的数组，而这42个值中并不是所有的都是合法的走法，合法的走法在allowedActions里，它最多是7个值。

接着变量所有allowedActions，使用takeAction得到它的孩子节点。这个孩子节点如果以及在MCTS.tree里，那么直接拿到，否则创建一个新的Node加到MCTS.tree里。同时创建一个Edge，把$P(a \vert s)$存放到Edge.states[“P”]里。

上面会用到Agent.get_preds来计算叶子节点的Value和走棋概率。

def get_preds(self, state):
	inputToModel = np.array([self.model.convertToModelInput(state)])
	
	preds = self.model.predict(inputToModel)
	value_array = preds[0]
	logits_array = preds[1]
	value = value_array[0]
	
	logits = logits_array[0]
	
	allowedActions = state.allowedActions
	
	mask = np.ones(logits.shape,dtype=bool)
	mask[allowedActions] = False
	logits[mask] = -100
	
	#SOFTMAX
	odds = np.exp(logits)
	probs = odds / np.sum(odds)
	
	return ((value, probs, allowedActions))

首先用Gen_Model.convertToModelInput把输入状态变成(1,2,6,7)的网络输入，这个函数前面讲过了。注意Keras的输入都是带batch的，输出也是，因此即使输入是一个也得是一个batch。接着调用predict进行预测，输出两个值：value和policy的logits。输出也是batch的，所以取第一个值。

然后就是根据logits使用softmax函数计算概率。因为模型输出的是42个action的概率，只有allowedActions里的是合法的走法，因此把不合法的走法的logits都设置成-100(exp(-100)趋近于0)。

上面介绍完了一次simulate的过程，我们再回到act函数。

def act(self, state, tau):

	#### run the simulation
	for sim in range(self.MCTSsimulations):
		self.simulate()
	
	#### get action values
	pi, values = self.getAV(1)
	
	####pick the action
	action, value = self.chooseAction(pi, values, tau)
	
	nextState, _, _ = state.takeAction(action)
	
	NN_value = -self.get_preds(nextState)[0]
	
	return (action, pi, value, NN_value)

getAV函数根据N(s,a)来计算$\pi_a$，代码为：

def getAV(self, tau):
	edges = self.mcts.root.edges
	pi = np.zeros(self.action_size, dtype=np.integer)
	values = np.zeros(self.action_size, dtype=np.float32)
	
	for action, edge in edges:
		pi[action] = pow(edge.stats['N'], 1/tau)
		values[action] = edge.stats['Q']
	
	pi = pi / (np.sum(pi) * 1.0)
	return pi, values

接着根据计算的$\pi$来选择一个走法：

def chooseAction(self, pi, values, tau):
	if tau == 0:
		actions = np.argwhere(pi == max(pi))
		action = random.choice(actions)[0]
	else:
		action_idx = np.random.multinomial(1, pi)
		action = np.where(action_idx==1)[0][0]
	
	value = values[action]
	
	return action, value

如果$\tau$是零，那么选择概率最大的走法；否则按照概率随机选择。

接着执行action得到新的状态，并且用网络预测新状态的得分(这个只是用于比较走之前的胜负预测和走之后的预测，如果两者相差很大，说明模型学习的不好)。

Agent.replay

这个函数用于训练新的模型。

def replay(self, ltmemory):
  for i in range(config.TRAINING_LOOPS):
    minibatch = random.sample(ltmemory, min(config.BATCH_SIZE, len(ltmemory)))
    
    training_states = np.array([self.model.convertToModelInput(row['state']) for 
        row in minibatch])
    training_targets = {'value_head': np.array([row['value'] for row in minibatch])
      , 'policy_head': np.array([row['AV'] for row in minibatch])} 
    
    fit = self.model.fit(training_states, training_targets, epochs=config.EPOCHS, 
        verbose=1, validation_split=0, batch_size = 32)

代码其实很简单，首先从ltmemory随机采样一个minibatch的训练数据，然后把它转成合适的输入格式(batch, 2, 6, 7)，输出格式(batch, 1)和(batch, 42)。然后调用fit进行训练。

测试代码

jupyter notebook的训练Cell是个死循环，我们训练一定时间(一天一般就足够了)，就可以停止掉(Kernel->Interrupt)，注意，训练的过程会写入大量的日志，尤其是MCTS模拟的日志，训练一天可能会产生超过10GB的日志文件。如果空间不够，可以注释掉相关代码。

然后运行下面的Cell，让它预测第一步应该怎么走：

gs = GameState(np.array([
	0,0,0,0,0,0,0,
	0,0,0,0,0,0,0,
	0,0,0,0,0,0,0,
	0,0,0,0,0,0,0,
	0,0,0,0,0,0,0,
	0,0,0,0,0,0,0
	]), 1)

preds = current_player.get_preds(gs)

print(preds)

输出是：
(array([-0.02830422], dtype=float32), array([
0.        , 0.        , 0.        , 0.        , 0.        ,
0.        , 0.        , 0.        , 0.        , 0.        ,
0.        , 0.        , 0.        , 0.        , 0.        ,
0.        , 0.        , 0.        , 0.        , 0.        ,
0.        , 0.        , 0.        , 0.        , 0.        ,
0.        , 0.        , 0.        , 0.        , 0.        ,
0.        , 0.        , 0.        , 0.        , 0.        ,
0.0458048 , 0.13997355, 0.18774767, 0.23204002, 0.18951856,
0.15696892, 0.04794649], dtype=float32), [35, 36, 37, 38, 39, 40, 41])

在没有MTCS的情况下，它确实预测到了最好的走法(走第4列)。

Connect4规则简介

获取代码

代码阅读

游戏规则

Game类的构造函数

Game.reset函数

Game.step函数

identities函数

GameState的构造函数：

_binary函数

_convertStateToId函数

_allowedActions函数

_checkForEndGame函数

_getValue函数

_getScore函数

takeAction函数

训练主要代码

Memory类

构造函数

commit_stmemory

commit_ltmemory

clear_stmemory

Residual_CNN

构造函数

convertToModelInput

_build_model

conv_layer

residual_layer

value_head

policy_head

Gen_Model

Agent

playMatches函数

Agent.act

buildMCTS

Node类

Edge类

changeRootMCTS

simulate

MCTS

Agent.replay

测试代码

FEATURED TAGS

FRIENDS