本文介绍Connectionist Temporal Classification(CTC)的基本概念和原理，接着通过一个验证码识别的例子介绍CTC的实际用法。更多文章请点击深度学习理论与实战：提高篇。
目录
CTC简介
前面介绍过，对于语音识别来说，训练数据的输入是一段音频，输出是它转录的文字(transcript)，但是我们是不知道字母和语音是怎么对齐(align)的。这使得训练语音识别比看起来更加复杂。
要人来标注这种对齐是非常困难而且容易出错的，因为很多音素的边界是很难区分，比如下图，人通过看波形或者频谱是很难准确的区分其边界的。之前基于HMM的语音识别系统在训练声学模型是需要对齐，我们通常会让模型进行强制对齐(forced alignment)。类似的在手写文字识别中，也会存在同样的问题，虽然看起来比声音简单一下，但是如下图所示，字母T和h在手写的时候是粘连在一起的，传统的识别方法可以首先需要一个分割(segmentation)算法，然后再识别。而CTC不要求训练数据的对齐，因此非常适合语音识别和手写文字识别这种问题，这里我会以语音识别为例介绍CTC，而后面我们会通过示例介绍使用CTC来进行验证码识别。
图：CTC工作原理
图：语音识别
图：手写文字识别
接下来在正式介绍CTC的算法之前，我们引入一些记号更加形式化的描述CTC要解决的问题。首先我们假设输入序列$X=[x_1, x_2, …, x_T]$，比如在语音识别中，它是T个帧，每一帧$x_t$是39维的MFCC特征。输出序列是$Y=[y_1, y_2, …, y_U]$。这个任务我们很难把它转化为简单的分类任务，因为：
- X和Y都是变长的
- X和Y的长度比也是变化的(X和Y的长度不存在简单的比例对应关系)
- 训练数据中没有X和Y的对齐
和后面介绍的NLP的很多问题(比如词性标注，命名实体识别等)相比，虽然语音识别和它们都是序列标注问题，但是NLP的任务存在清晰的边界。NLP的输入和输出都是逻辑上的符号，每个符号的边界是显然的，但是如上图所示，语音信号的边界是模糊不清的。
CTC可以解决这些问题，给定一个输入X，CTC可以对所有可能的Y计算$P(Y \vert X)$。有了这个概率，我们就可以推断最可能的输出或者计算某个Y的概率。在训练的时候，我们需要计算损失函数，并且通过梯度下降调整参数使得损失在训练数据上最小。为了实现训练，我们需要一种高效快速的方法来计算条件概率$P(Y \vert X)$，而且还要求它是可导的，这样我们才能计算梯度。而在预测的时候，给定输入X，我们需要计算最可能的Y：
\[Y^*=\underset{Y}{argmax}P(Y|X)\]CTC虽然没有精确的算法来高效的计算最优路径，但是它提供近似的算法使得我们能在合理的时间内找到较优的路径。
CTC算法详解
给定X时，CTC算法可以计算所有输出Y的概率。理解计算这个概率的关键是CTC怎么处理输入和输出的对齐。因此我们首先讨论输入和输出的对齐问题。
对齐
CTC算法是不需要对齐输入和输出的，为了计算给定X的条件下输出Y的概率，CTC会枚举所有可能的对齐方式然后把这些概率累积起来。要理解CTC算法，我们首先需要理解对齐。
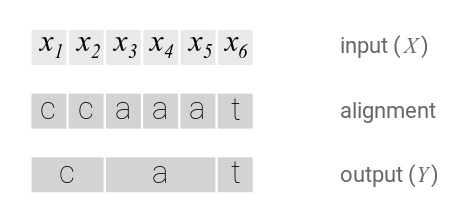
在介绍CTC的对齐之前，我们先看看一种简单的对齐方式。我们通过一个例子来说明它。我们假设输入长度为6，输出$Y=[c, a, t]$。一种简单的对齐方法是给每一个输入都对应Y中的一个字符（而且保证顺序）。比如如下图所示是一种合法的对齐方式，其中$x_1,x_2$对应c，$x_3,x_4,x_5$对应a，$x_6$对应t。
图：简单的对齐
这种简单的对齐有两个问题：
- 强制要求每个输入都对应实际的输出是不合理的，比如在语音识别中会有静音(silence)，这些输入不对应任何输出
- 没办法输出连续相同的字符，比如假设有一个单词caat，那么上面的对齐只能认为输出是cat。
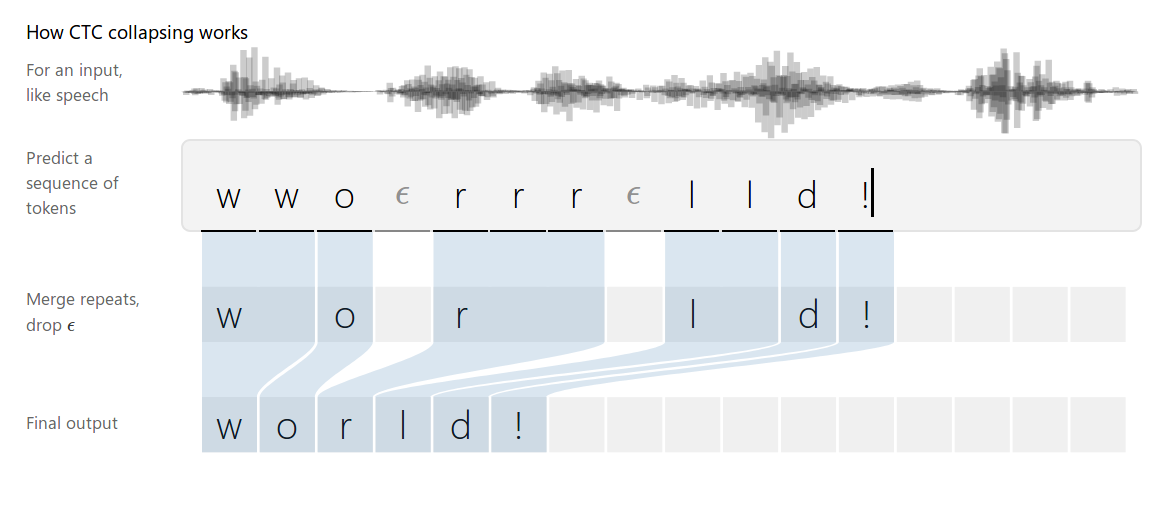
为了解决上述问题，CTC引入了一个新的特殊符号$\epsilon$，它表示空字符，在最后我们会去掉它。如下图所示，首先有些输入可以对应空字符，这样我们可以解决第一个问题。同样由于有了空字符，我们可以区分连续的字符。
图：CTC的对齐
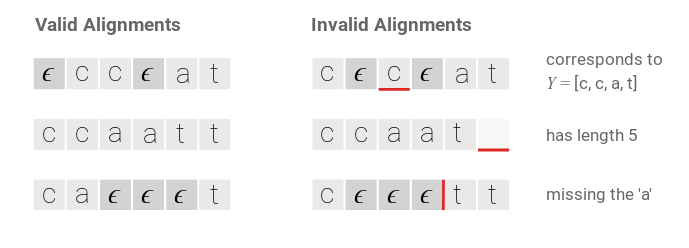
如果输出有两个连续相同的字符，那么它们之间一定要有至少一个空字符，这样我们就可以区分hello和helo了。对于之前长度为6的输入，输出为cat的例子，下图是一些合法的和非法的CTC对齐的例子。
图：CTC对齐示例
CTC对齐有如下一些特性。首先它是单调的，如果我们输入往前一步，那么输出可以保持不变，也可以往前一步。比如假设$x_1$是c，与之对于的y是c，我们往前走一步，有可能$x_2$还是c，那么y的输出是保持不变的。当然也可能$x_2$是a了，那么y的输出也往前走一步变成ca。第二个特点就是输入与输出是多对一的关系，输出的c可以对于$x_1,x_2$两个输入，但一个输入$x_1$只能对应一个输出。这个特性可以推出如下结论：输入序列的长度一定是大于等于输出长度的。
损失函数
有了CTC对齐之后，计算条件概率$P(Y \vert X)$就变得非常自然了，下图是计算过程的示意图，我们下面会详细介绍其计算过程。
图：CTC计算条件概率
在上图中，最上面是我们的输入序列，比如在语音识别中，输入是帧的序列，每一帧可以提取其MFCC作为其特征向量。然后我们可以把输入序列feed进一个RNN模型。这个RNN模型会计算每一个时刻t的输出的概率分布$p_t(a \vert X)$，表示t时刻输出字符a的概率，这这个例子里可能的字符是$\{h,e,l,o,\epsilon\}$。假设输入的长度为T，那么理论上有$5^T$中不同的对齐方式（路径），当然有些概率很低，我们可以忽略。这些路径中有一些的输出是一样的，比如都是”hello”，我们把它的概率加起来就得到了$P(“hello” \vert X)$的概率。
更加形式化地，假设一个输入输出对(X,Y)，我们有：
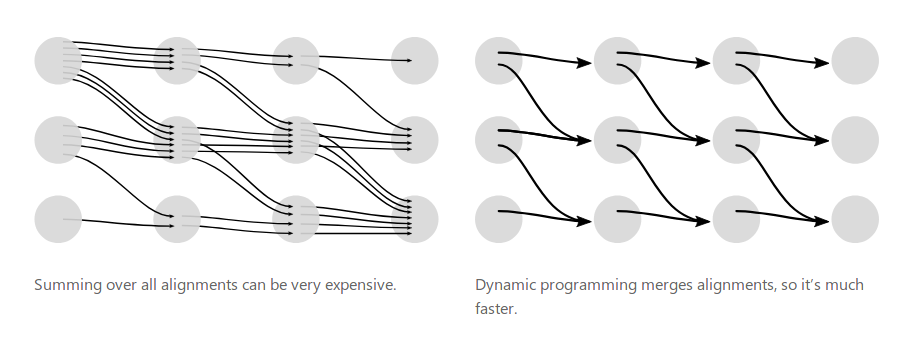
\[\begin{split} P(Y|X)= \underset{A \in \mathcal{A}_{X,Y}}{\sum} \prod_{t=1}^{T}p_t(a_t|X) \\ \end{split}\]在使用CTC的时候我们通常用RNN来估计每个时刻的输出$p_t(a_t \vert X)$。因为RNN可以很好的建模序列标注问题，但是CTC并没有要求一定用什么样的模型。给定X和Y，如果我们直接遍历所有的路径，那么效率会非常低，因为路径会随着T指数增加。不过我们可以使用动态规划技术来提高计算效率，这项技术在HMM里也用到过。
因为在输出Y的任意两个字符之间都可以对应空字符（比如语音识别的任意两个音素直接都可以有silence），所有我们在Y的每个字符直接都插入空字符得到$Z=[\epsilon, y_1, \epsilon, y_2, …, y_U, \epsilon]$。假设$\alpha_{s,t}$表示输入序列的前s个字符$X_{1:s}$和输出的前t个字符$Z_{1:t}$对齐时所有合法路径的概率和。有了t时刻之前的$\alpha$，我们就可以计算t时刻的$\alpha$，这样我们就能使用动态规划算法。最后得到T时刻的$\alpha$之后我们就可以得到$P(Y \vert X)$。
图：CTC的穷举和动态规划算法
我们在计算t时刻的$\alpha$的时候有两类情况：一类是对齐的时候可以不能跳过$z_{s-1}$的；另一类是能跳过$z_{s-1}$的。
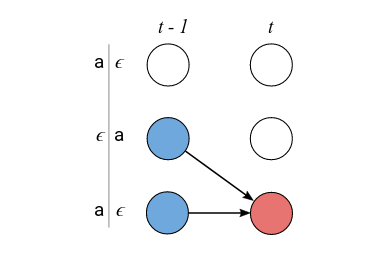
首先我们来看第一种情况，如下图所示。有两种条件是不能跳过$z_{s-1}$的，一种是$z_{s}=z_{s-2}$；另一种就是$z_s=\epsilon$。
我们先看第一种条件，比如图中所示$z_{s-2}=z_s=a$，现在我们要求输入$X_{1:t}$和输出$Z_{1:s}$对齐，因此$x_t$的输出是a或者空。那$X_{1:t-1}$可能和谁对齐呢？首先我们看$Z_{1:s}$，这是可能的，因为$x_{t-1}$输出a，而$x_t$也是输出a，所有输出Z的下标s不用后移。那么$Z_{1:s-1}$可能吗？这意味着$x_{t-1}$输出空，而$x_t$输出a，所以下标s和t同时后移一个。那么$Z_{1:s-2}$可能吗？这意味着$x_{t-1}$对齐$z_{s-2}$的a，而$x_t$对齐$z_s$的a，中间的空字符被跳过，这是不行的！因为连续两个时刻的输出都是a，而且中间没有空字符，那么输出只会有一个a。
类似的，如果$z_s=\epsilon$，假设$z_{s-1}=a$，那么$z_{s-2}$一定是$\epsilon$（请读者思考为什么）。那么$X_{1:t-1}$可以对齐到$Z_{1:s}$，这意味着$x_{t-1}$对齐$\epsilon$，而$x_t$也对齐$\epsilon$，两个连续的x都对齐空，这没有问题。还有一种情况就是$X_{1:t-1}$对齐到$Z_{1:s-1}$，这意味着$x_{t-1}$对齐到a，$x_t$对齐到a之后的$\epsilon$，下标s和t都后移一位。但是$X_{1:t-1}$能不能对齐到$Z_{1:t-2}$呢？这显然不行，因为输出的a被跳过了，没有输入和它对齐，这是不合法的对齐。
对于$z_{s-1}$不能被跳过的情况，我们可以得到：
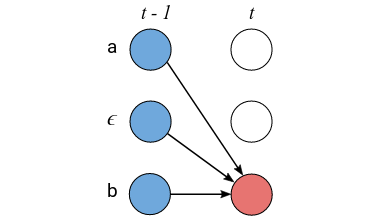
\[\alpha_{s,t}=(\alpha_{s-1,t-1} + \alpha_{s, t-1}) \cdot p_t(z_s|X)\]
图：不能跳过$z_{s-1}$的情况
第二种情况，如下图所示。$z_{s-2}=a, z_{s-1}=\epsilon, z_s=b$。和前面的分析一样，很明显$X_{1:t-1}$可以对齐到$Z_{1:s}$或者$Z_{1:s-1}$。那它能不能对齐到$Z_{1:s-2}$呢？这是可以的，因为可以让$x_{t-1}$对齐到a，$x_t$对齐到b，中间的$\epsilon$在这种情况下是可以跳过的。
对于第二种$z_{s-1}$可以被跳过的情况，我们有：
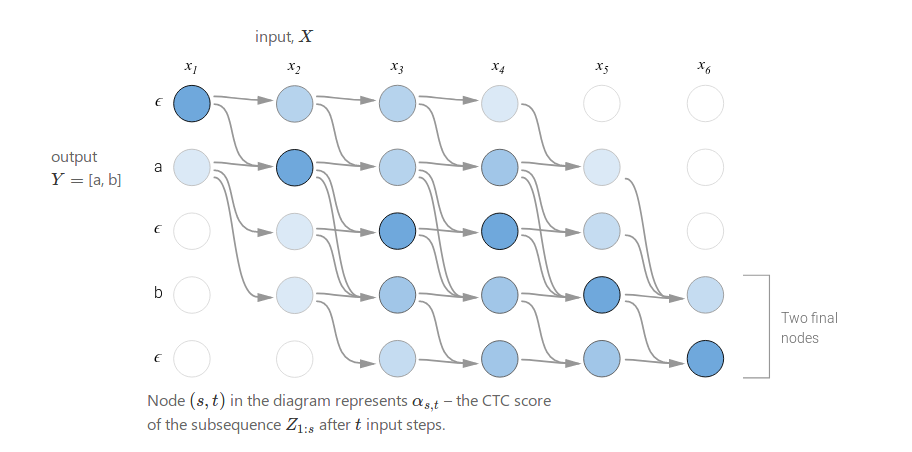
\[\alpha_{s,t}=(\alpha_{s-2,t-1} + \alpha_{s-1,t-1} + \alpha_{s, t-1}) \cdot p_t(z_s|X)\]
图：能跳过$z_{s-1}$的情况
有了前面的分析，我们就可以很容易的通过动态规划来计算$\alpha$了。计算过程如下图所示。在图中，输入为$x_1,…,x_6$，从左到右表示；输出为$\epsilon, a, \epsilon, b, \epsilon$，从上到下排列。$X_{1:1}=x_1$只有两种可能的对齐方式：$x_1$对齐到$\epsilon$或者a。我们可以验证前面的两种情况，拿第三行为例，第三行对应的$z_{s}=\epsilon$，所以第三行的点的入边只能是第三行或者第二行。这是第一种情况。而第四行对于的$z_{s}=b, z_{s-1}=\epsilon, z_{s-2}=b$，所以第四行的点的入边包括第四第三和第二行。
最后分析一下哪些节点是没有任何边经过的（也就是不在合法路径上）。首先第一列只有前两个是有边的，因为第一个输入只能对齐空或者第一个输出字符a；类似的最后一列之后最后两个是有边的，因为最后一个输入$x_6$要么对齐最后一个输出b要么对齐b之后的空。那第六行的第二列为什么是没有边的呢？因为它所在行是第一种情况，因此它的入边只能是第六行的第一列与第五行的第一列，这两个点都是无效的，因此它也是无效的。
这样我们就可以用动态规划高效的计算$P(Y \vert X)$，因为$P(Y \vert X)$是合法路径上点的累积，每个点对于$p_t(z_t \vert X)$，而$p_t(z_t \vert X)$又是一个可以求导的模型（比如RNN)，因此最终$P(Y \vert X)$是可以求导的。对于训练数据(X,Y)，我们的优化目标一般是最大化$P(Y \vert X)$，因此我们也可以定义损失函数为：
\[L=\underset{(X,Y) \in \mathcal{D}}{\sum}-log P(Y|X)\]
图：动态规划计算$\alpha$的过程
预测
模型训练好了之后，我们需要用它来预测最可能的结果。具体来说，我们需要解决如下问题：
\[Y^*=\underset{Y}{argmax}P(Y|X)\]最简单的方法是每一个时刻都选择概率最大的输出，这样可以得到概率最大的一条路径(一种对齐)：
\[A^*=\underset{A}{argmax}\prod_{t=1}^{T}p_t(a_t|X)\]最后我们把连续相同的字符合并，并去掉空字符就能得到最终的输出。对于有些应用，这种简单的方法是可以工作的，尤其是当模型的大部分概率集中在一条路径上的时候。但是另外一些应用可能有问题，因为一种输出可能对应多种可能的对齐，可能的情况是某种输出它的每种对齐分都不是特别高，但是加起来却很高。
举个例子，假设对齐$[a,a,\epsilon]$和$[a,a,a]$的概率都比$[b,b,b]$小，按照上面的算法我们会输出b，但是实际上$[a,a,\epsilon]$和$[a,a,a]$加起来的概率可能是大于$[b,b,b]$的，那么实际应该输出的是a。
我们可以使用一个改进版的Beam Search方法来搜索，虽然它不能保证找到最优解，但是我们可以调整beam的大小，beam越小，速度越快；beam越大，搜索的解越好。极限的情况是，如果beam是1那么它等价与前面的算法；如果beam是所有字母的个数，那么它会遍历所有路径，保证能找到最优解。
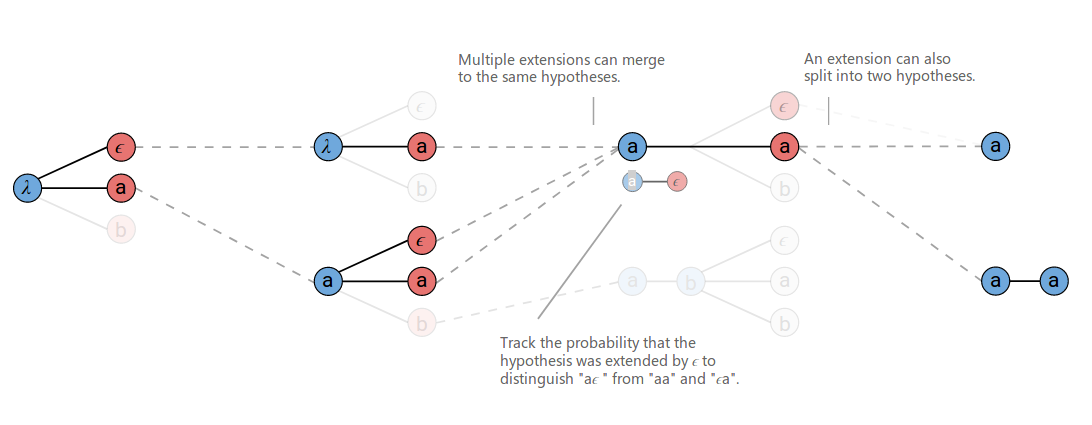
普通的Beam Search方法会在每个时刻保留最优的N条路径，然后在t+1时刻对这N条路径展开，然后从所有展开的路径中选择最优的N条路径，。。。，一直到最终时刻T。下图是使用普通Beam Search算法的示例。在图中，我们发现在t=3的时候，有两条路径的输出都是a(分别是$[a,\epsilon]$和$[\epsilon,a]$)，它们(有可能)是可以合并的（请读者思考为什么是有可能而不是一定？）。
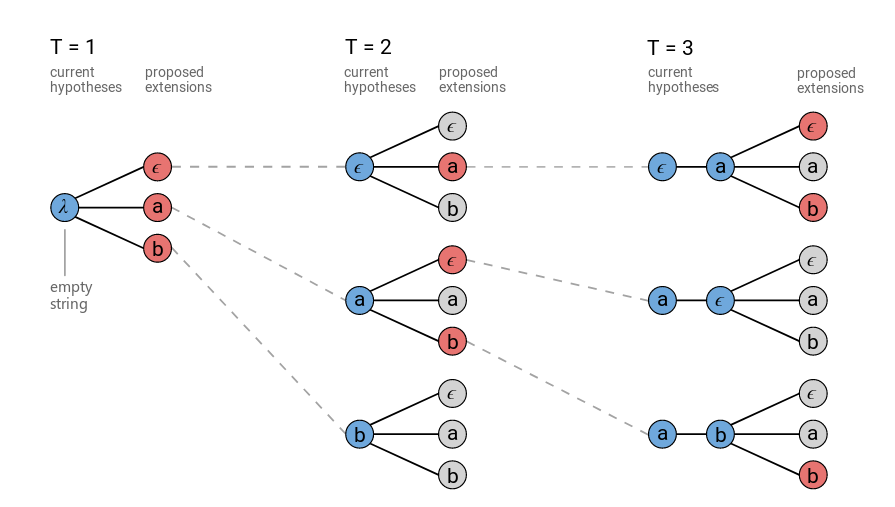图：普通的Beam Search算法，字母表为${a,b,\epsilon}$，beam大小是3
因此我们可以改进一些Beam Search算法，把相同输出的路径合并起来。这里的合并是把输出里相同的字符变成一个，并且去掉空字符，然后所有相同输出的概率累加起来。
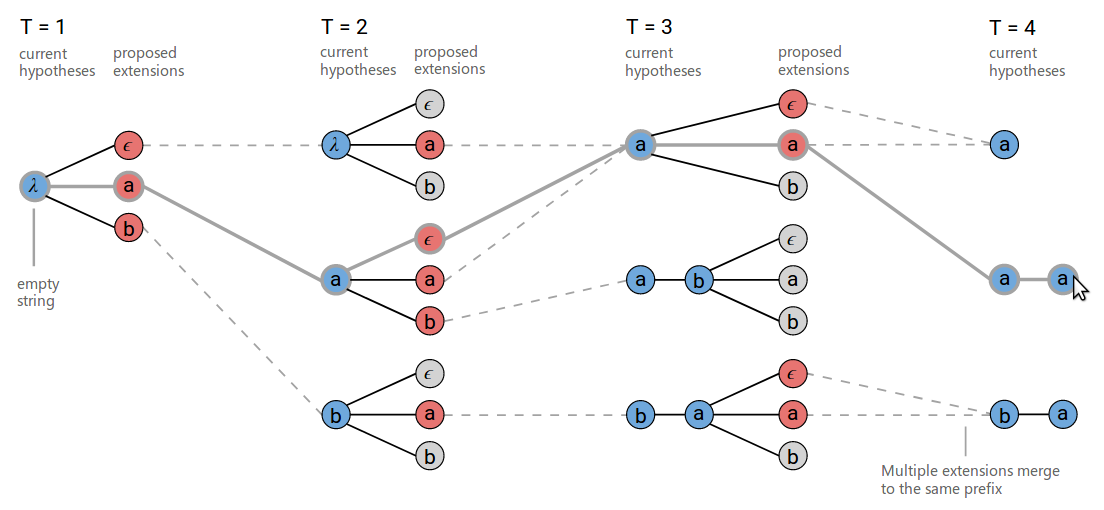
改进后的算法的搜索过程如下图所示。在t=3的时刻，在下方，$[b,a,\epsilon]$和$[b,a,a]$被合并成相同的结果$[b,a]$。另外需要注意的是t=3的时刻，上方$[a]$在扩展增加a的时候会输出两条路径$[a,a]$，与$[a]$。把两个a合并成一个这是显然的，但是不合并的路径需要注意。如下图所示，我们如果想在t=4时得到a-a。那么只有图中粗线条的一种路径($[a, \epsilon, a]$)，其它两条路径$[a,a,a]$和$[\epsilon,a,a]$都是无法输出a-a的，它们只能输出a。
为了区分，我们需要在t=2到t=3的合并的时候记下哪些路径的最后一个字符是空，哪些不是。在上图的例子中路径$[\epsilon,a]$和$[a,a]$的结尾不是空，而路径$[a,\epsilon]$的结尾是空，因此当t=3到t=4值遇到a的时候，前两条路径只能输出a，而后一条路径既能输出a也能输出a-a。
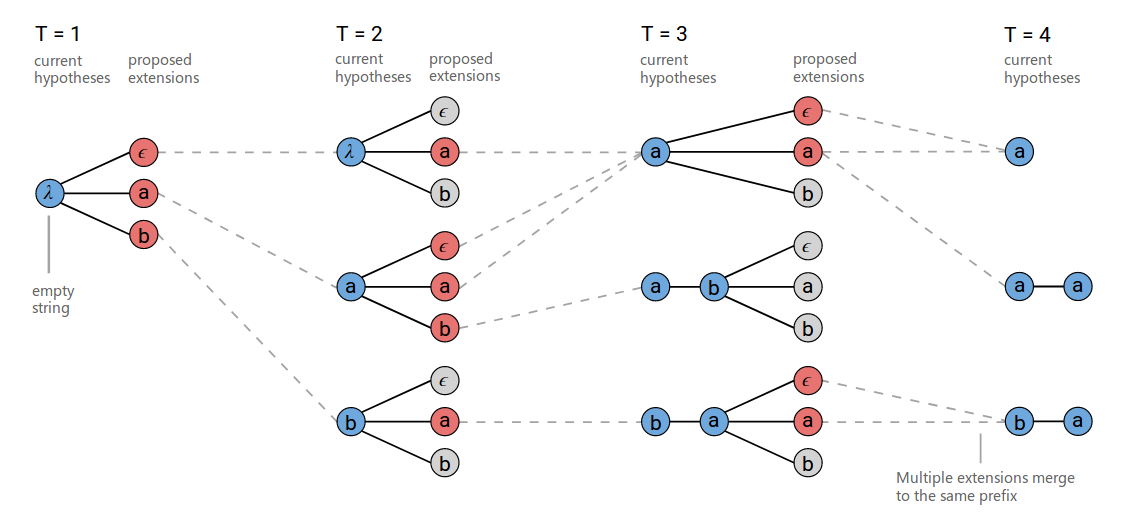图：改进的Beam Search算法，字母表为${a,b,\epsilon}$，beam大小是3
图：注意鼠标选中的aa的粗线条路径
因此我们可以再次改进搜索算法，如下图所示，在合并的时候，我们会记下以空结尾的路径的概率和。
图：在合并的时候记录是否有空结尾的路径以及它们的概率和
在语音识别中，我们一般需要在加入一个语言模型来提高识别效果，我们可以很容易的把语言模型集成进来：
\[Y^*=\underset{Y}{argmax}p(Y|X) \cdot p(Y)^\alpha \cdot L(Y)^\beta\]$P(Y)$就是语言模型，而$L(Y)$是一个语言模型长度的奖励，如果$L(Y)$是基于词的语言模型，那么$L(Y)$就是词的个数，如果$L(Y)$是基于字符(character)的语言模型，那么$L(Y)$就是字符的个数。因为越长的句子概率越小，如果不加这个奖励的话，语言模型总是会倾向于选择短的句子。超参数$\alpha$和$\beta$通常通过交叉验证来选择。
CTC算法的特性
条件独立
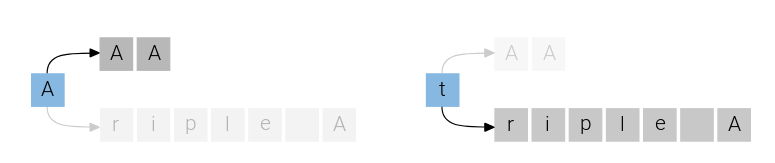
CTC经常被诟病的一个特点就是它的条件独立性。这个模型假设给定X的时候不同时刻的$y_t$是独立的，这个假设对于很多序列标注问题来说是不合理的。假设一个语音是要说”三个A“，它有两种说法：”三个A(triple A)”;”AAA”。如果第一个输出是A，那么第二个输出A的概率应该变大；类似的如果第一个输出是t（英文的triple的t)，那么输出triple A的概率更大，如下图所示。但是CTC无法建模这种关系。
图：triple A和AAA
也就是说CTC是无法建模输出序列之间的依赖关系的（不是说它无法建模输入序列的依赖关系！），也就是它不会学到任何语言模型的知识。因此像前面所说的，我们一般会加入额外的一个语言模型。但换个角度，这其实并不是坏事！因为让CTC只学习声学特征，而把语言学特征交个单独的语言模型，这会让它切换到一个新的领域变得更简单——我们只需要换另外一个领域的语言模型就可以了。
对齐
CTC算法不需要训练数据对齐，它会把所有相同输出的对齐合并。虽然CTC要求输入X和输出Y严格对齐，但是具体怎么对齐它并没有在模型层面加任何限制，是把概率比较均匀的分配给所有可能的路径还是把概率集中的分配给某些路径，这是不能确定的。
CTC要求对齐的方式是单调的，这对于语音识别是合适的假设，但是对于其它的任务，比如机器翻译，这种对齐是不合适的。因为一个不同语言的语序是不同的，比如英语a friend of mine和我的朋友，在英语里，friend在mine之前，但是在汉语里”我的”在”朋友”之前。
CTC的另外一个要求就是输入和输出是多对一的，有的任务可以要求严格的一对一关系，比如词性标注，那CTC也是不合适的。另外它也无法表示输入与输出的多对一的关系。比如在英语中，th是一个音素，一个输入可能要对于th这两个输出，CTC也是无法表示这种关系的。
最后一个就是CTC要求输出比输入短，虽然这在语音识别是合理的假设，但是其它的任务可能就不一定。
使用CTC进行变长验证码识别
问题描述和解决方法
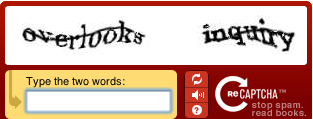
验证码的英文单词是CAPTCHA，它是”Completely Automated Public Turing test to tell Computers and Humans Apart”的缩写。它是一些任务，它的特点是人类很容易解决但是计算机很难解决(这不就是AI要实现的目标吗？)。这些任务可以用于防止计算机攻击系统，比如在12306提交火车票前需要输入验证码，如果计算机不能识别，那么就很难用一个程序自动刷票。我们这里介绍最常见的视觉验证码问题，也就是识别做过加噪声、扭曲和变形的字符串，如下图所示。
图：Captcha示例
我们要识别的验证码的字符个数是变化的，一种办法是先切割，然后再识别。但是验证码为了增加机器破解的难度，会加入很多噪音、粘连等操作，使得切割变得困难。我们可以用前面介绍过的CTC算法来解决这个问题。前面我们介绍的CTC解决的是序列的问题，但是和一维的语音不同，图像是二维的数据，不能直接用CTC。不过一般的文字的数字都是有方向的，比如我们这里生成的验证码是从左到右的，因此我们可以把图像的宽度(从左往右)看成序列的时间维度，而高度(从上往下)可以看成特征，这样我们就可以用上CTC了。比如输入的图像是64 x 40，我们可以认为输入序列的长度是40，每一个时刻的特征是64维。然后我们可以简单的把这个序列输入到LSTM中，然后使用CTC就可以了。不过实际这种方法收敛比较慢。
这里我们使用CNN+RNN+CTC的方法：首先把图像通过卷积，然后再把它输入到RNN中，最后用CTC来计算损失和预测。TensorFlow自带了tf.nn.ctc_loss，但是效率并不高，我们这里使用百度开源的WarpCTC。WarpCTC是一个CTC的并行实现，开源用多核并行或者GPU来加速。它是C++语言编写的代码，但是提供Tensorflow和PyTorch（非官方）的绑定(binding)。我们这里使用TensorFlow的绑定，它的实现原理是：warpCTC首先编译成一个动态库(libwarpctc.so)，然后在TensorFlow里实现一个自定义的Operation来使用这个动态库。由于WarpCTC最近没有太多的维护，所有和新版本的TensorFlow的基础有一些问题，所有首先介绍怎么安装WarpCTC以及TensorFlow的绑定。
安装WarpCTC
注：这是作者一年多前写的内容，当时作者是从源代码安装的Tensorflow 1.6.0，使用的是CUDA-9.1。如果读者是通过pip安装的，有些步骤可能需要注意和作者的环境差别。在最新版本的Tensorflow上作者没有尝试过，安装过程请参考WarpCTC官网，本节内容仅供参考。
得到tensorflow源代码
git clone https://github.com/tensorflow/tensorflow.git
git checkout r1.6.0
说明：如果读者使用的Tensorflow版本是别的版本，请checkout到相应的版本。
设置环境变量TENSORFLOW_SRC_PATH
#export TENSORFLOW_SRC_PATH=/path/to/tensorflow
读者请把这个环境变量设置成自己的路径。
修改配置
对于GCC5，我们需要加入C++选项 -D_GLIBCXX_USE_CXX11_ABI=0。
另外如果是新版本的Tensorflow，会出现import warpctc_tensorflow时会出现undefined symbol: _ZTIN10tensorflow8OpKernelE。 根据这个issue 以及知乎文章，我们需要链接时使用tensorflow_framework.so
此外新版本的Tensorflow nsync_cv.h文件的位置也会发生变化，因此需要做如下修改：
lili@lili-Precision-7720:~/codes/warp-ctc$ git diff CMakeLists.txt
diff --git a/CMakeLists.txt b/CMakeLists.txt
index cdb4b3e..ec20845 100644
--- a/CMakeLists.txt
+++ b/CMakeLists.txt
@@ -6,6 +6,7 @@ ENDIF()
project(ctc_release)
+set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -D_GLIBCXX_USE_CXX11_ABI=0 -L /home/lili/py3-env/lib/python3.5/site-packages/tensorflow -ltensorflow_framework")
上面是我做的修改，请读者根据自己的环境修改 tensorflow_framework.so的路径，也就是GCC的-L参数，作者的位置是/home/lili/py3-env/lib/python3.5/site-packages/tensorflow。
lili@lili-Precision-7720:~/codes/warp-ctc$ git diff tensorflow_binding/setup.py
...
--- a/tensorflow_binding/setup.py
+++ b/tensorflow_binding/setup.py
@@ -52,11 +52,13 @@ root_path = os.path.realpath(os.path.dirname(__file__))
tf_include = tf.sysconfig.get_include()
tf_src_dir = os.environ["TENSORFLOW_SRC_PATH"]
-tf_includes = [tf_include, tf_src_dir]
+tf_includes = [tf_include, tf_src_dir, ("/home/lili/py3-env/lib/python3.5/site-packages/tensorflow/include/external/nsync/public")]
...
extra_compile_args = ['-std=c++11', '-fPIC']
+extra_compile_args += [ '-D_GLIBCXX_USE_CXX11_ABI=0']
...
-
+import tensorflow as tf
+TF_LIB=tf.sysconfig.get_lib()
+print(TF_LIB)
ext = setuptools.Extension('warpctc_tensorflow.kernels',
sources = lib_srcs,
language = 'c++',
include_dirs = include_dirs,
- library_dirs = [warp_ctc_path],
+ library_dirs = [warp_ctc_path, TF_LIB],
runtime_library_dirs = [os.path.realpath(warp_ctc_path)],
- libraries = ['warpctc'],
+ libraries = ['warpctc','tensorflow_framework'],
extra_compile_args = extra_compile_args)
setup.py需要修改3个地方，第一个就是tf_includes里增加nsync_cv.h头文件的路径；第二个就是增加C++选项-D_GLIBCXX_USE_CXX11_ABI=0；第三个就是在setuptools.Extension里增加tensorflow_framework库和它的路径。
build
cd warp-ctc
mkdir build; cd build
cmake ..
make
安装
python setup.py install
测试安装是否成功
python
import warpctc_tensorflow
如果没有错误信息，那就说明成功了，否则读者需要根据错误反馈自行解决。
运行代码
首先需要安装依赖captcha，这会用来生成验证码(训练数据)。
pip install captcha
git clone https://github.com/fancyerii/lstm_ctc_ocr.git
cd lstm_ctc_ocr
./train.sh
代码阅读
我们这里介绍最新的beta版的代码，它的效果最好，经过几万次的迭代就能达到97%以上的准确率。
数据处理
最早的版本训练的时候提前把数据用验证码生成器生成出来，现在最新的版本是每次训练的时候实时的生成图片，这样不需要读取磁盘，但是CPU消耗更高。当然最主要的好处是每次都是完全不同的图片，这相对于有无穷多的训练数据，避免过拟合到特定的数据上。
生成验证码图片的代码注意在lib/lstm/utils/gen.py。它会使用captcha包的ImageCaptcha类来生成验证码。
def generateImg():
captcha=ImageCaptcha(fonts=[cfg.FONT])
if not os.path.exists(cfg.FONT):
print('cannot open the font')
theChars=gen_rand()
data=captcha.generate_image(theChars)
return np.array(data),theChars
生成的图像是彩色的，这里会把它转换成灰度图。生成了一个batch的数据后需要把它们整理成一个batch的数据：
def groupBatch(imgs,labels):
max_w = -sys.maxsize
time_steps = []
label_len = []
label_vec = []
img_batch = []
nh = cfg.IMG_HEIGHT
for i,img in enumerate(imgs):
if cfg.NCHANNELS==1: h,w = img.shape
else: h,w,_ = img.shape
nw = int(nh/h*w)
max_w = max(max_w,nw)
imgs[i] = cv2.resize(img,(nw,nh))
time_steps.append(nw//cfg.POOL_SCALE+cfg.OFFSET_TIME_STEP) # 这句代码的解释在后面
code = [encode_maps[c] for c in list(labels[i])]
label_vec.extend(code)
label_len.append(len(labels[i]))
max_w = math.ceil(max_w/cfg.POOL_SCALE)*cfg.POOL_SCALE
for img in imgs:
if cfg.NCHANNELS==1: h,w = img.shape
else: h,w,_ = img.shape
img = cv2.copyMakeBorder(img,0,0,0,max_w-w,cv2.BORDER_CONSTANT,value=0).
astype(np.float32)/255.
img = img.swapaxes(0, 1)
img = np.reshape(img,[-1,cfg.NUM_FEATURES])
img_batch.append(img)
return img_batch,label_vec,label_len,time_steps
上面的代码会把一个batch的图像保持宽高比的缩放，缩放后使得所有图片的高度都是32。然后把所有的图片都变成最大的宽度，它使用opencv的copyMakeBorder函数。这个函数会把输入图片复制到目标图像的正中间，然后其余像素的值通过插值得到。这样就保证所有的输入是一样大小的。当然CTC并不要求输入是定长的，这里为了简单就先处理成一样大小的输入了。
另外有一个小的trick就是这一行代码：
max_w = math.ceil(max_w/cfg.POOL_SCALE)*cfg.POOL_SCALE
它保证缩放后图像的宽度是cfg.POOL_SCALE(默认4)的整数倍，后面会解释为什么。实际在生成训练需要的图片时，会使用多个进程来提高效率，这里借鉴了Keras的代码，感兴趣的读者可以阅读gen.py里的GeneratorEnqueuer类，这里因为和算法本身关系不大，就不赘述了。
network.py
这个类把常见的网络层做了封装，比如：
@layer
def conv(self, input, k_h, k_w, c_o, s_h, s_w, name, c_i=None, biased=True,relu=True,
padding=DEFAULT_PADDING, trainable=True):
self.validate_padding(padding)
if not c_i: c_i = input.get_shape()[-1]
convolve = lambda i, k: tf.nn.conv2d(i, k, [1, s_h, s_w, 1], padding=padding)
with tf.variable_scope(name) as scope:
init_weights = tf.contrib.layers.xavier_initializer()
init_biases = tf.constant_initializer(0.0)
kernel = self.make_var('weights', [k_h, k_w, c_i, c_o], init_weights, trainable, \
regularizer=self.l2_regularizer(cfg.TRAIN.WEIGHT_DECAY))
if biased:
biases = self.make_var('biases', [c_o], init_biases, trainable)
conv = convolve(input, kernel)
if relu:
bias = tf.nn.bias_add(conv, biases)
return tf.nn.relu(bias)
return tf.nn.bias_add(conv, biases)
else:
conv = convolve(input, kernel)
if relu:
return tf.nn.relu(conv)
return conv
代码把卷积操作进行了封装，需要注意的是函数前面的@layer，这是Python的Decorator。当我们调用conv函数的时候，首先变成调用layer的layer_decorated函数：
def layer(op):
def layer_decorated(self, *args, **kwargs):
# Automatically set a name if not provided.
name = kwargs.setdefault('name', self.get_unique_name(op.__name__))
# Figure out the layer inputs.
if len(self.inputs)==0:
raise RuntimeError('No input variables found for layer %s.'%name)
elif len(self.inputs)==1:
layer_input = self.inputs[0]
else:
layer_input = list(self.inputs)
# Perform the operation and get the output.
layer_output = op(self, layer_input, *args, **kwargs)
# Add to layer LUT.
self.layers[name] = layer_output
# This output is now the input for the next layer.
self.feed(layer_output)
# Return self for chained calls.
return self
return layer_decorated
比如我们调用conv(args, kwargs)，就会变成调用layer_decorated，并且op对象就是conv函数。layer_decorated会使用op()进行真正的调用，然后把结果保存到self.layers[name]里。最后通过self.feed(layer_output)把当前op的结果放到self.inputs里作为下一步输入。network.py封装了很多常见的网络层，这里不详细介绍了。
LSTM_train类
这个类继承了Network类，是真正实现CNN-LSTM-CTC的地方。它的代码其实很简单，它只实现了构造函数和setup函数，我们先看构造函数：
class LSTM_train(Network):
class LSTM_train(Network):
def __init__(self, trainable=True):
self.inputs = []
#N*t_s*features*channels
self.data = tf.placeholder(tf.float32, shape=[None, None, cfg.NUM_FEATURES ], name='data')
self.labels = tf.placeholder(tf.int32,[None],name='labels')
self.time_step_len = tf.placeholder(tf.int32,[None], name='time_step_len')
self.labels_len = tf.placeholder(tf.int32,[None],name='labels_len')
self.keep_prob = tf.placeholder(tf.float32)
self.layers = dict({'data': self.data,'labels':self.labels,
'time_step_len':self.time_step_len,
'labels_len':self.labels_len})
self.trainable = trainable
self.setup()
构造函数首先定义4个placeholder：输入图像data，其shape是(batch, width, 32)；输出labels；labels_len；time_step_len。假设batch=2，两个样本的输出是[[1,2],[3,4,5]]，那么labels=[1,2,3,4,5]，labels_len=[2,3]。因为warpctc要求的输出是这种一维展开的形式化，同样的time_step_len也是每一个样本的输入长度，虽然我们这里把输入变成一样长(类似于padding)，但是CTC其实不要求定长。接下来把这4个placeholder都放到dict里，key是变量名。然后调用setup函数。
def setup(self):
(self.feed('data')
.conv_single(3, 3, 64 ,1, 1, name='conv1',c_i=cfg.NCHANNELS)
.max_pool(2, 2, 2, 2, padding='VALID', name='pool1')
.conv_single(3, 3, 128 ,1, 1, name='conv2')
.max_pool(2, 2, 2, 2, padding='VALID', name='pool2')
.conv_single(3, 3, 256 ,1, 1, name='conv3_1')
.conv_single(3, 3, 256 ,1, 1, name='conv3_2')
.max_pool(1, 2, 1, 2, padding='VALID', name='pool2')
.conv_single(3, 3, 512 ,1, 1, name='conv4_1', bn=True)
.conv_single(3, 3, 512 ,1, 1, name='conv4_2', bn=True)
.max_pool(1, 2, 1, 2, padding='VALID', name='pool3')
.conv_single(2, 2, 512 ,1, 1, padding = 'VALID', name='conv5', relu=False)
.reshape_squeeze_layer(d = 512 , name='reshaped_layer'))
(self.feed('reshaped_layer','time_step_len')
.bi_lstm(cfg.TRAIN.NUM_HID,cfg.TRAIN.NUM_LAYERS,name='logits'))
代码其实很直观，即使不去读conv_single的代码，我也能猜测其含义。我们这里通过输入Tensor的shape的变化来分析它的网络结构。
假设输入是(batch, 100, 32)，这里100是width,32是固定的height，这里和一般的图像表示方法不同，width在前，相当于图像做了个转置。因为我们这里是把width看成序列的时间轴，height看成特征。
1. 输入(batch, 100, 32)
2. conv1 -> (batch, 100, 32, 64) #默认的padding是same，所以大小不变
3. pool1 -> (batch, 50, 16, 64)
4. conv2 -> (batch, 50, 16, 128)
5. pool2 -> (batch, 25, 8, 128)
6. conv3_1 -> (batch, 25, 8, 256)
7. conv3_2 -> (batch, 25, 8, 256)
8. pool2 -> (batch, 25, 4, 256) # 注意这个max_pool会让width不变,height变小为一半
9. conv4_1 -> (batch, 25, 4, 512)
10. conv4_2 -> (batch, 25, 4, 512)
11. pool3 -> (batch, 25, 2, 512)
12. conv5 -> (batch, 24, 1, 512) # 这个卷积的kernel是2x2,而且没有padding(VALID)，因此width和height都减1
13. reshaped_layer -> (batch, 24*1, 512)
通过卷积，我们把高度从32压缩为1，把宽度变成100/4-1=24。最终得到(batch, 24, 512)的Tensor，把它当成长度为24的序列，序列的每个时刻的特征是512维的。然后把它输入到双向的LSTM里。
(self.feed('reshaped_layer','time_step_len')
.bi_lstm(cfg.TRAIN.NUM_HID,cfg.TRAIN.NUM_LAYERS,name='logits'))
time_step_len是长度为batch的整数列表，每个元素表示样本输入的长度，在这里是定长，而且是widht/4-1。这可以gen.py的如下代码中看到：
time_steps.append(nw//cfg.POOL_SCALE+cfg.OFFSET_TIME_STEP)
其中cfg.POOL_SCALE=4,cfg.OFFSET_TIME_STEP=-1
我们来看一下双向rnn的代码：
@layer
def bi_lstm(self, input, num_hids, num_layers, name,img_shape = None ,trainable=True):
img,img_len = input[0],input[1]
if img_shape:img =tf.reshape(img,shape = img_shape )
with tf.variable_scope(name) as scope:
lstm_fw_cell = tf.contrib.rnn.LSTMCell(num_hids//2,state_is_tuple=True)
lstm_bw_cell = tf.contrib.rnn.LSTMCell(num_hids//2,state_is_tuple=True)
output,_ = tf.nn.bidirectional_dynamic_rnn(lstm_fw_cell,lstm_bw_cell,img,img_len,dtype=tf.float32)
output = tf.concat(output,axis=2)
lstm_out = output
shape = tf.shape(img)
batch_size, time_step = shape[0],shape[1]
lstm_out = tf.reshape(lstm_out,[-1,num_hids])
init_weights = tf.contrib.layers.variance_scaling_initializer(factor=0.01,
mode='FAN_AVG', uniform=False)
init_biases = tf.constant_initializer(0.0)
W = self.make_var('weights', [num_hids, cfg.NCLASSES], init_weights, trainable, \
regularizer=self.l2_regularizer(cfg.TRAIN.WEIGHT_DECAY))
b = self.make_var('biases', [cfg.NCLASSES], init_biases, trainable)
logits = tf.matmul(lstm_out,W)+b
logits = tf.reshape(logits,[batch_size,-1,cfg.NCLASSES])
logits = tf.transpose(logits,(1,0,2))
return logits
代码其实很简单，请注意Tensor的shape的变换，理解了它基本代码就理解了。
参数num_hids=512
img=input[0]=reshaped_layer=(batch, 24, 512)
img_len=input[1]=time_step_len=(batch,) # 如前面的分析，这个示例batch里每一个样本的长度都是100/4-1=24
output,_ = tf.nn.bidirectional_dynamic_rnn -> output是双向的结果，两个shape是(batch, 24, 256)的Tensor
output = tf.concat(output,axis=2) -> output(batch, 24, 512)
lstm_out = tf.reshape(lstm_out,[-1,num_hids]) -> lstm_out(batch*24, 512)
logits = tf.matmul(lstm_out,W)+b -> logits(batch*24, NCLASSES)
logits = tf.reshape(logits,[batch_size,-1,cfg.NCLASSES]) -> logits(batch, 24, NCLASSES)
logits = tf.transpose(logits,(1,0,2)) -> logits(24, batch, NCLASSES) #因为warpctc要求时间主序。
接下来我们看一些怎计算CTC的Loss以及CTC decoder的用法，代码在network.py，请注意注释里Tensor的shape：
def build_loss(self):
time_step_batch = self.get_output('time_step_len') # (batch, )
logits_batch = self.get_output('logits') # (24, batch, NCLASSES)
labels = self.get_output('labels') # 展开的labels[[1,2,3],[4,5]] -> [1,2,3,4,5]
label_len = self.get_output('labels_len') # labels_len [3,2]
ctc_loss = warpctc_tensorflow.ctc(activations=logits_batch,flat_labels=labels,
label_lengths=label_len,input_lengths=time_step_batch)
loss = tf.reduce_mean(ctc_loss)
decoded, log_prob = tf.nn.ctc_beam_search_decoder(logits_batch,
time_step_batch, merge_repeated=True)
dense_decoded = tf.cast(tf.sparse_tensor_to_dense(decoded[0], default_value=0), tf.int32)
#...
return loss,dense_decoded
我们来看一下warpctc_tensorflow.ctc，它有4个参数：
- activations 3维的float Tensor，要求shape是(time, batch, NCLASSES)，是logits,CTC自己会对logits进行softmax
- flat_labels 1维的整数 Tensor，是输出的拼接
- label_lengths 输出的长度数组
- input_lengths 输入长度
- blank_label 空字符的ID，必须是0
它的输出是一个Tensor，对应每个输入的loss(-log概率)。因此对它进行reduce_mean就得到平均的损失。
接下来介绍ctc_beam_search_decoder，它的输入是：
- inputs 3维Tensor, (time, batch, NCLASSES)，也是没有进行softmax的logits
- sequence_length, 1维Tensor (batch)，表示每个样本的长度
- beam_width beam search的宽度
- top_paths 每个时刻保留top N个最优路径
- merge_repeated 默认True。比如路径是[b,a,a]如果为True，则合并成[b,a]
输出是一个Tuple(decoded, log_probabilities)：
-
decoded 长度为top_paths的list，表示最优的top_paths条路径。
其中decode[i]是一个SparseTensor，表示一条路径
-
log_probability (batch_size x top_paths)，表示路径的概率。
- 显示Disqus评论(需要科学上网)