本文介绍依存句法分析,包括基本原理和代码示例。更多文章请点击深度学习理论与实战:提高篇。
目录
- 简介
- 依存关系(Dependency Relation)
- 依存句法分析的定义
- 基于转换的(transition-based)依存句法分析算法
- 创建Oracle
- 算法
- 特征
- 效果评估
- 基于转换的依存句法分析代码示例
简介
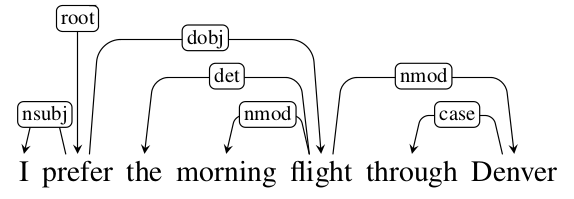
和成分句法分析不同,依存句法分析并不关注短语成分,而是直接关注词本身以及词之间的二元依存关系。比如下图所示,句子的中心词是动词prefer,它依赖于一个主语(nsub)”I”和一个直接宾语(dobj)flight。而flight依赖于定冠词(det)”The”、名词修饰词(nmod)”morning”和名词修饰词”Denvor”。而Denvor依赖于”through”。没有任何词依赖prefer,但是习惯上构造一个特殊的词”root”,它依赖于”prefer”。
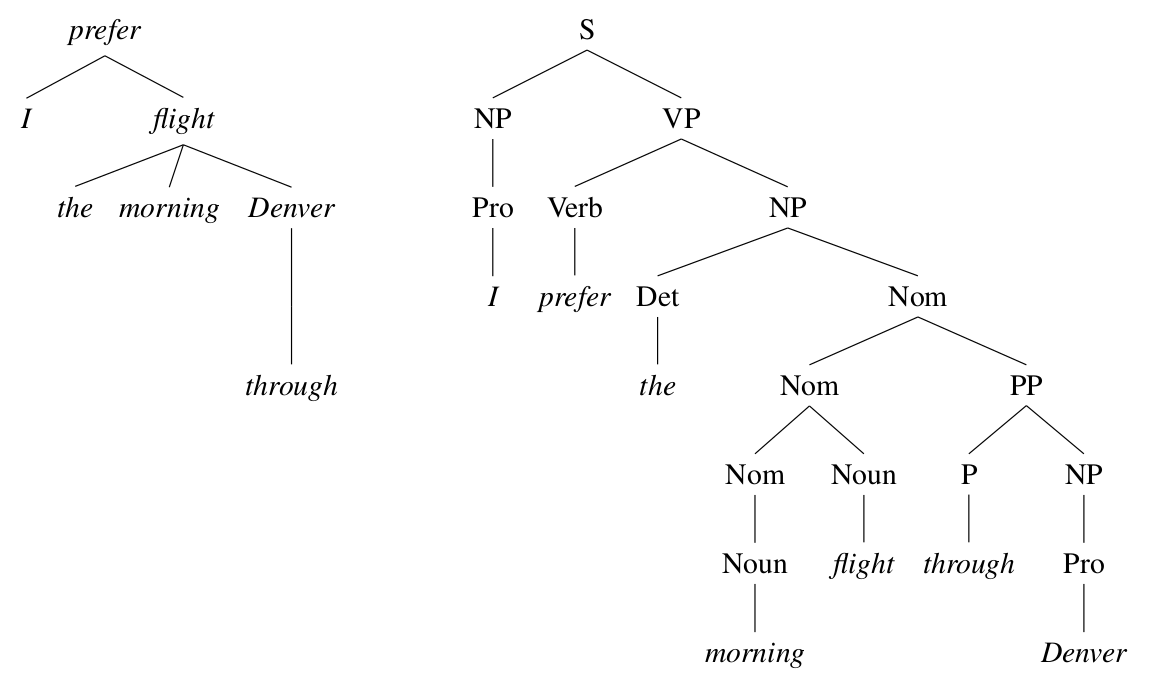
如下图所示,和成分句法分析相比,依存句法分析更加直接的分析出句子的主语谓语等成分。另外一点,依存句法分析的结果里,词的关系更加直接。比如上面的例子中动词prefer的直接宾语是flight,在依存句法分析树中,直接有prefer到flight的边,而在成分句法分析中这种关系是不直接的(但是也是有的)。
依存关系(Dependency Relation)
传统的语法关系(Grammatical Relation)是依存关系的基础,但是依存关系只是二元的关系。每一种依存关系都有一个中心词(Head)和一个依赖(Dependent),比如前面例子里的nsubj表示了prefer和I直接的依存关系是谓词依赖一个主语。语言学家定义了很多中依存关系,不同的语言可能也不一样。
在自然语言处理处理实践中不同的依存树库会使用不同的依存关系定义,当然一些最基本的关系是所有的树库都会有。对于英语来说,最常用的依存树库是Standord Dependency。它定义了一系列依存关系,并且提供工具从PTB把成分句法分析树转成依存句法树。当然对于中文,也有CTB转换成的中文依存树库。但是不同的语言都需要定义一套依存关系会比较麻烦,因此Stanford NLP Group定义了Universal Dependencies,这是一套使用与任何语言的依存关系集合,不过目前还属于早期推广阶段,有兴趣的读者可以点击这里了解更多细节。
依存句法分析的定义
作为最一般的形式,依存句法分析的结果是一个有向图G=(V, A),V代表节点,句子中的每一个词都对于一个节点。而A表示有向边(Arc),表示词之间的有依存关系,边有一个标签(label)表示具体的依存关系(比如prefer与I是nsub的关系)。但是通常我们假设依存分析的结果是一棵树(一种特殊的有向图),它满足如下条件:
- 有一个特殊的树根节点,它没有入边(例子中的prefer)
- 其它节点有且仅有一条入边(但是可以有多个或者零个出边)
- 对于每一个叶子节点(词),存在且仅存在一条从根到它的路径
这些条件可以保证每个词只有一个head(入边),它是连通的(每个词都可以有从根到它的路径)。因此我们通常把依存分析的结果表示成一棵依存树。除此之外,有的算法还要求依存树是Projective的。这个性质有点类似与CFGs的上下文无关特性。
我们首先定义边(arc)满足Projective的条件:假设这条边连接的是$w_i$和$w_j$,其中$i < j$,它的中心词是head(是$w_i,w_j$中的一个)。如果对于i和j之间的每一个词,都存在一条从head到它的路径,那么这条边就满足Projective性质。
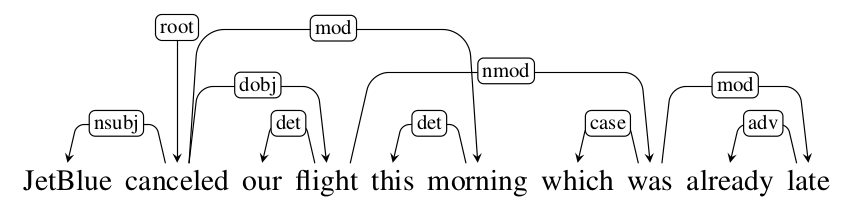
如果一棵依存树的每条边都满足Projective性质,那么这棵树就满足Projective性质。比如下图所示的依存树(请读者验证这是一棵树),有一条从flight(head)到was的边,它们之间包含3个单词”this morning which”,flight有到which的路径(flight->was->which),但是flight到”this”和”morning”都没有路径可达。因此这条边不满足Projective。
更加容易理解的说法是:如果一棵依存树是不满足projectivity性质的,那么画出来的这棵依存树至少有两条边是要相交的;而满足projectivity性质的依存树可以画出来而且没有边相交。比如上图我们可以看到”canceled->morning”和”flight->was”这两边是相交的。这种说法更加形式化的定义为:如果两条边对应的节点是(i, j)以及(k, l),这里$i<j$并且$k<l$。因为对称性,我们假设$i<k$。如果$j<k$或者$j>l$,那么它就是满足projectivity性质的。通过成分分析树转换得到的依存句法树都是满足projective性质的。
基于转换的(transition-based)依存句法分析算法
接下来我们介绍基于转换的算法来进行依存句法分析。基于转换的依存句法分析算法是受shift-reduce算法的启发。shift-reduce算法是一个用于parse CFGs的算法,它有一个栈(stack)和一个带处理的词的队列(queue)。刚开始stack是空,而队列包含了句子中所有词。每一步它有两种操作:把队列中的一个元素插入到stack中;把stack顶部的两个元素合并(reduce)成一个元素。通过这样的方法扫描一遍输入得到parsing tree,有兴趣的读者可以参考wiki。
基于转换的算法也有一个栈和一个词队列,除此之外还有一个已经parse的依存关系。这三个数据结构组合在一起叫作一种configuration。而在每种配置的时候有一个分类器来判断到底应该采取什么操作。
arc-standard算法
有很多种定义操作集合的方法,我们这里介绍最常见的arc standard方法,它包含如下3种操作:
- LEFT-ARC 栈顶和它下面的词构成依存关系,并且中心词是栈顶元素,把这两个词从栈中弹出,把这个依存关系加入到已parse的数据结构里,最后把中心词再加到栈中
- RIGHT-ARC 栈顶和它下面的词构成依存关系,中心词是下面的元素,把这两个词从栈中弹出,把这个依存关系加入到已parse的数据结构里,最后把中心词再加到栈中
- SHIFT 把队列中的一个词加入到栈顶
有了上面的操作,我们就可以实现如下图所示的算法。这个算法很简单,初始状态栈里只有一个root,而队列里是所有的词,然后循环直到状态是结束状态(栈中只有root,队列也为空)。循环的每一步是根据当前状态(配置)使用Oracle函数选择合适的操作,然后执行这个操作。注意:如果Oracle函数不”好”,那么最终的parse结果可能是错误的,但是可以证明对于任意一棵满足projective性质的依存树,都至少存在一个操作序列,使得这个操作序列可以得到正确的依存树。我们这里不做证明。而我们的模型需要根据训练数据学习到在不同的配置下应该采取怎么样的操作以便能得到正确的依存树。
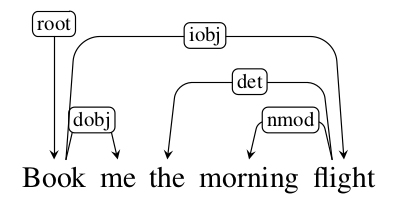
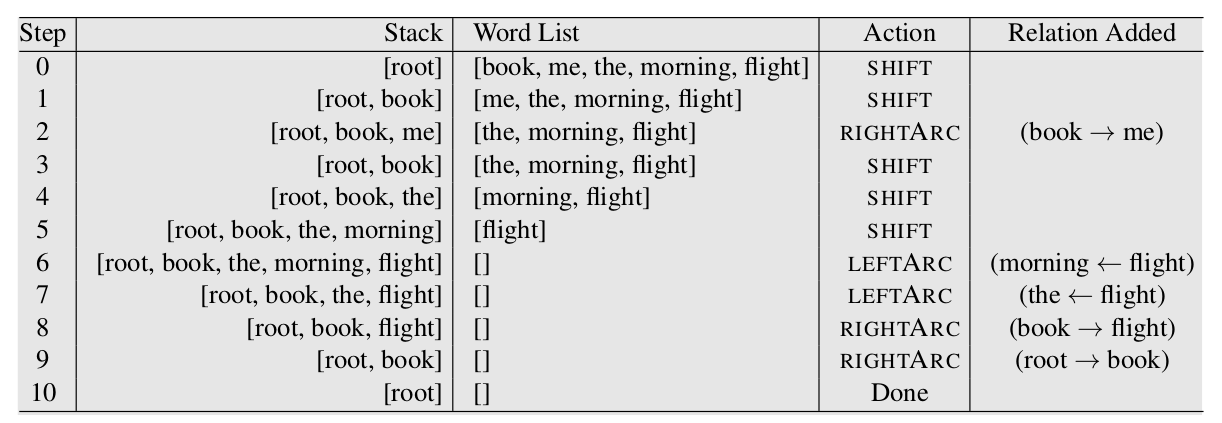
上面介绍的有些抽象,我们通过一个例子来说明它。比如句子”Book me the morning flight”,正确的依存树如下图所示。我们来看什么样的操作序列可以得到这棵树。
下图是一个正确的操作序列,注意,对于一个依存树,可能同时存在多于一个正确的操作序列。
下面我们来详细的分析这个过程。在第0步,状态是初始状态——栈里只有”root”,队列里是”[book, me, the, morning, flight]”,而已经parse的依存关系是空。前两步只能是SHIFT,因为栈里少于两个元素,不能LEFT-ARC或者RIGHT-ARC。第2步的操作是ARC-RIGHT,得到关系book -> me。注意栈顶在右边,因此ARG-RIGHT就是栈顶第二个元素指向栈顶的方向就是右。
接下来三个操作都是SHIFT,把”the morning flight”三个词都压倒栈中。这个时候栈中的元素为”[root, book, the, morning, flight]”,接下来的操作是LEFT-ARCT,得到关系”morning <- flight”,然后又是LEFT-ARC,得到”the <- flight”。最后两个RIGHT-ARC得到”book -> flight” 和”root -> book”。最终栈中只有root,而队列为空,parse结束。
上面的过程有一些需要注意的地方。首先正确的操作序列不是唯一的,前面我们已经提到过了。其次我们的算法要求Oracle函数每次都能找到正确的操作,这是一种贪心算法。如果Oracle不能找到正确的操作,由于这个算法没有任何回溯机制,那么它就得不到正确的依存树。最后上面介绍的是简化版本,我们只考虑两个词之间是否有依存关系,而没有考虑具体是什么类型的依存关系,实际的Oracle函数不但要输出一个操作,而且还有输出边上的label,比如可能输出LEFT-ARC(nsub)。这个时候模型输出就不是3个分类了,而是$3 \times \vert \text{依存关系集合}\vert$。
可以证明(这里略过):转换算法得到的依存树是满足projective性质的;对于每一个projective的依存树,至少存在一个操作序列可以得到这棵依存树。此外,长度为n个词的句子,操作序列的长度为2n,每个词都出队并且入栈一次(n次SHIFT操作),并且每个词都出栈一次。
arc-standard算法是一种自底向上(bottom-up)的算法,对于X->Y,只有当Y的子树都构造好了之后才会(能)把它们加到parse结果里,否则就得推迟到Y的子树都构建好了才能执行产生X->Y的操作。这让模型的学习变得困难,因为它要保存很长时间的记忆。
arc-eager算法
另外一种常见的算法就是arc-eager算法,它的操作集合为:
- SHIFT 和前面一样,把队列头部的元素出队,放到栈顶
- LEFT-ARC 和前面不一样,产生依存关系stack[-1] <- queue[0],然后把stack[-1]弹出(queue[0]不动)
- RIGHT-ARC 和之前不同,产生依存关系 stack[-1] -> queue[0],并且把queue[0]出队压入栈顶。
- REDUCE 弹出栈顶元素
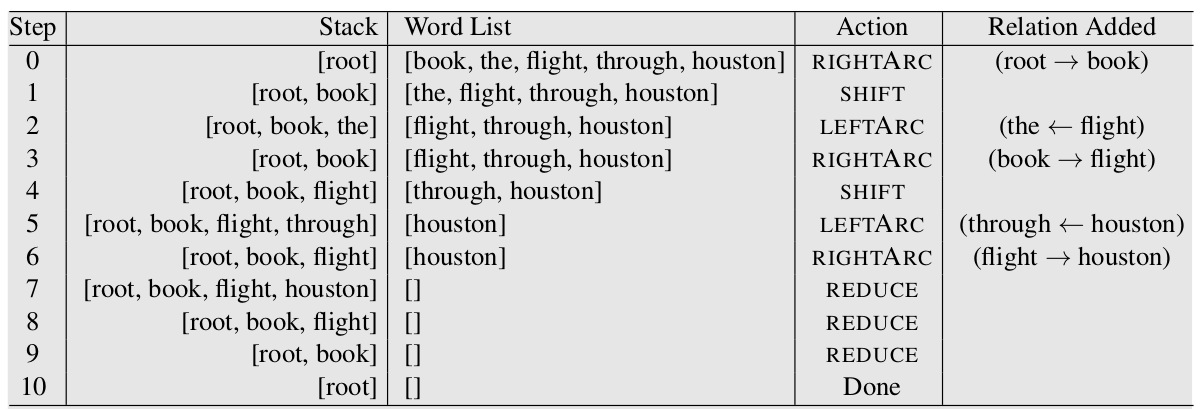
arc-eager多了一个REDUCE操作,并且RIGHT-ARC和LEFT-ARC的定义也发生了变化。arc-standard处理的是栈顶的两个元素,而arc-eager处理的是栈顶和队列头部的这两个元素。arc-eager的LEFT-ARC会减少一个元素,而RIGHT-ARC不会。下图是arc-eager算法的操作过程,它的输入还是之前的”Book the flight through Houston”。
我们可以对比一下不同之处。arc-standard里,root->book是最后等book的所有依赖(子树)都处理完了才加入。而在arc-eager里,root->book是第一个加入的,因此arc-eager是一种自顶向下(top-down)的方法。
和arc-standard类似,arc-eager有如下性质:arc-eager转换算法得到的依存树是满足projective性质的;对于每一个projective的依存树,至少存在一个操作序列可以得到这棵依存树。此外,长度为n个词的句子,操作序列的长度最多为2n。
创建Oracle
因此基于转换的依存句法分析算法的核心是训练一个分类器,它的输入是一个配置(状态),输出是一个操作。分类器当然我们很熟悉了,但是训练数据怎么得到呢?我们有的是一个依存树库,它包含很多句子和对应的依存树。我们怎么从这个依存树库得到用于Oracle的训练数据呢?
Oracle是一个函数,它的输入是一个正确的依存树,输出是一个操作序列。如果每一步我们都按照这个操作序列进行转换,那么最终我们可以得到正确的依存树。
arc-standard的oracle
我们回顾一下基于转换的算法的过程,在每一个时刻,输入是一个配置(状态),包括栈,队列和已经处理好的依存关系,输出是3个操作中的一个(我们先不考虑label)。因此对于一个标注好的依存树,我们需要根据它来生成每一个时刻正确的操作。我们先看具体怎么生成正确的操作,之后再详细解释它。给定一个配置和一个正确的依存树,我们根据如下的原则来选择正确的操作:
- 如果栈顶的两个元素执行LEFT-ARC之后得到的关系在包含在正确的依存树里,那么我们就选择LEFT-ARC
- 如果栈顶的两个运算执行RIGHT-ARC得到的关系包含在正确的依存树里,并且栈顶这个词的所有依赖都已经包含在已经处理好的关系列表里,那么就选择RIGHT-ARC
- 否则选择SHIFT
或者更加形式化的描述,假设当前的栈是S,当前得到的关系列表是$R_c$,正确的依存树的点集合是V,边集合是$R_p$。那么选择操作的伪代码如下:
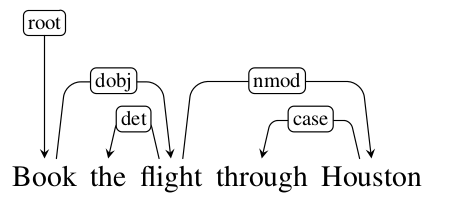
下面我们通过一个例子来介绍怎么生成训练数据,正确的依存树如下图所示。
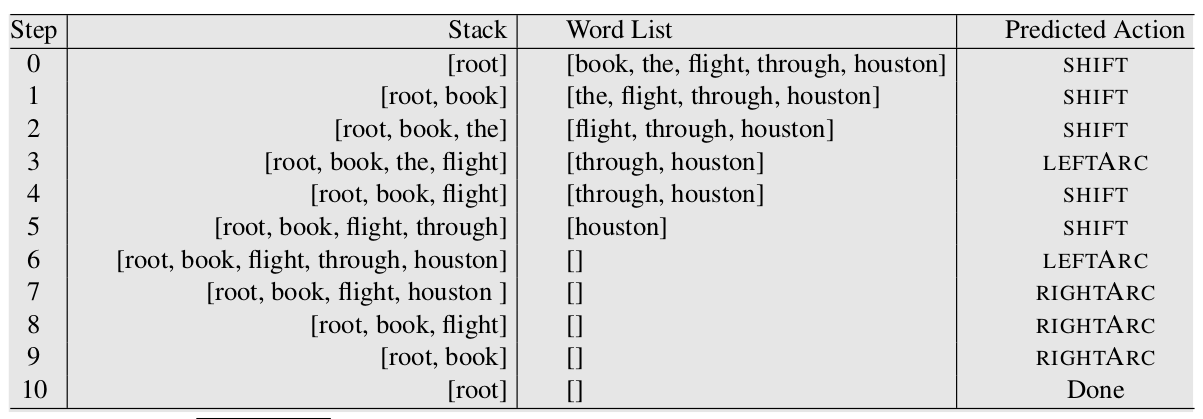
生成训练数据的过程如下图所示,我们下面来逐步分析。
第0步因为栈中只有一个元素,因此只能SHIFT。第1步时栈中有[root,book],而且正确的依存树里有root -> book,那么这个配置的正确操作是RIGHT-ARC吗?注意输出RIGHT-ARC还有第二个条件,也就是book在正确依存树里的所有依赖都已经处理完了。在这个配置下显然不是,book -> flight还没有被加到已处理关系集合里。因此这里不能输出RIGHT-ARC,只能输出SHIFT。
第2步很容易,因为book和the没有依存关系,因此只能SHIFT。第3不,存在the <- flight,因此根据第一条规则,输出LEFT-ARC。第4步和第1步类似,虽然book -> flight是正确的依赖,但是flight的其它依赖(flight -> huston)还没有处理,因此只能SHIFT。
第5步也是很简单,flight和through没有关系,只能SHIFT。第6步有through <- houston,因此输出LEFT-ARC。
第7步有 flight -> houston,而且huston的所有依赖(through <- houston)以及处理完毕,因此可以输出RIGHT-ARC。后面几步都是RIGHT-ARC,请读者验证是否满足前面的第二个条件。
通过这个例子,我们对怎么生成训练数据应该比较熟悉了,接着我们再来分析一些为什么要根据这3个条件来选择操作。根据前面的介绍,基于转换的算法是一种贪心算法,一个元素首先在队列里,然后只会通过一次SHIFT加入到栈里。
如果栈中的两个元素有$S_1 \leftarrow S_2$,我们就可以执行LEFT-ARC操作,因为根据projective性质,假设某条$S_1$为head的边,它的终点是$S_0$,那么$S_0$一定在$S_2$的左边,因此如下图所示的情况是不可能出现的。为什么呢?
根据$S_1 \rightarrow S_0$的projective性质,一定存在$S_1$到$S_2$的路径,同时这里$S_2 \rightarrow S_1$,因此存在回路而不是一棵树,这就产生矛盾。因此$S_0$和$S_1$一定在$S_2$之前进入堆栈,也因此正确的操作序列一定处理好了$S_1 \rightarrow S_0$。所以可以直接输出LEFT-ARC。
如果上面不好理解,我们还可以用projective的第二种定义来理解。假设如下图存在,现在我们考虑$S_2$,因为每个节点都有一个入边,入边的起点是$S_1,S_0$之外的其它点,因此它一定和边$S_1 \rightarrow S_0$相交,从而和这棵树是projective相矛盾。
而RIGHT-ARC就不同了,因为假设$S_1 \rightarrow S_2$,但是$S_2 \rightarrow S_0$,有可能$S_0$还没有从队列SHIFT到堆栈中,因此如果输出RIGHT-ARC,那么$S_2$就永远消失了,再也没有机会输出$S_2 \rightarrow S_0$了。
arc-eager的oracle
给定一个配置和一个正确的依存树,我们根据如下的原则来选择正确的操作:
- 如果可以LEFT-ARC,也就是栈顶元素和队列头部元素有stack[-1] <- queue[0],那么输出LEFT-ARC
- 如果可以RIGHT-ARC,也就是stack[-1] -> queue[0],那么输出RIGHT-ARC
- 如果stack[-1]所有的依赖(孩子)都以及处理完毕,并且它的head(入边)也找到了,那么REDUCE
- 否则输出SHIFT
算法
定义了arc-standard或者arc-eager算法的操作序列之后,parsing问题就变成寻找一个操作序列的问题。给定一个句子,依存分析的输出是一个操作序列。
贪心(greedy)算法
前面说了,依存分析的输出是一个序列。理论上,我们需要考虑整个操作序列才能得到最优解,因为有的序列前半部分可能比较好,能够得到一些正确的parse片段,但是最终可能parse出很多错误。而另外一种情况也可能存在——某个序列前面可能有一些错误,但是后面parse得非常好。而贪心算法每次只考虑当前的配置就直接做出决策,它只选择当前看起来不错的决策。
下图就是贪心算法。这个算法初始化完成之后就是一个循环,每次都根据当前配置选择最优的操作,然后执行这个操作直到进入终止状态(配置)。它的时间复杂度是O(n),这里n是句子的长度(词的个数)。因此它的速度是比较快的。
贪心算法的缺点是它不能回溯,因此会产生错误的累积(第一个错了后面就很难对了)。为了解决这个问题,我们通常有如下方法:
- 别出错!使用更加复杂的分类器,比如LSTM
- Beam Search
- Dynamic Oracle 错了也别影响后面的判断
第一个思路是使用更好更复杂的分类器,本来贪心算法的效果不好(使用传统的分类器),用的人很少了,但是2014年Manning使用了深度学习之后,由于它的简单易用,又让它进入了大家的视野,我们后面介绍Manning的这篇文章。
Beam Search
这是一种非常自然的改进方法,贪心算法每个时刻选择最优的一种操作,而Beam Search可以选择多于一个操作。比如t-1时刻有k=2个操作序列,那么t时刻会对这k个状态都选择k个最优的操作,这样可能得到k*k个操作序列,然后我们保留top-k个。
Dynamic Oracle
我们之前的创建Oracle部分介绍了怎么根据正确的依存树生成训练数据的过程,上面叫作静态的(static)oracle,而这里使用的是动态的(dynamic)oracle。静态的oracle指的是所有的操作都是根据正确的依存树产生的,因此这个操作序列一定可以最终生成正确的依存树。而动态的oracle使用现有模型预测的结果来执行。使用静态oracle的坏处是它学习的都是最终正确的操作序列对于的状态,但是实际parsing的过程中,肯定会出现错误的操作。因为静态的oracle训练时从没见过这样的情况,因此只要错一点,后面就错的非常厉害了,而动态oracle就可以避免这个问题——即使前面parse的不好,它也会尽量把剩下的parse好。实践也证明动态的oracle的效果要比今天oracle好。
如果读者还记得机器翻译的Teaching Force——我们给decoder的输入可以是参考答案也可以是decoder上一个时刻的输出。那么对比一下,Teaching Force就是static oracle,而非Teaching Force就是dynamic oracle。我们也可以交替的用static oracle和dynamic oracle训练模型。具体的dynamic oracle怎么生成后面的代码部分会介绍。
其它(非基于转换的算法)
基于转换的算法的一个缺点是只能parse projective的依存树。一种方法是对arc-standard进行改进,增加SWAP,使得它可处理non-projective的情况;另外就是使用其它的方法,比如基于图的方法。有兴趣的读者可以参考相关资料,本书不做讨论。
特征
有了训练数据之后,我们就可以训练模型了。我们可以使用的特征包括栈、队列和已经得到的依存关系,我们可以从这3个数据结构中抽取各种有用的特征。后面的例子我们会介绍一些常见的特征。
效果评估
因为依存分析其实就是给每个词指定head,因此我们只需要计算其准确率(accuracy)。计算准确率时也有UAS和LAS两种方法,前者只要依存关系(head)对了就行,而后者不但要求依存关系正确,而且要求label(比如nsub)也是正确的才算对。
基于转换的依存句法分析代码示例
我们这里实现一个非常简单的算法,使用感知机作为分类器,目的是为了让读者更加深入的了解算法的原理。代码来自这里,运行需要python2.7。
Parse类
首先我们定义保存已输出的依存关系的数据结构Parse类。
class Parse(object):
def __init__(self, n):
self.n = n
self.heads = [None] * (n - 1)
self.labels = [None] * (n - 1)
self.lefts = []
self.rights = []
for i in range(n + 1):
self.lefts.append(DefaultList(0))
self.rights.append(DefaultList(0))
def add(self, head, child, label=None):
self.heads[child] = head
self.labels[child] = label
if child < head:
self.lefts[head].append(child)
else:
self.rights[head].append(child)
成员变量n保存输入句子的词的个数(加上一个特殊的root),因此n-2是实际词的个数。heads保存每个词的入边对应的点(head),labels存储边上的label(比如nsub,nmod等)。而lefts和rights数组存储每个词的出边,入边只有一个,但是出边可能多个,因此这里需要用一个DefaultList来存储。注意:下标0用来表示特殊的start,2…n-1表示实际的n-2个词,n表示root。如下图所示。引入start的目的是让第一个词的下标是1,因为conll格式的下标是1开始而不是程序语言里的0开始的,这样下标一致,否则需要减一,比较麻烦。比如conll格式的一个句子为:
1 Some _ DET DT _ 2 advmod _ _
2 4,300 _ NUM CD _ 3 nummod _ _
3 institutions _ NOUN NNS _ 5 nsubj _ _
4 are _ VERB VBP _ 5 cop _ _
5 part _ NOUN NN _ 0 root _ _
6 of _ ADP IN _ 9 case _ _
7 the _ DET DT _ 9 det _ _
8 pension _ NOUN NN _ 9 compound _ _
9 fund _ NOUN NN _ 5 nmod _ _
10 . _ PUNCT . _ 5 punct _ _
我们之前介绍的是把root放在初始化的堆栈里,这里参考的是Ballesteros & Nivre 2013的论文Training Deterministic Parsers with Non-Deterministic Oracles,把root放到最后,初始堆栈为空。对于arc-eager算法,通常建议把root放到后面,从而推迟root->xxx,否则它可能太容易倾向于构建root->xxx。
transition函数
这里实现的是arc-hybrid算法,它的ARC-LEFT和arc-standard不同,下面我们通过代码来看不同之处。实现的地方是transition函数,代码为:
SHIFT = 0;
RIGHT = 1;
LEFT = 2;
MOVES = (SHIFT, RIGHT, LEFT)
def transition(move, i, stack, parse):
if move == SHIFT:
stack.append(i)
return i + 1
elif move == RIGHT:
parse.add(stack[-2], stack.pop())
return i
elif move == LEFT:
parse.add(i, stack.pop())
return i
这里RIGHT和SHIFT的实现和我们前面介绍的操作是完全一样的,注意stack里只压入词的下标而不是词本身,词队列是用一个数组存储的,它是永远不会被修改的,我们要出队一个元素其实就是修改一下它的下标。这里是用下标i来表示当前队列头部的词,对于SHIFT操作,我们首先把i压入栈中,同时返回i+1,告诉调用者队列的下标后移一位。而对于LEFT和RIGHT,返回的都是i,说明队列没有什么变化。
RIGHT操作是把 stack[-2] -> stack[-1]构成一条边,同时把栈顶的弹出。而LEFT操作把 stack[-1] <- i构成一条边,同时把栈顶的弹出。这和我们之前介绍的有些不同——我们之前介绍的是把stack[-2] <- stack[-1]构成一条边,然后把stack[-2]删掉。
parse算法
Parser这个类具体实现parsing算法。我们这里只看parse(预测)的部分,训练部分后面再看。
class Parser(object):
def parse(self, words):
n = len(words)
i = 2;
stack = [1];
parse = Parse(n)
tags = self.tagger.tag(words)
while stack or (i + 1) < n:
features = extract_features(words, tags, i, n, stack, parse)
scores = self.model.score(features)
valid_moves = get_valid_moves(i, n, len(stack))
guess = max(valid_moves, key=lambda move: scores[move])
i = transition(guess, i, stack, parse)
return tags, parse.heads
这里首先把第一个词放到栈里,然后队列的下标i等于2。接着构造一个Parse(n)对象用于保存已经parse的依存关系。然后用tagger进行词性标注。之后就是主循环,条件是栈非空或者队列非空。循环里首先提取特征,然后用模型进行预测(打分),然后得到当前配置的合法操作,然后在合法操作中选择得分最高的操作,最后调用transition函数执行这个操作。
get_valid_moves
get_valid_moves函数判断当前状态下的合法操作,如果队列非空(i+1<n)那么就可以SHIFT,如果堆栈有2个以上元素,那么就可以RIGHT,如果堆栈至少有一个元素,那么就可以LEFT。注意LEFT的条件,即使队列空了也可以LEFT,因为还有一个root在队列的第n个位置。
def get_valid_moves(i, n, stack_depth):
moves = []
if (i + 1) < n:
moves.append(SHIFT)
if stack_depth >= 2:
moves.append(RIGHT)
if stack_depth >= 1:
moves.append(LEFT)
return moves
extract_features
对于传统的机器学习算法来说,最重要的部分就是提取特征了。对于基于转换的算法来说,我们可以用到的信息就是配置(状态)里的信息,包括栈里的词、队列里的词和Parse里的结果。当然这里面用很多的信息,但是根据(语言学的)经验,最有用的信息是栈顶的3个词(n0, n1, n2,栈顶是n0)、队列最前面的3个词(s0, s1, s2)、s0最左边的3个孩子(s0b1, s0b2, s0b3)、s0最右边的3个孩子(s0f1, s0f2, s0f3)、n0最左边的3个孩子(n0b1, n0b2, n0b3)、n0最右边的3个孩子(n0f1, n0f2, n0f3)。这总共有18个词,我们可以使用它们的词、词性以及左右孩子的个数等特征。
extract_features首先定义了3个函数,分别用于返回栈(stack)、队列(这里叫buffer)和Parse结果里的关键词。代码如下:
def extract_features(words, tags, n0, n, stack, parse):
def get_stack_context(depth, stack, data):
if depth >= 3:
return data[stack[-1]], data[stack[-2]], data[stack[-3]]
elif depth >= 2:
return data[stack[-1]], data[stack[-2]], ''
elif depth == 1:
return data[stack[-1]], '', ''
else:
return '', '', ''
def get_buffer_context(i, n, data):
if i + 1 >= n:
return data[i], '', ''
elif i + 2 >= n:
return data[i], data[i + 1], ''
else:
return data[i], data[i + 1], data[i + 2]
def get_parse_context(word, deps, data):
if word == -1:
return 0, '', ''
deps = deps[word]
valency = len(deps)
if not valency:
return 0, '', ''
elif valency == 1:
return 1, data[deps[-1]], ''
else:
return valency, data[deps[-1]], data[deps[-2]]
get_stack_context返回从栈顶往下的3个词,如果不够,就补充空字符串。类似的get_buffer_context返回队列头部的前3个词。 get_parse_context有3个参数,word是带处理的词,比如s0,deps是Parse对象的lefts或者rights,而data就是单词序列(数组)。因此这个函数首先用deps = deps[word]得到当前待处理词的left或者right数组,然后返回最后两个值。注意:deps里存的是下标,实际的词是data[deps[-1]]。最终返回的是3个值,第一个值是一个整数,说明真正返回的词的个数,后面两个是真正的词(或者空字符串)。
接下来是真正提取特征的代码,比较冗长:
def extract_features(words, tags, n0, n, stack, parse):
features = {}
# Set up the context pieces --- the word (W) and tag (T) of:
# S0-2: Top three words on the stack
# N0-2: First three words of the buffer
# n0b1, n0b2: Two leftmost children of the first word of the buffer
# s0b1, s0b2: Two leftmost children of the top word of the stack
# s0f1, s0f2: Two rightmost children of the top word of the stack
depth = len(stack)
s0 = stack[-1] if depth else -1
Ws0, Ws1, Ws2 = get_stack_context(depth, stack, words)
Ts0, Ts1, Ts2 = get_stack_context(depth, stack, tags)
Wn0, Wn1, Wn2 = get_buffer_context(n0, n, words)
Tn0, Tn1, Tn2 = get_buffer_context(n0, n, tags)
Vn0b, Wn0b1, Wn0b2 = get_parse_context(n0, parse.lefts, words)
Vn0b, Tn0b1, Tn0b2 = get_parse_context(n0, parse.lefts, tags)
Vn0f, Wn0f1, Wn0f2 = get_parse_context(n0, parse.rights, words)
_, Tn0f1, Tn0f2 = get_parse_context(n0, parse.rights, tags)
Vs0b, Ws0b1, Ws0b2 = get_parse_context(s0, parse.lefts, words)
_, Ts0b1, Ts0b2 = get_parse_context(s0, parse.lefts, tags)
Vs0f, Ws0f1, Ws0f2 = get_parse_context(s0, parse.rights, words)
_, Ts0f1, Ts0f2 = get_parse_context(s0, parse.rights, tags)
# Cap numeric features at 5?
# String-distance
Ds0n0 = min((n0 - s0, 5)) if s0 != 0 else 0
features['bias'] = 1
# Add word and tag unigrams
for w in (Wn0, Wn1, Wn2, Ws0, Ws1, Ws2, Wn0b1, Wn0b2, Ws0b1, Ws0b2, Ws0f1, Ws0f2):
if w:
features['w=%s' % w] = 1
for t in (Tn0, Tn1, Tn2, Ts0, Ts1, Ts2, Tn0b1, Tn0b2, Ts0b1, Ts0b2, Ts0f1, Ts0f2):
if t:
features['t=%s' % t] = 1
# Add word/tag pairs
for i, (w, t) in enumerate(((Wn0, Tn0), (Wn1, Tn1), (Wn2, Tn2), (Ws0, Ts0))):
if w or t:
features['%d w=%s, t=%s' % (i, w, t)] = 1
# Add some bigrams
features['s0w=%s, n0w=%s' % (Ws0, Wn0)] = 1
features['wn0tn0-ws0 %s/%s %s' % (Wn0, Tn0, Ws0)] = 1
features['wn0tn0-ts0 %s/%s %s' % (Wn0, Tn0, Ts0)] = 1
features['ws0ts0-wn0 %s/%s %s' % (Ws0, Ts0, Wn0)] = 1
features['ws0-ts0 tn0 %s/%s %s' % (Ws0, Ts0, Tn0)] = 1
features['wt-wt %s/%s %s/%s' % (Ws0, Ts0, Wn0, Tn0)] = 1
features['tt s0=%s n0=%s' % (Ts0, Tn0)] = 1
features['tt n0=%s n1=%s' % (Tn0, Tn1)] = 1
# Add some tag trigrams
trigrams = ((Tn0, Tn1, Tn2), (Ts0, Tn0, Tn1), (Ts0, Ts1, Tn0),
(Ts0, Ts0f1, Tn0), (Ts0, Ts0f1, Tn0), (Ts0, Tn0, Tn0b1),
(Ts0, Ts0b1, Ts0b2), (Ts0, Ts0f1, Ts0f2), (Tn0, Tn0b1, Tn0b2),
(Ts0, Ts1, Ts1))
for i, (t1, t2, t3) in enumerate(trigrams):
if t1 or t2 or t3:
features['ttt-%d %s %s %s' % (i, t1, t2, t3)] = 1
# Add some valency and distance features
vw = ((Ws0, Vs0f), (Ws0, Vs0b), (Wn0, Vn0b))
vt = ((Ts0, Vs0f), (Ts0, Vs0b), (Tn0, Vn0b))
d = ((Ws0, Ds0n0), (Wn0, Ds0n0), (Ts0, Ds0n0), (Tn0, Ds0n0),
('t' + Tn0 + Ts0, Ds0n0), ('w' + Wn0 + Ws0, Ds0n0))
for i, (w_t, v_d) in enumerate(vw + vt + d):
if w_t or v_d:
features['val/d-%d %s %d' % (i, w_t, v_d)] = 1
return features
我们来看一部分代码,其余的都是类似的。首先得到这18个词以及它们对应的18个词性,接着可以增加词的unigram特征:
for w in (Wn0, Wn1, Wn2, Ws0, Ws1, Ws2, Wn0b1, Wn0b2, Ws0b1, Ws0b2, Ws0f1, Ws0f2):
if w:
features['w=%s' % w] = 1
比如特征’w=the’这个特征,只有单词’the’在这12个词中出现,那么它对应的值就是1,否则就是0。注意’w=xxx’是一个模板,xxx可以替换成任何词,这和我们前面介绍的CRF模板是类似的。我们也可以加入词-词性对的特征:
for i, (w, t) in enumerate(((Wn0, Tn0), (Wn1, Tn1), (Wn2, Tn2), (Ws0, Ts0))):
if w or t:
features['%d w=%s, t=%s' % (i, w, t)] = 1
比如特征’1 w=the, t=det’表示队列的第二个词(Wn1)是the,对应的词性是det。后面的代码都是类似的,就不详细介绍了,请读者自己阅读。
model.score
这里的模型是一个非常简单的感知机(Perceptron)算法,因为本文的重点不是介绍感知机算法,实际的应用中也没有人会用这个算法,不感兴趣的读者可以跳过。基本上感知机就是一个线性分类器,只不过它的学习过程是一种online的学习——每来一个样本,如果分类正确,那么参数不做任何修改;如果分类错误,那么跳转参数使得尽量往正确的方向移动。
class Perceptron(object):
def score(self, features):
all_weights = self.weights
scores = dict((clas, 0) for clas in self.classes)
for feat, value in features.items():
if value == 0:
continue
if feat not in all_weights:
continue
weights = all_weights[feat]
for clas, weight in weights.items():
scores[clas] += value * weight
return scores
训练
训练的代码如下:
class Parser(object):
def train_one(self, itn, words, gold_tags, gold_heads):
n = len(words)
i = 2;
stack = [1];
parse = Parse(n)
tags = self.tagger.tag(words)
while stack or (i + 1) < n:
features = extract_features(words, tags, i, n, stack, parse)
scores = self.model.score(features)
valid_moves = get_valid_moves(i, n, len(stack))
gold_moves = get_gold_moves(i, n, stack, parse.heads, gold_heads)
guess = max(valid_moves, key=lambda move: scores[move])
assert gold_moves
best = max(gold_moves, key=lambda move: scores[move])
self.model.update(best, guess, features)
i = transition(guess, i, stack, parse)
self.confusion_matrix[best][guess] += 1
return len([i for i in range(n - 1) if parse.heads[i] == gold_heads[i]])
因此主循环的步骤为:根据当前状态提取特征,用模型打分,然后用get_valid_moves得到所有合法的操作,接着在所有合法的走法中寻找得分最高的作为guess,同时get_gold_moves根据正确的依存树得到当前状态下所有的”正确”走法,然后用模型的得分选择得分最高的作为best。然后使用model.update更新模型参数——如果guess和best一样,那么不更新,否则进行适当的调整。最后使用guess来更新状态”i = transition(guess, i, stack, parse)”。但是动态oracle有一个问题:怎么知道某个“错误”状态下的“正确”操作?
get_gold_moves
这个函数返回一个状态下的”正确”走法,也就是实现动态oracle的核心代码。
def get_gold_moves(n0, n, stack, heads, gold):
def deps_between(target, others, gold):
for word in others:
if gold[word] == target or gold[target] == word:
return True
return False
valid = get_valid_moves(n0, n, len(stack))
if not stack or (SHIFT in valid and gold[n0] == stack[-1]):
return [SHIFT]
if gold[stack[-1]] == n0:
return [LEFT]
costly = set([m for m in MOVES if m not in valid])
# If the word behind s0 is its gold head, Left is incorrect
if len(stack) >= 2 and gold[stack[-1]] == stack[-2]:
costly.add(LEFT)
# If there are any dependencies between n0 and the stack,
# pushing n0 will lose them.
if SHIFT not in costly and deps_between(n0, stack, gold):
costly.add(SHIFT)
# If there are any dependencies between s0 and the buffer, popping
# s0 will lose them.
if deps_between(stack[-1], range(n0 + 1, n - 1), gold):
costly.add(LEFT)
costly.add(RIGHT)
return [m for m in MOVES if m not in costly]
首先定义函数deps_between,它有3个参数:target是一个词的下标,others是多个词的下标列表,gold是正确的依存关系,gold[i]存储的是第i个词的head(入边)词的下标。因此deps_between函数的作用是判断target和others是否有任何关系,只有target -> others[i]或者 target <- others[i],都返回True,如果所有的others[i]和target都没有任何关系,那么返回False。
get_gold_moves函数的参数是:n0是队列头部的下标;n是词的长度;stack是堆栈;gold在deps_between里解释过了。
if not stack or (SHIFT in valid and gold[n0] == stack[-1]):
return [SHIFT]
这段代码的意思是:如果栈为空,那么唯一合法的操作是SHIFT。或者如果SHIFT是合法的操作并且有 stack[-1] -> n0,那么就应该SHIFT,因为SHIFT之后栈中就是stack[-1]和n0,接下来我们就可以RIGHT得到一个正确的依存。
if gold[stack[-1]] == n0:
return [LEFT]
这段代码的意思是:如果 stack[-1] <- n0,那么当然应该直接LEFT得到正确的依存。接下来定义一个集合costly,初始化为所有不合法的操作。
if len(stack) >= 2 and gold[stack[-1]] == stack[-2]:
costly.add(LEFT)
这段代码的意思是:如果stack[-2] -> stack[-1],那么显然不应该执行LEFT操作。
if SHIFT not in costly and deps_between(n0, stack, gold):
costly.add(SHIFT)
这段代码的意思是:如果n0(队列头部)和栈中的任何元素有依存关系,就不能执行SHIFT,因为n0和栈中的某个元素有关系,显然前面两个条件已经排除了n0和栈顶stack[-1]的关系。那么假设为stack-k,stack[-k]和n0有依存关系,那么要么是n0 -> stack[-k],要么stack[-k] -> n0。如果是前者,那么如果n0入栈就没有机会了,因为只有LEFT操作能产生 <-的依存,也就是n0一定要在队列头部才能产生LEFT操作。如果是后者stack[-k] -> n0,因为它们之间隔了一个stack[-1],因此也是没有机会执行RIGHT操作的。
if deps_between(stack[-1], range(n0 + 1, n - 1), gold):
costly.add(LEFT)
costly.add(RIGHT)
这段代码的意思是:如果栈顶元素和n0+1之后的某个k有依存关系,那么就不能LEFT和RIGHT,因为这两个操作都会最终把栈顶元素弹出,从而使得没有机会让栈顶元素与k产生依存关系。
return [m for m in MOVES if m not in costly]
最终costly集合里是不正确的操作,用所有的操作集合MOVES减去costly就得到“正确”的操作。
- 显示Disqus评论(需要科学上网)