本教程是《深度学习理论与实战》草稿的部分内容,主要介绍语音识别的MFCC特征提取。更多文章请点击深度学习理论与实战:提高篇。
目录
- MFCC特征提取步骤
- 上述步骤的作用
- 美尔尺度(Mel Scale)
- 详细实现过程
- 计算梅尔滤波器组的参数
- Deltas和Delta-Deltas特征
- 代码实现
- Filter Bank特征 vs MFCC特征
语音识别的第一步是特征提取,也就是提取语音信号中有助于理解语言内容的部分而丢弃掉其它的东西(比如背景噪音和情绪等等)。
语音的产生过程如下:语音信号是通过肺部呼出气体,然后通过声门的开启与闭合产生的周期信号。再通过声道(包括舌头牙齿)对信号调制后产生。区分语音的关键就是声道的不同形状。不同的形状就对应不同的滤波器,从而产生了不同的语音。如果我们可以准确的知道声道的形状,那么我们就可以得到不同的音素(phoneme)的表示。声道的形状体现在语音信号短时功率谱的包络(envelope)中,因此好多特征提取方法需要准确的表示包络信息。
MFCC特征提取步骤
首先我们会介绍MFCC特征提取的步骤,然后会详细的介绍为什么要这么做。
- 对语音信号进行分帧处理
- 用周期图(periodogram)法来进行功率谱(power spectrum)估计
- 对功率谱用Mel滤波器组进行滤波,计算每个滤波器里的能量
- 对每个滤波器的能量取log
- 进行DCT变换
- 保留DCT的第2-13个系数,去掉其它
除此之外,通常(当然也不是一定)会把每一帧的能量作为一个特征,再加上12个DCT系数得到13维的特征向量。然后计算这13维特征向量的Delta以及Delta-Delta得到39维的MFCC特征。
上述步骤的作用
语音信号是时变的信号,为了便于处理,我们假设在一个很短的时间范围内它是一个稳定的(stationary)系统。因此我们通常把语音信号分成20-40毫秒(ms)的帧,为什么是这个长度呢?因为如果太短了每一帧的样本不够,无法估计频谱;而太长了则它的变化会太大从而不是我们假设的稳定系统。
下一步就是计算每一帧的功率谱。这是受人耳蜗(cochlea)的启发——根据输入声音的不同,它会在不同的地方共振。而根据共振位置的不同,不同的神经元会向大脑发送不同的信号告诉大脑这个声音对应哪些频率。我们用周期图来估计功率谱就是为了达到类似的效果。
但是上面得到的功率谱仍然包含了很多对于语音识别无用的信息。比如耳蜗不会太细微的区分两个频率,尤其是对于高频的信号,耳蜗的区分度就越小。因此我们会把频率范围划分成不同的桶(bin),我们把所有落到这个桶范围内的能量都累加起来。这就是通过Mel滤波器组来实现的:第一个滤波器非常窄,它会收集频率接近0Hz的频率;而越往后,滤波器变得越宽,它会收集更大范围内的频率,具体频率范围是怎么划分的后面我们会介绍。
接下来对于滤波器组的能量,我们对它取log。这也是受人类听觉的启发:人类对于声音大小(loudness)的感受不是线性的。为了使人感知的大小变成2倍,我们需要提高8倍的能量。这意味着如果声音原来足够响亮,那么再增加一些能量对于感知来说并没有明显区别。log这种压缩操作使得我们的特征更接近人类的听觉。为什么是log而不是立方根呢?因为log可以让我们使用倒谱均值减(cepstral mean subtraction)这种信道归一化技术(这可以归一化掉不同信道的差别)。
最后一步是对这些能量进行DCT变换。因为不同的Mel滤波器是有交集的,因此它们是相关的,我们可以用DCT变换去掉这些相关性,从而后续的建模时可以利用这一点(比如常见的GMM声学模型我们可以使用对角的协方差矩阵,从而简化模型)。为什么只取第2-13个系数呢?因为后面的能量表示的是变化很快的高频信号,在实践中发现它们会使识别的效果变差。
美尔尺度(Mel Scale)
美尔尺度是建立从人类的听觉感知的频率——Pitch到声音实际频率直接的映射。人耳对于低频声音的分辨率要高于高频的声音。通过把频率转换成美尔尺度,我们的特征能够更好的匹配人类的听觉感知效果。从频率到美尔频率的转换公式如下:
\[M(f)=1125 ln(1+f/700)\]而从美尔频率到频率的转换公式为:
\[M^{-1}(m)=700(e^{m/1125-1})\]详细实现过程
分帧
把信号分成20-40ms的帧,通常会分成25ms的。如果语音信号的采样频率是16kHz的,那么一帧就有16000*25/1000=400个样本点。通常我们会让相邻的帧有重叠的部分,我们会每次移动10ms(而不是25ms),这就意味着相邻的帧重叠的样本为(25-10)/1000*16000=240个。这样,第一帧是前400个样本点,第二帧是第160个到560个样本点。如果最后一帧不够400个样本点,我们一般在后面补0。
后面的步骤是应用到每一帧上的,从每一帧抽取12个特征。先介绍一些数学记号:$s(n)$表示时域信号;$s_i(n)$是第i帧的数据,其中n的范围是1-400;当我们介绍DFT的时候,$S_i(k)$表示的是第i帧的第k个复系数;$P_i(k)$是第i帧的功率谱。
对每帧信号进行DFT
\[S_i(k)=\sum_{n=1}^{N}s_i(n)h(n)e^{-j2\pi kn/N} 1 \le k \le N\]其中$h(n)$是一个N点的窗函数(比如Hamming窗),K是DFT的长度。有了$S_i(k)$我们就可以估计功率谱:
\[P_i(k)=\frac{1}{N}|S_i(k)|^2\]上式得到的是周期图的功率谱估计。通常我们会进行512点的DFT并且保留前257个系数。
计算美尔滤波器组
这是一组大约20-40(通常26)个三角滤波器组,它会对上一步得到的周期图的功率谱估计进行滤波。我们的滤波器组由26个(滤波器)长度为257的向量组成,每个滤波器的257个值中大部分都是0,只有对于需要采集的频率范围才是非零。输入的257点的信号会通过26个滤波器,我们会计算通过每个滤波器的信号的能量。
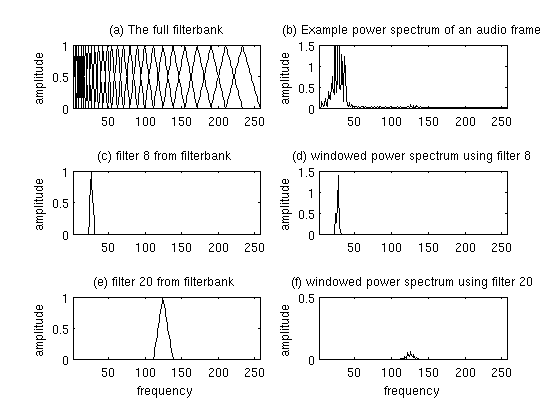
计算过程如下图所示,最后我们会保留这26个滤波器的能量。图(a)是26个滤波器;图(b)是滤波后的信号;图(c)是其中的第8个滤波器,它只让某一频率范围的信号通过;图(d)通过它的信号的能量;图(e)是第20个滤波器;图(f)是通过它的信号的能量。
能量取log
这一步非常简单,对26个能量取log。
DCT
对这26个点的信号进行DCT,得到26个倒谱系数(Cepstral Coefficents),最后我们保留2-13这12个数字,这12个数字就叫MFCC特征。对功率谱再做DCT的目的就是为了提取信号的包络。
计算梅尔滤波器组的参数
这里为了简便,我们的示例使用大小是10的滤波器组,实际我们通常使用26个。
首先我们需要选择频率的最大值和最小值,通常最小值我们选择300Hz,对于16kHz的语音,我们的最大值通常是8kHz。为什么这样选择呢?因为人类的听觉范围是20Hz-20kHz,但对于实际的语音,低于300Hz通常没有意义。而根据奈奎斯特(Nyquist)采样定理,16kHz的信号的范围就是8kHz,所以我们选择最大值是8kHz。当然如果我们的语音的采样频率是8kHz,那么我们的最大值就要是4kHz。计算步骤如下:
1.转换
使用上式把最小和最大频率转换成梅尔尺度的频率。300Hz就是401.25Mel,8kHz对应的是2834.99Mel。
2.划分
因为我们有10个滤波器,那么我们需要12个点(除去最大和最小频率外还需要10个点)。我们在Mel空间上平均的分配它们:
\[m(i) = 401.25, 622.50, 843.75, 1065.00, 1286.25, 1507.50, 1728.74, 1949.99, 2171.24, 2392.49, 2613.74, 2834.99\]3.把这12点的Mel频率变换成频率
这可以使用公式来得到:
\[h(i) = 300, 517.33, 781.90, 1103.97, 1496.04, 1973.32, 2554.33, 3261.62, 4122.63, 5170.76, 6446.70, 8000\]4.把这些频率对应最近接近的的FFT的bin里
因为FFT的频率没办法精确的与上面的频率对应,因此我们把它们对应到最接近的bin里。计算公式如下:
\[f(i) = floor((nfft+1)*h(i)/samplerate)\]这样得到:
\[f(i) = 9, 16, 25, 35, 47, 63, 81, 104, 132, 165, 206, 256\]5.创建滤波器组
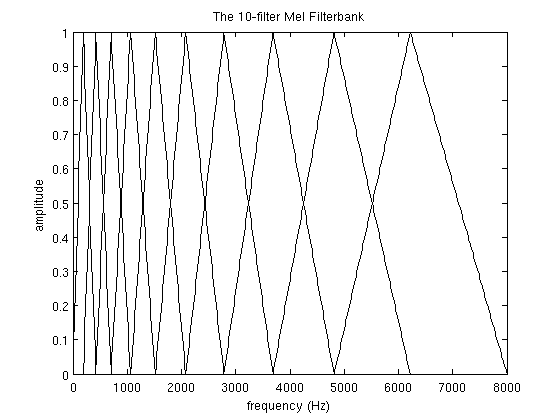
我们的第一个滤波器开始与第一个点(300Hz),峰值在第二个点(517Hz),结束与第三个点(781Hz);第二个滤波器开始与第二个点(517Hz),峰值在第三个点(781Hz),结束与第四个点(1103Hz);…,以此类推。具体的公式如下:
\[H_m(k)=\begin{cases} 0 & k < f(m-1) \\ \frac{k-f(m-1)}{f(m)-f(m-1)} & f(m-1) \le k \le f(m) \\ \frac{f(m+1)-k}{f(m+1)-f(m)} & f(m) \le k \le f(m+1) \\ 0 & k > f(m+1) \end{cases}\]最终我们得到10个的滤波器组如下图所示。
Deltas和Delta-Deltas特征
Deltas和Delta-Deltas通常也叫(一阶)差分系数和二阶差分(加速度)系数。MFCC特征向量描述了一帧语音信号的功率谱的包络信息,但是语音识别也需要帧之间的动态变化信息,比如MFCC随时间的轨迹,实际证明把MFCC的轨迹变化加入后会提高识别的效果。因此我们可以用当前帧前后几帧的信息来计算Delta和Delta-Delta:
\[d_t=\frac{\sum_{n=1}^{N}n(c_{t+n}-c_{t-n})}{2\sum_{n=1}^{N}n^2}\]上式得到的$d_t$是Delta系数,计算第t帧的Delta需要t-N到t+N的系数,N通常是2。如果对Delta系数$d_t$再使用上述公式就可以得到Delta-Delta系数,这样我们就可以得到3*12=36维的特征。上面也提到过,我们通常把能量也加到12维的特征里,对能量也可以计算一阶和二阶差分,这样最终可以得到39维的MFCC特征向量。
代码实现
代码来自这里。
我们首先来看它的用法:
(rate,sig) = wav.read("english.wav")
mfcc_feat = mfcc(sig,rate)
d_mfcc_feat = delta(mfcc_feat, 2)
fbank_feat = logfbank(sig,rate)
print(fbank_feat[1:3,:])
wav.read读取wav文件,返回采样率rate和语音信号sig。这里rate是8000,说明english.wav文件的采样率是8Khz;而sig是一个长度为34122的一维ndarry,表示语音信号。
接下来是mfcc函数,它用来提取13维的MFCC特征,这个函数的代码为:
def mfcc(signal,samplerate=16000,winlen=0.025,winstep=0.01,numcep=13,
nfilt=26,nfft=512,lowfreq=0,highfreq=None,preemph=0.97,ceplifter=22,appendEnergy=True,
winfunc=lambda x:numpy.ones((x,))):
"""从语音信号计算MFCC特征。
:param signal: 语音信号
:param samplerate: 采样率
:param winlen: 一帧的长度,单位秒,默认0.025s (25毫秒)
:param winstep: 帧移,单位秒,默认0.01s (10毫秒)
:param numcep: 返回的倒谱系数个数,默认13
:param nfilt: 滤波器组个数,默认26
:param nfft: FFT大小,默认512
:param lowfreq: 梅尔滤波器的最低频率,单位Hz,默认0
:param highfreq: 梅尔滤波器的最高频率,默认是:采样率/2
:param preemph: 预加重(preemphasis)系数,默认0.97
:param ceplifter: 对最终的倒谱系数进行提升, 默认22
:param appendEnergy: 是否增加能量,如果true,则把第一个系数替换成能量。
:param winfunc: 窗函数,比如使用汉明窗:winfunc=numpy.hamming
:returns: 返回一个numpy数字,大小是(NUMFRAMES, numcep)
"""
feat,energy = fbank(signal,samplerate,winlen,winstep,nfilt,nfft,lowfreq,highfreq,preemph,winfunc)
feat = numpy.log(feat)
feat = dct(feat, type=2, axis=1, norm='ortho')[:,:numcep]
feat = lifter(feat,ceplifter)
if appendEnergy:
# 把第一个系数换成能量(log)
feat[:,0] = numpy.log(energy)
return feat
它首先调用fbank函数计算MFCC特征,这个函数的代码为:
def fbank(signal,samplerate=16000,winlen=0.025,winstep=0.01,
nfilt=26,nfft=512,lowfreq=0,highfreq=None,preemph=0.97,
winfunc=lambda x:numpy.ones((x,))):
"""从语音信号计算MFCC特征
:param signal: 语音信号
:param samplerate: 采样率
:param winlen: 一帧的长度,单位秒,默认0.025s (25毫秒)
:param winstep: 帧移,单位秒,默认0.01s (10毫秒)
:param nfilt: 滤波器组个数,默认26
:param nfft: FFT大小,默认512
:param lowfreq: 梅尔滤波器的最低频率,单位Hz,默认0
:param highfreq: 梅尔滤波器的最高频率,默认是:采样率/2
:param preemph: 预加重(preemphasis)系数,默认0.97
:param winfunc: 窗函数,比如使用汉明窗:winfunc=numpy.hamming
:returns: 两个值,第一个是特征,大小是(NUMFRAMES, nfilt);第二个是能量。
"""
highfreq= highfreq or samplerate/2
signal = sigproc.preemphasis(signal,preemph)
frames = sigproc.framesig(signal, winlen*samplerate, winstep*samplerate, winfunc)
pspec = sigproc.powspec(frames,nfft)
energy = numpy.sum(pspec,1) # 每一帧的能量
# 如果能量是0,取log会有问题,因此需要后处理
energy = numpy.where(energy == 0,numpy.finfo(float).eps,energy)
fb = get_filterbanks(nfilt,nfft,samplerate,lowfreq,highfreq)
feat = numpy.dot(pspec,fb.T) # 计算滤波器组的能量
feat = numpy.where(feat == 0,numpy.finfo(float).eps,feat) # 同上,处理0的情况
return feat,energy
这个函数首先调用sigproc.preemphasis,这个函数对信号进行预加重(Pre-Emphasis)。因为高频信号的能量通常较低,因此需要增加高频部分的能量。具体来讲预加重有三个好处:增加高频部分的能量使得能量分布更加均衡;防止傅里叶变换的数值计算不稳定问题;有可能增加信噪比(Signal-to-Noise Ratio/SNR)。它的计算公式为:
\[y_t=x_t−\alpha x_{t-1}\]上式中$\alpha$就是预加重的系数,默认是0.97。代码也非常简单,只有一行:
def preemphasis(signal, coeff=0.95):
# 第一个时刻不需要处理;后面的是当前信号减去coeff乘以上一个时刻的信号
return numpy.append(signal[0], signal[1:] - coeff * signal[:-1])
接下来是把语音信号切分成25ms的帧,帧移是10ms,代码比较简单,请读者阅读注释。
def framesig(sig, frame_len, frame_step, winfunc=lambda x: numpy.ones((x,)), stride_trick=True):
"""把信号变成有重叠的帧
:param signal: 语音信号
:param frame_len: length of each frame measured in samples.
:param winlen: 一帧的长度,单位秒,默认0.025s (25毫秒)
:param winstep: 帧移,单位秒,默认0.01s (10毫秒)
:param winfunc: 窗函数,比如使用汉明窗:winfunc=numpy.hamming
:param stride_trick: 是否使用stride trick来加速计算
:returns: 一个数组,每一个元素是一帧的数据,大小是(NUMFRAMES, frame_len)
"""
# 本例为34122
slen = len(sig)
# 帧长0.025*8,000,200个点
frame_len = int(round_half_up(frame_len))
# 帧移0.010s*8,000,80个点
frame_step = int(round_half_up(frame_step))
# 计算帧数(426)
if slen <= frame_len:
numframes = 1
else:
numframes = 1 + int(math.ceil((1.0 * slen - frame_len) / frame_step))
# padding后点的总数(34200)
padlen = int((numframes - 1) * frame_step + frame_len)
# padding的点
zeros = numpy.zeros((padlen - slen,))
# 原始信号sig加上padding的
padsignal = numpy.concatenate((sig, zeros))
if stride_trick:
win = winfunc(frame_len)
frames = rolling_window(padsignal, window=frame_len, step=frame_step)
else:
indices = numpy.tile(numpy.arange(0, frame_len), (numframes, 1)) +
numpy.tile(numpy.arange(0, numframes * frame_step, frame_step),
(frame_len, 1)).T
indices = numpy.array(indices, dtype=numpy.int32)
frames = padsignal[indices]
win = numpy.tile(winfunc(frame_len), (numframes, 1))
return frames * win
前面的计算都是比较简单的,有难点的代码是padsignal之后的代码,我们只看stride_trick为False的情况,这个代码虽然长一点,但是容易理解。在介绍代码之前,我们首先熟悉一些numpy的tile函数,这个函数的第一个参数是一个numpy的数组,而第二个参数指定怎么重复。下面是来自文档的例子,请读者仔细阅读注释。
>>> a = np.array([0, 1, 2])
# a是(3,)的向量
>>> np.tile(a, 2)
# 把a重复两次,因此得到大小(6,)的向量
array([0, 1, 2, 0, 1, 2])
>>> np.tile(a, (2, 2))
# 结果是二维的,因此先broadcasting成(1, 3)的矩阵,
# 然后按照两个维度重复2倍,因此得到(2, 6)的矩阵
array([[0, 1, 2, 0, 1, 2],
[0, 1, 2, 0, 1, 2]])
>>> np.tile(a, (2, 1, 2))
# a按照3个维度重复,所以把a先broadcasting成(1, 1, 3)
# 然后三个维度分别复制(2, 1, 2),因此最终得到(2, 1, 6)的Tensor
array([[[0, 1, 2, 0, 1, 2]],
[[0, 1, 2, 0, 1, 2]]])
>>> b = np.array([[1, 2], [3, 4]])
# b是(2, 2)的矩阵
>>> np.tile(b, 2)
# 对b的最后一维进行复制,变成(2, 4)
array([[1, 2, 1, 2],
[3, 4, 3, 4]])
>>> np.tile(b, (2, 1))
# 对b的第一维进行2倍的复制;第二维进行1倍(不变)的复制。
# 最终得到(4, 2)的矩阵
array([[1, 2],
[3, 4],
[1, 2],
[3, 4]])
>>> c = np.array([1,2,3,4])
# (4,)的向量
>>> np.tile(c,(4,1))
# 结果是二维的,先broadcasting成(1, 4),
# 然后复制得到(4, 4)
array([[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4]])
numpy.arange(0, frame_len)=(0,1,…,199),这是一个(200,)的数组,通过tile变成(426,200)的矩阵,共426行,每一行都是(0,1,…,199)。
numpy.arange(0, numframes * frame_step, frame_step)是一个(426,)的数组,内容是(0, 80, 160, …, (426-1)80),然后通过tile变成(200,426)的矩阵,最后通过转置变成(426,200)的矩阵,这个矩阵200列,每一列都是(0, 80, 160, …, 42580)。
把这个两个矩阵相加得到的还是(426, 200)的矩阵indices,值为:
[[ 0 1 2 ... 197 198 199]
[ 80 81 82 ... 277 278 279]
[ 160 161 162 ... 357 358 359]
...
[33840 33841 33842 ... 34037 34038 34039]
[33920 33921 33922 ... 34117 34118 34119]
[34000 34001 34002 ... 34197 34198 34199]]
我们发现第一行就是第一帧的信号对应的下标,第二行是第二帧的下标,…。
接下来把indices从浮点数变成int32,然后frames = padsignal[indices]就得到每一帧的数据。这里frames是一个shape为(426, 200)的矩阵,每一行代表一帧。
然后用winfunc(frame_len)得到200个点的窗函数,类似的用tile变成(426,200)的win,最后把frames * win得到加窗后的分帧信号,其shape还是(426, 200)。
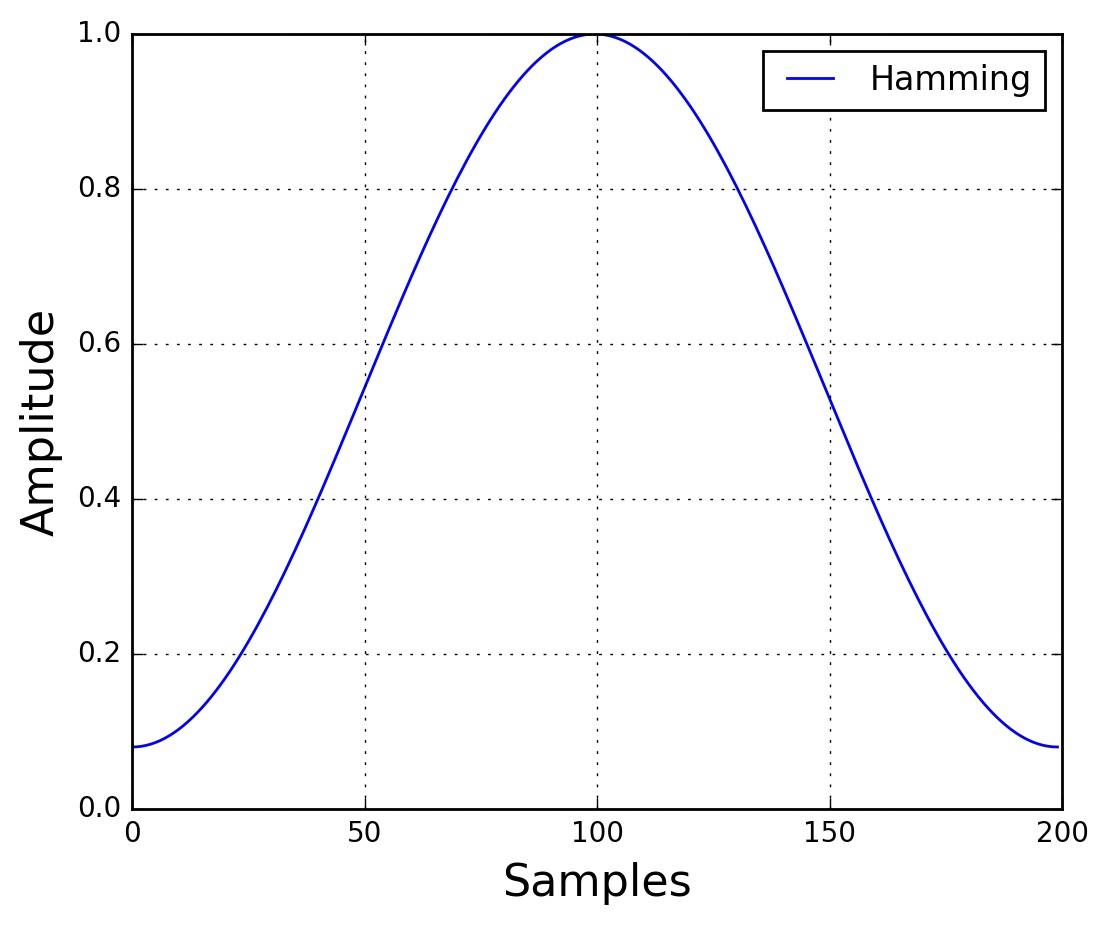
默认的窗函数是方窗,也就是值全为1,但是它的缺点是从1突然变成0会造成尖峰。比较常见的是汉明窗,如下图所示,它的函数形式为:
\[w[n] = 0.54 − 0.46 cos ( \frac{2\pi n}{N − 1} )\]如果使用stride tricks,代码的效率会更高一点,但是结果是一样的。有兴趣的读者请参考numpy文档和这篇文章。
接下来是调用powspec计算功率谱,”pspec = sigproc.powspec(frames,nfft)”,函数powspec的代码为:
def powspec(frames, NFFT):
return 1.0 / NFFT * numpy.square(magspec(frames, NFFT))
它首先调用magspec:
def magspec(frames, NFFT):
complex_spec = numpy.fft.rfft(frames, NFFT)
return numpy.absolute(complex_spec)
magspec对输入的frames(426,200)进行512点的FFT,得到(426,257)个复数值,然后用numpy.absolute求其模。然后用公式$P = \frac{|FFT(x_i)|^2}{N}$计算功率谱,结果是(426,257)的矩阵。
接下来的两行是处理能量为零的情况(也就是一行257个点都是0),如果直接取log会出问题,因此把零的行替换成很小(eps)的数值:
energy = numpy.sum(pspec,1)
energy = numpy.where(energy == 0,numpy.finfo(float).eps,energy)
接下来是用get_filterbanks函数得到滤波器组,前面我们已经介绍过了,这里就不分析其代码了,有兴趣的读者可以自行阅读,这个函数返回一个(26,257)的数组fb。把功率谱能量pspec乘以fb就得到(426,26)的矩阵,表示426帧每一帧是26个Filter Bank的特征。和能量类似,也要处理一些全是零的情况。最终函数fbank返回的是(426,26)的特征和(426,)的能量。到此为止我们得到了Filter Bank的特征。
接下来我们还有继续对log后的Filter Bank特征做DCT得到倒谱系数,代码如下:
feat,energy = fbank(....)
# 首先对Filter Bank特征取log
feat = numpy.log(feat)
# 做DCT
feat = dct(feat, type=2, axis=1, norm='ortho')[:,:numcep]
# 对结果做liftering
feat = lifter(feat,ceplifter)
# 除了能量替换
if appendEnergy:
feat[:,0] = numpy.log(energy)
return feat
lifter函数实现liftering,据说可以提高在噪声环境下的识别效果。
最后是使用delta函数计算delta特征(再对结果调用delta就得到delta-delta特征):
def delta(feat, N):
NUMFRAMES = len(feat)
denominator = 2 * sum([i**2 for i in range(1, N+1)])
delta_feat = numpy.empty_like(feat)
padded = numpy.pad(feat, ((N, N), (0, 0)), mode='edge')
for t in range(NUMFRAMES):
delta_feat[t] = numpy.dot(numpy.arange(-N, N+1), padded[t : t+2*N+1]) /
denominator # [t : t+2*N+1] == [(N+t)-N : (N+t)+N+1]
return delta_feat
Filter Bank特征 vs MFCC特征
前面我们介绍了MFCC特征,它是基于Filter Bank特征的。Filter Bank的特征是基于人耳的听觉机制,而MFCC引入的DCT去相关更多的是为了后面的GMM建模。为了计算方便我们假设GMM的协方差矩阵是对角矩阵,这就要求特征是不相关的。但是对于HMM-DNN系统来说这是不必要的,并且变换会丢失一些信息,因此很多HMM-DNN系统直接使用Filter Bank特征。
- 显示Disqus评论(需要科学上网)