本文主要介绍Policy Gradient,包括用Policy Gradient玩Pong游戏的代码分析。更多文章请点击深度学习理论与实战:提高篇。
目录
原理回顾
前面我们介绍过Policy Gradient的基本原理,我们这里简单的回顾一下。给定一个策略$\pi_\theta(a \vert s)$,我们可以计算一个Episode的trajectory的概率,假设trajectory $\tau$为$s_1,a_1,…,s_T,a_T,s_{T+1}=terminal$,为了简单,我们记为$s_1,a_1,…,s_T,a_T$,然后默认T+1时刻进入终止状态。则这个trajectory的概率为:
\[p_\theta(\tau)=p_\theta(s_1,a_1,...,s_T,a_T)=p(s_1)\prod_{t=1}^{T}\pi_\theta(a_t|s_t)p(s_{t+1}|s_t,a_t)\]上式中$p(s_1)$和$p(s_{t+1} \vert s_t,a_t)$都是由环境决定的,与策略无关,而$\pi_\theta(a_t \vert s_t)$由参数$\theta$决定。Policy Gradient算法期望找到最优的\(\theta^*\)使得期望的Reward最大,用数学语言描述就是:
\[\theta^* =\underset{\theta}{argmax}\mathbb{E}_{\tau \sim p_\theta(\tau)}[\sum_t r(s_t, a_t)]\]如果是Episode的情况,上面的公式按时间进行分解:
\[\theta^* =\underset{\theta}{argmax} \sum_{t=1}^{T}\mathbb{E}_{(s_t,a_t) \sim p_\theta(s_t, a_t)}[\sum_t r(s_t, a_t)]\]注意,我们前面知道的是联合概率分布$p_\theta(s_1,a_1,…,s_T,a_T)$,而这里要求的是边缘分布$p_\theta(s_t,a_t)$,当然有了联合分布,理论上是可以通过积分或者求和得到边缘分布。但如果是Continuous的情况,t可以区域无穷大,那么就只能写出如下的形式:
\[\theta^* =\underset{\theta}{argmax}\mathbb{E}_{(\mathbf{s},\mathbf{a}) \sim p_\theta((\mathbf{s},\mathbf{a}))}[\sum_t r(\mathbf{s},\mathbf{a})]\]这个公式和前面的用$\tau$的其实完全一样,因为$\tau$就是$(\mathbf{s},\mathbf{a})$。下面我们再来推导一下Policy Gradient,这比之前的推导更加简洁,注意这里的记号稍微有些不同,之前t时刻采取$a_t$,然后进入状态$s_{t+1}$并且得到reward $r_{t+1}$,而这里reward记作$r_t$。
\[\begin{aligned} J(\theta) & \equiv \mathbb{E}_{\tau \sim p_\theta(\tau)}[\sum_t r(s_t, a_t)] \\ & = \mathbb{E}_{\tau \sim p_\theta(\tau)}r(\tau) & \text{把} \sum_t r(s_t, a_t) \text{记作} r(\tau) \\ & = \int p_\theta(\tau) r(\tau) d\tau \\ \nabla J(\theta)=\int \nabla p_\theta(\tau) r(\tau) d\tau \\ & = p_\theta(\tau) \nabla log p_\theta(\tau) r(\tau) d\tau \\ & = \mathbb{E}_{\tau \sim p_\theta(\tau)}[\nabla log p_\theta(\tau) r(\tau)] \\ & = \mathbb{E}_{\tau \sim p_\theta(\tau)}[\nabla logp(s_1) +\sum_{t=1}^Tlog\pi_\theta(a_t|s_t) + logp(s_{t+1}|s_t,a_t) r(\tau)] \\ & = \mathbb{E}_{\tau \sim p_\theta(\tau)}[\nabla \sum_{t=1}^Tlog\pi_\theta(a_t|s_t) r(\tau)] & \text{前后两项与参数} \theta \text{无关} \\ & = \mathbb{E}_{\tau \sim p_\theta(\tau)}[\nabla \sum_{t=1}^Tlog\pi_\theta(a_t|s_t) \sum_{t=1}^{T}r(s_t,a_t)] \end{aligned}\]最后一个式子是求期望,而实际我们可以使用采样(MC)来实现,这样得到:
\[\begin{split} \nabla J(\theta) & = \mathbb{E}_{\tau \sim p_\theta(\tau)}[\nabla \sum_{t=1}^Tlog\pi_\theta(a_t|s_t) \sum_{t=1}^{T}r(s_t,a_t)] \\ \nabla J(\theta) & \approx \frac{1}{N} \sum_{i=1}^{N} \nabla \sum_{t=1}^Tlog\pi_\theta(a_t|s_t) \sum_{t=1}^{T}r(s_t,a_t) \end{split}\]根据”因果性”,我们认为$a_t$只能影响t及其之后时刻的reward,因此:
\[\nabla J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \nabla \sum_{t=1}^Tlog\pi_\theta(a_t|s_t) \sum_{t'=t}^{T}r(s_{t'},a_{t'})\]当然我们也可以对未来的reward进行discount:
\[\begin{split} \nabla J(\theta) & \approx \frac{1}{N} \sum_{i=1}^{N} \nabla \sum_{t=1}^Tlog\pi_\theta(a_t|s_t) \sum_{t'=t}^{T} \gamma^{t'-t}r(s_{t'},a_{t'}) \\ & = \frac{1}{N} \sum_{i=1}^{N} \nabla \sum_{t=1}^Tlog\pi_\theta(a_t|s_t) Q(s_t, a_t) \end{split}\]使用深度学习框架
下面我们来讨论实现的问题,我们需要计算$\nabla J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \nabla \sum_{t=1}^Tlog\pi_\theta(a_t \vert s_t) \sum_{t’=t}^{T}r(s_{t’},a_{t’})$,这并不困难,我们的神经网络就是拟合函数$pi_\theta(a \vert s)$,它的输入是状态s(连续的向量),而输出是采取不同action的概率,假设有n个不同的action,那么我们的网络输出就是n个logits值,然后用softmax变成概率就行了。我们需要计算$\nabla log\pi_\theta(a \vert s) \vert_{s=s_t, a=a_t} Q(s_t,a_t)$,这也并不困难,Tensorflow或者PyTorch都可以帮我们自动求梯度。但是我们需要手动更新参数(梯度上升),而且我们无法使用更加复杂的算法,比如Adam Optimizer等,因为这些算法都是用于梯度下降算法的。
为了能够复用这些工具,我们可以使用一个tricky的办法——定义一个损失函数,使得它的梯度就是$\nabla log\pi_\theta(a \vert s) \vert_{s=s_t, a=a_t}Q(s_t,a_t)$。什么损失函数的梯度就是它呢?我们先不看$Q(s_t,a_t)$,它只是一个常量。我们来看看$\nabla log\pi_\theta(a \vert s)$,$pi_\theta(a \vert s_t)$的输出是概率分布,真实的action是$a_t$,我们把它看成一个分类问题,输入是$s_t$,真实的标签是$a_t$,而模型的预测是$p(a_t \vert s_t)$,因此交叉熵就是$-logp(a_t \vert s_t)$。
因此我们可以把一个Policy Gradient算法看成一个分类问题,训练数据是$<s_1,a_1>, …, <s_T,a_T>$,然后使用梯度下降来优化分类的交叉熵,这样调整参数后就能增加期望的Reward $J(\theta)$。
但是还有一个问题:怎么处理Q(s_t,a_t)这个常量?也很简单,直接把它乘到loss里就行。因此我可以使用下面的伪(Tensorflow)代码来实现Policy Gradient算法:
states = tf.placeholder(dtype=tf.float32, shape=(None, s_dim))
actions = tf.placeholder(dtype=tf.float32, shape=(None, a_dim))
q_values = tf.placeholder(dtype=tf.float32, shape=(None,1))
logits = .... 定义网络输入是states,输出logits的shape是(None, a_dim),表示输出不同action的logits
negative_likelihoods = tf.nn.softmax_cross_entropy_with_logits(labels=actions, logits=logits)
weighted_negative_likelihoods = tf.multiply(negative_likelihoods, q_values)
loss = tf.reduce_mean(weighted_negative_likelihoods)
opt = tf.train.RMSPropOptimizer().minimize(loss)
用Policy Gradient玩Pong游戏
前面我们介绍了Policy Gradient的原理,它的核心是求Reward $J_\theta$对参数$\theta$的梯度,然后使用梯度上升算法调整参数使得Reward最大化。而Reward $J_\theta$是策略$\pi_\theta(a \vert s)$的函数,而$\pi_\theta(a \vert s)$又是$\theta$的函数。把深度学习用到Policy Gradient里是非常自然的,也就是用神经网络来你好函数$\pi_\theta(a \vert s)$,因此参数$\theta$就是神经网络的参数。下面我们介绍怎么用基于深度神经网络的Policy Gradient来玩Pong这个游戏。完整代码在这里下载。
游戏简介
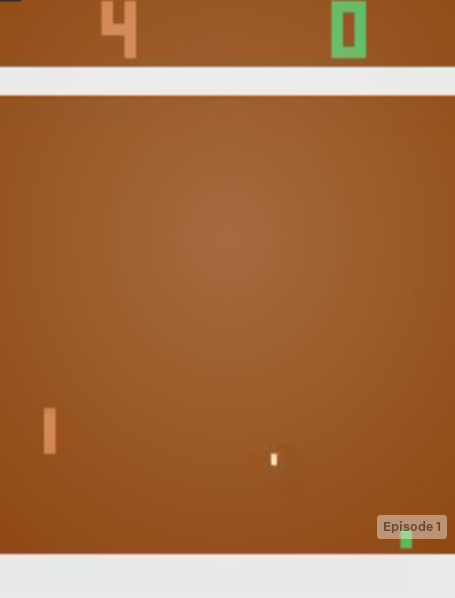
如下图所示,这个游戏有两个玩家,一个是电脑NPC,一个是玩家(现在我们也要用深度学习的Agent来实现)。有一个球弹来弹去,每个玩家都可以移动挡板,目的是把求弹到对方的方向,如果某个玩家没有接住球那么就算输了,而对手获胜。
这个游戏的输入也是连续输入的一帧帧的图片,我们这里会使用神经网络来实现策略函数$\pi_\theta(a vert s)$,我们通常把用于实现策略的神经网络叫做Policy Network;类似的我们会把拟合Value函数的神经网络叫做Value Network。在后面介绍的AlphaGo算法里我们也会看到这两个网络。
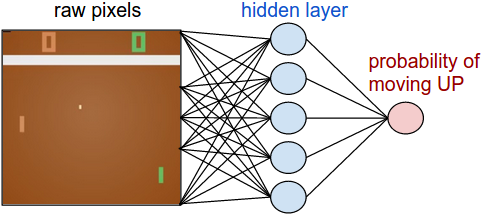
这个Policy Network的输入是(210, 160, 3)的图片,通过两个全连接网络之后输出一个值,表示UP操作的概率p(DOWN的概率就是1-p)。如下图所示。
预处理
但是我们并不直接把(210,160,3)的图像输入Policy Network,我们会做一下预处理,图像预处理代码如下,这是由OpenAI team的成员提供的:
def prepro(I): # I是游戏的一帧图像
""" 把210x160x3的uint8图像变成6400 (80x80)的1d的float向量"""
# 下面的代码是OpenAI team成员提供的
I = I[35:195] # 去掉无效的(球到不了的)区域 (160,160,3)
I = I[::2, ::2, 0] # 下采样 (80,80) RGB只保留R。
I[I == 144] = 0 # 类型1的背景值是144,变成0
I[I == 109] = 0 # 类型2的背景值是109,也变成0
I[I != 0] = 1 # 非背景(挡板和小球)变成1
return I.astype('float').ravel() # 变成1D的浮点数
和前面的breakout类似,我们用最近两帧的图像来表示当前状态,这样可以建模球的速度。但是这里和前面不同,直接用这两帧的差表示当前状态,因此神经网络的输入大小是6400的向量。
网络定义
网络定义非常简单,就是一个三层的全连接网络:
def make_network(pixels_num, hidden_units):
pixels = tf.placeholder(dtype=tf.float32, shape=(None, pixels_num))
actions = tf.placeholder(dtype=tf.float32, shape=(None, 1))
rewards = tf.placeholder(dtype=tf.float32, shape=(None, 1))
with tf.variable_scope('policy'):
hidden = tf.layers.dense(pixels, hidden_units, activation=tf.nn.relu, \
kernel_initializer=tf.contrib.layers.xavier_initializer())
logits = tf.layers.dense(hidden, 1, activation=None, \
kernel_initializer=tf.contrib.layers.xavier_initializer())
out = tf.sigmoid(logits, name="sigmoid")
cross_entropy = tf.nn.sigmoid_cross_entropy_with_logits(
labels=actions, logits=logits, name="cross_entropy")
loss = tf.reduce_sum(tf.multiply(rewards, cross_entropy, name="rewards"))
lr = 1e-3
decay_rate = 0.99
opt = tf.train.RMSPropOptimizer(lr, decay=decay_rate).minimize(loss)
tf.summary.histogram("hidden_out", hidden)
tf.summary.histogram("logits_out", logits)
tf.summary.histogram("prob_out", out)
merged = tf.summary.merge_all()
return pixels, actions, rewards, out, opt, merged
注意:这里的代码和前面的伪代码稍微有一些区别。前面假设输出是N个action的概率,所有网络的输出是logits,然后计算交叉熵。对于这个问题来说,输出的值只有两种可能,所以这里神经网络的输出是一个值,表示action UP的logits(不是概率)。然后计算交叉熵损失函数的时候使用了sigmoid_cross_entropy_with_logits计算。
我们也可以修改代码使得网络输出是两个值,然后使用softmax_cross_entropy_with_logits,这其实是等价的。我们之前也介绍过了,二分类的LR(sigmoid)是多分类的LR(softmax)的特殊情况。
discount_rewards
def discount_rewards(r):
gamma = 0.99
""" take 1D float array of rewards and compute discounted reward """
discounted_r = np.zeros_like(r)
running_add = 0
for t in reversed(range(0, len(r))):
if r[t] != 0:
# 游戏结束,开始一个新的episode
running_add = 0
running_add = running_add * gamma + r[t]
discounted_r[t] = running_add
return discounted_r
它的输入是一维的向量,表示多个Episode的reward,那怎么区分某个reward属于那个Episode呢?因为Pong比较特殊,除了游戏结束,其它时刻的reward都是0,游戏介绍agent获胜就是1,失败就是0。因此我们可以根据这个特点来判断Episode的结束。假设一个Episode的reward是$r_1,…,r_4$,那么G的计算如下:
\[\begin{split} G_1 & =r_1 +\gamma r_2 + \gamma^2 r_3 + \gamma^3 r_4 \\ G_2 & = r_2 +\gamma r_3 + \gamma ^2 r_4 \\ G_3 & = r_3 +\gamma r_4 \\ G_4 & = r_4 \end{split}\]这样计算效率不高,我们可以这样重写一下:
\[\begin{split} G_1 & =r_1 +\gamma G_2 \\ G_2 & = r_2 +\gamma G_3 \\ G_3 & = r_3 +\gamma G_4 \\ G_4 & = r_4 \end{split}\]这样计算量就小多了,但是需要从后往前先计算G。理解这个之后,代码就很好懂了,running_add就是上一个时刻的G。如果碰到非零值,就表示这是一个新的Episode,因此running_add需要清零。
训练主代码
pix_ph, action_ph, reward_ph, out_sym, opt_sym, merged_sym =
make_network(pixels_num, hidden_units)
...
while True:
cur_x = prepro(observation)
x = cur_x - prev_x if prev_x is not None else np.zeros((pixels_num,))
prev_x = cur_x
# 当前网络输出UP的概率,即使是一个数据,也要reshape成(batch, 6400)
tf_probs = sess.run(out_sym, feed_dict={pix_ph: x.reshape((-1, x.size))})
y = 1 if np.random.uniform() < tf_probs[0, 0] else 0
action = 2 + y
# 采取action
observation, reward, done, _ = env.step(action)
# 保存x(s),y(a)和reward
xs.append(x)
ys.append(y)
ep_ws.append(reward)
if done:
episode_number += 1
# 计算discount reward
discounted_epr = discount_rewards(ep_ws)
# normalize,因为不同的Episode长度不一样,所以需要normalize。
discounted_epr -= np.mean(discounted_epr)
discounted_epr /= np.std(discounted_epr)
# 每隔batch_size个episode训练一次
if episode_number % batch_size == 0:
step += 1
exs = np.vstack(xs)
eys = np.vstack(ys)
ews = np.vstack(batch_ws)
frame_size = len(xs)
stride = 20000
pos = 0
# 一个episode可能很长,我们每次训练20000个(s,a,r)对
while True:
end = frame_size if pos + stride >= frame_size else pos + stride
batch_x = exs[pos:end]
batch_y = eys[pos:end]
batch_w = ews[pos:end]
feed_dict={pix_ph:exs,action_ph:eys,reward_ph:ews})
tf_opt, tf_summary = sess.run([opt_sym, merged_sym], feed_dict=
{pix_ph: batch_x, action_ph: batch_y, reward_ph: batch_w})
pos = end
if pos >= frame_size:
break
xs = []
ys = []
batch_ws = []
observation = env.reset()
结果
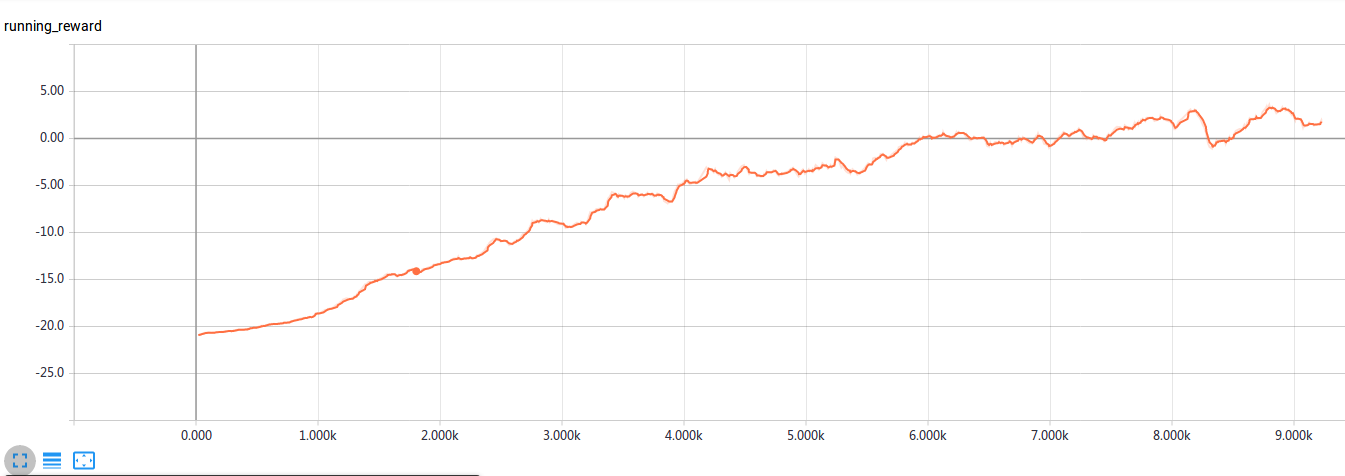
训练8k个minibatch之后agent对电脑的胜率就超过50%了,训练8k可能需要十几个小时。胜率的变化曲线如下图所示。
- 显示Disqus评论(需要科学上网)