强化学习简介(三)

本文介绍蒙特卡罗方法，详细介绍蒙特卡罗预测。接着会通过多臂老虎机和UCB来介绍探索-利用困境（exploration-exploitation dilemma），然后会介绍On-Policy和Off-Policy的蒙特卡罗预测，最后会简单的比较一下蒙特卡罗方法与动态规划的区别。每一个算法都会有相应的示例代码，通过一个简单的21点游戏来比较On-Policy和Off-Policy算法。

更多本系列文章请点击强化学习简介系列文章。更多内容请点击深度学习理论与实战：提高篇。

目录

• 蒙特卡罗预测(Monte Carlo Prediction)
• 21点游戏(Blackjack)
• 蒙特卡罗预测代码示例
  • Blackjack环境
  • 蒙特卡罗预测代码
• 蒙特卡罗控制
• 多臂老虎机和UCB
• On-Policy蒙特卡洛控制
• On-Policy蒙特卡罗控制代码示例
• Off-Policy蒙特卡罗预测
• Off-Policy蒙特卡罗控制
• Off-Policy蒙特卡罗控制代码示例
• 动态规划和蒙特卡罗方法的比较

接下来我们介绍解决MDP问题的另外一种方法——蒙特卡罗方法。前面的动态规划方法，我们需要完全的环境动力学$p(s’,r|s,a)$。而蒙特卡罗方法只需要经验(Experience)——通过与真实环境交互或者模拟得到的状态、行为和奖励的序列。如果从模拟学习，那么需要一个模型来建模环境，但是这个模型不需要完整的环境动力学，它只需要能采样即可。有的时候显示的定义一个概率分布是很困难的，但是从中获取样本却比较容易。

蒙特卡罗方法通过平均采样的回报(return)来解决强化学习问题。它要求任务是Episodic的，并且一个Episode进入终止状态后才能开始计算（后面介绍的Temporal Difference不需要任务是Episodic，即使Episodic的任务也不用等到一个Episode介绍才能计算）。

蒙特卡罗预测(Monte Carlo Prediction)

首先我们来使用蒙特卡罗方法解决预测问题——给定策略，计算状态价值函数的问题。回忆一下，状态的价值是从这个状态开始期望的回报——也就是期望的所有未来Reward的打折累加。因此很直观的想法就是从经验中估计——所有经过这个状态的回报的平均。我们的目标是估计$v_\pi$，但是我们有的只是一些经验的Episode，这些Episode是采样策略$\pi$得到的。也就是Episode $S_1,A_1,R_2,…,S_k \sim \pi$。而t时刻状态是s的回报是如下定义的：

而状态价值函数是采样策略$\pi$时期望的回报：

蒙特卡罗方法的思想是使用(采样的)平均回报来估计期望回报，根据大数定律，如果采样的次数趋于无穷，那么估计是无偏的。

比如我们要估计$v_\pi(s)$，我们用很多Episodic的经验，这些经验是使用策略$\pi$获得的。一个Episode里s的每次出现都叫做s的一次visit。当然在一个Episode里s可能多次出现，一种方法只考虑s的第一次visit，这就叫First-Visit蒙特卡罗方法；而另外一种就是每次visit都算，这就是Every-Visit蒙特卡罗方法。这两者的收敛在理论上有一些细微区别，我们这里不讨论，这里我们使用First-Visit蒙特卡罗方法。算法伪代码如下：

图：First-Visit蒙特卡罗方法伪代码

21点游戏(Blackjack)

在介绍蒙特卡罗预测的代码之前，我们来学习一下21点游戏的玩法，并且说明为什么之前的动态规划很难解决这个问题，后面我们会使用蒙特卡罗方法来估计状态的价值函数。

这个游戏有一个庄家和一个玩家(我们这里假设只有一个玩家)，有一副扑克牌，他们的目标是使得手中所有的牌加起来尽可能大，但是不能超过21（可以等于），最终谁大谁获胜，如果一样大就是平均(Draw)。所有的花牌(Face，也就是J、Q、K)都算作10，Ace可以算1也可以算11。游戏开始时庄家和玩家都会发到两张牌，庄家的一张牌是亮出来的，而玩家的两张牌是不亮的。如果这两张牌是21点(一个Ace和一个花牌或者一个10)，那么就叫一个natural，如果对手不是natural，那就获胜，否则是平局。如果都不是natural，那么玩家可以有两种选择，继续要牌(hit)或者不要(stick)。如果继续要牌之后超过21点，就叫爆了(goes bust)，那么庄家获胜。如果没有爆就停止要牌，那就轮到庄家要牌，庄家如果爆了，那就玩家获胜，否则就比最终的大小来区分胜负或者平局。

读者可以在继续阅读之前上网“搜索21点在线”来试玩一下，这样对这个游戏更加熟悉。进入网站点击”Try it free”可以免费单人试玩，请不要赌博！！

从游戏的技巧来看（作者在学习强化学习之前也没玩过，所有总结的不一定正确），玩家需要根据庄家亮的牌以及自己牌的和来决定是否继续要牌。同样庄家可能需要根据自己的点数以及玩家的牌的张数以及玩家要牌的快慢表情等(如果是跟机器玩可能就无表情了？机器能像人那样使用表情骗人吗？——明明分不高故意装得很有信心，从而引导对手爆掉)来决定是否继续要牌。另外就是Ace的使用，如果把Ace算成11也没有超过21点，那么再要牌肯定不会爆掉，但是有可能分变小，比如现在是3+Ace，我们可以认为是4点或者14点，但似乎都有点少，那么我们再要一张。如果是8，那么Ace只能算成1，否则就爆了(22)，这样的结果就是12点。

由于有两个角色——庄家和玩家，玩的好的Agent可能还要对对手建模，甚至还要利用对手的表情这样的信息，包括用表情来骗人。这里为了简单，我们假设看不到表情，而且我们的Agent是玩家，并且假设庄家使用一个固定的策略：如果得分达到或者超过17就stick，否则就一直hit。

我们可以用MDP来对这个游戏进行建模，这是个有限的MDP，而且是Episodic的，游戏肯定会结束。对于结束状态，获胜、失败和平局，Reward分别是+1、-1和0。没有结束的状态的Reward都是0,打折因子是1。玩家的Action只有stick和hit两种。状态是玩家的牌和庄家亮出来的那张牌（这部分信息是玩家可以获得的所有信息）。此外为了简单，我们假设发牌的牌堆是无限的（也就是每种牌都可能无限张，因此记住已经发过的牌是没有什么意义的，但实际的情况是有区别的，如果拿过一张Ace，那么再拿到Ace的概率会变化）。

玩家的状态有多少种呢？首先是自己的当前得分，因为如果当前不超过11点，那么必然可以要牌而不爆掉，因此状态是12-21共10种可能。而另外的信息就是庄家亮牌ace-10共十种（花牌和10没区别）。还有一点就是Ace，如果玩家有一个Ace而且可以把它算作11而不爆，那么这个Ace就叫可用(Usable)的Ace。如果Ace算作11就爆了，那么它只能算1，也就是不能再（根据不同情况）变化了，也就不“可用”了。如果Ace可以算11，那么我们一定把它算成11，因为如果算成1，那么分就一定小于等于11（否则就爆了），那么我们一定会继续要牌，这个状态是不需要决策的，直接变成一个新的状态。

关于“可用”的Ace算11可能有些难以理解，我们通过一个例子来说明。假设现在玩家手里的牌是2+3+Ace，这个Ace是“可用”的，我们现在的状态是16点并且有一个“可用”的Ace。如果我们把Ace当成1，那么也可以增加一个状态，2+3+Ace，但是这个状态我们一定会hit。所以我们不需要认为这种状态存在。因此这个MDP一共有10 * 10 * 2=200个状态。

如果现在的牌是9+Ace，正常它是两种状态：得分为10并且有可用的Ace；得分为20并且有可用的Ace。但是这两种状态可以合并为一个状态——得分为20并且有可用的Ace。因为如果你告诉我得分是20并且有可用的Ace，那么一定有一个Ace并且除了Ace之外的牌的分是9；同理你如果告诉我得分10并且有可用的Ace，我们通用可以推出出来一定有一个Ace并且其它牌得分是9(显然不能是-1)。那为什么不把这两种状态合并成得分为10并且有可用的Ace呢？其实也是可以的，但是我们之前把得分范围限定在[12,21]之间了，因为小于11是肯定可以要牌的，所以这样表示比较简单，否则得分的范围就是[1,21]了。

为什么这个问题很难用动态规划来解决呢？因为动态规划需要知道$p(s’,r|s,a)$，比如现在的牌是3+8+2，如果我们采取hit(要牌)，我们也许还能计算变成3+8+2+4的概率，但是reward是多少呢？此外如果我们stick，那么我们的状态会取决于庄家的行为并且最终进入终止状态，这个是很难计算的（因为我们不知道没有亮的牌是多少）。而使用蒙特卡罗方法就很简单，我们不需要知道这些概率，只需要根据某个策略来采取行为就可以了，而环境动力学我们只需要随机模拟就可以了。

蒙特卡罗预测代码示例

完整代码在这里。

Blackjack环境

首先我们来简单的阅读一些Blackjack环境代码。代码在envs/blackjack.py里。要点都在注释里了，请读者仔细阅读注释。

class BlackjackEnv(gym.Env):
    """简单的blackjack环境
    Blackjack是一个纸牌游戏，目的是纸牌的和尽量接近21但是不能超过。这里的玩家是和一个
    固定策略的庄家。
    花牌(Jack, Queen, King)是10。 have point value 10.
    Ace即可以看成11也可以看成1，如果可以看成11那么就叫Usable。
    这个游戏可以任务牌的数量是无限的。因此每次取牌的概率是固定的。
    游戏开始时玩家和庄家都有两张牌，庄家的一张牌是亮出来的。
    玩家可以要牌或者停止要牌。如果玩家的牌超过21点，则庄家获胜。
    如果玩家没有超过21点就停止要牌，则轮到庄家要牌，这里的庄家是采取固定的策略——如果没超过16就
    继续要牌，如果超过16（大于等于17）则停止要牌。如果庄家超过21点则玩家获胜，
    否则比较两人牌的大小，大者获胜，一样大则平局。赢的reward是1，输了-1，平局0。
    """
    def __init__(self, natural=False):
        self.action_space = spaces.Discrete(2)
        # Tuple-1 1-31表示玩家的牌的和，注意如果玩家到了21点肯定不会再要牌，
        # 因此即使爆了和最大也是20+11=31，其实根据我们的分析12以下也
        # 没必要有，不过有也没关系。
        # Tuple-2 1-10表示庄家亮牌的点数
        # Tuple-3 0和1表示是否有可用的Ace
        self.observation_space = spaces.Tuple((
            spaces.Discrete(32),
            spaces.Discrete(11),
            spaces.Discrete(2)))
        self.seed()

        # 这个Flag表示如果玩家natural赢了的奖励是1.5倍。
        self.natural = natural
        # 开始游戏
        self.reset()
        self.nA = 2

    def seed(self, seed=None):
        self.np_random, seed = seeding.np_random(seed)
        return [seed]

    def step(self, action):
        assert self.action_space.contains(action)
        if action:  # hit: 继续要牌
            self.player.append(draw_card(self.np_random))
            if is_bust(self.player):
                done = True
                reward = -1
            else:
                done = False
                reward = 0
        else:  # stick: 玩家不要牌了，模拟庄家的策略直到游戏结束。
            done = True
            while sum_hand(self.dealer) < 17:
                self.dealer.append(draw_card(self.np_random))
            reward = cmp(score(self.player), score(self.dealer))
            # 如果self.natural并且玩家通过natural获胜，这是1.5倍奖励
            if self.natural and is_natural(self.player) and reward == 1:
                reward = 1.5
        return self._get_obs(), reward, done, {}

    def _get_obs(self):
        return (sum_hand(self.player), self.dealer[0], usable_ace(self.player))

    def reset(self):
        # 每人都来两张牌
        self.dealer = draw_hand(self.np_random)
        self.player = draw_hand(self.np_random)

        # 如果玩家的牌没到12点就自动帮他要牌
        while sum_hand(self.player) < 12:
            self.player.append(draw_card(self.np_random))

        return self._get_obs()

玩家的牌存在self.player里，而庄家的牌存在self.dealer里，状态是3元组。3元组的第一个是spaces.Discrete(32)，Discrete(32)的范围是0-31。游戏中没有0的牌，1-31表示玩家的牌的和，注意如果玩家到了21点肯定不会再要牌，因此即使爆了最大和也最多是20+11=31，其实根据我们的分析12以下也没必要有，不过有也没关系。3元组的第二个是spaces.Discrete(10)，1-10表示庄家亮牌的点数。3元组的第三个元素用0和1表示是否有可用的Ace。

蒙特卡罗预测代码

代码如下，非常直观，请读者对照前面的伪代码阅读代码和注释。

def mc_prediction(policy, env, num_episodes, discount_factor=1.0):
    """
    蒙特卡罗预测算法。给定策略policy，计算它的价值函数。
    
    参数:
        policy: 一个函数，输入是状态(observation)，输出是采取不同action的概率。
        env: OpenAI gym 环境对象。
        num_episodes: 采样的次数。
        discount_factor:打折因子。
    
    返回:
        一个dictionary state -> value。
        state是一个三元组，而value是float。
    """

    # 记录每个状态的Return和出现的次数。
    returns_sum = defaultdict(float)
    returns_count = defaultdict(float)
    
    # 最终的价值函数
    V = defaultdict(float)
    
    for i_episode in range(1, num_episodes + 1):
        if i_episode % 1000 == 0:
            print("\rEpisode {}/{}.".format(i_episode, num_episodes), end="")
            sys.stdout.flush()

        # 生成一个episode.
        # 一个episode是三元组(state, action, reward) 的数组
        episode = []
        state = env.reset()
        for t in range(100):
            action = policy(state)
            next_state, reward, done, _ = env.step(action)
            episode.append((state, action, reward))
            if done:
                break
            state = next_state

        # 找到这个episode里出现的所有状态。
        states_in_episode = set([tuple(x[0]) for x in episode])
        for state in states_in_episode:
            # 找到这个状态第一次出现的下标
            first_occurence_idx = next(i for i,x in enumerate(episode) if x[0] == state)
            # 计算这个状态的Return
            G = sum([x[2]*(discount_factor**i) for i,x in enumerate(episode[first_occurence_idx:])])
            # 累加
            returns_sum[state] += G
            returns_count[state] += 1.0
            V[state] = returns_sum[state] / returns_count[state]

    return V

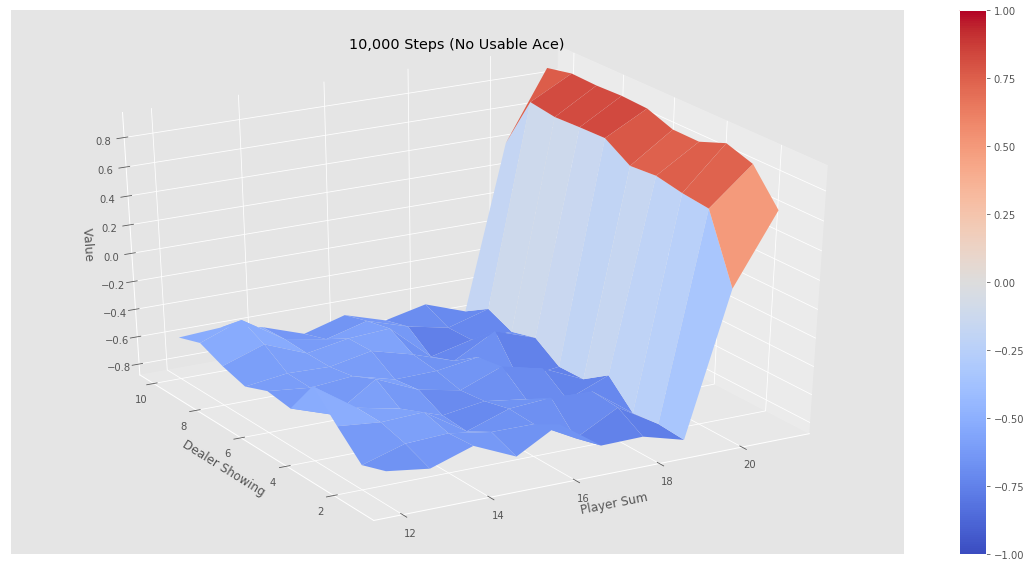
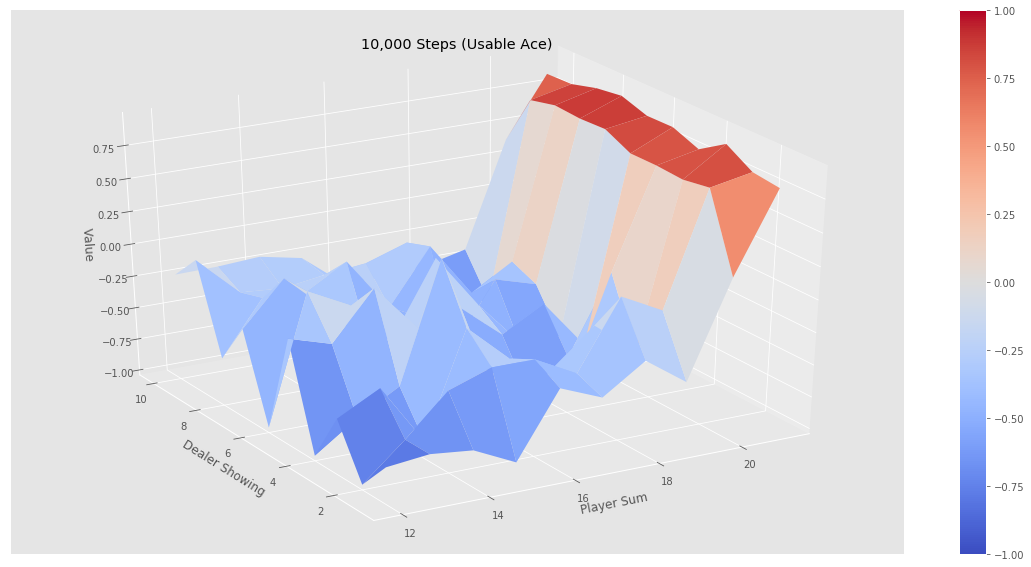
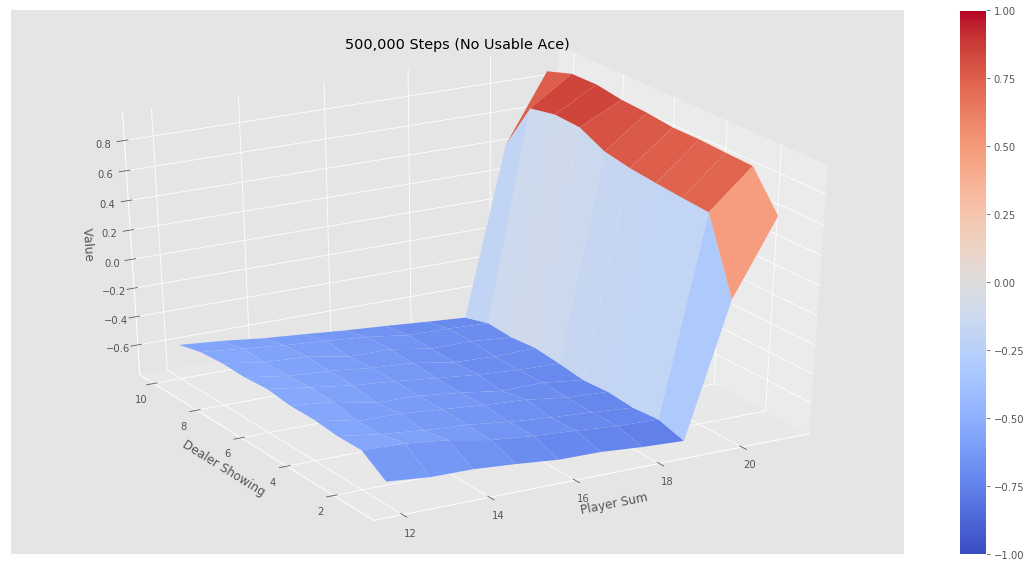
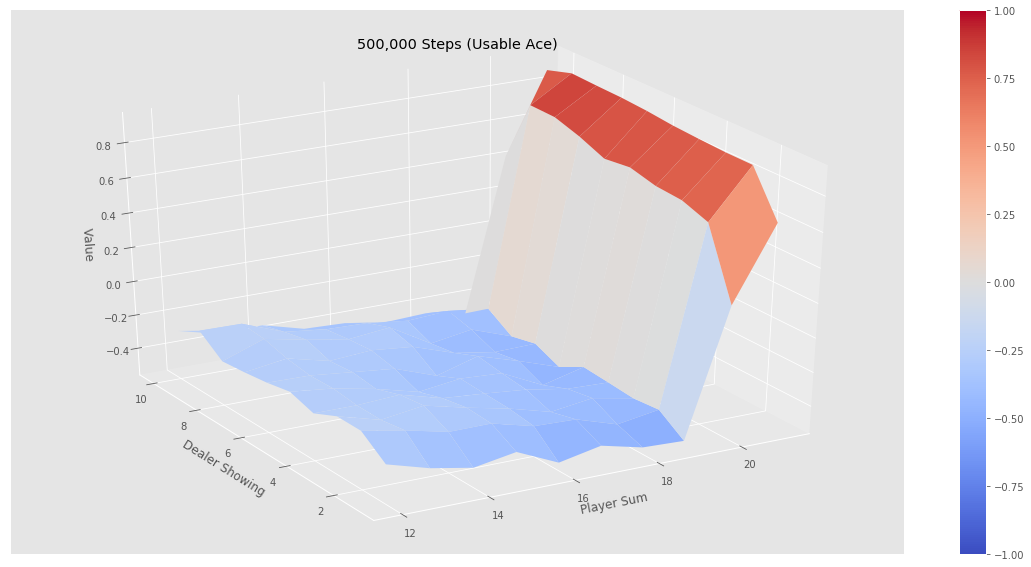
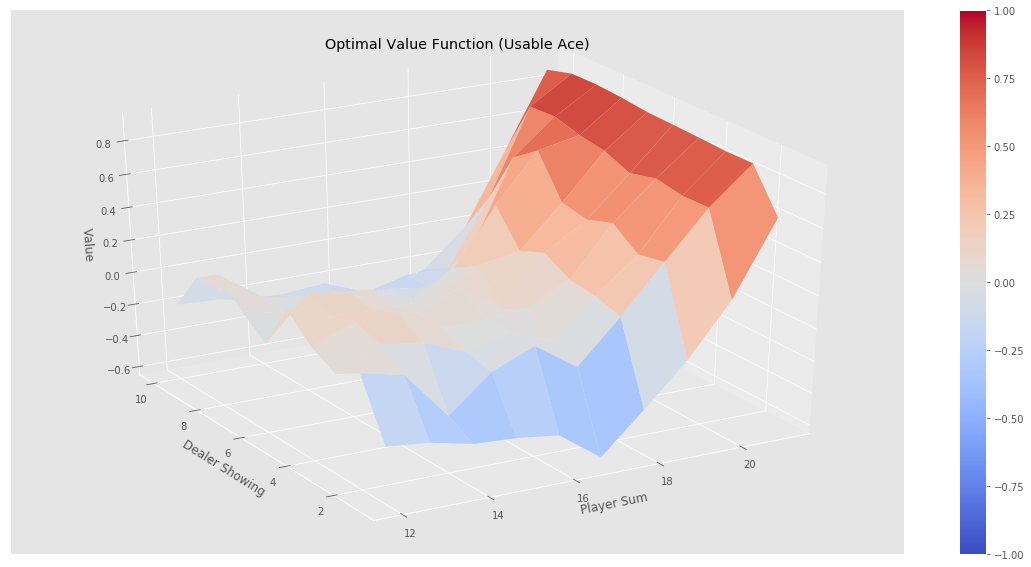
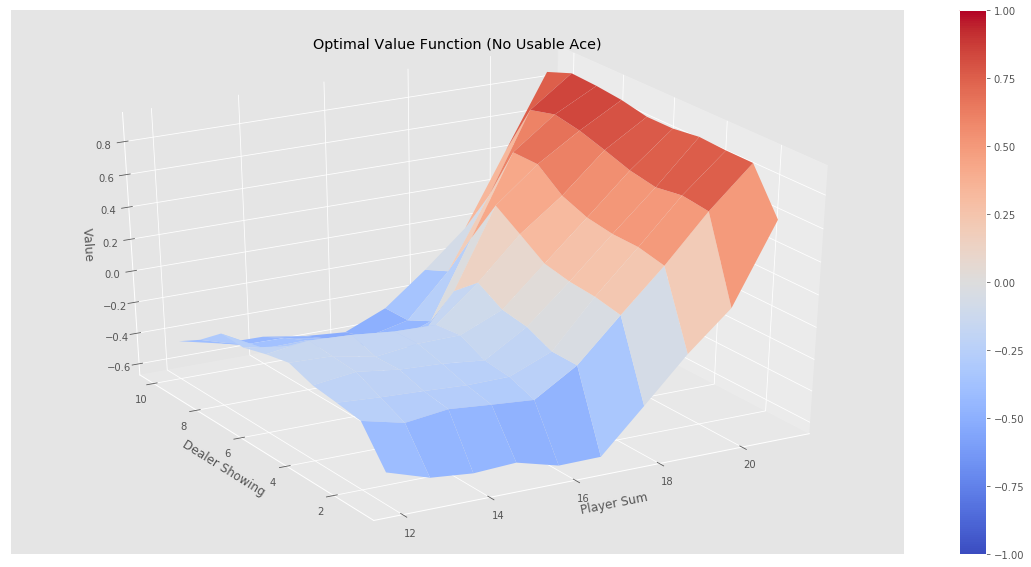
最后我们测试简单的策略——不到20就要牌，否则就停止的策略，看看它在不同状态下的价值函数：

如果我们运行jupyter notebook的代码，可以得到下图的结果。可以看到经过500k次迭代后价值函数非常平滑，而10k次迭代还是不平滑的，也就是误差比较大。我们发现(验证)这个策略并不好：从图中可以看出，只有一上来我们(agent)的点数大于20点才会赢，事实上如果我们知道庄家的策略，我们一上来到了18点就可以停止要牌了，但是我们很激进的要超过19才停止，这显然很容易爆掉。所以这个策略基本就是输的。

图：10k迭代没有Ace

图：10k迭代有Ace

图：500k迭代没有Ace

图：500k迭代有Ace

前面介绍的是使用蒙特卡罗方法来求解一个策略的状态价值函数，而行为状态函数也是类似的算法，只不过采样后累加的key是s-a而不是s而已。这里就不赘述了。

蒙特卡罗控制

和之前的策略迭代类似，我们可以用蒙特卡罗预测替代基于动态规划的策略评估，然后不断提升策略。这里我们计算的是行为价值函数q(s,a)而不是状态v(s)。

这里使用的策略提升是贪婪的方法：

为什么这个方法可以提升策略呢？我们仍然可以使用前面的策略提升定理来证明：

上面的证明第一行到第二行的等号稍微有点绕，但并不复杂：$arg\max_aq_{\pi_k}(s,a)$是遍历所有的a，找到使得$q_{\pi_k}(s,a)$最大的那个a，假设是\(a_*\)，那么\(q_{\pi_k}(s,a_*)\)，自然就是使得$\max_aq_{\pi_k}(s,a)$。第二行到第三行的不等式很容易，最大的那个a对应的q自然比任何其它($\pi_k(s)$)的q要大。

这个算法有两个假设：蒙特卡罗迭代的次数是无穷的（才能逼近真实的价值函数）；Exploring Start。前者我们可以忽略，因为迭代足够多次数一般就够了，而且我们之前也讨论过价值迭代，我们不需要精确的估计策略的价值就可以使用价值提升了。这里的关键问题是Exploring Start，初始状态$S_0$因为游戏是随机初始化的，因此所有可能的初始状态我们都可能遍历到，而且随着采样趋于无穷，每种可能初始状态的采样都是趋于无穷。与$S_0$对应的$A_0$可能有很多，但是有可能我们的策略会只选择其中一部分，那么有可能我们搜索的空间是不完整的。一种办法就是Exploring Start，就是强制随机的选择所有可能的($S_0$和$A(S_0)$)，但这样有问题——我们的策略探索过$(S_0,A_0)$之后发现它不好，正常的话，它碰到$S_0$后就避免$A_0$了，但是我们强迫它随机(平均)的探索$(S_0,A_0)$和$(S_0,A_1)$，其实是浪费的。这个问题我们留到后面来解决，我们首先假设是Exploring Start的，看看蒙特卡罗预测的伪代码。

图：蒙特卡罗控制算法伪代码

通过上面的算法，我们就可以得到最优的策略如下图所示。

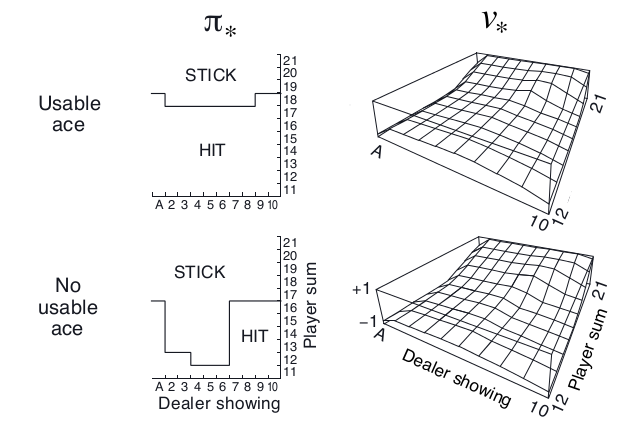图：使用Exploring Start的蒙特卡罗控制求解结果

这里学到的策略大致是：如果有可用的Ace，那么一直要牌直到18点，这显然是有道理的，因为我们知道庄家是要到17点为止。如果没有Ace，如果庄家亮出来的牌很小，那么我们到11或者12点就停止要牌了。为什么这是最优的？作者也不清楚，知道的读者可以留言告诉我。

这一节我们不会实现Exploring Start的算法，原因前面我们讲过了，这个算法并不高效和通用，我们之后的内容会介绍没有Explroing Start的算法并用它们来解决21点游戏。

多臂老虎机和UCB

上一节遇到的一个问题就是Exploring Start的问题，如果我们不“探索”所有可能的$(S_0,A_0)$，那么就可能“错过”好的策略。但是如果不“利用”以往的知识而把过多的时间浪费在明显不好的状态也似乎不明智，这就需要权衡“探索”(Explore)和“利用”(Exploit)。我们下面通过一个多臂老虎机的例子来介绍一下探索和利用的矛盾。

这是很简单的一个问题，但在很多地方都有应用，比如互联网广告，游戏厅有一个K臂的老虎机，你可以选择其中的一个投币，每个手臂都是一个产生一个随机的奖励，它们的均值是固定的（也有Nonstationary的多臂老虎机，我这里只考虑Stationary的）。你有N次投币的机会，需要想办法获得最大的回报(reward)。

当然如果我们知道这个K个手臂的均值，那么我们每次都选择均值最大的那个投币，那么获得的期望回报应该是最大的。

可惜我们并不知道。那么我们可能上来每个都试一下，然后接下来一直选择最大的那个。不过这样可能也有问题，因为奖励是随机的，所以一次回报高不代表真实的均值回报高。当然你可以每个都试两次，估计一下奖励的均值。如果还不放心，你可以每个都试三次，或者更多。根据大数定律，试的次数越多，估计的就越准。最极端的一种做法就是每个手臂都投一样多的次数；另外一种极端就是碰运气，把所有的机会都放到一个手臂上。后一种如果运气好是最优的，但是很可能你抽到的是回报一般的甚至很差的手臂，期望的回报其实就是K个手臂的平均值。前一种呢？回报也是K个手臂的平均值！我们实际的做法可能是先每个手臂都试探几次，然后估计出比较好的手臂（甚至几个手臂），然后后面重点尝试这个(些)手臂，当然偶尔也要试试不那么好的手臂，太差的可能就不怎么去试了。但这个“度”怎么控制就是一个很复杂的问题了。这就是exploit-explore的困境(dilemma)。利用之前的经验，优先“好”的手臂，这就是exploit；尝试目前看不那么“好”的手臂，挖掘“潜力股”，这就是explore。

一种策略(Policy)的Regret(损失)为：

不要被数学公式吓到了，用自然语言描述就是：最理想的情况是n次都是均值最大的那个手臂($\mu^*$)，不过我们并不知道，$\mu_j\mathbb{E}[T_j(n)]$是这个策略下选择第j个手臂的期望。那么R就是期望的损失，如果我们的策略非常理想，这个策略只尝试最好的手臂，其它不试，那么R就是0。

但是这样的理想情况存在吗？很明显不太可能存在（存在的一种情况是k个手臂的均值一样）。那么我们的策略应该尽量减少这个损失。Lai and Robbins证明了这个损失的下界是logn，也就是说不存在更好的策略，它的损失比logn小（这类似于算法的大O表示法）。所以我们的目标是寻找一种算法，它的损失是logn的。UCB就是其中的一种算法：

每次决策之前，它都用上面的公式计算每个手臂的UCB值，然后选中最大的那个手臂。公式右边的第一项是exploit项，是第j个手臂的平均回报的估计。这个值越大我们就越有可能再次选中它。第二项是explore项，$n_j$是第j个手臂的尝试次数，$n_j$越小这个值就越大，也就是说尝试次数越少的我们就越应该多尝试。当$n_j=0$时，第二项为无穷大，所以这个算法会首先尝试完所有的手臂（explore），然后才会选择回报最大的那个(exploit)，试了之后这个手臂的平均值可能变化，而且$n_j$增加，explore值变小，接着可能还是试最大的那个，也可能是第二大的，这要看具体情况。

我们来分析一些极端的情况，一种情况是最好的（假设下标是k)比第二好的要好很多，那么第一项占主导，那么稳定了之后大部分尝试都是最好的这个，当然随着$n_k$的增加explore项在减少(其它手表不变)，所以偶尔也试试其它手臂，但其它手臂的回报很少，所以很快又会回到第k个手臂。但是不管怎么样，即使n趋于无穷大，偶尔也会尝试一下其它的手臂的。不过因为大部分时间都在第k个手臂上，所以这个策略还是可以的。

另一种极端就是k个手臂都差不多（比如都是一样的回报），那么exploit项大家都差不多，起决定作用的就是explore项，那么就是平均的尝试这些手臂，由于k各手臂回报差不多，所以这个策略也还不错。处于中间的情况就是有一些好的和一些差的，那么根据分析，大部分尝试都是在好的手臂上，偶尔也会试一试差的，所以策略的结果也不会太差。

当然这个只是简单的直觉的分析，事实上可以证明这个算法的regret是logn的，具体证明细节请参看论文Finite-time Analysis of the Multiarmed Bandit Problem。

On-Policy蒙特卡洛控制

我们再回到前面蒙特卡洛控制的问题，需要Exploring Start，有什么办法可以避免吗？从理论上讲，如果蒙特卡洛实验的次数趋于无穷，那么所有的Action我们也需要尝试无穷次才能保证无偏的估计。我们这里先介绍On-Policy的方法，它的基本思想和UCB类似，把大多数时间花在当前策略认为好的Action上，但是也要花一些时间探索所有其它的Action。为什么叫On-Policy呢？这是和Off-Policy相对的，On-Policy指的是生成Episode的策略和最后使用来决策的策略是同一个策略；而Off-Policy有两个策略：一个策略用于生成Episode，而另一个策略是最终用了决策的策略。

On-Policy的策略通常是soft的，也就是$\forall s \in \mathcal{S}, a \in \mathcal{A}(s), \pi(a|s)>0$。因此soft的策略在状态s时对于所有的Action都有一定的概率去尝试，但是最终会有某个(些)Action的概率会比较大从而形成比较固定的策略。为什么蒙特卡罗控制要求策略是soft而之前的动态规划不需要呢（还记得之前的策略提升都是用到固定的贪婪的策略吗）？

图：动态规划的backup图

图：蒙特卡罗方法的backup图

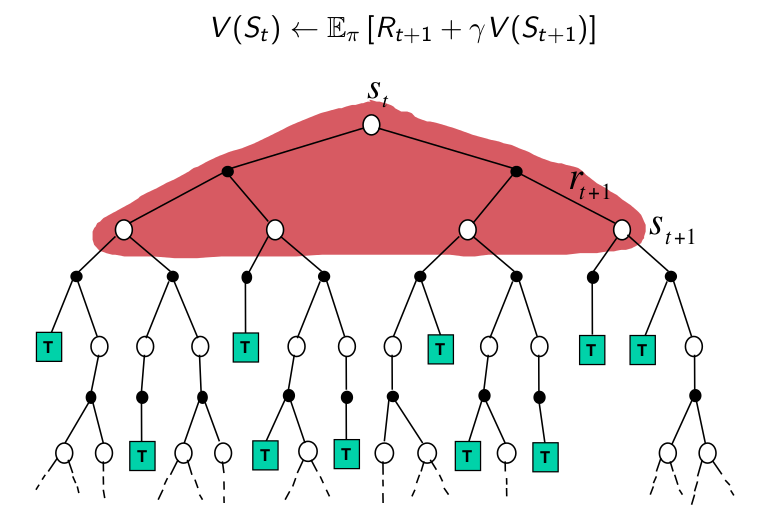
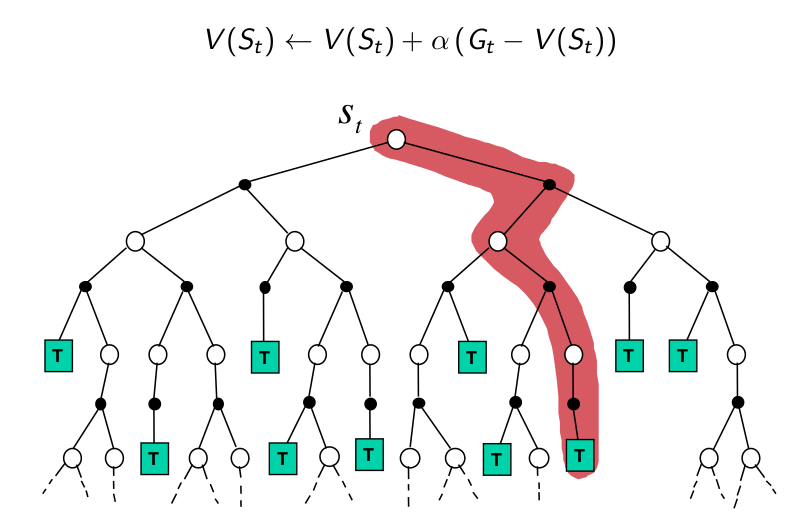
我们看一下这两种方法的backup图，从图中我们可以看出，在动态规划的时候，我们是“遍历”一个状态所有Action，以及Action的所有新状态。通过这种类似广度优先的方式递归的方式，我们遍历了所有空间。而蒙特卡罗方法我们是通过采样的方法一次访问一条“路径”，如果策略是固定的，那么我们每次都是访问相同的路径。

这一节我们会介绍ε-贪婪算法，它在大部分情况下(1-ε的概率)会使用贪婪的策略选择a使得q(s,a)最大，但是也会有ε的概率随机的选择策略。因此对于“最优”行为的概率是1-ε+ε/|A|（因为随机也可能随机到最优的行为），而其它行为的概率是ε/|A|。算法的伪代码如下：

图：On-Policy蒙特卡洛控制算法

ε-贪婪策略是ε-soft策略的一种特例。ε-soft策略定义如下：对于任意状态s和行为a，都有$\pi(s|a) \ge \epsilon$。也就是说：对于任何的(s,a)，我们都有至少ε的概率去尝试，这就是ε-soft策略。可以验证ε-贪婪策略是一种ε-soft策略，因为对于非“最优”行为，它们的概率s是$\frac{\epsilon}{\mathcal{A}(s)}$，如果“严格”的说，ε-贪婪策略是$\frac{\epsilon}{\mathcal{A}(s)}\text{-soft}$的策略。

假设策略$\pi$是一个ε-soft的策略，它的行为价值函数是$q_\pi(s,a)$，而$\pi’$是对$q_\pi$进行ε-贪婪之后得到的新策略（当然它也是一个ε-soft的策略），那么这个新策略$\pi’$相对于$\pi$是有提升的（新的策略比老的好）。下面我们来证明一下， $\forall s \in \mathcal{S}$，我们有：

这个证明难点是第二行到第三行的不等式，它利用了这样一个结论：n个数的“线性组合”小于等于最大的那个数。所谓的线性组合就是n个数分别乘以n个系数在加起来，这n个系数是大于等于0小于等于1并且和为1的。我们以两个数为例，假设$x_1\le x_2$：

同样三个数的情况可以用类似的方法证明。我们再回过头来看上面的不等式，假设状态s下有n种行为，那么第三行就是n个数($a_\pi(s,a)$)的线性组合，因为这n个数的系数都是大于0小于1的，而且其和是1：

上面用到的一点是$\sum_a\pi(a|s)=1$，这是很明显的。

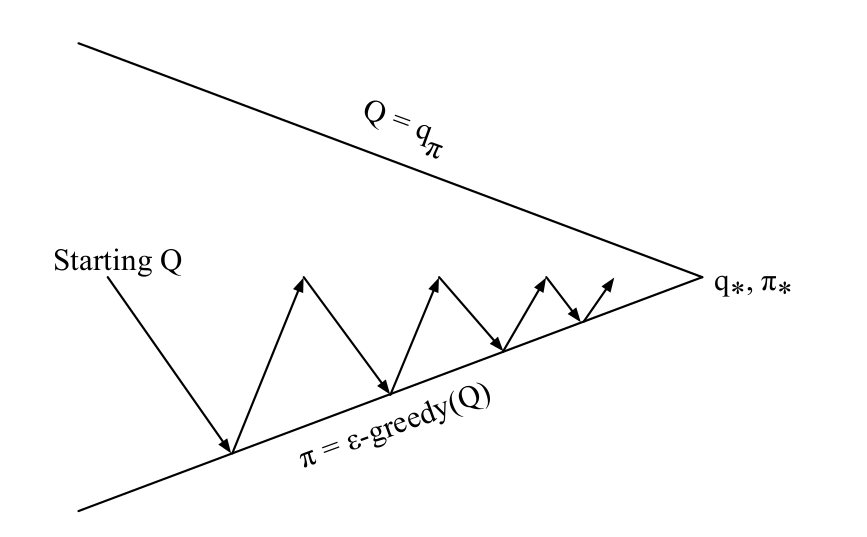
我们在蒙特卡罗方法（包括后面的TD）使用的不是状态价值函数V(s)而是行为价值函数Q(s,a)，为什么呢？我们首先回顾一下GPI，参考下图。假设使用V(s)，我们首先有个初始的策略$\pi$，我们用蒙特卡罗预测来估计$v_\pi(s)$，然后我们使用ε-贪婪获得一个更好的策略，然后再估计这个新的策略的价值函数，不断的迭代。这里我们需要根据V(s)来计算这个ε-贪婪的策略如下：

要计算最优的策略，我们需要知道MDP的动力系统$p(s’,r|s,a)$，这对于动态规划来说是没有问题的，因为它是必须要知道的。但是对于蒙特卡罗方法来说，我们不能也没有必要知道它。而如果我们使用Q(s,a)，有了Q后计算贪婪策略（ε-贪婪也是类似）就不需要知道它了：

如下图所示，蒙特卡罗控制是这样优化的，注意和动态规划不同，蒙特卡罗控制一上来 是有Q，然后做ε-贪婪的提升，然后计算新的Q，不过因为蒙特卡罗是采样的近似，所以图中的蒙特卡罗的预测不是精确的预测$Q_\pi(s,a)$，而是它的近似，所以图中的线没有接近上端。

图：蒙特卡罗控制的GPI

On-Policy蒙特卡罗控制代码示例

代码在这里。首先我们定义函数make_epsilon_greedy_policy，它的输入是一个Q函数和epsilon，输出一个实现ε-贪婪的策略的函数。

def make_epsilon_greedy_policy(Q, epsilon, nA):
    """
    给定一个Q函数和epsilon，构建一个ε-贪婪的策略
    
    参数:
        Q: 一个dictionary其key-value是state -> action-values.
            key是状态s，value是一个长为nA(Action个数)的numpy数组，
            表示采取行为a的概率。
        epsilon:  float 
        nA: action的个数
    
    返回值:
        返回一个函数，这个函数的输入是一个状态/观察(observation)，
        输出是一个长度为nA的numpy数组，表示采取不同Action的概率

    """
    def policy_fn(observation):
        A = np.ones(nA, dtype=float) * epsilon / nA
        best_action = np.argmax(Q[observation])
        A[best_action] += (1.0 - epsilon)
        return A
    return policy_fn

然后是实现ε-贪婪策略的蒙特卡罗控制函数mc_control_epsilon_greedy：

def mc_control_epsilon_greedy(env, num_episodes, discount_factor=1.0, epsilon=0.1):
    """
    使用Epsilon-贪婪策略的蒙特卡罗控制，寻找最优的epsilon-greedy策略。
    
    参数:
        env: OpenAI gym environment
        num_episodes: 采样的episode个数
        discount_factor: 打折因子
        epsilon: Float
    
    返回:
        一个tuple(Q, policy).
        Q函数 state -> action values。key是状态，value是长为nA的numpy数组，表示Q(s,a)
        policy 最优的策略函数，输入是状态，输出是nA长的numpy数组，
        表示采取不同action的概率。
    """
    
    # 记录每个状态的回报累加值和次数
    returns_sum = defaultdict(float)
    returns_count = defaultdict(float)
    
    # Q函数state -> (action -> action-value)。key是状态s，value又是一个dict，其key是a，value是Q(s,a)
    Q = defaultdict(lambda: np.zeros(env.action_space.n))
    
    # epsilon-贪婪的策略
    policy = make_epsilon_greedy_policy(Q, epsilon, env.action_space.n)
    
    for i_episode in range(1, num_episodes + 1):
        if i_episode % 1000 == 0:
            print("\rEpisode {}/{}.".format(i_episode, num_episodes), end="")
            sys.stdout.flush()

        # 生成一个episode。
        # 一个episode是一个数组，每个元素是一个三元组(state, action, reward)
        episode = []
        state = env.reset()
        for t in range(100):
            probs = policy(state)
            action = np.random.choice(np.arange(len(probs)), p=probs)
            next_state, reward, done, _ = env.step(action)
            episode.append((state, action, reward))
            if done:
                break
            state = next_state

        # 找到episode里出现的所有(s,a)对epsilon。
        # 把它变成tuple以便作为dict的key。
        sa_in_episode = set([(tuple(x[0]), x[1]) for x in episode])
        for state, action in sa_in_episode:
            sa_pair = (state, action)
            # 找到(s,a)第一次出现的下标
            first_occurence_idx = next(i for i,x in enumerate(episode)
                                       if x[0] == state and x[1] == action)
            # 计算(s,a)的回报
            G = sum([x[2]*(discount_factor**i) for i,x in enumerate(episode[first_occurence_idx:])])
            # 累计计数
            returns_sum[sa_pair] += G
            returns_count[sa_pair] += 1.0
            Q[state][action] = returns_sum[sa_pair] / returns_count[sa_pair]
        
        # 策略已经通过Q“隐式”的提高了！
    
    return Q, policy

注意和伪代码比，我们没有“显式”定义新策略$\pi’$，而是把当前策略定义为Q(s,a)的一个函数policy = make_epsilon_greedy_policy(Q, epsilon, env.action_space.n)，因此Q(s,a)发生变化时，对于的函数就会发生变化。

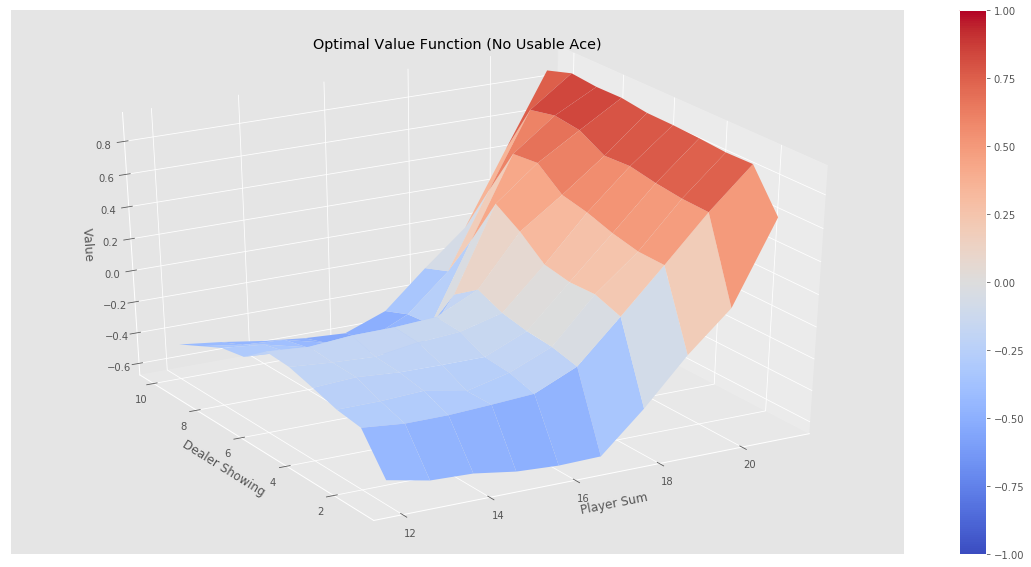
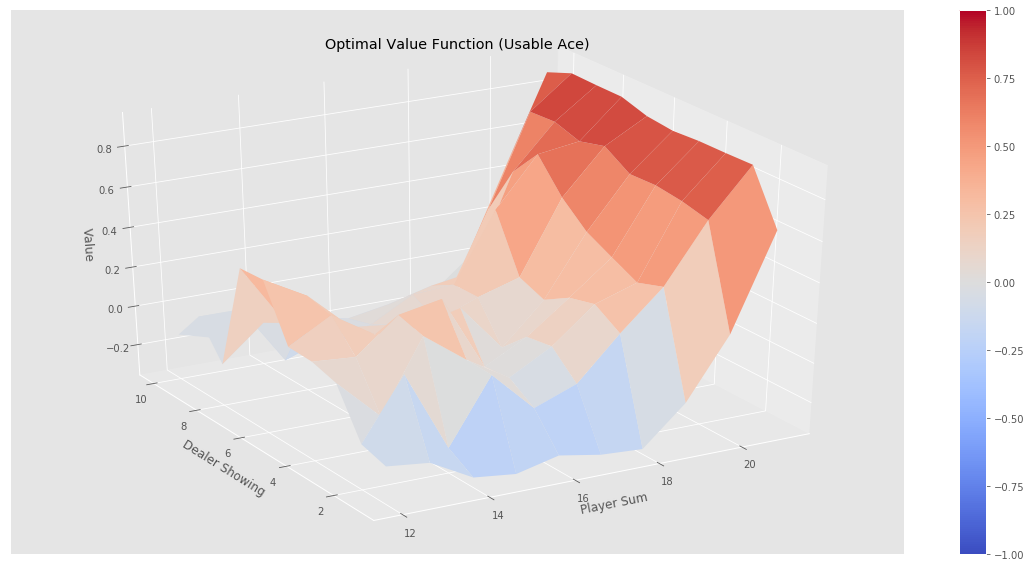
运行后我们把V(s)画出来，如下图所示。

图：无Ace时最佳值函数

图：有Ace时最佳值函数

我们可以看出，如果一上来手上的牌就大于18，我们最优的胜率是大于0的(当然也会可能输，因为庄家大于17就停止要牌，仍然有一定概率比我们大)。

Off-Policy蒙特卡罗预测

前面的ε-贪婪策略可以解决Exploring Start的问题，但是带来一个新的问题，它永远只能学到ε-soft的策略，用于决策的时候还去“探索”其实是不好的。本节我们介绍Off-Policy的蒙特卡罗预测，和前面的On-Policy策略相比，Off-Policy有两个不同策略：目标策略(target policy)和行为策略(behavior policy)。目标策略就是我们解决问题需要学习的策略；而行为策略是用来生成Episode的策略。如果目标策略和行为策略相同，那就是On-Policy策略了。

本节我们解决预测问题，假设目标策略和行为策略都已知的情况下计算其价值函数。假设目标策略是$\pi$，而行为策略是b，我们的目的是根据b生成的Episode采样来计算$v_\pi(s)或q_\pi(s,a)$。为了通过b生成的Episode能够用来估计$\pi$，我们要求如果$\pi(a|s)>0$则$b(s|a)>0$，这叫做b是$\pi$的coverage。为什么要有coverage的要求？因为如果我们要估计的策略$\pi(a|s)>0$，而$b(a|s)=0$，那么就不可能有Episode会在状态s是采取行为a，那么就无法估计$\pi(a|s)$了。

coverage的另外一种说法就是：如果$b(a|s)=0$那么一定有$\pi(a|s)=0$。因此策略b一定是随机的策略，为什么？因为b如果是确定的策略，对于任何状态$s_i$，只有一个$a_j$使得$b(a_j|s_i)=1$，其余的都是0。因为b是$\pi$的coverage，所以除了j，其余所有的$\pi(a_k|s_i)=0$，因此只有$\pi(a_j|s_i)>0$，因此它必须是$\pi(a_j|s_i)=1$，这样$\pi$和b就是相同的策略，这显然不是Off-Policy策略。

因此在Off-Policy控制里，行为策略通常是随机的，它会“探索”，而目标策略通常是固定的贪心的策略，它更多的是“利用”。几乎所有的Off-Policy策略都使用重要性采样(Importance Sampling)方法，这是根据一个概率分布来估计另外一个不同的概率分布的常见方法。我们希望估计的是策略$\pi$，而实际采样用的是b生成的Episode。因此我们在计算平均的回报时需要对它乘以一个采样重要性比例(importance-sampling ratio)来加权。通俗的解释就是：$b(a|s)$的概率是0.2，而$\pi(a|s)=0.4$，那么我们需要乘以2。给定初始状态$S_t$和策略$\pi$，再给定任意状态-行为轨迹(trajectory)，我们可以就是其条件概率——在给定策略下出现这个轨迹的概率。

其中$p(S_{k+1}|S_k,A_k)$是状态转移概率，可以对$p(s’,r|s,a)$的r进行求和/积分得到。因此我们可以计算这个轨迹在策略$\pi$和b下相对的重要性比例如下：

虽然轨迹的概率是和MDP的转移概率$p(s’|s,a)$有关，但是两个策略的重要性比例是和它无关的，它只跟两个策略相关。

为了介绍后面的算法，我们先介绍一个数学记号，请读者在继续阅读之前熟悉这些记号。首先我们把很多的Episode使用统一的时刻来标志，也就是把所有的Episode顺序的串起来。比如有两个Episode，$e_1$是105个时间单位，$e_2$是50个。那么我们用1到155来标识这过两个Episode。$e_2$的第一个时刻是106，$e_2$的最后一个时刻是155。我们介绍一个记号$\tau(s)$，如果是every-visit的方法，它代表状态s在同样时间里的下标集合；如果是first-visit的方法，那么每个Episode只算第一次的出现。举例来说：比如两个Episode是$\{s_1,s_1,s_2,s_3\}$和$\{s_2,s_3,s_2,s_1\}$。如果是every-visit的方法，则$\tau(s_1)=\{1,2,8\}$；如果是first-visit方法，则$\tau(s_1)=\{1,8\}$。然后是记号T(t)，它表示t时刻之后的第一个结束时刻。对于上面的例子T(2)=4,T(5)=8，表示第2个时刻之后的第一个结束时刻是4，第5个时刻之后的第一个结束时刻是8。其实就是这个时刻所在Episode的结束时刻。再就是记号G(t)，它表示从t时刻到T(t)时刻的回报(Return)，也就是t时刻的回报。因此记号\(\{G(t)\}_{t \in \tau(s)}\)表示所有这些Episode里状态s的回报的集合。$\{\rho_{t:T(t)-1}\}_{t \in \tau(s)}$表示与之对应的采样重要性比例。

为了估计$v_\pi(s)$，我们可以简单的用重要性比例加权平均回报：

这种平均方法加普通重要性采样(ordinary importance sampling)，另外一种叫加权重要性采样(weighted importance sampling)：

普通重要性采样是无偏的估计，而加权重要性采样是有偏的估计；前者的方差很大，而后者较小。Off-Policy预测的伪代码如下：

图：Off-Policy蒙特卡罗预测

上面的伪代码就是加权重要性采样的实现，和前面描述的差别在于：为了提高计算效率，我们这里使用了增量(incremental)的实现。假设某个状态s对应的回报是$G_1,G_2,…,G_{n-1}$，其对应的重要性比例是$W_i=\rho_{t:T(t)-1}$，则这n-1个回报的加权平均是： \(V_n \equiv \frac{\sum_{k=1}^{n-1}W_kG_k}{\sum_{k=1}^{n-1}W_k}\) 假设s经过新的一次采样得到$G_n$，我们需要计算n个回报的加权平均，一种办法是使用上面的公式从新计算，还有一种更高效的方法是利用n-1个的$V_n$。为了利用n-1个的平均，我们还需要n-1个回报时的权重累加和$C_n$，它的递归定义是： \(C_{n+1}=C_n+W_{n+1}\) 有了这些值，我们就可以用前n-1个的值$V_n$来计算n个的值$V_{n+1}$： \(V_{n+1}=V_{n}+\frac{W_n}{C_n}[G_n-V_n]\) 请读者自行验证上面公式的正确性。理解了这个之后读者再阅读伪代码就很简单了。我们的Episode是从后往前遍历的，因此$G \leftarrow \gamma G +R_{t+1}$，请读者理解这种Return的计算方式。还有需要注意的就是如果某个$\pi(a|s)=0$，W以后总是0，因此C和Q都不会变化，就没有必要计算了。这就是off-policy蒙特卡罗方法的问题——一旦$\pi(a|s)$是0，那么之前的模拟完全就是浪费的了，所以它的效率不高。我们之前也说了，实际的off-policy蒙特卡罗控制我们要学的$\pi$通常是固定的策略，也就是只有一个$\pi(a|s)=1$而其余的是0。

Off-Policy蒙特卡罗控制

有了Off-Policy预测之后，我们很容易得到Off-Policy蒙特卡罗控制。伪代码如下：

图：Off-Policy蒙特卡罗控制

注意这个代码和上面代码最后两行的差别。首先因为我们的策略$\pi$是确定的策略，因此只有一个Action的概率是1，其余的是0。因此如果状态是$S_t$，那么策略$\pi$会选择Q最大的那个a，也就是$arg\max_aQ(S_t,a)$，如果$A_t \ne \pi(S_t)$，则说明$p(A_t|S_t)=0$，因此和上面算法的条件一样，可以退出for循环，否则就更新W，如果执行到最后一行代码，说明$p(A_t|S_t)=1$，所以分子是1。

Off-Policy蒙特卡罗控制代码示例

完整代码在这里。

核心的函数是mc_control_importance_sampling，代码和伪代码几乎一样，请读者参考伪代码阅读：

def mc_control_importance_sampling(env, num_episodes, behavior_policy, discount_factor=1.0):
    """
    使用加权重要性采样的Off-Policy蒙特卡罗控制
    
    参数:
        env: OpenAI gym env对象
        num_episodes: 采样的Episode次数
        behavior_policy: 用来生成episode的行为策略。
            它是一个函数，输入是状态，输出是一个向量，表示这个状态下每种策略的概率
        discount_factor: 打折因子
    
    返回值:
        一个tuple (Q, policy)
        Q 是一个dictionary state -> action values
        policy是一个函数，输入是状态，输出是一个向量，表示这个状态下每种策略的概率，
        这里返回的策略是一个固定的贪心的策略。
    """
    
    # action-value function.
    # 一个dictionary：state -> action values
    Q = defaultdict(lambda: np.zeros(env.action_space.n))
    # 权重的累加值，也是一个dictionary：state -> action权重累加值
    C = defaultdict(lambda: np.zeros(env.action_space.n))
    
    # 我们想学的策略pi，我们通过修改Q来间接修改它。
    target_policy = create_greedy_policy(Q)
        
    for i_episode in range(1, num_episodes + 1):
        if i_episode % 1000 == 0:
            print("\rEpisode {}/{}.".format(i_episode, num_episodes), end="")
            sys.stdout.flush()

        # 生成episode.
        # 一个episode是一个数值，每个元素是一个三元组(state, action, reward) 
        episode = []
        state = env.reset()
        for t in range(100):
            # 使用行为策略采样Action
            probs = behavior_policy(state)
            action = np.random.choice(np.arange(len(probs)), p=probs)
            next_state, reward, done, _ = env.step(action)
            episode.append((state, action, reward))
            if done:
                break
            state = next_state
        
        # 打折回报的累加和
        G = 0.0
        # 采样重要性比例 (回报的权重)
        W = 1.0
        # 当前episode从后往前遍历
        for t in range(len(episode))[::-1]:
            state, action, reward = episode[t]
            # 计算t时刻到最后时刻的回报
            G = discount_factor * G + reward
            # 更新C
            C[state][action] += W
            # 使用增量更新公式更新Q
            # 通过更新Q也间接的更新了目标策略pi
            Q[state][action] += (W / C[state][action]) * (G - Q[state][action])
            # 如果行为策略选择的Action不是目标策略的Action，则p(s|a)=0，我们可以退出For循环
            if action !=  np.argmax(target_policy(state)):
                break
            W = W * 1./behavior_policy(state)[action]
        
    return Q, target_policy

运行后我们把V(s)画出来，如下图所示。

图：Off-Policy算法无Ace时最佳值函数

图：Off-Policy算法有Ace时最佳值函数

我们可以看出结果和前面的On-Policy算法差不多，但是运算速度会快很多，读者可以自行比较一下。

动态规划和蒙特卡罗方法的比较

• 是否有模型

动态规划需要模型p(s’,r|s,a)；而蒙特卡罗方法不需要，它只需要能获得采样的Episode就行。因此动态规划也称为基于模型的(model based)方法；而蒙特卡罗方法被称为无模型的(model free)方法。基于模型的方法需要知道环境的动力系统，有些问题我们很容易知道环境动力系统，但是还有很多问题我们无法直接获得。如果我们还想使用动态规划，我们就必须用一个模型来建模环境，这本身就是一个很复杂的问题。比如前面我们的21点游戏，想完全建模其动力系统是很困难的。

• bootstrapping

动态规划是有bootstrapping的，$v(s)$和$q(s,a)$都需要先有估计(初始值)，然后通过迭代的方法不断改进这个估计。

• online/offline

蒙特卡罗方法是offline的，需要一个Episode结束之后才能计算回报。等介绍过TD(λ)之后，与constant-α MC(一种后面我们会介绍的蒙特卡罗方法)等价的TD(1)可以实现online计算。这样如果不是Episode的任务（比如用于不结束状态的连续的任务），或者有些任务如果策略不对可能永远无法结束，比如后面我们会介绍的Windy Gridworld。

注意动态规划并没有online/offline只说，因为它不是采样的方法。这是蒙特卡罗方法的一个缺点，后面的时间差分学习能解决这个问题。

• full/sampling backup

如下图所示，动态规划会”遍历”所有的子树，而蒙特卡罗方法只采样一条路径。

图：蒙特卡罗算法只采样一条路径

图：动态规划会递归的遍历所有子树

• ← Previous Post
• Next Post →