本文介绍n步方法、TD-λ、Eligibility Trace和函数近似。
更多本系列文章请点击强化学习简介系列文章。更多内容请点击深度学习理论与实战:提高篇。
目录
n步方法
MC方法是用Episode结束时的回报来作为更新目标,而TD(0)使用一步之后的回报来作为更新目标:
\[\begin{split} \text{1步回报(TD(0))} & G_{t:t+1}\equiv R_{t+1}+\gamma V_t(S_{t+1}) \\ \text{2步回报} & G_{t:t+2} \equiv R_{t+1} + \gamma R_{t+2} + \gamma^2V_{t+1}(S_{t+2}) \\ ... \\ \infty \text{步回报(MC)} & G_{t:\infty}=G_t \equiv R_{t+1}+\gamma R_{t+2} + ... + \gamma^{T-1}R_T \end{split}\]根据上面的推广,我们可以定义n步回报(n-step Return)为:
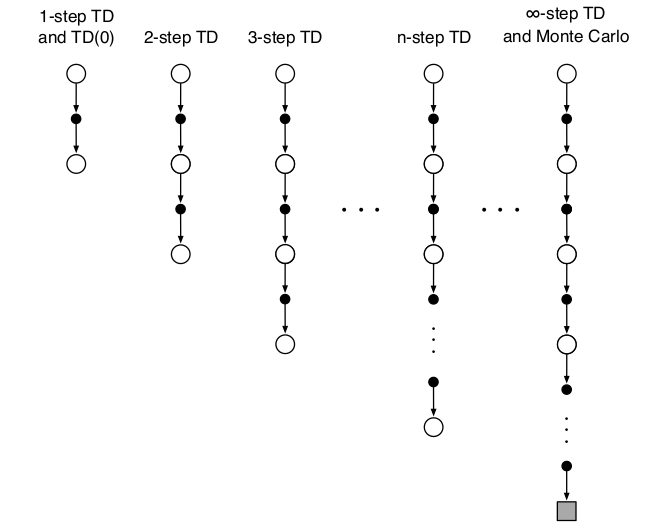
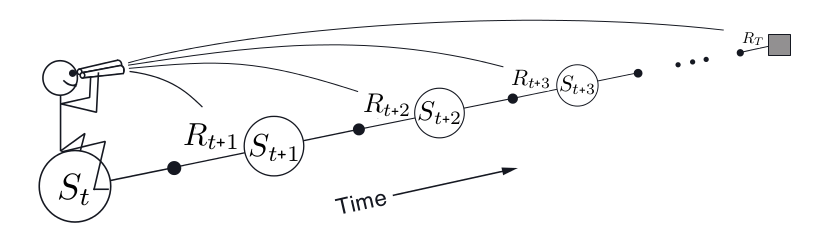
\[G_{t:t+n} \equiv R_{t+1} + \gamma R_{t+2} + ... + \gamma^{n-1}R_{t+n}+\gamma^{n}V_{t+n-1}(S_{t+n})\]这些方法的backup diagram如下图所示。
有了n步回报之后,我们就可以n步TD学习算法的更新公式: \(V_{t+n}(S_t) \leftarrow V_{t+n-1}(S_t)+\alpha[G_{t:t+n}-V_{t+n-1}(S_t)],\;0 \le t < T\)
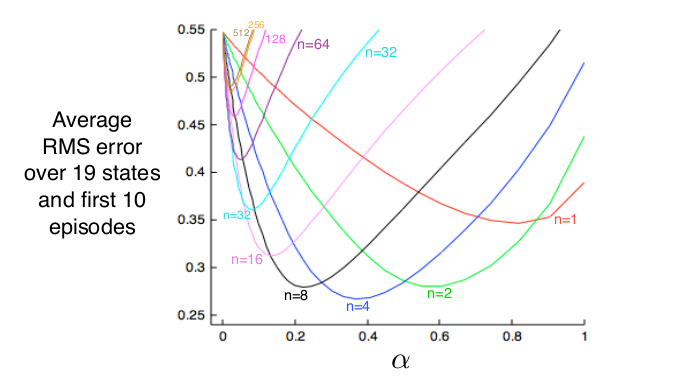
下面是不同的n在一个19状态的Random Walk(由于篇幅,本书不介绍这个任务)中的对比效果如下图所示,可以看出n=1(TD)和n很大(MC)的效果都不如中间的某个n好。
有了n步的预测,再加上ε-贪婪的策略提升,我们就可以实现n步的On-Policy策略n步SARSA算法。由于篇幅,我们就不讨论具体的算法了。同样的我们也可以使用重要性采样方法得到n步的Off-Policy算法。
TD-$\lambda$
$\lambda$-回报
前面我们介绍了n步回报,不同的n有不同的效果,那么还有一种方法就是把多个n步回报进行加权平均。比如我们可以把2步回报和4步如图回报加权平均起来:
\[G=\frac{1}{2}G_{t:t+2}+\frac{1}{2}G_{t:t+4}\]我们甚至可以把无穷多个n步回报加权平均起来,而λ-回报就是一种无穷多个n步回报的加权方式。无穷多个怎么加权呢?
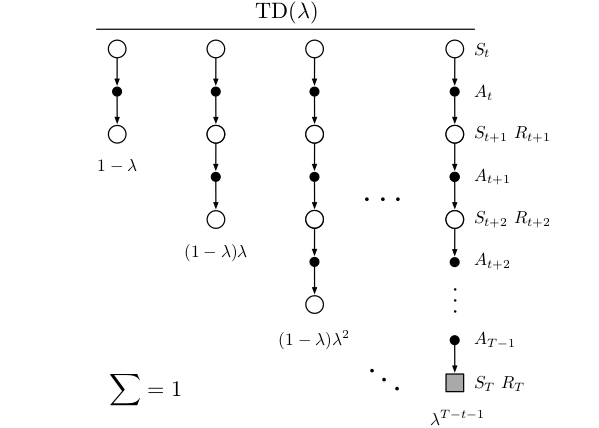
如上图所示,我们把无穷多个n步回报加权平均起来(因为当n大于T的时候,$G_{t:t+n}$就等于真实的回报$G_t$了。所有后面无穷项的系数都累加起来是$\lambda^{T-t-1}$,读者请先接受这个数字,我们后面会证明它。
从图中可以看出,1步回报的权重是$1-\lambda$,2步回报的是$(1-\lambda)\lambda$,3步回报是$(1-\lambda)\lambda^2$,…,一共有无穷项:
\[G_t^{\lambda}=(1-\lambda)\sum_{n=1}^{\infty}\lambda^{n-1}G_{t:t+n}\]我们首先证明这无穷项的和是1。这需要一个简单的无穷级数公式:
\[\frac{1}{1-\lambda}=1+\lambda+\lambda^2+... =\sum_{n=0}^{\infty}\lambda^n\; 0 < \lambda < 1\]有了这个公式之后,我们就能计算所有回报的系数和:
\[(1-\lambda)\sum_{n=1}^{\infty}\lambda^{n-1}=(1-\lambda)\frac{1}{1-\lambda}=1\]注意,因为当n=T-t及其以后$G_{t:t+n}$就等于真实的回报$G_t$了(因为到了Episode结束)。所以从n=T-t之后的项的回报是相同的,所以可以把后面无穷项合并起来:
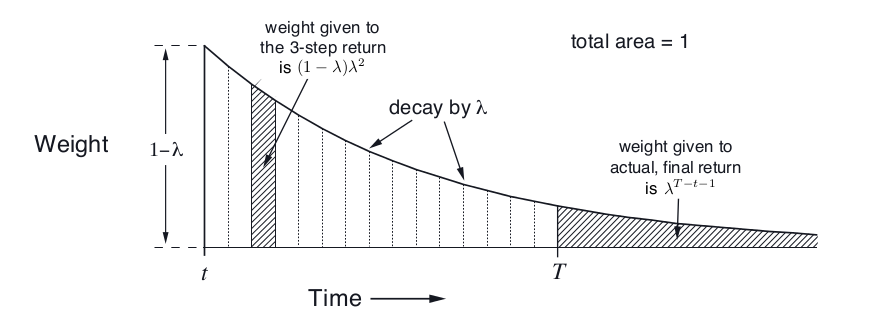
\[\begin{split} & (1-\lambda)\sum_{n=T-t}^{\infty}\lambda^{n-1} G_t \\ & =(1-\lambda)\sum_{n=T-t}^{\infty}\lambda^{n-1} \frac{\lambda^{T-t-1}}{\lambda^{T-t-1}} G_t \\ & =(1-\lambda)\lambda^{T-t-1}\sum_{n=T-t}^{\infty}\lambda^{n-T+t} G_t \\ & \text{令n'=n-T+t}做下标变换 \\ & =(1-\lambda)\lambda^{T-t-1}\sum_{n'=0}^{\infty}\lambda^{n'} G_t\\ & =(1-\lambda)\lambda^{T-t-1}\frac{1}{1-\lambda}G_t \\ & =\lambda^{T-t-1}G_t \end{split}\]因此从n=1到T-t的n步回报的权重分配如图下图所示。这样,我们可以把$G_t^{\lambda}$写出有限项的和:
\[G_t^{\lambda}=(1-\lambda)\sum_{n=1}^{T-t-1}\lambda^{n-1}G_{t:t+n}+\lambda^{T-t-1}G_t\]有了$\lambda$-回报的计算公式之后,我们就可以用它得到TD-λ算法的更新目标,从而就可以进行预测了。
\[V(S_t) \leftarrow V(S_t)+\alpha(G_t^\lambda-V(S_t))\]这就是著名的TD-$\lambda$算法了,根据这个算法,Gerald Tesauro在1992年设计了TD-Gammon程序,它会学习西洋双陆棋(backgammon),并且达到了人类顶尖高手的水平。
注意zhong这种TD-$\lambda$算法是所谓的前向视角(Forward View)得出的,和MC一样,它要等到Episode结束才能计算,而且不能用于非Episode的任务。
另外,我们看一下λ的两个特殊值,$\lambda=0$和$\lambda=1$的特例。根据公式,当$\lambda=0$时,第二项是零,第一项只有当n=0时的系数是非零的1,因此变成了TD(0)算法。当$\lambda=1$时,只有第二项,因此变成了MC算法。
Eligibility Trace
到这为止前面所有介绍的方法都可以归为Forward View的算法,在t时刻我们往前看一步或者多步,然后得到更新的目标。如上图所示。接下来我们会介绍另外一种视角Backward View。我们首先需要介绍一个概念Eligibility Trace,Backward View的算法大部分都是基于这个概念。
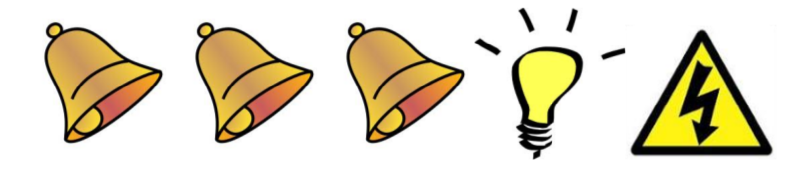
我们来看一个Credit分配的问题(其实强化学习的本质就是要判断很久以前的某个行为/状态对未来的影响大小,当然机器学习也是分析哪些因素是某个事件发生的重要原因,但是强化学习的难点在于行为会改变未来),如下图所示,有两个行为响铃和开灯,最终导致电击事件的发生。那到底是那个行为造成的呢?也许你会说是响铃,因为响铃了很多次,根据经验,如果某个事件发生前经常有另一件事情发生,那么它们很可能存在某种联系。但也许会有人说是灯光导致电击的发生,因为它就在电击事件的前一刻发生,根据经验,离某个事件越近的事件越有可能是诱因。
那到底哪种说法正确呢?两种都对!因此我们在分配Credit的时候要同时考虑这两个因素。把这两个综合起来就可以得到Eligibility Trace:
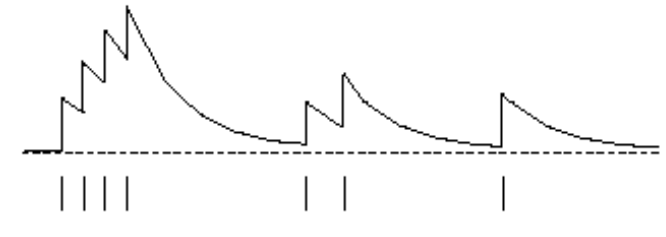
\[\begin{split} & E_0(s)=0 \\ & E_t(s)=\gamma \lambda E_{t-1}(s) + \mathbb{1}(S_t=s) \end{split}\]根据上面的公式,$E_t$分为两部分,一部分来自之前的$E_{t-1}$,但是会衰减成原来的$\lambda$倍($\gamma$是打折因子,这里暂不讨论);另外一部分就是当前状态是否是s。
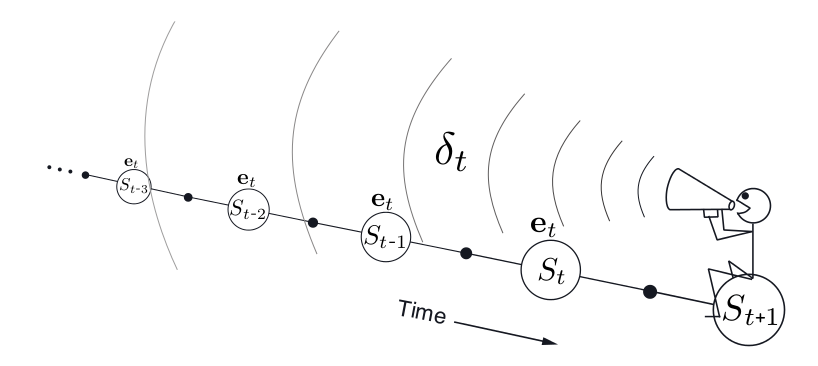
我们来看上图,开始是E(s)是0,然后连续4次$S_t$都是s,因此E(s)不断增加,接着的状态都不是s,因此E(s)逐渐衰减,然后又有两次的状态是s,…。因此我们可以把$E_t(s)$看成状态s对于最终的结果的“责任”,有点像之前反向传播算法的错误$\delta$。这样我们就可以得到backward view的TD-$\lambda$算法的更新如下:
\[\begin{split} & \delta_t=R_{t+1}+\gamma V(S_{t+1})-V(S_t) \\ & V(s) \leftarrow V(s)+\alpha \delta_t E_t(s) \end{split}\]这个算法和之前的forward view实现不同,它不需要等到Episode结束就可以更新V(s)了。更新的量是$\delta_t$乘以$E_t(s)$再乘以学习率$\alpha$。因此如果$E_t(s)$很大,那说明状态s的“责任”也很大,因此它需要更新的比较多。那些状态的s对应的$E_t(s)$大呢?显然如果$S_t=s$,那么它会较大,另外如果在这之前的$S_i=s$,那么也会有非零的值,但是i距离t越远,衰减的就越多。如果在t时刻之前状态s完全没有出现过,那么E就是0。因为是根据当前的错误往前找“责任”,所以就是所谓的backward view,如下图所示。
注意:上面公式会对所有的状态都进行V(s)的更新,而不(只)是更新$V(S_t)$,当然如果$E_t(s)=0$,那么时间更新量是零。
这看起来有些道理,但是这种方法怎么就和前面的forward view是一样的效果呢?下面我们来简单的验证一下。首先来验证一种特例,当$\lambda=0$时:
\[\begin{split} & E_t(s)=\mathbb{1}(S_t=s) \\ & V(s) \leftarrow V(s)+\alpha \delta_t E_t(s) \end{split}\]也就是只有$S_t$会有更新,其余的状态的$E_t(s)$都是0,所有上式就是:
\[V(S_t) \leftarrow V(S_t)+ \alpha \delta_t\]这正是TD(0)。
 Backward View和Forward View等价定理
Backward View和Forward View等价定理
这个定理我们不做证明,但我们需要“读懂”它的意思。offline更新指的是等到一个Episode完成之后做一次更新,而不是每一步都更新,与之相反的是online更新。我们通过一个例子来说明其中的区别,假设一个Episode是:
\[s, a_1, r_1, t, a_2, r_1, s, a_2, ...\]那么算法会对状态s更新两次,对t更新一次。如果是online的,第二次计算使用的是第一次的结果来更新:
\[\begin{split} & V_2(s) \leftarrow \delta_1 + V_1(s)\\ & V_3(s) \leftarrow \delta_2 + V_2(s) \end{split}\]这里的$\delta_1$会依赖于$V_1(s)$,$\delta_2$会依赖于$V_2(s)$。最终的效果是:
\[V_3(s) \leftarrow \delta_1+\delta_2+V_1(s)\]而offline更新公式是一样的,但是$\delta_1$和$\delta_2$都只依赖于$V_1(s)$。
关于定理,另外一点就是公式里的s是Episode里出现的所有状态。这其实s是Forward View和Backward View的区别。Forward View在每一个时刻t只更新一个状态$S_t$的V值,因为t会影响所有后面的状态,所以它要往前看知道终止时刻T,而Backward View一次更新所有的状态。因此offline的算法可以根据最初的值计算每个时刻的错误$\delta_t$,然后累加起来就是整个Episode对状态s的更新。
我们不证明(验证)这个定理,但是验证一个特例($\lambda=1$)。假设一个Episode状态s只出现了一次,并且出现在时刻k。根据$E_t(s)$的公式:
\[\begin{split} E_t(s)&=\gamma E_{t-1}(s)+\mathbb{1}(S_t=s) \\ &=\begin{cases} 0 & \text{ if } t<k \\ \gamma^{t-k} & \text{ if } t \ge k \end{cases} \end{split}\]因为s只在时刻k出现一次,因此k时刻前E(s)都是0,而k时刻是,k+1时刻是$\gamma$,…。根据前面TD(1)的Backward View的算法,我们可以计算到Episode结束时关于状态s累积的错误是:
\[\sum_{t=1}^{T-1}\alpha\delta_tE_t(s)=\alpha\sum_{t=k}^{T-1}\gamma^{t-k}\delta_t=\alpha(G_k-V(S_k))\]首先我们看一下上个公式的第一个等号就是代入,最后一个等号的部分就是MC的$\delta$。如果第二个等号成立,那么就说明TD(1)和MC是等价的。之前的Forward View我们已经说明了MC和TD(1)是等价的,如果MC又和TD(1)的Backward View等价,那么就证明了TD(1)的Forward View和Backward View是等价的,我们来证明一下第二个等式$\sum_{t=k}^{T-1}\gamma^{t-k}\delta_t=(G_k-V(S_k))$如下(为了之前的习惯,我们把k换成了t):
\[\begin{split} & \delta_t + \gamma \delta_{t+1}+\gamma^2\delta_{t+2}+...+\gamma^{T-t-1}\delta_{T-1} \\ = & R_{t+1}+\gamma V(S_{t+1})-V(S_t) \\ & + \gamma R_{t+2} +\gamma^2 V(S_{t+2}) - \gamma V(S_{t+1}) \\ & + \gamma^2 R_{t+3} +\gamma^3 V(S_{t+3}) -\gamma^2 V(S_{t+2})\\ & . \\ & . \\ & . \\ & + \gamma^{T-t-1}R_T+\gamma^{T-t}V(S_T) +\gamma^{T-t-1}V(S_{T-1}) \\ = & R_{t+1}+\gamma R_{t+2}+\gamma^2 R_{t+3} +...+\gamma^{T-t-1} R_T-V(S_t)\\ = & G_t-V(S_t) \end{split}\]上面的每一行的最后一列和前以后的第二列抵消掉,只剩下第一列,第二列的最后一个的$\gamma^{T-t}V(S_T)$和第三列的第一个$-V(S_t)$。因为$V(S_T)=0$,所以就得到上面的结果。
上面只是证明了一个状态s,因此TD(1)的Backward View是和First-Visit MC大致等价的。不完全等价的原因是MC方法是Online更新的。也存在和Online的TD Backward View的算法,它和Online的Forward View等价,我们这里不介绍了。
函数近似(Function Approximation)
前面我们介绍的都是表格(Tabular)的方法,比如Q(s,a),我们可以把状态看成行,action看成列,则这个表格的大小是$
|\mathcal{S}| \times |\mathcal{A}|$。这种方法只能解决状态和action空间是离散而且比较小的问题。但是很多实际的问题的状态空间和action空间都是很大甚至是连续的空间。比如我们让Agent玩一个视频弹球游戏,状态是当前时刻和之前时刻(为了能表示弹球的速度)的两帧图像。假设图像大小是80x80,图像是RGB的,那么状态空间的大小是$256^{3 \times 80 \times 80}$,存储这么大的空间是不可能的。而且即使能够存下,训练时模拟的Episode也不能每种状态都见过。
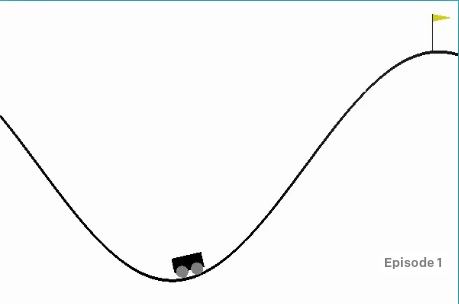
对于连续的状态空间,我们可以通过量化把它变成离散的空间,比如后面我们会用到的gym里的MountainCar,如下图所示。它的状态包括两个连续值,位置和速度,速度的范围是(-0.07,0.07),位置的范围是(-1.2,0.6),我们可以把这个范围均匀的切分为40个区间,每个区间的大小分别是0.0035和0.045。
但是怎么量化本身就是一个复杂的问题,量化的区间太大,那么就会丢失信息,而量化的区间太小,就会使得状态空间爆炸。而且有的值不是均匀分布的,某些范围可能要用比较精细的划分而另外的范围不需要精细的划分。
对于连续的复杂的问题,更好的办法是使用一个函数来近似这个表格,这就叫做函数近似方法。比如把Q(s,a)表示为参数$w$的函数$Q_w (s,a)$。这样不过$|\mathcal{S}| \times |\mathcal{A}|$有多大,它的实际存储和计算只取决于参数$w$和模型结构(简单的线性模型还是复杂的多层神经网络)。
使用函数近似Q(s, a)还有一个好处就是它的泛化能力会增强,比如我们在模拟学习的时候可能没有经历过状态(0.53, 0.12),但是我们有类似的状态(0.54, 0.11)。如果根据表格的方法,状态(0.53, 0.12)的值函数是未知的,但是使用函数之后就能计算出它们有近似的Value(通常的模型都是连续的函数)。
我们来看一个简单的函数近似方法,使用函数来近似状态值函数$v_\pi(s)$,假设函数为$\hat{v}(s, w)$。那么我们可以把普通的MC求$v_\pi(s)$的方法改造成函数近似的算法:
“真实”的Value可以用采样的$G_t$来近似,因此我们需要让函数$\hat{v}$来近似$G_t$,我们可以定义类似的loss函数为$\frac{1}{2} || G_t(S_t)-\hat{v}(S_t,w)||^2$,因此对上式求梯度就得到$-[G_t-\hat{v}(S_t,w)]\nabla \hat{v}(S_t,w)$,然后使用类似梯度下降的方法乘以步长$\alpha$就得到上面的更新公式。
当然,我们也可以使用TD来作为Value的近似,只需要把参数更新公式改为:
\[w \leftarrow w + \alpha[R +\gamma \hat{v}(S_{t+1},w) = \hat{v}(S_t,w)]\nabla \hat{v}(S_t,w)\]注意:TD需要计算$v(S_t)$和$v(S_{t+1})$的Value,这里用$\hat{v}(S_{t}$和$\hat{v}(S_{t+1}$来近似。
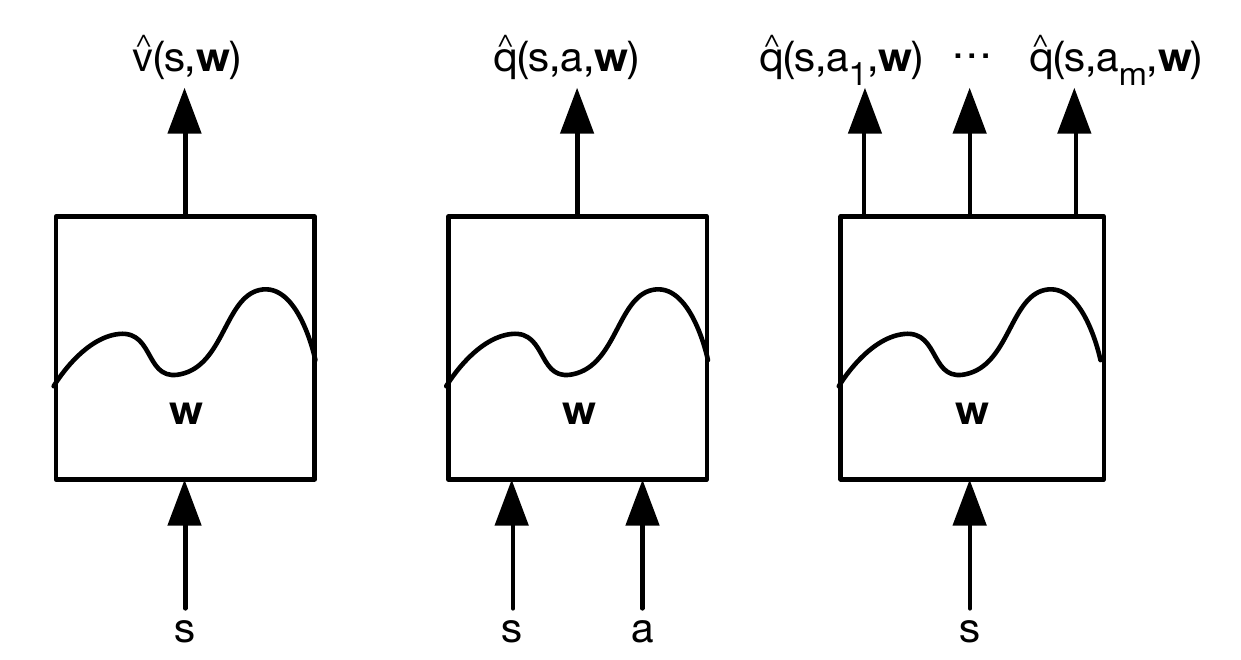
对于Q(s),输入是状态s,输出是value;对于Q(s,a),输入是状态s和行为a,输出是value。如果行为a的空间有限比如是m个值,那么也可以采用如下图右所示的方式,让函数的输入是s,输出m个值分别表示$Q(s, a_1),…,Q(s,a_m)$。这样做的好处是一次可以计算出多个Q(s,a),比如在Q-Learning中,我们需要计算$max_aQ(s,a)$,需要计算状态s下采取所有不同action中得分最高的,那么这种方法就可以一次算好。
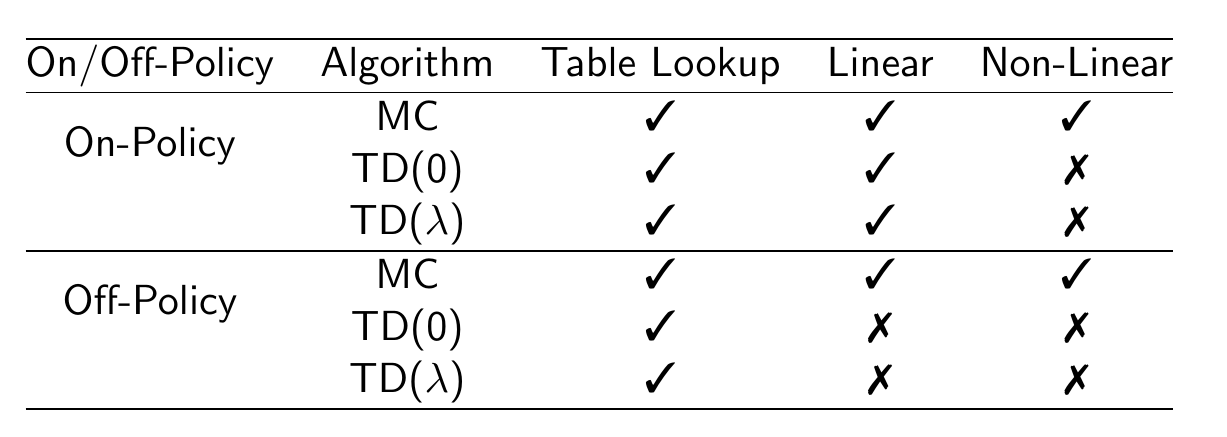
函数近似使用的函数可以有不同的函数形式,从最简单的线性函数到复杂的神经网络。对于不同的函数和不同的算法组合,有不同程度的收敛性保证。下图列举了不同预测算法使用不同函数近似下的收敛性保证。
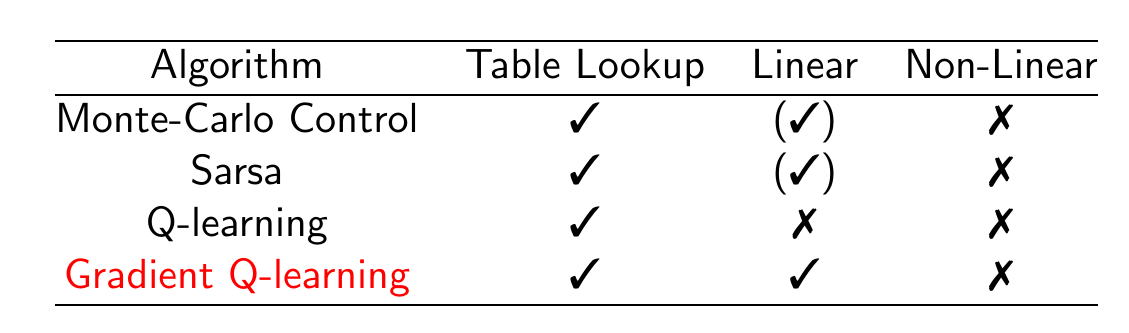
下图列举了不同控制算法的收敛性保证。
注意:没有收敛性保证不代表这个算法对于某个具体问题一定不收敛。比如Q-Learning和非线性的函数近似是不保证收敛的,但是在实际很多问题中,我们会使用非常复杂的神经网络来进行Q-Learning(Deep Q-Networks),这显然是非线性的,不能保证收敛,但是在很多问题中效果很好。
- 显示Disqus评论(需要科学上网)