本文是《深度学习理论与实战》草稿中的内容，一些不太相关或者出版时可能有版权的文章会放到《深度学习理论与实战》拾遗里。
本文介绍RNN/LSTM的基本概念。本文的LSTM部分主要参考了colah的博客文章理解LSTM。RNN代码参考了karpathy的博客文章The Unreasonable Effectiveness of Recurrent Neural Networks附带的代码。
RNN
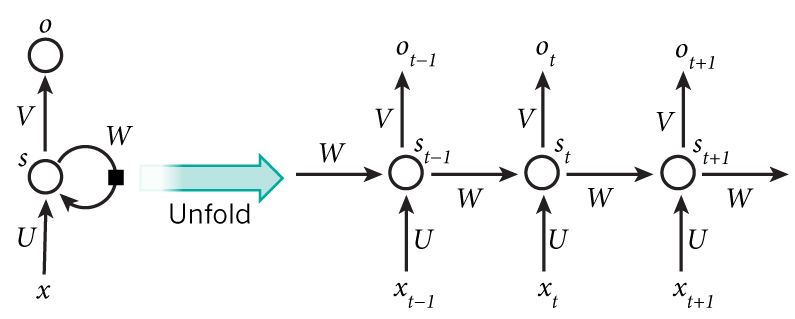
之前我们介绍的神经网络假设所有的输入是相互独立的，对于某些任务来说这不是一个好的假设。比如你想预测一个句子的下一个词，知道之前的词是有帮助的。而RNN的特点是利用时序的信息，RNN被称为循环的(recurrent)原因就是它会对一个序列的每一个元素执行同样的操作，并且之后的输出依赖于之前的计算。我们可以认为RNN有一些“记忆”能力，它能捕获之前计算过的一些信息。理论上RNN能够利用任意长序列的信息，但是实际中它能记忆的长度是有限的。
图：RNN展开图
上图显示了怎么把一个RNN展开成一个完整的网络。比如我们考虑一个包含5个词的句子，我们可以把它展开成5层的神经网络，每个词是一层。RNN的计算公式如下：
-
$x_t$是t时刻的输入。
-
$s_t$是t时刻的隐状态。
它是网络的“记忆”。 $s_t$的计算依赖于前一个时刻的状态和当前时刻的输入： $s_t=f(Ux_t+Ws_{t−1})$。函数f通常是诸如tanh或者ReLU的非线性函数。$s_{−1}$，这是用来计算第一个隐状态，通常我们可以初始化成0。
-
$o_t$是t时刻的输出。
有一些事情值得注意：
-
你可以把$s_t$看成是网络的“记忆”。
$s_t$ 捕获了从开始到前一个时刻的所有(感兴趣)的信息，输出 $o_t$ 只基于当前时刻的记忆。不过实际应用中 $s_t$ 很难记住很久以前的信息。
-
参数共享
传统的神经网络每层使用不同的参数，而RNN的参数(上文的U, V, W)是在所有时刻共享(一样)的。我们每一步都在执行同样的操作，只不过输入不同而已。这种结构极大的减少了我们需要学习的参数。
-
每一个时刻都有输出
每一个时刻都有输出，但我们不一定都要使用。比如我们预测一个句子的情感倾向是我们只关注最后的输出，而不是每一个词的情感。类似的，我们也不一定每个时刻都有输入。RNN最主要的特点是它有隐状态(记忆)，它能捕获一个序列的信息。
RNN的扩展
双向RNN(Bidirectional RNNs)
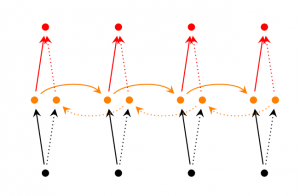
双向RNN如下图所示，它的思想是t时刻的输出不但依赖于之前的元素，而且还依赖之后的元素。比如，我们做完形填空，在句子中“挖”掉一个词，我们想预测这个词，我们不但会看前面的词，也会分析后面的词。双向RNN很简单，它就是两个RNN堆叠在一起，输出依赖两个RNN的隐状态。
图：双向RNN
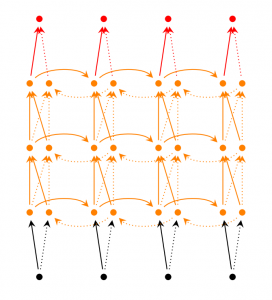
深度双向RNN(Deep Bidirectional RNNs)
深度双向RNN如下图所示，它和双向RNN类似，不过多加几层。当然它的表示能力更强，需要的训练数据也更多。
图：深度双向RNN
RNN代码示例
接下来我们通过简单的代码来演示的RNN，用RNN来实现一个简单的Char RNN语言模型。为了让读者了解RNN的一些细节，本示例会使用numpy来实现forward和backprop的计算。RNN的反向传播算法一般采用BPTT，如果读者不太明白也不要紧，但是forward的计算一定要清楚。RNN代码参考了karpathy的博客文章The Unreasonable Effectiveness of Recurrent Neural Networks附带的代码。代码总共一百来行，我们下面逐段来阅读。
数据预处理
data = open('./tiny-shakespeare.txt', 'r').read() # should be simple plain text file
chars = list(set(data))
data_size, vocab_size = len(data), len(chars)
print('data has %d characters, %d unique.' % (data_size, vocab_size))
char_to_ix = {ch: i for i, ch in enumerate(chars)}
ix_to_char = {i: ch for i, ch in enumerate(chars)}
上面的代码读取莎士比亚的文字到字符串data里，通过set()得到所有不重复的字符并放到chars这个list里。然后得到char_to_ix和ix_to_char两个dict，分别表示字符到id的映射和id到字符的映射，id从零开始。
模型超参数和参数定义
# 超参数
hidden_size = 100 # 隐藏层神经元的个数
seq_length = 25 # BPTT时最多的unroll的步数
learning_rate = 1e-1
# 模型参数
Wxh = np.random.randn(hidden_size, vocab_size) * 0.01 # 输入-隐藏层参数
Whh = np.random.randn(hidden_size, hidden_size) * 0.01 # 隐藏层-隐藏层参数
Why = np.random.randn(vocab_size, hidden_size) * 0.01 # 隐藏层-输出层参数
bh = np.zeros((hidden_size, 1)) # 隐藏层bias
by = np.zeros((vocab_size, 1)) # 输出层bias
上面的代码定义超参数hidden_size，seq_length和learning_rate，以及模型的参数Wxh, Whh和Why。
损失函数
def lossFun(inputs, targets, hprev):
"""
inputs,targets都是整数的list
hprev是Hx1的数组，是隐状态的初始值
返回loss，梯度和最后一个时刻的隐状态
"""
xs, hs, ys, ps = {}, {}, {}, {}
hs[-1] = np.copy(hprev)
loss = 0
# forward pass
for t in xrange(len(inputs)):
xs[t] = np.zeros((vocab_size, 1)) # encode in 1-of-k representation
xs[t][inputs[t]] = 1
hs[t] = np.tanh(np.dot(Wxh, xs[t]) + np.dot(Whh, hs[t - 1]) + bh) # hidden state
ys[t] = np.dot(Why, hs[t]) + by # unnormalized log probabilities for next chars
ps[t] = np.exp(ys[t]) / np.sum(np.exp(ys[t])) # probabilities for next chars
loss += -np.log(ps[t][targets[t], 0]) # softmax (cross-entropy loss)
# backward pass: compute gradients going backwards
dWxh, dWhh, dWhy = np.zeros_like(Wxh), np.zeros_like(Whh), np.zeros_like(Why)
dbh, dby = np.zeros_like(bh), np.zeros_like(by)
dhnext = np.zeros_like(hs[0])
for t in reversed(xrange(len(inputs))):
dy = np.copy(ps[t])
dy[targets[t]] -= 1 # 参考http://cs231n.github.io/neural-networks-case-study/#grad
dWhy += np.dot(dy, hs[t].T)
dby += dy
dh = np.dot(Why.T, dy) + dhnext # backprop into h
dhraw = (1 - hs[t] * hs[t]) * dh # backprop through tanh nonlinearity
dbh += dhraw
dWxh += np.dot(dhraw, xs[t].T)
dWhh += np.dot(dhraw, hs[t - 1].T)
dhnext = np.dot(Whh.T, dhraw)
for dparam in [dWxh, dWhh, dWhy, dbh, dby]:
np.clip(dparam, -5, 5, out=dparam) # clip to mitigate exploding gradients
return loss, dWxh, dWhh, dWhy, dbh, dby, hs[len(inputs) - 1]
我们这里只阅读一下forward的代码，对backward代码感兴趣的读者请参考代码。
# forward pass
for t in xrange(len(inputs)):
xs[t] = np.zeros((vocab_size, 1)) # encode in 1-of-k representation
xs[t][inputs[t]] = 1
hs[t] = np.tanh(np.dot(Wxh, xs[t]) + np.dot(Whh, hs[t - 1]) + bh) # hidden state
ys[t] = np.dot(Why, hs[t]) + by # unnormalized log probabilities for next chars
ps[t] = np.exp(ys[t]) / np.sum(np.exp(ys[t])) # probabilities for next chars
loss += -np.log(ps[t][targets[t], 0]) # softmax (cross-entropy loss)
上面的代码遍历每一个时刻t，首先把字母的id变成one-hot的表示，然后计算hs[t]。计算方法是：hs[t] = np.tanh(np.dot(Wxh, xs[t]) + np.dot(Whh, hs[t - 1]) + bh)。也就是根据当前输入xs[t]和上一个状态hs[t-1]计算当前新的状态hs[t]，注意如果t=0，则hs[t-1] = hs[-1] = np.copy(hprev)，也就是函数参数传入的隐状态的初始值hprev。接着计算ys[t] = np.dot(Why, hs[t]) + by。然后用softmax把它变成概率：ps[t] = np.exp(ys[t]) / np.sum(np.exp(ys[t]))。最后计算交叉熵的损失：loss += -np.log(ps[t][targets[t], 0])。注意：ps[t]的shape是[vocab_size,1]。
sample函数
这个函数随机的生成一个句子（字符串）。
def sample(h, seed_ix, n):
"""
使用rnn模型生成一个长度为n的字符串
h是初始隐状态，seed_ix是第一个字符
"""
x = np.zeros((vocab_size, 1))
x[seed_ix] = 1
ixes = []
for t in xrange(n):
h = np.tanh(np.dot(Wxh, x) + np.dot(Whh, h) + bh)
y = np.dot(Why, h) + by
p = np.exp(y) / np.sum(np.exp(y))
ix = np.random.choice(range(vocab_size), p=p.ravel())
x = np.zeros((vocab_size, 1))
x[ix] = 1
ixes.append(ix)
return ixes
sample函数会生成长度为n的字符串。一开始x设置为seed_idx：x[seed_idx]=1(这是one-hot表示)，然后和forward类似计算输出下一个字符的概率分布p。然后根据这个分布随机采样一个字符(id) ix，把ix加到结果ixes里，最后用这个ix作为下一个时刻的输入：x[ix]=1。
训练
n, p = 0, 0
mWxh, mWhh, mWhy = np.zeros_like(Wxh), np.zeros_like(Whh), np.zeros_like(Why)
mbh, mby = np.zeros_like(bh), np.zeros_like(by) # memory variables for Adagrad
smooth_loss = -np.log(1.0 / vocab_size) * seq_length # loss at iteration 0
while True:
# prepare inputs (we're sweeping from left to right in steps seq_length long)
if p + seq_length + 1 >= len(data) or n == 0:
hprev = np.zeros((hidden_size, 1)) # reset RNN memory
p = 0 # go from start of data
inputs = [char_to_ix[ch] for ch in data[p:p + seq_length]]
targets = [char_to_ix[ch] for ch in data[p + 1:p + seq_length + 1]]
# sample from the model now and then
if n % 1000 == 0:
sample_ix = sample(hprev, inputs[0], 200)
txt = ''.join(ix_to_char[ix] for ix in sample_ix)
print('----\n %s \n----' % (txt,))
# forward seq_length characters through the net and fetch gradient
loss, dWxh, dWhh, dWhy, dbh, dby, hprev = lossFun(inputs, targets, hprev)
smooth_loss = smooth_loss * 0.999 + loss * 0.001
if n % 1000 == 0:
print('iter %d, loss: %f' % (n, smooth_loss)) # print progress
# perform parameter update with Adagrad
for param, dparam, mem in zip([Wxh, Whh, Why, bh, by],
[dWxh, dWhh, dWhy, dbh, dby],
[mWxh, mWhh, mWhy, mbh, mby]):
mem += dparam * dparam
param += -learning_rate * dparam / np.sqrt(mem + 1e-8) # adagrad update
p += seq_length # move data pointer
n += 1 # iteration counter
上面是训练的代码，首先初始化mWxh, mWhh, mWhy。因为这里实现的是Adgrad，所以需要这些变量来记录每个变量的“delta”，有兴趣的读者可以参考CS231n的notes 。
接下来是一个无限循环来不断的训练，首先是得到一个训练数据，输入是data[p:p + seq_length]，而输出是data[p+1:p + seq_length+1]。然后是lossFun计算这个样本的loss、梯度和最后一个时刻的隐状态（用于下一个时刻的隐状态的初始值），然后用梯度更新参数。每1000次训练之后会用sample函数生成一下句子，可以通过它来了解目前模型生成的效果。
完整代码在这里。
LSTM/GRU
长距离依赖(Long Term Dependency)问题
RNN最有用的地方在于它(可能)把之前的信息传递到当前时刻，比如在理解一个视频的当前帧时利用之前的帧是非常有用的。如果RNN可以做到这一点，那么它会非常有用。但是它能够实现这个目标吗？
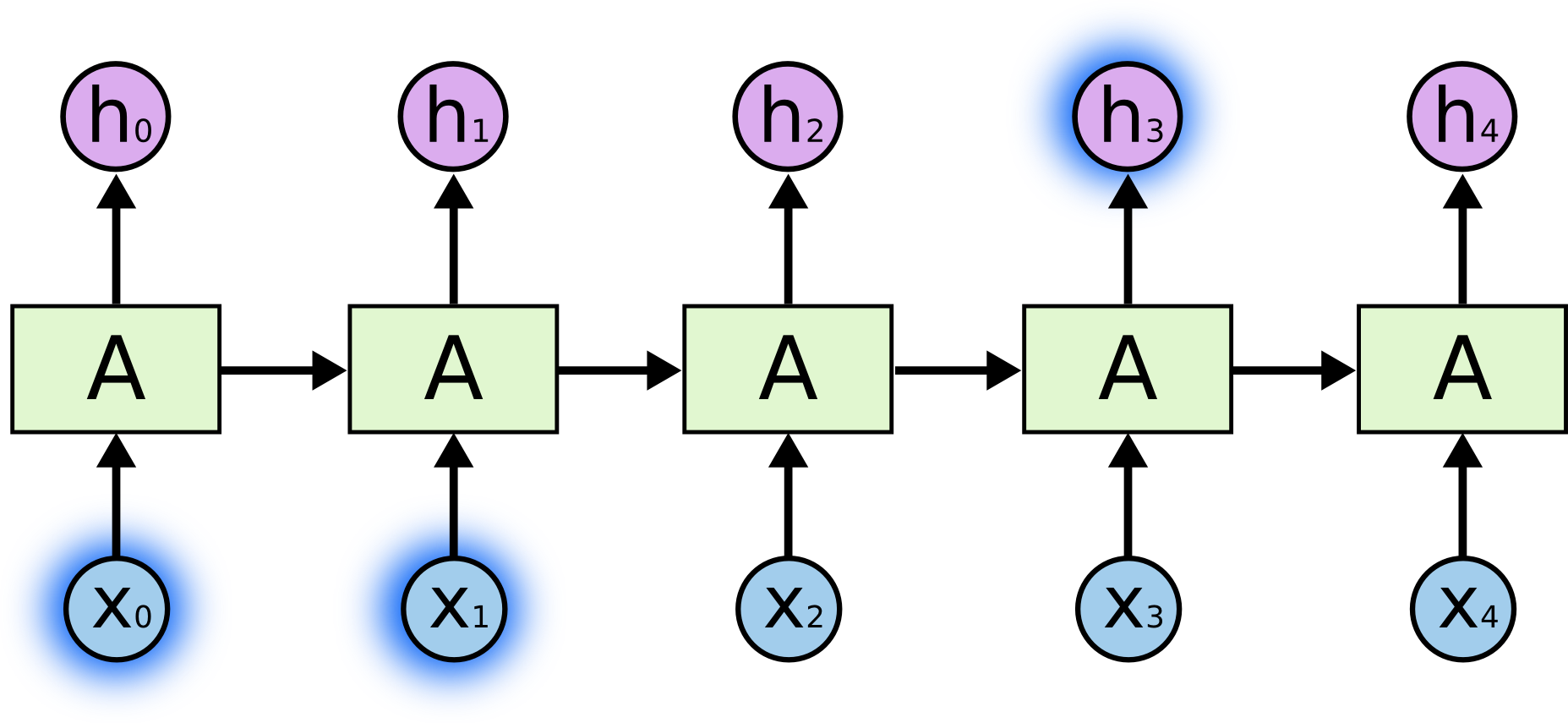
有的时候，我们只需要最近的一些信息就可以很好的预测当前的任务。比如在语言模型里，我们需要预测”the clouds are in the ?”的下一个单词，我们很容易根据之前的这几个此就可以预测最可能的词是”sky”。如下图所示，我们要预测的$h_3$需要的信息$x_0,x_1$距离不是太远。
图：RNN的短距离依赖
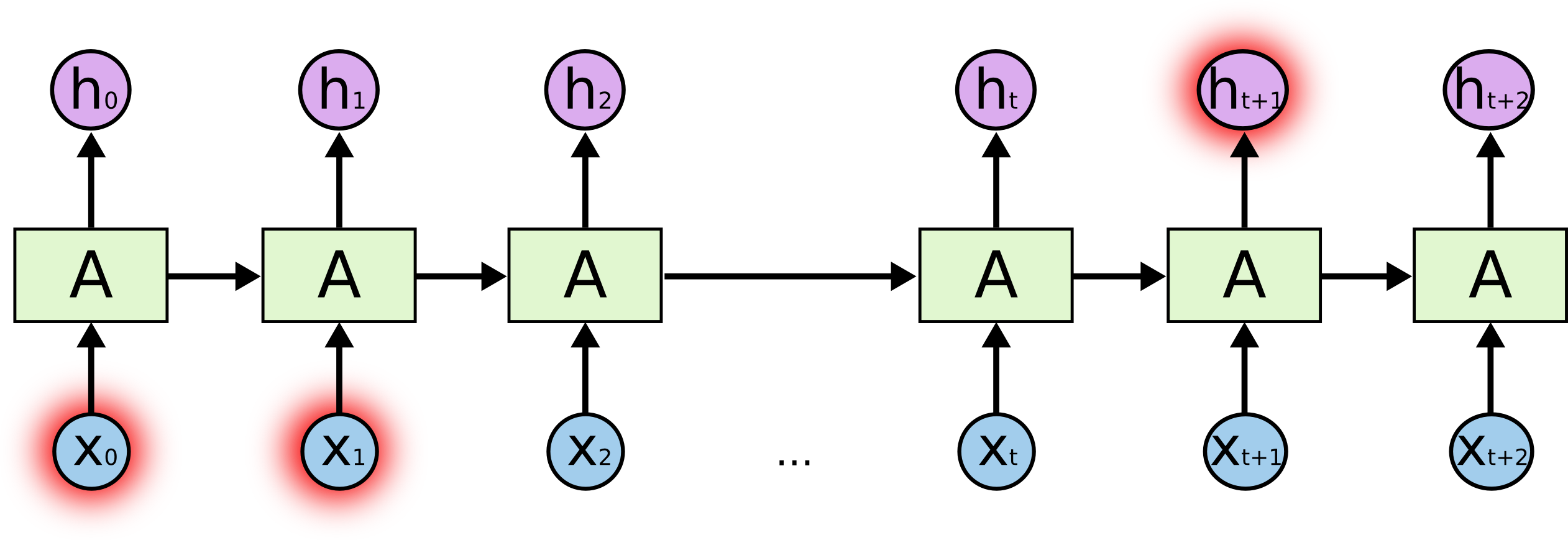
但是有的时候我们需要更多的上下文信息来预测，比如”I grew up in France… I speak fluent ?”。最近的信息”I speak fluent”暗示后面很可能是一种语言，但是我们无法确定是哪种语言，除非我们有更久之前的上下文”I grew up in France”。因此为了准确的预测，我们可能需要依赖很长距离的上下文。如下图所示，为了预测$x_{t+1}$，我们需要很远的$x_0,x_1$。理论上，如果我们的参数学得足够好，RNN是可以学习到这种长距离依赖关系的。但是在实际应用中RNN很难学到。
图：RNN的长距离依赖
接下来会介绍的LSTM就是试图解决这个问题。
Long Short Term Memory(LSTM) 基本概念
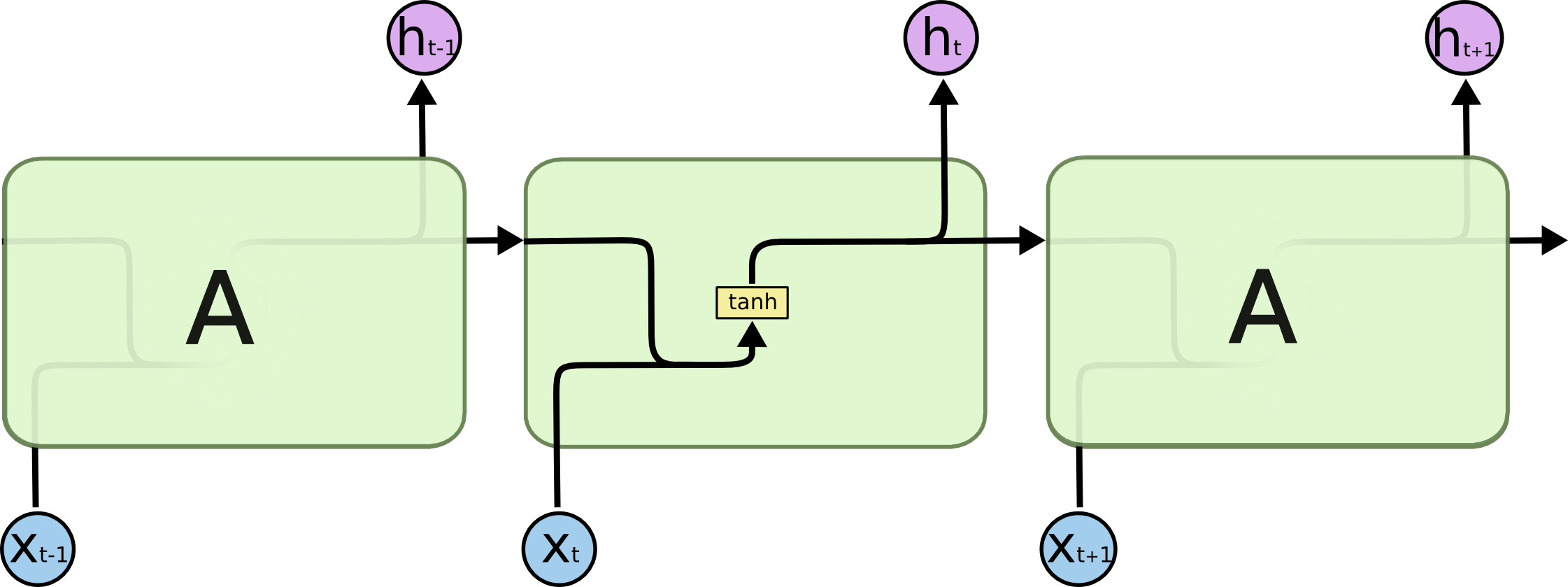
LSTM是一种特殊的RNN网络，它使用门(Gate)的机制来解决长距离依赖的问题。回顾一下，所有的RNN都是如下图所示的结构，把RNN看成一个黑盒子的话，它会有一个“隐状态”来“记忆”一些重要的信息。当前时刻的输出除了受当前输入影响之外，也受这个“隐状态”影响。并且在这个时刻结束时，除了输出之外，这个“隐状态”的内容也会发生变化——它“记忆”了新的信息同时有“遗忘”了一些旧的信息。
图：RNN的结构
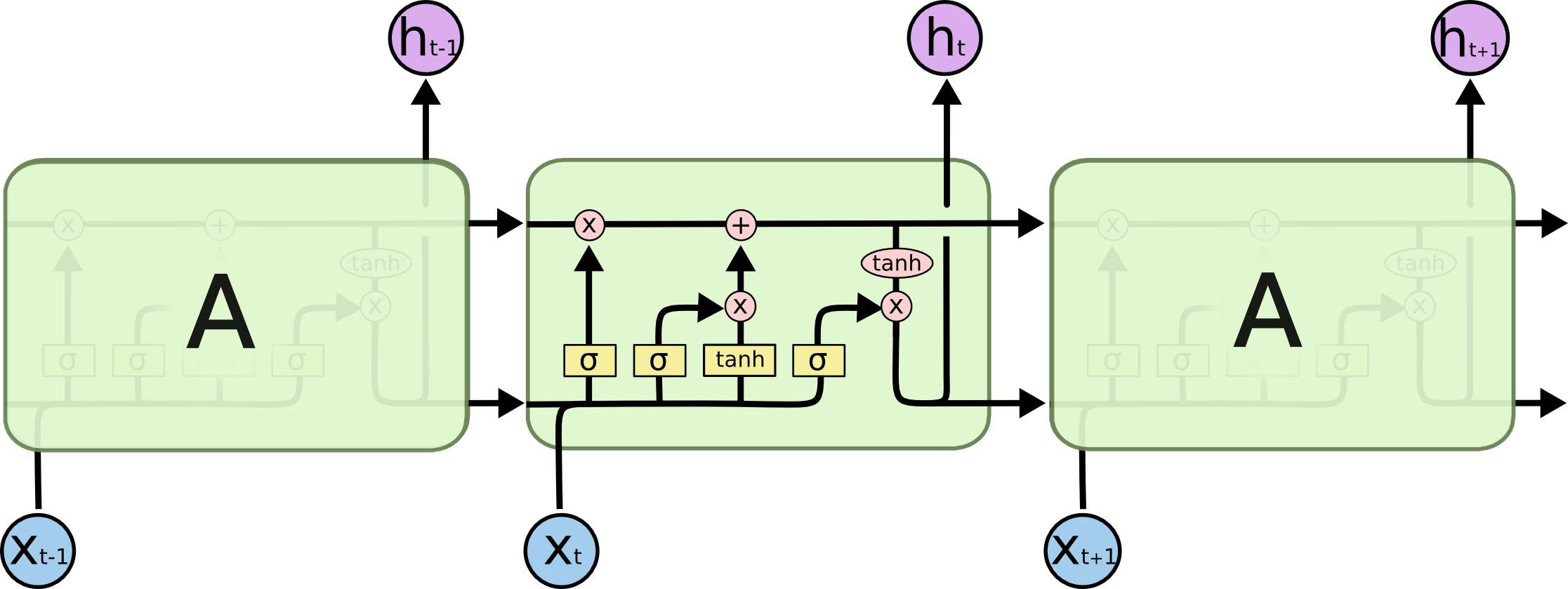
LSTM也是这样的结构，但相比于原始的RNN，它的内部结构更加复杂。普通的RNN就是一个全连接的层，而LSTM有四个用于控制”记忆”和运算的门，如下图所示。
图：LSTM
这个图初看比较复杂，我们后面会详细解释里面的细节。在介绍之前，我们首先来熟悉图中的一下部件，如下图所示。
图：RNN的结构
在上图中，每条有向边代表向量，黄色的方框代表神经网络层，粉色的圆圈代表逐点运算(Pointwise Operation)。两条边的合并代表向量的拼接(concatenation)，边的分叉代表把一个向量复制到两个地方。
LSTM核心思想
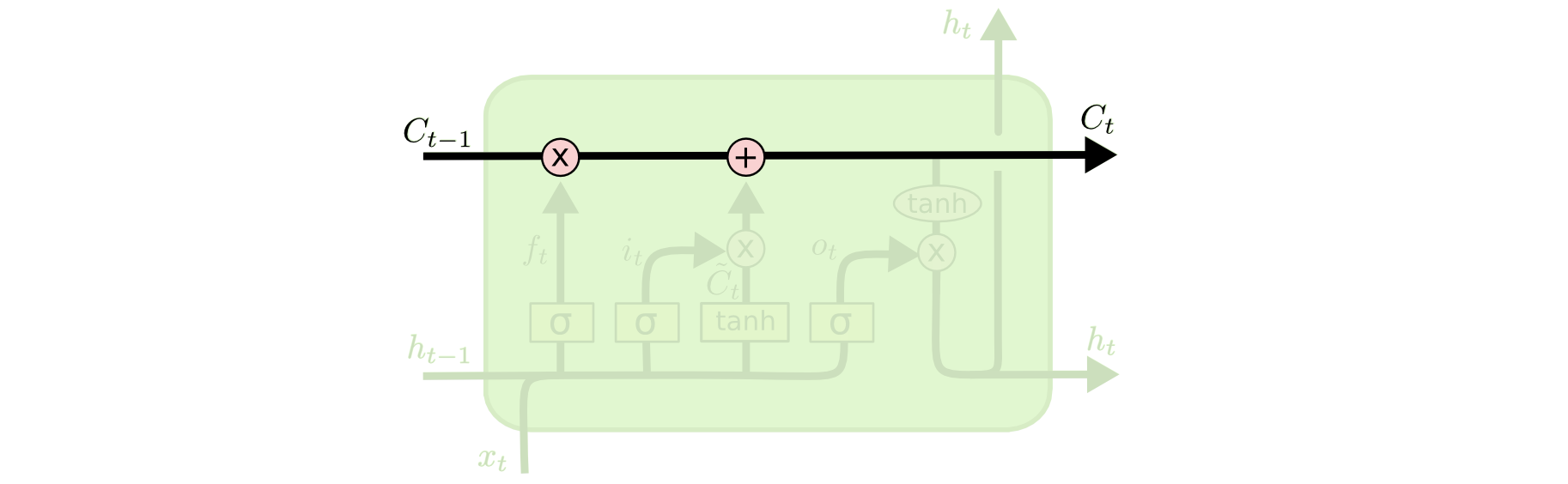
LSTM除了有普通RNN的隐状态$h_t$之外还有一个Cell状态$C_t$，它可以从上一个时刻直接通到下一个时刻的（后面会介绍修改它的操作），所以以前的重要记忆可以很容易保存下来，如下图所示，图上从$C_{t-1}$到$C_t$存在直接的通道。
图：LSTM Cell State的通道
当然如果LSTM只是原封不动的保存之前的记忆，那就没有太多价值，它还必须根据需要，能够增加新的记忆同时擦除旧的无用的记忆。LSTM是通过一种叫作门的机制来控制怎么擦除旧记忆写入新记忆的，下面我们逐步来介绍它的这种机制。
如下图所示，门可以用来控制信息是否能够通过，它是一个激活函数是sigmoid的层，0表示阻止任何信息通过，1表示所有信息通过，而0～1之间的值表示部分通过。
图：LSTM的Gate
LSTM门的细节
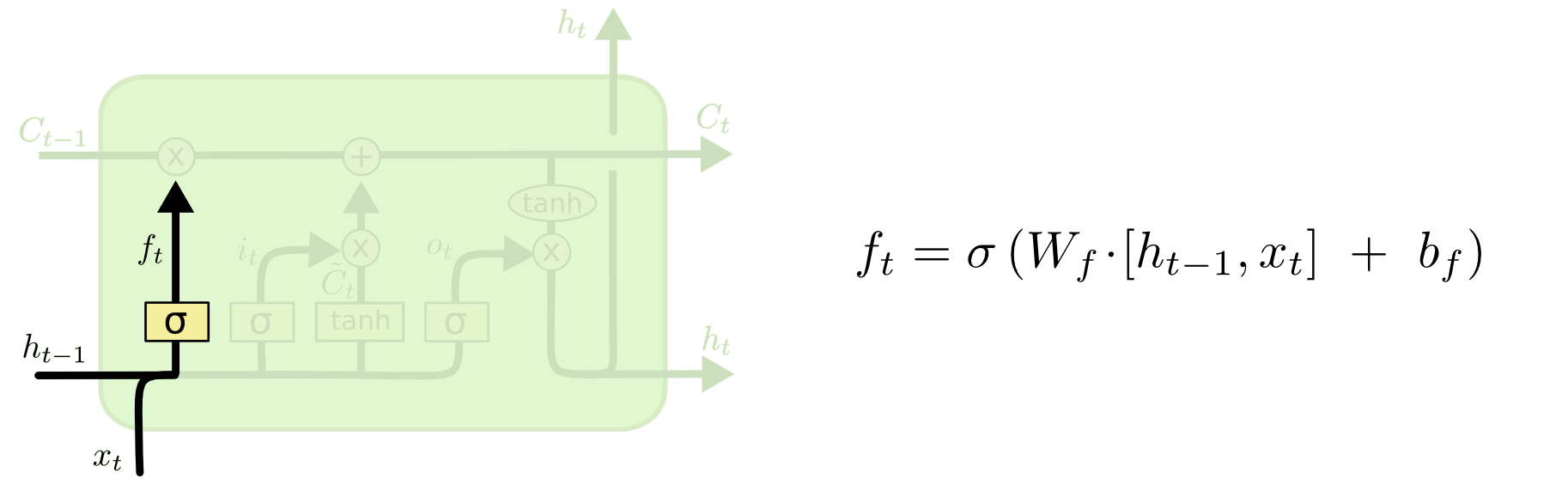
首先我们来了解LSTM的遗忘门(Forget Gate)，它会决定遗忘多少之前的记忆。它的输入是上一个时刻的隐状态$h_{t-1}$和当前时刻的输入$x_t$，它的输出是0-1之间的数，0表示完全遗忘之前的记忆，而1表示完全保留原来的记忆。
如下图所示：$f_t=\sigma(W_f · [h_{t-1}, x_t]+b_f)$。这个$f_t$乘以$C_{t-1}$就表示上一个时刻的Cell状态 $C_{t-1}$需要遗忘多少信息。
图：LSTM的遗忘门
接下来LSTM有一个输入门(Input Gate)：$i_t=\sigma(W_i · [h_{t-1}, x_t]+b_i)$，它用来控制输入的信息多少可以进入LSTM。t时刻的输入候选\(\tilde{C}_t=tanh(W_C · [h_{t-1}, x_t]+b_C)\)，注意$\tilde{C}_t$的激活函数是tanh，因为输入的范围我们不能限制，因此用(-1,1)的tanh；而门我们要求它的范围是(0,1)，因用sigmoid激活。
然后把输入门和输入候选点乘起来，表示当前时刻有多少信息应该进入Cell状态，如下图所示。
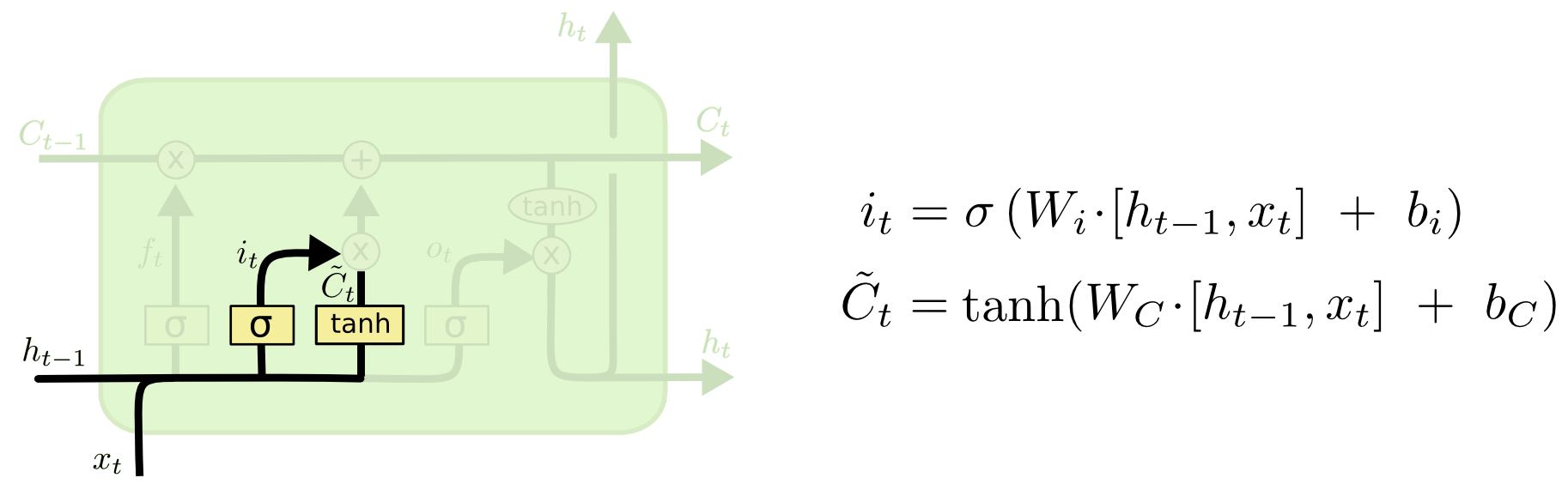图：LSTM的输入门
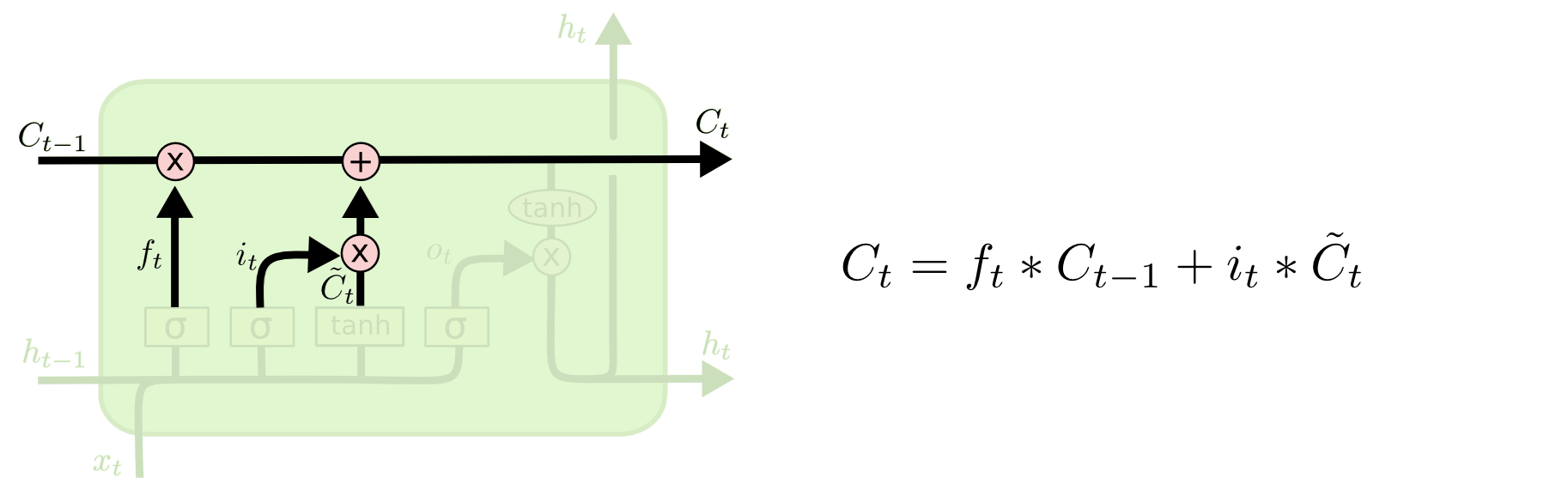
接着把上一个时刻未遗忘的信息\(C_{t-1} \times f_t\)和当前时刻候选$\tilde{C}_t$累加得到新的\(C_t\)，如下图：\(C_t=C_{t-1} \times f_t +\tilde{C}_t\)。
图：LSTM计算t时刻的$C_t$
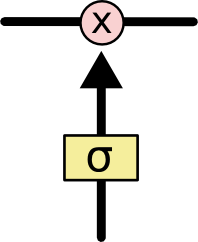
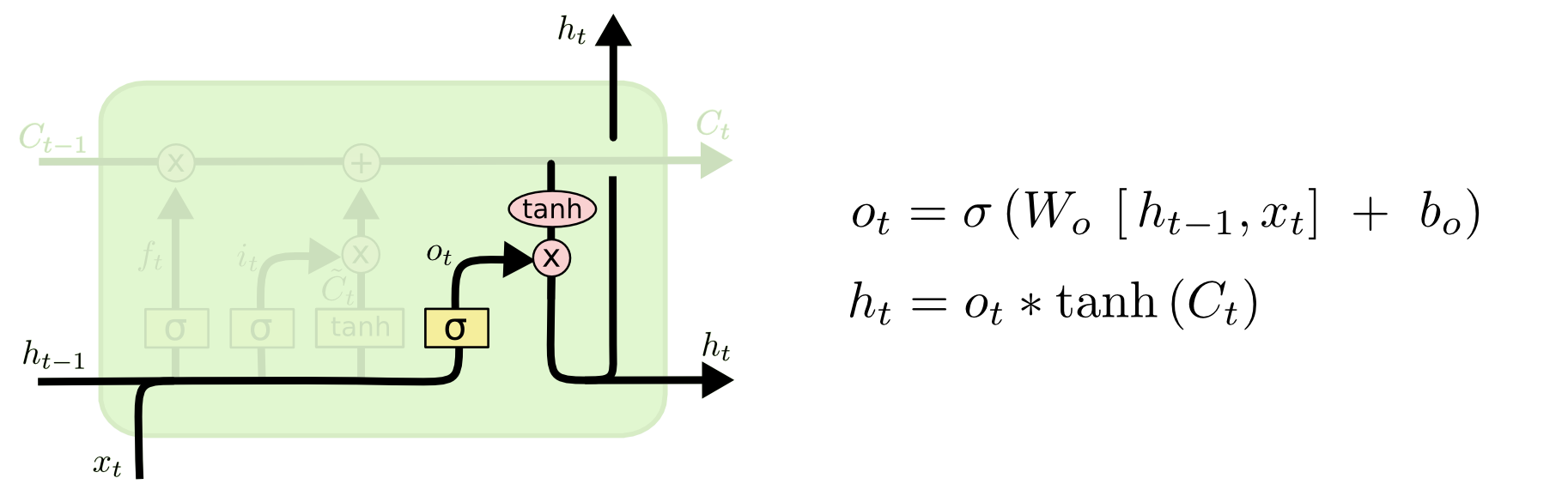
最后我们需要计算当前时刻的输出$h_t$(它就是隐状态)，它是使用当前的$C_t$使用tanh计算后再通过一个输出门(Output Gate)得到，如下图所示。
\[\begin{split} & o_t=\sigma(W_o · [h_{t-1}, x_t]+b_o \\ & h_t=o_t * tanh(C_t) \end{split}\]
图：$o_t$的计算
LSTM的变种
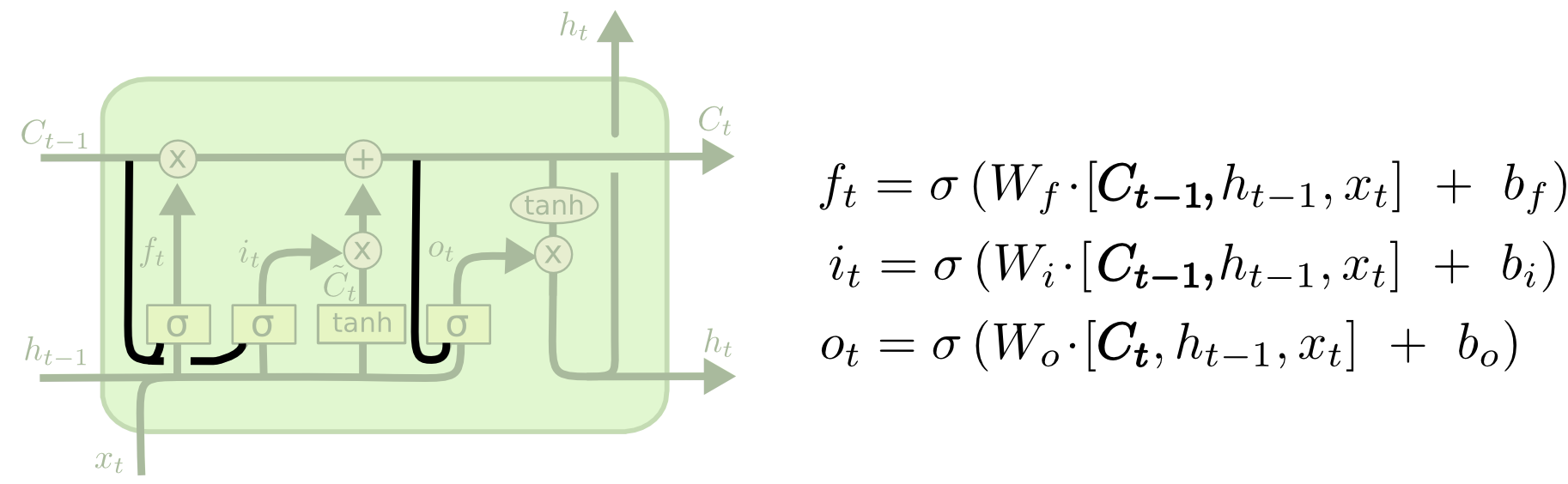
下面介绍一些常见的LSTM变种，包括很流行的GRU(Gated Recurrent Unit)。第一种变体是计算三个门时不只利用$h_{t-1}$和$x_t$，还使用$C_{t-1}$，也就是从$C_{t-1}$有一个peephole的边，如下图所示。
图：有peephole连接的LSTM
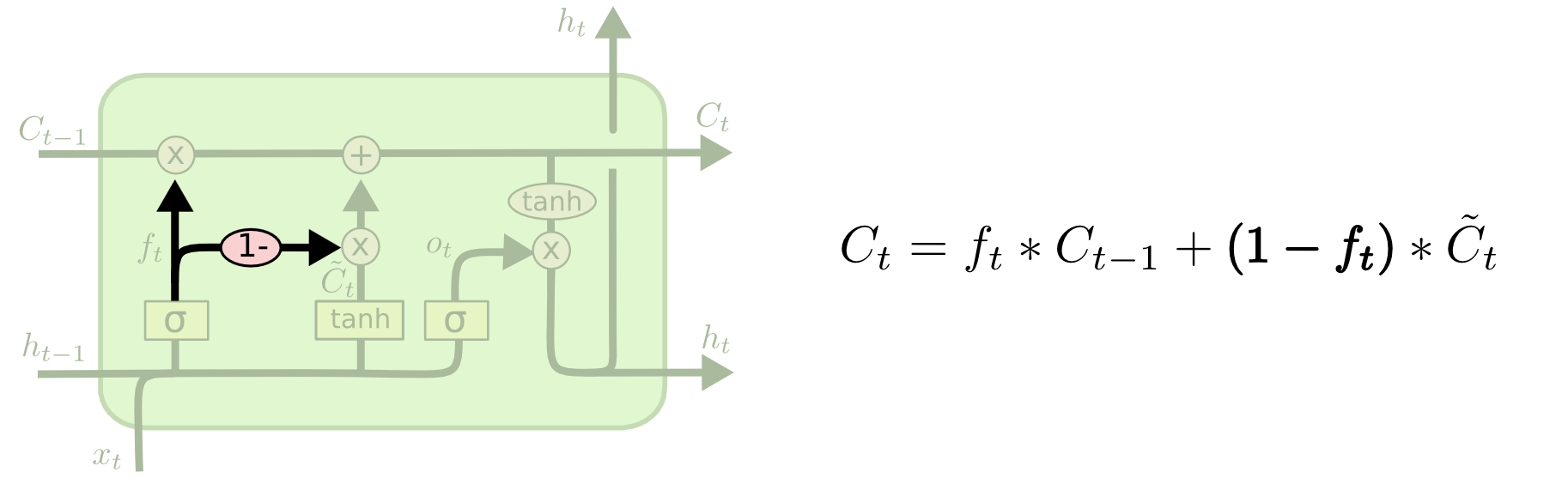
第二种变体就是遗忘门$f_t$不但决定遗忘多少$C_{t-1}$的信息，而且$1-f_t$会乘以$\tilde{C}_t$中用于控制多少新的信息进入$C_t$，如下图所示。
图：LSTM变种2
第三种就是GRU，它把遗忘门和输入门合并成一个更新门(Update Gate)，并且把Cell State和Hidden State也合并成一个Hidden State，它的计算如下图所示。
图：GRU
和LSTM不同，在计算$ \tilde h_t$的时候会用$r_t$乘以$h_{t-1}$，类似与LSTM的遗忘门。而在计算新的$h_t$时，$(1-z_t)$表示从$h_{t-1}$里保留的信息比例，而$z_t$表示从$\tilde{h}_t$里更新的信息比例。
- 显示Disqus评论(需要科学上网)