本文介绍序列标注算法,经典的HMM、MEMM和CRF模型。更多文章请点击深度学习理论与实战:提高篇。
目录
NLP很多任务都可以转化成序列标注任务,比如词性标注、命名实体识别和中文分词等。这类任务的输入是一个序列,输出是一个相同长度的序列。
词性标注(Part-of-speech/POS tagging)
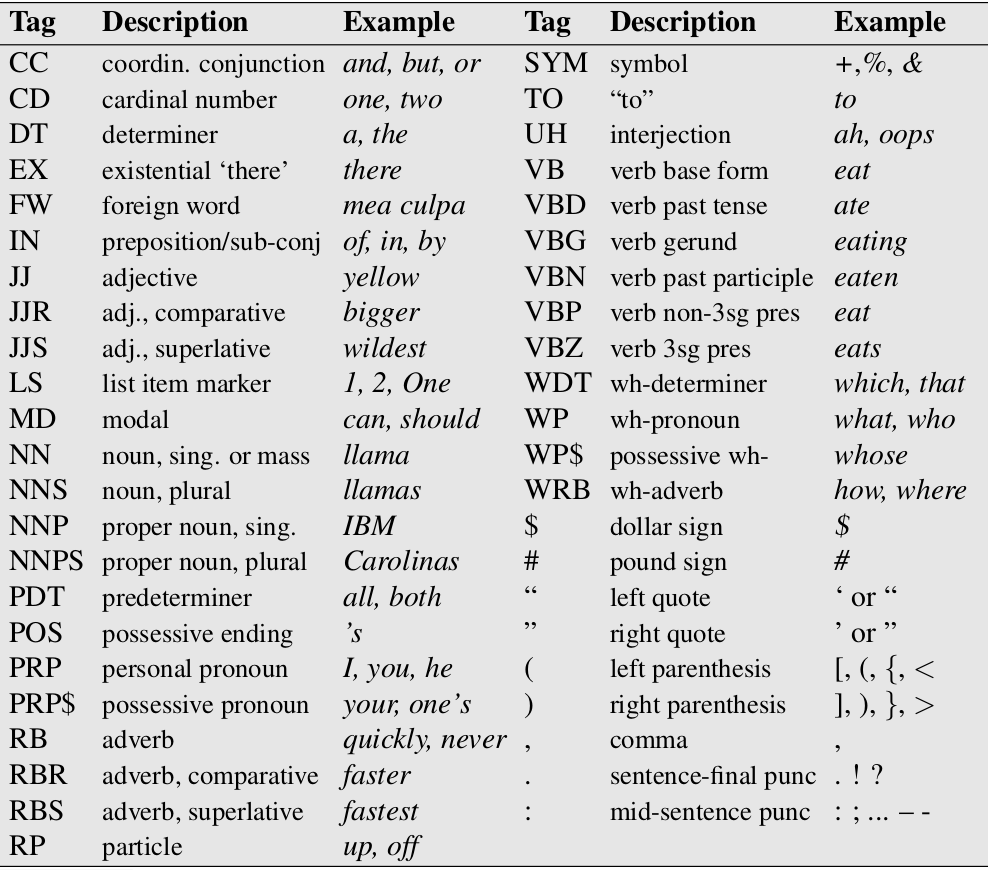
词性标注是一个典型的序列标注问题,输入是一个词序列,输出是对应的词性序列。词性(part-of-speech)是一个语言学的概念,对于英语来说,常见的词性包括名词(noun)、动词(verb)、形容词(adjectives)和副词(adverb)等等。不同的语言有不同的词性集合(tagset),而且对于一种语言,我们也可以定义不同的tagset。常见的tagset是Penn Treebank,对于英语它定义了45个词性tag。如下图所示。
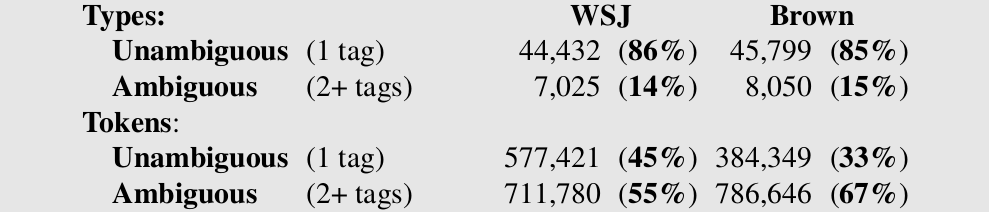
通常我们把词性用”/”放到词后面,比如 “The/DT grand/JJ jury/NN commented/VBD on/IN a/DT number/NN of/IN other/JJ topics/NNS ./.”。我们分析一下这个任务的难易程度,下图是对于华尔街日报(WSJ)和布朗(Brwon)语料库的一个统计。
以WSJ为例,86%的词是无歧义的词(只有一个词性)。但是高频词通常歧义比较多,因此以Token(同一个词出现两次就是2个Token)来统计,无歧义的Token占比是45%。当然一个词的词性比例是不同的,一般会有某个词性的比例很高。所以我们可以实现一个这样的Baseline系统:如果一个词(在训练数据量)只有一个词性,那么直接预测这个词性,否则用出现比例最高的词性作为这个词的词性。这样的一个简单Baseline系统在WSJ语料上的准确率能达到92.34%。我们后面介绍的算法能够达到97%以上的准确率。
词性标注有两个难题,第一个就是前面介绍的歧义,消除歧义需要依赖与上下文的信息。而第二个就是新词,很多词在训练数据中从来没有出现过,那要“猜测”新词的词性,更是需要上下文的信息。我们判断一个词的词性主要有两部分信息,一是词本身的信息,一个有多个词性的词它的词性分布不是均匀的,肯定有些词性会高频出现,而有些很少出现。而另一部分信息来自于这个词的上下文。
用HMM来进行序列标注
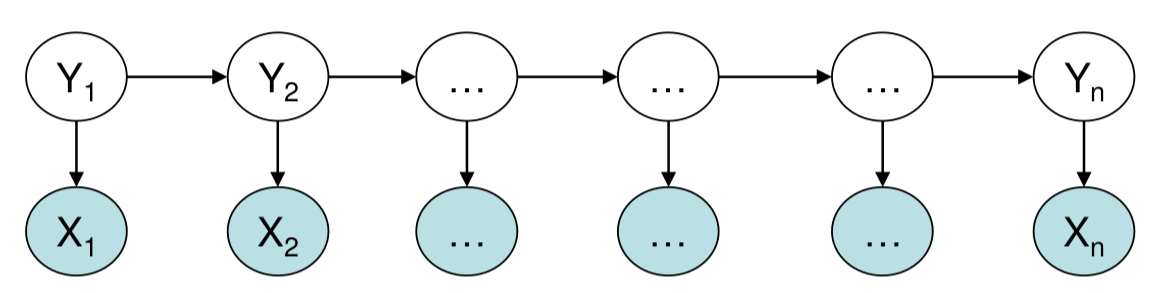
用HMM来进行词性标注要比语音识别容易很多,原因在于NLP(包含词性标注)的任务的标注是对齐的。比如词性标注,观察序列是”The grand jury commented on a number of other topics .”,而状态序列是”DT JJ NN VBD IN DT NN IN JJ NNS .”。它们是一一对应的,输入和输出序列的长度是一样的。而在语音识别里,观察序列是$o_1,o_2,…,o_T$,而状态序列是$s_1,s_2,…,s_N$,它们的长度是不同的,而且我们不知道它们的对齐关系的——我们并不知道$o_2$对应的是$s_1$还是$s_2$。而在词性标注中,我们知道The对应的标签(状态)就是DT。另外HMM的观察是连续的高维的向量,因此需要GMM模型来建模;而词性标注的观察是离散的一维的标量,因此直接可以估计$b_j(v)$。
在语音识别中,每一个因子的都是一个HMM,一个词由它对应的因子的HMM拼接成一个大的HMM,而一个句子是由词拼接成的更大的一个HMM;而在词性标注中只有一个HMM。因此语音识别的解码器的搜索空间非常巨大,而词性标注可以用Viberbi算法求解,原因在于它只有一个HMM,并且它的状态(Tag)个数也非常少。
在语音识别里,我们需要使用前向后向算法来估计参数。因为我们不知道每个观察对应的状态是什么,所以需要用EM算法。而在NLP的序列标注任务中,观察对应的状态是已知的,因此可以直接最大似然的估计跳转和发射概率。
学习
根据前面的讨论,HMM用于词性标注的学习过程非常简单,因为我们已经知道每个观察的状态。最大似然估计就变为简单的计数。
比较我们要估计$P(NN \vert DT)$,那么我们数一下有多少个NN跟在DT后面,我们记为C(DT,NN)。同时我们可以统计DT出现了多少次,我们可以记为C(DT),那么$\hat{P}(NN \vert DT)=\frac{C(DT,NN)}{C(DT)}$
因为观察(输出)是一维的离散的,所以估计发射概率也很简单。C(race,NN)表示状态为NN并且观察为单词race出现的次数,那么$\hat{P}(race \vert NN)=\frac{C(race,NN)}{C(NN)}$
预测
因为只有一个HMM模型,预测使用Viterbi算法就可以了。
HMM的问题
HMM的问题是很难融入更多的特征,比如判断一个词的词性(尤其是未登录词),前后缀会很有帮助。我们用HMM很难融入生成模型,因为它建模的是联合概率P(x,y)。每引入一个特征都要都要保证概率分布的要求,因此通常要做很多独立性的假设。而这些独立性假设通常并不成立,因为很多特征是高度相关的。
此外,HMM的每个状态只和之前状态以及当前观察有关系,这个假设在很多NLP的序列标注任务是不成立的。比如命名实体识别任务,New是不是实体,与它后面的词很有关系,比如后面是York,那么New就是一个实体。
另外一个问题就是建模联合概率P(x,y)会建模P(x)和$P(y \vert x)$,对于分类或者序列标注问题,有$P(y \vert x)$就足够了。这样会导致我们优化的目标和实际预测不匹配——我们训练学习的是联合概率分布,但是我们预测是却只使用条件概率分布。
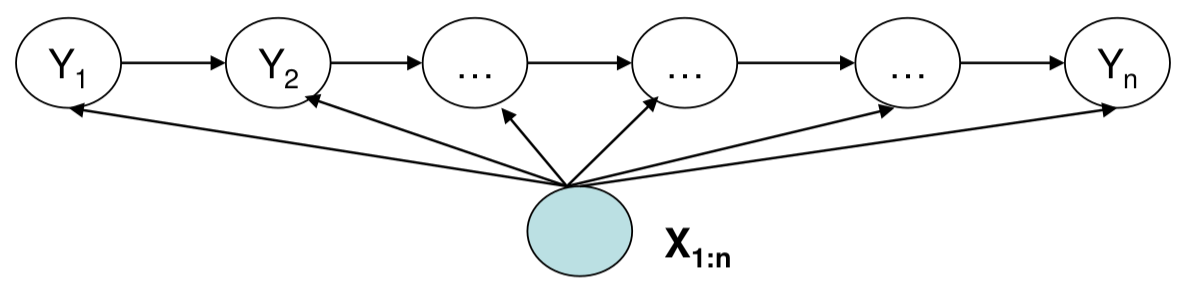
如下图所示,状态$Y_i$只和$X_i$直接有关,而和其它的比如$X_{j-1}$没有直接关系,如果$X_{j-1}$想影响$Y_i$,那么只有间接通过$Y_{i-1}$来影响。但是跳转概率只和状态有关,因此很难表示复杂的关系。
MEMM
HMM的好处是可以利用状态的跳转信息,而最大熵模型可以融入很多上下文特征,因此把它们结合起来就可以得到更好的模型。这就是MEMM模型,它也叫对数线性标注(log-linear tagging)模型。HMM建模的联合概率分布$p(x_1,x_2,…,x_n,y_1,y_2,…,y_n)$;而MEMM建模的是条件概率分布$p(y_1,y_2,…,y_n \vert x_1,x_2,…,x_n)$。
我们首先来定义条件标注模型(Conditional Tagging Models)
条件标注模型
条件标注模型满足如下条件:
-
一个词典集合$\mathcal{X}$,可以是无穷集合
-
一个有限的标签集合$\mathcal{Y}$
-
一个满足如下条件的函数$p(y_1,…,y_n \vert x_1,…,x_n)$
a. 对于任何的观察/状态序列$<x_1,…,x_n,y_1,…,y_n> \in \mathcal{S}$,其中$x_i \in \mathcal{X}, y_i \in \mathcal{Y}$。
\[p(y_1,...,y_n|x_1,...,x_n) \ge 0\]b. 对于任意的观察序列$x_1,…,x_n$,有:
\[\sum_{y_1,...,y_n \in \mathcal{Y}^n} p(y_1,...,y_n|x_1,...,x_n)=1\]给定条件标注模型时,标注任务就变成寻找最优的状态序列:
\[f(x_1,...,x_n)=\underset{y_1,...,y_n \in \mathcal{Y}^n}{argmax}p(y_1,...,y_n|x_1,...,x_n)\]现在我们有三个问题:
- 怎么定义条件标注模型$p(y_1,…,y_n \vert x_1,…,x_n)$满足上面的条件
- 怎么根据训练数据估计模型的参数
- 给定模型和观察序列$x_1,…,x_n$,怎么高效的寻找最优状态序列$\underset{y_1,…,y_n \in \mathcal{Y}^n}{argmax}p(y_1,…,y_n \vert x_1,…,x_n)$
Trigram MEMM
我们这节介绍Trigram MEMM,它的状态依赖于之前两个状态。MEMM就是一种常见的条件标注模型,后面我们介绍的CRF模型也是条件标注模型。
\[\begin{split} & P(Y_1=y_1,...,Y_n=y_n|X_1=x_1,...,X_n=x_n) \\ & =\prod_{i=1}^{n}P(Y_i=y_i|X_1=x_1,...,X_n=x_n, Y_1=y_1,...,Y_{i-1}=y_{i-1}) \\ & =\prod_{i=1}^{n}P(Y_i=y_i|X_1=x_1,...,X_n=x_n, Y_{i-2}=y_{i-2},Y_{i-1}=y_{i-1}) \end{split}\]上式的第一个等号是概率的链式规则,而第二个等号使用了二阶马尔科夫假设——当前状态只依赖于之前的两个状态,而与更早之前的状态无关。我们假设$y_{-1}=y_0=*$,用于表示序列开始的特殊符号。这里的二阶马尔科夫假设为:
\[P(Y_i=y_i|X_1=x_1,...,X_n=x_n, Y_1=y_1,...,Y_{i-1}=y_{i-1})= \\ P(Y_i=y_i|X_1=x_1,...,X_n=x_n, Y_{i-2}=y_{i-2},Y_{i-1}=y_{i-1})\]它和HMM的马尔科夫假设有点类似:
\[P(Y_i=y_i| Y_1=y_1,...,Y_{i-1}=y_{i-1})=P(Y_i=y_i|Y_{i-2}=y_{i-2},Y_{i-1}=y_{i-1})\]区别在于HMM和状态$y_i$是与观察$x_1,…,x_n$无关,而这里的$y_i$是依赖于整个观察序列$x_1,…,x_n$的。接下来使用对数线性模型(最大熵模型MM)来建模$P(Y_i=y_i \vert X_1=x_1,…,X_n=x_n, Y_{i-2}=y_{i-2},Y_{i-1}=y_{i-1})$。为了简化,我们引入记号$h_i$:
\[h_i=<x_1,...,x_n,y_{i-2},y_{i-1}>\]它包含预测标签$y_i$时可以用到的信息:包括整个输入训练,前两个时刻的状态,以及位置i。我们需要定义特征映射函数$f(h_i,y) \in R^d$,比如两个可能的特征为:
\[\begin{split} f_1(h_i,y) & =\begin{cases} 1 \text{ if } x_i=the and y=DT \\ 0 \text{, 其它} \end{cases} \\ f_2(h_i,y) & =\begin{cases} 1 \text{ if } y_{i-1}=V and y=DT \\ 0 \text{, 其它} \end{cases} \\ \end{split}\]我们的对数线性模型为:
\[P(Y_i=y_i|X_1=x_1,...,X_n=x_n, Y_{i-2}=y_{i-2},Y_{i-1}=y_{i-1}) = \frac{exp(w \cdot f(h_i,y_i))}{\sum_{y \in \mathcal{Y}}exp(w \cdot f(h_i,y))}\]MEMM的参数估计
MEMM的参数分为两部分,状态跳转概率和对数线性模型的参数。前者和HMM的参数估计类似,简单的最大似然估计就行,只不过上一节我们介绍的是一阶的HMM,而这里是二阶的。对数线性模型的参数估计和前面分类任务里完全一样。唯一的区别就是训练数据的不同,前面每一个训练数据是一个(x,y)对;而这里是$(x_1,…,x_n, y_1,…,y_n)$,我们可以根据它构造出n个训练数据$(y_1,h_1=<x_1,…,x_n,y_{-1},y_0>), (y_2,h_1=<x_1,…,x_n,y_{0},y_1>), …,(y_n,h_n=<x_1,…,x_n,y_{n-2},y_{n-1}>)$。
MEMM的解码算法
我们的目标是寻找最优的序列,使得概率最大:
\[\underset{y_1,...,y_n \in \mathcal{Y}^n}{argmax}p(y_1,...,y_n|x_1,...,x_n) \\ =\underset{y_1,...,y_n \in \mathcal{Y}^n}{argmax}\prod_{i=1}^{n}p(y_i|h_i;w)\]当然最简单的办法是遍历所有序列,然后逐一计算寻找最大的。这个复杂度是$O(n^{\vert \mathcal{Y} \vert})$。和HMM一样,我们可以使用Viterbi算法对MEMM进行解码。
我们首先定义几个记号。$S(k,u,v)$表示所有的序列$y_{-1}y_0…y_k$并且$y_{k-1}=u,y_k=v$,也就是长度为k(不计算$y_{-1}y_0$)的序列中满足第k-1个时刻是状态u并且第k个时刻是状态v的那些序列。
\[\pi(k,u,v)=\underset{y_{-1}y_0...y_k \in S(k,u,v)}{argmax}\prod_{i=1}^{k}p(y_i|h_i;w)\]因此$\pi(k,u,v)$表示长度为k并且最后两个时刻的状态为u和v的所有序列中概率最大的哪个状态序列对于的概率值。我们可以递归(递推)的计算$\pi(k,u,v)$,公式为:
\[\pi(k,u,v)=\underset{w \in \mathcal{Y_{k-2}}}{max}\pi(k-1,w,u)p(v|h;w)\]上式中\(\mathcal{Y_{-1}}=\mathcal{Y_{0}}=*\),而\(\mathcal{Y_{k}}=\mathcal{Y}, i=1,2,...,n\)。也就是-1和0两个特殊时刻,状态只能是\*,而其它时刻的状态集合是$\mathcal{Y}$。
我们可以这样解读这个递推公式:k时刻是v,k-1时刻是u的最优路径是从k-2是w,k-1是u的最优路径中选择出来的,然后还要乘以$p(v \vert h;w)$。这样得到$\vert \mathcal{Y_{k-2}}\vert$条路径,然后我们从这么多路径中寻找最优的。注意h是和w相关的,不同的w对于不同的h。$h_k=<x_1,…,x_n,w,u>$。因此最优路径既要$\pi(k-1,w,u)$比较大,同时也需要$p(v \vert <x_1,…,x_n,w,u>;w)$比较大。
递归的出口是\(\pi(0,*,*)=1\)。带backtrace的完整的伪代码如下图所示。
MEMM相比HMM的好处
如下图所示,MEMM在每个时刻估计标签$y_t$的时候都可以用到全部输入训练$x_1,…,x_n$的特征,因此我们可以方便的加入输入任意位置的信息作为特征,比如判断当前词的词性时,我们可以看前一个词,看后一个词,看前一个词/后一个词的组合,甚至看前一个词的后缀。这些特征明显不是完全独立的(前一个词和前后词组合是有关系的),这在HMM里是很难加入的。另外相对于HMM,MEMM只建模条件概率$p(y \vert x)$,因此不存在学习和预测不匹配的问题。
MEMM的label bias问题
MEMM最大的问题就是Label Bias,下面我们通过一个例子来说明。
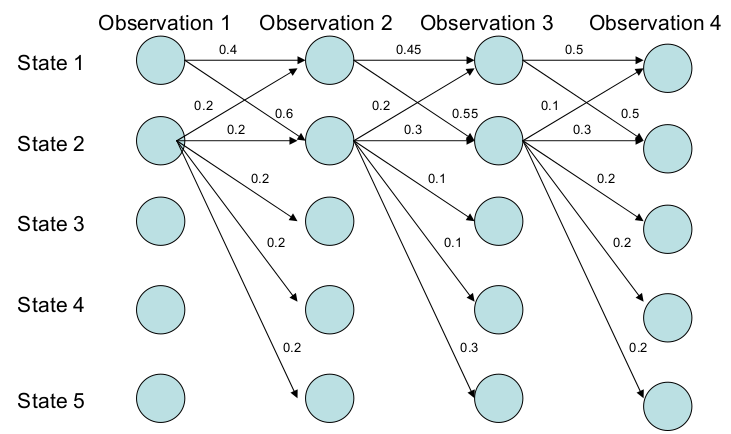
比如如下图所示,横轴表示4个时刻,纵轴表示5个状态。从图中,我们可以看成状态1倾向于跳转到状态2(0.4 vs 0.6;0.45 vs 0.55;0.5 vs 0.5);状态2也倾向于跳转到自己(2->2的概率是2->{1,2,3,4,5}中最大的)。因此我们期望最优的路径会包含状态2。事实是这样吗?我们可以简单的计算一下:
\[P(1->1->1->1)= 0.4 \times 0.45 \times 0.5 = 0.09 \\ P(2->2->2->2)= 0.2 \times 0.3 \times 0.3 = 0.018 \\ P(1->2->1->2)= 0.6 \times 0.2 \times 0.5 = 0.06 \\ P(1->1->2->2)= 0.4 \times 0.55 \times 0.3 = 0.066\]最优的路径竟然是1->1->1->1!原因是什么呢?我们仔细分析可以发现,状态1的概率比较集中,它只能跳转到1和2,虽然跳转到2的概率稍大,但是跳到1的概率也不小(0.45)。而状态2的概率比较分散,它可以跳转到5个状态,虽然2跳到2的概率是最大的但也只有0.3。因此选择最优路径的时候它倾向于比较集中的那些label,这就是所谓的label bias。
为什么存在label bias问题呢?关键问题在于MEMM模型的概率需要locally normalized,也就是1->1+1->2必须等于1;2->{1,2,3,4,5}加起来也必须等于1。因为MEMM在每个时刻都是一个概率模型$P(y_t \vert h_t;w)$,一次它要求$\sum_{y_t}P(y_t \vert h_t;w)=1$。如果我们能够不要求locally normalized,就不会有label bias的问题。
比如下图所示,我们不要求2->{1,2,3,4,5}的值加起来等于1。那么就不会有这个问题,因为即使我们(训练数据)要求2出去的概率比较分散,但是模型也可能学到2出去的概率都比较大。这样最优的路径就有可能包含状态2,这里实际最优的路径是1->2->2->2。
满足上面要求的条件标注模型就是CRF模型。
CRF
定义
首先介绍(全局)特征函数$\Phi(x,y) \in R^d$,这个函数的输入是观察序列x和状态序列y,输出是d维特征空间的一个(特征)向量。CRF是如下形式的一个对数线性模型:
\[\label{eq:crf} p(y|x;w)=p(y_1,...,y_m|x_1,...,x_m;w)=\frac{exp(w \cdot \Phi(x,y))}{\sum_{y' \in \mathcal{Y}^m}exp(w \cdot \Phi(x,y'))}\]从函数形式看,它和MEMM的最大熵模型一样,但是它们是有重要的区别的。
首先MEMM输出的是$y_i$,而CRF的输出是整个序列y,假设$\vert \mathcal{Y} \vert=10$,那么MEMM的输出可能值只有10个,而CRF有$10^m$个(m是序列的长度),它们的差别是非常大的。其次,MEMM的$h_i=<x_1,…,x_m,y_{i-1}>$(我们这里假设一阶的MEMM),模型的输入除了输入序列x之外还有前一个时刻的状态;而CRF不需要,因为CRF是一次计算的。比如要计算$p(y_1,..,y_m \vert x_1,…,x_m)$,MEMM要用MM模型计算m次,$\prod_{t=1}^{m}p(y_t \vert h_t;w)$。而CRF是一次直接计算出$p(y \vert x)=p(y_1,…,y_m \vert x_1,…,y_m)$,因此CRF更加“全局”。
其次分母归一化项的计算量也差别很大,MEMM只需要对$\vert \mathcal{Y} \vert$个数求和,而CRF要对$\vert \mathcal{Y} \vert^m$个数求和。这看起来使得CRF无法使用,因为我们如果老老实实计算概率的话需要$\vert \mathcal{Y} \vert^m$次求和,那么前面介绍的词性标注任务,假设$\vert \mathcal{Y} \vert =45$,句子长度为10,那么$45^{10}$这样的计算量是根本不可能算出来的。后面我们会介绍怎么解决这个问题。
接下来的问题就是特征函数是怎么定义的问题,我们这里介绍最简单的线性链(Linear Chain)的CRF,它的特征函数是如下形式:
\[\Phi(x,y)=\sum_{j=1}^{m}\phi(x,j,y_{j-1},y_j)\]或者更加具体的:
\[\Phi_k(x,y)=\sum_{j=1}^{m}\phi_k(x,j,y_{j-1},y_j)\]也就是每个特征都只考虑输入序列,当前状态和前一个时刻的状态,这和一阶MEMM是类似的。我们来看一个具体特征的例子。比如词性标注的任务:
\[\phi_1(x_j,y_j,y_{j-1})=\begin{cases} 1 \text{ if } x_j=NN and y_{j-1}=ADJ \\ 0 \text{, 其它} \end{cases}\]这个特征在判断当前词性是否NN是会参考前一个词的词性是否ADJ,通常如前一个词是ADJ,那么当前词更可能是NN,因此一个好的模型应该学到对于的参数$w_1>0$。注意MEMM也会有完全类似的特征,但是它只由于某个时刻t,而CRF里是把m个时刻都加起来的:
\[\Phi_1(x,y)=\phi_1(x_1,y_0,y_1) + ... + \phi_1(x_m,y_{m-1},y_m)\]因此MEMM我们可以说$\phi_1$是一个Local的特征,而CRF里的$\Phi_1$是一个Global的特征。
CRF模型的Decoding
CRF模型的decoding为如下问题:
\[\underset{y \in \mathcal{Y}^m}{argmax}p(y|x;w)\]也就是选择路径(状态序列)使得概率最大。
\[\begin{split} & \underset{y \in \mathcal{Y}^m}{argmax}p(y|x;w)=\underset{y \in \mathcal{Y}^m}{argmax} \frac{exp(w \cdot \Phi(x,y))}{\sum_{y' \in \mathcal{Y}^m}exp(w \cdot \Phi(x,y'))} \\ & = \underset{y \in \mathcal{Y}^m}{argmax} \; exp(w \cdot \Phi(x,y)) \\ & = \underset{y \in \mathcal{Y}^m}{argmax} \; w \cdot \Phi(x,y) \\ & = \underset{y \in \mathcal{Y}^m}{argmax} \; w \cdot \sum_{j=1}^{m}\phi(x,j,y_{j-1},y_j) \\ & = \underset{y \in \mathcal{Y}^m}{argmax} \; \sum_{j=1}^{m}w \cdot \phi(x,j,y_{j-1},y_j) \end{split}\]第一步推导是直接使用公式;而第二步是因为分母对于y’求和之后与y’无关,只是x的函数,因此对于的argmax可以忽略它。之前我们说CRF的分母很难计算,但是在Decoding的时候根本不需要计算分母。因此CRF的decoding最终变成寻找这样的状态序列:
\[\underset{y \in \mathcal{Y}^m}{argmax} \; \sum_{j=1}^{m}w \cdot \phi(x,j,y_{j-1},y_j)\]这是比较符合直觉的,从状态$y_{j-1}$跳到状态$y_j$对于的得分是$w \cdot \phi(x,j,y_{j-1},y_j)$。这个得分可以认为是边的权重,它可正可负。如果得分较大,那么从状态$y_{j-1}$跳到状态$y_j$的可能性就较大。当然我们最终考虑的是“全局”的最优,因此我们要选择路径上所有边的得分加起来是最大的。我们可以用动态规划来求解这个问题,和MEMM类似。我们首先定义:
\[\pi[t,s]=\underset{s_1,...,s_{t-1}s}{\sum_{j=1}^{t} w \cdot \phi(x,j,s_{j-1},s_j)}\]在所有长度为t的路径(序列)里,满足t时刻处于状态s的路径边的得分最大的值。
我们首先进行初始计算:
\[\pi[1,s]=w \cdot \phi(x,1,*,s) for s \in \mathcal{Y}\]其中*表示初始化状态。接着我们递推的计算j时刻:
\[\pi[j,s]=\underset{s' \in \mathcal{Y}}{max}[ \pi[j-1,s'] + w \cdot \phi(x,j,s',s)]\]最终有:
\[\underset{s_1,...,s_m}{max}\sum_{j=1}^{m} w \cdot \phi(x,j,s',s)=\underset{s }{max}\pi[m,s]\]我们可以这样来”读”上面的公式:$\pi[m,s]$是m时刻状态为s的最优路径,s共有$\vert \mathcal{Y} \vert$中可能,那么长度为m的最优路径一定是这$\vert \mathcal{Y} \vert$条路径中的某一条,因此我们求最大的就得到了全局最优的路径。当然这里只是求最优路径的得分,如果要求路径,我们还需要backtrace路径的上一个状态。
CRF模型的参数学习
我们假设有n个训练数据${x^i,y^i}{i=1}^n$。其中$x^i=x_1^i,…x{m_i}^i$,$y^i=y_1^i,…y_{m_i}^i$。和MEMM类似,我们可以定义对数似然概率:
\[L(w)=\sum_{i=1}^{n}logp(y^i|x^i;w) - \frac{1}{w} \lambda \left\Vert w \right \Vert^2\]我们需要找到最优的参数:
\[w^*=\underset{w \in \mathbb{R}^n}{argmax}\sum_{i=1}^{n}logp(y^i|x^i;w) - \frac{1}{w} \lambda \left\Vert w \right \Vert^2\]因为它仍然是一个对数线性模型,从而是一个凸函数,因此我们可以使用梯度下降或者L-BFGS求解。要使用这两种方法求解,我们都需要计算梯度$\frac{\partial L(w)}{\partial w_k}$。
由于CRF的函数形式和对数线性模型完全一样,因此它的梯度公式也和对数线性模型的公式完全一样:
\[\frac{\partial}{\partial w_k}L(w)=\sum_i\Phi_k(x^i,y^i)-\sum_i\sum_{s \in \mathcal{Y}^m}p(s|x^i;w)\Phi_k(x^i,s) -\lambda w_k\]第一项很容易计算,我们只需要遍历所有样本的所有时刻,把对应的$\phi_k$加起来:
\[\sum_i\Phi_k(x^i,y^i)=\sum_i\sum_{j=1}^m\phi_k(x^i,j,y^i_{j-1},y^i_j)\]第二项比较复杂,因为它需要遍历所有的$\mathcal{Y}^m$,它的大小是$\vert \mathcal{Y} \vert^m$,直接穷举是不可能的。
和Decoding一样,这些路径中包含大量重复的计算,因此可以使用动态规划求解。我们这里只看第i个样本的计算。
\[\begin{split} \sum_{s \in \mathcal{Y}^m}p(s|x^i;w)\Phi_k(x^i,s) \\ & = \sum_{s \in \mathcal{Y}^m}p(s|x^i;w) \sum_{j=1}^m \phi_k(x^i,j,y^i_{j-1},y^i_j) \\ & = \sum_{j=1}^m \sum_{s \in \mathcal{Y}^m}p(s|x^i;w) \phi_k(x^i,j,y^i_{j-1},y^i_j) \\ & = \sum_{j=1}^m \sum_{a \in \mathcal{Y}} \sum_{a \in \mathcal{Y}} \sum_{s \in \mathcal{Y} : s_{j-1}=a, s_j=b} p(s|x^i;w) \phi_k(x^i,j,y^i_{j-1},y^i_j) \\ & = \sum_{j=1}^m \sum_{a \in \mathcal{Y}} \sum_{a \in \mathcal{Y}} \phi_k(x^i,j,y^i_{j-1},y^i_j)\sum_{s \in \mathcal{Y} : s_{j-1}=a, s_j=b} p(s|x^i;w) \\ & = \sum_{j=1}^m \sum_{a \in \mathcal{Y}} \sum_{a \in \mathcal{Y}} \phi_k(x^i,j,y^i_{j-1},y^i_j) q_j^i(a,b) \end{split}\]上面的公式推导比较简单,基本就是使用求和换序。最后一步为了简化,引入了一个记号:
\[q_j^i(a,b)=\sum_{s \in \mathcal{Y} : s_{j-1}=a, s_j=b} p(s|x^i;w)\]$q_j^i(a,b)$表示所有j-1时刻的状态为a并且j时刻为b的路径的概率的和。这个概率可以用类似HMM的前向后向算法来计算:先定义$\alpha,\beta$,然后就可以计算$q_j^i(a,b)$。这里就不详细介绍了。
CRF实战
接下来我们通过使用CRFsuite软件来熟悉CRF的应用,CRFsuite是使用SGD进行训练的一个CRF库。最早流行的CRF软件是Crf++,它使用L-BFGS算法,一次对所有训练数据求梯度因此训练速度较慢。而SGD一次对一个minibatch的数据求梯度,速度会快很多。
这里读者可能会奇怪为什么Crf++不用SGD?其实这和机器学习的发展过程有关。在早期,大家都习惯使用梯度下降,因为理论上它能保证收敛(当然更多的还是一种习惯,而且那个时代机器学习都是在学术界使用,数据量也不大)。但是在实际应用中训练数据太大,对所有数据求一次梯度虽然方向是loss下降最快的,但是速度太慢,而且当数据量达到无法放到内存里是根本无法计算。因此Léon Bottou等人2007年发了关于用SGD算法求解SVM的论文(当然后来也可以用于CRF),实验证明了SGD速度比普通的梯度下降更快,而且在实际问题中效果相当甚至更好,并且从理论上做了分析,保证了随机梯度下降的最终收敛。
现在我们对SGD习以为常,但是在那个年代神经网络并不流行。当时流行的模型比如SVM或者CRF的目标函数最终都可以转化成一个凸函数,凸函数有一个非常好的性质:局部最优解就是全局最优解。从而可以用梯度下降求最优解(当然SVM更流行用SMO算法)。对于神经网络这种“非凸”的目标函数,大家都是心存疑惑的——没有理论保证它能找到全局最优解(即使现在也是)。
在CRFsuite之前,Crf++是最流行的CRF工具,它最大的特点就是提供了模板的方法来定义特征。CRFsuite并不提供,而是需要使用代码自己来生成。这使用起来麻烦一点,但好处是使用者能更加深入的了解CRF到底生成了哪些特征。如果看模板,CRF模型好像没有多少特征,但是一旦展开,那可能几百万甚至上千万。另外的好处就是CRFsuite可以自己随意定义任何特征,而CRF++只能使用模板语法支持的特征,我们只能使用它支持的特征模板。这也是所有软件框架的缺陷——它可能会提供一些便利性,但是会丧失很多灵活性,过度依赖框架就很难理解更底层的原理。因此本书介绍的模型尽量不使用高层框架(比如NMT或者Tensor2Tensor),尽量从最底层来实现。
CRFsuite安装
这里我们使用C++版本的CRFsuite,如果读者想用Python,可以尝试sklearn-crfsuite,它是用Python对crfsuite做的封装。
读者可以去这里下载最新版本的CRFsuite,CRFsuite依赖libLBFGS,作者使用的crfsuite-0.12和liblbfgs-1.10。读者可能会问,既然CRFsuite是SGD算法,为什么还有libLBFGS呢?笔者也不清楚,也许是作者为了实验对比,也许是给读者更多选择?
安装可以参考INSTALL文件,如果是Linux系统,使用标准的命令编译和安装:
cd liblbfgs-1.10
./configure
make
sudo make install
因为需要把so复制到/usr/local/lib下,所以需要root权限,如果没有,那么可以使用:
./configure --prefix=/home/user/liblbfgs-1.10
这样make install的时候就会把so等文件拷贝到指定的位置,不过如果不是标准的位置,程序运行时会找不到so,需要把它加到LD_LIBRARY_PATH里。除此之外也有很多其它的办法,请读者根据自己的操作系统参考网络资料。
接下来用类似的方法编译和安装crfsuite。如果系统找不到liblbfgs.so,那么可能需要sudo ldconfig更新一下。安装后执行”crfsuite -h”检查是否安装成功:
$ crfsuite -h
CRFSuite 0.12 Copyright (c) 2007-2011 Naoaki Okazaki
USAGE: crfsuite <COMMAND> [OPTIONS]
COMMAND Command name to specify the processing
OPTIONS Arguments for the command (optional; command-specific)
COMMAND:
learn Obtain a model from a training set of instances
tag Assign suitable labels to given instances by using a model
dump Output a model in a plain-text format
For the usage of each command, specify -h option in the command argument.
Text chunking任务描述
我们这里使用CRFsuite来做Text chunking任务。Text chunking可以认为是简化版本的parsing(shallow parsing),比如句子“He reckons the current account deficit will narrow to only # 1.8 billion in September.”,它期望的输出是:
[NP He ] [VP reckons ] [NP the current account deficit ] [VP will narrow ] [PP to ] [NP only # 1.8 billion ] [PP in ] [NP September ] .
NP代表名词短语(Noun Phrase)、VP代表动词短语(Verb Phrase)。NP(或者其它部分)可以由很多词组成,比如”the current account deficit”这四个词组成一个大的NP,而”will narrow”组成一个VP。
我们可以把Text chunking的任务转化成序列标注的任务,比如用B-NP表示NP的开始,而I-NP表示NP后续的词。而O表示其它我们不关注的词。比如上面的例子可以这样来标注:
B-NP He
B-VP reckons
B-NP the
I-NP current
I-NP account
I-NP deficit
B-VP will
I-VP narrow
B-PP to
B-NP only
I-NP #
I-NP 1.8
I-NP billion
B-PP in
B-NP September
O .
“the current account deficit”被标注成”B-NP I-NP I-NP I-NP”。这样我们把它转化成了一个序列标注任务。如果我们的模型可以标注每个词的Tag,那么我们就可以找到NP。比如上面的标签序列,我们发现He是B-NP,而它后面的不是I-NP,因此He这个词独立组成一个NP。又比如will是B-VP,而narrow是I-VP,而后面没有I-VP,所以”will narrow”组成一个VP。
注意:并不是所有的标注序列都是“合法”的,比如”B-NP I-VP”。I-VP前面一定要有”B-VP”。“好”的模型不会输出这样的序列,因为它们能学到I-VP前一定是B-VP,但是可能也会出现意外(目前的机器学习都会这样)。如果出现了,就需要后处理一下。
下载数据
原始数据在官方地址,不过好像年久失修了,还好网上有备份,我们使用下面的命令下载数据。
wget https://raw.githubusercontent.com/teropa/nlp/master/resources/corpora/conll2000/train.txt
wget https://raw.githubusercontent.com/teropa/nlp/master/resources/corpora/conll2000/test.txt
下面是这两个文件的格式:
$ less train.txt.gz
... (snip) ...
London JJ B-NP
shares NNS I-NP
closed VBD B-VP
moderately RB B-ADVP
lower JJR I-ADVP
in IN B-PP
thin JJ B-NP
trading NN I-NP
. . O
At IN B-PP
Tokyo NNP B-NP
, , O
the DT B-NP
Nikkei NNP I-NP
index NN I-NP
of IN B-PP
225 CD B-NP
selected VBN I-NP
issues NNS I-NP
was VBD B-VP
up IN B-ADVP
112.16 CD B-NP
points NNS I-NP
to TO B-PP
35486.38 CD B-NP
. . O
... (snip) ...
每个词为一行,第一列是词本身,第二列是词性(已知),第三列是真实的tag。句子结束用一个空行表示。因此如果读者要实际用模型对一个句子进行Chunking的话,首先要对它进行词性标注。
特征生成
传统机器学习最重要的步骤就是提取特征,特征的好坏直接决定效果的好坏。这里使用了19类特征:
w[t-2], w[t-1], w[t], w[t+1], w[t+2]
w[t-1]|w[t], w[t]|w[t+1]
pos[t-2], pos[t-1], pos[t], pos[t+1], pos[t+2]
pos[t-2]|pos[t-1], pos[t-1]|pos[t], pos[t]|pos[t+1], pos[t+1]|pos[t+2],
pos[t-2]|pos[t-1]|pos[t], pos[t-1]|pos[t]|pos[t+1], pos[t]|pos[t+1]|pos[t+2]
w[t]表示当前时刻的词,w[t-2]表示前两个时刻的词。w[t-1]\|w[t]表示前一个词和当前词的组合。pos[t]表示前一个词的词性,而pos[t-2]\|pos[t-1]表示前两个时刻和前一个时刻的词性组合。
注意:这里词的组合特征用的比较少,只有前一个词和当前词以及当前词和下一个词,而词性有很多组合,而且还有3个时刻的组合。为什么这样呢?原因是词性的类别相当较少(比如45),因此泛化能力较强;而词特别多(几万几十万),如果3个词组合结果就太多了,训练数据中很少出现数据系数,从而学到的不是稳定的特征。我们用一个例子来展示实际提取的特征。
He PRP B-NP
reckons VBZ B-VP
t --> the DT B-NP
current JJ I-NP
account NN I-NP
比如现在我们需要计算t时刻的特征$\phi_t(x,t,y_{t-1},y_t)$。提取t时刻的特征可以用到整个输入$x=x_1,…,x_m$,但是只能用到当前和前一个时刻的状态(标签)。CRFsuite实现的是一阶的CRF模型,因此“类似”HMM,特征都是只和当前tag相关的;另外CRFsuite为使用前后状态的组合作为特征。因此CRFsuite可以实现如下的特征:
\[\begin{split} f_1(x,t,y_{t-1},y_t) & =\begin{cases} 1 \; if \; \text{ 当前tag=B-NP and 前一个词|当前词=reckons|the} \\ 0 \; \text{否则} \end{cases} \\ f_2(x,t,y_{t-1},y_t) & =\begin{cases} 1 \; if \; \text{ 当前tag=B-NP and 前一个词性=VBZ} \\ 0 \; \text{否则} \end{cases} \\ f_3(x,t,y_{t-1},y_t) & =\begin{cases} 1 \; if \; \text{ 当前tag=B-NP and 前一个词性=VBZ} \\ 0 \; \text{否则} \end{cases} \\ f_4(x,t,y_{t-1},y_t) & =\begin{cases} 1 \; if \; \text{ 当前tag=B-NP and 前一个tag=B-VP} \\ 0 \; \text{否则} \end{cases} \end{split}\]但是它无法实现这样的特征:
\[\begin{split} f_5(x,t,y_{t-1},y_t)=\begin{cases} 1 if \text{当前tag=B-NP and 前一个tag=B-VP and 当前词=the} \\ 0 \text{否则} \end{cases} \\ \end{split}\]CRFsuite要求的输入格式为:”LABEL
# Unigram
U00:%x[-2,0]
U01:%x[-1,0]
U02:%x[0,0]
U03:%x[1,0]
U04:%x[2,0]
U05:%x[-1,0]/%x[0,0]
# Bigram
B
因此在这一点上CRF++更加灵活,我们可以开启这个特征,也可以不开启;而CRFsuite只能开启。比如下面是特征文件的示例:
$ less train.crfsuite.txt
... (snip) ...
B-NP w[0]=He w[1]=reckons w[2]=the w[0]|w[1]=He|reckons pos[0]=P
RP pos[1]=VBZ pos[2]=DT pos[0]|pos[1]=PRP|VBZ pos[1]|pos[2]=VB
Z|DT pos[0]|pos[1]|pos[2]=PRP|VBZ|DT __BOS__
B-VP w[-1]=He w[0]=reckons w[1]=the w[2]=current w[-1]|w[
0]=He|reckons w[0]|w[1]=reckons|the pos[-1]=PRP pos[0]=VBZ pos[1]=D
T pos[2]=JJ pos[-1]|pos[0]=PRP|VBZ pos[0]|pos[1]=VBZ|DT pos[1]|p
os[2]=DT|JJ pos[-1]|pos[0]|pos[1]=PRP|VBZ|DT pos[0]|pos[1]|pos[2]=VBZ
|DT|JJ
B-NP w[-2]=He w[-1]=reckons w[0]=the w[1]=current w[2]=acc
ount w[-1]|w[0]=reckons|the w[0]|w[1]=the|current pos[-2]=PRP pos[-1]=
VBZ pos[0]=DT pos[1]=JJ pos[2]=NN pos[-2]|pos[-1]=PRP|VBZ
pos[-1]|pos[0]=VBZ|DT pos[0]|pos[1]=DT|JJ pos[1]|pos[2]=JJ|NN pos[-2]|
pos[-1]|pos[0]=PRP|VBZ|DT pos[-1]|pos[0]|pos[1]=VBZ|DT|JJ pos[0]|pos[1]|po
s[2]=DT|JJ|NN
I-NP w[-2]=reckons w[-1]=the w[0]=current w[1]=account w[2]=def
icit w[-1]|w[0]=the|current w[0]|w[1]=current|account pos[-2]=VBZ
pos[-1]=DT pos[0]=JJ pos[1]=NN pos[2]=NN pos[-2]|pos
[-1]=VBZ|DT pos[-1]|pos[0]=DT|JJ pos[0]|pos[1]=JJ|NN pos[1]|pos[2]=NN|NN
pos[-2]|pos[-1]|pos[0]=VBZ|DT|JJ pos[-1]|pos[0]|pos[1]=DT|JJ|NN pos
[0]|pos[1]|pos[2]=JJ|NN|NN
I-NP w[-2]=the w[-1]=current w[0]=account w[1]=deficit w[2]=wil
l w[-1]|w[0]=current|account w[0]|w[1]=account|deficit pos[-2]=
DT pos[-1]=JJ pos[0]=NN pos[1]=NN pos[2]=MD pos[-2]|
pos[-1]=DT|JJ pos[-1]|pos[0]=JJ|NN pos[0]|pos[1]=NN|NN pos[1]|pos[2]=NN
|MD pos[-2]|pos[-1]|pos[0]=DT|JJ|NN pos[-1]|pos[0]|pos[1]=JJ|NN|NN pos[0]|p
os[1]|pos[2]=NN|NN|MD
... (snip) ...
| 我们简单的看一下第一行的前几个特征,”B-NP w[0]=He w[1]=reckons w[2]=the w[0] | w[1]=He | reckons”。 |
w[0]=He表示如果当前词是He并且输出为B-NP的特征,如果这个特征对于的权值(参数)越大,那么模型月倾向于把它tag成B-NP。而”w[0]|w[1]=He|reckons”表示当前词和下一个词是”He,reckons”并且输出为B-NP的特征。注意特征一定要带上当前的tag,比如:
It PRP B-NP
was VBD B-VP
t -> like IN B-PP
a DT B-NP
comedy NN I-NP
of IN B-PP
errors NNS B-NP
在特征文件里有一个特征w[0]=like,表示”当前词是like并且当前输出为B-PP”。而
behind IN B-PP
their PRP$ B-NP
ears NNS I-NP
just RB B-PP
t -> like IN I-PP
traditional JJ B-NP
pencils NNS I-NP
made VBN B-VP
在特征文件里也要w[0]=like,它表示”当前词是like并且当前输出为I-PP”,这和上面不是一个特征!
我们可以使用任何工具来生成,对于CONLL2000的任务,CRFsuite提供了生成特征的Python脚本,因此不需要我们自己来写,用兴趣的读者可以分析怎么生成特征,这在做别的任务时就会有用到。
~/soft/crfsuite-0.12/example$ cat train.txt |./chunking.py > train.crfsuite.txt
~/soft/crfsuite-0.12/example$ cat test.txt |./chunking.py > test.crfsuite.txt
除了上面的模板特征,chunking.py还对句子开通的词和结尾的词分别加了”__BOS__“和”__EOS__“特征。
CRFsuite的特征没有任何要求,只要是一个字符串就行,它会把相同的字符串映射到一个唯一的整数。我们习惯的”w[0]=like”只是为了让人好读而已,如果我们把所有的这个特征(字符串)替换成”xxxyyy”,CRFsuite不会觉得有什么不同(也许会映射到不同的整数ID而已)。
训练
crfsuite learn -m CoNLL2000.model train.crfsuite.txt
如果要用一边训练一边用测试数据进行验证
crfsuite learn -e2 train.crfsuite.txt test.crfsuite.txt
测试
crfsuite tag -m CoNLL2000.model test.crfsuite.txt
上面的命令会输出每一行(一个词)对于的tag,如果只想评估最终的效果,可以使用:
crfsuite tag -qt -m CoNLL2000.model test.crfsuite.txt
结果为:
$ crfsuite tag -qt -m CoNLL2000.model test.crfsuite.txt
Performance by label (#match, #model, #ref) (precision, recall, F1):
B-NP: (12000, 12359, 12407) (0.9710, 0.9672, 0.9691)
B-PP: (4707, 4872, 4805) (0.9661, 0.9796, 0.9728)
I-NP: (13982, 14482, 14359) (0.9655, 0.9737, 0.9696)
B-VP: (4466, 4662, 4653) (0.9580, 0.9598, 0.9589)
I-VP: (2549, 2698, 2643) (0.9448, 0.9644, 0.9545)
B-SBAR: (448, 498, 534) (0.8996, 0.8390, 0.8682)
O: (5939, 6114, 6174) (0.9714, 0.9619, 0.9666)
B-ADJP: (322, 403, 438) (0.7990, 0.7352, 0.7658)
B-ADVP: (711, 835, 866) (0.8515, 0.8210, 0.8360)
I-ADVP: (54, 82, 89) (0.6585, 0.6067, 0.6316)
I-ADJP: (110, 137, 167) (0.8029, 0.6587, 0.7237)
I-SBAR: (2, 15, 4) (0.1333, 0.5000, 0.2105)
I-PP: (34, 42, 48) (0.8095, 0.7083, 0.7556)
B-PRT: (80, 102, 106) (0.7843, 0.7547, 0.7692)
B-LST: (0, 0, 4) (0.0000, 0.0000, 0.0000)
B-INTJ: (1, 1, 2) (1.0000, 0.5000, 0.6667)
I-INTJ: (0, 0, 0) (******, ******, ******)
B-CONJP: (5, 7, 9) (0.7143, 0.5556, 0.6250)
I-CONJP: (10, 12, 13) (0.8333, 0.7692, 0.8000)
I-PRT: (0, 0, 0) (******, ******, ******)
B-UCP: (0, 0, 0) (******, ******, ******)
I-UCP: (0, 0, 0) (******, ******, ******)
Macro-average precision, recall, F1: (0.639228, 0.602505, 0.611077)
Item accuracy: 45420 / 47321 (0.9598)
Instance accuracy: 1175 / 2011 (0.5843)
Elapsed time: 0.360145 [sec] (5586.6 [instance/sec])
CRF的缺点
CRF的缺点其实就是传统机器学习的缺点——需要人工提取特征,而特征都是one-hot的,从而泛化能力弱。比如CRF有如下的特征w[0]=China,如果训练数据中China很多但是Japan很少,那么在预测China可能比较准确,但是Japan可能就不准,词在传统机器学习里就是最小的单位(可能会有前后缀)。而使用Embedding的深度学习的最小单位不是词而是更底层的(潜)语义,而且Embedding是根据任务学习出来的,因而泛化能力更强。
- 显示Disqus评论(需要科学上网)