基于HMM的语音识别系统中最复杂的是解码器,它需要融合来自声学模型、发音词典和语言模型的信息,在巨大的搜索空间里寻找最优的路径。WFST提供了统一的框架,能够用统一的方式表示这些模型并且融合起来,从而可以达到很快的搜索速度。本文介绍WFST的基本概念以及它在语音识别中的应用。更多文章请点击深度学习理论与实战:提高篇。
目录
在介绍加权有限状态转换器(Weighted Finite State Transducer, WFST)的概念之前,我们首先介绍有穷自动机(有限状态自动机)。
有穷自动机(FA)
自动机(automaton,复数是Automata)来源于希腊单词”αὐτόματα”,它表示一个根据预先设置的指令序列自动执行的机器。一个包含有限个状态的自动机就叫作有穷自动机(Finite Automaton)或者有限状态机(Finite State Machine)。
确定有穷自动机(Deterministic Finite Automaton, DFA)
一个确定有穷自动机由一个五元组$(Q, \Sigma, \delta, q_0, F)$表示,其中:
- Q是一个有限的状态集合
- $\Sigma$是字母表
- $\delta$是状态转移函数:$\delta: Q \times \Sigma \to Q$
- $q_0$是初始状态,$q_0 \in Q$
- F是终止状态的集合,$F \subseteq Q$
字母表(Alphabeta)是任意有限符号的集合,比如$\Sigma=\{a,b,c,d\}$就是一个字母表,它包含符号”a”,”b”,”c”,”d”。字符串(String)是由字母表中的字符组成的串。比如”cabcad”就是$\Sigma=\{a,b,c,d\}$上的一个合法字符串,而”abf”则不是,因为”f”不是字母表中的符号。字符串中符号的个数叫作字符串的长度,比如字符串”cabcad”的长度是6。长度为0的字符串叫作空字符串,一般记作$\lambda$或者$\epsilon$。两个字符串的拼接(concatenation)就是把两个字符串的字符按照顺序拼接起来。
$\Sigma_i$表示字母表$\Sigma$上所有长度为i的字符串的集合。比如$\Sigma=\{a,b\}$,那么$\Sigma_1=\{a,b\}$,$\Sigma_2=\{aa, ab, ba, bb\}$,而$\Sigma_0=\{\lambda\}$。Kleene Star是定义在字母表上的一个一元操作,它是字母表上所有字符串的集合。\(\Sigma^*=\Sigma_0 \cup \Sigma_1 ...\)。如果$\Sigma=\{a,b\}$,那么\(\Sigma^{*} = \{ \lambda, a, b, aa, ab, ba, bb, ... \}\)。而Kleene Plus操作和Keene Star类似,只是它不包含空字符串。
一个语言(Language)是\(\Sigma^*\)的一个子集,比如$\Sigma=\{a,b\}$上所有长度为2的字符串就构成了一个语言$L=\{aa, ab, ba, bb\}$。
我们可以用一个图来表示一个状态机,其中:
- 点代表状态
- 边代表状态之间的跳转,边上的字符代表跳转的输入
- 我们在初始状态所在的点上画一条入边来表示它是初始状态
- 终止状态用两个圈表示
比如我们有一个状态机:
- $Q=\{a,b,c\}$
- $\Sigma=\{0,1\}$
- $q_0=a$
- $F=\{c\}$
它对应的状态转移表如下表:
| 状态/输入 | 0 | 1 |
|---|---|---|
| a | a | b |
| b | c | a |
| c | b | c |
- 表:示例DFA的转移函数
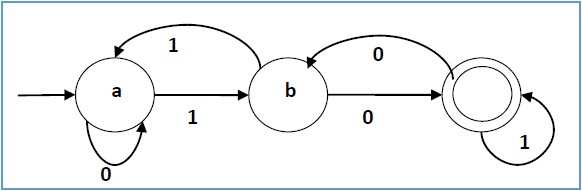
下图是一个DFA的图形表示。
一个DFA识别的语言定义为这样的字符串——从初始状态根据字符串的字符来跳转,最终把字符串“消费”完成后停止在终止状态。给定一个DFA和一个字符串,我们可以这样来判断:首先状态机的状态是初始状态,然后根据字符串的第一个字符跳转到第二个状态,然后根据第二个字符串跳转到第三状态,…,根据最后所有的字符都处理完成后的状态机所在的状态来判断状态机是否“接受”这个字符串——如果是终止状态就接受,否则拒绝。
根据上面的方法,理论上我们可以这样得到状态机识别的语言:变量所有可能的字符串,然后用上面的方法判断这个字符串是否被DFA接受,接受的话加到识别的集合里。当然实际我们无法这样操作(或者通常也不需要列举出某个DFA识别的所有字符串,因为通常DFA识别的字符串是无穷的)。
比如字符串”1101011”是上面DFA识别语言中的一个字符串,而”100”不是。读者可以思考一下这个自动机表示的语言到底包含(不包含)哪些字符串。
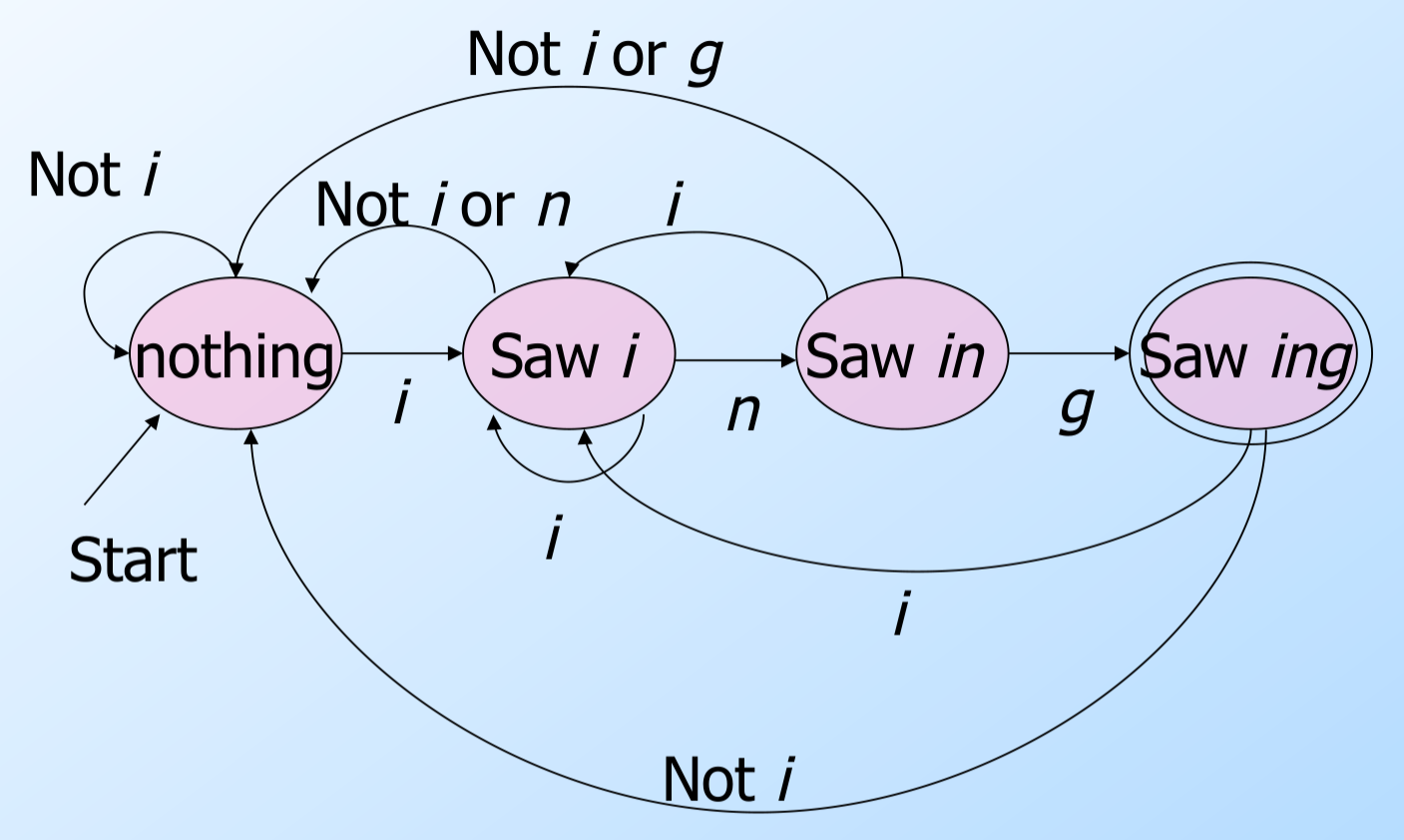
因此DFA的一个用途可以是“识别”一种语言——也就是判断一个字符串是否属于这个语言。可以证明,任何正则表达式描述的语言都可以找到一个等价的DFA,反之亦然。比如图\ref{fig:dfa_ing}的DFA可以识别以”ing”结尾的字符串。请读者验证一下它确实可以(且仅可以)识别”ing”结尾的字符串。然后我们再来思考一下如果我们自己来设计一个DFA来识别”ing”应该怎么做?
我们来分析一下为什么这个DFA可以识别”ing”结尾的字符串。首先它初始化状态是”nothing”表示没有识别到”ing”的任何部分。而这个状态如果遇到”i”,那么就会进入”Saw i”(见到i)的状态;如果它遇到非i的字符,仍然处于”nothing”状态。在”Saw i”的状态遇到n会进入”Saw n”的状态;遇到i那么还是状态不变;而遇到i和n之外的其它字符都是跳到”nothing”的状态。而在”Saw n”的状态遇到g就进入”Saw ing”的状态,这个状态是一个终止状态;如果遇到i它会跳到”Saw i”的状态;遇到其它字符就好跳到”nothing”状态。注意在”Saw n”状态遇到n还是跳到”nothing”,比如字符串doinn,在第二个n的时候说明前面的in不可能是ing了,所以必须回到”nothing”状态从新搜索”ing”。在”Saw ing”的终止状态如果遇到了i,那么还是进入”Saw i”的状态,否则就回到”nothing”状态。
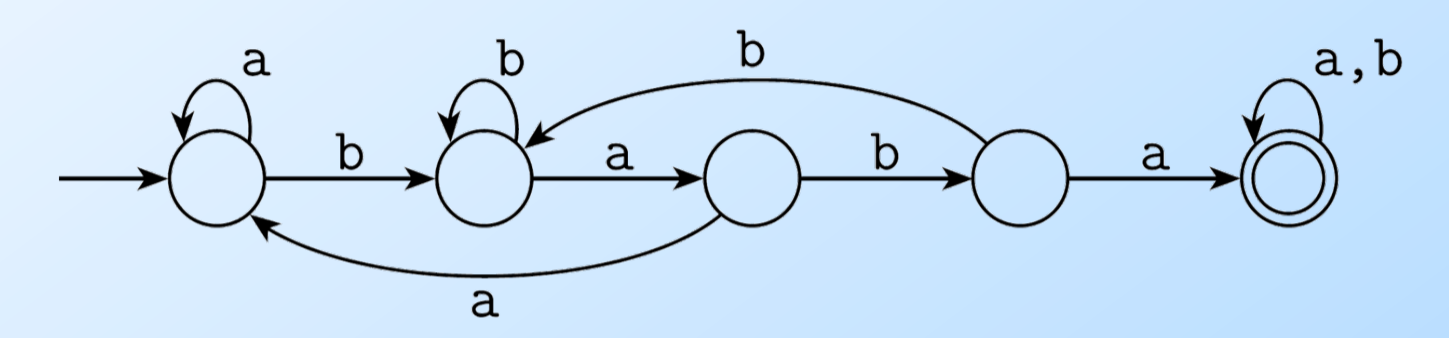
我们再来看一个DFA,如下图所示,它识别包含baba的字符串。
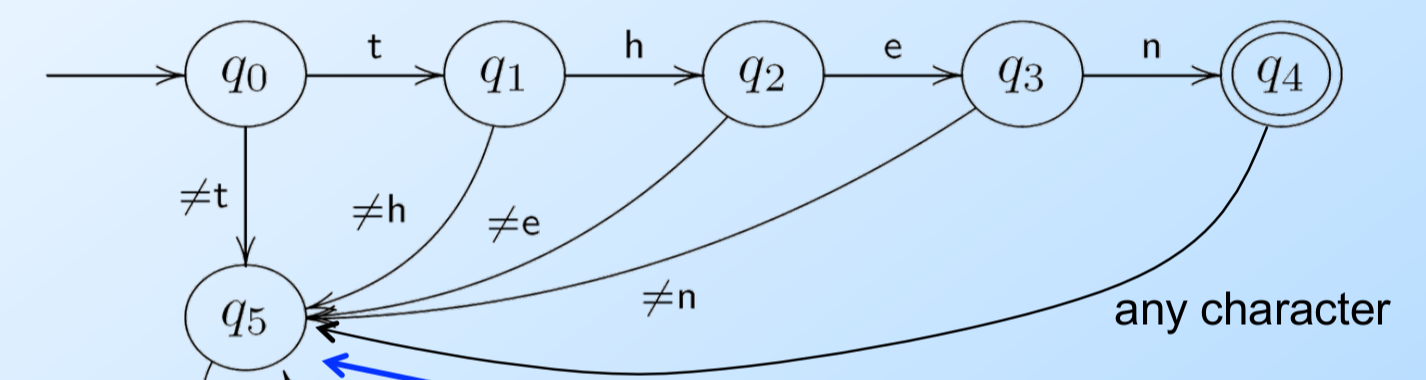
DFA的每一个状态在遇到一个字符的时候有且只有一条边跳到另一个状态(或者跳到自己),这样的FA是确定的。如果字母表的大小是N,那么每个点出发的边一定也是N。为了简化,我们通常假设有一个“死”的状态,它不是终止状态,并且进入这个状态后遇到任何输入都是跳转到自己上。如下图所示,我们的DFA只识别”then”这个字符串,因此第一个状态只有遇到t会跳到下一个状态,其它非t的输入都会跳转到“死”状态。为了简化,我们通常可以把死状态以及跳到死状态的边去掉。这样如果DFA在某个状态遇到某个输入无法跳转(没有边可以走)就认为它进入“死”状态了。
非确定有穷自动机(Non-deterministic Finite Automaton/NFA)
DFA每个状态遇到任何一个输入有且仅有一个跳转(边),我们可以对DFA进行扩展,使得一个状态遇到一个输入可以(当然不一定)有多余一条边。那这就带来一个问题:状态机执行的时候有多条边到底跳到哪个状态呢?答案是多条边都“同时”跳转,有点像状态机的“分裂”,原来只有一个状态机,现在遇到某个输入有多个跳转,一个状态机就“分裂”成多个状态机,然后到下一个输入的时候同时执行多个状态机,当然往后也可能继续“分裂”。当然某些分裂的状态机会遇到不能跳转的情况(进入死状态),我们就认为它“死”掉了。最后字符串的字符都消费完了之后,如果至少一个分裂的状态机停止在终止状态,那么我们就认为这个状态机接受这个字符串,否则不接受。
这样看起来,NFA是“包含”DFA的,或者说DFA是一种特殊的NFA,它的每个状态在遇到一个输入字符是有且只有一条边。因此DFA描述的语言是包含在NFA里的。或者更加正式的说法是:任意给定一个DFA,我们可以构造一个NFA,这个NFA识别的语言是和DFA相同的(语言是一个集合,语言相同就是集合相同的意思,通常我们证明两个集合A和B相同的方法是证明$A \subseteq B$并且$B \subseteq A$)。这是很显然的,我们构造一个和这个DFA一模一样的另外一个DFA,然后把它“叫作”NFA就行了。
但是是否存在一个NFA,我们没有办法构造出一个与之等价的DFA呢?从直觉上似乎应该存在,因为看起来NFA的描述能力更强。不过这个直觉是错误的,虽然NFA看起来更强大,但是对于任意一个NFA,我们都可以构造出一个与之等价的DFA来,下面的章节会介绍怎么构造,我们这里先承认这个结论就行了。这就有个问题:既然NFA不比DFA强大,那么我们研究它还有什么用处吗?答案是:为了识别某种语言,NFA更容易构造出来。我们用一个例子来说明这一点。
比如假设字母表是\(\Sigma=\{0,1\}\),我们需要识别一种语言$L=\{w| w的最后一个字符是1\}$。这看起来是个很简单的语言,我们尝试用DFA来识别它。读者可以拿出纸笔来试一试。
如图是一个可以识别这个语言的一个DFA,请读者验证其正确性。我们可以发现,如果给了我们一个DFA,然后我们来验证,就会很容易的发现:“哦,确实这个DFA可以识别这个语言/字符串”。但是让我们来想(构造)出一个识别这个语言的DFA就会觉得很难。但是NFA却不是这样,有了一些经验之后,我们会发现设计一个NFA很容易,甚至我们可以把构造的过程变成固定的“流程”,这意味着可以用程序来构造NFA。当然并不是所有的语言都可以用NFA/DFA来识别,后面我们会介绍正则表达式,任何一个正则表达式都可以很容易的构造出一个等价的NFA来。注意我们在很多语言或者工具里提供的正则表达式很多都不是“真正”的正则表达式,它们加了很多“扩展”从而导致它们的表达能力更强,但是它们表达的语言无法用DFA/NFA来识别,比如back reference。
下面我们来“设计”一个NFA识别倒数第3个字符是1的字符串的语言。如下图所示,我们首先有个$q_0$状态,它遇到1就跳到$q_1$状态,这表示它是倒数第3个位置,然后不管输入是0还是1都跳到$q_2$——倒数第二个位置。然后不管输入是什么,$q_2$都跳到$q_3$——被接受的最后一个字符。为什么它就能够识别倒数第3个是1的字符串呢?
我们来分析一下,开始我们在状态$q_0$,如果遇到0,那么它还是在这个状态。如果遇到1,它既可以留着状态$q_0$,也可以跳到状态$q_1$。状态$q_1$是我们“猜测”的可能的倒数第三个位置(但是我们现在不可能知道后面还有几个字符,我们只是猜测有这种可能),如果我们没猜对呢?也没关系,还有一个“分裂”的状态机在状态$q_0$。如果运气好猜对了,那么后面不过输入什么我们都跳到$q_2$,再不过输入是什么我们都跳到$q_3$,然后结束(因为我们猜对了,所以$q_1$后面有且仅有两个字符)。
我们用一个例子来验证一下。比如”010101”是L中的一个字符串,因为倒数第3个字符是1。NFA的分裂过程如下表所示:
| 时刻/状态 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 输入字符 | 0 | 1 | 0 | 1 | 0 | 1 |
| $q_0$ | $q_0$ | $q_1$ | $q_2$ | $q_3$ | X(dead) | X |
| $q_0$ | $q_0$ | $q_1$ | $q_2$ | $q_3$(accepted) | ||
| $q_0$ | $q_0$ | $q_1$ | ||||
| $q_1$ |
我们可以发现,在时刻2(遇到第一个1),NFA猜测了一次它是倒数第三个字符(分裂了一次),但是到第5个时刻发现不是(因为这个时候它至少是倒数第4个字符了)。在时刻4又猜测了一次,这次运气很好猜对了。在时刻6又猜测了一次,结果没有猜对,因为它是最后一个1,后面没有别的字符了。
通过子集构造把NFA转换成DFA
我们这里介绍把NFA转换成DFA的子集构造法,我们只介绍怎么使用这个算法,不会证明这种方法构造出来的DFA和NFA是等价的,有兴趣的读者可以找一些形式语言与自动机的资料(可能有些编译原理课程也会介绍)。
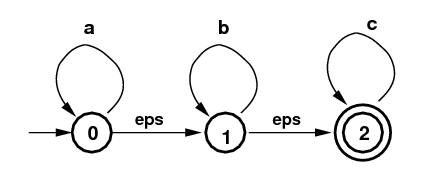
子集构造的核心概念是$\epsilon$-闭包($\epsilon-closure$)算法。比如下图所示的NFA,它可以识别的语言是”a*b*c*“(请读者验证)。$\epsilon$-闭包算法的输入是一个NFA的状态集合,比如{1},它的输出也是一个状态集合,其中输出集合的每一个状态都是可以从输入状态经过全是$\epsilon$的边跳转到这个状态。因此如果输入是{1},那么它的$\epsilon$-闭包是集合{1,2},因为1可以通过空跳转到自己,而1也可以通$\epsilon$跳转到2。类似的输入{0}的$\epsilon$-闭包是集合{0,1,2},因为0可以通过$\epsilon$跳转到1,而1又可能通过$\epsilon$跳转到2。
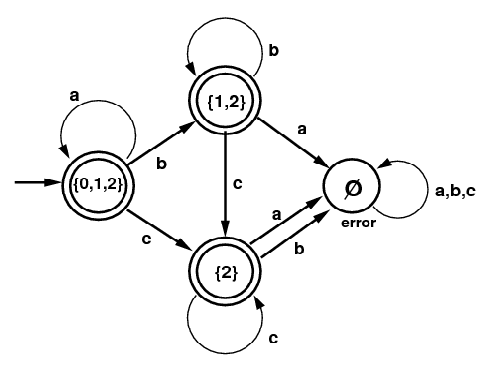
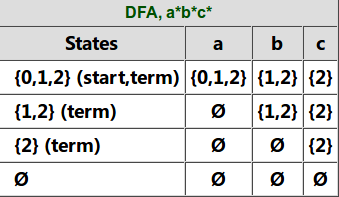
子集构造的过程如下图所示。NFA的初始状态是0,我们首先得到它的$\epsilon$-闭包{0,1,2},我们把它作为DFA的一个状态,因为它包含NFA的初始状态0,因此它也是DFA的初始状态;同时它包含NFA的终止状态2,因此它也是DFA的终止状态。
接着我们看DFA的状态{0,1,2}输入字母a的情况,状态0输入a还是0,而状态1和2不能输入a,因此{0,1,2}输入a可以得到0,而0的$\epsilon$-闭包是{0,1,2},因此{0,1,2} -a->{0,1,2}。再看{0,1,2}输入b的情况,0和2不能输入b,只有状态1遇到b后还是状态1,因此{0,1,2}遇到b的”直接”输出是{1},而{1}的$\epsilon$-闭包是{1,2},因此最终{0,1,2}-b->{1,2}。类似的,我们可以得到{0,1,2}-c->{2}。
这个时候的状态除了{0,1,2}又多了{1,2}和{2},我们再来看第二行状态{1,2}的跳转。首先是{1,2}输入a,跳不到任何状态,因此输出是空集$\emptyset$,空集的$\epsilon$-闭包还是空集。然后是{1,2}输入b,2遇到b没有,1遇到b还是1,然后1的$\epsilon$-闭包是{1,2},因此{1,2}-b->{1,2}。后面的过程都是类似的,当处理完空集后没有产生任何新的状态,因此整个过程结束。
DFA的Minimization
给定一个DFA A,存在一个”最小的”DFA min(A),这个DFA的状态数是所有与A等价的DFA中最小的。DFA最小化之后可以进一步压缩空间和提高识别速度,我们这里就不介绍具体的算法了。有兴趣的读者可以参考wiki或者其它资料。
加权有限状态转换器(WFST)
传统的语音识别模型的组件比如HMM、发音词典、语言模型等都可以用WFST来表示。FST与FSA相比每条边多了一个输出字符串,这样FST可以看成一个关系,把输入字符串映射成另外一个字符串(可能完全不同的字母表)输出出来。而WFST在FST的基础上每条边以及结束状态上有一个权重,从而每一个可接受输入字符串都对应一条路径,路径上的权重以及终止状态(可接受的字符串最终要走到终止状态)的权重通过某个运算整合起来(最常见的比如加起来)就是输入字符串对应的权重。在语音识别里权重通常用来表示概率,但WFST的理论其实不要求它有什么具体意义。
注意:WFST定义了一种关系而不是一个函数。给定一个输入(字符串),函数只有一个唯一确定的输出(字符串);而关系不同,给定一个输入(字符串),可以有多个输出(字符串)
基本概念
加权的接受器(Weighted Acceptors)
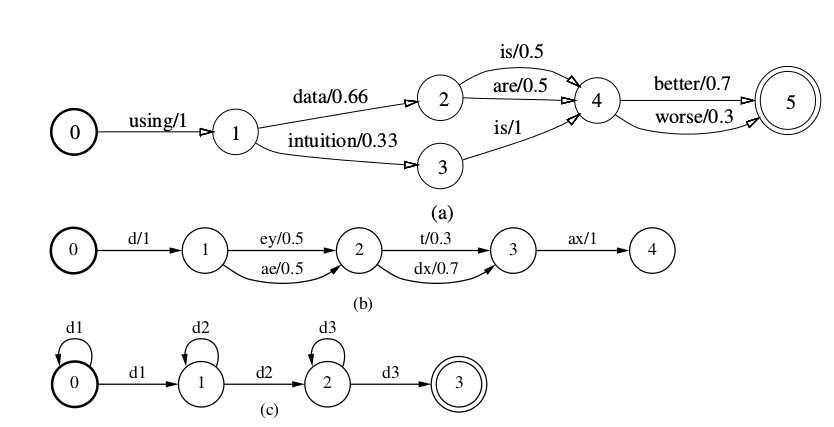
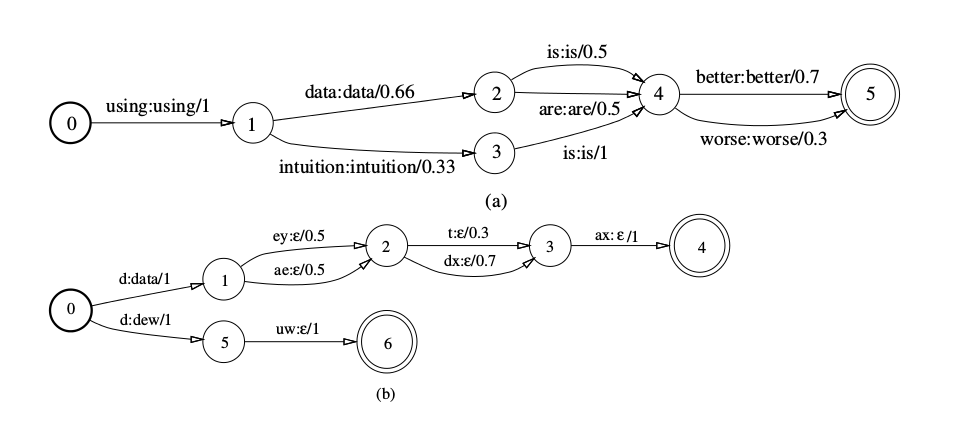
WFSA在FSA的基础上输出一个权重,下图是在语音识别中使用WFSA的几个例子。下图(a)是语言模型的例子,下图(b)是发音词典,而下图(c)是一个音子的HMM,每个音子都三状态从左到右的HMM,因此它可以接受”d1+ d2+ d3+”,+表示出现一次或者多次。
我们这里不用形式化的定义,而用自然语言来描述:一个WFSA有很多状态,有一个初始状态(图中一般话成粗的圆圈),一个或者多个终止状态。边表示状态的跳转,除了对应的起点和终点,边上还有一个原标签(source label,也叫输入标签)和一个权值(weight)。我们可以把WFSA看作一个Python的dict:string->double,输入一个字符串,首先可以告诉你这个字符串是否在在dict里(WFSA是否接受这个字符串),如果在dict里,还可以知道它对于的权值。
加权的转换器(Weighted Transducers)
在语音识别中我们通常使用WFST,因为我们通常需要把语言模型和发音词典“融合”起来使用。WFST和WFSA类似,只是边上除了输入标签之外还多了一个输出标签。在下图中,(a)是语言模型的WFST,和WFSA基本一样,输入和输出字符串一模一样,因为语言模型是最终的输出,所以我们这样来构造。而(b)是发音词典的WFST,输入是因子,输入是单词。注意这个WFST不是确定的,因此我们看到输入”d”的时候,两条边都要尝试,如果接下来我们输入的是”uw”,则输出”dew”+”eps”=”dew”。后面我们会讲到WFST的确定化(Determinization),确定的WFST在每个状态的每个输入字母最多只有一条边,这样识别就会非常简单(和NFA->DFA的确定化类似)。我们可以把图(c)也扩展成WFST,其中输入是音子的id,输出就是pdf-id。因此WFST可以看成输入和输出的二元关系(注意它不是函数,因为一个输入可能有多条路径从而对应多个输出,如果对抽象代数不了解的读者可以忽略这些形式化的术语,简单来说就是给定一个输入字符串,WFST可以输出0个或者多个)。
下面介绍WFST的常见运算(Operation)。
复合(Composition)操作
复合操作用来把两个不同层级的WFST“整合”成一个WFST。比如发音词典会告诉我们一个单词对应的因子,因此我们可以构造一个WFST L来把因子的序列转换成单词的序列以及对应的概率,如上图(b)所示。此外我们有一个文法(或者统计语言模型)告诉我们单词序列概率,我们也可以构造一个G来表示这个文法或者统计语言模型,如上图(a)所示,不过G的特点是输入和输出是一样的,我们其实只关系其权值(概率),这样我们通过复合操作$L \circ G$来得到一个新的WFST,它的输入是一个因子的序列,输出是(所有)单词序列及其对于概率。
我们下面来非形式化的定义复合操作$T_1 \circ T_2$:如果在$T_1$中有一条路径把输入字符串u映射到输出字符串w,并且在$T_2$中有一条路径把输入字符串从w映射成v,那么在$T_1 \circ T_2$中就存在一条路径把输入字符串u映射到v,而且其权值是$T_1$映射的权值与$T_2$映射的权值计算出来的,如果我们认为权值是概率,那么这个操作通常就是乘法,如果是log之后的概率,那么操作就是加法。当然这是对于语音识别任务来说的,从数学上来讲,任何二元操作(函数)都是可以的,只要它和路径权值的计算那个操作可以构成一个半环(semiring)即可。这里稍微有一些抽象代数的群环域知识,计算机专业课程离散数学也会有介绍,不了解的读者可以忽略,不影响继续阅读。
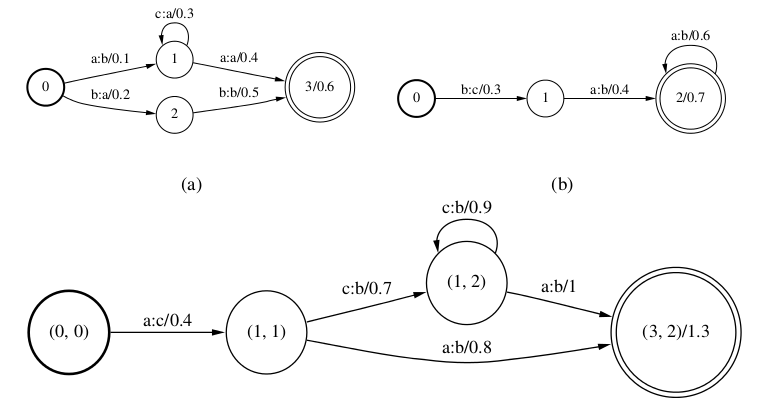
我们来看一个复合操作的例子,参考下图请读者自己动手做一做简单的练习,这个图是把a和b的WFST复合成c的WFST为了简单,我们把图a、图b和图c的WFST叫做A,B,C。首先我们构造C的状态,理论上A的每一个状态和B的每一个状态都可以组成一个C中的状态,比如A有4个状态,B有3个状态,那么C就有$4 \times 3 = 12$个状态,但是因为很多状态都不能从初始化状态走达,其实也就没有意义存在,所以实际我们可以从初始化状态开始,需要的时候才增加c的状态(lazy)。
因此我们第一步把A的初始状态0和B的初始状态0“复合”成C的初始状态(0,0)。在A中0 -a:b/0.1-> 1,而在B中有0 -b:c/0.3 -> 1,因此在C中有 (0,0) -a:c/0.4->(1,1)。同理,在A中有1 -c:a/0.3 -> 1,在B中有1 -a:b/0.4 -> 2,因此在C中有(1,1) -c:b/0.7 -> (1,2)。其它的边请读者一一验证。因为3是A的终止状态(之一),2是B的终止状态(之一),因此(3,2)是C的终止状态(之一)。(3,2)的权值是1.3是1的权值0.6加上2的权值0.7。
最后,我们来验证一些复合操作的效果。我们可以发现WFST A中会有映射 aca:baa/1.4(1.4=0.1+0.3+0.4+0.6),B中有baa:cbb/2,而在C中确实有aca:cbb/3.4。
确定化(Determinization)操作
前面说了,如果WFST有$\epsilon$空转移的边,或者从一个状态遇到一个字母会有两条及其以上的边,那么它就是非确定的。非确定的WFST/WFSA/FSA相比于确定的WFST/WFSA/FSA会更加难于判定某个字符串是否是它可以接受的。确定化的算法就是把一个非确定的WFST转换成等价的确定的WFST的算法。两个WFST等价的定义是:如果第一个WFST接受输入x并且可以把它映射成y且权重是w,那么第二个WFST也一定接受输入x并且能把它映射成y,权重也是w;反之亦然。
我们可以采样类似FSA/FST的子集构造(subset construction)方法来实现从非确定性WFST到等价确定WFST的转换,但是和FSA/FST不同,并不是所有的非确定的WFST都可以转换成一个等价的确定的WFST,不过还好,对于语音识别来说,大部分WFST都是可以的,某些即使不可以,我们有可以通过一些简单的变化使得它可以。后面会介绍这些技巧。
为了消除冗余的路径,我们需要一个操作(operation)合并相同标签(label)的路径的权值。如果每条路径都代表不同的一个事件,而路径的权值表示事件的概率,那么操作就是加法。而如果我们只保留最可能的路径,那么操作就是max函数,这就叫viterbi近似(viterbi approximation)。如果权值表示概率的负log(-log(prob)),那么加法就要变成log加法,而max就要变成min函数。一般情况,我们用符号$\bigotimes$表示计算路径权值的操作(怎么把边的权值整合成路径的权值),而用符号$\bigoplus$来合并相同路径的权值。常见的$\bigoplus 和 \bigotimes$组合包括$(max,+),(+,*),(min,+),(-log(e^{-x}+e^{-y}),+)$。在语音识别中,前两个的权值表示概率,后两个表示概率的负log值。后面我们会看到操作并不限于这些,只有它们能构成半环即可。$(min,+),(-log(e^{-x}+e^{-y}),+)$分别叫做热带半环(tropical semiring)和log半环。热带半环这个名字听起来有些奇怪,真实原因是发现这个半环的数学家来自巴西,巴西是个热带国家,因此就叫做热带半环了。。。
普通的NFA可以通过前面我们介绍过的子集构造来变成确定性的DFA,给定输入字符串,所有可以从初始状态消费掉这个字符串后到达的状态都放到一个集合里组成一个新的状态。但是在WFST/WFSA里,相同的输入字符串可能有多条不同权重的路径,我们也会把最终到达的状态合并成一个,边则采用最短的那条。但是我们还是需要把那些较长的变多余的weight记录下来。
如下图所示,左图是一个非确定的WFSA,而右图是与之等级的确定的WFSA。
从状态0出发输入a后可以进入1和2两个状态,路径的weight分别是1和2,我们可以把状态1和2合并成一个状态<1,2>,但是状态0到状态<1,2>的weight是最短的1,然后我们在合并后的状态<1,2>里记录剩下的(remaining)的权重,记为<(1,0), (2,1)>。它的意思是进入状态1之后剩下的权重就是0了,而如果进入的是状态2,那么剩余的权重是1。接下来我们发现左图状态1和2都可以进入状态3,1->3的权重是5,2->3的权重是6,因此合并后的状态<(1,0), (2,1)>可以进入状态<(3,0)>。1->3的权重是5,而1的剩余权重是0,所以最终权重是5+0=5;而2->3的权重是6,2的剩余权重是1,因此最终的权重是6+1=7。
最小化(Minimization)操作
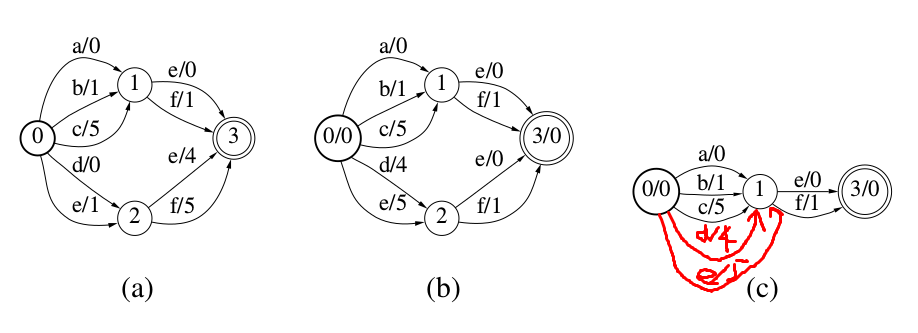
和DFA一样,WFST也可以通过Minimiaztion来进一步压缩空间和提高识别速度。通过把label和weight对(a, w)都看成字符串,我们可以把一个加权的FST/FSA看成一个普通的FST/FSA。比如下图(a)中,我们可以把”a/0”看成一个普通的label,然后使用普通的FSA的Minimization算法。
但是图(a)所示的WFST如果通过上面的方法进行Minimization之后仍然不变,因为所有的label都是不同的。但是我们可以通过weight pushing的方法进一步Minimization。
如下图(b)所示,我们可以把(a)的WFST的weight 往前pushing。我们把e/4和f/5的weight往前pushing到d/0和e/1中,这样状态1和2就可以合并成一个了,如图(c)所示。
weight pushing是一种特殊的reweighting,我们下面用tropical 半环为例来说明reweighting,其它半环是类似的。关于半环(semi-ring)后面会有介绍,读者暂时不用管它。
一个WFSA可以有无穷多种reweighting的方式而且保证reweighting之后的WFSA是等价的。为什么有无穷多种呢?比如i是WFSA A的初始状态,f是A的终止状态(因为任何一个WFSA有一个等价的WFSA,这个WFSA只有一个终止状态)。函数$V: Q \rightarrow \mathbb{R}$是一个势(potential)函数,它把状态映射成一个数值。假设t是一个跳转(边),w[t]是它的weight,p[t]是边的起点,n[t]是边的终点。那么我们可以把原理的w[t]通过势函数修改为:
\[w[t] \leftarrow w[t] + (V(n[t]) - V(p[t]))\]同时把终止状态的weight改成: \(\rho[f] \leftarrow \rho[f] + (V(i) - V(f))\)
如果我们考虑一条从初始状态i到终止状态f的路径:
\[i \overset{t_1}{\rightarrow} v_1 \overset{t_2}{\rightarrow} v_2 \overset{t_3}{\rightarrow} f\]原来的weight是:
\[\rho[i] + w[t_1] + w[t_2] + w[t_3] + \rho[f]\]而reweighting之后为:
\[\begin{split} & \rho[i] + w[t_1] +(V(v_1)-V(i) + w[t_2] +(V(v_2)-V(v_1)) + \\ & \;\;\;\;\;\;\;\;\;\; w[t_3]+(V(f)-V(v_2)) + \rho[f] +(V(i) -V(f)) \\ & = \rho[i] + w[t_1] + w[t_2] + w[t_3] + \rho[f] +[V(v_1)-V(i)+V(v_2)-V(v_1)+V(f)-V(v_2)+V(i)-V(f)] \\ & = \rho[i] + w[t_1] + w[t_2] + w[t_3] + \rho[f] \end{split}\]算法实现
WFST的Composition、Determinization和Minimization的具体算法这里就不详细介绍,有兴趣的读者可以阅读Speech Recognition with Weighted Finite State Transducers等相关论文。我们通常也不需要自己实现这些算法,OpenFst等开源库提供了高效的实现,而语音识别工具Kaldi更是对OpenFst进行了封装,使得它更加适合语音识别的任务。
半环和WFST的形式化定义
前面通过非形式化的方式介绍了WFST,下面我们形式化的定义WFST,但是先要了解一下半环的概念。这是属于抽象代数(计算机的离散数学课程可能会介绍),不感兴趣的读者可以跳过。
之前提到过,WFST的路径上的权值需要通过两个操作“整合”起来,这两个操作在权重(实数集合)上就构成了一个半环(semiring),我们我们来正式的定义半环。
半环是一个五元组$(\mathbb{K}, \bigoplus, \bigotimes, \bar{0}, \bar{1})$,其中$\mathbb{K}$是一个集合,比如实数集合$\mathbb{R}$,$\bigoplus$和$\bigotimes$是定义在$\mathbb{K}$上的二元函数,分别叫做“加法”和“乘法”,注意这个两个函数不(一定就)是我们学过的加法和乘法,但是它和实数集上的加法以及乘法有类似的结构,所以我们把它们也叫做加法和乘法,但是记号上用一个圈区别一下。$\bar{0}$和$\bar{1}$是属于$\mathbb{K}$的两个特殊元素,分别叫做加法单位元和乘法单位元,因为它们和实数中的0和1有类似的性质,因此也叫零元和幺元。如果满足如下条件,那么这个五元组就是一个半环:
-
加法满足交换律和结合律
也就是$\forall x,y\;$,有:
\[x \bigoplus y = y \bigoplus x\] \[(x \bigoplus y) \bigoplus z = x \bigoplus (y \bigoplus z)\] -
零元加任何元素不变
\[\bar{0} \bigoplus x =x \bigoplus \bar{0} =x\] -
乘法满足结合律和对加法的分配率
\[(x \bigotimes y) \bigotimes z = x \bigotimes (y \bigotimes z)\] \[(x \bigoplus y) \bigotimes z= x \bigotimes z \bigoplus y \bigotimes z\] \[x \bigotimes (y \bigoplus z)= x \bigotimes y \bigoplus x \bigotimes z\] -
零元乘以数也不变
\[\bar{1} \bigotimes x=x \bigotimes \bar{1}=x\] -
零元乘以任何数等于零(吸收律)
\[\bar{0} \bigotimes x =x \bigotimes \bar{0} = \bar{0}\]
如果乘法满足交换律,那么这个半环叫交换半环。我们之后讨论的半环都是交换半环。 实数上的加法和乘法是个半环,不过我们这里用不到,下面介绍几个WFST里可能用到的半环:
| 名称 | 集合 | $\bigoplus$ | $\bigotimes$ | $\bar{0}$ | $\bar{1}$ |
|---|---|---|---|---|---|
| 布尔半环 | ${0,1}$ | $\vee$ | $\wedge$ | 0 | 1 |
| 概率半环 | $\mathbb{R}_+$ | + | $\times$ | 0 | 1 |
| 对数半环 | $\mathbb{R} \cup {-\infty, +\infty}$ | $\bigoplus_{log}$ | + | $+\infty$ | 0 |
| 热带半环 | $\mathbb{R} \cup {-\infty, +\infty}$ | min | + | $+\infty$ | 0 |
其中$x \bigoplus_{log} y \equiv -log(e^{-x}+e^{-y})$。我们验证一下热带半环确实是一个半环。
- 加法满足交换律和结合律
- 零元加任何元素不变
- 乘法满足结合律和对加法的分配率
- 零元乘以数也不变
- 零元乘以任何数等于零(吸收律)
因此热带半环确实是一个半环。有了半环的定义之后,我们现在可以形式化的定义WFST。
半环$\mathbb{K}$之上的一个weighted finite-state transducer(加权有效状态转录机, WFST) $T=(\mathcal{A}, \mathcal{B}, Q, I, F, E, \lambda, \rho)$包括如下部分。
- $\mathcal{A}$是一个有限的输入字母表
- $\mathcal{B}$是一个有限的输出字母表
- Q是一个有限的状态集合
- $I \subseteq Q$是初始状态集合
- $F \subseteq Q$是终止状态集合
- $E \subseteq Q \times (\mathcal{A} \cup {\epsilon}) \times (\mathcal{B} \cup {\epsilon}) \times \mathbb{K} \times Q$
- $\lambda : I \rightarrow \mathbb{K}$,给初始状态一个weight
- $\rho: F \rightarrow \mathbb{K}$,给终止状态一个weight
另外我们用记号$E(q)$表示离开状态q的所有转移(边),而$\vert T \vert$表示T中所有状态和边的个数总和。给定一个转移e,p[e]表示起点(状态),n[e]表示终点(状态),i[e]表示输入字母,o[e]表示输出字母,w[e]表示权重。一条路径$\pi=e_1…e_k$是一连串的边,并且前后两条边的点是连接在一起的(也就是说后一条边的起点是前一条边的终点),即$n[e_{i-1}]=p[e_i], i=2,3,…,k$。如果一条路径的开始状态和状态是同一个状态,那么这条路径就是一个cycle,即$p[e_1]=n[e_k]$。如果一个cycle的所有边的输入和输出符号都是$\epsilon$,那么这个cycle就叫$\epsilon-cycle$。
我们也可以把函数n,p和w从边扩展到路径上,$n(\pi)=n(e_k)$,$p(\pi)=p(e_1)$,$w[\pi]=w[e_1] \bigotimes … \bigotimes w[e_k]$。
接着我们可以形式化的定义WFST的composition,假设$T_1$和$T_2$是两个WFST,其中$T_1$的输入字母表是$\mathcal{A}$,输出字母表是$\mathcal{B}$;而$T_2$的输入字母表是$\mathcal{B}$,输出字母表是$\mathcal{C}$。则$T_1$和$T_2$的composition定义为:
\[T_1 \circ T_2(x, y) = \underset{z \in \mathcal{B}^*}{\bigoplus}T_1(x,z) \bigotimes T_2(z,y)\]WFST在语音识别中的应用
前面介绍了WFST的基本原理和一些常见操作,下面我们介绍WFST在语音识别中的应用。我们回顾一下,一个WFST定义了一个关系(而不是一个函数),它的输入是一个字母表上的字符串,而输出是另一个字母表上的多个(或者零个)字符串以及对应的概率。我们可以把它看成一个一对多的”函数”,输入一个字符串,输出多个字符串及其概率。
我们可以把语音识别的组件都用WFST来表示,而它们的组合使用WFST的composition来表示。在语音识别中有4个WFST transducer,我们下面逐个介绍。
G
G表示语言模型。它是一个WFSA,它的输入是一个词序列,然后G可以判断这个词序列是否符合语法以及它的概率。对于固定的文法来说,它只能识别符合文法的句子;而对于N-Gram来说,所有的句子都是可能的,只不过概率有高有低。
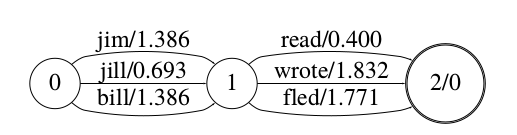
比如下图的WFSA它接受的语法只能识别”jim read”、”jim wrote”、”jim fled”等9个句子。
L
L是发音词典。它的输入(上下文无关的)因子序列,输出是词序列。比如上面文法对应的发音词典:
bill b ih l
jill jh ih l
jim jh ih m
read r eh d
read r iy d
red r eh d
...
注意:read有两种发音/r eh d/和/r iy d/,这当然没有什么问题。但是如果两个词有相同的发音就会有问题,比如read和red都可以发音成/r eh d/,我们后面会介绍怎么解决不同词有相同发音的问题。
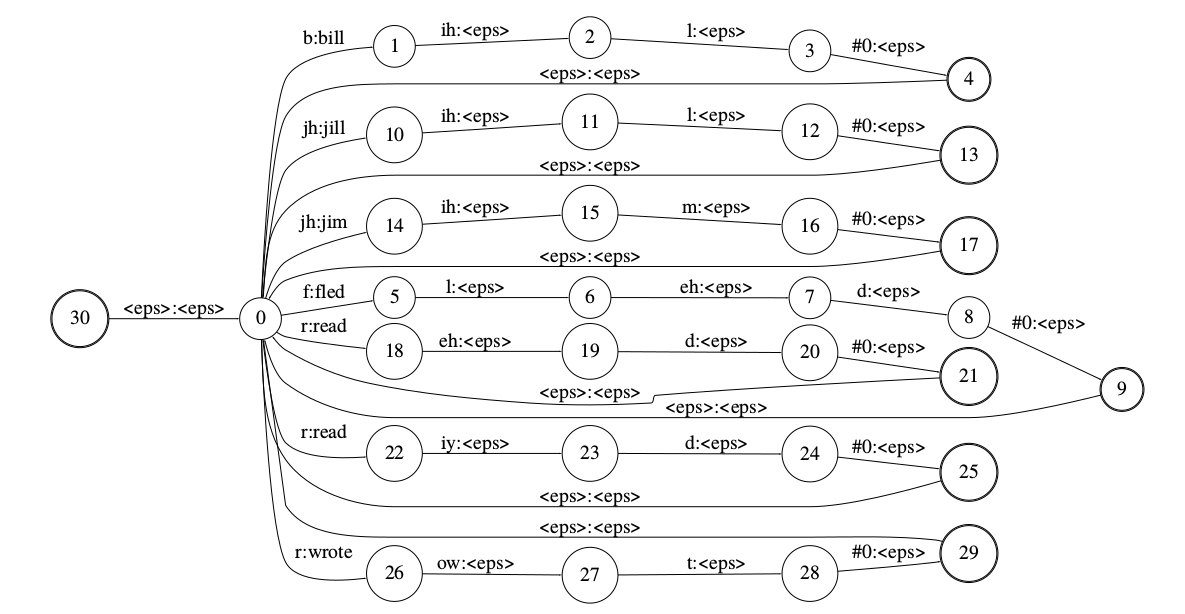
我们可以根据这个发音词典构造L,如下图所示。这个WFST的输入可以是词典里任意词的因子的序列,而输出是词的序列,比如输入是”b ih l b ih l b ih l”,那么输出就是”bill bill bill”,当然这并不符合G的文法,但这没关系,我们后面把它们进行composition之后,也就是$L \circ G$,它就只能输出符合G文法的句子了。
那这个L是怎么构造出来的呢?我们先假设不同的词的发音都不相同的情况。那么很简单,我们构造一个初始状态(30),然后构造一个状态0,初始状态可以通过$\epsilon$跳转到0,然后词典里的每个词都展开成一个状态链条。比如”bill b ih l”,我们把3个因子[b ih l]分别构造3个状态和3条边:
\[0-(b:bill)->1,1-(ih:\epsilon)->2,2-(l:\epsilon)->3\]注意,第一条边就输出了单词bill,而后面的边输出的是$\epsilon$。最后我们再加一条特殊的边来表示单词的结束:
\[3-(\#1:\epsilon)->4\]状态4是接受状态,这样就可以识别一个单词,为了识别多个单词,我们需要在每个单词的接受状态通过$\epsilon$跳转又调回到状态0。
注意,这个WFST是非确定性的。比如输入是[jh il m],状态0有两条边可以输入jh(jim和jill),因此我们同时进入状态10和14,接着输入il,状态机进入11和15。接着输入m,状态11无法处理,直接”死掉”,而状态15输入m后进入状态16,接着输入特殊的#0(我们后面会讨论),然后进入状态17,这是一个接受状态。如果后面再没有输入了,那么WFST的输出就是单词jim。如果后面还有”f l eh d #0”,那么它就通过$\epsilon$跳转到状态0,然后识别”f l eh d #0”,最终进入状态9,这也是一个接受状态。如果后面再没有输入,WFST就输出”jim fled”。
非确定性的WFST是比较容易构造的(类似于NFA比DFA容易构造一样),但是识别的时候需要递归或者回溯,因此效率较低,我们可以把它转换成等价的确定性WFST。前面的假设是所有的单词的发音都不相同,因此(可能但也并一定)存在一个与之等价的确定性的WFST。但是如果两个单词的发音完全相同,比如read和red的发音都是/r eh d/,那么显然不可能存在等价的确定性的WFST。那怎么办呢?假设最多k个不同的词有相同的发音,我们可以引入特殊的消歧符号#0、#1…#(k-1)。我们在发音词典的每一个词后面都加一个消歧符号,比如:
read r eh d #0
red r eh d #1
C
C 是把上下文相关的因子序列转换成上下文无关的因子序列的WFST。声学模型的输出是上下文相关的因子序列,而L要求的输入是上下文无关的因子序列,因此我们需要C来把上下文相关的因子序列转换成上下文无关的。
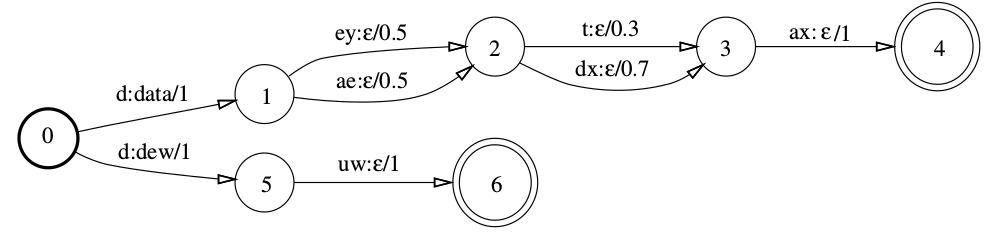
比如下图所示的发音词典,为了更好的效果,我们需要使用上下文相关的因子,比如ae/k_t表示当前的因子是ae而它的上一个因子是k而下一个因子是t。
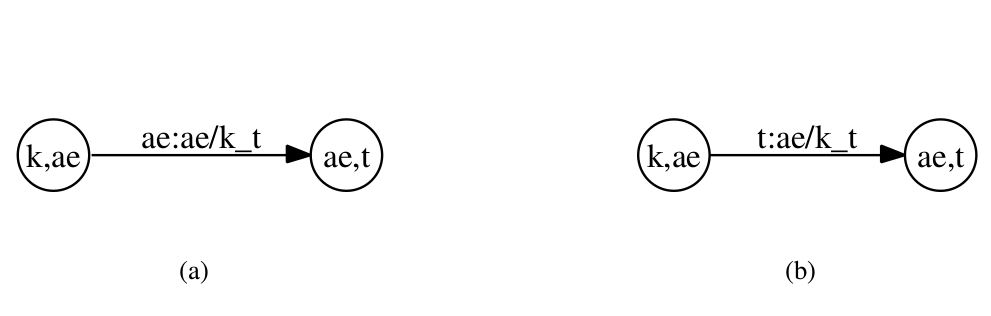
下图是一个示例。图(a)是非确定的WFST;而图(b)是确定的WFST。
我们先看图(a),状态”k,ae”表示当前因子是k而下一个因子是ae(这类似与NFA的猜测),这个状态下只能输入ae。当输入ae之后进入状态”ae,t”,表示新的当前因子是ae而下一个因子是t(猜测)。因此如果下一个输入不是t的话,这个猜测分支就会”死掉”,不过这没有关系,会有别的分支来正确的识别。
比如输入如果是[“k”, “ae”, “t”]的话,初始状态是”eps, eps”,表示当前因子是空(什么也不是),下一个是*(表示所有可能)。遇到输入k就进入状态”k,ae”并且输出”k/eps_ae”,接着遇到ae就进入状态”ae,t”并且输出”ae/k_t”,接着遇到t就进入状态”t, eps”并且输出”t/ae_eps,这是一个接受状态,因此最终它把上下文无关的因子序列[k ae t]转换成上下文相关的序列[k/eps_ae, ae/k_t, t/ae_eps]。
但如果输入是[“k”, “ae”, “f”],则上面的过程走到状态”ae,t”就走不下去的,但是另外一个识别[“k”, “ae”, “f”]的路径会成功识别并且把它转化成上下文相关的序列。
当然我们要的是把上下文相关的序列转换成上下文无关的序列,上面得到的是相反的WFST,这可以通过WFST的求逆运算把它反过来。
但是前面图(a)的WFST是非确定性的,我们可以采样图(b)的方式来把它变成确定性的。
在图(b)中,状态”k,ae”表示当前因子是ae而前一个因子是k,这和之前是不同的,之前状态”k,ae”表示当前状态是k而下一个因子是ae!
在图(a)中,状态”k,ae”只能输入”ae”,因为它猜测k后面是ae,而图(b)中”k,ae”可以输入很多个,比如:
"k,ae" -t-> ae/k_t
"k,ae" -d-> ae/k_d
....
相对于图(a),图(b)的输出有一个时刻的延迟,比如图中输入t的时候输出的是前一个因子ae的结果”ae/k_t”,因此需要在最后加一个特殊的结束符号以便输出最后一个因子的结果。
H
H是把声学观察序列变成上下文相关因子序列的WFST。这个WFST代表声学模型,它的输入是观察序列,输出是上下文相关因子序列及其概率。
最终我们可以把这4个WFST用composition操作组合起来得到$H \circ C \circ L \circ G$,这个大的WFST的输入是观察序列,而输出就是词序列,我们通过搜索最短路径(因为是热带半环,-log概率,因此最短路径等价与最大概率)来找到最可能的路径,也就是实现了解码算法。
不过为了使WFST能够变成确定的,我们需要对H、C和L做一些特殊处理,包括加入消歧符号和self-loop等操作,具体细节这里就不介绍,有兴趣的读者可以参考相关论文。最终我们得到$\tilde{H}, \tilde{C}, \tilde{L}$,我们是把它们composite起来得到$\tilde{H} \circ \tilde{C} \circ \tilde{L} \circ G$。这个WFST不是确定的,因此我们需要把它变成确定的并且变成最小的WFST,当然这有很多方法,最常见的就是:
\[N=\pi_\epsilon(min(det(\tilde{H} \circ det(\tilde{C} \circ det(\tilde{L} \circ G)))))\]- 显示Disqus评论(需要科学上网)