HMM和WFST代码示例

前面介绍了HMM和WFST的原理，下面我们通过简单的例子来更加深入的了解HMM和WFST在语音识别中的应用。更多文章请点击深度学习理论与实战：提高篇。

转载请联系作者(fancyerii at gmail dot com)！

代码和安装
HMM代码
WFST代码

代码和安装

完整代码在这里。这部分内容参考了danijel3的代码。

运行代码需要安装OpenFst和PyFst，OpenFst是一个开源的WFST库，后面介绍的Kaldi也会使用OpenFst。而PyFst是OpenFst的一个wrapper，我们可以通过它来了解OpenFst的基本用法。我们需要首先安装OpenFst，作者安装的是openfst-1.6.9。安装比较简单，就是标准的安装流程：

./configure
make
sudo make install

注意最后的安装(把头文件和so文件复制到系统路径，把二进制可执行程序放到系统路径)需要root权限。安装好了OpenFst之后需要按照PyFst，PyFst网站只能使用版本1.3的openfst，还好placebokkk fix了这个问题。安装过程如下：

git clone https://github.com/placebokkk/pyfst.git
安装python3(建议使用virtualenv)
pip install cython
python setup.py install

HMM代码

HMM回顾

Rabiner的论文提到了HMM有3个问题：

给定模型(参数)，计算观察的概率，也就是$P(O|M)$ - 这需要使用前向算法
给定模型(参数)和观察，计算最可能的状态序列，也就是$\underset{S}{argmax}P(S|O;M)$。这需要使用Viterbi算法。
学习问题，调整模型参数，使得概率$P(O|M)$最大(最大似然)。这需要Baum-Welch算法，也叫前向后向算法。

HMM有如下的参数定义：

发射概率

通常我们使用高斯混合模型(GMM)，但是我们也可以使用深度神经网络(比如MLP)。为了与Rabiner的论文一致，我们假设输出是离散的。因此可以用概率分布函数$b_{jk}$来描述。它表示给定状态j出现观察k的概率。
隐状态

在我们的例子中，隐状态是我们需要识别的单元：比如因素(phonemes)，但是也有可能是其它的单元比如词。
转移概率——从一个状态跳转到另一个状态的概率
先验概率 - 系统处于不同初始状态的概率

为了便于阅读，我们这里使用和Rabiner论文一致的记号：

发射概率我们用$b_{jk}$表示
跳转概率用$a_{ij}$表示
先验概率用$\pi_i$表示

示例模型

这里我们会随机的生成一些值来演示算法。我们这里的示例HMM有3个状态，观察有4种可能值。观察的长度是5。我们把这些值定义为常量，方便后面引用：

N=3
M=4
T=5

我们先随机生成一个观察序列，它的长度是5：

O=np.random.randint(0,M,T)
print(O)
# [2 2 0 2 1]

发射概率可以用一个矩阵来表示。这个矩阵的大小是3x4，每一行表示一个状态，$b_{jk}$表示状态j发射观察k的概率。

b=np.random.random((N,M))
b/=np.array(b.sum(axis=1, keepdims=True))
print(b)
#输出：
[[0.48229459 0.27721979 0.12239203 0.11809359]
 [0.11822906 0.14038183 0.42902164 0.31236747]
 [0.34614273 0.10475221 0.38320261 0.16590244]]

因为是概率，因此要求$\sum_kb_{jk}=1$，也就是每一行加起来等于1。我们来验证一下：

print(b.sum(axis=1))
# [1. 1. 1.] 

给定这些概率和一个观察序列，我们很容易计算不同时刻处于不同状态的发射概率：

ob=np.zeros((T,N))
for t in range(T):
    for i in range(N):
        ob[t,i]=b[i,O[t]]
print(ob)
# 输出：
[[0.12239203 0.42902164 0.38320261]
 [0.12239203 0.42902164 0.38320261]
 [0.48229459 0.11822906 0.34614273]
 [0.12239203 0.42902164 0.38320261]
 [0.27721979 0.14038183 0.10475221]]

或者更加简洁高效的写法（但是更难懂一点）：

ob=b.T[O]

我们下面的代码会有两个版本的实现，一个是使用for循环的版本，一个是Numpy的版本，前者可读性更好容易理解，而后者更加简洁和高效，读者至少需要能理解for循环的版本。

我们这里的示例使用的是离散的输出，我们用一个发射概率矩阵就可以表示了，但是在实际的系统中，我们通常使用一个模型，比如GMM或者MLP来表示这个发射概率。这里为了简单起见我们使用了离散的输出，但是读者应该知道在实际的系统中很少使用离散的输出。状态转移矩阵是一个3x3的矩阵，它的每一行加起来是1：

a=np.random.random((N,N))
a/=np.array([a.sum(axis=-1)]).T
print(a)
print(a.sum(axis=1))
# 输出：
[[0.39884173 0.3486846  0.25247367]
 [0.08072832 0.59021607 0.32905562]
 [0.25993654 0.25873506 0.4813284 ]]
[1. 1. 1.]

下面我们随机的生成先验概率。我们可以设置随机值，也可以让所有的状态的先验概率相等。

pi=np.random.random(N)
pi/=pi.sum()
print(pi)
# 输出：
[0.23738012 0.47646268 0.28615719]

为了更容易阅读，我们把这些概率放到一个tuple里：

hmm=(O,pi,a,b,N,M,T)

我们把模型保存到磁盘文件里：

import pickle

with open('../data/hmm.pkl','wb') as f:
    pickle.dump(hmm,f,pickle.HIGHEST_PROTOCOL)

前向算法

下面会直接实现Rabiner的论文里的算法。注意原文的下标是1开始的，而程序的下标是0开始。

def forward(O,pi,a,b,N,M,T):
    fwd=np.zeros((T,N))

    #初始化
    for i in range(N):
        fwd[0,i]=pi[i]*b[i,O[0]]

    #递推
    for t in range(T-1):
        for j in range(N):
            s=0
            for i in range(N):
                s+=fwd[t,i]*a[i,j]
            fwd[t+1,j]=s*b[j,O[t+1]]
            
    return fwd

print(forward(*hmm))

代码和伪代码一样，请读者对照前面我们介绍的算法阅读。最终得到的是3x5的前向概率$\alpha_t(i)$。

我们也可以使用Numpy更加高效的实现：

def forward(O,pi,a,b,N,M,T):
    fwd=np.zeros((T,N))

    #初始化
    fwd[0]=pi*b[:,O[0]]

    #递推:
    for t in range(T-1):
        fwd[t+1]=np.dot(fwd[t],a)*b[:,O[t+1]]
    
    return fwd

前面计算了到最后一个时刻的某个状态的所有路径的概率累加和，为了计算所有路径的累加和，我们需要把最后一个时刻的所有概率再加起来：

def full_prob(fwd):
    return fwd[-1].sum()

print(full_prob(forward(*hmm)))

Viterbi算法

我们先看最简单算法——只考虑某一个时刻最可能的状态，也就是根据发射概率找出最可能的状态。$s_i=argmax_sP(o_i|s)$。用代码实现就是：

np.argmax(ob,axis=1)
# array([0, 0, 2, 0, 2])

上面的序列不会考虑上下文。但是HMM认为有些状态之间的跳转概率更大，因此即使某个发射概率可能比另外一个稍大一些，但是如果从前面的状态跳转到它的概率很低的话，我们也应该选择跳转概率更大的那个。所以我们需要考虑整个序列，综合考虑跳转概率和发射概率。

def viterbi(O,pi,a,b,N,M,T):
    d=np.zeros((T,N))
    ph=np.zeros((T,N),dtype=np.int)

    #初始化
    for i in range(N):
        d[0,i]=pi[i]*b[i,O[0]]
        ph[0,i]=0

    #递推
    for t in range(1,T):
        for j in range(N):
            m=np.zeros(N)
            for i in range(N):
                m[i]=d[t-1,i]*a[i,j]
            ph[t,j]=m.argmax()
            d[t,j]=m.max()*b[j,O[t]]

    #结束时刻
    m=np.zeros(N)
    for i in range(N):
        m[i]=d[T-1,i]
    Pv=m.max()

    #back-tracking
    Q=np.zeros(T,dtype=np.int)
    Q[T-1]=m.argmax()
    for t in reversed(range(T-1)):
        Q[t]=ph[t+1,Q[t+1]]
        
    return Q

print(viterbi(*hmm))
#　[0 1 2 1 2]

Viterbi和前向算法很像，只不过前向算法是计算到当前时刻t的某个状态的所有路径的概率累加和；而Viterbi算法只计算概率最大的一条路径。

更快一点的Numpy实现：

def viterbi(O,pi,a,b,N,M,T):
    d=np.zeros((T,N))
    ph=np.zeros((T,N),dtype=np.int)

    #初始化
    d[0]=pi*b[:,O[0]]
    ph[0]=0

    #递推
    for t in range(1,T):
        m=d[t-1]*a.T        
        ph[t]=m.argmax(axis=1)
        d[t]=m[np.arange(N),ph[t]]*b[:,O[t]]    

    #结束时刻
    Q=np.zeros(T,dtype=np.int)
    Q[T-1]=np.argmax(d[T-1])
    Pv=d[T-1,Q[T-1]]

    #back-tracking
    for t in reversed(range(T-1)):
        Q[t]=ph[t+1,Q[t+1]]

    return Q

这个结果和之前的不考虑上下文是不同的，如果我们把先验概率和转移概率设置成均匀分布，那么Viterbi得到的路径和前面最大似然的路径是相同的。

前向后向算法

前向算法已经实现过了，这里我们实现后向算法：

def backward(O,pi,a,b,N,M,T):
    bk=np.zeros((T,N))
    #初始化
    for i in range(N):
        bk[T-1,i]=1
    #推导:
    for t in reversed(range(T-1)):
        for i in range(N):
            s=0
            for j in range(N):
                s+=a[i,j]*b[j,O[t+1]]*bk[t+1,j]            
            bk[t,i]=s
    return bk

print(backward(*hmm))

numpy的实现：

def backward(O,pi,a,b,N,M,T):
    bk=np.zeros((T,N))
    #初始化:
    bk[T-1]=1
    #递推:
    for t in reversed(range(T-1)):
        bk[t]=np.dot(bk[t+1]*b[:,O[t+1]],a.T)
    return bk

根据定义，前向概率是$P(o_1,…,o_t,s_t=j|M)$，而后向概率是$P(o_{t+1},…,o_T \vert s_t=j;M)$。状态占用概率$\gamma_t(j)=P(s_t=j \vert O)=\frac{\alpha_t(j)\beta_t(j)}{P(O)}$，而P(O)就是full_prob函数得到的结果。在语音识别章节有详细的推导过程，请读者参考相关内容。

def gamma(fwd,bk,fp):
    gm=np.zeros((T,N))
    for t in range(T):
        for i in range(N):
            gm[t,i]=(fwd[t,i]*bk[t,i])/fp
    return gm

如果使用numpy可以一行实现：

def gamma(fwd,bk,fp):
    return (fwd*bk)/fp

print(gamma(forward(*hmm),backward(*hmm),full_prob(forward(*hmm))))

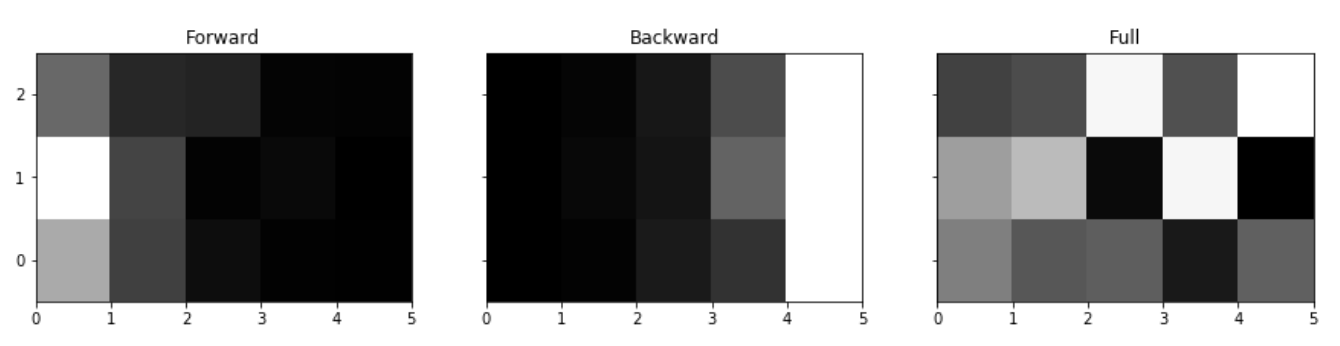
我们可以把这3个概率绘制出来进行比较。我们可以发现前向概率随着时间的增加指数衰减(后向算法也类似，只是方向相反)。把它们加到一起就可以找到每个时刻最可能的状态。

fig,ax=P.subplots(1,3,figsize=(15,3),sharey=True)


ax[0].pcolormesh(forward(*hmm).T,cmap=P.cm.gray)
ax[0].set_yticks(np.arange(0,N)+.5)
ax[0].set_yticklabels(np.arange(0,N))
ax[0].set_title('Forward')

ax[1].pcolormesh(backward(*hmm).T,cmap=P.cm.gray)
ax[1].set_title('Backward')

g=gamma(forward(*hmm),backward(*hmm),full_prob(forward(*hmm)))
ax[2].pcolormesh(g.T,cmap=P.cm.gray)
ax[2].set_title('Full')

结果如下图所示，白色表示概率较大，因此从图中我们可以知道1-5个时刻最优的状态是[1,1,2,1,2]，这回Viterbi算法得到的[0,1,2,1,2]是很接近的。

图：三个概率的可视化

注意我们可以抽取很多序列，它们的含义是不同的。

我们可以根据观察逐个时刻(独立，不考虑上下文)的计算每个时刻最可能的状态，这个状态下发射这个观察的概率最大，这不会考虑状态的跳转。我们把这个序列叫做最近观察(得到的状态)序列
我们也可以考虑最佳的前向或者后向的概率，它只考虑单个方向的信息。
我们可以计算状态占用概率，得到某个时刻最可能的状态，注意这不是最优路径，它只是说明某个时刻的最可能的状态，但是它们串起来可能就不是最优的。
最后我们可以通过Viterbi算法得到最优状态序列。

print('Best observation sequence: {}'.format(np.argmax(ob,axis=1)))
print('Best forward prob. sequence: {}'.format(np.argmax(forward(*hmm),axis=1)))
print('Best backward prob. sequence: {}'.format(np.argmax(backward(*hmm),axis=1)))
g=gamma(forward(*hmm),backward(*hmm),full_prob(forward(*hmm)))
print('Best full prob. sequence: {}'.format(np.argmax(g,axis=1)))
print('Best Viterbi sequence: {}'.format(viterbi(*hmm)))
# 输出：
Best observation sequence: [0 0 2 0 2]
Best forward prob. sequence: [1 1 2 1 2]
Best backward prob. sequence: [0 1 0 1 0]
Best full prob. sequence: [1 1 2 1 2]
Best Viterbi sequence: [0 1 2 1 2]

Baum-Welch算法

总共有5个时刻，但是最后一个时刻没有跳转，而每个时刻都有3x3种可能的跳转，因此我们可以得到一个4x3x3的tensor。这就是我们介绍过$\epsilon_t(i,j)$(这里用xi表示)，它表示t时刻的状态是i而t+1时刻是状态j的概率，它可以这样计算： $\epsilon_t(i,j)=\frac{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}{P(O \vert \lambda)}$。

def xi(fwd,bk,fp,O,pi,a,b,N,M,T):
    ret=np.zeros((T-1,N,N))
    for t in range(T-1):
        for i in range(N):
            for j in range(N):
                ret[t,i,j]=(fwd[t,i]*a[i,j]*b[j,O[t+1]]*bk[t+1,j])/fp                
    return ret

Numpy版本：

def xi(fwd,bk,fp,O,pi,a,b,N,M,T):
    return fwd[:-1].reshape((T-1,N,1))*a.reshape((1,N,N))*b[:,O[1:]].T.reshape((T-1,1,N))
		    *bk[1:].reshape((T-1,1,N))/fp

我们可以估计先验概率pi——也就是初始状态的概率，它就是0时刻的状态占用概率：

def exp_pi(gamma):
    return gamma[0]

接下来我们可以估计跳转概率，它的计算公式为： $\hat{a}_{ij}=\frac{\sum_t\epsilon_t(i,j)}{\sum_j \sum_t\epsilon_t(i,j)}=\frac{\sum_t\epsilon_t(i,j)}{\sum_t\gamma_t(i)}$ 。

公式看起来比较复杂，其实意思很简单：分子是所有的状态i->j的概率累加和，而分母是所有状态为i的概率和。

def exp_a(gamma,xi,N):
    e_a=np.zeros((N,N))
    for i in range(N):
        for j in range(N):
            e_a[i,j]=np.sum(xi[:,i,j])/np.sum(gamma[:-1,i])
            
    return e_a

#前向概率
fw=forward(*hmm)
#后向概率
bk=backward(*hmm)
#观察全概率
fp=full_prob(fw)
#就是状态占用概率gamma
g=gamma(fw,bk,fp)
#就是状态跳转概率epsilon(xi)
x=xi(fw,bk,fp,*hmm)
#估计新的跳转概率
ea=exp_a(g,x,N)

Numpy的版本：

def exp_a(gamma,xi,N):
    return xi[:].sum(axis=0)/gamma[:-1].sum(axis=0).reshape(N,1)

最后，我们可以估计发射概率，它的计算公式为：$\hat{b}_{jk}=\frac{\sum_t[o_t=k]\gamma_t(j)}{\sum_t\gamma_t(j)}$。它的意思是：观察为k并且状态为j的概率和除以状态为j的概率。

def exp_b(gamma,O,N,M):
    e_b=np.zeros((N,M))
    for j in range(N):
        for k in range(M):        
            e_b[j,k]=np.sum(gamma[O==k,j])/np.sum(gamma[:,j])
    return e_b

#前向概率
fw=forward(*hmm)
#后向概率
bk=backward(*hmm)
#观察全概率
fp=full_prob(fw)
#就是状态占用概率
g=gamma(fw,bk,fp)
#更新发射概率，然后打印
print(exp_b(g,O,N,M)) 

Baum-Welch算法是一种EM算法，首先我们随机初始化一组参数，然后就可以用前向和后向算法计算前向后向概率，然后根据它们计算状态占用概率$\gamma_t(i)$和状态跳转概率$\epsilon_t(i,j)$，接下来就可以用这两个概率重新估计pi,$a_{ij},b_{jk}$。每次迭代都可以增加训练数据上的似然概率，我们可以不断的迭代直到收敛(到局部最优解)。

print('Initial probability: {}'.format(full_prob(forward(*hmm))))

hmm_new=hmm
# 15次EM迭代
for i in range(15):
    # E-step
    # 前向概率
    fw=forward(*hmm_new)
    # 后向概率
    bk=backward(*hmm_new)
    # 观察全概率
    fp=full_prob(fw)
    # 状态占用概率 gamma
    g=gamma(fw,bk,fp)
    # 状态跳转概率 epsilon
    x=xi(fw,bk,fp,*hmm_new)
	
    # M-step
    # 更新参数pi
    pi_new=exp_pi(g)
    # 更新跳转概率a
    a_new=exp_a(g,x,N)
    # 更新发射概率b
    b_new=exp_b(g,O,N,M)
    
    err=np.concatenate(((pi_new-hmm_new[1]).ravel(),(a_new-hmm_new[2]).ravel(),
			(b_new-hmm_new[3]).ravel()))
    
    hmm_new=(O,pi_new,a_new,b_new,N,M,T)

    print('Update #{} probability: {} -- mean error:
		    {}'.format(i+1,full_prob(forward(*hmm_new)),np.mean(err**2)))

通常我们用HMM来建模一个语音单元比如因子，通常使用3-5个状态来建模一个因子，通过发音词典，我们直到一个单词对应的因子序列，我们可以把每个因子的HMM拼接起来(所有通常在语音识别系统中HMM有一个开始状态和结束状态，这样便于拼接HMM)得到一个词的HMM。类似的我们也可以把一个句子中所有词的HMM拼接起来得到一个很大的句子的HMM。我们实际标注的粒度一般是句子级别的，因此我们可以用数据来训练这个很大的HMM的参数，但是这个大的HMM是”临时”拼凑的HMM，真正的参数还是在因子级别。

而对于HMM-DNN的混合系统，我们通常不适用EM算法。对于深度神经网络，我们通常使用区分性(discriminative)训练。这要求我们的标注是帧级别的(也就是标注每一帧属于那个因子)，这显然不可能让人来标注，实际通常使用Viterbi算法来进行Force-Alignment。什么叫Force Alignment呢？普通的Viterbi算法的是在所有的路径里搜索最有的状态序列，而对于训练数据，我们是有句子级别的标注的，我们可以利用这个信息。

举个例子，句子”go home”，如果不做限制，它是在所有可能的路径里搜索，可能(虽然理论上可能性较低)解码成”/b/ae/t/”，而Force Alignment已经知道句子是”go home”了，因此已经知道HMM模型是/g əʊ h əʊ m/。假设观察序列是： $o_1,o_2,…,o_{10}$ 那么所有可能的对齐方式为：

g g əʊ əʊ əʊ h əʊ əʊ m
g əʊ əʊ əʊ əʊ h əʊ əʊ m
...

它只需要从这些对齐里选择最可能的路径就行了。而不可能是：

b b ae ae ae ae ae ae ae t

当然，我们也可以不用HMM而使用其它损失函数(比如CTC)，使用End-to-End的深度学习模型，完全抛弃HMM模型，后面我们也会介绍。

用于语音识别的HMM拓扑结构

如果要实际使用HMM来进行语音识别，我们需要扩展HMM模型的定义。我们之前定义的HMM只能用于识别一个词。

假设我们创建了一个声学模型(acoustic model)而不是简单的发射概率矩阵，声学模型可以根据声学观察(比较短时傅里叶变换滤波器组的输出)识别出因子序列。我们可以用神经网络来实现声学模型，我们可以认为神经网络的输出就是发射概率(但实际并不是，神经网络是区分性模型，它的输出是$P(s \vert o_t)$而不是$P(o_t \vert s)$)。把它替换掉原来的GMM，我们就可以把观察序列转换(识别)成因子序列。但是我们需要识别词，因此我们还需要识别词，因此我们还需要一个模型把因子训练变成词序列(实际更加复杂，声学模型输出的通常是上下文相关的因子序列，我们首先需要把它转换成上下文无关的因子序列，然后通过发音词典把它转换成词序列，最后通过语言模型选择最可能的词序列。

注意：声学模型输出的不是一个因子序列，而是很多可能的上下文相关的因子序列，当然每个序列有不同的概率得分；类似的一个上下文无关的因子序列可以转换成很多可能的词序列，它们也有不同的概率，这样的组合会非常大，我们需要从这些可能的组合中寻找概率最大的那个。

但是我们发现把观察序列变成上下文相关的因子序列的HMM H、把上下文相关的因子序列变成上下文无关的C、把上下文无关的因子序列变成词的L和把词序列变成词序列的语言模型L。都可以统一的用WFST来表示(某些复杂的文法或者N-gram需要通过近似的方法变成WFST)，而它们的层级关系可以通过WFST的composition来实现。这样我们可以把一个复杂的多层的搜索网络用WFST来表示，而且我们可以使用WFST的Determinization和Minimization算法来压缩和提高搜索速度。

WFST代码

WFST定义了一种关系，给定一个输入字符串，它可以输出多个(或者零个)字符串已经对应的weight。

例子

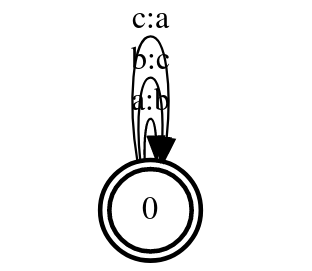
我们这里使用PyFst库，它是对OpenFst的封装。我们可以定义如下的WFST：

f=fst.Transducer()
f.add_arc(0,0,'a','b')
f.add_arc(0,0,'b','c')
f.add_arc(0,0,'c','a')
f[0].final=True

这个WFST如下图所示，它只有一个状态，但是有3个跳转(边)。

图：示例WFST

下面我们再来创建另一个WFST，它的输入和输出是完全相同的。输入和输出完全相同的WFST其实就是一个WFSA，我们有时候也称之为acceptor。我们可以使用那还是linear_chain来生成一个类似链条的acceptor：

i=fst.linear_chain(['a','a','c','b'],syms=f.isyms)

上面代码生成的WFST如下图所示，它形成一个链条。

图：链式WFST

Composition

WFST最有用的操作就是composition。这个操作的输入是两个WFST，第一个WFST的输入字母表是A，输出字母表是B；第二个的输入字母表是B输出字母表是C，则Composition之后的WFST的输入字母表是A而输出字母表是C。我们可以使用重载的»运算符实现Composition操作，比如i»f就是把i和f进行Composition。

o=i>>f
o.project_output()

如下图所示，我们发现把i和f composition的作用就是把i的符号做一个替换——a变成b，b变成c，c变成a。

图：WFST的composition

我们也可以定义3个(链式的)WFST，然后使用union把它们并联成一个大的WFST，同时我们使用remove_epsilon去除$\epsilon$。

f=fst.Transducer()
f.add_arc(0,0,'a','b')
f.add_arc(0,0,'b','c')
f.add_arc(0,0,'c','a')
f.add_arc(0,0,'d','f')
f.add_arc(0,0,'e','g')
f.add_arc(0,0,'f','h')
f.add_arc(0,0,'g','e')
f.add_arc(0,0,'h','f')
f.add_arc(0,0,'x','x')
f.add_arc(0,0,'y','y')
f.add_arc(0,0,'z','z')
f[0].final=True

i1=fst.linear_chain(['a','b','c','d','e'],syms=f.isyms)
i2=fst.linear_chain(['a','b','x','y','z'],syms=f.isyms)
i3=fst.linear_chain(['g','h','c','d','e'],syms=f.isyms)
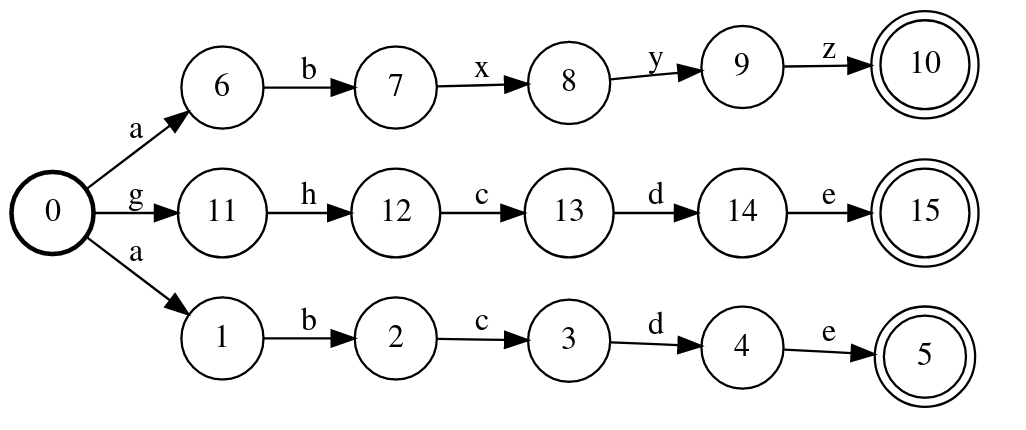
i=i1.union(i2)
i=i.union(i3)
i.remove_epsilon()

三个链式WFST的union结果如下图所示。

图：WFST的Union

我们发现里面有一些重复路径，比如从状态0->1和0->6都是a，因此这个WFST是非确定的WFST，它的搜索需要回溯。我们可以使用determinize函数先把它变成确定的WFST，然后使用minimize函数得到最小的WFST，从而压缩空间和提高搜索速度。

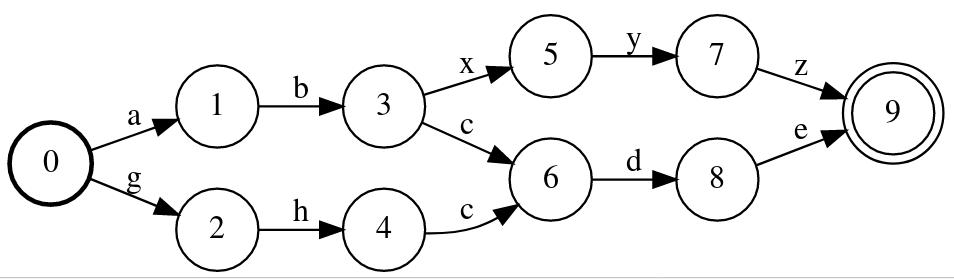
i=i.determinize()
i.minimize()

最终得到的WFST如下图所示，它确定性的WFST，而且状态是最小的，请读者验证这个WFST和前面是等价的。

图：WFST的determinize和minimize

HMM使用WFST的例子

我们可以用WFST来实现语音识别的解码器。比如我们可以使用一个WFST把观察序列转换成上下文相关的因子序列、接着使用一个WFST把它转换成上下文无关的因子序列、再用发音词典把它转化成词序列，最后用语言模型给这个词序列加上语言模型概率得分。我们把这几个WFST composite在一起，然后使用determinize和minimize优化这个WFST。有了这个WFSt之后，给定观察序列，我们直接就可以用WFST得到最可能的词序列。

下面我们修改前面HMM的代码，首先我们构造把观察变成状态(因子)的WFSA：

def obs_mat(O,b,N,T):
    f=fst.StdAcceptor()
        
    for t in range(T):
        for j in range(N):
            f.add_arc(t,t+1,str(j),-np.log(b[j,O[t]]))
        
    f[T].final=True
    return f

obs_fsa=obs_mat(O,b,N,T)

注意：在WFST里weight的表示方法和HMM不同，这里我们使用热带半环，把(发射)概率用-log来表示。

上面的代码得到如下图所示的WFST。

图：编码发射概率的WFST

这个FSA的输入是状态序列，输出这个状态序列的发射概率。比如给定当前的5个观察，我们可以计算状态(因子)序列为[0 0 1 1 2]的发射概率为：0.62 + 2.26 + 0.9 + 0.41 + 1.59。HMM除了发射概率之外还有状态的先验概率和跳转概率，我们也可以把它变成WFST：

def trans_mat(pi,a,N):
    f=fst.StdAcceptor()
    
    for i in range(N):
        f.add_arc(0,i+1,str(i),-np.log(pi[i]))
    
    for i in range(N):
        for j in range(N):
            f.add_arc(i+1,j+1,str(j),-np.log(a[i,j]))
        
    for i in range(N):
        f[i+1].final=True
    
    return f

tr_fsa=trans_mat(pi,a,N)

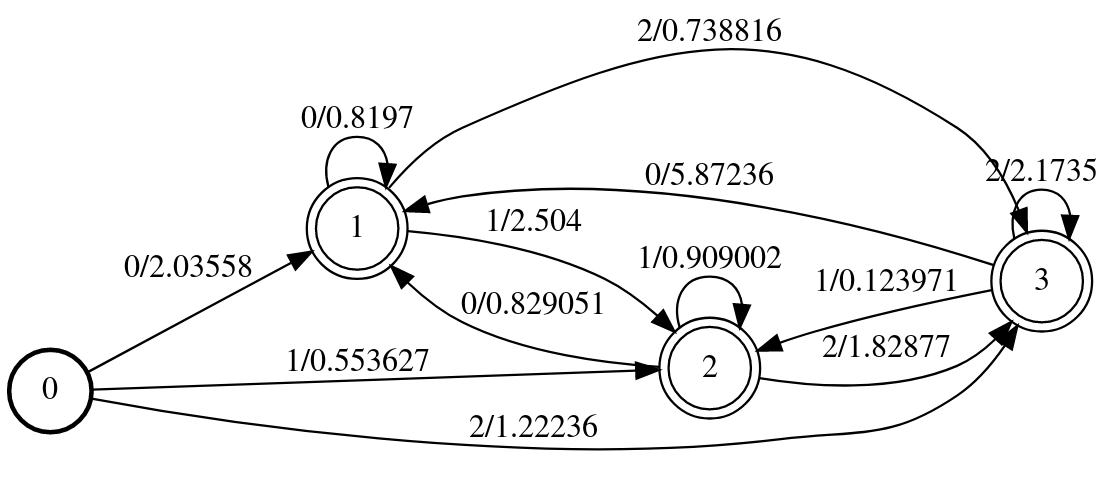
得到的WFST如下图所示，它编码了转移概率的信息。

图：编码先验和转移概率的WFST

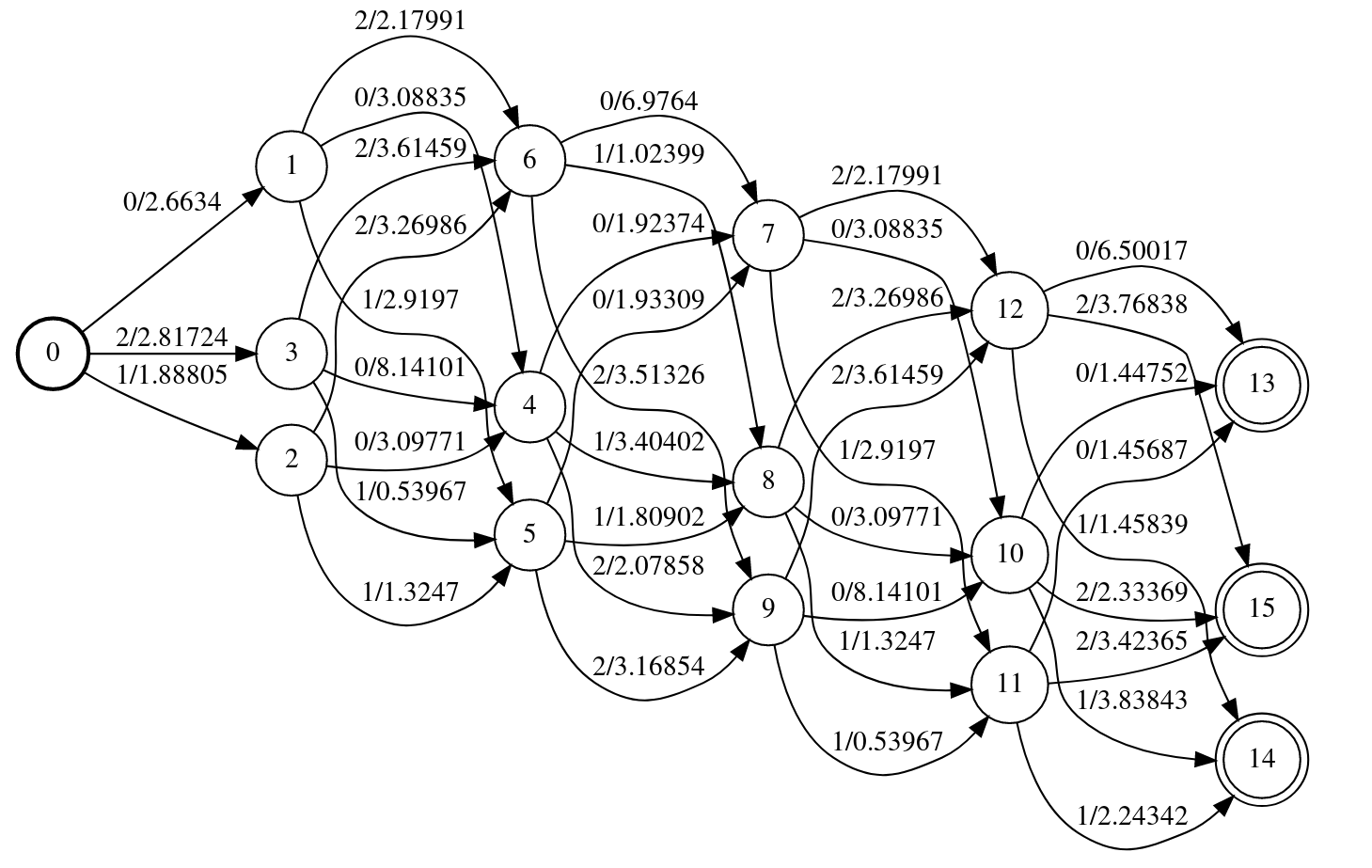
我们可以把这两个FSA composition起来，得到如下图所示的WFST。

out_fsa=obs_fsa>>tr_fsa

图：发射概率和转移概率WFST的composition

上面的WFST有些复杂，它的输入是状态序列，而输出是这个状态序列的概率(先验+跳转+发射，而且是-log空间上的)，因此我们可以使用shortest_path来寻找最优的路径(-log最小，也就是log最大，也就是概率最大的路径），这等价于Viterbi算法：

sh_p=out_fsa.shortest_path()shp_l=[]
for p in sh_p.paths():
    for s in p:
        shp_l.append(sh_p.osyms.find(s.olabel))
print(shp_l)
# 输出：
['0', '1', '2', '1', '2']
# 这和Viterbi算法的结果完全一样：
print(viterbi(*hmm))
[0 1 2 1 2]

上面的演示了用WFST实现简单HMM解码的过程，实际的语音识别解码器需要H、C、L和G这4个WFST，实现从观察到词序列的解码过程。