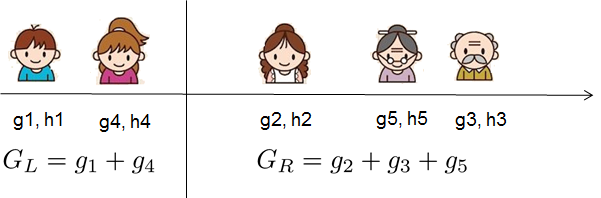本文简单的介绍Xgboost算法的原理,主要是参考了Introduction to Boosted Trees。当然也加入了作者的理解,用语也更加通俗简单。更多内容请点击深度学习理论与实战:提高篇。
本文假设读者理解决策树、ID3等基本的概念和算法,不了解的读者可以上网搜索相关资料。
CART树简介
梯度提升(Gradient Boosting)是一种算法,最早的论文是《Greedy Function Approximation: A Gradient Boosting Machine》,它可以应用到很多模型上,但是最常见的是用到决策树上,也就是GBDT(Gradient Boosting Decision Tree)。我们这里介绍XGBoost,它是一种GBDT的实现。
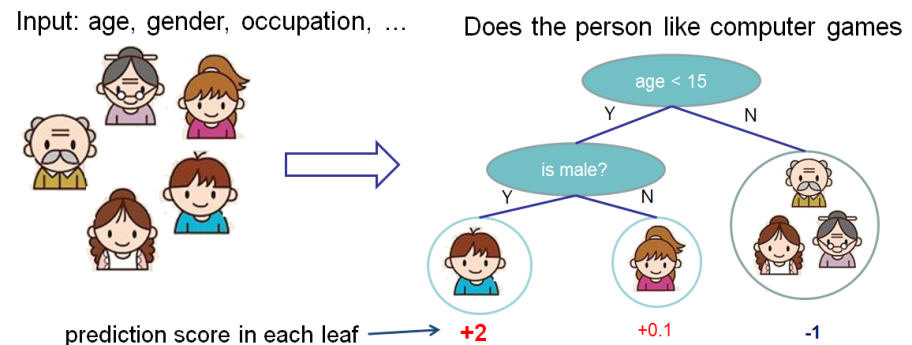
介绍Xgboost之前我们先了解一下分类与回归树(Classification And Regression Tree/CART)。它也是一种决策树,可以用于分类和回归。CART的每次划分都把一棵树划分成两棵子树,如下图所示。
对于二值的属性,很容易划分成两棵树;如果是多个取值的离散属性,我们也可以划分成两个集合,比如前面决策树里的例子,outlook有三个取值$\{sunny, overcast, rainy\}$,我们可以划分成$\{sunny, rainy\}$和$\{overcast\}$两个集合。某个属性如果有k种取值,那么就有$2^k-2$种划分方法(把所有元素全划分到一个集合是没有意义的,所以要减去2)。如果是有偏序关系的(通常是连续的,但是离散的也是可以的)集合,则可以根据它是否小于某个值来划分,比如上图根据$age<15$来划分子树。对于连续的属性怎么选择切分点呢?理论上我们可以选择所有的值,这显然无法穷尽。但是我们可以把实际出现过的值进行排序,比如age,假设在训练数据里出现的是:
10,20,24,40,60,80
那么我们选择22或者23还是23.987654321作为切分点是没有什么区别,因为对于这个训练数据来说这3个切分点的值都是把数据切分成${10,20}$和${24,40,60,80}$两个集合。所以排序后我们通常选择两个值的平均值作为切分点,对于上面的例子,切分点的值是:
15, 22, 32, 50, 70
另外如果两个排序后的值都是属于一个分类的话,那么可以把这两个值合并在一起,因为我们选择的切分点没有必要把它们分开,这样可以减少切分点的个数。
如果是分类问题,那么叶子节点的输出是一个分类标签,通常是选择这个叶子节点中出现最多的类别(当然最理想的是叶子节点的数据都是属于一个分类);如果是回归问题,那么叶子节点直接输出一个实数值,通常是这个叶子节点的数据的平均值。
对于任何一个节点都有很多属性以及切分点可以选择,CART算法会从所有这些可能中选择最”好”的一个。对于回归来说,我们可以使用均方误差(MSE)损失函数$L=\frac{1}{2}\sum_i(y_i-pred_i)^2$,也就是期望预测的$pred_i$和实际的$y_i$尽量接近。对于分类来说可以使用前面的熵,也就是期望叶子节点尽量都是一个分类。我们这里考虑回归的问题,比如上图的输出是根据一个人的年龄等属性来预测他对于游戏的兴趣得分(score)。
Boost算法
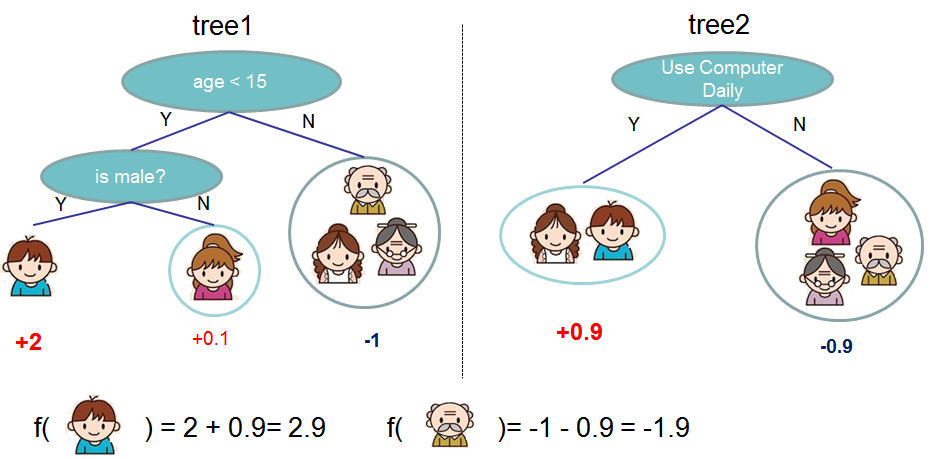
我们可以把多个CART进行融合,如下图所示,我们可以把两棵树的输出加起来得到最终的输出。
上图的两棵树是互补的,也就是说每棵树都学到部分的score,而最终的score是把它们加起来,我们也可以推广到k棵树:
\[\hat{y}_i = \sum_{k=1}^K f_k(x_i), f_k \in \mathcal{F}\]上式中K是CART树的个数,而$f_k$是第k个CART树。那这k个树是怎么学习出来的呢?我们首先需要定义损失函数:
\[\text{obj}(\theta) = \sum_i^n l(y_i, \hat{y}_i) + \sum_{k=1}^K \Omega(f_k)\]这里需要注意的是参数$\theta$在上面的公式中看不出来,一个CART树其实也是一个函数,它的输入是一个向量X,输出是一个实数值y。只不过这个函数不太好用闭式(closed-form)表示出来,但是它还是一个函数——给定一个输入对应唯一的一个输出。所以这里我们还是假设函数的参数是$\theta$,把损失函数定义为参数$\theta$的函数。此外上式的右边的$\Omega(f_k)$是第k个树的复杂度,用来对模型进行正则化防止过拟合。
Xgboost是一种boost算法(这就是Gradient Boost中boost的含义),所谓的boost就是提升的意思。我们首先有一个模型$f_1(x)$,这个模型预测的可能不准,然后我们再加一个$f_2(x)$变成$f_1(x)+f_2(x)$,这个$f_2(x)$学习的就是$f_1(x)$和真实值的误差。如果效果还不够理想再加一个$f_3(x)$,它学习真实值和$f_1+f_2$的误差。
XgBoost算法
上面的过程可以用下面的公式来描述:
\[\begin{split}\hat{y}_i^{(0)} &= 0\\ \hat{y}_i^{(1)} &= f_1(x_i) = \hat{y}_i^{(0)} + f_1(x_i)\\ \hat{y}_i^{(2)} &= f_1(x_i) + f_2(x_i)= \hat{y}_i^{(1)} + f_2(x_i)\\ &\dots\\ \hat{y}_i^{(t)} &= \sum_{k=1}^t f_k(x_i)= \hat{y}_i^{(t-1)} + f_t(x_i)\end{split}\]上式中经过t次boost之后的模型对于输入$x_i$的预测值记为$\hat{y}_i$。我们把t轮后的损失记为$obj^t$,它的计算公式为:
\[\begin{split} \text{obj}^{(t)} & = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t)}) + \sum_{i=1}^t\Omega(f_i) \\ & = \sum_{i=1}^n l(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) + \Omega(f_t) + \mathrm{constant} \end{split}\]假设我们使用MSE损失函数,则上式可以继续简化为:
\[\begin{split} \text{obj}^{(t)} & = \sum_{i=1}^n (y_i - (\hat{y}_i^{(t-1)} + f_t(x_i)))^2 + \sum_{i=1}^t\Omega(f_i) \\ & = \sum_{i=1}^n [2(\hat{y}_i^{(t-1)} - y_i)f_t(x_i) + f_t(x_i)^2] + \Omega(f_t) + \mathrm{constant} \end{split}\]但是有的损失函数可能没有这么简单的形式,为了让Xgboost可以使用更加复杂的损失函数,我们可以对前面的式子进行泰勒展开:
\[\text{obj}^{(t)} = \sum_{i=1}^n [l(y_i, \hat{y}_i^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t) + \mathrm{constant}\]其中$g_i$和$h_i$定义为:
\[\begin{split}g_i &= \partial_{\hat{y}_i^{(t-1)}} l(y_i, \hat{y}_i^{(t-1)})\\ h_i &= \partial_{\hat{y}_i^{(t-1)}}^2 l(y_i, \hat{y}_i^{(t-1)})\end{split}\]在做第t次boost的时候1到t-1时刻的模型都是固定的,因此$[l(y_i, \hat{y}_i^{(t-1)})$是一个常量,我们把上面的损失函数去掉常量后得到:
\[\sum_{i=1}^n [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t)\]我们再来分析一些这个损失函数,它是$f_t(x_i)$的函数,给定训练数据$x_i$和$y_i$以及1到t-1时刻的模型。我们把$\hat{y}_i^{(t-1)}$看成一个变量,则$l(y_i, \hat{y}_i^{(t-1)})$是这个变量的函数,因此可以求它对$\hat{y}_i^{(t-1)}$的导数。比如MSE的例子,$g_i=(\hat{y}_i^{(t-1)} - y_i)f_t(x_i)$。类似的$h_i$是损失函数对$\hat{y}_i^{(t-1)}$的二阶导数在$\hat{y}_i^{(t-1)}$点的值。
上面的损失函数分为两项,一项是预测值与真实值的差异带来的损失,另一项是模型的复杂度也就是正则项。我们先来看模型的复杂度怎么定义,一棵CART树可以由它的结构和权重唯一确定。所谓的结构就是从树的每一个节点的划分条件,比如上图,根节点的条件是$age<15$,如果把它变成$age < 30$或者$is male$,则就变成了另外一种结构。而任一叶子的权重发生变换,则这棵树(函数)也会发生变化。
前面我们提过CART虽然我们很难写出闭式的函数,但是它本质上还是一个函数,其输入x是空间$R^d$中的一个点,输出是一个实数。但是CART这个函数有一点比较特殊,虽然它的定义域(输入)是$R^d$,但是它的值域确实一个有限的大小为T的集合,这里T是CART树叶子的个数。为什么呢?因为任意给定一个输入$x \in R^d$,经过决策树的一系列决策之后最终一定落到某个叶子节点上,然后输出这个叶子节点的权重。
因此任何一个CART都可以定义为如下形式:
\[f_t(x) = w_{q(x)}, w \in R^T, q:R^d\rightarrow \{1,2,\cdots,T\} .\]上式中w是树叶的权重,我们把T个叶子编码成$1,2,…T$,对应的权重是$w_1,w_2,…,w_T$。而函数q(x)是决策函数,它把输入$x \in R^d$映射都某个叶子(的下标)。
有了上面的定义,我们可以定义CART的复杂度为:
\[\Omega(f) = \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2\]根据上面的定义,树的叶子越多(从而节点也越多,因为节点个数=2*叶子数-1),复杂度越高,此外权重越大也越复杂,参数$\lambda$用来控制这两者的比重。
接下来我们把$f_t$和$\Omega(f_t)$代入前面的损失函数中得到:
\[\begin{split}\text{obj}^{(t)} &\approx \sum_{i=1}^n [g_i w_{q(x_i)} + \frac{1}{2} h_i w_{q(x_i)}^2] + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2\\ &= \sum^T_{j=1} [(\sum_{i\in I_j} g_i) w_j + \frac{1}{2} (\sum_{i\in I_j} h_i + \lambda) w_j^2 ] + \gamma T\end{split}\]上式中$I_j = \{i | q(x_i)=j \}$,这看起来很难理解,但其实很简单,它是训练数据中所有落到叶子j的训练数据(的下标)。因为所有的训练样本最终都要落到某个叶子上,所以原来对于训练样本的求和下标i可以变成叶子节点的下标j。为了简化,我们再定义$G_j = \sum_{i\in I_j} g_i$和$H_j = \sum_{i\in I_j} h_i$。$G_j$就是所有落到叶子j的训练数据中的导数之和,而$H_j$是二阶导数之和。如果树的结构给定了(但是叶子的权重可以不给定),则映射函数$q$是已知的,因此$G_j$和$H_j$也是已知的。这里可以看成$G_j$和$H_j$只依赖与是树的结构q,而与权重w无关。
有了上面的记号,损失函数可以进一步化简:
\[\text{obj}^{(t)} = \sum^T_{j=1} [G_jw_j + \frac{1}{2} (H_j+\lambda) w_j^2] +\gamma T\]回顾一下,我们的目标是在所有的CART树里选择损失最少的那个作为当前的$f_t(x)$。这当然有太多选择,我们无法穷尽。但是我们先假设树的结构是固定的,因此$G_j$和$H_j$是已知的,那么$\text{obj}^{(t)}$只是参数$w_j$的二次函数,因此我们直接求出最优的$w_j^\ast$和对应的$\text{obj}^\ast$:
\[\begin{split}w_j^\ast &= -\frac{G_j}{H_j+\lambda}\\ \text{obj}^\ast &= -\frac{1}{2} \sum_{j=1}^T \frac{G_j^2}{H_j+\lambda} + \gamma T\end{split}\]如下图所示,假定树的结构给定,因此我们可以把5个训练数据分别映射到3个叶子节点上,图中样本1映射到第一个叶子,样本4映射到第二个叶子,而剩下的2、3和5被映射到第三个。 也就是$I_1=\{1\}, I_2=\{4\}, I_3=\{2,3,5\}$,因此我们可以计算$G_1,G_2,G_3$和$H_1,H_2,H_3$。最后我们可以求出3个叶子最优的权重$w_1^\ast,w_2^\ast,w_3^\ast$。
我们的目标是求出所有CART树中$obj^t$最小的那棵树,理论上我们应该可以穷尽所有的树结构,解出这种结构最优的$w^\ast$和$obj^\ast$,然后在所有的结构里选择最好的一个。
但是树的结构太多了,实际我们没法穷举,因此实际中我们使用贪心的算法,这不能保证找到全局最优解,但是通常能够找到还不错的解。
和前面的决策树类似,每次分裂时我们选择损失最小的分裂方式。当然这不能保证全局最优,因为有可能某个全局最优解的前几次分类看起来并不好,但是后面就越来越好了。
我们可以定义一种分裂方式的Gain:
\[Gain = \frac{1}{2} \left[\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}\right] - \gamma\]它其实就是分裂后的loss减去分裂前的loss,读者可以自行验证一下。
我们从所有的分裂方式中选择Gain最大的那个,如果最大的Gain是小于零的,就可以停止分裂了。也就是说分裂减少的误差还不足以弥补模型变复杂带来的损失,那么就没有必要在分裂下去了。
比如前面的例子,在树根有很多中分裂方式,最好的是根据条件$age<15$来分裂,如下图所示。分离后变成左右两棵子树,可以计算其Gain,这个Gain是最大的。
通过上面的贪心算法,我们可以得到t时刻的最优的CART树。通过类似的方式,我们可以继续求t+1,t+2,…时刻的CART树。
- 显示Disqus评论(需要科学上网)