目录
本章中,您将学习如何使用代理对象(Proxy Objects)和惰性求值(Lazy Evaluation)来推迟某些代码的执行直到需要时。使用代理对象可以在幕后实现优化,同时保持暴露给用户的接口不变。
本章涵盖内容:
- 惰性求值与即时求值
- 使用代理对象避免冗余计算
- 在与代理对象一起工作时重载操作符
引入惰性求值与代理对象
首先,本章介绍的技术用于在库中向库的用户隐藏优化。这样做很有用,因为将每一种优化技术都暴露为一个单独的函数,需要库用户投入大量的注意力和学习成本。它还会使代码库充斥着大量特定功能的函数,使其难以阅读和理解。通过使用代理对象,我们可以在幕后实现优化;最终的代码既优化又具有可读性。
惰性求值 vs. 即时求值
惰性求值(Lazy Evaluation)是一种将操作推迟到真正需要其结果时才执行的技术。与此相反,操作立即执行的方式称为即时求值(Eager Evaluation)。在某些情况下,即时求值是不可取的,因为我们可能最终构造了一个从未被使用的值。
为了演示即时求值和惰性求值之间的区别,假设我们正在编写某种具有多个关卡的游戏。每当一个关卡完成时,我们需要显示当前得分。在这里,我们将关注游戏的几个组件:
- 一个
ScoreView类,负责显示用户的得分,如果获得了奖励,还会显示可选的奖励图像。 - 一个
Image类,代表加载到内存中的图像。 - 一个
load()函数,用于从磁盘加载图像。
在本示例中,类和函数的具体实现并不重要,但声明如下所示:
class Image { /* ... */ }; // Buffer with JPG data
auto load(std::string_view path) -> Image; // Load image at path
class ScoreView {
public:
// Eager, requires loaded bonus image
void display(const Image& bonus);
// Lazy, only load bonus image if necessary
void display(std::function<Image()> bonus);
// ...
};
这里提供了两个版本的 display():第一个版本需要一个完全加载的奖励图像,而第二个版本接受一个函数,该函数仅在需要奖励图像时才会被调用。
使用第一个即时(eager)版本如下所示:
// 总是即时加载奖励图像
const auto eager = load("/images/stars.jpg");
score.display(eager);
使用第二个惰性(lazy)版本如下所示:
// 仅在需要时惰性加载默认图像
auto lazy = [] { return load("/images/stars.jpg"); };
score.display(lazy);
即时版本将始终把默认图像加载到内存中,即使它从未显示。然而,奖励图像的惰性加载将保证仅在 ScoreView 真正需要显示奖励图像时,图像才会被加载。
这是一个非常简单的例子,但其核心思想是,您的代码表达方式几乎与即时声明时相同。隐藏代码是惰性求值这一事实的一种技术是使用代理对象。
代理对象
代理对象是库的内部对象,不打算暴露给库的用户。它们的任务是推迟操作直到需要时,并收集表达式的数据直到可以对其进行求值和优化。然而,代理对象在幕后工作;库的用户应该能够处理这些表达式,就好像代理对象不存在一样。换句话说,通过使用代理对象,您可以在库中封装优化,同时保持接口不变。
您现在将学习如何使用代理对象,以便惰性地求值更高级的表达式。
代理对象:避免构造对象与惰性求值
即时求值(Eager Evaluation)可能产生不希望的效果,即对象被不必要地构造。通常这不是问题,但如果对象的构造开销很大(例如,因为涉及堆分配),那么就有合理的理由去优化,避免不必要地构造那些没有实际用途的短命对象。
使用代理对象比较连接后的字符串
我们现在将通过一个使用代理对象的极简示例,让您了解代理对象是什么以及它们的用途。这并不是为了提供一个通用的、可用于生产环境的字符串比较优化解决方案。
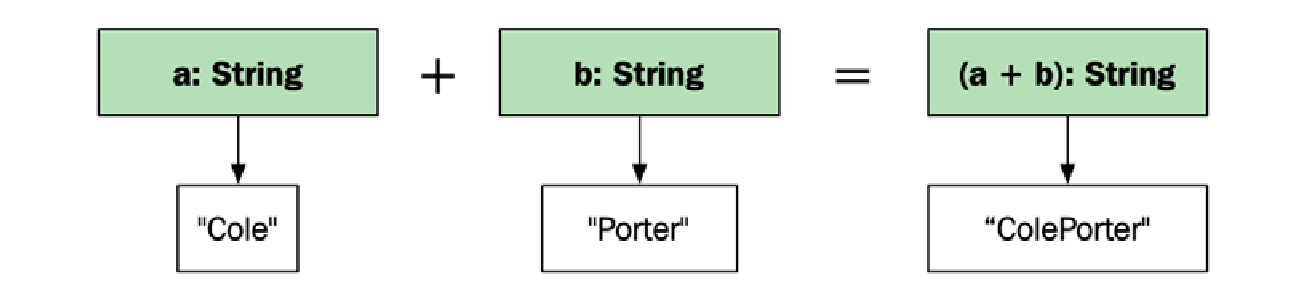
话虽如此,请看这段代码片段,它连接了两个字符串并比较了结果:
auto a = std::string{"Cole"};
auto b = std::string{"Porter"};
auto c = std::string{"ColePorter"};
auto is_equal = (a + b) == c; // true
这里的问题在于 (a + b) 构造了一个新的临时字符串,以便将其与 c 进行比较。与其构造一个新字符串,不如直接比较连接后的内容,如下所示:
auto is_concat_equal(const std::string& a, const std::string& b,
const std::string& c) {
return
a.size() + b.size() == c.size() &&
std::equal(a.begin(), a.end(), c.begin()) &&
std::equal(b.begin(), b.end(), c.begin() + a.size());
}
然后我们可以像这样使用它:
auto is_equal = is_concat_equal(a, b, c);
从性能角度来看,我们取得了胜利,但从语法角度来看,一个充斥着这种特殊便利函数的代码库会很难维护。因此,让我们看看如何在保持原始语法不变的情况下实现这种优化。
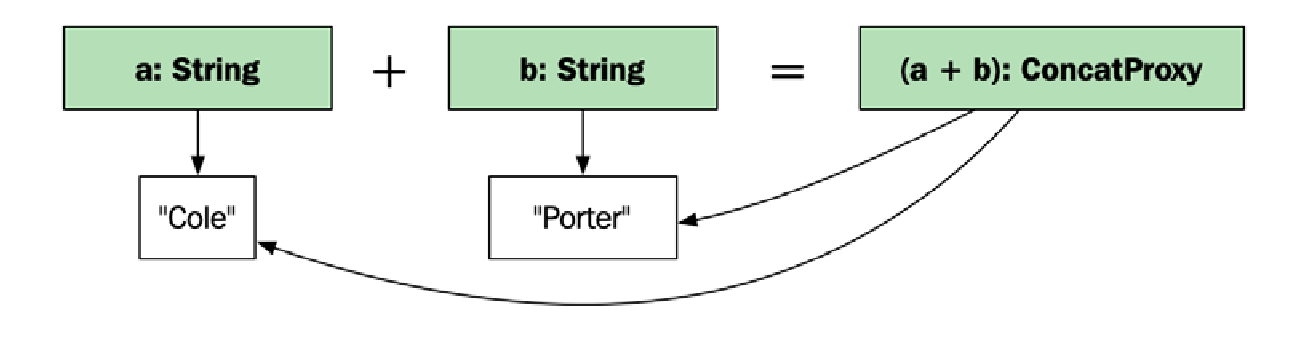
实现代理对象
首先,我们将创建一个表示两个字符串连接的代理类:
struct ConcatProxy {
const std::string& a;
const std::string& b;
};
然后,我们将构造一个包含 std::string 和重载 operator+() 函数的自定义 String 类。请注意,这是一个关于如何制作和使用代理对象的示例;我不建议您创建自己的 String 类:
class String {
public:
String() = default;
String(std::string str) : str_{std::move(str)} {}
std::string str_{};
};
auto operator+(const String& a, const String& b) {
return ConcatProxy{a.str_, b.str_};
}
最后,我们将创建一个全局的 operator==() 函数,它会反过来使用优化的 is_concat_equal() 函数,如下所示:
auto operator==(ConcatProxy&& concat, const String& str) {
return is_concat_equal(concat.a, concat.b, str.str_);
}
现在我们万事俱备,可以获得两全其美的效果:
auto a = String{"Cole"};
auto b = String{"Porter"};
auto c = String{"ColePorter"};
auto is_equal = (a + b) == c; // true
换句话说,我们获得了 is_concat_equal() 的性能,同时保留了使用 operator==() 的富有表现力的语法。
右值修饰符
在前面的代码中,全局的 operator==() 函数只接受 ConcatProxy 右值:
auto operator==(ConcatProxy&& concat, const String& str) { // ...
如果我们接受一个 ConcatProxy 左值,我们可能会意外地滥用代理,如下所示:
auto concat = String{"Cole"} + String{"Porter"};
auto is_cole_porter = concat == String{"ColePorter"};
这里的问题是,当比较执行时,保存 "Cole" 和 "Porter" 的两个临时 String 对象已经被销毁了,这会导致失败。(请记住,ConcatProxy 类只持有对这些字符串的引用。)但由于我们强制 concat 对象必须是右值,前面的代码将不会编译,从而避免了可能的运行时崩溃。当然,你可以通过使用 std::move(concat) == String("ColePorter") 将其转换为右值来强制编译,但这不太可能是一个现实情况。
赋值连接代理
现在,您可能会想,如果我们实际上想将连接后的字符串存储为一个新字符串,而不是仅仅比较它,该怎么办?我们只需重载一个 operator String() 函数,如下所示:
struct ConcatProxy {
const std::string& a;
const std::string& b;
operator String() const && { return String{a + b}; }
};
两个字符串的连接现在可以隐式地将自身转换为一个 String:
String c = String{"Marc"} + String{"Chagall"};
不过,这里有一个小问题:我们不能使用 auto 关键字初始化新的 String 对象,因为这会导致 c 被推导为 ConcatProxy:
auto c = String{"Marc"} + String{"Chagall"};
// 由于这里的 auto 关键字,c 是一个 ConcatProxy
遗憾的是,我们没有办法绕过这个问题;结果必须被显式地转换为 String。
是时候看看我们优化的版本比普通情况快多少了。
性能评估
为了评估性能优势,我们将使用以下基准测试,它连接并比较 10,000 个大小为 50 的字符串:
template <typename T>
auto create_strings(int n, size_t length) -> std::vector<T> {
// Create n random strings of the specified length
// ...
}
template <typename T>
void bm_string_compare(benchmark::State& state) {
const auto n = 10'000, length = 50;
const auto a = create_strings<T>(n, length);
const auto b = create_strings<T>(n, length);
const auto c = create_strings<T>(n, length * 2);
for (auto _ : state) {
for (auto i = 0; i < n; ++i) {
auto is_equal = a[i] + b[i] == c[i];
benchmark::DoNotOptimize(is_equal);
}
}
}
BENCHMARK_TEMPLATE(bm_string_compare, std::string);
BENCHMARK_TEMPLATE(bm_string_compare, String);
BENCHMARK_MAIN();
在使用 Intel Core i7 CPU 执行时,我使用 GCC 实现了 40 倍的加速。直接使用 std::string 的版本在 1.6 毫秒内完成,而使用 String 的代理版本仅在 0.04 毫秒内完成。当对长度为 10 的短字符串运行相同的测试时,加速约为 20 倍。造成巨大差异的一个原因是,小字符串会利用在第 7 章《内存管理》中讨论的小字符串优化来避免堆分配。基准测试表明,当我们避免了临时字符串及其可能带来的堆分配时,使用代理对象的加速是相当可观的。
ConcatProxy 类帮助我们在比较字符串时隐藏了一个优化。希望这个简单的例子能激励您开始思考如何在保持 API 设计简洁的同时实现性能优化的方法。
接下来,您将看到另一个可以隐藏在代理类后面的有用优化。
推迟 $\text{sqrt}$ 计算
本节将向您展示如何使用代理对象(proxy object)来推迟,甚至避免,在比较二维向量长度时使用计算量大的 $\text{std::sqrt()}$ 函数。
一个简单的二维向量类
我们从一个简单的二维向量类开始。它有 $x$ 和 $y$ 坐标,以及一个名为 $\text{length()}$ 的成员函数,用于计算从原点到位置 $(x, y)$ 的距离。我们将该类命名为 $\text{Vec2D}$。定义如下:
class Vec2D {
public:
Vec2D(float x, float y) : x_{x}, y_{y} {}
auto length() const {
auto squared = x_ * x_ + y_ * y_;
return std::sqrt(squared);
}
private:
float x_{};
float y_{};
};
以下是客户端如何使用 $\text{Vec2D}$ 的示例:
auto a = Vec2D{3, 4};
auto b = Vec2D{4, 4};
auto shortest = a.length() < b.length() ? a : b;
auto length = shortest.length();
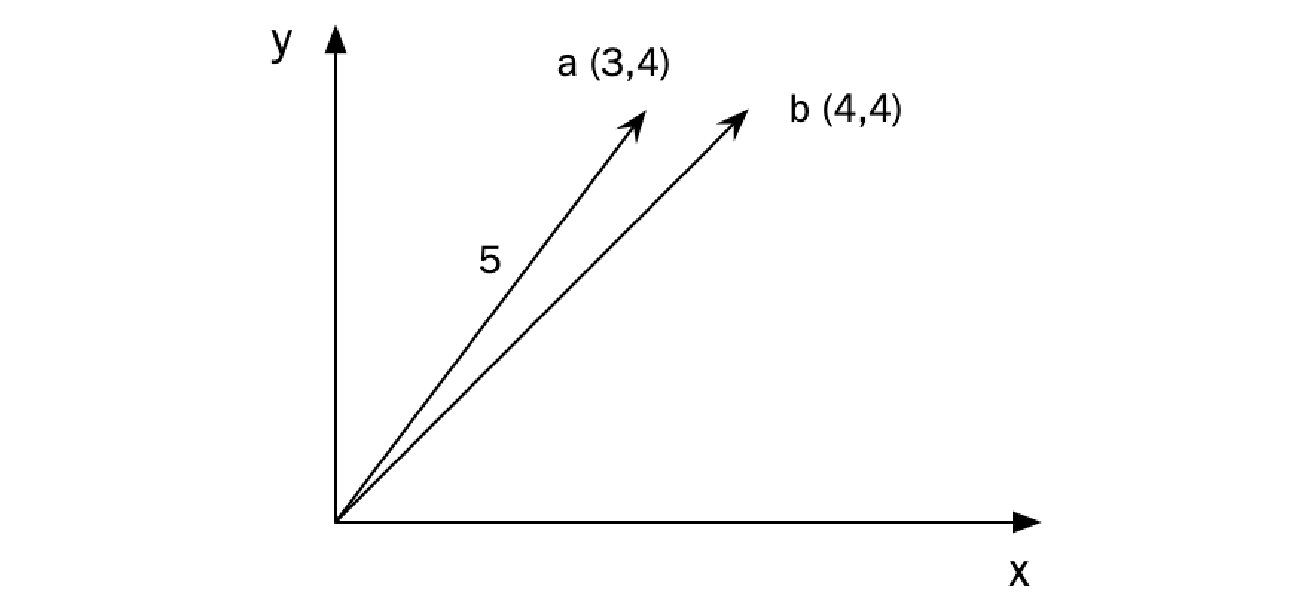
std::cout << length; // Prints 5
该示例创建了两个向量并比较它们的长度。然后将最短向量的长度打印到标准输出。下图说明了向量及其到原点的计算长度。
数学原理
深入研究计算的数学原理,您可能会注意到一些有趣的地方。用于计算长度的公式如下:
\[L = \sqrt{x^2 + y^2}\]然而,如果我们只需要比较两个向量之间的距离,那么平方长度就足够了,如下面的公式所示:
\[L_a < L_b \quad \Leftrightarrow \quad L_a^2 < L_b^2\]平方根可以使用函数 $\text{std::sqrt()}$ 来计算。但是,如前所述,如果我们只是想比较两个向量之间的长度,则不需要平方根操作,因此可以省略它。好处是 $\text{std::sqrt()}$ 是一个相对较慢的操作,这意味着如果我们通过长度比较大量的向量,就可以获得一些性能提升。问题是,如何在保持简洁语法的同时实现这一点?让我们看看如何使用代理对象来在底层进行这种优化,同时为库提供简单的接口。
为了清晰起见,我们从原始的 $\text{Vec2D}$ 类开始,但我们将 $\text{length()}$ 函数拆分为两部分——$\text{length_squared()}$ 和 $\text{length()}$,如下所示:
class Vec2D {
public:
Vec2D(float x, float y) : x_{x}, y_{y} {}
auto length_squared() const {
return x_ * x_ + y_ * y_;
}
auto length() const {
return std::sqrt(length_squared());
}
private:
float x_{};
float y_{};
};
现在,我们的 $\text{Vec2D}$ 类的客户端可以在只比较不同向量的长度时,使用 $\text{length_squared()}$ 来获得一些性能提升。
假设我们想要实现一个方便的工具函数,它返回一系列 $\text{Vec2D}$ 对象的最小长度。我们现在有两种选择:在进行比较时使用 $\text{length()}$ 函数或 $\text{length_squared()}$ 函数。它们对应的实现如下例所示:
// Simple version using length()
auto min_length(const auto& r) -> float {
assert(!r.empty());
auto cmp = [](auto&& a, auto&& b) {
return a.length() < b.length();
};
auto it = std::ranges::min_element(r, cmp);
return it->length();
}
使用 $\text{length_squared()}$ 进行比较的第二个优化版本将如下所示:
// Fast version using length_squared()
auto min_length(const auto& r) -> float {
assert(!r.empty());
auto cmp = [](auto&& a, auto&& b) {
return a.length_squared() < b.length_squared(); // Faster
};
auto it = std::ranges::min_element(r, cmp);
return it->length(); // But remember to use length() here!
}
第一个使用 $\text{length()}$ 的版本在 $\text{cmp}$ 内部的优势是更具可读性且更容易写对,而第二个版本的优势是更快。提醒一下,第二个版本提速的原因是我们在 $\text{cmp}$ lambda 内部避免了对 $\text{std::sqrt()}$ 的调用。
最佳解决方案将是拥有第一个版本使用 $\text{length()}$ 的语法,以及第二个版本使用 $\text{length_squared()}$ 的性能。
根据 $\text{Vec2D}$ 类将被使用的上下文,暴露 $\text{length_squared()}$ 这样的函数可能有很好的理由。但让我们假设我们团队中的其他开发人员不理解存在 $\text{length_squared()}$ 函数的原因,并认为该类令人困惑。因此,我们决定想出更好的方法来避免出现两个暴露向量长度属性的函数版本。
您可能已经猜到了,是时候使用代理类来隐藏这种复杂性了。
为了实现这一点,$\text{length()}$ 成员函数不再返回 $\text{float}$ 值,而是返回一个对用户隐藏的中间对象。根据用户使用这个隐藏代理对象的方式,它应该避免 $\text{std::sqrt()}$ 操作,直到真正需要为止。在接下来的部分中,我们将实现一个名为 $\text{LengthProxy}$ 的类,它将是 $\text{Vec2D::length()}$ 返回的代理对象的类型。
实现 $\text{LengthProxy}$ 对象
是时候实现 $\text{LengthProxy}$ 类了,它包含一个表示平方长度的 $\text{float}$ 数据成员。为了防止类的用户将平方长度与常规长度混淆,实际的平方长度永远不会被暴露。相反,$\text{LengthProxy}$ 有一个隐藏的 $\text{friend}$ 函数,用于比较其平方长度和常规长度,如下所示:
class LengthProxy {
public:
LengthProxy(float x, float y) : squared_{x * x + y * y} {}
bool operator==(const LengthProxy& other) const = default;
auto operator<=>(const LengthProxy& other) const = default;
friend auto operator<=>(const LengthProxy& proxy, float len) {
return proxy.squared_ <=> len * len; // C++20
}
operator float() const { // Allow implicit cast to float
return std::sqrt(squared_);
}
private:
float squared_{};
};
我们定义了 $\text{operator float()}$ 来允许 $\text{LengthProxy}$ 隐式转换为 $\text{float}$。 $\text{LengthProxy}$ 对象也可以相互比较。通过使用新的 $\text{C++20}$ 比较,我们简单地默认了相等运算符和三路比较运算符,让编译器为我们生成所有必要的比较运算符。
接下来,我们重写 $\text{Vec2D}$ 类,使其返回 $\text{LengthProxy}$ 类的对象,而不是实际的 $\text{float}$ 长度:
class Vec2D {
public:
Vec2D(float x, float y) : x_{x}, y_{y} {}
auto length() const {
return LengthProxy{x_, y_}; // Return proxy object
}
float x_{};
float y_{};
};
有了这些添加,是时候使用我们新的代理类了。
使用 $\text{LengthProxy}$ 比较长度
在这个示例中,我们将比较两个向量 $a$ 和 $b$,并确定 $a$ 是否比 $b$ 短。请注意,代码的语法看起来与我们没有使用代理类时完全相同:
auto a = Vec2D{23, 42};
auto b = Vec2D{33, 40};
bool a_is_shortest = a.length() < b.length();
在底层,最后一个语句展开类似于这样:
// These LengthProxy objects are never visible from the outside
LengthProxy a_length = a.length();
LengthProxy b_length = b.length();
// Member operator< on LengthProxy is invoked,
// which compares member squared_
auto a_is_shortest = a_length < b_length;
太棒了! $\text{std::sqrt()}$ 操作被省略了,而 $\text{Vec2D}$ 类的接口仍然完好无损。我们之前实现的简单版 $\text{min_length()}$ 现在可以更有效地执行其比较,因为 $\text{std::sqrt()}$ 操作被省略了。
以下是简单实现,它现在也变得高效了:
// Simple and efficient
auto min_length(const auto& r) -> float {
assert(!r.empty());
auto cmp = [](auto&& a, auto&& b) {
return a.length() < b.length();
};
auto it = std::ranges::min_element(r, cmp);
return it->length();
}
$\text{Vec2D}$ 对象之间优化的长度比较现在在底层发生。实现 $\text{min_length()}$ 函数的程序员不需要知道此优化即可从中受益。让我们看看如果我们需要实际长度,它会是什么样子。
使用 $\text{LengthProxy}$ 计算长度
当请求实际长度时,调用代码会发生一点变化。为了触发到 $\text{float}$ 的隐式转换,我们必须在声明下面的 $\text{len}$ 变量时明确指定 $\text{float}$ 类型;也就是说,我们不能像通常那样只使用 $\text{auto}$:
auto a = Vec2D{23, 42};
float len = a.length(); // Note, we cannot use auto here
如果我们只写 $\text{auto}$,那么 $\text{len}$ 对象将是 $\text{LengthProxy}$ 类型而不是 $\text{float}$。我们不希望代码库的用户显式处理 $\text{LengthProxy}$ 对象;代理对象应该在后台运行,只应利用它们的结果(在这种情况下,是比较结果或实际距离值,即 $\text{float}$)。尽管我们不能完全隐藏代理对象,但让我们看看如何收紧它们以防止误用。
防止 $\text{LengthProxy}$ 的误用
您可能已经注意到,存在使用 $\text{LengthProxy}$ 类可能导致性能变差的情况。在以下示例中,根据程序员对长度值的请求,$\text{std::sqrt()}$ 函数被多次调用:
auto a = Vec2D{23, 42};
auto len = a.length();
float f0 = len; // Assignment invoked std::sqrt()
float f1 = len; // std::sqrt() of len is invoked again
尽管这是一个人为的示例,但在现实世界中可能会发生这种情况,我们希望强制 $\text{Vec2D}$ 的用户每个 $\text{LengthProxy}$ 对象只调用一次 $\text{operator float()}$。为了防止误用,我们使 $\text{operator float()}$ 成员函数只能在右值 (rvalues) 上调用;也就是说,$\text{LengthProxy}$ 对象只有在没有绑定到变量时才能转换为浮点数。
我们通过在 $\text{operator float()}$ 成员函数上使用 && 修饰符来强制实现此行为。 && 修饰符的作用类似于 $\text{const}$ 修饰符,但 $\text{const}$ 修饰符强制成员函数不修改对象,而 && 修饰符强制函数在临时对象上操作。
修改后的代码如下:
operator float() const && { return std::sqrt(squared_); }
如果我们在绑定到变量的 $\text{LengthProxy}$ 对象上调用 $\text{operator float()}$,例如以下示例中的 $\text{len}$ 对象,编译器将拒绝编译:
auto a = Vec2D{23, 42};
auto len = a.length(); // len is of type LenghtProxy
float f = len; // Doesn't compile: len is not an rvalue
但是,我们仍然可以直接在从 $\text{length()}$ 返回的右值上调用 $\text{operator float()}$,如下所示:
auto a = Vec2D{23, 42};
float f = a.length(); // OK: call operator float() on rvalue
后台仍会创建一个临时 $\text{LengthProxy}$ 实例,但由于它没有绑定到变量,我们被允许将其隐式转换为 $\text{float}$。这将防止误用,例如多次在一个 $\text{LengthProxy}$ 对象上调用 $\text{operator float()}$。
性能评估
为了说明这一点,让我们看看我们实际获得了多少性能提升。我们将对以下版本的 $\text{min_element()}$ 进行基准测试:
auto min_length(const auto& r) -> float {
assert(!r.empty());
auto it = std::ranges::min_element(r, [](auto&& a, auto&& b) {
return a.length() < b.length();
});
return it->length();
}
为了将代理对象优化与某种东西进行比较,我们将定义一个替代版本 $\text{Vec2DSlow}$,它总是使用 $\text{std::sqrt()}$ 计算实际长度:
struct Vec2DSlow {
float length() const { // Always compute
auto squared = x_ * x_ + y_ * y_; // actual length
return std::sqrt(squared); // using sqrt()
}
float x_, y_;
};
使用 Google Benchmark 和函数模板,我们可以看到在查找 $\text{1,000}$ 个向量的最小长度时我们获得了多少性能提升:
template <typename T>
void bm_min_length(benchmark::State& state) {
auto v = std::vector<T>{};
std::generate_n(std::back_inserter(v), 1000, [] {
auto x = static_cast<float>(std::rand());
auto y = static_cast<float>(std::rand());
return T{x, y};
});
for (auto _ : state) {
auto res = min_length(v);
benchmark::DoNotOptimize(res);
}
}
BENCHMARK_TEMPLATE(bm_min_length, Vec2DSlow);
BENCHMARK_TEMPLATE(bm_min_length, Vec2D);
BENCHMARK_MAIN();
在 $\text{Intel i7 CPU}$ 上运行此基准测试生成了以下结果:
- 使用未优化的 $\text{Vec2DSlow}$ 和 $\text{std::sqrt()}$ 耗时 $7,900$ 纳秒
- 使用带有 $\text{LengthProxy}$ 的 $\text{Vec2D}$ 耗时 $1,800$ 纳秒
这种性能提升对应于超过 4 倍的加速。
这是我们如何避免在某些情况下不必要的计算的一个示例。但我们没有使 $\text{Vec2D}$ 的接口复杂化,而是成功地将优化封装在代理对象内部,从而使所有客户端都能受益于优化,而不牺牲清晰度。
一种相关的优化 C++ 表达式的技术是表达式模板(expression templates)。它使用模板元编程在编译时生成表达式树。该技术可用于避免临时对象并实现惰性求值(lazy evaluation)。表达式模板是 Boost Basic Linear Algebra Library 和 Eigen 中使线性代数算法和矩阵运算快速的技术之一。您可以在 Bjarne Stroustrup 的《The C++ Programming Language},第 4 版》中阅读更多关于如何在设计矩阵类时使用表达式模板和融合操作的内容。
我们将通过查看将代理对象与重载运算符结合使用时获得好处的其他方式来结束本章。
创意性的操作符重载与代理对象
您可能已经知道,C++ 能够重载多种操作符,包括加减等标准数学操作符。重载的数学操作符可用于创建行为类似于内置数值类型的自定义数学类,从而提高代码的可读性。另一个例子是流操作符,它在标准库中被重载,用于将对象转换为流,如下所示:
std::cout << "iostream " << "uses " << "overloaded " << "operators.";
然而,一些库在其他上下文中也使用重载。如前所述,Ranges 库使用重载来组合视图(Views),如下所示:
const auto r = {-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5};
auto odd_positive_numbers = r
| std::views::filter([](auto v) { return v > 0; })
| std::views::filter([](auto v) { return (v % 2) == 1; });
接下来,我们将探索如何将管道操作符 (|) 与代理类 (Proxy Classes) 结合使用。
管道操作符作为扩展方法
与其他语言(例如 C#、Swift 和 JavaScript)相比,C++ 不支持扩展方法;也就是说,您不能在本地为一个类添加一个新的成员函数来扩展它。
例如,您不能为 $\text{std::vector}$ 扩展一个 $\text{contains(T val)}$ 函数,并像这样使用:
auto numbers = std::vector{1, 2, 3, 4};
auto has_two = numbers.contains(2);
然而,您可以通过重载管道操作符来实现几乎等效的语法:
auto has_two = numbers | contains(2);
通过使用代理类,可以轻松实现这一点。
管道操作符的实现
我们的目标是实现一个简单的管道操作符,以便我们可以编写以下代码:
auto numbers = std::vector{1, 3, 5, 7, 9};
auto seven = 7;
bool has_seven = numbers | contains(seven);
用于管道语法的 $\text{contains()}$ 函数有两个参数:$\text{numbers}$(左侧)和 $\text{seven}$(右侧)。由于左侧参数 $\text{numbers}$ 可以是任何类型,我们需要重载操作符的右侧参数包含一些独特的东西。因此,我们创建了一个名为 $\text{ContainsProxy}$ 的结构体模板,用于持有右侧的参数值。这样,重载的管道操作符就能够识别这个重载:
template <typename T>
struct ContainsProxy { const T& value_; };
template <typename Range, typename T>
auto operator|(const Range& r, const ContainsProxy<T>& proxy) {
const auto& v = proxy.value_;
return std::find(r.begin(), r.end(), v) != r.end();
}
现在,我们可以像这样使用 $\text{ContainsProxy}$:
auto numbers = std::vector{1, 3, 5, 7, 9};
auto seven = 7;
auto proxy = ContainsProxy<decltype(seven)>{seven};
bool has_seven = numbers | proxy;
管道操作符工作正常,但语法仍然不够优雅,因为我们需要手动指定类型。为了使语法更简洁,我们可以简单地创建一个便利函数,它接受值并创建一个包含该值的代理对象:
template <typename T>
auto contains(const T& v) { return ContainsProxy<T>{v}; }
这就是我们所需要的一切;现在我们可以将它用于任何类型或容器:
auto penguins = std::vector<std::string>{"Ping","Roy","Silo"};
bool has_silo = penguins | contains("Silo");
本节所涵盖的示例展示了实现管道操作符的基本方法。像 $\text{Ranges}$ 库和 Fit 库(作者 $\text{Paul Fultz}$,可在 $\text{https://github.com/pfultz2/Fit}$ 获取)等库实现了适配器,它们接受一个普通函数,并赋予该函数使用管道语法调用的能力。
总结
在本章中,您学习了惰性求值(Lazy Evaluation)和急切求值(Eager Evaluation)之间的区别。您还学习了如何使用隐藏的代理对象在幕后实现惰性求值,这意味着您现在了解了如何在保持类易于使用的接口的同时实现惰性求值优化。将复杂的优化隐藏在库类内部,而不是在应用程序代码中暴露它们,使得应用程序代码更具可读性,并减少出错的可能性。
在下一章中,我们将把重点转向使用 C++ 进行并发和并行编程。
- 显示Disqus评论(需要科学上网)