目录
- 并行性的重要性
- 并行算法
- 并行标准库算法 (Parallel standard library algorithms)
- 总结
前面的章节重点介绍了如何利用线程和协程在程序中引入并发(concurrency)和异步(asynchrony)。本章将重点讨论独立任务的并行执行,这与并发相关但又有所区别。
在早期的章节中,我强调我更喜欢使用标准库算法而不是手工编写 for 循环。在本章中,您将看到使用 C++17 引入的执行策略(execution policies)的标准库算法所带来的巨大优势。
本章不会深入探讨并行化算法或并行编程的一般理论,因为这些主题过于复杂,无法在一章中涵盖。此外,关于这个主题的书籍也很多。相反,本章将采取更实际的方法,演示如何扩展现有的 C++ 代码库以利用并行性,同时保持代码库的可读性。换句话说,我们不希望并行性妨碍可读性;相反,我们希望并行性被抽象出来,以便代码的并行化仅仅是更改算法的一个参数的问题。
在本章中,您将学到:
- 实现并行算法的各种技术
- 如何评估并行算法的性能
- 如何调整代码库以使用标准库算法的并行扩展
并行编程是一个复杂的话题,所以在开始之前,您需要理解引入并行性的根本动机。
并行性的重要性
从程序员的角度来看,如果当今的计算机硬件是一个 $100\text{ GHz}$ 单核 CPU 而不是 $3\text{ GHz}$ 多核 CPU,那将会非常方便;我们就不必关心并行性了。不幸的是,让单核 CPU 越来越快已经触及了物理极限。因此,随着计算机硬件的发展朝着多核 CPU 和可编程 GPU 的方向发展,程序员必须使用高效的并行模式才能最大程度地利用硬件。
并行算法允许我们通过在多核 CPU 或 GPU 上同时(at the exact same time)执行多个独立任务或子任务来优化程序。
并行算法
正如在第 $11$ 章《并发》中提到的,并发和并行这两个术语可能有点难以区分。回顾一下,如果一个程序在重叠的时间段内运行多个独立的控制流,则称其为并发运行。另一方面,并行程序会同时执行多个任务或子任务,这需要具有多核的硬件。我们使用并行算法来优化延迟(latency)或吞吐量(throughput)。如果我们没有可以同时执行多个任务以实现更好性能的硬件,那么并行化算法就没有意义。
接下来将介绍一些简单的公式,帮助您理解在评估并行算法时需要考虑哪些因素。
在本章中,加速比(Speedup)被定义为算法的串行版本与并行版本之间的时间比率,如下所示:
\[\text{加速比} = \frac{T_1}{T_n}\]其中 $T_1$ 是使用在一个核心上执行的串行算法解决问题所需的时间,$T_n$ 是使用$n$ 个核心解决相同问题所需的时间。时间指的是墙钟时间(wall-clock time),而不是 CPU 时间。
并行算法通常比其串行等效算法更复杂,并且需要更多的计算资源(例如 CPU 时间)。并行版本的优势来自于能够将算法分散到多个处理单元上的能力。
考虑到这一点,值得注意的是,并非所有算法在并行运行时都能获得相同的性能提升。并行算法的效率(Efficiency)可以通过以下公式计算:
\[\text{效率} = \frac{T_1}{T_n \cdot n}\]在这个公式中,$n$ 是执行算法的核心数量。由于 $T_1/T_n$ 表示加速比,因此效率也可以表示为 $\text{加速比}/n$。
如果效率为 $1.0$,则该算法是完美并行化的。例如,这意味着我们在具有八个核心的计算机上执行并行算法时实现了 $8$ 倍的加速比。然而,实际上,有许多参数限制了并行执行,例如创建线程、内存带宽和上下文切换,正如第 $11$ 章《并发》中所提到的。因此,通常情况下,效率远低于 $1.0$。
并行算法的效率取决于每块工作可以被独立处理的程度。例如,std::transform() 并行化起来非常简单,因为每个元素都与所有其他元素完全独立地处理。这将在本章后面进行演示。
效率还取决于问题规模和核心数量。例如,由于并行算法的复杂性增加所带来的开销,并行算法在小型数据集上表现可能很差。同样,在大量核心上执行程序可能会触及计算机中的其他瓶颈,例如内存带宽。当改变核心数量和/或输入规模时,如果效率保持不变,我们就说该并行算法是可扩展(scales)的。
再次回顾 Amdahl 定律
同样重要的是要记住,并非程序的所有部分都可以并行化。即使我们拥有无限数量的核心,这一事实也限制了程序的理论最大加速比。我们可以使用 Amdahl 定律来计算最大的可能加速比,该定律在第 $3$ 章《分析和测量性能》中介绍过。
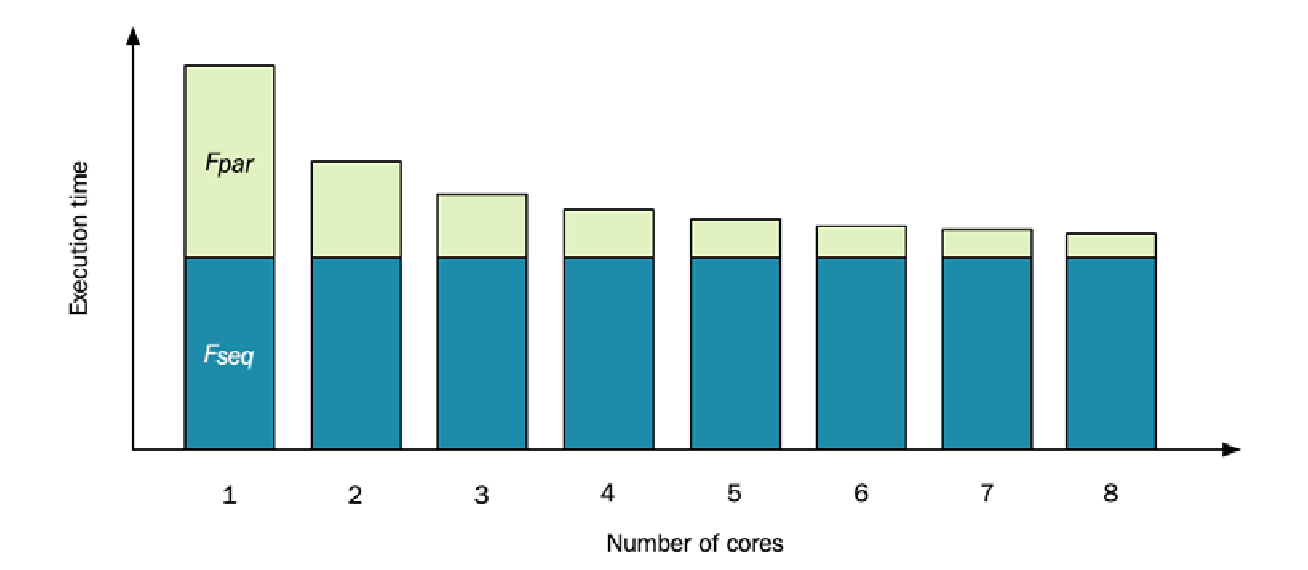
在这里,我们将 Amdahl 定律应用于并行程序。它是这样运作的:程序的总运行时间可以分成两个不同的部分或比例:
- $F_{seq}$:只能串行执行的程序部分比例。
- $F_{par}$:可以并行执行的程序部分比例。
由于这两个部分共同构成了整个程序,这意味着 $F_{seq} = 1 - F_{par}$。现在,Amdahl 定律告诉我们,在 $n$ 个核心上执行的程序的最大加速比是:
\[\text{最大加速比} = \frac{1}{\frac{F_{par}}{n} + F_{seq}} = \frac{1}{\frac{F_{par}}{n} + (1 - F_{par})}\]为了可视化该定律的效果,下图显示了一个程序的执行时间,其中串行部分在底部,并行部分在顶部。增加核心数量只会影响并行部分,这为最大加速比设定了限制:
在上图中,当在单个 CPU 上运行时,串行部分占执行时间的 $50\%$。因此,通过添加更多核心来执行此类程序,我们可以实现的最大加速比是 $2$ 倍。
为了让您了解并行算法是如何实现的,我们现在将介绍几个示例。我们将从 std::transform() 开始,因为它相对容易拆分成多个独立的部分。
实现并行 std::transform()
尽管从算法角度来看,std::transform() 易于实现,但在实践中,即使是实现一个基本的并行版本也比乍看起来要复杂得多。
算法 std::transform() 对序列中的每个元素调用一个函数,并将结果存储在另一个序列中。一个串行版本的 std::transform() 的可能实现可能如下所示:
template<class SrcIt, class DstIt, class Func>
auto transform(SrcIt first, SrcIt last, DstIt dst, Func func) {
while (first != last) {
*dst++ = func(*first++);
}
}
标准库版本还会返回 dst 迭代器,但在我们的示例中将忽略这一点。为了理解并行版本 std::transform() 所面临的挑战,我们从一个朴素(Naive)的方法开始。
朴素实现 (Naive Implementation)
一个朴素的并行实现 std::transform() 可能会采用以下步骤:
- 将元素划分成块(chunks),块的数量对应于计算机中的核心数量。
- 在单独的任务中处理每个块。
- 等待所有任务完成。
使用 std::thread::hardware_concurrency() 来确定支持的硬件线程数,一个可能的实现可能如下所示:
template <typename SrcIt, typename DstIt, typename Func>
auto par_transform_naive(SrcIt first, SrcIt last, DstIt dst, Func f) {
auto n = static_cast<size_t>(std::distance(first, last));
// 确定任务数(至少为 1)
auto n_cores = size_t{std::thread::hardware_concurrency()};
auto n_tasks = std::max(n_cores, size_t{1});
// 计算每个块的大小
auto chunk_sz = (n + n_tasks - 1) / n_tasks;
auto futures = std::vector<std::future<void>>{};
// 在单独的任务中处理每个块
for (auto i = 0ul; i < n_tasks; ++i) {
auto start = chunk_sz * i;
if (start < n) {
auto stop = std::min(chunk_sz * (i + 1), n);
// 异步启动一个任务
auto fut = std::async(std::launch::async,
[first, dst, start, stop, f]() {
// 对当前块执行串行 transform
std::transform(first + start, first + stop, dst + start, f);
});
futures.emplace_back(std::move(fut));
}
}
// 等待每个任务完成
for (auto&& fut : futures) {
fut.wait();
}
}
请注意,如果由于某种原因 hardware_concurrency() 无法确定,它可能会返回 $0$,因此这里将其限制为至少为 $1$。
std::transform() 和我们的并行版本之间有一个细微的区别:它们对迭代器的要求不同。std::transform() 可以操作输入和输出迭代器,例如绑定到 std::cin 的 std::istream_iterator<>。然而,这对于 par_transform_naive() 是不可能的,因为迭代器是从多个任务中复制和使用的。如您所见,本章中展示的并行算法都不能操作输入和输出迭代器。相反,并行算法至少需要前向迭代器,它允许多遍遍历(multi-pass traversal)。
性能评估 (Performance Evaluation)
继续朴素的实现,让我们通过与在单个 CPU 核心上执行的串行版本 std::transform() 进行比较,来衡量其性能。
在此测试中,我们将测量墙钟时间(Time/Wall clock)和消耗的总 CPU 时间,同时改变输入数据的大小。
我们将使用 Google Benchmark 来设置这个基准测试,这在第 $3$ 章《分析和测量性能》中介绍过。为了避免代码重复,我们将实现一个函数来为我们的基准测试设置测试夹具(test fixture)。该夹具需要一个包含示例值的源范围、一个用于结果的目标范围,以及一个转换函数:
auto setup_fixture(int n) {
auto src = std::vector<float>(n);
std::iota(src.begin(), src.end(), 1.0f); // 值从 1.0 到 n
auto dst = std::vector<float>(src.size());
auto transform_function = [](float v) {
auto sum = v;
// 确保计算量足够大,以便看到并行优势
for (auto i = 0; i < 500; ++i) {
sum += (i * i * i * sum);
}
return sum;
};
return std::tuple{src, dst, transform_function};
}
现在我们的夹具已设置好,是时候实现实际的基准测试了。将有两个版本:一个用于串行的 std::transform(),另一个用于我们的并行版本 par_transform_naive():
void bm_sequential(benchmark::State& state) {
auto [src, dst, f] = setup_fixture(state.range(0));
for (auto _ : state) {
std::transform(src.begin(), src.end(), dst.begin(), f);
}
}
void bm_parallel(benchmark::State& state) {
auto [src, dst, f] = setup_fixture(state.range(0));
for (auto _ : state) {
par_transform_naive(src.begin(), src.end(), dst.begin(), f);
}
}
只有 for 循环内的代码会被测量。通过使用 state.range(0) 作为输入大小,我们可以通过向每个基准测试添加一系列值来生成不同的值。实际上,我们需要为每个基准测试指定一些参数,因此我们创建一个辅助函数来应用所有需要的设置:
void CustomArguments(benchmark::internal::Benchmark* b) {
b->Arg(50)->Arg(10'000)->Arg(1'000'000) // 输入大小
->MeasureProcessCPUTime() // 测量所有线程的总 CPU 时间
->UseRealTime() // 使用墙钟时间作为循环控制
->Unit(benchmark::kMillisecond); // 使用 ms 作为单位
}
关于自定义参数需要注意几点:
- 我们将值 $50$、$10,000$ 和 $1,000,000$ 作为参数传递给基准测试。它们在
setup_fixture()函数中用于创建向量时的输入大小。这些值在测试函数中通过state.range(0)访问。 - 默认情况下,Google Benchmark 只测量主线程上的 CPU 时间。但是由于我们对所有线程的总 CPU 时间感兴趣,因此我们使用
MeasureProcessCPUTime()。 - Google Benchmark 决定每个测试需要重复多少次才能达到统计稳定的结果。我们希望库使用墙钟时间来进行此判断,而不是 CPU 时间,因此我们应用了
UseRealTime()设置。
就这样了。最后,注册基准测试并调用 main:
BENCHMARK(bm_sequential)->Apply(CustomArguments);
BENCHMARK(bm_parallel)->Apply(CustomArguments);
BENCHMARK_MAIN();
使用开启优化(使用 gcc 和 -O3)编译此代码后,我在一个使用八个核心的笔记本电脑上执行了此基准测试。下表显示了使用 $50$ 个元素时的结果:
| 算法 | CPU Time | Time | Speedup |
|---|---|---|---|
| std::transform() | $0.02\text{ ms}$ | $0.02\text{ ms}$ | $1.0\text{x}$ |
| par_transform_naive() | $0.17\text{ ms}$ | $0.08\text{ ms}$ | $0.25\text{x}$ |
CPU Time 是在 CPU 上花费的总时间。Time 是墙钟时间,这是我们最感兴趣的。Speedup 是将串行版本的经过时间与并行版本进行比较时的相对加速比(在本例中为 $0.02 / 0.08$)。
显然,对于只有 $50$ 个元素的这个小数据集,串行版本优于并行算法。然而,使用 $10,000$ 个元素时,我们确实开始看到并行化的好处:
| 算法 | CPU Time | Time | Speedup |
|---|---|---|---|
| std::transform() | $0.89\text{ ms}$ | $0.89\text{ ms}$ | $1.0\text{x}$ |
| par_transform_naive() | $1.95\text{ ms}$ | $0.20\text{ ms}$ | $4.5\text{x}$ |
最后,使用 $1,000,000$ 个元素使我们获得了更高的效率,如下表所示:
| 算法 | CPU Time | Time | Speedup |
|---|---|---|---|
| std::transform() | $9071\text{ ms}$ | $9092\text{ ms}$ | $1.0\text{x}$ |
| par_transform_naive() | $9782\text{ ms}$ | $1245\text{ ms}$ | $7.3\text{x}$ |
在这种最后一次运行中,并行算法的效率非常高。它在八个核心上执行,因此效率是 $7.3\text{x} / 8 \approx 0.925$。这里展示的结果(无论是绝对执行时间还是相对加速比)都不应过分依赖。结果取决于计算机架构、OS 调度程序以及执行测试时机器上当前运行的其他工作量等因素。尽管如此,基准测试结果证实了前面讨论的几个重要观点:
- 对于小数据集,串行版本
std::transform()比并行版本快得多,因为创建线程等带来的开销。 - 与
std::transform()相比,并行版本总是使用更多的计算资源(CPU Time)。 - 对于大数据集,在测量墙钟时间时,并行版本优于串行版本。在具有八个核心的机器上运行时,加速比超过 $7$ 倍。
我们的算法效率高(至少在大型数据集上)的一个原因是计算成本均匀分布,并且每个子任务高度独立。然而,情况并非总是如此。
朴素实现的缺陷
如果每块工作具有相同的计算成本,并且算法在没有其他应用程序占用硬件的环境中执行,那么朴素实现可能做得很好。然而,这种情况很少发生;相反,我们需要一个既高效又可扩展的通用并行实现。
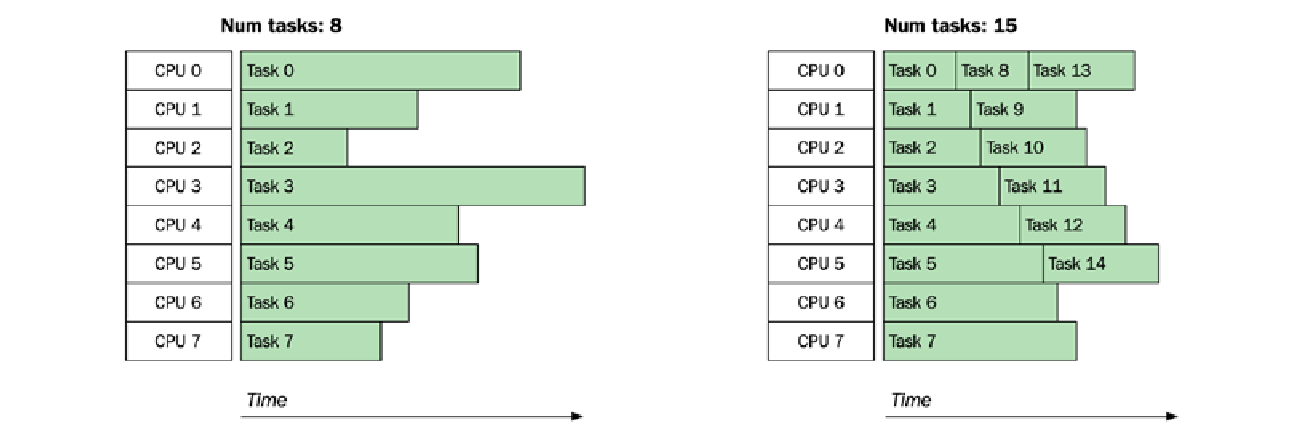
以下插图显示了我们希望避免的问题。如果每块工作的计算成本不相等,则实现受限于耗时最长的那一块工作:
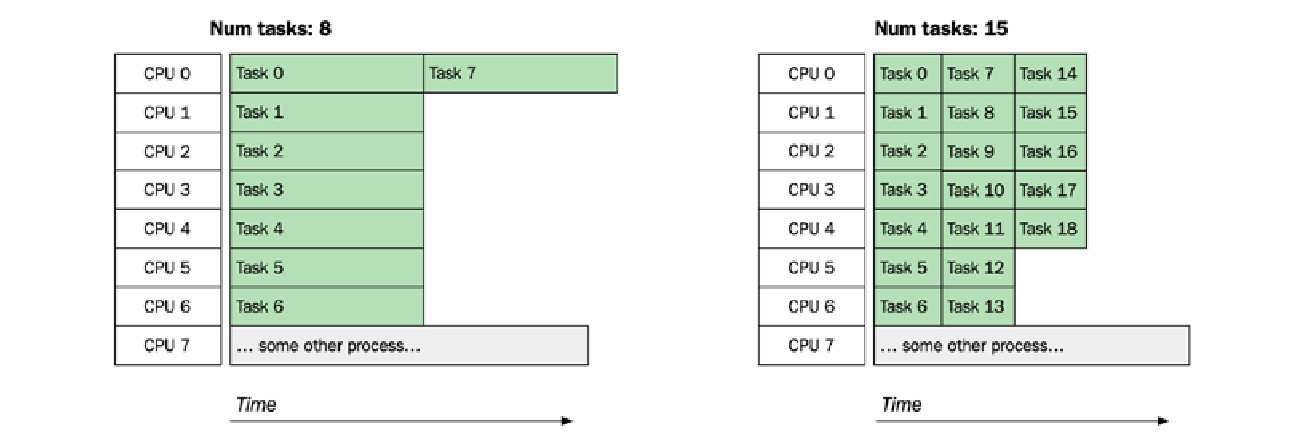
如果应用程序和/或操作系统还有其他进程需要处理,则操作将不会并行处理所有块:
正如您在上图中所见,将操作拆分成更小的块可以使并行化适应当前条件,避免单个任务拖慢整个操作。
还要注意,朴素实现对于小数据集是不成功的。有许多方法可以调整朴素实现以使其性能更好。例如,我们可以通过将核心数乘以大于 $1$ 的某个因子来创建更多、更小的任务。或者,为了避免在小数据集上产生显著开销,我们可以让块大小决定要创建的任务数等等。
您现在已经掌握了如何实现和评估一个简单并行算法的知识。我们不会对朴素实现进行任何微调;相反,我将展示在实现并行算法时要使用的另一种有用技术。
分治法 (Divide and Conquer)
将问题分解为更小子问题的算法技术称为分治法(Divide and Conquer)。我们将在这里使用分治法实现另一个版本的并行 transform 算法。它的工作原理如下:如果输入范围小于指定的阈值(threshold),则处理该范围;否则,该范围被拆分为两部分:
- 第一部分在一个新分支的任务上处理。
- 另一部分在调用线程上递归处理。
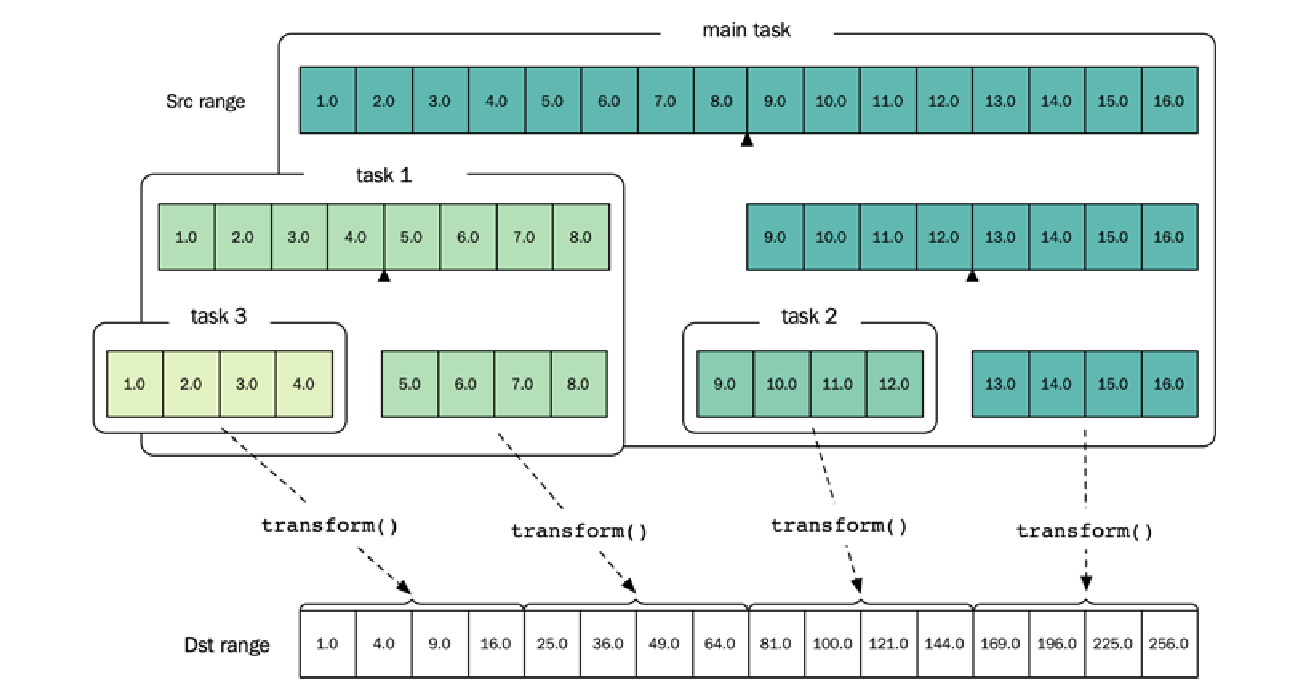
下图显示了分治算法将如何使用以下数据和参数递归地转换一个范围:
- 范围大小:$16$
- 源范围包含从 $1.0$ 到 $16.0$ 的浮点数
- 块大小:$4$
- 转换函数:
[](auto x) { return x*x; }
在上图中,您可以看到主任务派生了两个异步任务(任务 $1$ 和任务 $2$),并最终转换了范围内的最后一个块。任务 $1$ 派生了任务 $3$,然后转换了剩余的包含值 $5.0, 6.0, 7.0, 8.0$ 的元素。
在实现方面,代码量相当小。传入的范围被递归地分成两个块;第一个块作为新任务被调用,而第二个块在同一任务上递归处理:
template <typename SrcIt, typename DstIt, typename Func>
auto par_transform(SrcIt first, SrcIt last, DstIt dst,
Func func, size_t chunk_sz) {
const auto n = static_cast<size_t>(std::distance(first, last));
// 达到阈值,执行串行转换并返回
if (n <= chunk_sz) {
std::transform(first, last, dst, func);
return;
}
// 找到范围的中间点
const auto src_middle = std::next(first, n / 2);
// 将第一部分分支出去,作为另一个异步任务
auto future = std::async(std::launch::async, [=, &func] {
par_transform(first, src_middle, dst, func, chunk_sz);
});
// 递归处理第二部分(在当前线程上)
const auto dst_middle = std::next(dst, n / 2);
par_transform(src_middle, last, dst_middle, func, chunk_sz);
// 等待第一个异步任务完成
future.wait();
}
像这样将递归与多线程结合可能需要一段时间才能理解。在接下来的示例中,您将看到这种模式也可以用于实现更复杂的算法。但首先,让我们看看它的性能如何。
性能评估:分治法
为了评估我们的新版本,我们将修改基准测试夹具,更新转换函数,使其耗时取决于输入值。通过使用 std::iota() 填充范围来增加输入值的范围。这样做意味着算法需要处理大小不同的作业。
这是新的 setup_fixture() 函数:
auto setup_fixture(int n) {
auto src = std::vector<float>(n);
std::iota(src.begin(), src.end(), 1.0f); // 从 1.0 到 n
auto dst = std::vector<float>(src.size());
auto transform_function = [](float v) {
auto sum = v;
auto n = v / 20'000; // v 越大,
for (auto i = 0; i < n; ++i) { // 计算量越大
sum += (i * i * i * sum);
}
return sum;
};
return std::tuple{src, dst, transform_function};
}
我们现在可以通过对块大小使用递增参数来尝试找到分治算法要使用的最佳块大小。与此新的需要处理大小不同作业的夹具相比,查看我们的分治算法与朴素版本的性能也很有趣。这是完整的代码:
// 分治版本
void bm_parallel(benchmark::State& state) {
auto [src, dst, f] = setup_fixture(10'000'000);
auto n = state.range(0); // 块大小被参数化
for (auto _ : state) {
par_transform(src.begin(), src.end(), dst.begin(), f, n);
}
}
// 朴素版本
void bm_parallel_naive(benchmark::State& state) {
auto [src, dst, f] = setup_fixture(10'000'000);
for (auto _ : state) {
par_transform_naive(src.begin(), src.end(), dst.begin(), f);
}
}
void CustomArguments(benchmark::internal::Benchmark* b) {
b->MeasureProcessCPUTime()
->UseRealTime()
->Unit(benchmark::kMillisecond);
}
BENCHMARK(bm_parallel)->Apply(CustomArguments)
->RangeMultiplier(10) // 块大小从
->Range(1000, 10'000'000); // 1k 到 10M
BENCHMARK(bm_parallel_naive)->Apply(CustomArguments);
BENCHMARK_MAIN();
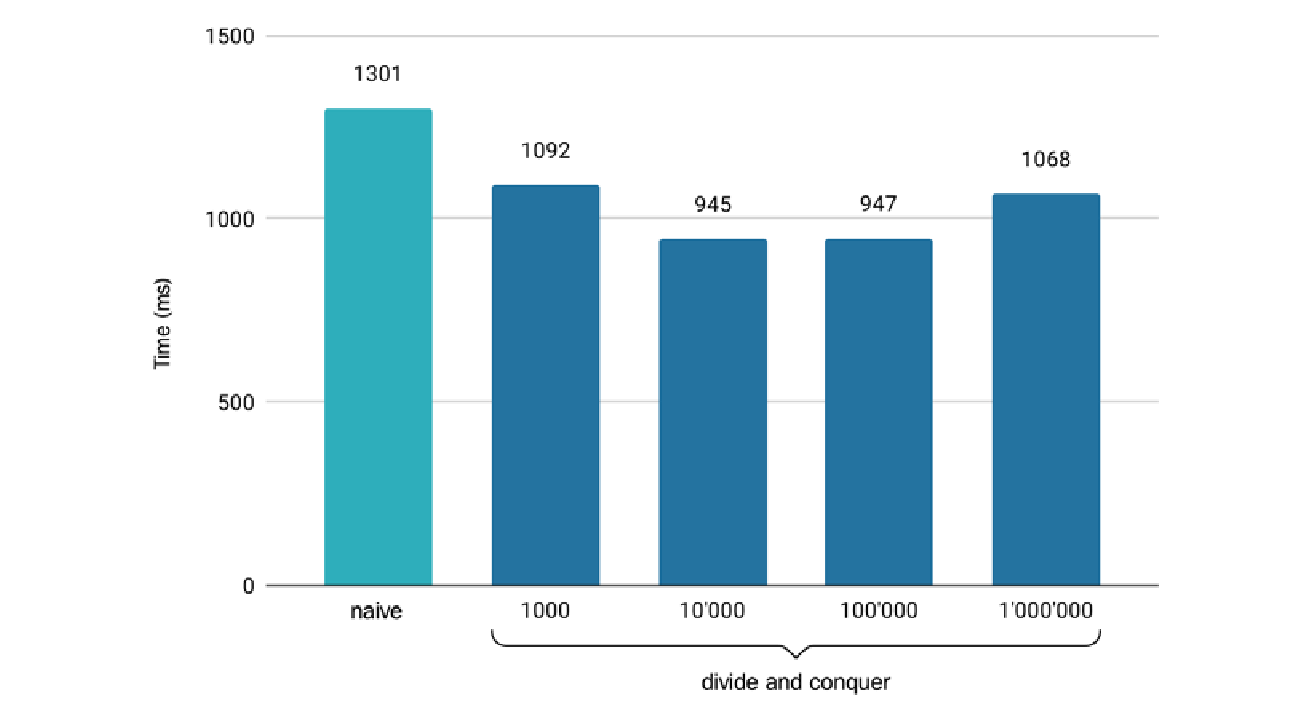
下面的图表揭示了我在 macOS 上使用八核 Intel Core i7 CPU 运行测试时所取得的结果:
在使用大约 $10,000$ 个元素的块大小时,实现了最佳效率,这创建了 $1,000$ 个任务。块越大,性能在处理最终块所需的时间上成为瓶颈,而块太小则导致创建和调用任务的开销相对于计算量太大。
从这个示例中可以得出,调度 $1,000$ 个较小任务而不是几个大任务的性能损失在这里不是问题。可以使用线程池来限制线程数,但在这种情况下,std::async() 似乎运行良好。一个通用的实现会选择使用相当大的任务数,而不是试图匹配确切的核心数。
在实现并行算法时,找到块大小和任务数的最佳值是一个实际问题。如您所见,它取决于许多变量,也取决于您是优化延迟(latency)还是吞吐量(throughput)。获得见解的最佳方法是在您的算法应该运行的环境中进行测量。
现在您已经了解了如何使用分治法实现并行 transform 算法,接下来让我们看看相同的技术如何应用于其他问题。
实现并行 std::count_if()
分治法的一个优点是它可以应用于许多问题。我们可以轻松地使用相同的技术来实现并行版本的 std::count_if(),不同之处在于我们需要累加返回的值,如下所示:
template <typename It, typename Pred>
auto par_count_if(It first, It last, Pred pred, size_t chunk_sz) {
auto n = static_cast<size_t>(std::distance(first, last));
// 达到阈值,执行串行 count_if 并返回
if (n <= chunk_sz)
return std::count_if(first, last, pred);
auto middle = std::next(first, n/2);
// 异步处理第一部分
auto fut = std::async(std::launch::async, [=, &pred] {
return par_count_if(first, middle, pred, chunk_sz);
});
// 递归处理第二部分(在当前线程)
auto num = par_count_if(middle, last, pred, chunk_sz);
// 累加结果并返回
return num + fut.get();
}
如您所见,这里唯一的区别是我们需要在函数末尾对结果求和。
如果您想让块大小取决于核心数量,您可以轻松地将 par_count_if() 包装在一个外部函数中:
template <typename It, typename Pred>
auto par_count_if(It first, It last, Pred pred) {
auto n = static_cast<size_t>(std::distance(first, last));
auto n_cores = size_t{std::thread::hardware_concurrency()};
// 启发式地计算块大小(核心数 * 32 或至少 1000)
auto chunk_sz = std::max(n / n_cores * 32, size_t{1000});
return par_count_if(first, last, pred, chunk_sz);
}
这里的魔法数字 $32$ 是一个有些随意的因子,它会使得当给定一个大输入范围时,我们能有更多和更小的块。通常,我们需要测量性能才能确定一个好的常量。现在让我们继续尝试解决一个更复杂的并行算法。
实现并行 std::copy_if()
我们已经看过了 std::transform() 和 std::count_if(),它们在串行和并行实现上都相当容易。如果我们再看一个容易串行实现的算法 std::copy_if(),事情在并行执行时就变得困难得多。
串行实现 std::copy_if() 就像这样简单:
template <typename SrcIt, typename DstIt, typename Pred>
auto copy_if(SrcIt first, SrcIt last, DstIt dst, Pred pred) {
for (auto it = first; it != last; ++it) {
if (pred(*it)) {
*dst = *it;
++dst;
}
}
return dst;
}
为了演示它的用法,请考虑以下示例:我们有一个包含整数序列的范围,我们只想将奇数复制到另一个范围:
const auto src = {1, 2, 3, 4};
auto dst = std::vector<int>(src.size(), -1);
auto new_end = std::copy_if(src.begin(), src.end(), dst.begin(),
[](int v) { return (v % 2) == 1; });
// dst 是 {1, 3, -1, -1}
dst.erase(new_end, dst.end()); // dst 现在是 {1, 3}
现在,如果我们想实现 copy_if() 的并行版本,我们立即会遇到问题,因为我们不能并发地写入目标迭代器。这是一个有未定义行为(Undefined Behavior)的失败尝试,因为两个任务都将写入目标范围中的同一位置:
// 警告:未定义行为
template <typename SrcIt, typename DstIt, typename Func>
auto par_copy_if(SrcIt first, SrcIt last, DstIt dst, Func func) {
auto n = std::distance(first, last);
auto middle = std::next(first, n / 2);
auto fut0 = std::async([=]() {
return std::copy_if(first, middle, dst, func);
});
auto fut1 = std::async([=]() {
return std::copy_if(middle, last, dst, func);
});
auto dst0 = fut0.get();
auto dst1 = fut1.get();
// 由于并发写入,dst0 和 dst1 都是无效的
return *std::max(dst0, dst1); // 只是为了返回一些东西...
}
现在我们有两种简单的方法:要么我们同步我们写入的索引(通过使用原子/无锁变量),要么我们将算法拆分成两个部分。接下来我们将探讨这两种方法。
方案一:使用同步的写入位置
我们可能考虑的第一个方法是使用 std::atomic_size_t 和 fetch_add() 成员函数来同步写入位置,正如您在第 $11$ 章《并发》中学到的。每当一个线程尝试写入一个新元素时,它会原子地获取当前索引并加一;因此,每个值都被写入到唯一的索引。
在我们的代码中,我们将算法拆分为两个函数:一个内部函数和一个外部函数。原子写入索引将在外部函数中定义,而算法的主要部分将在内部函数中实现。
1. 内部函数 (inner_par_copy_if_sync)
内部函数需要一个 std::atomic_size_t 来同步写入位置。由于算法是递归的,它不能自己存储 std::atomic_size_t;它需要一个外部函数来调用该算法:
template <typename SrcIt, typename DstIt, typename Pred>
void inner_par_copy_if_sync(SrcIt first, SrcIt last, DstIt dst,
std::atomic_size_t& dst_idx,
Pred pred, size_t chunk_sz) {
const auto n = static_cast<size_t>(std::distance(first, last));
// 达到阈值,执行串行处理
if (n <= chunk_sz) {
std::for_each(first, last, [&](const auto& v) {
if (pred(v)) {
// 原子地获取当前索引并递增
auto write_idx = dst_idx.fetch_add(1);
*std::next(dst, write_idx) = v; // 写入唯一位置
}
});
return;
}
auto middle = std::next(first, n / 2);
// 异步处理第一部分
auto future = std::async([first, middle, dst, chunk_sz, &pred, &dst_idx] {
inner_par_copy_if_sync(first, middle, dst, dst_idx, pred, chunk_sz);
});
// 递归处理第二部分(在当前线程)
inner_par_copy_if_sync(middle, last, dst, dst_idx, pred, chunk_sz);
future.wait();
}
这仍然是一个分治算法,希望您已经开始看到我们正在使用的模式。对写入索引 dst_idx 的原子更新确保了多个线程永远不会写入目标序列中的同一索引。
2. 外部函数 (par_copy_if_sync)
从客户端代码调用的外部函数只是一个 std::atomic_size_t 的占位符,它被初始化为零。然后该函数调用内部函数,进一步并行化代码:
template <typename SrcIt, typename DstIt, typename Pred>
auto par_copy_if_sync(SrcIt first,SrcIt last,DstIt dst,
Pred p, size_t chunk_sz) {
auto dst_write_idx = std::atomic_size_t{0}; // 初始化原子索引
inner_par_copy_if_sync(first, last, dst, dst_write_idx, p, chunk_sz);
// 返回新的结束迭代器位置
return std::next(dst, dst_write_idx);
}
一旦内部函数返回,我们就可以使用 dst_write_idx 来计算目标范围的结束迭代器。现在让我们看看解决同一问题的另一种方法。
方案二:将算法拆分成两部分
第二种方法是将算法拆分成两个部分。首先,并行执行条件复制,然后将生成的稀疏范围挤压成一个连续范围。
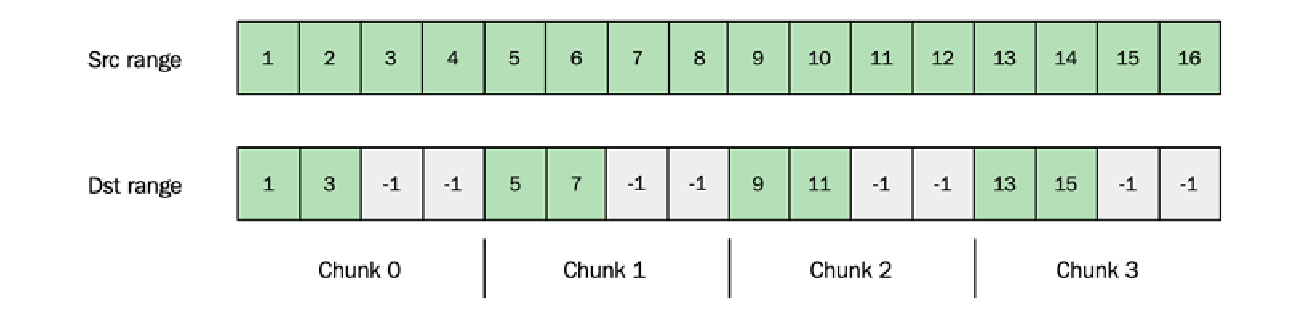
第一部分:将元素并行复制到目标范围
第一部分按块复制元素,从而产生如下图所示的稀疏目标数组。每个块都并行地进行条件复制,并且生成的范围迭代器存储在 std::future 对象中以供稍后检索:
以下代码实现了算法的前半部分:
template <typename SrcIt, typename DstIt, typename Pred>
auto par_copy_if_split(SrcIt first, SrcIt last, DstIt dst,
Pred pred, size_t chunk_sz) -> DstIt {
auto n = static_cast<size_t>(std::distance(first, last));
auto futures = std::vector<std::future<std::pair<DstIt, DstIt>>>{};
futures.reserve(n / chunk_sz); // 预留 future 空间
// 循环并创建任务,每个任务处理一个块
for (auto i = size_t{0}; i < n; i += chunk_sz) {
const auto stop_idx = std::min(i + chunk_sz, n);
auto future = std::async([=, &pred] {
auto dst_first = dst + i;
// 串行 copy_if 到目标范围的当前块
auto dst_last = std::copy_if(first+i, first+stop_idx,
dst_first, pred);
return std::make_pair(dst_first, dst_last);
});
futures.emplace_back(std::move(future));
}
// To be continued ...
// ...
我们现在已经将应该复制的元素复制到了稀疏目标范围中。是时候通过将元素向左移动来填补空白了。
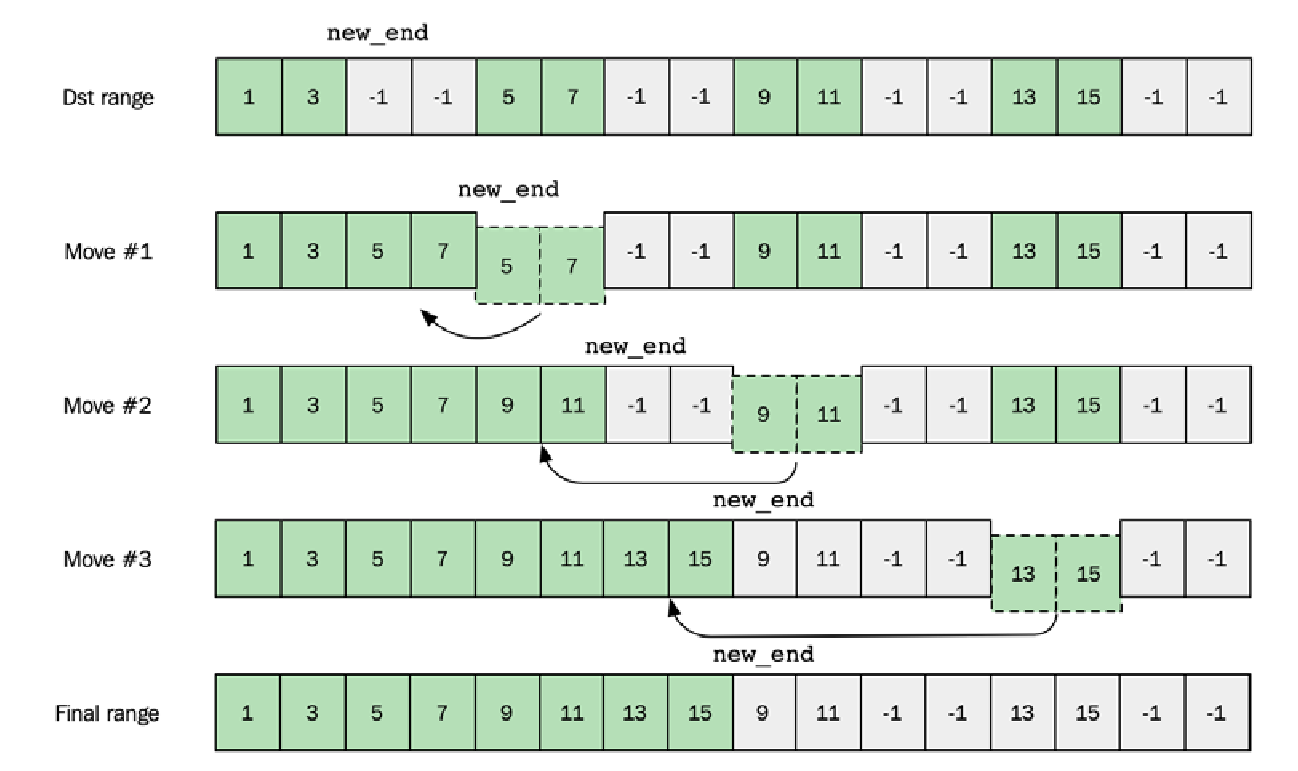
第二部分:将稀疏范围串行移动到连续范围
当稀疏范围创建完成后,它使用每个 std::future 的结果值进行合并。由于各个部分重叠,因此串行执行合并:
// ...接上文...
// 第二部分:串行执行稀疏范围的合并
// 等待第一个 future 结束,并获取第一个子范围的 new_end
auto new_end = futures.front().get().second;
for (auto it = std::next(futures.begin()); it != futures.end(); ++it)
{
auto chunk_rng = it->get(); // 获取下一个子范围的 (first, last) 迭代器
// 使用 std::move 将当前块的数据移动到上一个块的 new_end 处
new_end = std::move(chunk_rng.first, chunk_rng.second, new_end);
}
return new_end;
} // par_copy_if_split 结束
算法的第二部分将所有子范围移动到范围开头,如下图所示:
性能评估
使用这种并行版本的 copy_if() 带来的性能提升很大程度上取决于谓词(predicate)的开销。因此,我们在基准测试中使用了两个计算成本不同的谓词。
不昂贵的谓词: 检查奇偶性。
auto is_odd = [](unsigned v) {
return (v % 2) == 1;
};
昂贵的谓词: 检查其参数是否为质数。
auto is_prime = [](unsigned v) {
if (v < 2) return false;
if (v == 2) return true;
if (v % 2 == 0) return false;
for (auto i = 3u; (i * i) <= v; i+=2) {
if ((v % i) == 0) {
return false;
}
}
return true;
};
请注意,这不是实现 is_prime() 的特别优化的方法,仅用于基准测试的目的。
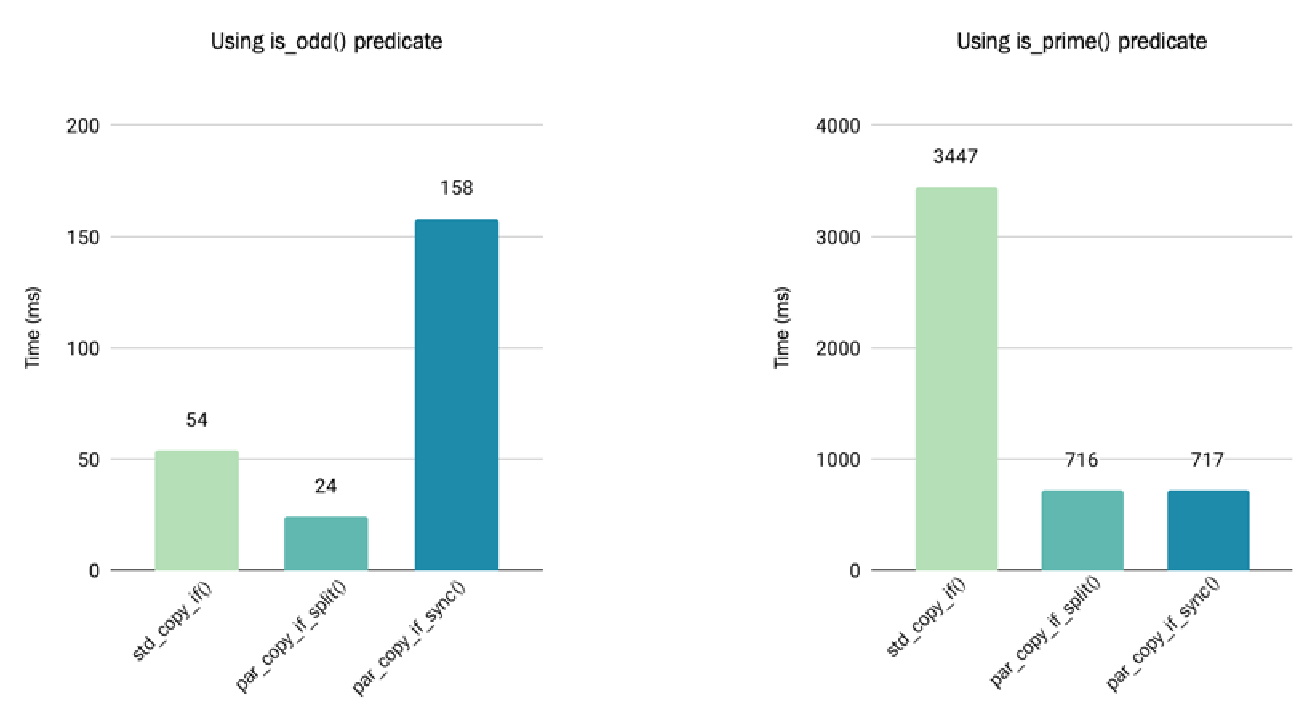
这里没有写出基准测试代码,但包含在随附的源代码中。比较了三种算法:std::copy_if(), par_copy_if_split(), 和 par_copy_if_sync()。下图显示了使用 Intel Core i7 CPU 测量的结果。并行算法在此基准测试中使用了 $100,000$ 的块大小。
测量性能时最明显的观察结果是,当使用不昂贵的 is_odd() 谓词时,同步版本 par_copy_if_sync() 慢得荒谬。灾难性的性能实际上并不是由于原子写入索引;而是因为硬件的缓存机制被破坏了,这是由于多个线程写入同一个缓存行(cache line)所致(正如您在第 $7$ 章《内存管理》中学到的)。
因此,有了这个知识,我们现在理解了为什么 par_copy_if_split() 表现更好。对于不昂贵的谓词 is_odd(),par_copy_if_split() 比 std::copy_if() 快大约 $2$ 倍,但对于昂贵的谓词 is_prime(),效率提高到将近 $5$ 倍。效率提高是由于大部分计算(即谓词的执行)发生在算法的第一部分,该部分是并行执行的。
您现在应该掌握了一些可用于并行化算法的技术。这些新的见解将帮助您理解使用标准库中的并行算法时的要求和期望。
并行标准库算法 (Parallel standard library algorithms)
从 C++17 开始,标准库已经扩展了大多数(但不是全部)算法的并行版本。将您的算法更改为允许并行执行仅仅是添加一个参数的问题,该参数告诉算法使用哪种并行执行策略。
正如本书前面所强调的,如果您的代码库基于标准库算法,或者至少您有使用算法编写 C++ 的习惯,那么通过在适当的地方添加执行策略,您几乎可以免费获得即时的性能提升:
auto v = std::vector<std::string>{
"woody", "steely", "loopy", "upside_down"
};
// 并行排序
std::sort(std::execution::par, v.begin(), v.end());
一旦您指定了执行策略,您就进入了并行算法的领域,与它们的原始串行版本相比,它们有一些显着的差异。
- 最小迭代器类别要求从输入迭代器更改为前向迭代器。
- 您的代码(从复制构造函数或传递给算法的函数对象)抛出的异常永远不会到达您。相反,算法要求调用
std::terminate()。 - 由于并行实现的复杂性增加,算法的复杂性保证(时间和内存)可能会放宽。
使用标准库算法的并行版本时,您需要指定一个执行策略(execution policy),该策略说明允许算法如何并行化执行。不过,实现可能会决定串行执行该算法。如果您比较不同标准库实现中并行算法的效率和可扩展性,您可能会看到很大的差异。
策略:Execution policies
执行策略通知算法是否以及如何可以并行化执行。标准库的并行扩展中包含四种默认的执行策略。编译器和第三方库可以针对特定的硬件和条件扩展这些策略。例如,使用特定于供应商的策略,已经可以从标准库算法中利用现代图形卡的并行能力。
执行策略定义在 <execution> 头文件中,并位于 std::execution 命名空间中。目前有四种不同的标签类型(tag types),每种执行策略对应一种。您不能实例化这些类型;相反,每种类型都有一个预定义的对象。例如,并行执行策略有一个名为 std::execution::parallel_policy 的类型,此类型的预定义实例名为 std::execution::par。每种策略都有一个类型(而不是一个带有多个预定义实例的类型)的原因是,库可以在编译时区分您提供的策略。
1. 序列化策略 (Sequenced policy)
序列化执行策略 std::execution::seq 使算法串行执行,不进行并行化,类似于没有额外执行策略参数的算法运行方式。然而,每当您指定执行策略时,这意味着您使用的是具有放宽复杂性保证和更严格迭代器要求的算法版本;它还假定您提供的代码不会抛出异常,否则算法将调用 std::terminate()。
2. 并行策略 (Parallel policy)
并行执行策略 std::execution::par 可以被认为是并行算法的标准执行策略。您提供给算法的代码需要是线程安全的。理解这个要求的一种方式是考虑您即将使用的算法的串行版本中的循环体。例如,考虑本章前面我们写出的 copy_if() 的串行版本:
template <typename SrcIt, typename DstIt, typename Pred>
auto copy_if(SrcIt first, SrcIt last, DstIt dst, Pred pred) {
for (auto it = first; it != last; ++it)
{ // 循环体开始
if (pred(*it)) { // 调用谓词
*dst = *it; // 复制构造/赋值
++dst;
}
} // 循环体结束
return dst;
}
在此算法中,循环体内的代码将调用您提供的谓词并调用范围内元素的复制赋值运算符。如果您将 std::execution::par 传递给 copy_if(),则您有责任保证这些部分是线程安全的,并且可以安全地并行执行。
让我们看一个提供不安全代码的示例,然后看看我们可以做些什么。假设我们有一个字符串向量:
auto v = std::vector<std::string>{"Ada", "APL" /* ... */ };
如果我们要使用并行算法计算向量中所有字符串的总大小,一个不恰当的方法是使用 std::for_each(),像这样:
auto tot_size = size_t{0};
std::for_each(std::execution::par, v.begin(), v.end(),
[&](const auto& s) {
tot_size += s.size(); // 未定义行为,数据竞争!
});
由于函数对象的主体不是线程安全的(因为它从多个线程更新一个共享变量),这段代码表现出未定义行为。当然,我们可以使用 std::mutex 来保护 tot_size 变量,但这会违背并行执行此代码的全部目的,因为互斥锁将只允许一次一个线程进入主体。使用 std::atomic 数据类型将是另一个选择,但这也会降低效率。
这里的解决方案是根本不要使用 std::for_each() 来解决这个问题。相反,我们可以使用专门为此类工作量身定制的 std::transform_reduce() 或 std::reduce()。以下是如何使用 std::reduce() 来完成:
auto tot_size = std::reduce(std::execution::par, v.begin(), v.end(),
size_t{0}, [](auto i, const auto& s) {
return i + s.size(); // OK!线程安全
});
通过摆脱 lambda 内部的可变引用,lambda 的主体现在是线程安全的。对 std::string 对象的 const 引用是没问题的,因为它永远不会改变任何字符串对象,因此不会引入任何数据竞争(data races)。
通常,您传递给算法的代码是线程安全的,除非您的函数对象通过引用捕获对象或具有其他副作用,例如写入文件。
3. 未序列化策略 (Unsequenced policy)
未序列化策略是在 C++20 中添加的。它告诉算法允许使用例如 SIMD 指令进行向量化(vectorization)。在实践中,这意味着您不能在传递给算法的代码中使用任何同步原语,因为这可能导致死锁(deadlocks)。
为了理解死锁是如何发生的,我们将回到前面计算向量中所有字符串总大小的不恰当示例。假设我们使用互斥锁来保护 tot_size 变量,而不是使用 std::reduce(),像这样:
auto v = std::vector<std::string>{"Ada", "APL" /* ... */ };
auto tot_size = size_t{0};
auto mut = std::mutex{};
std::for_each(std::execution::par, v.begin(), v.end(),
[&](const auto& s) {
auto lock = std::scoped_lock{mut}; // 加锁
tot_size += s.size();
} // 解锁
);
这段代码现在使用 std::execution::par 执行是安全的,但效率非常低。如果我们把执行策略改为 std::execution::unseq,结果将不仅是一个低效的程序,而且是一个有死锁风险的程序!
未序列化执行策略告诉算法它可以以优化编译器通常不允许的方式重新排序我们的代码指令。
为了使算法受益于向量化,它需要从输入范围读取多个值,然后一次将 SIMD 指令应用于多个值。让我们分析 for_each() 循环中两次迭代在有和没有重新排序时可能是什么样子。这是没有重新排序的两次循环迭代:
{ // 第一次迭代
const auto& s = *it++;
mut.lock();
tot_size += s.size();
mut.unlock();
}
{ // 第二次迭代
const auto& s = *it++;
mut.lock();
tot_size += s.size();
mut.unlock();
}
算法被允许以以下方式合并这两次迭代:
{ // 迭代 1 和 2 合并
const auto& s1 = *it++;
const auto& s2 = *it++;
mut.lock();
mut.lock(); // 死锁!
tot_size += s1.size(); // 替换为向量化指令
tot_size += s2.size();
mut.unlock();
mut.unlock();
}
尝试在同一线程上执行这段代码将导致死锁,因为我们试图连续两次锁定同一个互斥锁。换句话说,当使用 std::execution::unseq 策略时,您必须确保您提供给算法的代码不会获取任何锁。
请注意,优化编译器随时可以自由地对您的代码进行向量化。但是,在那些情况下,编译器有责任保证向量化不会改变程序的含义,就像编译器和硬件允许执行的任何其他优化一样。这里的区别是,当显式地向算法提供 std::execute::unseq 策略时,您保证您提供的代码是安全的,可以进行向量化。
4. 并行未序列化策略 (Parallel unsequenced policy)
并行未序列化策略 std::execution::par_unseq 像并行策略一样并行执行算法,此外它还可能对循环进行向量化。
除了这四种标准执行策略之外,标准库供应商还可以为您提供具有自定义行为并对输入施加其他限制的附加策略。例如,Intel Parallel STL 库定义了四种自定义执行策略,它们只接受随机访问迭代器。
异常处理 (Exception handling)
如果您向算法提供四种标准执行策略之一,则您的代码不得抛出异常,否则算法将调用 std::terminate()。这与正常的单线程算法有很大的不同,正常的单线程算法总是将异常传播回调用者:
auto v = {1, 2, 3, 4};
auto f = [](auto) { throw std::exception{}; };
try {
std::for_each(v.begin(), v.end(), f); // 串行版本
} catch (...) {
std::cout << "Exception caught\n"; // 捕获到异常
}
使用执行策略运行相同的代码会导致调用 std::terminate():
try {
std::for_each(std::execution::seq, v.begin(), v.end(), f);
} catch (...) {
// 抛出的 std::exception 永远不会到达我们。
// 相反,std::terminate() 已经被调用了
}
您可能认为这意味着并行算法被声明为 noexcept,但事实并非如此。许多并行算法需要分配内存,因此标准并行算法本身允许抛出 std::bad_alloc。
还应该说明的是,其他库提供的执行策略可能会以不同的方式处理异常。
现在,我们将继续讨论 C++17 中首次引入并行算法时添加和修改的一些算法。
好的,这是您提供的文本的翻译和格式化版本,保留了所有代码:
并行算法的添加和更改
标准库中的大多数算法都提供了并行版本。然而,也有一些值得注意的例外,包括 std::accumulate() 和 std::for_each(),因为它们的原始规范要求按顺序执行。
std::accumulate() 与 std::reduce()
std::accumulate() 算法无法并行化,因为它必须按照元素的顺序执行,这是并行化不可能实现的。取而代之的是,添加了一个名为 std::reduce() 的新算法,它的工作原理与 std::accumulate() 相似,不同之处在于它是无序执行的。
对于可交换(commutative)操作,由于累加的顺序无关紧要,它们的结果是相同的。换句话说,给定一个整数范围:
const auto r = {1, 2, 3, 4};
通过加法或乘法累加它们:
auto sum =
std::accumulate(r.begin(), r.end(), 0, std::plus<int>{});
auto product =
std::accumulate(r.begin(), r.end(), 1, std::multiplies<int>{});
将产生与调用 std::reduce() 相同的结果,因为整数的加法和乘法都是可交换的。例如:
但是,如果操作不可交换,结果将是非确定性(non-deterministic)的,因为它取决于参数的顺序。例如,如果我们要累加一个字符串列表,如下所示:
auto v = std::vector<std::string>{"A", "B", "C"};
auto acc = std::accumulate(v.begin(), v.end(), std::string{});
std::cout << acc << '\n'; // 打印 "ABC"
这段代码将始终生成字符串 "ABC"。但是,通过使用 std::reduce(),结果字符串中的字符顺序可能以任何顺序出现,因为字符串连接是不可交换的。换句话说,字符串 "A" + "B" 不等于 "B" + "A"。因此,使用 std::reduce() 的以下代码可能会产生不同的结果:
auto red = std::reduce(v.begin(), v.end(), std::string{});
std::cout << red << '\n';
// 可能的输出:"CBA" 或 "ACB" 等
与性能相关的一个有趣的观点是浮点数学不是可交换的。通过对浮点值使用 std::reduce(),结果可能会有所不同,但这也意味着 std::reduce() 可能比 std::accumulate() 快得多。这是因为 std::reduce() 允许以 std::accumulate() 在使用严格浮点数学时不允许的方式重新排序操作和利用 SIMD 指令。
std::transform_reduce()
作为对标准库算法的补充,std::transform_reduce() 也被添加到了 <numeric> 头文件中。它正如其名:它像 std::transform() 一样转换一个元素范围,然后应用一个函数对象。这会像 std::reduce() 一样无序地累加它们:
auto v = std::vector<std::string>{"Ada","Bash","C++"};
auto num_chars = std::transform_reduce(
v.begin(), v.end(), size_t{0},
[](size_t a, size_t b) { return a + b; }, // 归约(Reduce)
[](const std::string& s) { return s.size(); } // 转换(Transform)
);
// num_chars 是 10
std::reduce() 和 std::transform_reduce() 都是在 C++17 引入并行算法时添加的。另一个必要的更改是调整 std::for_each() 的返回类型。
std::for_each()
std::for_each() 一个不常用的特性是它返回传入的函数对象。这使得可以使用 std::for_each() 在有状态函数对象内累加值。以下示例演示了一个可能的用例:
struct Func {
void operator()(const std::string& s) {
res_ += s;
};
std::string res_{}; // 状态
};
auto v = std::vector<std::string>{"A", "B", "C"};
auto s = std::for_each(v.begin(), v.end(), Func{}).res_;
// s 是 "ABC"
这种用法类似于我们可以使用 std::accumulate() 实现的功能,因此在尝试并行化它时也表现出相同的问题:无序执行函数对象将产生非确定性结果,因为调用顺序是未定义的。因此,std::for_each() 的并行版本简单地返回 void。
并行化基于索引的 for 循环
尽管我推荐使用算法,但有时特定任务需要一个原始的、基于索引的 for 循环。标准库算法通过在库中包含 std::for_each() 来提供基于范围的 for 循环的等效项。然而,没有算法等效于基于索引的 for 循环。换句话说,我们不能通过简单地添加并行策略来轻松并行化以下代码:
auto v = std::vector<std::string>{"A", "B", "C"};
for (auto i = 0u; i < v.size(); ++i) {
v[i] += std::to_string(i+1);
}
// v 现在是 { "A1", "B2", "C3" }
但让我们看看如何通过组合算法来构建一个。正如您已经得出的结论,实现并行算法是复杂的。但在这种情况下,我们将使用 std::for_each() 作为构建块来构建一个 parallel_for() 算法,从而将复杂的并行化留给 std::for_each()。
结合 std::for_each() 与 std::views::iota()
基于标准库算法的基于索引的 for 循环可以通过将 std::for_each() 与来自 Ranges 库的 std::views::iota()(参见第 $6$ 章《Ranges 和 Views》)相结合来创建。它看起来像这样:
auto v = std::vector<std::string>{"A", "B", "C"};
auto r = std::views::iota(size_t{0}, v.size());
std::for_each(r.begin(), r.end(), [&v](size_t i) {
v[i] += std::to_string(i + 1);
});
// v 现在是 { "A1", "B2", "C3" }
然后可以通过使用并行执行策略进一步并行化:
std::for_each(std::execution::par, r.begin(), r.end(), [&v](size_t i) {
v[i] += std::to_string(i + 1);
});
如前所述,当像这样将引用传递给将从多个线程调用的 lambda 时,我们必须非常小心。通过只通过唯一的索引 i 访问向量元素,我们避免了在更改向量中的字符串时引入数据竞争。
通过包装器简化构造
为了以简洁的语法迭代索引,前面的代码被包装到一个名为 parallel_for() 的实用函数中,如下所示:
template <typename Policy, typename Index, typename F>
auto parallel_for(Policy&& p, Index first, Index last, F f) {
auto r = std::views::iota(first, last);
std::for_each(p, r.begin(), r.end(), std::move(f));
}
然后可以直接使用 parallel_for() 函数模板,如下所示:
auto v = std::vector<std::string>{"A", "B", "C"};
parallel_for(std::execution::par, size_t{0}, v.size(),
[&](size_t i) { v[i] += std::to_string(i + 1); });
由于 parallel_for() 是基于 std::for_each() 构建的,它接受 std::for_each() 接受的任何策略。
在 GPU 上执行算法
本章将以关于 GPU 以及它们现在和将来如何用于并行编程的简短介绍性概述作结。
图形处理单元 (GPU) 最初是为处理计算机图形渲染的点和像素而设计和使用的。简单来说,GPU 的作用是检索像素数据或顶点数据的缓冲区,对每个缓冲区独立执行一个简单的操作,并将结果存储在新缓冲区中(最终显示)。
以下是一些早期可以在 GPU 上执行的简单、独立操作的示例:
- 将点从世界坐标转换为屏幕坐标。
- 在特定点执行光照计算(光照计算指计算图像中特定像素的颜色)。
由于这些操作可以并行执行,GPU 被设计用于并行执行小型操作。后来,这些图形操作变得可编程,尽管程序是以计算机图形术语编写的(即,内存读取是以从纹理中读取颜色的方式完成的,结果总是作为颜色写入纹理)。这些程序被称为着色器(shaders)。
随着时间的推移,引入了更多的着色器类型程序,着色器获得了越来越多的低级选项,例如从缓冲区而不是从纹理中读取和写入原始值。
从技术上讲,CPU 通常由少数通用缓存核心组成,而 GPU 由大量高度专业化的核心组成。这意味着可扩展性好的并行算法非常适合在 GPU 上执行。
GPU 有自己的内存,在算法可以在 GPU 上执行之前,CPU 需要在 GPU 内存中分配内存并将数据从主内存复制到 GPU 内存。接下来发生的事情是 CPU 在 GPU 上启动一个例程(也称为内核/kernel)。最后,CPU 将数据从 GPU 内存复制回主内存,使其可供在 CPU 上执行的“正常”代码访问。在 CPU 和 GPU 之间来回复制数据所产生的开销是 GPU 更适合批处理任务(吞吐量比延迟更重要)的原因之一。
今天有许多库和抽象层可用于从 C++ 进行 GPU 编程,但标准 C++ 在这方面几乎没有提供任何东西。然而,并行执行策略 std::execution::par 和 std::execution::par_unseq 允许编译器将标准算法的执行从 CPU 转移到 GPU。这方面的一个例子是 NVIDIA HPC 编译器 NVC++。它可以配置为编译标准 C++ 算法,以便在 NVIDIA GPU 上执行。
如果您想了解更多关于 C++ 和 GPU 编程的当前状态,我强烈推荐 ACCU 2019 会议上 Michael Wong 的演讲:“GPU Programming with modern C++”。
总结
在本章中,您了解了手工编写并行执行算法的复杂性。您现在也知道如何分析、测量和调整并行算法的效率。在学习并行算法时获得的见解加深了您对 C++ 标准库中并行算法的要求和行为的理解。C++ 带有四种标准执行策略,可以由编译器供应商扩展。这为利用 GPU 执行标准算法打开了大门。
下一个 C++ 标准 C++23 极有可能会增加对 GPU 上的并行编程的支持。
您现在已经读完了本书。恭喜!性能是代码质量的一个重要方面。但通常情况下,性能是以牺牲其他质量方面(例如可读性、可维护性和正确性)为代价的。掌握编写高效、简洁代码的艺术需要实践训练。我希望您从本书中学到的知识能够融入您的日常工作,创造出令人惊叹的软件。
解决性能问题通常归结为愿意进一步研究事物。它往往需要足够了解硬件和底层操作系统,才能从测量数据中得出结论。在我觉得有必要时,本书已经触及了这些领域的表面。在编写完本第二版中关于 C++20 的特性后,我现在期待着在我的软件开发职业中开始使用这些特性。正如我之前提到的,本书中介绍的许多代码在今天的编译器中只得到部分支持。我将继续更新 GitHub 仓库并添加有关编译器支持的信息。祝您好运!
- 显示Disqus评论(需要科学上网)