第三章：分析和测量性能

渐近复杂度与大 O 记法
- 增长率
- 均摊时间复杂度
测量什么以及如何测量？
了解你的代码和热点
- 插入式性能分析器（Instrumentation Profilers）
- 采样式探查器 (Sampling Profilers)
微基准测试 (Microbenchmarking)
总结

这本书旨在编写高效运行的 C++ 代码，因此我们需要涵盖一些关于如何衡量软件性能和评估算法效率的基础知识。本章中的大多数主题并非 C++ 所特有，当你面临性能问题时都可以使用。

你将学习如何使用大 O 记法 (big O notation) 来评估算法效率。在从 C++ 标准库中选择算法和数据结构时，这是必不可少的知识。如果你不熟悉大 O 记法，这部分可能需要一些时间来消化。但不要放弃！这是一个非常重要的主题，对于理解本书的其余部分，更重要的是，对于成为一名具备性能意识的程序员至关重要。如果你需要对这些概念进行更正式或更实用的介绍，有大量专门针对此主题的书籍和在线资源。

另一方面，如果你已经掌握了大 O 记法，并且知道均摊时间复杂度 (amortized time complexity) 是什么，你可以略读下一节，直接进入本章的后续部分。

本章包含以下几个部分：

使用大 O 记法评估算法效率
一种建议的代码优化工作流程，以避免在没有充分理由的情况下浪费时间进行微调
CPU 性能分析器（CPU profilers）——它们是什么以及为什么要使用它们
微基准测试 (Microbenchmarking)

让我们首先看看如何使用大 O 记法来评估算法效率。

渐近复杂度与大 O 记法

通常有不止一种方法可以解决一个问题，如果效率是你关注的问题，你应该首先通过选择正确的算法和数据结构来专注于高层次的优化。评估和比较算法的一个有用方法是分析它们的渐近计算复杂度 (asymptotic computational complexity)——即分析随着输入规模的增加，运行时间或内存消耗如何增长。此外，C++ 标准库为所有容器和算法都指定了渐近复杂度，这意味着如果你使用这个库，对这个主题的基本理解是必须的。如果你已经对算法复杂度和大 O 记法有很好的理解，可以安全地跳过这一部分。

让我们从一个例子开始。假设我们想编写一个算法，如果它在一个数组中找到一个特定的键（key），则返回 true，否则返回 false。为了弄清楚我们的算法在传入不同大小的数组时的行为，我们希望将该算法的运行时间作为其输入规模的函数进行分析：

bool linear_search(const std::vector<int>& vals, int key) noexcept {
    for (const auto& v : vals) {
        if (v == key) {
            return true;
        }
    }
    return false;
}

该算法非常简单。它遍历数组中的元素，并将每个元素与键进行比较。如果运气好，我们在数组开头就找到了键，它会立即返回；但也可能遍历整个数组都找不到键。这将是该算法的最坏情况 (worst case)，通常，这也是我们想要分析的情况。

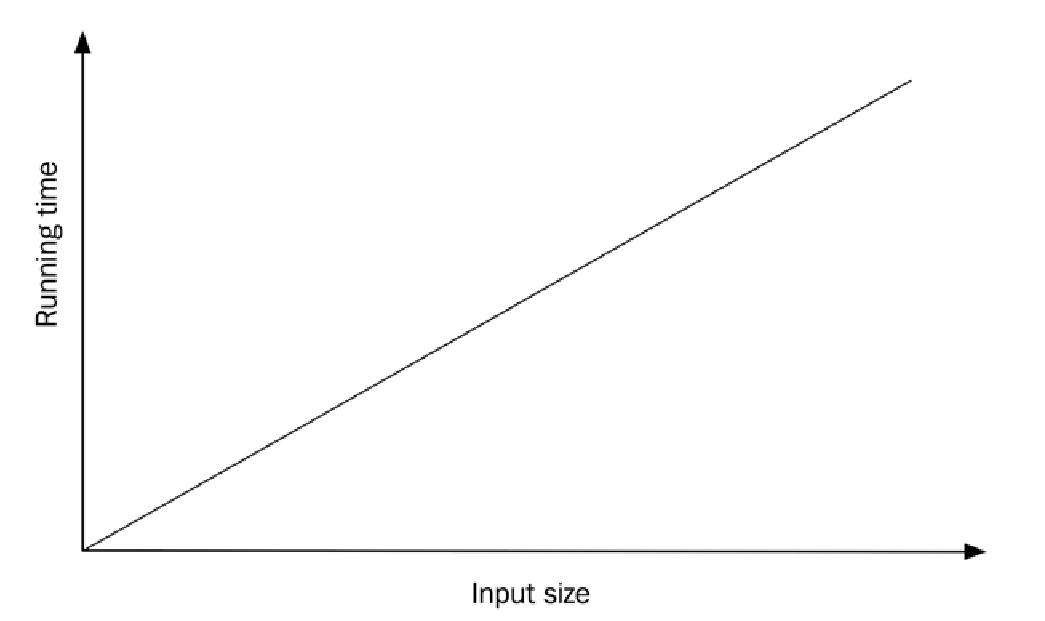
但是，当我们增加输入规模时，运行时间会发生什么变化呢？假设我们将数组的大小增加一倍。那么，在最坏的情况下，我们需要比较数组中的所有元素，这将使运行时间增加一倍。输入规模和运行时间之间似乎存在一种线性关系。我们称之为线性增长率 (linear growth rate)：

现在考虑以下算法：

struct Point {
    int x_{};
    int y_{};
};

bool linear_search(const std::vector<Point>& a, const Point& key) {
    for (size_t i = 0; i < a.size(); ++i) {
        if (a[i].x_ == key.x_ && a[i].y_ == key.y_) {
            return true;
        }
    }
    return false;
}

我们正在比较点而不是整数，并且我们使用下标运算符和索引来访问每个元素。这些变化对运行时间有什么影响？绝对运行时间可能比第一个算法更高，因为我们做了更多的工作——例如，点的比较涉及到两个整数而不是每个元素只涉及一个整数。然而，在这个阶段，我们感兴趣的是算法所表现出的增长率，如果我们将运行时间与输入规模作图，我们仍然会得到一条直线，如前面图中所示。

作为搜索整数的最后一个例子，让我们看看如果假设数组中的元素已排序，我们是否能找到一个更好的算法。我们第一个算法（线性搜索）无论元素顺序如何都适用，但如果我们知道它们已排序，我们就可以使用二分搜索 (binary search)。它的工作原理是查看数组中间的元素，以确定是应该继续在数组的前半部分还是后半部分搜索。为简单起见，索引 high、low 和 mid 的类型是 int，需要进行 static_cast。一个更好的选择是使用迭代器，这将在后续章节中介绍。下面是这个算法：

bool binary_search(const std::vector<int>& a, int key) {
    auto low = 0;
    auto high = static_cast<int>(a.size()) - 1;
    while (low <= high) {
        const auto mid = std::midpoint(low, high); // C++20
        if (a[mid] < key) {
            low = mid + 1;
        } else if (a[mid] > key) {
            high = mid - 1;
        } else {
            return true;
        }
    }
    return false;
}

正如你所见，这个算法比简单的线性扫描更难正确实现。它通过猜测键在数组的中间来寻找指定的键。如果不在，它会将键与中间的元素进行比较，以决定应该继续在数组的哪一半中寻找键。因此，在每次迭代中，它都会将数组减半。

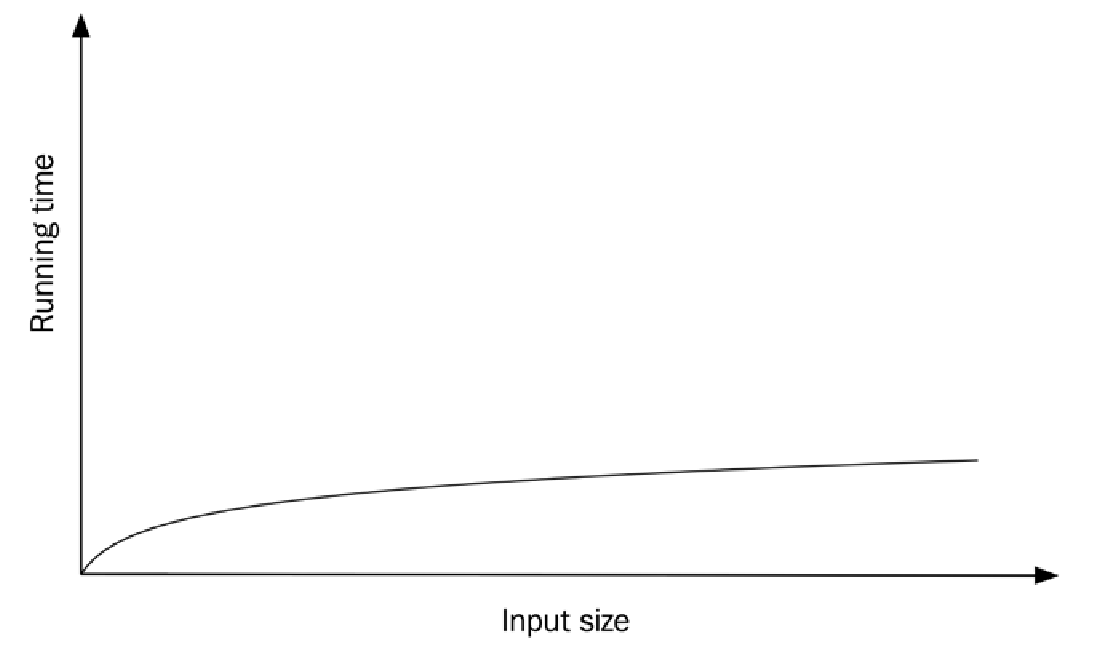
假设我们使用一个包含 64 个元素的数组调用 binary_search()。在第一次迭代中，我们排除了 32 个元素；在下一次迭代中，我们排除了 16 个元素；再下一次迭代中，我们排除了 8 个元素，依此类推，直到没有更多的元素可比较，或者直到我们找到键。对于 64 的输入规模，最多会有 7 次循环迭代。如果我们把输入规模加倍到 128 呢？由于我们在每次迭代中都将规模减半，这意味着我们只需要多一次循环迭代。显然，增长率不再是线性的——它实际上是对数增长 (logarithmic growth)。如果我们测量 binary_search() 的运行时间，我们会看到增长率看起来类似于下图：

在我的机器上，对这三个算法使用各种输入规模 ($n$) 重复调用 10,000 次的快速计时结果如下表所示：

比较算法 1 和 2，我们可以看到比较点比比较整数花费更多时间，但即使输入规模增加，它们仍然处于相同的数量级。然而，当我们比较所有这三个算法在输入规模增加时的情况，真正重要的是算法所展现的增长率。通过利用数组已排序的事实，我们可以用非常少的循环迭代来实现搜索功能。对于大型数组，与线性扫描数组相比，二分搜索实际上是免费的。

在你确定为问题选择了正确的算法和数据结构之前，花费时间调整代码通常不是一个好主意。

如果我们能够以一种有助于我们决定使用哪种算法的方式来表达算法的增长率，那不是很好吗？这就是大 O 记法 (big O notation) 派上用场的地方。

非正式定义如下：

如果 $f(n)$ 是一个函数，它指定了输入规模为 $n$ 的算法的运行时间，我们说 $f(n)$ 是 $O(g(n))$，如果存在一个常数 $k$，使得 $f(n) \le k \cdot g(n)$。

这意味着我们可以说 linear_search() 的时间复杂度 (time complexity) 是 $O(n)$，无论是针对整数版本还是针对点版本；而 binary\_search() 的时间复杂度是 $O(\log n)$，或称作大 O 对数 n。

实际上，当我们想找到一个函数的大 O 时，我们可以通过消除除了增长率最大的项之外的所有项，然后移除任何常数因子来实现。例如，如果一个算法的时间复杂度由 $f(n) = 4n^2 + 30n + 100$ 描述，我们选出增长率最高的项 $4n^2$。接下来，我们移除常数因子 4，得到 $n^2$，这意味着我们可以说我们的算法运行在 $O(n^2)$ 中。

找到一个算法的时间复杂度可能很困难，但当你开始在编写代码时思考它，就会变得越来越容易。在大多数情况下，跟踪循环和递归函数就足够了。

让我们尝试找到以下排序算法的时间复杂度：

void insertion_sort(std::vector<int>& a) {
    for (size_t i = 1; i < a.size(); ++i) {
        auto j = i;
        while (j > 0 && a[j-1] > a[j]) {
            std::swap(a[j], a[j-1]);
            --j;
        }
    }
}

输入规模是数组的大小 $n$。运行时间可以大致通过查看遍历所有元素的循环来估算。首先，有一个外层 for 循环，它迭代 $n-1$ 个元素。内层 while 循环则不同：我们第一次到达 while 循环时，$j$ 是 1，循环只运行一次。在下一次迭代中，$j$ 从 2 开始，递减到 0。对于外层 for 循环的每次迭代，内层循环都需要做越来越多的工作。最后，$j$ 从 $n-1$ 开始，这意味着在最坏的情况下，我们执行了 $\text{swap}()$ $1 + 2 + 3 + \dots + (n-1)$ 次。

我们可以注意到这是一个等差数列 (arithmetic series)，并用 $n$ 来表示：

\[1 + 2 + \dots + k = \frac{k(k + 1)}{2}\]

因此，如果我们设 $k = (n - 1)$，排序算法的时间复杂度是：

\[\frac{(n - 1)((n - 1) + 1)}{2} = \frac{n(n - 1)}{2} = \frac{n^2 - n}{2} = \frac{1}{2}n^2 - \frac{1}{2}n\]

我们现在可以通过首先消除除了增长率最大的项之外的所有项来找到这个函数的大 O，留下 $\frac{1}{2}n^2$。之后，我们移除常数 $\frac{1}{2}$，得出结论：该排序算法的运行时间是 $O(n^2)$。

增长率

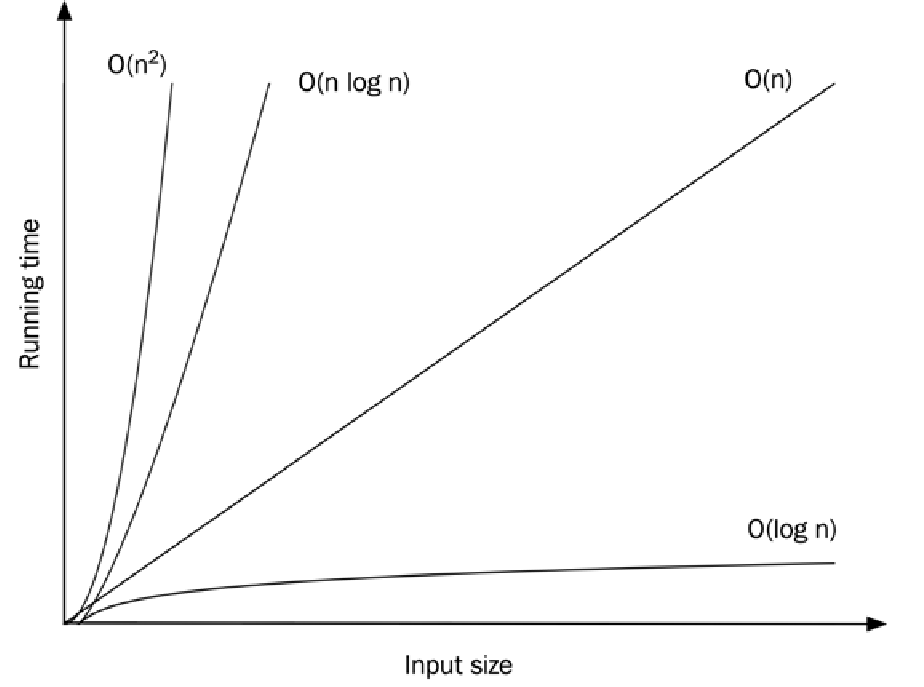
如前所述，确定复杂度函数的大 O 记法的第一步是移除除增长率最高的项之外的所有项。为此，我们必须了解一些常见函数的增长率。在下图中，我绘制了一些最常见的函数：

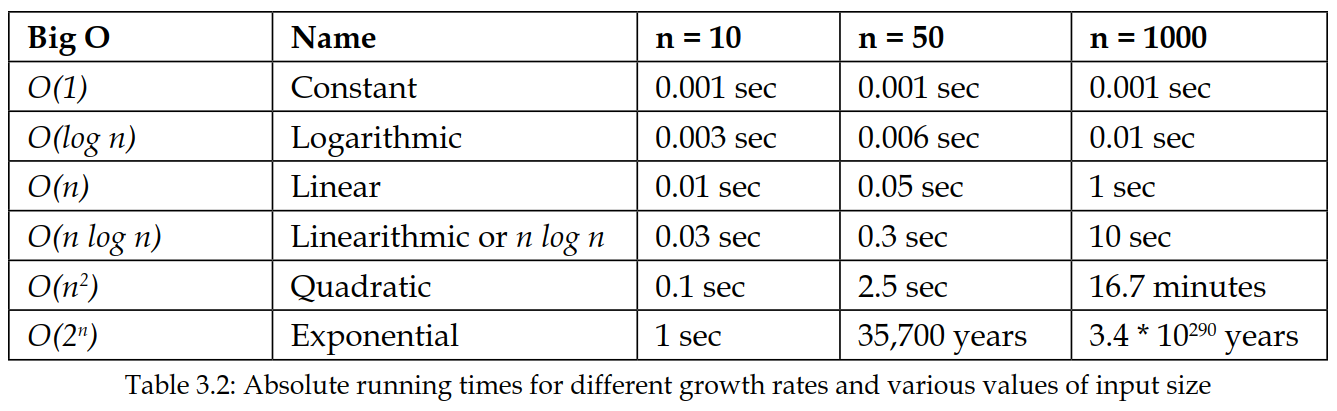
这些增长率独立于机器、编码风格等因素。当两个算法的增长率不同时，在输入规模足够大时，增长率较慢的算法将永远胜出。让我们假设执行 1 单位的工作需要 1 毫秒（ms），看看不同增长率下运行时间会发生什么变化。下表列出了增长函数、它的常用名称以及不同的输入规模 $n$：

请注意，右下角的数字是一个 291 位的数字！相比之下，宇宙的年龄是 $13.7 \times 10^9$ 年，仅是一个 11 位的数字。

接下来，我将介绍均摊时间复杂度 (amortized time complexity)，它在 C++ 标准库中经常使用。

均摊时间复杂度

通常，一个算法在不同的输入下表现不同。回到我们在线性搜索数组中元素的算法，我们分析的是键根本不在数组中的情况。对于该算法而言，这是最坏情况 (worst case)——即它使用了算法所需的最多资源。最好情况 (best case) 指的是算法所需的最少资源量，而平均情况 (average case) 则指定了算法在不同输入下平均将使用的资源量。

标准库通常指的是对容器操作的函数的均摊运行时间 (amortized running time)。如果一个算法以常数均摊时间运行，这意味着它在几乎所有情况下都将运行在 $O(1)$ 中，只有极少数情况表现会更差。乍一看，均摊运行时间可能会与平均时间相混淆，但正如你将看到的，它们并不相同。

为了理解均摊时间复杂度，我们将花一些时间思考 std::vector::push_back()。让我们假设 vector 内部有一个固定大小的数组来存储所有元素。当调用 push_back() 时，如果固定大小的数组中有空间容纳更多元素，则该操作将以常数时间 $O(1)$ 运行——也就是说，只要内部数组有空间再容纳一个元素，它就不依赖于 vector 中已经有多少元素：

if (internal_array.size() > size) {
    internal_array[size] = new_element;
    ++size;
}

但是当内部数组满了时会发生什么？处理 vector 增长的一种方法是创建一个更大的新的空内部数组，然后将所有元素从旧数组移动到新数组。这显然不再是常数时间了，因为我们需要对数组中的每个元素进行一次移动——即 $O(n)$。如果我们将此视为最坏情况，那将意味着 push_back() 是 $O(n)$。然而，如果我们多次调用 push_back()，我们知道昂贵的 push_back() 不会经常发生，因此，如果我们知道 push_back() 是连续多次调用的，那么说 push_back() 是 $O(n)$ 将是悲观的，且不是很有用。

均摊运行时间用于分析一系列操作，而不是单个操作。我们仍在分析最坏情况，但针对的是一系列操作的最坏情况。均摊运行时间可以通过先分析整个序列的总运行时间，然后除以序列的长度来计算。假设我们执行了一个长度为 $m$ 的操作序列，其总运行时间为 $T(m)$：

\[T(m) = t_0 + t_1 + t_2 \dots + t_{m-1}\]

其中 $t_0 = 1$，$t_1 = n$，$t_2 = 1$，$t_3 = n$，依此类推。换句话说，一半的操作以常数时间运行，另一半以线性时间运行。所有 $m$ 个操作的总时间 $T$ 可以表达如下：

\[T(m) = n \cdot \frac{m}{2} + 1 \cdot \frac{m}{2} = \frac{(n + 1)m}{2}\]

每个操作的均摊复杂度是总时间除以操作次数 $m$，结果是 $O(n)$：

\[\frac{T(m)}{m} = \frac{(n + 1)m}{2m} = \frac{n + 1}{2} = O(n)\]

然而，如果我们可以保证昂贵操作的次数与常数时间操作的次数相比数量级不同，我们将获得更低的均摊运行成本。例如，如果我们能保证在一个序列 $T(n) + T(1) + T(1) + \dots$ 中，昂贵操作只发生一次，那么均摊运行时间就是 $O(1)$。因此，均摊运行时间取决于昂贵操作的频率。

现在，回到 std::vector。C++ 标准规定 push_back() 需要以均摊常数时间 $O(1)$ 运行。库供应商是如何实现这一点的呢？如果每次 vector 满时，容量都以固定数量的元素增加，那么我们将得到类似于前面运行时间为 $O(n)$ 的情况。即使我们使用一个很大的常数，容量变化仍然会以固定的间隔发生。关键的见解是，vector 需要指数级增长，才能使昂贵的操作发生得足够稀少。在内部，vector 使用一个增长因子，使得新数组的容量是当前大小乘以该增长因子。

大的增长因子可能会浪费更多的内存，但会使昂贵的操作发生频率降低。为了简化计算，让我们使用一个常见的策略，即每次 vector 需要增长时都将容量加倍。我们现在可以估算昂贵调用的发生频率。对于大小为 $m$ 的 vector，我们需要增长内部数组 $\log_2(m)$ 次，因为我们一直在将大小加倍。每次我们增长数组时，都需要移动数组中当前的所有元素。第 $i$ 次增长数组时，将有 $2^i$ 个元素需要移动。因此，如果执行 $m$ 次 push_back() 操作，增长操作的总运行时间将是：

\[T(m) = \sum_{i=1}^{\log_2(m)} 2^i\]

这是一个几何级数 (geometric series)，也可以表达为：

\[\frac{2 - 2^{\log_2(m) + 1}}{1 - 2} = 2m - 2 = O(m)\]

将此除以序列的长度 $m$，我们得到均摊运行时间 $O(1)$。

正如我已经说过的，均摊时间复杂度在标准库中被大量使用，因此理解这种分析很有好处。思考 push_back() 如何能在均摊常数时间内实现，帮助我记住了均摊常数时间的简化版本：它在几乎所有情况下都将以 $O(1)$ 运行，只有极少数情况表现会更差。

关于渐近复杂度，我们只介绍到这里。现在我们将转向如何解决性能问题并通过优化代码有效工作。

测量什么以及如何测量？

优化几乎总是会增加代码的复杂性。高层次的优化，比如选择算法和数据结构，可以使代码的意图更清晰，但在大多数情况下，优化会使代码更难阅读和维护。因此，我们需要绝对确定我们添加的优化对于我们试图在性能方面实现的目标确实有实际影响。我们真的需要让代码运行得更快吗？以何种方式？代码真的使用了太多内存吗？为了理解哪些优化是可能的，我们需要对延迟 (latency)、吞吐量 (throughput) 和内存使用 (memory usage) 等要求有很好的理解。

优化代码很有趣，但也很容易迷失方向而没有获得任何可衡量的收益。本节将从一个建议的代码调整工作流程开始：

定义目标：如果你有一个定义明确、定量的目标，就更容易知道如何优化以及何时停止优化。对于某些应用来说，要求从一开始就很清楚，但在许多情况下往往比较模糊。即使代码运行速度明显太慢，了解“足够好”的标准是什么也很重要。每个领域都有自己的限制，所以请确保你理解与你的应用相关的限制。以下是一些更具体的例子：
- 用户交互式应用的响应时间为 100 毫秒 (ms)；参考 https://www.nngroup.com/articles/response-times-3-important-limits。
- 每秒 60 帧 (FPS) 的图形意味着每帧有 16 毫秒的处理时间。
- 在 44.1 kHz 采样率下，使用 128 个样本缓冲区的实时音频意味着略低于 3 毫秒的处理时间。
测量：一旦我们知道要测量什么以及限制是什么，我们就可以开始测量应用当前的性能。从步骤 1 中，应该清楚我们对平均时间、峰值、负载等中的哪一个感兴趣。在这一步中，我们只关注测量我们设定的目标。根据应用的不同，测量可以是任何事情，从使用秒表到使用高度复杂的性能分析工具。
找到瓶颈：接下来，我们需要找到应用的瓶颈 (bottlenecks)——那些运行太慢并导致应用无用的部分。在这一点上不要相信你的直觉！也许你在步骤 2 中通过测量代码的各个点获得了一些见解——这很好，但你通常需要进一步分析 (profile) 你的代码，以找到最重要的热点 (hot spots)。
做出有根据的猜测：提出一个关于如何提高性能的假设。可以使用查找表 (lookup table) 吗？我们可以缓存 (cache) 数据以提高整体吞吐量吗？我们可以改变代码，以便编译器可以向量化 (vectorize) 它吗？我们可以通过重用内存来减少关键部分中的分配次数吗？如果你知道这些只是有根据的猜测，提出想法通常并不难。犯错是可以的——你稍后会发现它们是否有影响。
优化：让我们实现我们在步骤 4 中草拟的假设。在你确定它确实有效之前，不要花太多时间使这一步完美无缺。准备好拒绝这个优化。它可能没有达到预期的效果。
评估：再次测量。执行与步骤 2 中完全相同的测试并比较结果。我们获得了什么？如果我们没有获得任何收益，拒绝该代码并返回步骤 4。如果优化确实产生了积极影响，你需要问自己是否值得花更多时间。这个优化有多复杂？它值得付出努力吗？这是一个普遍的性能提升，还是高度特定于某个案例/平台？它是否可维护？我们可以封装它，还是它会蔓延到整个代码库？如果你不能证明这个优化的合理性，请返回步骤 4，否则继续进行最后一步。
重构：如果你遵循了步骤 5 中的说明，并且一开始没有花太多时间编写完美的代码，那么现在是时候重构 (refactor) 优化，使其更简洁。优化几乎总是需要一些注释来解释我们为什么要以一种不寻常的方式做事。

遵循此流程将确保你保持在正确的轨道上，不会因为引入没有充分理由的复杂优化而告终。花时间定义具体目标和测量的重要性怎么强调都不为过。为了在这一领域取得成功，你需要了解哪些性能属性与你的应用相关。

性能属性

在你开始测量之前，你必须知道哪些性能属性对于你正在编写的应用是重要的。在本节中，我将解释一些性能测量中常用的术语。根据你正在编写的应用，某些属性比其他属性更相关。例如，如果你正在编写在线图像转换服务，吞吐量可能比延迟更重要的属性，而当你编写具有实时要求的交互式应用时，延迟是关键。下面是一些在性能测量过程中值得熟悉的有价值的术语和概念：

延迟/响应时间 (Latency/Response time)：根据领域不同，延迟和响应时间可能具有非常精确和不同的含义。然而，在本书中，我指的是请求和操作响应之间的时间——例如，图像转换服务处理一张图像所需的时间。
吞吐量 (Throughput)：这指的是每单位时间处理的事务数（操作、请求等）——例如，图像转换服务每秒可以处理的图像数量。
I/O 密集型或 CPU 密集型 (I/O bound or CPU bound)：一个任务通常将其大部分时间花在 CPU 上计算事物或等待 I/O（硬盘、网络等）上。如果 CPU 更快，任务会运行得更快，则称该任务为 CPU 密集型。如果通过使 I/O 更快，任务会运行得更快，则称该任务为 I/O 密集型。有时你也会听说内存密集型 (memory-bound) 任务，这意味着主内存的数量或速度是当前的瓶颈。
功耗 (Power consumption)：对于在带电池的移动设备上执行的代码来说，这是一个非常重要的考虑因素。为了降低功耗，应用需要更有效地利用硬件，就像我们优化 CPU 使用率、网络效率等一样。除此之外，应该避免高频轮询，因为它会阻止 CPU 进入休眠状态。
数据聚合 (Data aggregation)：在性能测量期间收集大量样本时，通常需要聚合数据。有时平均值 (mean values) 是衡量程序性能的足够好的指标，但更常见的是中位数 (median) 能告诉你更多关于实际性能的信息，因为它对异常值 (outliers) 更健壮。如果你对异常值感兴趣，你可以随时测量最小值和最大值（或者例如第 10 个百分位数）。

这个列表绝不是详尽无遗的，但这是一个很好的开始。这里要记住的重要一点是，我们在测量性能时可以使用既定的术语和概念。花一些时间定义我们真正想通过优化代码达成的目标，有助于我们更快地实现目标。

执行时间的加速比

当我们比较程序或函数的两个版本之间的相对性能时，通常会谈论加速比 (speedup)。在这里，我将给出比较执行时间（或延迟）时的加速比的定义。假设我们已经测量了某个代码的两个版本的执行时间：一个较旧的较慢版本（$T_{\text{old}}$），以及一个较新的较快版本（$T_{\text{new}}$）。执行时间的加速比可以相应地计算如下：

\[\text{加速比}_{\text{执行时间}} = \frac{T_{\text{old}}}{T_{\text{new}}}\]

其中 $T_{\text{old}}$ 是代码初始版本的执行时间，而 $T_{\text{new}}$ 是优化版本的执行时间。这种加速比的定义意味着加速比为 1 时表示完全没有加速。

我们通过一个例子来确保你知道如何测量相对执行时间。假设我们有一个函数执行时间为 10 ms ($T_{\text{old}} = 10 \text{ ms}$)，经过一些优化后，我们设法使其运行时间为 4 ms ($T_{\text{new}} = 4 \text{ ms}$)。那么我们可以计算加速比如下：

\[\text{加速比} = \frac{T_{\text{old}}}{T_{\text{new}}} = \frac{10 \text{ ms}}{4 \text{ ms}} = 2.5\]

换句话说，我们新的优化版本提供了 2.5 倍的加速比。如果想将这种改进表示为百分比，我们可以使用以下公式将加速比转换为百分比改进：

\[\text{百分比改进} = 100 \left(1 - \frac{1}{\text{加速比}}\right) = 100 \left(1 - \frac{1}{2.5}\right) = 60\%\]

因此，我们可以说新版本的代码比旧版本快 60%，这相当于 2.5 倍的加速比。在本书中，我将始终使用加速比而不是百分比改进来比较执行时间。

最终，我们通常对执行时间感兴趣，但时间并不总是最好的衡量指标。通过检查硬件上的其他数值，硬件可能会给我们一些其他有用的指导，以便优化我们的代码。

性能计数器

除了执行时间和内存使用等显而易见的属性外，测量其他指标有时也是有益的。这可能是因为它们更可靠，或者因为它们可以为我们提供更好的洞察力，以了解导致代码运行缓慢的原因。

许多 CPU 都配备了硬件性能计数器 (hardware performance counters)，可以为我们提供诸如指令数、CPU 周期数、分支预测错误 (branch mispredictions) 和缓存未命中 (cache misses) 等指标。我在这本书中尚未介绍这些硬件方面的内容，我们也不会深入探讨性能计数器。然而，了解它们的存在以及所有主要操作系统都有现成的工具和库（可通过 API 访问）来在程序运行时收集性能监控计数器 (Performance Monitoring Counters, PMC) 是有益的。

对性能计数器的支持因 CPU 和操作系统而异。Intel 提供了一个名为 VTune 的强大工具，可用于监控性能计数器。FreeBSD 提供了 pmcstat。macOS 带有 DTrace 和 Xcode Instruments。Microsoft Visual Studio 提供了在 Windows 上收集 CPU 计数器的支持。

另一个流行的工具是 perf，它在 GNU/Linux 系统上可用。运行以下命令：

perf stat ./your-program

将揭示许多有趣的事件，例如上下文切换次数 (context switches)、页面错误 (page faults)、分支预测错误 (mispredicted branches) 等。以下是运行一个小型程序时它输出的示例：

 Performance counter stats for './my-prog':

129.86 msec task-clock              # 1.000 CPUs utilized
           8 context-switches            # 0.007 K/sec
           0 cpu-migrations              # 0.000 K/sec
810 page-faults                 # 0.087 M/sec
968 043 041 cycles                    # 3.512 GHz
250 538 491 stalled-cycles-frontend   # 31.52% frontend cycles idle
225 466 stalled-cycles-backend    # 12.53% backend cycles idle
237 037 204 instructions              # 1.57 insn per cycle
                                         # 0.20 stalled cycles per insn
853 556 742 branches                  # 1640.516 M/sec
486 026 branch-misses             # 0.19% of all branches

130355771 sec time elapsed
026068000 sec user
104210000 sec sys

现在我们将继续强调测试和评估性能时的一些最佳实践。

性能测试——最佳实践

出于某种原因，涵盖功能需求的回归测试比涵盖性能需求或其他非功能需求的测试更为常见。性能测试通常进行得比较零星 (sporadically)，而且往往在开发过程中太晚才进行。我建议通过将性能测试添加到你的夜间构建 (nightly builds) 中，尽早进行测量并尽快检测到性能退化（regression）。

如果算法和数据结构需要处理大规模输入，请明智地选择它们，但不要在没有充分理由的情况下对代码进行微调 (fine-tune)。尽早使用逼真的测试数据来测试你的应用也很重要。在项目初期就询问关于数据规模的问题。应用应该能够处理多少行表格数据才能保持流畅滚动？不要只用 100 个元素试一下就希望你的代码能够扩展——去测试它！

绘制你的数据图表是理解你所收集数据的非常有效的方法。现在有许多优秀且易于使用的绘图工具可用，所以没有理由不进行绘图。RStudio 和 Octave 都提供了强大的绘图功能。其他例子包括 gnuplot 和 Matplotlib (Python)，它们可以在各种平台上使用，并且只需要最少的脚本编写就能在你收集数据后生成有用的图表。一张图表不必漂亮才能有用。一旦你绘制了数据图表，你就会看到异常值 (outliers) 和模式 (patterns)，而这些在满是数字的表格中通常很难发现。

至此，我们的“测量什么以及如何测量？”部分就结束了。接下来，我们将探讨如何找到代码中浪费过多资源的关键部分。

了解你的代码和热点

帕累托原则 (Pareto principle)，即 80/20 法则，自 100 多年前意大利经济学家维尔弗雷多·帕累托首次观察到以来，已被应用于各个领域。他证明了 20% 的意大利人口拥有 80% 的土地。在计算机科学中，它被广泛使用，甚至可能被过度使用。在软件优化中，它暗示了20% 的代码消耗了程序所使用的80% 的资源。

当然，这只是一个经验法则 (rule of thumb)，不应太过字面理解。尽管如此，对于尚未优化的代码来说，通常会发现一些相对较小的热点 (hot spots) 消耗了总资源的绝大部分。作为一名程序员，这实际上是个好消息，因为它意味着我们可以在编写大部分代码时不用费心进行性能调整，而是专注于保持代码的简洁。这也意味着在进行优化时，我们需要知道在哪里进行优化；否则，我们很有可能会优化对整体性能没有影响的代码。在本节中，我们将探讨用于找到那 20% 值得优化的代码的方法和工具。

使用性能分析器 (profiler) 通常是识别程序中热点最有效的方法。性能分析器会分析程序的执行情况，并输出一个统计摘要（即配置文件，profile），说明程序中的函数或指令被调用的频率。

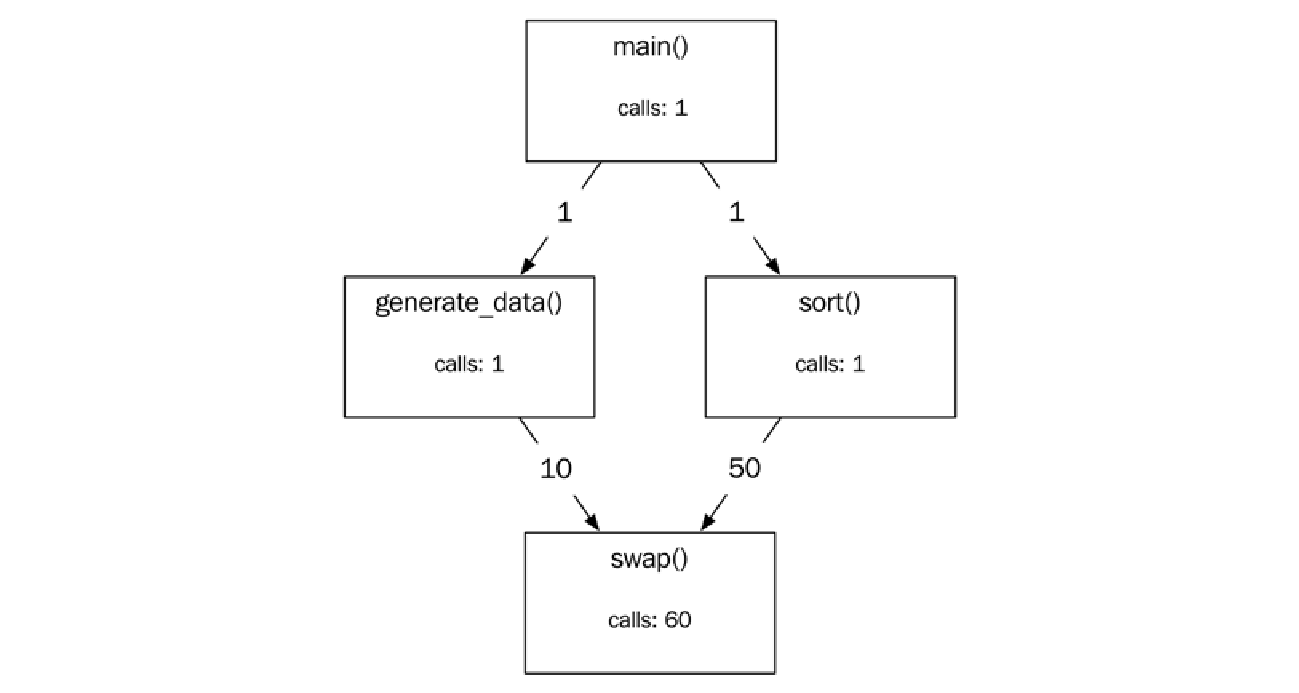
此外，性能分析器通常还会输出一个调用图 (call graph)，显示函数调用之间的关系，即在分析期间调用的每个函数的调用者 (callers) 和被调用者 (callees)。在下图中，你可以看到 sort() 函数是从 main()（调用者）调用的，并且 sort() 调用了 swap() 函数（被调用者）：

性能分析器主要分为两大类：采样性能分析器 (sampling profilers) 和插入式性能分析器 (instrumentation profilers)。这两种方法也可以混合使用，创建采样和插装的混合体。Unix 性能分析工具 gprof 就是一个例子。

接下来的部分将重点介绍插入性能分析器和采样性能分析器。

插入式性能分析器（Instrumentation Profilers）

我所说的插入（instrumentation），是指在待分析的程序中插入代码，以收集有关每个函数执行频率的信息。通常，插入的探查代码会记录每个进入点和退出点。您可以手动插入代码来编写自己的基本插入式探查器，也可以使用工具，在构建过程中自动插入必要的代码。

一个简单的实现可能足以满足您的目的，但请注意，添加的代码可能会对性能产生影响，从而可能导致探查结果产生误导。这种朴素实现的另一个问题是，它可能会阻止编译器优化或面临被优化掉的风险。

为了给您一个插入式性能分析器的示例，这里是一个我在先前项目中使用的计时器类的简化版本：

class ScopedTimer {
public:
    using ClockType = std::chrono::steady_clock;
    
    ScopedTimer(const char* func)
    : function_name_{func}, start_{ClockType::now()} {}
    
    ScopedTimer(const ScopedTimer&) = delete;
    ScopedTimer(ScopedTimer&&) = delete;
    auto operator=(const ScopedTimer&) -> ScopedTimer& = delete;
    auto operator=(ScopedTimer&&) -> ScopedTimer& = delete;
    
    ~ScopedTimer() {
        using namespace std::chrono;
        auto stop = ClockType::now();
        auto duration = (stop - start_);
        auto ms = duration_cast<milliseconds>(duration).count();
        std::cout << ms << " ms " << function_name_ << '\n';
    }

private:
    const char* function_name_{};
    const ClockType::time_point start_{};
};

ScopedTimer 类将测量从它被创建到它超出作用域（即被析构）所花费的时间。我们使用了 $\text{C}++11$ 以来可用的 std::chrono::steady_clock 类，它专为测量时间间隔而设计。steady_clock 是单调的（monotonic），这意味着在连续两次调用 clock_type::now() 之间，它永远不会减少。例如，系统时钟就不是单调的，因为它随时可以被调整。

现在，我们可以通过在每个函数的开头创建一个 ScopedTimer 实例来测量程序中的每个函数：

auto some_function() {
    ScopedTimer timer{"some_function"};
    // ...
}

尽管我们通常不推荐使用预处理器宏，但这可能是一个可以使用宏的场景：

#if USE_TIMER
#define MEASURE_FUNCTION() ScopedTimer timer{__func__}
#else
#define MEASURE_FUNCTION()
#endif

我们使用了 c++11 以来可用的函数局部预定义变量 __func__ 来获取函数的名称。 c++20 还引入了方便的 std::source_location 类，它为我们提供了 function_name()、file_name()、line() 和 column() 等函数。如果您的编译器尚不支持 std::source_location，还有一些被广泛支持的非标准预定义宏，它们对于调试目的非常有用，例如 __FUNCTION__、__FILE__ 和 __LINE__。

现在，我们的 ScopedTimer 类可以像这样使用：

auto some_function() {
    MEASURE_FUNCTION();
    // ...
}

假设我们在编译计时器时定义了 USE_TIMER，那么每次 some_function() 返回时，它将产生以下输出：

2.3 ms some_function

我已经演示了如何通过插入代码来手动探查（manually instrument）我们的代码，这些代码打印出代码中两点之间经过的时间。尽管这在某些场景下是一个方便的工具，但请注意，这样一个简单的工具可能会产生误导性的结果。在下一节中，我将介绍一种不需要修改执行代码的探查方法。

采样式探查器 (Sampling Profilers)

采样式探查器通过以固定的时间间隔——通常是每 $\text{10 ms}$——查看运行中程序的状态来创建性能剖析（profile）。

采样式探查器对程序实际性能的影响通常最小，并且还可以在启用所有优化的情况下以发布模式（release mode）构建程序。采样式探查器的一个缺点是它的不精确性和统计学方法，但只要你意识到这一点，这通常不是问题。

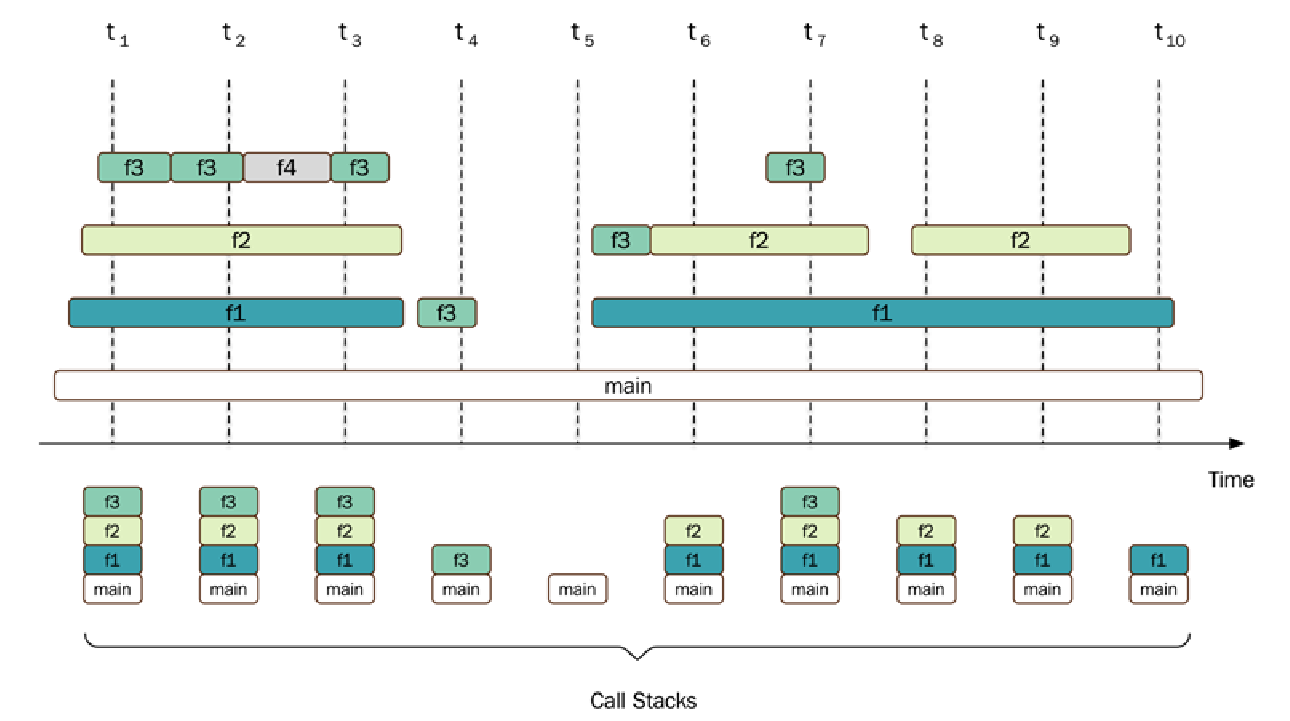
下面的图表展示了一个运行中的程序（包含 $\text{main()、f1()、f2()、f3()}$ 和 $\text{f4()}$ 五个函数）的采样会话。标签 $\text{t1} - \text{t10}$ 表示进行每次采样的时间点。方框表示每个正在执行的函数的进入点和退出点：

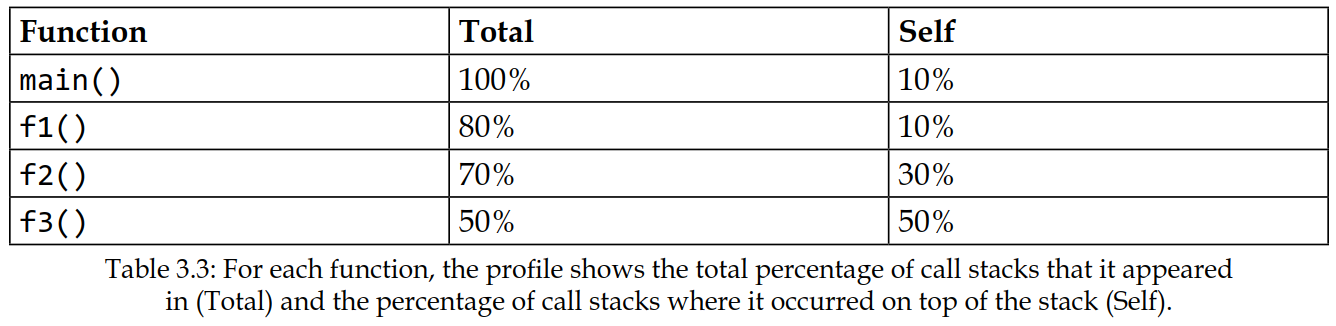
性能剖析总结在下表中：

上表中的“总计” (Total) 列显示了包含某个函数的调用堆栈（call stacks）的百分比。在我们的示例中，main 函数出现在所有 10 个调用堆栈中（100%），而 f2() 函数仅在 7 个调用堆栈中被检测到，对应于所有调用堆栈的 70%。

“自身” (Self) 列显示了每个函数出现在调用堆栈顶部的次数。main() 函数在第 t5 次采样时被检测到一次位于调用堆栈顶部，而 f2() 函数在 t6、t8 和 t9 次采样时位于调用堆栈顶部，对应于 3/10 = 30%。

f3() 函数的自身值最高（5/10），并且在每次被检测到时都位于调用堆栈的顶部。

从概念上讲，采样式探查器以固定的时间间隔存储调用堆栈的样本。它检测当前 $\text{CPU}$ 正在运行什么。纯采样式探查器通常只检测当前正在运行状态（running state）的线程中正在执行的函数，因为休眠（sleeping）的线程不会被调度到 $\text{CPU}$ 上。这意味着，如果一个函数正在等待锁（lock），导致线程休眠，那么这部分时间将不会出现在时间剖析中。这一点很重要，因为您的性能瓶颈可能正是由线程同步引起的，而采样式探查器可能无法察觉。

f4() 函数发生了什么？根据图表，它在第 $\text{t2}$ 和 $\text{t3}$ 次采样之间被 f2() 函数调用，但它从未出现在我们的统计性能剖析中，因为它从未被记录到任何调用堆栈中。这是采样式探查器的一个重要特性。如果两次采样之间的时间间隔太长，或者总的采样会话太短，那么简短且不常调用的函数将不会出现在性能剖析中。这通常不是问题，因为这些函数很少是您需要优化的函数。您可能会注意到 f3() 函数在 $\text{t5}$ 和 $\text{t6}$ 之间也被错过了，但由于 f3() 被频繁调用，它仍然对性能剖析产生了很大的影响。

请务必理解您的时间探查器实际记录了什么。了解其局限性和优势，才能尽可能有效地使用它。

微基准测试 (Microbenchmarking)

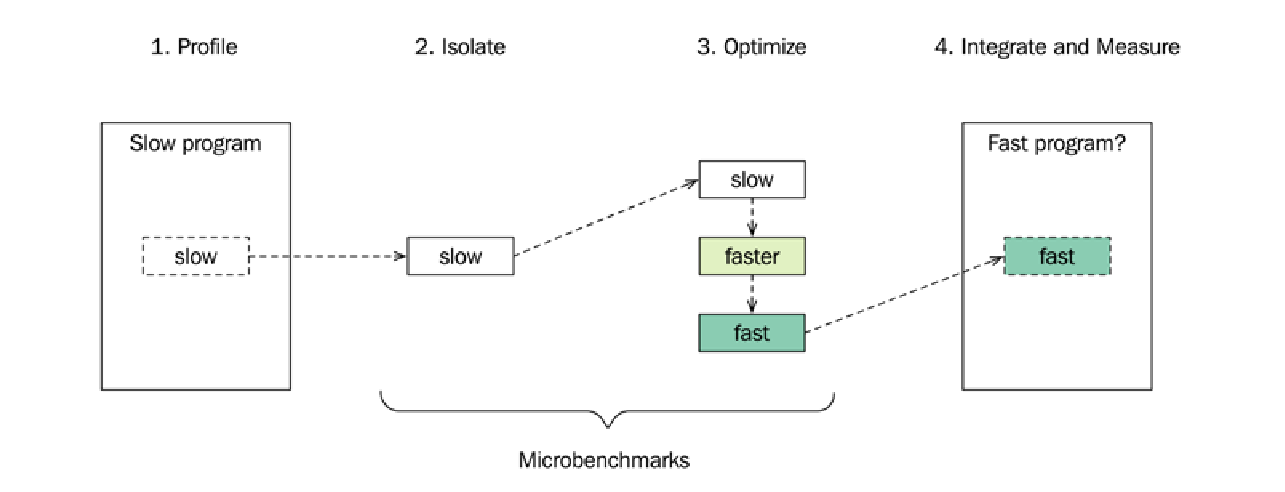
性能探查（Profiling）可以帮助我们找到代码中的瓶颈。如果这些瓶颈是由低效的数据结构（参见第 4 章：数据结构）、错误的算法选择（参见第 5 章：算法）或不必要的竞争（参见第 11 章：并发）引起的，那么应该首先解决这些更大的问题。但有时我们会发现一个需要优化的小函数或小代码块，在这种情况下，我们可以使用一种称为微基准测试 ($\text{microbenchmarking}$) 的方法。通过这个过程，我们创建了一个微基准 ($\text{microbenchmark}$)——一个将一小段代码与程序的其余部分隔离运行的程序。

微基准测试过程包括以下步骤：

找到一个需要调整的热点（hot spot），最好是使用探查器找到。
将其与程序的其余代码分离，并创建一个独立的微基准。
优化该微基准。在优化过程中，使用基准测试框架来测试和评估代码。
将新优化的代码集成到程序中，并再次测量，以查看在更大数据背景和相关输入下运行时，这些优化是否仍然有效。

微基准测试很有趣。然而，在开始尝试让某个特定函数运行得更快之前，我们应该首先确保：

当程序运行时，在该函数内部花费的时间显著影响我们想要加速的程序的整体性能。性能探查和阿姆达尔定律（Amdahl’s law）将帮助我们理解这一点。阿姆达尔定律将在下文解释。
我们不能轻易减少该函数的调用次数。消除对开销大函数的调用通常是优化程序整体性能最有效的方法。

使用微基准测试进行代码优化通常应被视为最后的手段。预期的整体性能增益通常很小。然而，有时我们无法避免需要通过调整实现来使相对较小的代码块运行得更快，在这些情况下，微基准测试可能会非常有效。

接下来，您将了解微基准测试带来的加速如何影响程序的整体加速。

阿姆达尔定律 (Amdahl’s Law)

在使用微基准测试时，必须牢记孤立代码的优化对整个程序的影响有多大（或多小）。根据我们的经验，人们很容易在改进微基准测试时过于兴奋，结果却发现整体效果几乎可以忽略不计。这种徒劳无功的风险部分可以通过使用可靠的探查技术来解决，但也要始终牢记优化带来的总体影响。

假设我们正在优化程序中一个孤立的部分（即微基准测试）。那么整个程序的总体加速的上限可以通过阿姆达尔定律来计算。我们需要知道两个值才能计算总体加速：

首先，我们需要知道孤立部分的执行时间占总执行时间的比例。我们将这个比例执行时间的值表示为字母 $p$。
其次，我们需要知道我们正在优化的部分的加速比（即微基准测试的加速比）。我们将这个局部加速比的值表示为字母 $s$。

使用 $p$ 和 $s$，我们现在可以使用阿姆达尔定律来计算总体加速：

\[\text{总体加速} = \frac{1}{(1 - p) + \frac{p}{s}}\]

希望这个公式看起来不会太复杂，因为它在实际应用中非常直观。为了对阿姆达尔定律有一个直观的理解，您可以看看当使用 $p$ 和 $s$ 的各种极端值时，总体加速会变成多少：

设置 $p = 0$ 且 $s = 5 \text{x}$ 意味着我们优化的部分对总体执行时间没有影响。因此，无论 $s$ 的值是多少，总体加速将始终是 $\text{1x}$。
设置 $p = 1$ 且 $s = 5 \text{x}$ 意味着我们优化的部分占了程序全部执行时间。在这种情况下，总体加速将始终等于我们在优化的部分中实现的加速比——在本例中为 $\text{5x}$。
设置 $p = 0.5$ 且 $s = \infty$ 意味着我们完全消除了程序中占总执行时间一半的部分。那么总体加速将是 $\text{2x}$。

结果总结在下表中：

一个完整的示例将演示我们如何在实践中使用阿姆达尔定律。假设您正在优化一个函数，优化后的版本比原始版本快 $\text{2}$ 倍，即加速比为 $\text{2x}$ ($s = 2$)。此外，假设这个函数仅占程序总执行时间的 $\text{1\%}$ ($p = 0.01$)，那么整个程序的总体加速可以计算如下：

\[\text{总体加速} = \frac{1}{(1 - p) + \frac{p}{s}} = \frac{1}{(1 - 0.01) + \frac{0.01}{2}} = \frac{1}{0.99 + 0.005} = \frac{1}{0.995} \approx 1.005\]

因此，即使我们成功地使我们的孤立代码快了 $\text{2}$ 倍，总体加速也只有 $\text{1.005}$ 倍——这并不是说这个加速比一定可以忽略不计，但我们始终需要回头看看我们所获得的收益与大局之间的比例关系。

微基准测试的陷阱 (Pitfalls of Microbenchmarking)

在测量软件性能，尤其是在进行微基准测试时，存在许多隐藏的难点。在这里，我将列出进行微基准测试时需要注意的一些事项：

结果可能被过度概括，并被视为普遍真理。
编译器对隔离代码的优化方式，可能与在完整程序中的优化方式不同。例如，一个函数可能在微基准测试中被内联（inlined），但在编译完整程序时却没有。或者，编译器可能会预先计算（precompute）微基准测试中的部分代码。
基准测试中未使用的返回值，可能会导致编译器移除我们试图测量的函数。
微基准测试中提供的静态测试数据，可能在优化代码时给编译器带来不切实际的优势。例如，如果我们硬编码（hardcode）了一个循环的执行次数，并且编译器知道这个硬编码的值恰好是 $\text{8}$ 的倍数，它可能会以不同的方式对循环进行向量化（vectorize），跳过那些可能未与 $\text{SIMD}$ 寄存器大小对齐的部分的序言和尾声（prologue and epilogue）。而在实际代码中，当这个硬编码的编译时常量被一个运行时值取代时，这种优化就不会发生。
- 不切实际的测试数据在运行基准测试时也会影响分支预测（branch prediction）。
多次测量之间的结果可能因为多种因素而有所不同，例如频率调节（frequency scaling）、缓存污染（cache pollution）以及其他进程的调度（scheduling）。
代码性能的限制因素可能是由于缓存未命中（cache misses），而不是执行指令实际花费的时间。因此，在许多场景中，微基准测试的一条重要规则是：在测量之前，你必须清除缓存（thrash the cache），否则你测量的可能根本不是你想要测量的东西。

我希望有一个简单的公式可以避免上面列出的所有陷阱，但不幸的是，没有。不过，在下一节中，我们将看一个具体的例子，了解如何通过使用微基准测试支持库来解决其中一些陷阱。

微基准测试示例 (A Microbenchmark Example)

我们将通过回到本章中最初关于线性搜索（linear search）和二分搜索（binary search）的例子，并演示如何使用基准测试框架来对它们进行基准测试，从而结束本章。

本章开头，我们比较了在 std::vector 中搜索一个整数的两种方法。如果我们知道向量已经排序，我们就可以使用二分搜索，它的性能优于简单的线性搜索算法。我在此不再重复这些函数的定义，但它们的声明如下所示：

bool linear_search(const std::vector<int>& v, int key);
bool binary_search(const std::vector<int>& v, int key);

一旦输入数据足够大，这些函数执行时间的差异就会非常明显，但这足以作为我们目的的一个好例子。我们将从只测量 linear_search() 开始。然后，当我们建立了一个可用的基准测试后，我们将添加 binary_search() 并比较这两个版本。

为了制作一个测试程序，我们首先需要一种生成已排序整数向量的方法。如下所示的简单实现就足以满足我们的需求：

auto gen_vec(int n) {
    std::vector<int> v;
    for (int i = 0; i < n; ++i) {
        v.push_back(i);
    }
    return v;
}

返回的向量将包含 $0$ 到 $n - 1$ 之间的所有整数。一旦准备好这个函数，我们就可以创建这样一个朴素的测试程序：

int main() { // 不要像这样进行性能测试！
    ScopedTimer timer("linear_search");
    int n = 1024;
    auto v = gen_vec(n);
    linear_search(v, n);
}

我们正在搜索值 $n$，我们知道它不在向量中，因此该算法将展示其最坏情况性能。这是这个测试的好处。除此之外，它还存在许多使其基准测试结果毫无用处的缺陷：

使用优化来编译这段代码很可能会完全移除这些代码，因为编译器可以看到函数的结果没有被使用。
我们不希望测量创建和填充 std::vector 所花费的时间。
只运行一次 linear_search() 函数，我们无法获得具有统计稳定性的结果。
测试不同的输入大小很麻烦。

让我们看看如何通过使用微基准测试支持库来解决这些问题。有各种用于基准测试的工具/库，但我们将使用 Google Benchmark (https://github.com/google/benchmark)，因为它应用广泛，而且作为额外福利，它也可以在 http://quick-bench.com 页面上轻松在线测试，无需任何安装。

下面是使用 $\text{Google Benchmark}$ 时 linear_search() 的一个简单微基准测试示例：

#include <benchmark/benchmark.h> // 非标准头文件
#include <vector>

bool linear_search(const std::vector<int>& v, int key) { /* ... */ }
auto gen_vec(int n) { /* ... */ }

static void bm_linear_search(benchmark::State& state) {
    auto n = 1024;
    auto v = gen_vec(n);
    for (auto _ : state) {
        benchmark::DoNotOptimize(linear_search(v, n));
    }
}
BENCHMARK(bm_linear_search); // 注册基准测试函数
BENCHMARK_MAIN();

就是这样！我们唯一尚未解决的事实是输入大小被硬编码为 $\text{1024}$。我们稍后会解决这个问题。编译并运行此程序将生成类似如下的输出：

-------------------------------------------------------------------
Benchmark             Time             CPU   Iterations
-------------------------------------------------------------------
bm_linear_search     361 ns         361 ns      1945664

最右侧列报告的迭代次数 ($\text{Iterations}$) 是在获得统计稳定结果之前，循环需要执行的次数。传递给我们的基准测试函数的 state 对象决定了何时停止。每迭代的平均时间在两列中报告：Time 是挂钟时间（wall-clock time），CPU 是主线程花费在 $\text{CPU}$ 上的时间。在这个例子中，它们是相同的，但如果 linear_search() 曾被阻塞等待 $\text{I/O}$（例如），$\text{CPU}$ 时间就会低于挂钟时间。

另一个需要注意的重要事项是，生成向量的代码没有包含在报告的时间内。唯一被测量的是这个循环内的代码：

for (auto _ : state) { // 只有这个循环被测量
    benchmark::DoNotOptimize(binary_search(v, n));
}

我们的搜索函数返回的布尔值被封装在 benchmark::DoNotOptimize() 内部。这是用来确保返回值不会被优化掉的机制，否则可能导致整个对 linear_search() 的调用消失。

现在，让我们通过改变输入大小，让这个基准测试更有趣一些。我们可以通过使用 state 对象将参数传递给我们的基准测试函数来实现。方法如下：

static void bm_linear_search(benchmark::State& state) {
    auto n = state.range(0);
    auto v = gen_vec(n);
    for (auto _ : state) {
        benchmark::DoNotOptimize(linear_search(v, n));
    }
}

BENCHMARK(bm_linear_search)->RangeMultiplier(2)->Range(64, 256);

这将从输入大小 $\text{64}$ 开始，并将其加倍，直到达到 $\text{256}$。在我的机器上，该测试生成了以下输出：

-------------------------------------------------------------------
Benchmark             Time             CPU   Iterations
-------------------------------------------------------------------
bm_linear_search/64 17.9 ns         17.9 ns     38143169
bm_linear_search/128 44.3 ns         44.2 ns     15521161
bm_linear_search/256 74.8 ns         74.7 ns      8836955

作为最后一个示例，我们将对 linear_search() 和 binary_search() 函数进行基准测试，使用可变的输入大小，并尝试让框架估计我们函数的时间复杂度。这可以通过使用 SetComplexityN() 函数将输入大小提供给 state 对象来实现。完整的微基准测试示例如下所示：

#include <benchmark/benchmark.h>
#include <vector>

bool linear_search(const std::vector<int>& v, int key) { /* ... */ }
bool binary_search(const std::vector<int>& v, int key) { /* ... */ }
auto gen_vec(int n) { /* ... */ }

static void bm_linear_search(benchmark::State& state) {
    auto n = state.range(0);
    auto v = gen_vec(n);
    for (auto _ : state) {
        benchmark::DoNotOptimize(linear_search(v, n));
    }
    state.SetComplexityN(n);
}

static void bm_binary_search(benchmark::State& state) {
    auto n = state.range(0);
    auto v = gen_vec(n);
    for (auto _ : state) {
        benchmark::DoNotOptimize(binary_search(v, n));
    }
    state.SetComplexityN(n);
}

BENCHMARK(bm_linear_search)->RangeMultiplier(2)->
Range(64, 4096)->Complexity();
BENCHMARK(bm_binary_search)->RangeMultiplier(2)->
Range(64, 4096)->Complexity();

BENCHMARK_MAIN();

运行基准测试时，我们将获得以下结果打印到控制台：

-------------------------------------------------------------------
Benchmark             Time             CPU   Iterations
-------------------------------------------------------------------
bm_linear_search/64 18.0 ns         18.0 ns     38984922
bm_linear_search/128 45.8 ns         45.8 ns     15383123
...
bm_linear_search/8192 1988 ns        1982 ns       331870
bm_linear_search_BigO  0.24 N         0.24 N
bm_linear_search_RMS   4 %            4 %

bm_binary_search/64 4.16 ns         4.15 ns    169294398
bm_binary_search/128 4.52 ns         4.52 ns    152284319
...
bm_binary_search/4096 8.27 ns         8.26 ns     80634189
bm_binary_search/8192 8.90 ns         8.90 ns     77544824
bm_binary_search_BigO  0.67 lgN         0.67 lgN
bm_binary_search_RMS   3 %            3 %

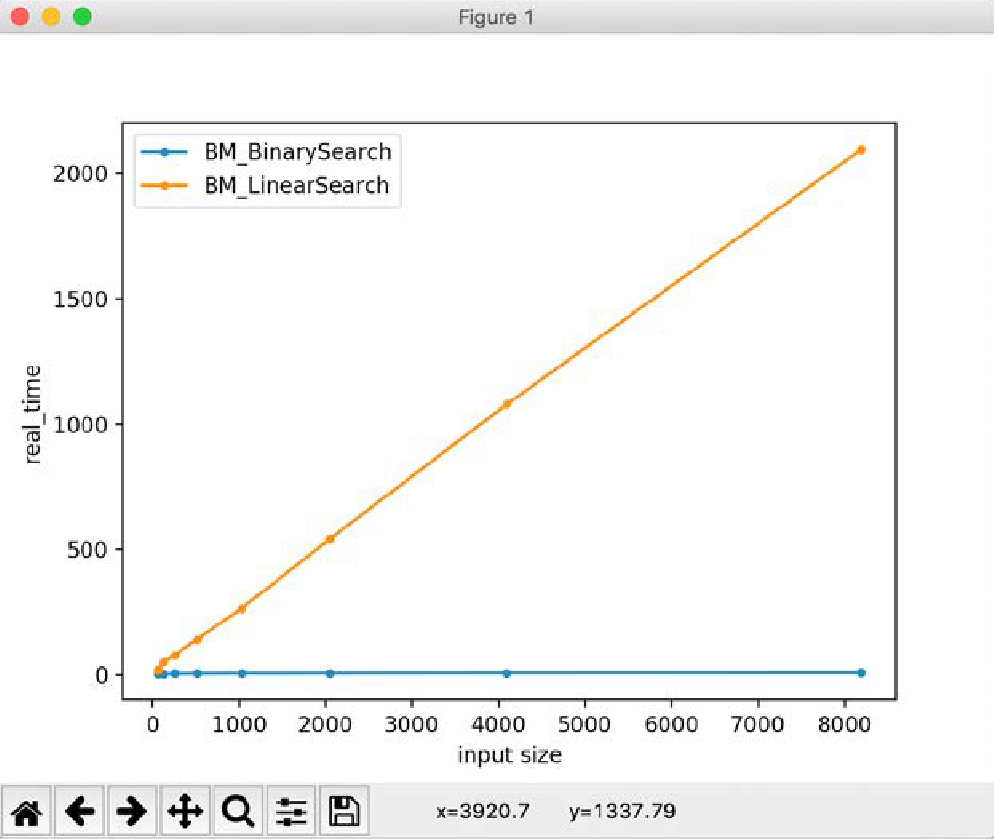
输出结果与我们本章的初步结果一致，我们得出结论，这两种算法分别表现出线性运行时 ($\mathcal{O}(N)$) 和对数运行时 ($\mathcal{O}(\log N)$)。如果我们将这些值绘制成图表，我们可以清楚地看到函数的线性和对数增长率。

您现在拥有了大量用于查找和改进代码性能的工具和见解。在进行性能工作时，我再怎么强调测量和设定目标的重要性也不为过。引用 $\text{Andrei Alexandrescu}$ 的一句话来结束本节：

“测量让你比不需要测量的专家更胜一筹。” — Andrei Alexandrescu, 2015, Writing Fast Code I, code::dive conference 2015, https://codedive.pl/2015/writing-fast-code-part-1.

总结

在本章中，您学习了如何使用大 $\mathcal{O}$ 记法来比较算法的效率。您现在知道 $\text{C}++$ 标准库为算法和数据结构提供了复杂度保证。所有标准库算法都指定了它们的最坏情况或平均情况性能保证，而容器和迭代器则指定了均摊或精确复杂度。

您还发现了如何通过测量延迟 ($\text{latency}$) 和吞吐量 ($\text{throughput}$) 来量化软件性能。

最后，您学习了如何使用 $\text{CPU}$ 探查器来检测代码中的热点 ($\text{hot spots}$)，以及如何执行微基准测试 ($\text{microbenchmarking}$) 来改进程序的孤立部分。

在下一章中，您将了解如何高效地使用 $\text{C}++$ 标准库提供的数据结构。