目录
在前一章中,我们讨论了如何分析时间和内存复杂度以及如何衡量性能。在本章中,我们将讨论如何选择和使用标准库中的数据结构。为了理解为什么某些数据结构在当今的计算机上表现出色,我们首先需要了解一些计算机内存的基础知识。在本章中,你将学习以下内容:
- 计算机内存的属性
- 标准库容器:序列容器和关联容器
- 标准库容器适配器
- 并行数组
在我们开始详细介绍标准库提供的容器和其他一些有用的数据结构之前,我们将简要讨论一下计算机内存的一些属性。
计算机内存的属性
C++ 将内存视为一系列单元格。每个单元格的大小为 1 字节,并且每个单元格都有一个地址。通过地址访问内存中的一个字节是一个常数时间操作,即 $O(1)$,换句话说,它与内存单元格的总数无关。在 32 位机器上,理论上你可以寻址 $2^{32}$ 个字节,大约 $4 \text{ GB}$,这限制了一个进程一次可以使用的内存量。在 $\text{64}$ 位机器上,理论上你可以寻址 $2^{64}$ 个字节,这个容量非常大,几乎没有耗尽地址的风险。
下面的图展示了内存中一系列排列的内存单元格。每个单元格包含 $\text{8}$ 位。十六进制数字是内存单元格的地址:
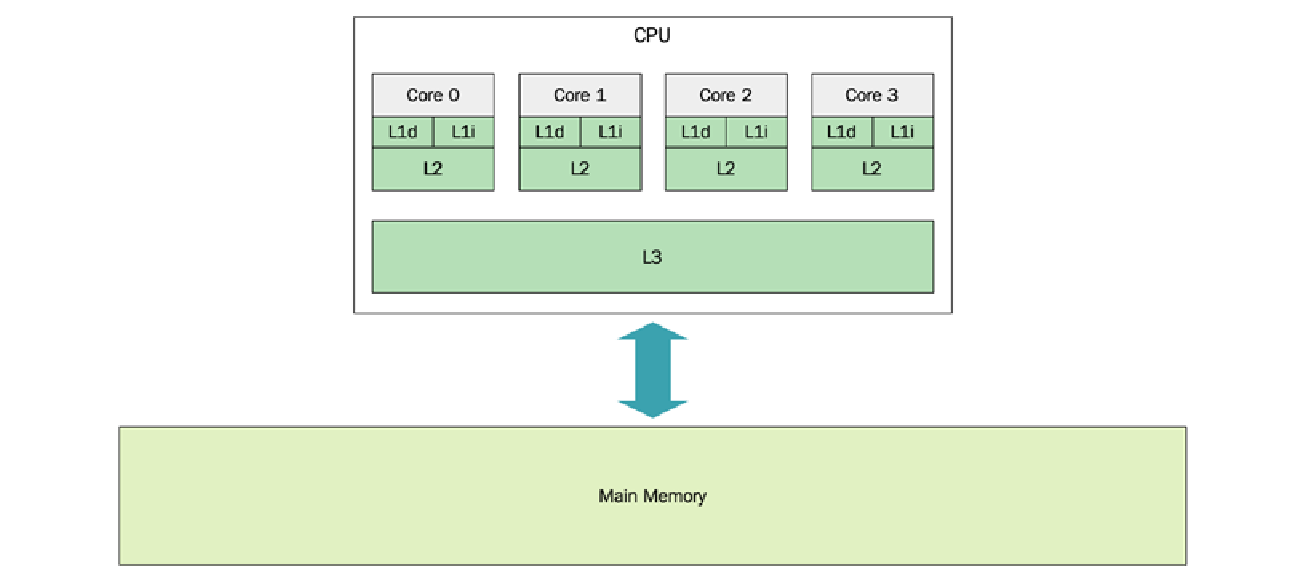
由于通过地址访问一个字节是一个 $O(1)$ 操作,从程序员的角度来看,很容易相信每个内存单元格的访问速度是相同的。这种内存处理方法在很多情况下都是简单且有用的,但是当选择数据结构以实现高效使用时,你需要考虑现代计算机中存在的内存层次结构 ($\text{memory hierarchy}$)。内存层次结构的重要性日益增加,因为与当今处理器的速度相比,从主内存 ($\text{main memory}$) 读取和写入所需的时间变得更加昂贵。下面的图展示了一个包含一个 $\text{CPU}$ 和四个核心的机器架构:
我目前正在一台 $\text{2018}$ 年的 $\text{MacBook Pro}$ 上撰写本章,它配备了 $\text{Intel Quad-Core i7 CPU}$。在这个处理器上,每个核心都有自己的 $\text{L1}$ 和 $\text{L2}$ 缓存,而 $\text{L3}$ 缓存则由所有四个核心共享。在终端运行以下命令:
sysctl -a hw
除了其他信息外,还会给我以下信息:
hw.memsize: 17179869184
hw.cachelinesize: 64
hw.l1icachesize: 32768
hw.l1dcachesize: 32768
hw.l2cachesize: 262144
hw.l3cachesize: 8388608
报告的 hw.memsize 是主内存的总量,在本例中是 $\text{16 GB}$。
hw.cachelinesize 报告为 $\text{64}$ 字节,是缓存行 ($\text{cache lines}$),也称为块 ($\text{blocks}$) 的大小。当访问内存中的一个字节时,机器不会只获取所请求的那个字节;相反,机器总是获取一个缓存行,在本例中是 $\text{64}$ 字节。$\text{CPU}$ 和主内存之间的各种缓存跟踪的是 $\text{64}$ 字节的块,而不是单个字节。
hw.l1icachesize 是 $\text{L1}$ 指令缓存的大小。这是一个 $\text{32 KB}$ 的缓存,专门用于存储 $\text{CPU}$ 最近使用的指令。hw.l1dcachesize 也是 $\text{32 KB}$,专门用于存储数据,而不是指令。最后,我们可以读取 $\text{L2}$ 缓存和 $\text{L3}$ 缓存的大小,分别是 $\text{256 KB}$ 和 $\text{8 MB}$。一个重要的观察结果是,与可用的主内存量相比,缓存非常小。
虽然没有提供访问缓存层次结构中每一层所需的实际周期数的详细数据,但一个非常粗略的指导原则是,相邻层(例如 $\text{L1}$ 和 $\text{L2}$)之间的延迟 ($\text{latency}$) 存在数量级的差异。下表摘自 $\text{Peter Norvig}$ 在 $\text{2001}$ 年发表的文章《$\text{Teach yourself programming in ten years}$》中提供的延迟数字。完整的表格通常被称为《每个程序员都应该知道的延迟数字》 ($\text{Latency numbers every programmer should know}$) 并归功于 $\text{Jeff Dean}$:
| 内存层次 | 延迟 ($\text{Latency}$) | 相对速度 (以 $\text{L1}$ 为 1) |
|---|---|---|
| L1 缓存引用 | $0.5 \text{ ns}$ | $1\times$ |
| L2 缓存引用 | $7 \text{ ns}$ | $14\times$ 慢 |
| 主内存引用 | $100 \text{ ns}$ | $200\times$ 慢 |
以充分利用缓存的方式组织数据,可以对性能产生显著影响。访问最近使用过的数据(因此可能已驻留在缓存中)将使你的程序运行得更快。这被称为时间局部性 ($\text{temporal locality}$)。
此外,访问位于你正在使用的某些其他数据附近的数据,会增加你所需的数据已存在于先前从主内存中取出的缓存行中的可能性。这被称为空间局部性 ($\text{spatial locality}$)。
在内层循环中不断清除缓存行可能会导致非常糟糕的性能。这有时被称为缓存抖动 ($\text{cache thrashing}$)。让我们看一个例子:
constexpr auto kL1CacheCapacity = 32768; // The L1 Data cache size
constexpr auto kSize = kL1CacheCapacity / sizeof(int);
using MatrixType = std::array<std::array<int, kSize>, kSize>;
auto cache_thrashing(MatrixType& matrix) {
auto counter = 0;
// 快版本: matrix[i][j]
for (auto i = 0; i < kSize; ++i) {
for (auto j = 0; j < kSize; ++j) {
matrix[i][j] = counter++;
}
}
}
这个版本在我的电脑上运行大约需要 $\text{40 ms}$。然而,仅仅将内层循环中的行更改为以下内容,函数完成所需的时间就从 $\text{40 ms}$ 增加到超过 $\text{800 ms}$:
matrix[j][i] = counter++;
在第一个使用 matrix[i][j] 的示例中,大部分时间我们将访问已在 $\text{L1}$ 缓存中的内存;而在使用 matrix[j][i] 的修改版本中,每次访问都会导致一次 $\text{L1}$ 缓存未命中 ($\text{cache miss}$)。几张图可能有助于你理解发生了什么。这里我们不绘制完整的 $\text{32768} \times \text{32768}$ 矩阵,而是使用一个微小的 $\text{3} \times \text{3}$ 矩阵作为示例:
尽管这可能是我们对矩阵如何驻留在内存中的心理图像,但并没有“二维内存”这种东西。相反,当这个矩阵被布置在一维内存空间中时,它看起来像这样:
也就是说,它是一个按行 ($\text{row by row}$) 连续排列的元素数组。在我们算法的快速版本中,数字是按照它们在内存中连续排列的相同顺序被依次访问的,如下所示:
而在算法的慢速版本中,元素的访问模式则完全不同。使用慢速版本访问前四个元素现在看起来像这样:
由于空间局部性差 ($\text{poor spatial locality}$),以这种方式访问数据会慢得多。现代处理器通常还配备有预取器 ($\text{prefetcher}$),它可以自动识别内存访问模式,并尝试将可能在不久的将来被访问的数据从内存预取到缓存中。预取器通常在较小的步幅 ($\text{strides}$) 下表现最佳。你可以在 $\text{Randal E. Bryant}$ 和 $\text{David R. O’Hallaron}$ 所著的优秀书籍《$\text{Computer Systems, A Programmer’s Perspective}$》中阅读更多相关内容。
总结本节,尽管内存访问是常数时间操作,但缓存 ($\text{caching}$) 可以对访问内存所需的实际时间产生巨大的影响。这是在使用或实现新数据结构时需要始终牢记的一点。
接下来,我将介绍 C++ 标准库中的一组数据结构,称为容器 ($\text{containers}$)。
好的,这是对您提供的文本内容的翻译和格式化,保留了代码部分:
标准库容器
C++ 标准库提供了一组非常有用的容器 ($\text{container}$) 类型。容器是一种包含元素集合的数据结构。容器负责管理其所持有的元素的内存。这意味着我们不必显式地创建和删除放入容器中的对象。我们可以将在栈上创建的对象传递给容器,容器将复制并将其存储在自由存储区 ($\text{free store}$,即堆内存) 上。
迭代器 ($\text{Iterators}$) 用于访问容器中的元素,因此它是理解标准库中算法和数据结构的一个基本概念。迭代器概念将在第 $\text{5}$ 章《算法》中介绍。对于本章来说,只需要知道迭代器可以被视为指向元素的指针,并且迭代器定义了不同的运算符,具体取决于它们所属的容器。例如,类似数组的数据结构为其元素提供了随机访问迭代器 ($\text{random access iterators}$)。这些迭代器支持使用 + 和 - 的算术表达式,而链表的迭代器则只支持 ++ 和 -- 运算符。
容器分为三类:序列容器 ($\text{sequence containers}$)、关联容器 ($\text{associative containers}$) 和容器适配器 ($\text{container adaptors}$)。本节将简要介绍这三类中的容器,并讨论在性能成为问题时需要考虑的最重要事项。
序列容器
序列容器按照我们添加元素的顺序来保持元素的顺序。标准库中的序列容器有 std::array、std::vector、std::deque、std::list 和 std::forward_list。本节还将介绍 std::basic_string,尽管它并非正式的通用序列容器,因为它只处理字符类型的元素。
在选择序列容器之前,我们应该知道以下问题的答案:
- 元素的数量级是多少?
- 使用模式是什么?你多久添加一次数据?读取/遍历数据?删除数据?重新排列数据?
- 你最常在序列的哪个位置添加数据?在末尾、在开头还是在序列中间?
- 你需要对元素进行排序吗?或者你是否关心元素的顺序?
根据这些问题的答案,我们可以确定哪些序列容器更适合或不太适合我们的需求。但要做到这一点,我们需要对每种序列容器的接口和性能特征有基本的了解。
接下来的部分将简要介绍不同的序列容器,从总体上最广泛使用的容器之一开始。
向量和数组
std::vector 可能是最常用的容器类型,这是有充分理由的。向量是一个动态增长的数组。添加到向量中的元素保证在内存中是连续布局的,这意味着你可以通过索引在常数时间内访问数组中的任何元素。这也意味着,由于前面提到的空间局部性 ($\text{spatial locality}$),按元素布局的顺序遍历元素时,它提供了出色的性能。
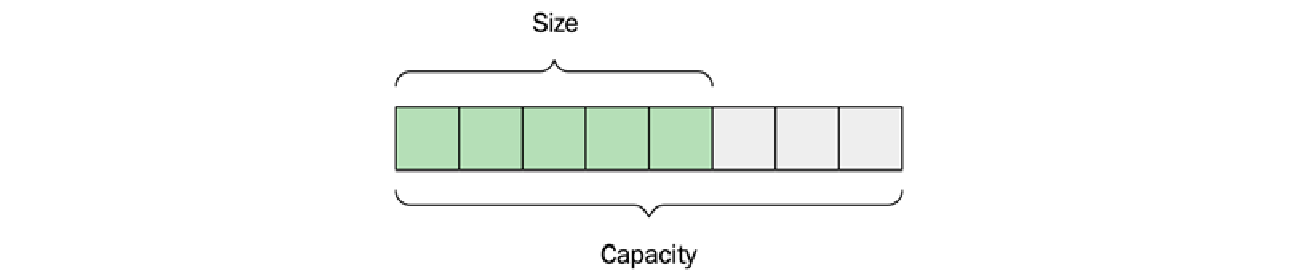
一个向量有两个属性:大小 ($\text{size}$) 和容量 ($\text{capacity}$)。大小是容器中当前持有的元素数量,而容量是向量在需要分配更多空间之前可以容纳的最大元素数量:
使用 push_back() 函数在向量末尾添加元素是快速的,只要大小小于容量。当添加一个元素且没有更多空间时,向量将分配一个新的内部缓冲区,然后将所有元素移动到新空间。容量将以一种很少发生重新分配的方式增长,因此使得 push_back() 成为一个均摊常数时间 ($\text{amortized constant-time}$) 操作,正如我们在第 $\text{3}$ 章《分析和衡量性能》中讨论的那样。
std::vector<Person> 类型的向量模板实例将以值的方式存储 $\text{Person}$ 对象。当向量需要重新排列 $\text{Person}$ 对象时(例如,作为 $\text{insert}$ 操作的结果),这些值将被复制构造 ($\text{copy constructed}$) 或移动 ($\text{moved}$)。如果对象具有 $\text{nothrow}$ 移动构造函数,则它们将被移动。否则,对象将被复制构造,以保证强异常安全 ($\text{strong exception safety}$):
Person(Person&& other) { // Will be copied
// ...
}
Person(Person&& other) noexcept { // Will be moved
// ...
}
在内部,std::vector 使用 std::move_if_noexcept 来确定对象应该被复制还是被移动。<type_traits> 头文件可以帮助你在编译时验证你的类在移动时是否保证不会抛出异常:
static_assert(std::is_nothrow_move_constructible<Person>::value);
如果你正在向向量添加新创建的对象,你可以利用 emplace_back() 函数,它会原地构造对象,而不是先创建对象再使用 push_back() 函数将其复制/移动到向量中:
persons.emplace_back("John", 65);
向量的容量可以通过以下方式改变:
- 当
capacity == size时向向量添加元素 - 调用
reserve() - 调用
shrink_to_fit()
除此之外,向量不会改变容量,因此也不会分配或释放动态内存。例如,成员函数 clear() 会清空向量,但不会改变其容量。这些内存保证使得向量即使在实时上下文 ($\text{real-time contexts}$) 中也可用。
自 C++20 起,还有两个自由函数可以从 std::vector 中擦除元素。在 C++20 之前,我们必须使用擦除-移除习语 ($\text{erase-remove idiom}$),我们将在第 $\text{5}$ 章《算法》中讨论。然而,现在从 std::vector 中擦除元素的推荐方法是使用 std::erase() 和 std::erase_if()。这是一个关于如何使用这些函数的简短示例:
auto v = std::vector{-1, 5, 2, -3, 4, -5, 5};
std::erase(v, 5); // v: [-1, 2, -3, 4, -5]
std::erase_if(v, [](auto x) { return x < 0; }); // v: [2, 4]
作为动态大小向量的替代方案,标准库还提供了一个名为 std::array 的固定大小版本,它通过使用栈 ($\text{stack}$) 而不是自由存储区来管理其元素。数组的大小是一个在编译时指定的模板参数,这意味着大小和元素类型成为具体类型的一部分:
auto a = std::array<int, 16>{};
auto b = std::array<int, 1024>{};
在这个示例中,a 和 b 不是相同的类型,这意味着当你将该类型用作函数参数时,你必须指定大小:
auto f(const std::array<int, 1024>& input) {
// ...
}
f(a); // Does not compile, f requires an int array of size 1024
这乍一看可能有点繁琐,但这实际上是它相对于内置数组类型 ($C$ 数组) 的巨大优势,内置数组在作为函数参数传递时会丢失大小信息,因为它会自动转换为指向数组第一个元素的指针:
// input looks like an array, but is in fact a pointer
auto f(const int input[]) {
// ...
}
int a[16];
int b[1024];
f(a); // Compiles, but unsafe
数组丢失其大小信息通常被称为数组衰退 ($\text{array decay}$)。你将在本章后面看到,通过使用 std::span 向函数传递连续数据时,可以避免数组衰退。
双端队列
有时,你会发现自己需要频繁地在序列的开头和结尾添加元素。如果你正在使用 std::vector 但需要加快在前端插入元素的速度,你可以转而使用 std::deque(双端队列 $\text{double-ended queue}$ 的缩写)。
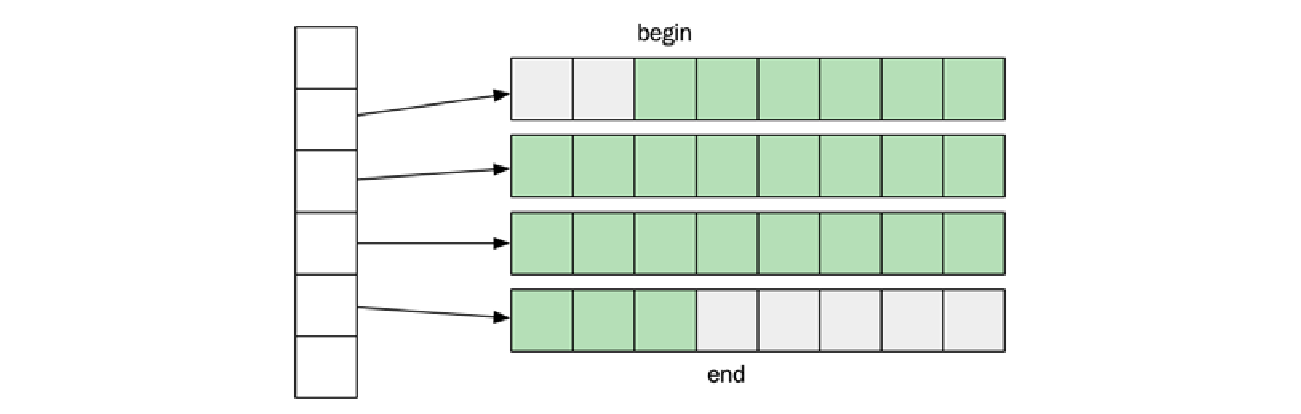
std::deque 通常实现为一系列固定大小的数组的集合。这使得它能够以常数时间 ($O(1)$) 通过索引访问元素。然而,正如你在下图中看到的,并非所有元素都存储在内存中连续的位置,这与 std::vector 和 std::array 的情况不同。
双向链表和单向链表
std::list 是一个双向链表 ($\text{doubly linked list}$),这意味着每个元素都有一个指向下一个元素的链接和一个指向上一个元素的链接。这使得列表可以向前和向后迭代。
标准库中还有一个单向链表 ($\text{singly linked list}$),名为 std::forward_list。你不总是选择双向链表而非 std::forward_list 的原因是,双向链表中的后向指针会占用额外的内存。因此,如果你不需要向后遍历列表,就应该使用 std::forward_list。
std::forward_list 的另一个有趣特性是它针对非常短的列表进行了优化。当列表为空时,它只占用一个字长 ($\text{word}$),这使得它成为稀疏数据 ($\text{sparse data}$) 的可行数据结构。
请注意,即使元素在序列中是有序的,它们在内存中也不是连续布局的,这与 $\text{vector}$ 和 $\text{array}$ 不同。这意味着与 $\text{vector}$ 相比,遍历链表更有可能产生大量的缓存未命中 ($\text{cache misses}$)。
总结一下:
std::list是一个双向链表,包含指向下一个和上一个元素的指针:
std::forward_list是一个单向链表,只包含指向下一个元素的指针:
std::forward_list 由于只有一个指向下一个元素的指针,因此内存效率更高。
列表也是唯一支持拼接 ($\text{splicing}$) 的容器。拼接是一种在列表之间传输元素的方式,无需复制或移动元素。这意味着,例如,可以在常数时间 ($O(1)$) 内将两个列表连接成一个列表。其他容器进行此类操作至少需要线性时间 ($O(N)$)。
好的,这是对您提供的关于 $\text{std::basic_string}$ 和关联容器的文本的翻译和格式化,保留了代码部分:
基本字符串
我们将在本节中介绍的最后一个模板类是 std::basic_string。std::string 是 std::basic_string<char> 的类型别名 ($\text{typedef}$)。
历史上,std::basic_string 不保证在内存中是连续布局的。这种情况在 C++17 中发生了变化,这使得可以将字符串传递给需要字符数组的 $\text{API}$。例如,以下代码将整个文件读入一个字符串:
auto in = std::ifstream{"file.txt", std::ios::binary | std::ios::ate};
if (in.is_open()) {
auto size = in.tellg();
auto content = std::string(size, '\0');
in.seekg(0);
in.read(&content[0], size);
// "content" now contains the entire file
}
通过使用 std::ios::ate 打开文件,位置指示符被设置到流的末尾,这样我们就可以使用 tellg() 来获取文件的大小。之后,我们将输入位置设置回流的起始位置并开始读取。
大多数 std::basic_string 的实现利用了一种称为小对象优化 ($\text{small object optimization}$) 的技术,这意味着如果字符串的大小很小,它们就不会分配任何动态内存。我们将在本书后面讨论小对象优化。现在,让我们继续讨论关联容器。
关联容器
关联容器是根据元素本身的值来放置其元素的。例如,与 std::vector::push_back() 或 std::list::push_front() 不同,我们不可能在关联容器的末尾或开头添加元素。相反,元素的添加方式使得无需扫描整个容器即可找到该元素。因此,关联容器对我们想要存储的对象有一些要求。我们稍后会查看这些要求。
关联容器主要分为两大类:
-
有序关联容器 ($\text{Ordered associative containers}$): 这些容器基于树 ($\text{trees}$); 它们使用树来存储元素。它们要求元素必须通过小于运算符 (
<) 进行排序。在基于树的容器中,添加、删除和查找元素的操作时间复杂度均为 $O(\log n)$。这些容器包括std::set、std::map、std::multiset和std::multimap。 -
无序关联容器 ($\text{Unordered associative containers}$): 这些容器基于哈希表 ($\text{hash tables}$); 它们使用哈希表来存储元素。它们要求元素必须使用相等运算符 (
==) 进行比较,并且必须有一种方法可以基于元素计算出哈希值 ($\text{hash value}$)。稍后会详细介绍这一点。在基于哈希表的容器中,添加、删除和查找元素的操作时间复杂度均为 $O(1)$。这些容器包括std::unordered_set、std::unordered_map、std::unordered_multiset和std::unordered_multimap。
自 C++20 起,所有关联容器都配备了一个名为 contains() 的函数,当你想要知道容器是否包含某个特定元素时,应该使用这个函数。在 C++ 的早期版本中,需要使用 count() 或 find() 来判断容器是否包含一个元素。
始终使用专门的函数,例如
contains()和empty(),而不是使用count() > 0或size() == 0。专门的函数保证是效率最高的。
有序集合和映射
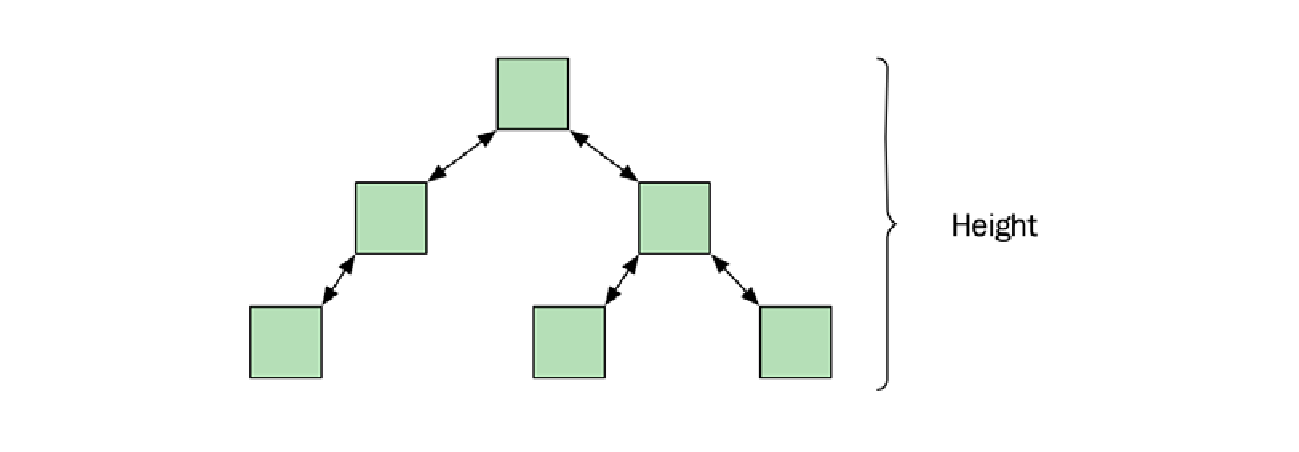
有序关联容器保证插入、删除和查找操作可以在对数时间 ($O(\log n)$) 内完成。如何实现这一点取决于标准库的实现。然而,我们所知的实现都使用某种自平衡二叉搜索树 ($\text{self-balancing binary search tree}$)。树保持大致平衡对于控制树的高度至关重要,因此也控制了访问元素时的最坏情况运行时间。
树不需要预先分配内存,因此,通常情况下,每当插入一个元素时,树就会在自由存储区上分配内存,并在擦除元素时释放内存。
请看下面的图表,它展示了一个平衡树的高度是 $O(\log n)$:
无序集合和映射
集合 ($\text{set}$) 和映射 ($\text{map}$) 的无序版本提供了一种基于哈希 ($\text{hash-based}$) 的替代方案,以替代基于树的版本。这种数据结构通常被称为哈希表 ($\text{hash tables}$)。
理论上,哈希表提供了均摊常数时间 ($O(1)$) 的插入、添加和删除操作,这可以与基于树的版本 ($O(\log n)$) 相媲美。然而,在实践中,这种差异可能并不那么明显,特别是如果你的容器中存储的元素数量不是非常大的话。
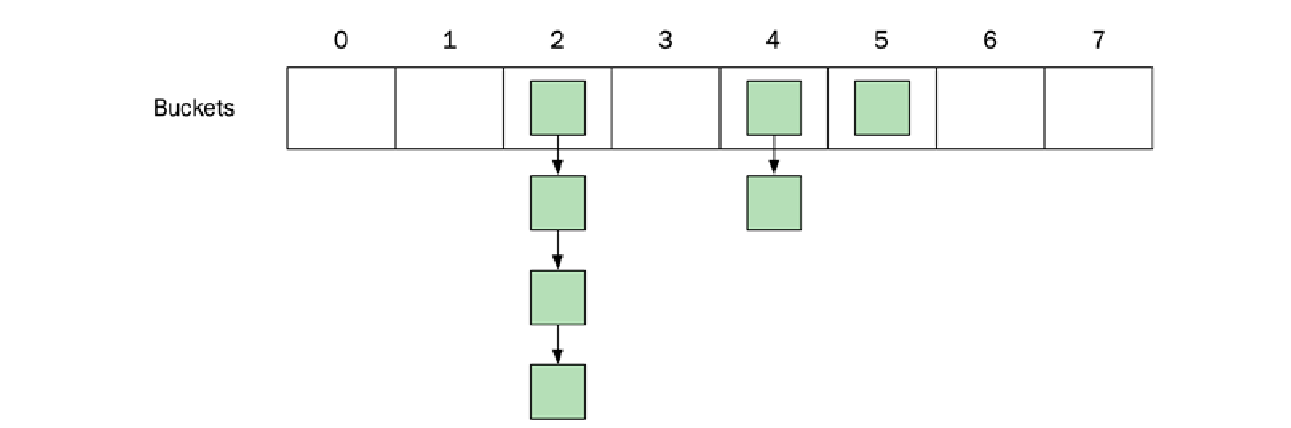
让我们看看哈希表如何能提供 $O(1)$ 操作。哈希表将其元素保存在某种桶 ($\text{buckets}$) 数组中。当向哈希表添加一个元素时,会使用哈希函数 ($\text{hash function}$) 为该元素计算出一个整数。这个整数通常被称为元素的哈希值 ($\text{hash}$)。然后,哈希值通常被限制在数组的大小范围内(例如,通过使用取模运算),以便将这个新的受限值用作数组的索引。一旦计算出索引,哈希表就可以将元素存储在数组的该索引位置。元素的查找工作方式类似,首先计算我们正在查找的元素的哈希值,然后访问数组。
除了计算哈希值之外,这种技术似乎很简单。但这只是故事的一半。如果两个不同的元素生成了相同的索引怎么办?无论是它们产生了相同的哈希值,还是两个不同的哈希值被限制到了相同的索引。当两个不相等的元素最终落在同一个索引处时,我们称之为哈希冲突 ($\text{hash collision}$)。
这不仅仅是一种极端情况:即使我们使用了一个好的哈希函数,这种情况也会经常发生,特别是当数组大小相对于我们添加的元素数量较小时。有各种方法可以处理哈希冲突。在这里,我们将重点介绍标准库中使用的方法,它被称为独立链式法 ($\text{separate chaining}$)。
独立链式法解决了两个不相等元素落在同一个索引处的问题。它不是直接将元素存储在数组中,而是将数组设置为一系列桶 ($\text{buckets}$)。每个桶可以包含多个元素,即所有哈希到同一索引的元素。因此,每个桶也是某种容器。用于桶的具体数据结构没有被定义,并且可能因不同的实现而异。然而,我们可以将其视为一个链表,并假设在特定桶中查找元素是慢的,因为它需要线性扫描 ($\text{scan linearly}$) 桶中的元素。
下图展示了一个包含八个桶的哈希表。元素落在了三个不同的桶中。索引为 $2$ 的桶包含四个元素,索引为 $4$ 的桶包含两个元素,而索引为 $5$ 的桶只包含一个元素。其他桶都是空的:
哈希与相等
哈希值(相对于容器大小而言,可以在常数时间内计算)决定了一个元素将被放置在哪个桶中。由于可能不止一个对象会生成相同的哈希值,从而最终落入同一个桶中,因此每个键还需要提供一个相等函数 ($\text{equals function}$),用于将我们正在查找的键与桶中的所有键进行比较。
如果两个键相等,则要求它们必须生成相同的哈希值。然而,两个对象返回相同的哈希值而彼此不相等是完全合法的。
一个好的哈希函数应具备以下特点:计算速度快,并且能够将键均匀地分布到各个桶中,以最大限度地减少每个桶中的元素数量。
下面是一个非常糟糕但有效的哈希函数的示例:
auto my_hash = [](const Person& person) {
return 47; // Bad, don't do this!
};
它是有效的,因为它会为两个相等的对象返回相同的哈希值。这个哈希函数也很快。然而,由于所有元素都会产生相同的哈希值,所有键最终都会落入同一个桶中,这意味着查找一个元素的时间复杂度将是 $O(n)$,而不是我们追求的 $O(1)$。
另一方面,一个好的哈希函数确保元素在桶中均匀分布,以最大限度地减少哈希冲突。C++ 标准对此有一个说明,指出哈希函数为两个不同对象生成相同哈希值的情况应该非常罕见。
幸运的是,标准库已经为我们提供了基本类型的良好哈希函数。在很多情况下,我们在为用户定义类型编写自己的哈希函数时,可以重用这些函数。
假设我们想在一个 std::unordered_set 中使用一个 $\text{Person}$ 类作为键。$\text{Person}$ 类有两个数据成员:age(一个 int)和 name(一个 std::string)。
我们首先编写相等判断式 ($\text{equal predicate}$):
auto person_eq = [](const Person& lhs, const Person& rhs) {
return lhs.name() == rhs.name() && lhs.age() == rhs.age();
};
要使两个 $\text{Person}$ 对象相等,它们需要具有相同的姓名和年龄。
我们现在可以通过结合包含在相等判断式中的所有数据成员的哈希值来定义哈希判断式 ($\text{hash predicate}$)。不幸的是,C++ 标准中还没有用于组合哈希值的函数,但在 $\text{Boost}$ 中有一个很好的函数,我们将在此处使用:
#include <boost/functional/hash.hpp>
auto person_hash = [](const Person& person) {
auto seed = size_t{0};
boost::hash_combine(seed, person.name());
boost::hash_combine(seed, person.age());
return seed;
};
注意: 如果由于某种原因你不能使用 $\text{Boost}$,
boost::hash_combine()实际上只是一个单行代码,可以从文档中复制,文档位于 https://www.boost.org/doc/libs/1。
定义了相等函数和哈希函数后,我们最终可以创建我们的 unordered_set:
using Set = std::unordered_set<Person, decltype(person_hash),
decltype(person_eq)>;
auto persons = Set{100, person_hash, person_eq};
一个好的经验法则是:在生成哈希值时,始终使用所有在相等函数中用到的数据成员。这样,我们既遵守了相等性和哈希之间的契约,同时又能提供一个有效的哈希值。例如,仅在计算哈希值时使用 name 是正确的,但效率低下,因为这意味着所有同名的 $\text{Person}$ 对象都会落入同一个桶中。然而,更糟糕的是在哈希函数中包含未在相等函数中使用的数据成员。这很可能会导致一场灾难,即你在 unordered_set 中无法找到实际上比较相等的对象。
哈希策略
除了创建能够将键均匀地分布到桶中的哈希值之外,我们还可以通过拥有更多的桶来减少冲突的数量。
每个桶中元素的平均数量称为负载因子 ($\text{load factor}$)。在前面的示例中,我们创建了一个包含 $100$ 个桶的 unordered_set。如果我们向集合中添加 $50$ 个 $\text{Person}$ 对象,load_factor() 将返回 $0.5$。
max_load_factor 是负载因子的上限,当达到该值时,集合将需要增加桶的数量,因此,还需要对集合中当前的所有元素重新哈希 ($\text{rehash}$)。也可以使用 rehash() 和 reserve() 成员函数手动触发重新哈希。
现在,让我们继续看第三类容器:容器适配器 ($\text{container adaptors}$)。
这是一段关于容器适配器和优先队列的详细解释和示例代码。
容器适配器
标准库中有三种容器适配器:std::stack(栈)、std::queue(队列)和 std::priority_queue(优先队列)。
容器适配器与序列容器和关联容器有很大不同,因为它们表示抽象数据类型 ($\text{abstract data types}$),可以由底层序列容器实现。例如,栈 ($\text{stack}$) 是一种后进先出 ($\text{LIFO}$) 的数据结构,支持在栈顶进行 $\text{push}$ 和 $\text{pop}$ 操作,它可以通过使用 std::vector、std::list、std::deque 或任何其他支持 back()、push_back() 和 pop_back() 的自定义序列容器来实现。队列 ($\text{queue}$)(一种先进先出 ($\text{FIFO}$) 的数据结构)和优先队列 ($\text{priority_queue}$) 也是如此。
在本节中,我们将重点关注 std::priority_queue,它是一种非常有用但容易被遗忘的数据结构。
优先队列
优先队列提供对具有最高优先级元素的常数时间 ($O(1)$) 查找。优先级是使用元素的小于运算符 ($\text{less than operator}$) 定义的。插入和删除操作都运行在对数时间 ($O(\log n)$)。
优先队列是一种部分有序的数据结构,它可能不如完全排序的数据结构(例如,树或排序的向量)那么直观。但在某些情况下,优先队列可以提供你所需的功能,而且成本低于完全排序的容器。
标准库已经提供了一个部分排序算法 ($\text{partial sort algorithm}$),所以我们不需要自己编写。但让我们看看如何使用优先队列来实现一个部分排序算法。
假设我们正在编写一个根据查询搜索文档的程序。匹配的文档(搜索结果)应该按排名 ($\text{rank}$) 排序,而我们只对查找排名前 $\text{m}$ 位的搜索结果感兴趣。
文档由以下类表示:
class Document {
public:
Document(std::string title) : title_{std::move(title)} {}
private:
std::string title_;
// ...
};
搜索时,算法会选择匹配查询的文档并计算搜索结果的排名。每个匹配的文档由一个 $\text{Hit}$ 结构体表示:
struct Hit {
float rank_{};
std::shared_ptr<Document> document_;
};
最后,我们需要对这些 $\text{Hit}$ 进行排序并返回排名前 $m$ 的文档。
对 $\text{Hit}$ 进行排序有哪些选择?
- 如果 $\text{Hit}$ 包含在一个提供随机访问迭代器 ($\text{random access iterators}$) 的容器中,我们可以使用
std::sort()并只返回前 $m$ 个元素。 - 如果 $\text{Hit}$ 的总数 $n$ 远大于我们要返回的文档数 $m$,我们可以使用
std::partial_sort(),这将比std::sort()更高效。
但是,如果我们没有随机访问迭代器怎么办?也许匹配算法只提供对 $\text{Hit}$ 的前向迭代器 ($\text{forward iterators}$)。在这种情况下,我们可以使用优先队列,仍然可以得到一个高效的解决方案。我们的排序接口如下所示:
template<typename It>
auto sort_hits(It begin, It end, size_t m) -> std::vector<Hit> {
我们可以使用定义了自增运算符 ($\text{increment operator}$) 的任何迭代器调用此函数。
接下来,我们创建一个由 std::vector 支持的 std::priority_queue,并使用自定义比较函数来将排名最低的 $\text{Hit}$ 保留在队列的顶部:
auto cmp = [](const Hit& a, const Hit& b) {
return a.rank_ > b.rank_; // 注意,我们使用的是大于号
};
auto queue = std::priority_queue<Hit, std::vector<Hit>,
decltype(cmp)>{cmp};
我们将最多只向优先队列中插入 $m$ 个元素。优先队列将包含目前为止遇到的排名最高的 $m$ 个 $\text{Hit}$。在当前位于优先队列中的元素中,排名最低的 $\text{Hit}$ 将是最顶部的元素(队头):
for (auto it = begin; it != end; ++it) {
if (queue.size() < m) {
queue.push(*it);
}
else if (it->rank_ > queue.top().rank_) {
queue.pop();
queue.push(*it);
}
}
现在,我们已经在优先队列中收集了排名最高的 $\text{Hit}$,剩下的唯一事情就是将它们以相反的顺序放入一个 $\text{vector}$ 中并返回 $m$ 个已排序的 $\text{Hit}$:
auto result = std::vector<Hit>{};
while (!queue.empty()) {
result.push_back(queue.top());
queue.pop();
}
std::reverse(result.begin(), result.end());
return result;
} // end of sort_hits()
这个算法的复杂度是多少?如果我们用 $n$ 表示 $\text{Hit}$ 的数量,用 $m$ 表示返回的 $\text{Hit}$ 数量,我们可以看到内存消耗是 $O(m)$,而时间复杂度是 $O(n \cdot \log m)$。这是因为我们迭代了 $n$ 个元素。此外,在每次迭代中,我们可能需要执行一次 $\text{push}$ 和/或一次 $\text{pop}$,这两个操作的运行时间都是 $O(\log m)$。
我们现在将离开标准库容器,专注于一些与标准容器密切相关的新颖且有用的类模板。
使用视图
在本节中,我们将讨论 C++ 标准库中一些相对较新的类模板:C++17 中的 std::string_view 和 C++20 中引入的 std::span。
这些类模板不是容器 ($\text{containers}$),而是轻量级视图 ($\text{views}$)(或切片 $\text{slices}$),用于观察连续元素序列。视图是小对象 ($\text{small objects}$),设计目的是按值复制。它们不分配内存,也不对它们指向的内存的生命周期提供任何保证。换句话说,它们是非拥有引用类型 ($\text{non-owning reference types}$),这与本章前面描述的容器有显著不同。同时,它们又与 std::string、std::array 和 std::vector 密切相关,我们很快就会看到。我将从描述 std::string_view 开始。
使用string_view避免复制
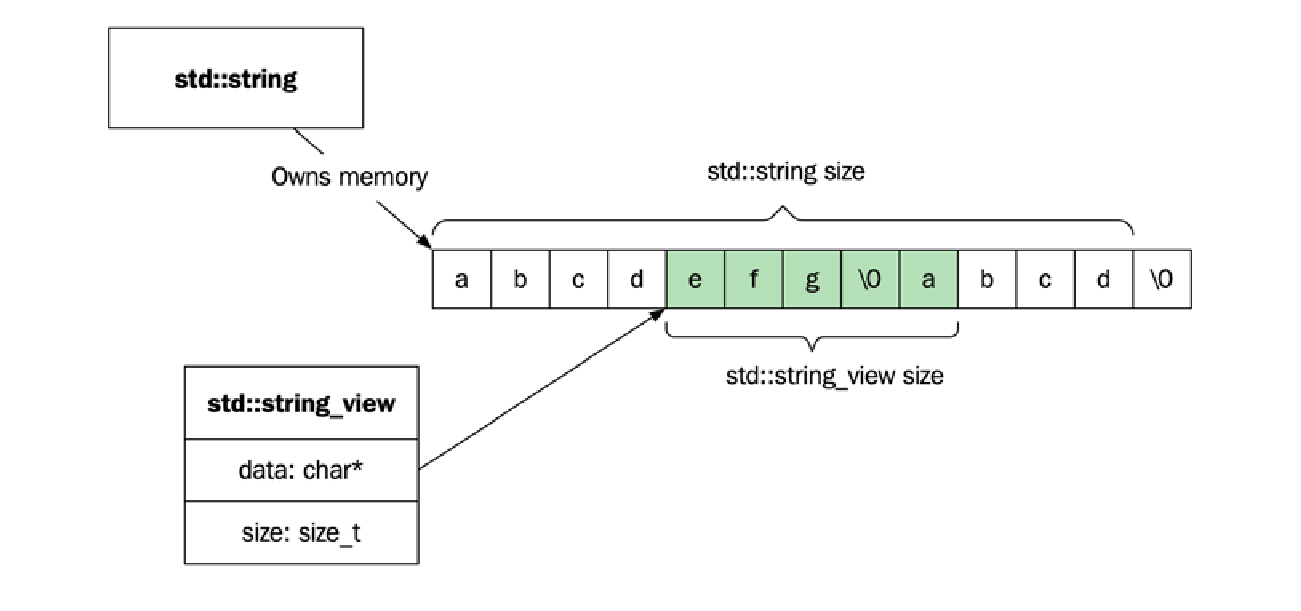
一个 std::string_view 包含一个指向不可变字符串缓冲区开头的指针和一个大小。由于字符串是连续的字符序列,因此指针和大小完整地定义了一个有效的子字符串范围。通常,std::string_view 指向由 std::string 拥有的内存,但它也可以指向具有静态存储持续时间的字符串字面量,或者像内存映射文件这样的东西。
下图展示了一个 std::string_view 指向由 std::string 拥有的内存:
由 std::string_view 定义的字符序列不需要以空字符终止,但序列中包含空字符是完全有效的。另一方面,std::string 需要能够通过 c_str() 返回一个空终止的字符串,这意味着它总是在序列末尾存储一个额外的空字符。
$\text{string_view}$ 不需要空终止符的事实意味着它比 $\text{C}$ 风格字符串或 std::string 能够更高效地处理子字符串,因为它不必为了添加空终止符而创建新的字符串。使用 std::string_view 的 substr() 复杂度是常数时间 ($O(1)$),而 std::string 的 substr() 版本则需要线性时间 ($O(N)$)。
在将字符串传递给函数时,性能也有所提升。考虑以下代码:
auto some_func(const std::string& s) {
// process s ...
}
some_func("A string literal"); // Creates a std::string
当将一个字符串字面量传递给 some_func() 时,编译器需要构造一个新的 std::string 对象以匹配参数类型。然而,如果让 some_func() 接受一个 std::string_view,就不再需要构造 std::string:
auto some_func(std::string_view s) { // Pass by value
// process s ...
}
some_func("A string literal");
一个 std::string_view 实例可以从 std::string 和字符串字面量高效地构造,因此它非常适合作为函数参数的类型。
使用std::span消除数组退化
在本章前面讨论 std::vector 和 std::array 时,我提到了当内置数组被传递给函数时,会发生数组退化 ($\text{array decay}$),即丢失数组的大小信息:
// buffer 看起来像一个数组,但实际上是一个指针
auto f1(float buffer[]) {
const auto n = std::size(buffer); // 无法编译!
for (auto i = 0u; i < n; ++i) { // 大小信息丢失!
// ...
}
}
我们可以通过添加一个大小参数来解决这个问题:
auto f2(float buffer[], size_t n) {
for (auto i = 0u; i < n; ++i) {
// ...
}
}
虽然这在技术上可行,但向这个函数传递正确的数据既容易出错又繁琐,而且如果 $\text{f2()}$ 将该缓冲区传递给其他函数,它需要记住传递正确大小的变量 $n$。$\text{f2()}$ 的调用点可能看起来像这样:
float a[256];
f2(a, 256);
f2(a, sizeof(a)/sizeof(a[0])); // 一个常见且繁琐的模式
f2(a, std::size(a));
数组退化是许多与边界相关 $\text{bug}$ 的根源。在需要使用内置数组(出于某种原因)的情况下,std::span 提供了一种更安全的方式来将数组传递给函数。由于 $\text{span}$ 将指向内存的指针和大小一起保存在一个对象中,因此在将元素序列传递给函数时,我们可以将其用作单一类型:
auto f3(std::span<float> buffer) { // Pass by value
for (auto&& b : buffer) { // 基于范围的 for 循环
// ...
}
}
float a[256];
f3(a); // OK!数组作为带大小的 span 传递
auto v = std::vector{1.f, 2.f, 3.f, 4.f};
f3(v); // OK!
span 也比内置数组更方便使用,因为它表现得更像一个支持迭代器的常规容器。
std::string_view 和 std::span 在数据成员(指针和大小)以及成员函数方面有许多相似之处。但也有一些显著的差异:
std::span指向的内存是可变的,而std::string_view总是指向常量内存。std::string_view还包含特定于字符串的函数,例如hash()和substr(),这些函数自然不是std::span的一部分。- 最后,
std::span中没有compare()函数,因此不可能直接在std::span对象上使用比较运算符。
现在是时候强调一些与使用标准库数据结构时的性能相关的通用要点了。
一些性能考量
我们现在已经涵盖了三个主要的容器类别:序列容器 ($\text{sequence containers}$)、关联容器 ($\text{associative containers}$) 和容器适配器 ($\text{container adaptors}$)。本节将为您提供一些在使用容器时需要考虑的一般性性能建议。
平衡复杂度保证与开销
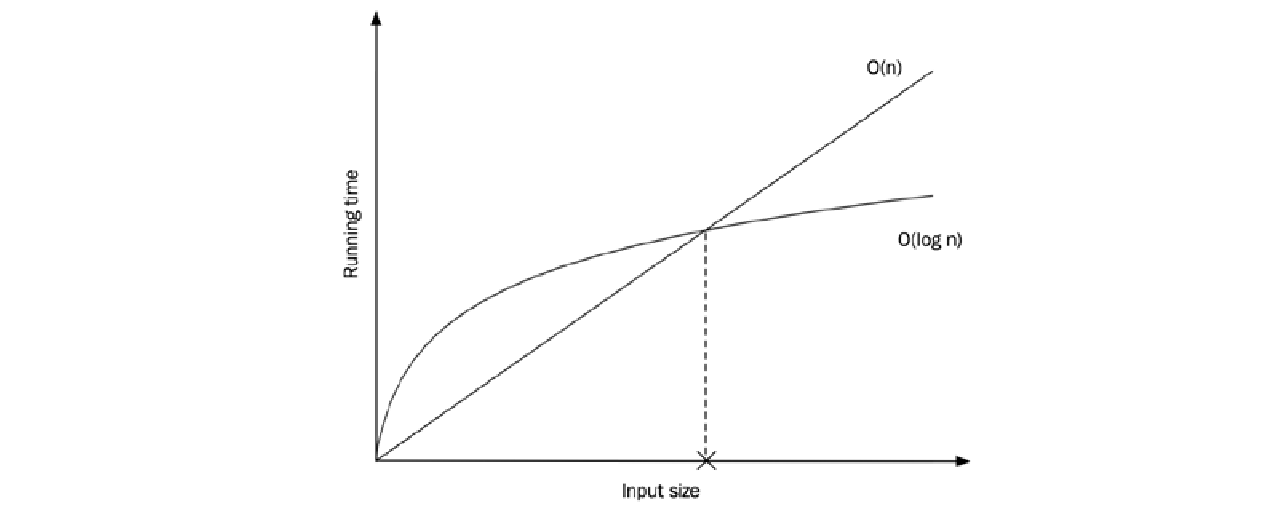
了解数据结构的时间和内存复杂度 ($\text{complexity}$) 在选择容器时非常重要。但同样重要的是要记住,每种容器都会受到开销 ($\text{overhead}$) 的影响,这种开销对较小数据集的性能影响更大。复杂度保证只对足够大的数据集才变得有意义。然而,判断“足够大”在你的用例中意味着什么,则取决于你。在这里,你需要再次通过在程序执行时进行测量 ($\text{measure}$) 来获得洞察。
此外,由于计算机配备了内存缓存 ($\text{memory caches}$),使用对缓存友好的数据结构更有可能表现得更好。这通常有利于 std::vector,因为它具有较低的内存开销,并且将其元素连续存储 ($\text{contiguously}$) 在内存中,使得访问和遍历更快。
下图显示了两种算法的实际运行时间。一种以线性时间 ($O(n)$) 运行,另一种以对数时间 ($O(\log n)$) 运行,但具有更大的开销。当输入大小低于标记的阈值时,对数算法比线性时间算法慢:
我们需要记住的下一个要点更为具体,它强调了使用最合适的 $\text{API}$ 函数的重要性。
了解并使用适当的API函数
在 C++ 中,通常有不止一种方法可以完成同一件事。语言和库不断发展,但很少有功能被弃用。当新的函数被添加到标准库中时,我们应该学习何时使用它们,并反思我们可能使用过哪些模式来弥补以前缺失的功能。
在这里,我们将重点关注标准库中可以找到的两个小而重要的函数:contains() 和 empty()。
- 检查元素是否存在于关联容器中时,请使用
contains()。 - 如果你想知道容器是否包含任何元素或是否为空,请使用
empty()。
除了更清晰地表达意图外,它还具有性能优势。检查链表 ($\text{linked list}$) 的大小是一个 $O(n)$ 的操作,而调用链表的 empty() 则在常数时间 ($O(1)$) 内运行。
在 C++20 引入 contains() 函数之前,每次我们想检查关联容器中是否存在某个值时,都必须绕道而行。你很可能偶然发现过使用各种方式来查找元素存在的代码。假设我们使用 std::multiset 实现了一个词袋 ($\text{bag-of-words}$):
auto bag = std::multiset<std::string>{}; // Our bag-of-words
// Fill bag with words ...
如果我们想知道某个特定的词是否在我们的词袋中,有许多方法可以实现。一种选择是使用 count(),像这样:
auto word = std::string{"bayes"}; // Our word we want to find
if (bag.count(word) > 0) {
// ...
}
这看起来很合理,但它可能会有轻微的开销,因为它会计算所有匹配我们单词的元素。另一种替代方法是使用 find(),但它具有相同的开销,因为它返回所有匹配的单词,而不仅仅是第一次出现:
if (bag.find(word) != bag.end()) {
// ...
}
在 C++20 之前,推荐的方法是使用 lower_bound(),因为它只返回第一个匹配的元素,像这样:
if (bag.lower_bound(word) != bag.end()) {
// ...
}
现在,随着 C++20 和 contains() 的引入,我们可以更清晰地表达我们的意图,并且还可以确保当我们的目标仅仅是检查元素是否存在时,库将为我们提供最有效的实现:
if (bag.contains(word)) { // Efficient and with clear intent
// ...
}
一般规则是:如果有一个专门的成员函数或自由函数是为特定容器设计的,并且它符合你的需求,那么就使用它。它将是高效的,并且会更清晰地表达意图。不要因为你没有学习完整的 $\text{API}$ 或因为你有以某种方式做事的旧习惯而使用前面所示的那些“绕道”方法。
还应该说,零开销原则 ($\text{zero-overhead principle}$) 特别适用于像这样的函数,所以不要花费时间试图通过手工编写自己的函数来超越库实现者。
我们现在将继续看一个更长的示例,说明如何以不同的方式重新排序数据,以优化特定用例的运行时性能。
并行数组
本章将通过讨论元素的迭代以及探索如何在使用类数组数据结构 时提高迭代性能来结束。
我已经提到了影响数据访问性能的两个重要因素:空间局部性 和时间局部性 。当我们迭代存储在内存中连续的元素时,由于空间局部性,如果我们设法保持对象较小,那么我们需要的数据就已经被缓存的概率就会增加。显然,这将对性能产生巨大影响。
回想本章开头展示的缓存颠簸 ($\text{cache-thrashing}$) 示例(我们迭代一个矩阵)。它表明,即使数据表示相当紧凑,我们有时也需要考虑访问数据的方式。
接下来,我们将比较迭代不同大小对象所需的时间。我们首先定义两个结构体 SmallObject 和 BigObject:
struct SmallObject {
std::array<char, 4> data_{};
int score_{std::rand()};
};
struct BigObject {
std::array<char, 256> data_{};
int score_{std::rand()};
};
SmallObject 和 BigObject 是相同的,只是初始数据数组的大小不同。这两个结构体都包含一个名为 score_ 的 int,我们将其初始化为随机值仅用于测试目的。我们可以使用 sizeof 运算符让编译器告诉我们对象的大小:
std::cout << sizeof(SmallObject); // 可能的输出是 8
std::cout << sizeof(BigObject); // 可能的输出是 260
我们需要大量的对象来评估性能。创建一百万个每种类型的对象:
auto small_objects = std::vector<SmallObject>(1'000'000);
auto big_objects = std::vector<BigObject>(1'000'000);
现在进行迭代。假设我们想要对所有对象的分数求和。我们倾向于使用 std::accumulate(),我们将在本书后面介绍,但现在,一个简单的 $\text{for}$ 循环就足够了。我们将此函数写成模板,这样我们就不必手动为每种对象类型编写一个版本。该函数迭代对象并对所有分数求和:
template <class T>
auto sum_scores(const std::vector<T>& objects) {
ScopedTimer t{"sum_scores"}; // 参见第 3 章
auto sum = 0;
for (const auto& obj : objects) {
sum += obj.score_;
}
return sum;
}
现在,我们准备好查看对小对象求和与对大对象求和所需的时间:
auto sum = 0;
sum += sum_scores(small_objects);
sum += sum_scores(big_objects);
为了获得可靠的结果,我们需要重复测试几次。在我的计算机上,计算小对象的总和大约需要 $1 \text{ ms}$,而计算大对象的总和需要 $10 \text{ ms}$。这个例子类似于本章开头的缓存颠簸示例,造成巨大差异的一个原因,再次是由于计算机使用缓存层次结构 ($\text{cache hierarchy}$) 从主内存中获取数据的方式。
通过缩小类大小来优化迭代
在处理比前面示例更真实的场景时,我们如何利用迭代较小对象集合比迭代较大对象更快的事实呢?
显然,我们可以尽力保持类的体积较小,但这往往说起来容易做起来难。而且,如果我们正在处理一个已经发展了一段时间的旧代码库,我们很有可能会遇到一些数据成员过多、职责过大的巨大类。
我们现在来看一个代表在线游戏系统中用户的类,并看看如何将其分解成更小的部分。该类具有以下数据成员:
struct User {
std::string name_;
std::string username_;
std::string password_;
std::string security_question_;
std::string security_answer_;
short level_{};
bool is_playing_{};
};
一个用户有一个经常使用的名字,以及一些很少使用的身份验证信息。该类还记录了玩家当前所在的等级 ($\text{level}$)。最后,$\text{User}$ 结构体还通过存储 $\text{is_playing_}$ 布尔值来知道用户是否正在玩游戏。
当为 $64$ 位架构编译时,sizeof 运算符报告 User 类的大小为 $128$ 字节。
所有用户都保存在一个 std::vector 中,并且有两个全局函数被非常频繁地调用,需要快速运行:num_users_at_level() 和 num_playing_users()。这两个函数都迭代所有用户,因此我们需要让用户向量上的迭代变得快速。
第一个函数返回达到特定等级的用户数:
auto num_users_at_level(const std::vector<User>& users, short level) {
ScopedTimer t{"num_users_at_level (using 128 bytes User)"};
auto num_users = 0;
for (const auto& user : users)
if (user.level_ == level)
++num_users;
return num_users;
}
第二个函数计算当前正在玩游戏的用户数:
auto num_playing_users(const std::vector<User>& users) {
ScopedTimer t{"num_playing_users (using 128 bytes User)"};
return std::count_if(users.begin(), users.end(),
[](const auto& user) {
return user.is_playing_;
});
}
在这里,我们使用了算法 std::count_if() 而不是像在 num_users_at_level() 中那样手写循环。std::count_if() 将为用户向量中的每个用户调用我们提供的谓词,并返回谓词返回 true 的次数。这基本上也与我们在第一个函数中所做的一样,所以我们也可以在第一个案例中使用 std::count_if()。这两个函数都以线性时间运行。
使用包含一百万用户的向量调用这两个函数的结果输出为:
11 ms num_users_at_level (using 128 bytes User)
10 ms num_playing_users (using 128 bytes User)
我们假设通过使 $\text{User}$ 类更小,迭代向量会更快。如前所述,密码和安全数据字段很少使用,可以分组到一个单独的结构体中。这将给我们以下类:
struct AuthInfo {
std::string username_;
std::string password_;
std::string security_question_;
std::string security_answer_;
};
struct User {
std::string name_;
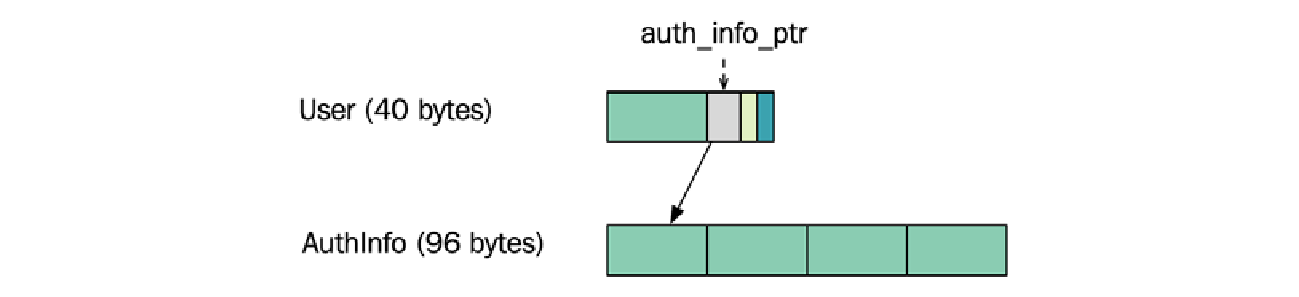
std::unique_ptr<AuthInfo> auth_info_; // 使用指针指向认证信息
short level_{};
bool is_playing_{};
};
此更改将 $\text{User}$ 类的大小从 $128$ 字节减少到 $40$ 字节。我们使用一个指针来引用新的 $\text{AuthInfo}$ 对象,而不是在 $\text{User}$ 类中存储四个字符串。这个改变从设计的角度来看也是有意义的。将身份验证数据保存在一个单独的类中有助于增加 $\text{User}$ 类的内聚性 ($\text{cohesion}$)。
当然,用户数据占用的总内存量没有减少,但现在重要的是缩小 $\text{User}$ 类,以便加速迭代所有用户的函数。
从优化的角度来看,我们必须再次测量以验证我们关于数据较小的假设是否有效。结果表明,使用较小的 $\text{User}$ 类后,这两个函数的运行速度都快了两倍以上。运行修改后版本的输出为:
4 ms num_users_at_level with User
3 ms num_playing_users with User
接下来,我们将尝试一种更激进的方式来缩减我们需要迭代的数据量,即使用并行数组 ($\text{parallel arrays}$)。
⚠️ 警告: 这种优化在许多情况下有太多缺点,不适合作为可行的替代方案。不要将其视为一种通用技术,不假思索地应用。在查看几个示例后,我们将回到并行数组的优缺点。
使用并行数组,我们只是将大型结构体分解为更小的类型,类似于我们对 $\text{User}$ 类的身份验证信息所做的那样。但我们不使用指针来关联对象,而是将较小的结构体存储在大小相等的单独数组中。不同数组中共享相同索引的较小对象构成了完整的原始对象。
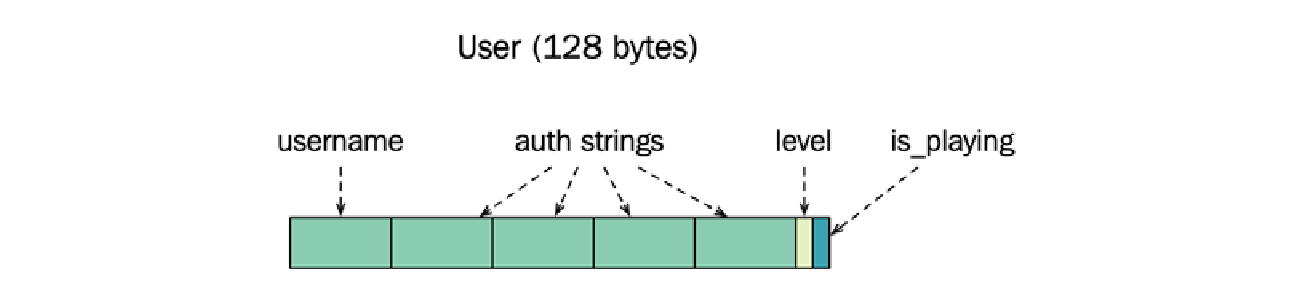
一个示例将阐明这种技术。我们使用的 $\text{User}$ 类现在由 $40$ 字节组成。它现在只包含一个用户名字符串、一个指向身份验证信息的指针、一个用于当前等级的整数和 $\text{is_playing_}$ 布尔值。通过使用户对象更小,我们看到迭代对象时的性能有所提高。
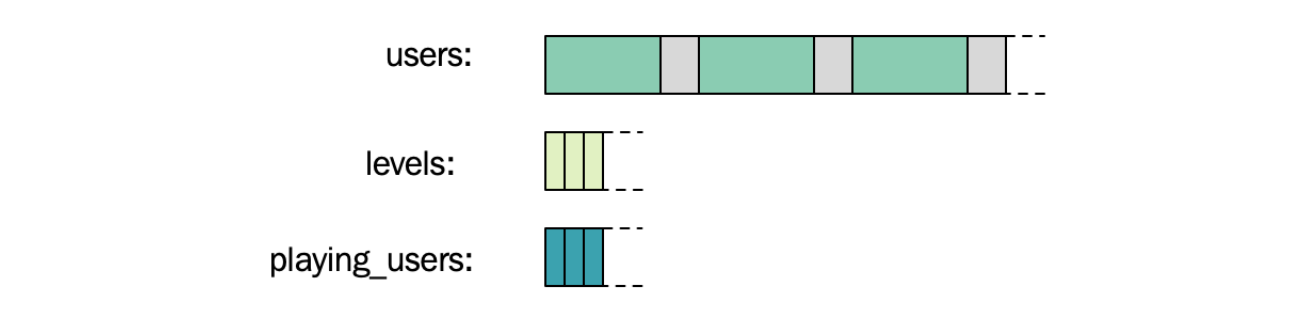
现在,我们不使用包含用户对象的一个向量,而是将所有的 $\text{short}$ 类型等级和 $\text{is_playing_}$ 标志存储在单独的向量中。用户数组中索引 $0$ 处用户的当前等级也存储在等级数组的索引 $0$ 处。这样,我们就可以避免使用指向等级的指针,而是仅使用索引来连接数据字段。我们可以对 $\text{is_playing_}$ 布尔字段做同样的事情,最终得到三个并行数组而不是一个。这三个向量的内存布局如下图所示:
我们使用三个并行数组来快速迭代一个特定的字段。num_users_at_level() 函数现在可以通过仅使用等级数组来计算特定等级的用户数。现在的实现简单地封装了 std::count():
auto num_users_at_level(const std::vector<int>& users, short level) {
ScopedTimer t{"num_users_at_level using int vector"};
return std::count(users.begin(), users.end(), level);
}
同样,num_playing_users() 函数只需要迭代布尔值的向量来确定正在玩游戏的用户数。我们再次使用 std::count():
auto num_playing_users(const std::vector<bool>& users) {
ScopedTimer t{"num_playing_users using vector<bool>"};
return std::count(users.begin(), users.end(), true);
}
使用并行数组,我们根本不必使用用户数组。提取出的数组所占用的内存量远小于用户数组,所以让我们再次检查对一百万用户运行这些函数时性能是否有所改善:
auto users = std::vector<User>(1'000'000);
auto levels = std::vector<short>(1'000'000);
auto playing_users = std::vector<bool>(1'000'000);
// Initialize data
// ...
auto num_at_level_5 = num_users_at_level(levels, 5);
auto num_playing = num_playing_users(playing_users);
使用整数数组计算特定等级的用户数仅需约 $0.7 \text{ ms}$。回顾一下,最初使用 $128$ 字节 $\text{User}$ 类的版本大约需要 $11 \text{ ms}$。较小的 $\text{User}$ 类执行时间为 $4 \text{ ms}$,而现在,仅使用 levels 数组,我们降到了 $0.7 \text{ ms}$。这是一个相当显著的变化。
对于第二个函数 num_playing_users(),变化甚至更大——计算当前正在玩游戏的用户数仅需约 $0.03 \text{ ms}$。之所以能这么快,归功于一种名为位数组 ($\text{bit arrays}$) 的数据结构。事实证明,std::vector<bool> 根本不是 C++ $\text{bool}$ 对象的标准向量。相反,在内部,它是一个位数组。像 count() 和 find() 这样的操作可以在位数组中得到非常高效的优化,因为它一次可以处理 $64$ 位(在 $64$ 位机器上),甚至可能通过使用 $\text{SIMD}$ 寄存器处理更多位。
缺点和总结
这一切都很棒,但我警告过你一些缺点。
- 代码结构影响: 将字段从它们所属的类中提取出来,将对代码的结构产生巨大影响。在某些情况下,将大型类拆分成较小的部分是完全合理的,但在其他情况下,它会完全破坏封装 ($\text{encapsulation}$),并暴露本可以隐藏在具有更高抽象级别的接口后面的数据。
- 难以同步: 确保数组保持同步是麻烦的,我们总是需要确保构成一个对象的字段存储在所有数组中的相同索引处。这种隐式关系 ($\text{Implicit relationships}$) 难以维护且容易出错。
- 多字段访问变慢: 最后一个缺点实际上与性能有关。在前面的例子中,你看到了对于一次迭代一个字段的算法,性能有很大的提升。然而,如果我们的算法需要访问已被提取到不同数组中的多个字段,那么它将比迭代一个包含较大对象的数组慢得多。
因此,正如在处理性能时总是如此,没有什么是没有代价的,而暴露数据并将一个简单数组拆分成多个数组的代价可能很高,也可能不高。这完全取决于你所面临的场景以及你在测量后遇到的性能提升。在真正面临性能问题之前,不要考虑并行数组。始终优先选择稳健的设计原则,并倾向于使用显式的方式来表达对象之间的关系,而不是隐式的方式。
总结
在本章中,我们介绍了标准库中的容器类型 。你了解了我们组织数据的方式对我们执行某些操作的效率有很大的影响。在选择不同的数据结构时,标准库容器的渐近复杂度规范 是需要考虑的关键因素。
此外,你了解了现代处理器中的缓存层次结构 如何影响我们需要组织数据的方式,以实现高效的内存访问。高效利用缓存级别的重要性怎么强调都不为过。这也是为什么连续存储元素的容器(例如 std::vector 和 std::string)成为最常用的容器之一的原因。
在下一章中,我们将探讨如何使用迭代器 和算法 来高效地操作容器。
- 显示Disqus评论(需要科学上网)