第五章：算法 - 李理的博客

引入标准库算法
- 标准库算法的演变
- 解决日常问题
迭代器和范围
标准算法的特性
编写和使用通用算法
最佳实践
总结

标准库容器在 C++ 程序员中被广泛采用。例如，很少能找到没有引用 std::vector 或 std::string 的 C++ 代码库。然而，根据我的经验，标准库算法的使用频率要低得多，尽管它们提供了与容器相同的优势：

它们可以作为解决复杂问题的构建块。
它们有完备的文档（包括参考资料、书籍和视频）。
许多 C++ 程序员已经对它们很熟悉。
它们的空间和运行时成本是已知的（复杂度保证）。
它们的实现经过精心设计且高效。

此外，C++ 的特性，如 $\text{lambda}$ 表达式、执行策略 ($\text{execution policies}$)、概念 ($\text{concepts}$) 和 $\text{Ranges}$ (范围库)，都使得标准算法更加强大，同时也更加友好易用。

在本章中，我们将研究如何使用算法库 ($\text{Algorithm library}$) 在 C++ 中编写高效的算法。你将了解在应用程序中使用标准库算法作为构建块的益处，无论是在性能方面还是在可读性方面。

本章你将学到：

C++ 标准库中的算法。
迭代器 ($\text{Iterators}$) 和范围 ($\text{Ranges}$) —— 容器和算法之间的粘合剂。
如何实现可以操作标准容器的通用算法 ($\text{generic algorithm}$)。
使用 C++ 标准算法时的最佳实践。

让我们从了解标准库算法以及它们如何发展到今天开始。

引入标准库算法

将标准库算法集成到你的 C++ 词汇表中非常重要。在本介绍中，我将展示一组可以使用标准库算法有效解决的常见问题。

C++20 通过引入 $\text{Ranges}$ 库和 C++ 概念 ($\text{concepts}$) 语言特性，给算法库带来了巨大的变化。因此，在我们开始之前，我们需要简要回顾一下 C++ 标准库的历史背景。

标准库算法的演变

你可能听说过 $\text{STL}$ 算法或 $\text{STL}$ 容器。希望你也听说过随 C++20 引入的新的 $\text{Ranges}$ 库。 C++20 对标准库进行了大量的补充。在继续之前，我需要澄清一些术语。我们从 $\text{STL}$ 开始。

$\text{STL}$，或标准模板库 ($\text{Standard Template Library}$)，最初是 $1990$ 年代添加到 C++ 标准库中的一个库的名称。它包含算法、容器、迭代器和函数对象。这个名称一直沿用下来，我们习惯于听到和谈论 $\text{STL}$ 算法和容器。

然而，C++ 标准没有提及 $\text{STL}$；相反，它谈论的是标准库及其各个组成部分，例如迭代器库 ($\text{Iterator library}$) 和算法库 ($\text{Algorithm library}$)。在本书中，我将尽量避免使用 $\text{STL}$ 这个名称，而是根据需要谈论标准库或各个子库。

现在我们来看 $\text{Ranges}$ 库以及我称之为受约束的算法 ($\text{constrained algorithms}$)。$\text{Ranges}$ 库是 C++20 添加到标准库中的一个库，它引入了一个全新的头文件 <ranges>，我们将在下一章详细讨论。但 $\text{Ranges}$ 库的添加也通过引入所有先前存在算法的重载版本，对 <algorithm> 头文件产生了巨大影响。我将这些算法称为受约束的算法，因为它们使用 C++ 概念 (C++ $\text{concepts}$) 进行了约束。因此，<algorithm> 头文件现在包括旧的基于迭代器的算法和新的使用 C++ 概念约束的、可以操作范围 ($\text{ranges}$) 的算法。这意味着我们将在本章讨论的算法有两种风格，如下例所示：

#include <algorithm>
#include <vector>

auto values = std::vector{9, 2, 5, 3, 4};

// Sort using the std algorithms (旧版基于迭代器)
std::sort(values.begin(), values.end());

// Sort using the constrained algorithms under std::ranges (新版基于范围)
std::ranges::sort(values);
std::ranges::sort(values.begin(), values.end());

请注意，sort() 的这两种版本都位于 <algorithm> 头文件中，但它们通过不同的命名空间和签名进行区分。本章将使用这两种风格，但通常，我建议尽可能使用新的受约束算法。阅读完本章后，其优势希望会变得显而易见。

现在，你已准备好开始学习如何使用现成的算法来解决常见问题。

解决日常问题

我将在此列出一些常见的场景和有用的算法，只是为了让你对标准库中可用的算法有所了解。库中算法很多，本节我只介绍其中一小部分。

1. 迭代序列

拥有一个可以打印序列元素的简短辅助函数非常有用。以下通用函数适用于任何包含可以打印到输出流（使用 operator<<()）的元素的容器：

void print(auto&& r) {
    std::ranges::for_each(r, [](auto&& i) { std::cout << i << ' '; });
}

print() 函数使用了 for_each()，这是一个从 <algorithm> 头文件导入的算法。 for_each() 会对范围内的每个元素调用我们提供的函数一次。我们提供的函数的返回值被忽略，对我们传递给 for_each() 的序列没有影响。我们可以使用 for_each() 来实现副作用 ($\text{side effects}$)，例如打印到标准输出（如本例所示）。

一个类似的、非常通用的算法是 transform()。它也对序列中的每个元素调用一个函数，但它不忽略返回值，而是将函数的返回值存储在输出序列中，像这样：

auto in = std::vector{1, 2, 3, 4};
auto out = std::vector<int>(in.size());
auto lambda = [](auto&& i) { return i * i; };

std::ranges::transform(in, out.begin(), lambda);
print(out);
// Prints: "1 4 9 16 "

这段代码片段也演示了我们如何使用前面定义的 print() 函数。 transform() 算法将对输入范围内的每个元素调用一次我们的 $\text{lambda}$。为了指定输出的存储位置，我们向 transform() 提供了一个输出迭代器，即 out.begin()。我们将在本章后面详细讨论迭代器。

有了我们的 print() 函数以及一些最通用算法的演示，我们将继续研究一些用于生成元素的算法。

2. 生成元素

有时我们需要用一些初始值来赋值一个序列的元素或重置整个序列。以下示例用值 $-1$ 填充一个向量：

auto v = std::vector<int>(4);
std::ranges::fill(v, -1);
print(v);
// Prints "-1 -1 -1 -1 "

下一个算法 generate() 会为每个元素调用一个函数，并将函数的返回值存储在当前元素中：

auto v = std::vector<int>(4);
std::ranges::generate(v, std::rand);
print(v);
// Possible output: "1804289383 846930886 1681692777 1714636915 "

在前面的示例中，std::rand() 函数为每个元素调用了一次。

我将提到的最后一个生成算法是来自 <numeric> 头文件的 std::iota()。它以递增顺序生成值。起始值必须指定为第二个参数。这是一个生成 $0$ 到 $5$ 之间值的简短示例：

auto v = std::vector<int>(6);
std::iota(v.begin(), v.end(), 0);
print(v); // Prints: "0 1 2 3 4 5 "

这个序列已经排序，但更常见的情况是你的元素集合是无序的，需要排序，这也是我们接下来要看的。

排序元素

排序元素是一种非常常见的操作。有一些排序算法的替代方案值得了解，但在这个介绍中，我将只展示最常规的版本，简单命名为 sort()：

auto v = std::vector{4, 3, 2, 3, 6};
std::ranges::sort(v);
print(v); // Prints: "2 3 3 4 6 "

如前所述，这不是唯一的排序方法，有时我们可以使用部分排序算法 ($\text{partial sorting algorithm}$) 来提高性能。我们将在本章后面详细讨论排序。

查找元素

另一个非常常见的任务是查找特定值是否在集合中。也许我们想知道某个特定值在集合中出现了多少次。如果我们知道集合已经排序，那么这些搜索值的算法可以实现得更高效。你在第 3 章《分析和测量性能》中看到了这一点，我们在其中比较了线性搜索和二分搜索。

这里我们从 find() 算法开始，它不要求集合已排序：

auto col = std::list{2, 4, 3, 2, 3, 1};
auto it = std::ranges::find(col, 2);
if (it != col.end()) {
    std::cout << *it << '\n'; // Output: 2
}

如果找不到我们正在查找的元素，find() 会返回集合的 end() 迭代器。在最坏的情况下，find() 需要检查序列中的所有元素，因此它以 $O(n)$ 时间运行。

使用二分搜索查找

如果我们知道集合已经排序，我们可以使用二分搜索 ($\text{binary search}$) 算法之一：binary_search()、equal_range()、upper_bound() 或 lower_bound()。如果我们将这些函数用于提供随机访问 ($\text{random access}$) 的容器，则它们都保证以 $O(\log n)$ 时间运行。当我们稍后在本章讨论迭代器和范围（有一个有趣的部分名为“迭代器和范围”）时，你将更好地理解算法如何提供复杂度保证，即使它们操作的是不同的容器。

在以下示例中，我们将使用一个已排序的 std::vector：

binary_search() 函数返回 true 或 false，取决于是否找到了我们搜索的值：

auto v = std::vector{2, 2, 3, 3, 3, 4, 5}; // Sorted!
bool found = std::ranges::binary_search(v, 3);
std::cout << std::boolalpha << found << '\n'; // Output: true

在调用 binary_search() 之前，你应该绝对确定集合已排序。我们可以使用 is_sorted() 在代码中轻松断言这一点，如下所示：

assert(std::ranges::is_sorted(v));

此检查将以 $O(n)$ 运行，但只会在断言被激活时调用，因此不会影响你最终程序的性能。

我们正在处理的已排序集合包含多个 $3$。如果我们想知道集合中第一个 $3$ 或最后一个 $3$ 的位置怎么办？在这种情况下，我们可以使用 lower_bound() 来查找第一个 $3$，或使用 upper_bound() 来查找紧跟在最后一个 $3$ 之后的元素：

auto v = std::vector{2, 2, 3, 3, 3, 4, 5};
auto it = std::ranges::lower_bound(v, 3);
if (it != v.end()) {
    // 使用 std::distance 获取索引
    auto index = std::distance(v.begin(), it); 
    std::cout << index << '\n'; // Output: 2
}

这段代码将输出 $2$，因为那是第一个 $3$ 的索引。要从迭代器获取元素的索引，我们使用来自 <iterator> 头文件的 std::distance()。

以同样的方式，我们可以使用 upper_bound() 来获取紧跟在最后一个 $3$ 之后的元素的迭代器：

const auto v = std::vector{2, 2, 3, 3, 3, 4, 5};
auto it = std::ranges::upper_bound(v, 3);
if (it != v.end()) {
    auto index = std::distance(v.begin(), it);
    std::cout << index << '\n'; // Output: 5
}

如果你想要上界和下界两者，你可以改用 equal_range()，它返回包含所有 $3$ 的子范围 ($\text{subrange}$)：

const auto v = std::vector{2, 2, 3, 3, 3, 4, 5};
auto subrange = std::ranges::equal_range(v, 3);
if (subrange.begin() != subrange.end()) {
    auto pos1 = std::distance(v.begin(), subrange.begin()); // 第一个 3 的索引 (下界)
    auto pos2 = std::distance(v.begin(), subrange.end());   // 紧跟在最后一个 3 之后的索引 (上界)
    std::cout << pos1 << " " << pos2 << '\n';
} // Output: "2 5"

现在让我们探索一些用于检查集合的其他有用算法。

检查特定条件

有三个非常方便的算法，称为 all_of()、any_of() 和 none_of()。它们都接受一个范围 ($\text{range}$)、一个一元谓词 ($\text{unary predicate}$，即接受一个参数并返回 true 或 false 的函数) 以及一个可选的投影函数 ($\text{projection function}$)。

假设我们有一个数字列表和一个用于确定数字是否为负数的小 $\text{lambda}$ 表达式：

const auto v = std::vector{3, 2, 2, 1, 0, 2, 1};
const auto is_negative = [](int i) { return i < 0; };

我们可以使用 none_of() 检查是否没有数字是负数：

if (std::ranges::none_of(v, is_negative)) {
    std::cout << "Contains only natural numbers\n";
}

接下来，我们可以使用 all_of() 询问列表中的所有元素是否都是负数：

if (std::ranges::all_of(v, is_negative)) {
    std::cout << "Contains only negative numbers\n";
}

最后，我们可以使用 any_of() 查看列表是否包含至少一个负数：

if (std::ranges::any_of(v, is_negative)) {
    std::cout << "Contains at least one negative number\n";
}

很容易忘记这些存在于标准库中的小巧方便的构建块。但是，一旦你养成了使用它们的习惯，你就再也不会回头自己手写这些代码了。

计数元素

计算等于某个值的元素数量，最明显的方法是调用 count()：

const auto numbers = std::list{3, 3, 2, 1, 3, 1, 3};
int n = std::ranges::count(numbers, 3);
std::cout << n; // Prints: 4

count() 算法以线性时间 ($O(n)$) 运行。然而，如果我们知道序列已经排序，并且我们使用的是 $\text{vector}$ 或其他随机访问数据结构，我们可以改用 equal_range()，它将以 $O(\log n)$ 时间运行。示例如下：

const auto v = std::vector{0, 2, 2, 3, 3, 4, 5};
assert(std::ranges::is_sorted(v)); // O(n), but not called in release
auto r = std::ranges::equal_range(v, 3);
int n = std::ranges::size(r);
std::cout << n; // Prints: 2

equal_range() 函数找到包含所有我们想要计数的值的元素的子范围 ($\text{subrange}$)。一旦找到子范围，我们就可以使用 <ranges> 头文件中的 size() 来检索子范围的长度。

最小值、最大值和钳制

我想提一组对于经验丰富的 C++ 程序员来说至关重要的、小而极其有用的算法。std::min()、std::max() 和 std::clamp() 函数有时会被遗忘，我们常常发现自己在写这样的代码：

const auto y_max = 100;
auto y = some_func();
if (y > y_max) {
    y = y_max;
}

这段代码确保了 y 的值在一个特定的限制内。这段代码可以工作，但我们可以通过使用 std::min() 来避免可变变量和 if 语句，如下所示：

const auto y = std::min(some_func(), y_max);

通过使用 std::min()，代码中混乱的可变变量和 if 语句都被消除了。我们可以将 std::max() 用于类似的情况。

如果我们想将一个值限制在最小值和最大值之间，我们可能会这样做：

const auto y = std::max(std::min(some_func(), y_max), y_min);

但是，从 C++17 开始，我们现在有了 std::clamp()，它在一个函数中为我们完成了这项工作。因此，我们可以直接使用 clamp() 如下：

const auto y = std::clamp(some_func(), y_min, y_max);

有时我们需要找到一个未排序集合中元素的极值。为此，我们可以使用 minmax()，它（毫不奇怪）返回序列的最小值和最大值。结合结构化绑定，我们可以打印极值，如下所示：

const auto v = std::vector{4, 2, 1, 7, 3, 1, 5};
const auto [min, max] = std::ranges::minmax(v);
std::cout << min << " " << max; // Prints: "1 7"

我们还可以通过使用 min_element() 或 max_element() 来查找最小或最大元素的位置。它们不返回元素值，而是返回指向我们正在查找的元素的迭代器。在下面的示例中，我们正在查找最小元素：

const auto v = std::vector{4, 2, 7, 1, 1, 3};
const auto it = std::ranges::min_element(v);
std::cout << std::distance(v.begin(), it); // Output: 3

这段代码输出了3，这是找到的第一个最小值的索引。

这是对标准库中一些最常用算法的简要介绍。算法的运行时成本在 C++ 标准中指定，所有库实现都必须遵守这些规范，尽管确切的实现可能因平台而异。为了理解在处理许多不同类型的容器时，通用算法如何保持复杂度保证，我们需要更仔细地研究迭代器和范围。

这是对“迭代器和范围”部分的翻译和格式化，保留了代码部分：

迭代器和范围

正如在前面的示例中所见，标准库算法操作的是迭代器 ($\text{iterators}$) 和范围 ($\text{ranges}$)，而不是容器类型。本节将重点介绍迭代器以及 C++20 中引入的范围这一新概念。一旦你掌握了迭代器和范围，正确使用容器和算法就会变得容易。

引入迭代器

迭代器构成了标准库算法和范围的基础。迭代器是数据结构和算法之间的粘合剂。正如你已经看到的，C++ 容器以截然不同的方式存储它们的元素。迭代器提供了一种通用的方式来导航序列中的元素。通过让算法操作迭代器而不是容器类型，算法变得更加通用和灵活，因为它们不依赖于容器的类型以及容器在内存中排列元素的方式。

迭代器的核心是一个表示序列中位置的对象。它有两个主要职责：

在序列中导航。
读取和写入其当前位置的值。

迭代器抽象绝不是 C++ 独有的概念，它存在于大多数编程语言中。 C++ 实现的迭代器概念与其他编程语言的不同之处在于，C++ 模仿了原始内存指针的语法。

基本上，迭代器可以被视为具有与原始指针相同属性的对象；它可以步进到下一个元素并解引用（如果指向一个有效地址）。尽管迭代器在内部可能是一个遍历类似树状 std::map 的“重”对象，但算法只使用了指针允许的少数操作。

大多数直接位于 std 命名空间下的算法只操作迭代器，而不是容器（即 std::vector、std::map 等）。许多算法返回迭代器而不是值。

为了能够在序列中导航而不越界，我们需要一种通用的方式来判断迭代器何时到达了序列的末尾。这就是哨兵值 ($\text{sentinel values}$) 的作用。

哨兵值和越界迭代器

哨兵值（或简称哨兵 ($\text{sentinel}$）) 是一个指示序列结束的特殊值。哨兵值使得迭代一个序列成为可能，而无需事先知道序列的大小。使用哨兵值的一个例子是空字符终止的 $\text{C}$ 风格字符串（在这种情况下，哨兵是 '\0' 字符）。通过不跟踪空字符终止字符串的长度，指向字符串开头的指针和末尾的哨兵就足以定义一个字符序列。

受约束的算法使用一个迭代器来定义序列中的第一个元素，使用一个哨兵来指示序列的结束。对哨兵的唯一要求是它可以与迭代器进行比较，这在实践中意味着应该定义 operator==() 和 operator!=() 来接受哨兵和迭代器的组合：

bool operator!=(sentinel s, iterator i) {
    // ...
}

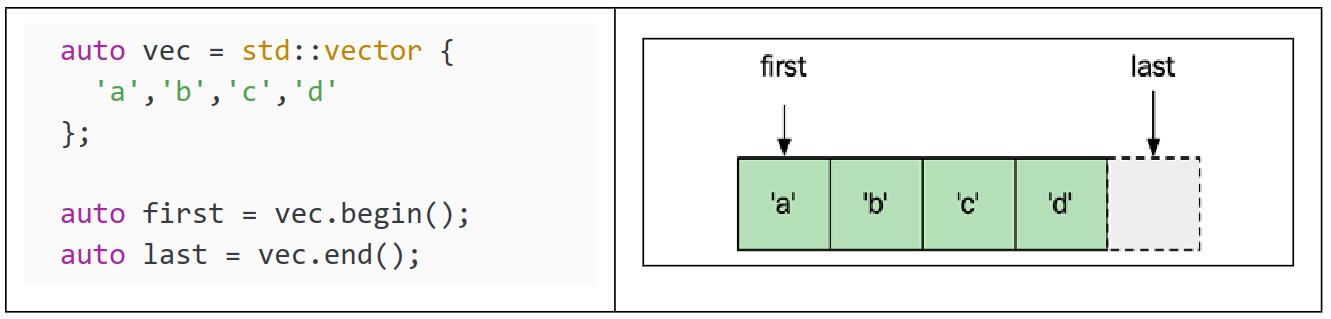
现在你知道了什么是哨兵，我们如何创建一个哨兵来指示序列的结束呢？这里的技巧是使用一个称为越界迭代器 ($\text{past-the-end iterator}$) 的东西作为哨兵。它只是一个指向我们定义的序列中最后一个元素之后（或越过）的元素的迭代器。请看下面的代码片段和图示：

如上图所示，last 迭代器现在指向 ‘d’ 之后的一个假想元素。这使得可以使用一个循环来迭代序列中的所有元素：

for (; first != last; ++first) {
    char value = *first; // Dereference iterator
    // ...

我们可以使用这个越界哨兵来与我们的迭代器 it 进行比较，但我们不能解引用这个哨兵，因为它不指向范围内的任何元素。

这种越界迭代器的概念历史悠久，甚至适用于内置 $\text{C}$ 数组：

char arr[] = {'a', 'b', 'c', 'd'};
char* end = arr + sizeof(arr);
for (char* it = arr; it != end; ++it) { // Stop at end
    std::cout << *it << ' ';
}
// Output: a b c d

再次注意，end 实际上指向越界的位置，所以我们不允许解引用它，但我们允许读取指针值并将其与我们的 it 变量进行比较。

这是对“范围和迭代器类别”部分的翻译和格式化，保留了代码部分：

范围

范围是我们引用元素序列时所使用的迭代器-哨兵对 ($\text{iterator-sentinel pairs}$) 的替代品。 <ranges> 头文件包含多个概念 ($\text{concepts}$)，它们定义了不同类型范围的要求，例如 input_range、random_access_range 等。这些都是最基本概念 $\text{range}$ 的细化，该概念定义如下：

template<class T>
concept range = requires(T& t) {
    ranges::begin(t);
    ranges::end(t);
};

这意味着任何暴露 begin() 和 end() 函数的类型都被视为一个范围（假设这些函数返回迭代器）。

对于 C++ 标准容器，begin() 和 end() 函数将返回相同类型的迭代器，但在 C++20 范围中，这通常不成立。迭代器和哨兵类型相同的范围满足 std::ranges::common_range 概念。新的 C++20 视图 ($\text{views}$，下一章介绍) 返回的迭代器-哨兵对可以是不同类型的。然而，它们可以使用 std::views::common 转换为迭代器和哨兵具有相同类型的视图。

std::ranges 命名空间中的受约束算法 ($\text{constrained algorithms}$) 可以操作范围，而不是迭代器对。由于所有标准容器（vector、map、list 等）都满足范围概念，我们可以直接将范围传递给受约束算法，如下所示：

auto vec = std::vector{1, 1, 0, 1, 1, 0, 0, 1};
std::cout << std::ranges::count(vec, 0); // Prints 3

范围是对可迭代事物（可以循环遍历的事物）的抽象，并在一定程度上隐藏了 C++ 迭代器的直接使用。然而，迭代器仍然是 C++ 标准库的主要部分，并在 $\text{Ranges}$ 库中被广泛使用。

接下来你需要理解的是存在的不同类型的迭代器。

迭代器类别

现在你对范围的定义方式以及如何知道何时到达序列末尾有了更好的理解，是时候更仔细地研究迭代器为了导航、读取和写入值所能支持的操作了。

序列中的迭代器导航可以通过以下操作完成：

向前步进： std::next(it) 或 ++it
向后步进： std::prev(it) 或 --it
跳转到任意位置： std::advance(it, n) 或 it += n

在迭代器表示的位置读取和写入值是通过解引用迭代器完成的。它是这样的：

读取： auto value = *it
写入： *it = value

这些是容器暴露的迭代器最常见的操作。但此外，迭代器可能操作数据源，其中写入或读取意味着向前步进。此类数据源的示例可以是用户输入、网络连接或文件。这些数据源需要以下操作：

只读并向前步进： auto value = *it; ++it;
只写并向前步进： *it = value; ++it;

这些操作只能用两个连续的表达式来表达。第一个表达式的后置条件是第二个表达式必须有效。这也意味着我们只能对一个位置读取或写入一次值。如果我们要读取或写入一个新值，我们必须首先将迭代器推进到下一个位置。

并非所有迭代器都支持上述列表中的所有操作。例如，一些迭代器只能读取值并向前步进，而其他迭代器可以同时读取、写入并跳转到任意位置。

现在，如果我们考虑一些基本算法，很明显，对迭代器的要求在不同算法之间是不同的：

如果一个算法计数一个值的出现次数，它需要读取和向前步进操作。
如果一个算法用一个值填充一个容器，它需要写入和向前步进操作。
对已排序集合的二分搜索算法需要读取和跳转操作。

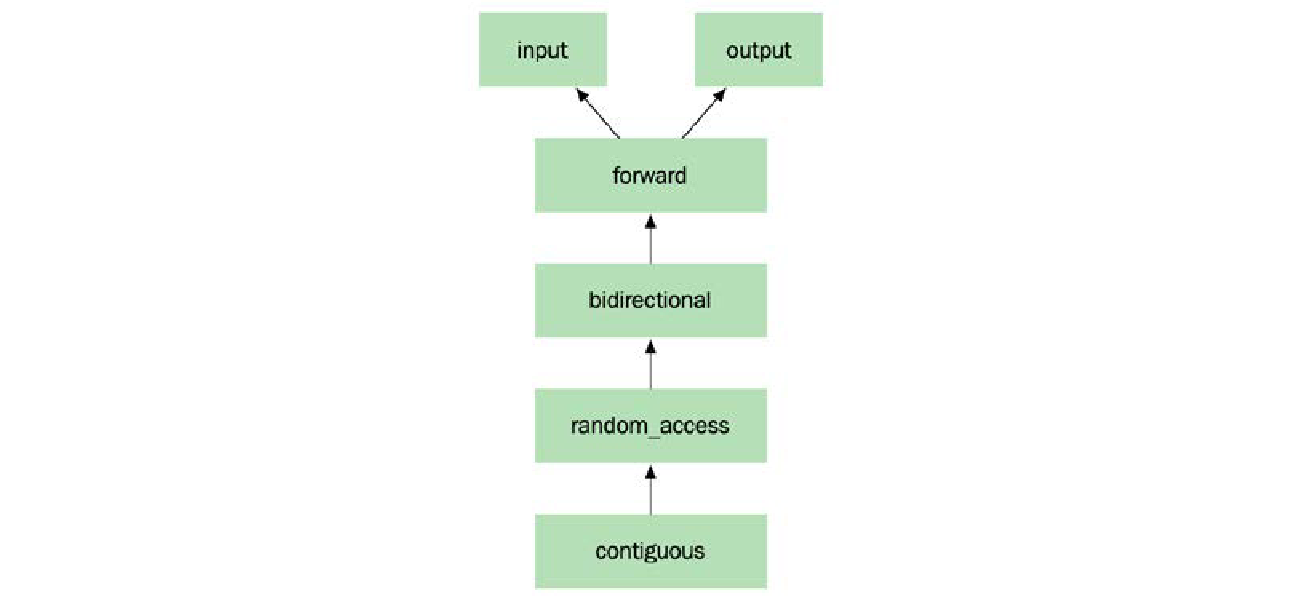
一些算法可以根据迭代器支持的操作实现得更高效。就像容器一样，标准库中的所有算法都有复杂度保证（使用大 $O$ 符号）。为了让算法满足特定的复杂度保证，它对其操作的迭代器提出了要求。这些要求被归类为六个基本迭代器类别，它们之间的关系如下图所示：

箭头表示一个迭代器类别也具有其指向的类别的所有功能。例如，如果一个算法需要一个向前迭代器 ($\text{forward iterator}$)，我们也可以传递给它一个双向迭代器 ($\text{bidirectional iterator}$)，因为双向迭代器拥有向前迭代器的所有功能。

这六个要求由以下概念正式规定：

std::input_iterator (输入迭代器)：支持只读和向前步进（一次）。std::count() 等单趟算法 ($\text{One-pass algorithms}$) 可以使用输入迭代器。std::istream_iterator 是输入迭代器的一个示例。
std::output_iterator (输出迭代器)：支持只写和向前步进（一次）。请注意，输出迭代器只能写入，不能读取。std::ostream_iterator 是输出迭代器的一个示例。
std::forward_iterator (向前迭代器)：支持读取和写入以及向前步进。当前位置的值可以读取或写入多次。std::forward_list 等单向链表暴露向前迭代器。
std::bidirectional_iterator (双向迭代器)：支持读取、写入、向前步进和向后步进。双向链表 std::list 暴露双向迭代器。
std::random_access_iterator (随机访问迭代器)：支持读取、写入、向前步进、向后步进和以常数时间 ($\text{constant time}$) 跳转到任意位置。std::deque 内部的元素可以使用随机访问迭代器访问。
std::contiguous_iterator (连续迭代器)：与随机访问迭代器相同，但还保证底层数据是连续的内存块，例如 std::string、std::vector、std::array、std::span 和（很少使用的）std::valarray。

迭代器类别对于理解算法的时间复杂度要求非常重要。对底层数据结构有很好的理解，可以很容易地知道哪些迭代器通常属于哪些容器。

我们现在准备更深入地研究大多数标准库算法使用的常见模式。

标准算法的特性

为了更好地理解标准算法，最好了解一下 <algorithm> 头文件中所有算法所使用的特性和常见模式。如前所述，std 和 std::ranges 命名空间下的算法有很多共同点。我们将从对 std 算法和 std::ranges 下的受约束算法都成立的通用原则开始，然后在下一节中，我们将讨论 std::ranges 下的受约束算法所特有的特性。

算法不改变容器的大小

来自 <algorithm> 的函数只能修改指定范围内的元素；它们永远不会从底层容器中添加或删除元素。因此，这些函数永远不会改变它们操作的容器的大小。

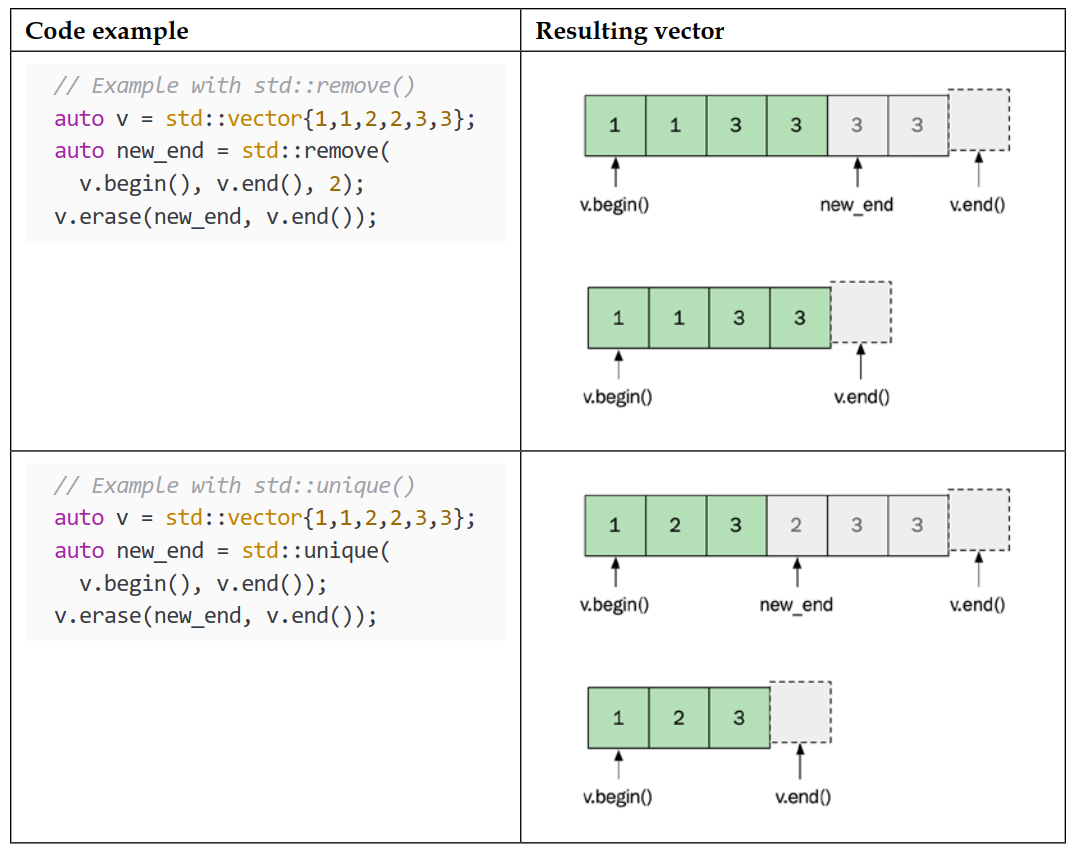
例如，std::remove() 或 std::unique() 实际上并不会从容器中删除元素（尽管它们的名字如此）。相反，它们将应该保留的元素移动到容器的前面，然后返回一个定义有效元素新末尾的哨兵：

C++20 新特性： C++20 向 <vector> 头文件添加了新版本的 std::erase() 和 std::erase_if() 函数，它们可以直接从 $\text{vector}$ 中删除值，无需先调用 $\text{remove()}$ 再调用 $\text{erase()}$。

标准库算法永远不会改变容器大小的这一事实意味着，当我们调用会产生输出的算法时，我们需要自己分配数据。

产出结果的算法需要分配数据

将数据写入输出迭代器 ($\text{output iterator}$) 的算法，例如 std::copy() 或 std::transform()，要求为输出预留已分配的数据空间。由于算法只使用迭代器作为参数，它们无法自行分配数据。为了增大它们操作的容器，这些算法依赖于迭代器本身具有增大容器的能力。

如果将一个空容器的迭代器作为输出来传递给这些算法，程序很可能会崩溃。下面的例子说明了这个问题，其中 squared 是空的：

const auto square_func = [](int x) { return x * x; };
const auto v = std::vector{1, 2, 3, 4};
auto squared = std::vector<int>{}; // 空容器
// 错误：试图写入未分配的内存，程序很可能会崩溃
std::ranges::transform(v, squared.begin(), square_func); 

相反，你必须执行以下操作之一：

预先分配结果容器所需的尺寸，或者
使用插入迭代器 ($\text{insert iterator}$)，它在迭代时将元素插入到容器中。

1. 预先分配空间

以下代码片段展示了如何使用预先分配的空间：

const auto square_func = [](int x) { return x * x; };
const auto v = std::vector{1, 2, 3, 4};
auto squared = std::vector<int>{};

squared.resize(v.size()); // 预分配所需的尺寸

std::ranges::transform(v, squared.begin(), square_func);

优化提示：如果你在操作 $\text{std::vector}$ 并知道结果容器的预期大小，可以在执行算法之前使用 $\text{reserve()}$ 成员函数来预留内存，以避免不必要的重新分配。否则，$\text{vector}$ 可能会在算法执行期间多次重新分配新的内存块。

2. 使用插入迭代器

以下代码片段展示了如何使用 std::back_inserter() 和 std::inserter() 将值插入到未预分配的容器中：

const auto square_func = [](int x) { return x * x; };
const auto v = std::vector{1, 2, 3, 4};

// 使用 std::back_inserter 插入到 vector 的末尾 (要求容器支持 push_back)
auto squared_vec = std::vector<int>{};
auto dst_vec = std::back_inserter(squared_vec); // 自动调用 push_back
std::ranges::transform(v, dst_vec, square_func);

// 使用 std::inserter 插入到 std::set 中 (要求容器支持 insert)
auto squared_set = std::set<int>{};
// 自动调用 insert(hint, value)，hint 为 squared_set.end()
auto dst_set = std::inserter(squared_set, squared_set.end()); 
std::ranges::transform(v, dst_set, square_func);

默认情况下算法使用 `operator==()` 和 `operator<()`

默认情况下，算法依赖于基本的 == 和 < 运算符进行比较，就像整数的情况一样。为了能够在算法中使用你自己的类，你必须提供 operator==() 和 operator<()，要么由类提供，要么作为参数传递给算法。

通过使用三路比较运算符 ($\text{three-way comparison operator}$) operator<=>()，我们可以让编译器生成必要的运算符。下面的示例展示了一个简单的 $\text{Flower}$ 类，其中 std::find() 使用了 operator==()，而 std::max_element() 使用了 operator<()：

struct Flower {
    // C++20：使用 default 生成所有比较运算符
    auto operator<=>(const Flower& f) const = default; 
    bool operator==(const Flower&) const = default;
    int height_{};
};

auto garden = std::vector<Flower>{ {67}, {28}, {14}};

// std::max_element() 使用 operator<()
auto tallest = std::max_element(garden.begin(), garden.end());

// std::find() 使用 operator==()
auto perfect = *std::find(garden.begin(), garden.end(), Flower{28});

除了对当前类型使用默认的比较函数外，还可以使用自定义比较器函数 ($\text{custom comparator function}$)，我们接下来将探讨这一点。

自定义比较器函数

有时我们需要在不使用默认比较运算符的情况下比较对象，例如，按字符串长度进行排序或查找。在这些情况下，可以提供一个自定义函数作为额外的参数。虽然原始算法使用一个值（例如 std::find()），但具有特定操作的版本名称后附加了 _if（例如 std::find_if()、std::count_if() 等）：

auto names = std::vector<std::string> {
    "Ralph", "Lisa", "Homer", "Maggie", "Apu", "Bart"
};

// 使用 lambda 表达式作为自定义比较器，按字符串长度排序
std::sort(names.begin(), names.end(),
    [](const std::string& a,const std::string& b) {
        return a.size() < b.size(); 
    });
// names is now "Apu", "Lisa", "Bart", "Ralph", "Homer", "Maggie"

// 使用 std::find_if() 查找长度为 3 的名字
auto x = std::find_if(names.begin(), names.end(),
    [](const auto& v) { return v.size() == 3; });

// x points to "Apu"

受约束算法使用投影

std::ranges 下的受约束算法 ($\text{constrained algorithms}$) 为我们提供了一个便捷的特性，称为投影 ($\text{projections}$)，它减少了编写自定义比较函数的需要。前一节中的示例可以使用标准的谓词 ($\text{predicate}$) std::less 结合自定义投影来重写：

auto names = std::vector<std::string>{
    "Ralph", "Lisa", "Homer", "Maggie", "Apu", "Bart"
};

// 使用 std::less<> 进行比较，但比较的是 std::string::size 的结果
std::ranges::sort(names, std::less<>{}, &std::string::size); 
// names is now "Apu", "Lisa", "Bart", "Ralph", "Homer", "Maggie"

// 查找 size() == 3 的元素，比较的是投影的结果 3 和 目标值 3
auto x = std::ranges::find(names, 3, &std::string::size);
// x points to "Apu"

也可以传递一个 $\text{lambda}$ 表达式作为投影参数，当你想要在投影中组合多个属性时，这会非常方便：

struct Player {
    std::string name_{};
    int level_{};
    float health_{};
    // ...
};

auto players = std::vector<Player>{
    {"Aki", 1, 9.f},
    {"Nao", 2, 7.f},
    {"Rei", 2, 3.f}};

// 投影函数：返回一个包含 level 和 health 的元组
auto level_and_health = [](const Player& p) {
    return std::tie(p.level_, p.health_);
};

// 使用 std::greater<> 进行比较，按照 level 降序，然后按照 health 降序排序
std::ranges::sort(players, std::greater<>{}, level_and_health);

将投影对象传递给标准算法的可能性是一个非常受欢迎的特性，它极大地简化了自定义比较的使用。

编写和使用通用算法

算法库包含通用算法 ($\text{generic algorithms}$)。为了尽可能具体，我将展示一个如何实现通用算法的示例。这将为你提供一些关于如何使用标准算法的见解，同时演示实现一个通用算法并不困难。我将刻意避免在这里解释示例代码的所有细节，因为我们将在本书的后面花费大量时间在通用编程上。

在接下来的示例中，我们将一个简单的非通用算法转换为一个功能齐全的通用算法。

非通用算法

通用算法是一种可以用于各种元素范围（$\text{ranges}$），而不仅仅是一种特定类型（如 std::vector）的算法。以下算法是一个非通用算法的示例，它只适用于 std::vector<int>：

auto contains(const std::vector<int>& arr, int v) {
    for (int i = 0; i < arr.size(); ++i) {
        if (arr[i] == v) { return true; }
    }
    return false;
}

为了找到我们正在查找的元素，我们依赖于 std::vector 的接口，该接口为我们提供了 size() 函数和下标运算符 (operator[]())。然而，并非所有容器都为我们提供这些函数，而且我也不建议你像这样编写裸循环 ($\text{raw loops}$)。相反，我们需要创建一个操作迭代器的函数模板。

通用算法

通过将 std::vector 替换为两个迭代器，并将 int 替换为模板参数，我们可以将算法转换为通用版本。以下版本的 contains() 可以用于任何容器：

template <typename Iterator, typename T>
auto contains(Iterator begin, Iterator end, const T& v) {
    for (auto it = begin; it != end; ++it) {
        if (*it == v) { return true; }
    }
    return false;
}

例如，要与 std::vector 一起使用它，你必须传递 begin() 和 end() 迭代器：

auto v = std::vector{3, 4, 2, 4};
if (contains(v.begin(), v.end(), 3)) {
    // Found the value...
}

我们可以通过提供一个接受范围 ($\text{range}$) 而不是两个单独的迭代器参数的版本来改进这个算法：

auto contains(const auto& r, const auto& x) {
    auto it = std::begin(r);
    auto sentinel = std::end(r);
    return contains(it, sentinel, x);
}

这个算法不强制客户端提供 begin() 和 end() 迭代器，因为我们已将它们的操作移到了函数内部。我们使用 C++20 的简化函数模板语法 ($\text{abbreviated function template syntax}$) 来避免明确写出这是一个函数模板。作为最后一步，我们可以为我们的参数类型添加约束 ($\text{constraints}$)：

auto contains(const std::ranges::range auto& r, const auto& x) {
    auto it = std::begin(r);
    auto sentinel = std::end(r);
    return contains(it, sentinel, x);
}

正如你所看到的，创建一个健壮的通用算法实际上不需要太多代码。我们传递给算法的数据结构唯一的要求是它能够暴露 begin() 和 end() 迭代器。你将在第 $8$ 章《编译期编程》中学习更多关于约束和概念的知识。

可供通用算法使用的数据结构

这引导我们认识到，我们创建的新的自定义数据结构只要暴露 begin() 和 end() 迭代器或一个范围，就可以被标准通用算法使用。作为一个简单的例子，我们可以实现一个二维 $\text{Grid}$ 结构，其中行被暴露为一对迭代器，如下所示：

struct Grid {
    Grid(std::size_t w, std::size_t h) : w_{w}, h_{h} {
        data_.resize(w * h);
    }
    auto get_row(std::size_t y); // Returns iterators or a range
    std::vector<int> data_{};
    std::size_t w_{};
    std::size_t h_{};
};

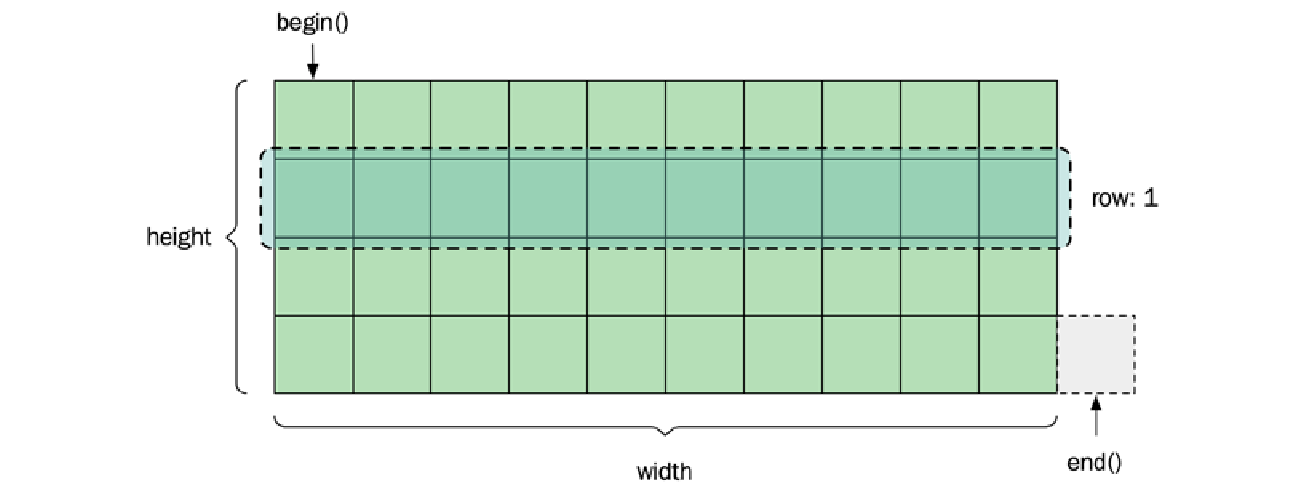
下图说明了 $\text{Grid}$ 结构及其迭代器对的布局：

get_row() 的一种可能实现将返回一个包含表示行开头和结尾的迭代器的 std::pair：

auto Grid::get_row(std::size_t y) {
    auto left = data_.begin() + w_ * y;
    auto right = left + w_;
    return std::make_pair(left, right);
}

表示一行的迭代器对随后可以被标准库算法利用。在下面的示例中，我们使用了 std::generate() 和 std::count()：

auto grid = Grid{10, 10};
auto y = 3;
auto row = grid.get_row(y);
std::generate(row.first, row.second, std::rand);
auto num_fives = std::count(row.first, row.second, 5);

虽然这样做可行，但使用 std::pair 有点笨拙，而且它还要求客户端知道如何处理迭代器对。没有什么明确说明 $\text{first}$ 和 $\text{second}$ 成员实际上表示一个半开区间 ($\text{half-open range}$)。如果它可以暴露一个强类型范围 ($\text{strongly typed range}$) 而不是一对迭代器，会不会更好呢？幸运的是，我们将在下一章探讨的 $\text{Ranges}$ 库为我们提供了一个名为 std::ranges::subrange 的视图类型。现在，get_row() 函数可以像这样实现：

auto Grid::get_row(std::size_t y) {
    auto first = data_.begin() + w_ * y;
    auto sentinel = first + w_;
    return std::ranges::subrange{first, sentinel};
}

我们甚至可以更“懒”一些，使用专为这种情况量身定制的便捷视图，称为 std::views::counted()：

auto Grid::get_row(std::size_t y) {
    auto first = data_.begin() + w_ * y;
    return std::views::counted(first, w_);
}

从 $\text{Grid}$ 类返回的行现在可以与任何接受范围而不是迭代器对的受约束算法一起使用：

auto row = grid.get_row(y);
std::ranges::generate(row, std::rand);
auto num_fives = std::ranges::count(row, 5);

这就完成了我们关于编写和使用支持迭代器对和范围的通用算法的示例。希望这能为你提供一些关于如何以通用方式编写数据结构和算法的见解，以避免由于必须为所有类型的数据结构编写专用算法而导致的组合爆炸 ($\text{combinatorial explosion}$)。

最佳实践

让我们考虑一些在你使用我们讨论过的算法时会有所帮助的做法。我将首先强调利用标准算法的重要性。

使用受约束算法

C++20 引入的 std::ranges 下的受约束算法 ($\text{constrained algorithms}$) 比 $\text{std}$ 下基于迭代器的算法提供了一些优势。受约束算法具有以下特点：

支持投影 ($\text{Support projections}$)，简化了元素的自定义比较。
支持范围 ($\text{Support ranges}$) 而不是迭代器对。无需将 begin() 和 end() 迭代器作为单独的参数传递。
易于正确使用，并且由于受到 C++ 概念 ($\text{concepts}$) 的约束，在编译期间能提供描述性错误消息。

我的建议是开始使用受约束算法来替代基于迭代器的算法。

ℹ️ 注意：你可能已经注意到本书在很多地方使用了基于迭代器的算法。原因在于，在撰写本书时，并非所有标准库实现都支持受约束算法。

仅对你需要检索的数据进行排序

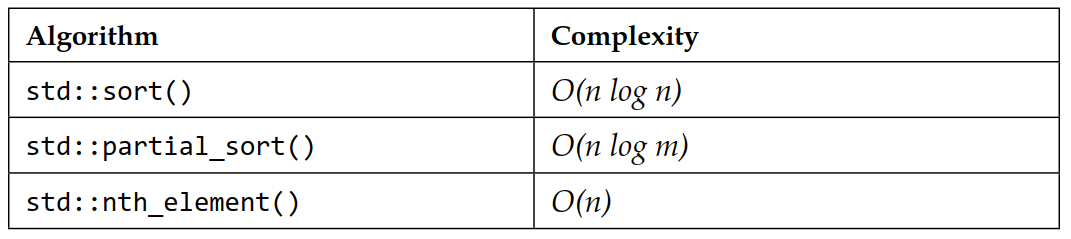
算法库包含三个基本的排序算法：sort()、partial_sort() 和 nth_element()。此外，它还包含这些算法的一些变体，包括 stable_sort()，但我们将重点关注这三个，因为根据我的经验，很容易忘记在许多情况下可以通过使用 nth_element() 或 partial_sort() 来避免完全排序。

虽然 sort() 排序整个范围，但 partial_sort() 和 nth_element() 可以被认为是用于检查该排序范围的特定部分的算法。在许多情况下，你只对排序范围的某个特定部分感兴趣，例如：

如果你想计算一个范围的中位数 ($\text{median}$)，你需要排序范围中间的值。
如果你想创建一个适用于某个人口群体平均身高 $80\%$ 的人体扫描仪，你需要排序范围中的两个值：一个位于距离最高者 $10\%$ 的值，另一个位于距离最矮者 $10\%$ 的值。

下图说明了 std::nth_element 和 std::partial_sort 与完全排序的范围相比，如何处理一个范围：

下表显示了它们的算法复杂度；请注意 $m$ 表示被完全排序的子范围的大小：

用例

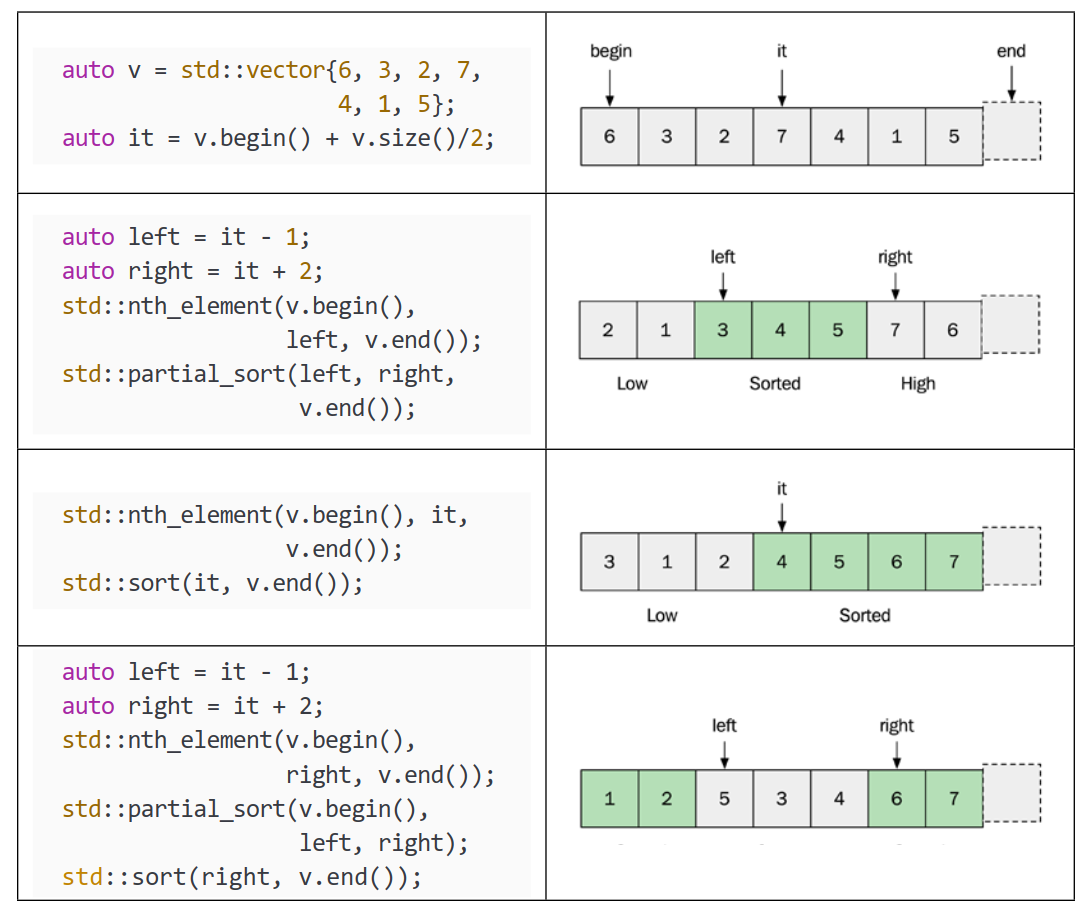
既然你对 std::nth_element() 和 std::partial_sort() 有了深入了解，让我们看看如何结合它们来检查范围的某些部分，就像整个范围已排序一样：

如你所见，通过结合使用 std::sort()、std::nth_element() 和 std::partial_sort()，在并非绝对需要时有很多方法可以避免对整个范围进行排序。这是提高性能的有效方法。

这是对“性能评估与最佳实践”部分的翻译和格式化，保留了代码和图表：

性能评估

让我们看看 std::nth_element() 和 std::partial_sort() 与 std::sort() 相比，性能表现如何。我们使用了一个包含 $10,000,000$ 个随机整数元素的 std::vector 进行了测量：

最佳实践：使用标准算法优于裸循环

很容易忘记复杂的算法可以通过组合标准库中的算法来实现。这可能是因为一种旧习惯，即试图手工解决问题，并立即开始手工编写 $\text{for}$ 循环，采用命令式 ($\text{imperative}$) 方法来解决问题。如果这对你来说很熟悉，我的建议是充分了解标准算法，以便将它们视为首选。

我提倡使用标准库算法而不是裸 $\text{for}$ 循环，原因如下：

标准算法提供性能。即使标准库中的某些算法看起来微不足道，但它们通常以乍一看并不明显的方式进行了最优设计。
标准算法提供安全性。即使是简单的算法也可能存在边界情况 ($\text{corner cases}$)，这些情况很容易被忽略。
标准算法是面向未来的。如果你希望在稍后阶段利用 $\text{SIMD}$ 扩展、并行化甚至 $\text{GPU}$（参见第 $14$ 章《并行算法》），给定的算法可以被更合适的算法替换。
标准算法有详尽的文档。

此外，通过使用算法而不是 $\text{for}$ 循环，每个操作的意图都通过算法的名称清晰地表明。如果你使用标准算法作为构建块，代码的读者无需检查裸 $\text{for}$ 循环内部的细节来确定你的代码做了什么。

一旦你养成了以算法方式思考的习惯，你就会意识到许多 $\text{for}$ 循环通常只是少数简单算法的变体，例如 std::transform()、std::any_of()、std::copy_if() 和 std::find()。

使用算法还会使代码更简洁。你通常可以在没有嵌套代码块的情况下实现函数，同时避免可变变量。这将在下面的示例中得到证明。

示例 1: 可读性问题和可变变量

我们的第一个示例来自一个真实世界的代码库，尽管变量名已被伪装。由于它只是一个片段，你不必理解代码的逻辑。这里的示例只是为了向你展示与嵌套 $\text{for}$ 循环相比，使用算法时复杂度如何降低。

原始版本如下所示：

// Original version using a for-loop
auto conflicting = false;
for (const auto& info : infos) {
    if (info.params() == output.params()) {
        if (varies(info.flags())) {
            conflicting = true;
            break;
        }
    }
    else {
        conflicting = true;
        break;
    }
}

在 $\text{for}$ 循环版本中，很难理解 conflicting 何时或为何被设置为 true，而在以下算法版本中，你可以本能地看出如果 info 满足某个谓词 ($\text{predicate}$)，就会发生冲突。此外，标准算法版本不使用可变变量，并且可以使用一个简短的 $\text{lambda}$ 和 any_of() 组合编写。它是这样的：

// Version using standard algorithms
const auto in_conflict = [&](const auto& info) {
    return info.params() != output.params() || varies(info.flags());
};
const auto conflicting = std::ranges::any_of(infos, in_conflict);

尽管可能有些夸大其词，但想象一下，如果我们要跟踪一个 $\text{bug}$ 或对其进行并行化，使用 $\text{lambda}$ 和 any_of() 的标准算法版本会更容易理解和推断。

示例 2: 不幸的异常和性能问题

为了进一步说明使用算法而不是 $\text{for}$ 循环的重要性，我想展示一些你在使用手工编写的 $\text{for}$ 循环而不是标准算法时可能遇到的不那么明显的问题。

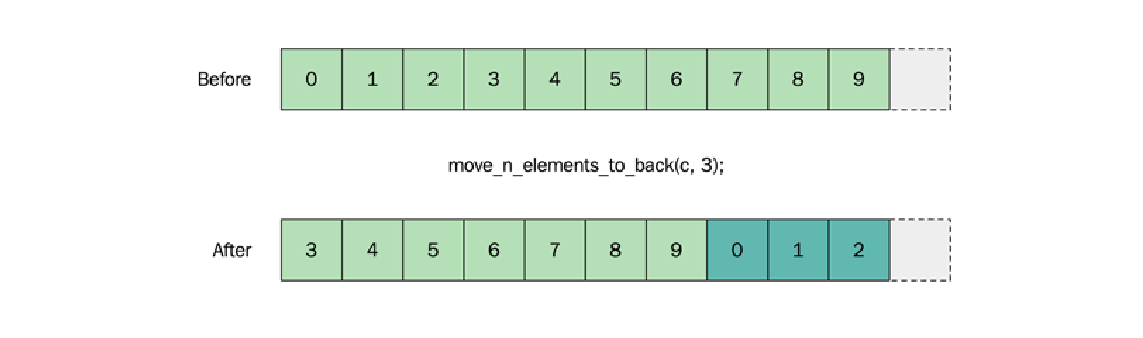
假设我们需要一个函数，它将容器中前 $n$ 个元素从前面移动到后面，像这样：

方法 1: 使用传统的for循环

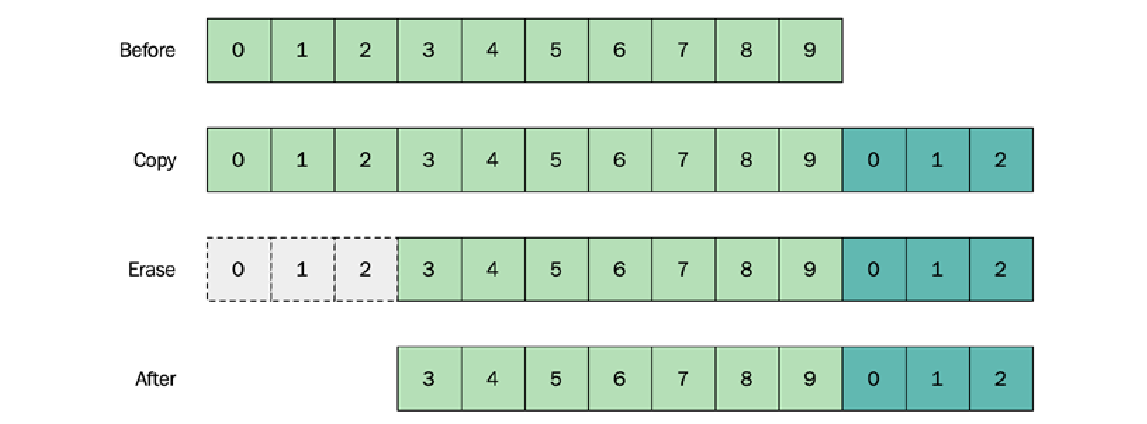
一个幼稚的方法是，在迭代前 $n$ 个元素时，将其复制到末尾，然后删除前 $n$ 个元素：

以下是相应的实现：

template <typename Container>
auto move_n_elements_to_back(Container& c, std::size_t n) {
    // Copy the first n elements to the end of the container
    for (auto it = c.begin(); it != std::next(c.begin(), n); ++it) {
        c.emplace_back(std::move(*it));
    }
    // Erase the copied elements from front of container
    c.erase(c.begin(), std::next(c.begin(), n));
}

乍一看，它似乎是合理的，但仔细检查会发现一个严重的问题：如果容器在迭代过程中由于 emplace_back() 而重新分配内存，迭代器 it 将不再有效。当算法试图访问一个无效迭代器时，算法将进入未定义行为 ($\text{undefined behavior}$)，最好的情况是程序崩溃。

方法 2: 安全的for循环

由于未定义行为是一个明显的问题，我们必须重写算法。我们仍然使用手工编写的 $\text{for}$ 循环，但我们将利用索引而不是迭代器：

template <typename Container>
auto move_n_elements_to_back(Container& c, std::size_t n) {
    for (size_t i = 0; i < n; ++i) {
        auto value = *std::next(c.begin(), i);
        c.emplace_back(std::move(value));
    }
    c.erase(c.begin(), std::next(c.begin(), n));
}

该解决方案可行；它不再崩溃了。但现在，它有一个微妙的性能问题。该算法在 std::list 上的速度明显慢于 std::vector。

原因是：在 std::list::iterator 上使用 std::next(it, n) 是 $O(n)$ 的，而在 std::vector::iterator 上是 $O(1)$ 的。由于 std::next(it, n) 在 $\text{for}$ 循环的每一步都被调用，因此该算法在 std::list 等容器上的时间复杂度将是 $O(n^2)$。除了这个性能限制之外，上述代码还有以下限制：

由于 emplace_back()，它不适用于 std::array 等静态大小的容器。
它可能会抛出异常，因为 emplace_back() 可能会分配内存并失败（尽管这可能很少见）。

方法 3: 查找并使用合适的标准库算法

当我们达到这个阶段时，我们应该浏览标准库，看看它是否包含一个合适的算法可以作为构建块使用。凑巧的是，<algorithm> 头文件提供了一个名为 std::rotate() 的算法，它正是我们想要的，同时避免了前面提到的所有缺点。以下是我们使用 std::rotate() 算法的最终版本：

template <typename Container>
auto move_n_elements_to_back(Container& c, std::size_t n) {
    auto new_begin = std::next(c.begin(), n);
    std::rotate(c.begin(), new_begin, c.end());
}

让我们看看使用 std::rotate() 的优势：

该算法不会抛出异常，因为它不分配内存（尽管所包含的对象可能会抛出异常）。
它适用于大小不能更改的容器，例如 std::array。
性能是 $O(n)$，无论它操作的容器是什么。
它的实现很可能针对特定的硬件进行了优化。

你可能会觉得这种 $\text{for}$ 循环和标准算法之间的比较不公平，因为这个问题还有其他既优雅又高效的解决方案。尽管如此，在现实世界中，当标准库中有算法正在等待解决你的问题时，看到像你刚才看到的那些实现并不罕见。

这是对文本的翻译和格式化，保留了代码和表格：

示例 3: 利用标准库优化

这最后一个示例强调了一个事实：即使看起来非常简单的算法，也可能包含你不会考虑到的优化。例如，让我们看看 std::find()。乍一看，它似乎无法进一步优化了。下面是 std::find() 算法的一种可能实现：

template <typename It, typename Value>
auto find_slow(It first, It last, const Value& value) {
    for (auto it = first; it != last; ++it)
        if (*it == value)
            return it;
    return last;
}

然而，查看 $\text{GNU libstdc}++$ 的实现，当与随机访问迭代器 ($\text{random_access_iterator}$，即 std::vector、std::string、std::deque 和 std::array) 一起使用时，$\text{libc}++$ 的实现者将主循环展开 ($\text{unrolled}$) 为一次四个循环块，导致比较 (it != last) 的执行次数减少了四分之三。

这是从 $\text{libstdc}++$ 库中提取的 std::find() 优化版本：

template <typename It, typename Value>
auto find_fast(It first, It last, const Value& value) {
    // Main loop unrolled into chunks of four
    auto num_trips = (last - first) / 4;
    for (auto trip_count = num_trips; trip_count > 0; --trip_count) {
        if (*first == value) {return first;} ++first;
        if (*first == value) {return first;} ++first;
        if (*first == value) {return first;} ++first;
        if (*first == value) {return first;} ++first;
    }
    // Handle the remaining elements
    switch (last - first) {
        case 3: if (*first == value) {return first;} ++first;
        case 2: if (*first == value) {return first;} ++first;
        case 1: if (*first == value) {return first;} ++first;
        case 0:
        default: return last;
    }
}

请注意，实际利用这种循环展开优化的是 std::find_if()，而不是 std::find()。但 std::find() 是使用 std::find_if() 实现的。

除了 std::find() 之外，$\text{libstdc}++$ 中的大量算法都是使用 std::find_if() 实现的，例如 any_of()、all_of()、none_of()、find_if_not()、search()、is_partitioned()、remove_if() 和 is_permutation()，这意味着所有这些算法都比手工编写的 $\text{for}$ 循环稍微快一些。

而我说的“稍微”快一些，是真的稍微；加速大约是 $1.07$ 倍，如下表所示：

然而，即使收益几乎可以忽略不计，通过使用标准算法，你可以免费获得它。

“与零比较”优化 ($\text{“Compare with zero” optimization}$)

除了循环展开之外，一个非常微妙的优化是 trip_count 向后迭代，以便与零进行比较而不是一个值。在某些 $\text{CPU}$ 上，与零进行比较比与其他任何值进行比较稍微快一些，因为它使用另一条汇编指令（在 $\text{x86}$ 平台上，它使用 test 而不是 cmp）。

下表显示了使用 $\text{gcc 9.2}$ 时的汇编输出差异：

尽管这种优化在标准库实现中受到鼓励，但不要重新排列你手工编写的循环以从这种优化中受益，除非它是一个（非常）热点 ($\text{hot spot}$)。这样做会严重降低代码的可读性；应该让算法来处理这些类型的优化。

这是我关于使用算法而不是 $\text{for}$ 循环的建议的结尾。如果你还没有使用标准算法，我希望我已经为你提供了一些论据来说服你尝试一下。现在我们将转向我关于有效使用算法的最后一个建议。

避免容器复制

我们将在本章结束时强调一个在使用算法库中的多个算法时遇到的常见问题：很难避免底层容器不必要的复制。

一个例子将澄清我的意思。假设我们有一个 Student 类来表示某个年份、具有特定考试分数和姓名的学生，像这样：

struct Student {
    int year_{};
    int score_{};
    std::string name_{};
    // ...
};

如果我们要在一个大型的学生集合中找到二年级中分数最高的学生，我们可能会对 score_ 使用 max_element()，但由于我们只想考虑二年级的学生，这就变得棘手了。

本质上，我们希望将 copy_if() 和 max_element() 组合起来构成一个新算法，但算法库无法实现算法的组合 ($\text{composing algorithms}$)。相反，我们必须将所有二年级的学生复制到一个新容器中，然后迭代新容器以找到最高分数：

auto get_max_score(const std::vector<Student>& students, int year) {
    auto by_year = [=](const auto& s) { return s.year_ == year; };

    // 为了按年份进行过滤，学生列表需要被复制
    auto v = std::vector<Student>{};
    std::ranges::copy_if(students, std::back_inserter(v), by_year);

    // 在新的容器 v 上找到分数最高的元素
    auto it = std::ranges::max_element(v, std::less{}, &Student::score_);
    
    return it != v.end() ? it->score_ : 0;
}

这就是一个很容易诱惑你从头开始编写自定义算法而不再利用标准算法的地方。但正如你将在下一章中看到的，对于这样的任务，没有必要放弃标准库。组合算法的能力是使用 $\text{Ranges}$ 库的关键动机之一，我们接下来将介绍它。

总结

在本章中，你学习了如何使用算法库中的基本概念、将它们用作构建块而非手写 $\text{for}$ 循环的优势，以及为什么使用标准算法库有利于在后期优化你的代码。我们还讨论了标准算法的保证和权衡，这意味着从现在起你可以自信地使用它们。

通过利用算法的优势而不是手动 $\text{for}$ 循环，你的代码库为本书后续章节将讨论的并行化技术做好了充分准备。标准算法缺少的一个关键特性是组合算法的可能性，这在我们试图避免不必要的容器复制时得到了强调。在下一章中，你将学习如何使用 C++ $\text{Ranges}$ 库中的视图 ($\text{views}$) 来克服标准算法的这一限制。