本文介绍DeepFM模型的原理、代码和用于CTR预估的示例,同时也会介绍相关的FM模型。
目录
问题简介
点击率(Click Through Rate, CTR)预估是程序化广告里的一个最基本而又最重要的问题。比如在竞价广告里,排序的依据就是$ctr \times bid$。通过选择$ctr \times bid$最大的广告就能最大化平台的eCPM。从机器学习的角度来说这是一个普通的回归问题,但是它的特殊性在于训练数据只有0/1的值——因为我们没有办法给同一个用户展示同一个广告1万次,然后统计点击的次数来估计真实的点击率。另外有人也许会有这样的看法:对于某一个特定的曝光,某个用户是否点击某个广告是确定的,第一次不点,第二次也不会点,因此点击率是一个0/1的固定值而不是一个0-1之间的概率值。这个说法有一些道理,原因是第二次实验和第一次使用不是独立同分布的。“真正”的做法是第二次做实验前要擦除用户第一次实验的记忆,然后在一模一样的场景(时间、地点……)下做N次独立实验。但是我们也可能从另外一个角度理解点击率:有很多用户比较类似,比如类似的用户有1万个,在相同的条件下他们点击的次数和除以1万可以看成点击率。如果从“上帝”视角来看,如果能预知未来,那么确实可以知道每一个用户是否会点击某个广告,然后能够准确的估计这一次是否会点击。但是实际由于我们信息的缺失和计算能力的限制,我们不可能准确的提前预估。如果在训练数据上精确的预估了0/1这样的点击率,那么更可能是过拟合了。
另外有一点就是我们采集的数据是有偏的。比如在CPC的竞价广告中,我们收集到的都是竞价获胜的广告,而竞价又是受CTR的影响,因此会产生放大作用——CTR估计的越低,则竞价获胜的可能性越低,曝光的次数也越少,从而点击率估计的也有偏。
评价指标
评价CTR的最常见指标是logloss和AUC。logloss就是计算真实分布和预测分布的交叉熵,计算公式为:
\[logloss = \sum_{i=1}^N [- y_ilog\; ctr(x_i) - (1-y_i) log (1-ctr(x_i))]\]其中$y_i$是真实的值(0/1),而$ctr(x_i)$是模型预测的点击率。
下面我们来介绍AUC,这里主要参考了这篇文章。在介绍AUC之前,我们先介绍一下二分类的混淆矩阵。下表是每个测试数据的真实值和模型的预测值:
| 真实值 | 模型1预测 | 模型2预测 |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
| 1 | 1 | 0 |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
下表是两个模型的混淆矩阵:
| 模型1 | 真实值为1 | 真实值为0 |
|---|---|---|
| 预测为1 | 3(TP) | 2(FP) |
| 预测为0 | 1(FN) | 1(TN) |
| 模型2 | 真实值为1 | 真实值为0 |
|---|---|---|
| 预测为1 | 2(TP) | 0(FP) |
| 预测为0 | 2(FN) | 3(TN) |
读者可能对于TP、TN、FP和FN这些缩写搞不清楚,但是其实并不复杂。第一个T表示预测和真实值是否一样,如果是则为T(true)否则为F(false);第二个字母N(Negative)表示模型预测为不点击而P(Positive)表示预测为点击。因此TP指的是真实为1(点击)并且预测也是1(点击),TN指的是真实为0(不点击)而预测也为0(不点击),FP表示预测错误,预测为点击(P)因此推理出真实为不点击,而FN也是预测错误,把点击预测为不点击。
所以有两种预测正确的情况:TP和TN,分别是正确预测点击和不点击的样例。而预测错误也有两种情况:FN和FP,分别是把点击的预测为不点击、把不点击的预测为点击。下面是一些常见的细化指标,FPR和TPR,分别表示预测为Positive(点击)的错误率和正确率,具体计算公式为:
\[FPR(FP Rate)=\frac{FP}{FP+TN} \\ TPR(TP Rate)=\frac{TP}{TP+FN} \\\]显然FPR(错误)我们希望越小越好,而TPR越大越好。
如果要”记住”这个公式很简单:FPR的分子肯定是FP,分母肯定也要有FP,然后分母再加上TN(字母和FP完全不重合);TPR也是类似。
另外FPR和TPR这两个指标是正相关的,比如为了提升FPR,我们可以把阈值调的很低,则模型把没有把握的样本尽量分类成1,因此分类成0的都非常有把握,因此FP会很少,从而FPR(可能)会减少。但是阈值低会让模型尽量把True识别成Positive,所以TPR也会增加。我们的目标是希望FPR尽量小而TPR尽量大,但是我们的目标很难只通过调整阈值达到,因为FPR小TPR也会小,FPR大TPR也会大。那么怎么达到目标呢?当然是优化模型的预测能力,而不是靠调阈值这种旁门左道。
当阈值为1时,所有的样本都预测成Negative,也就是FP=TP=0,因此FPR和TPR都为0。而当阈值为0时,所有的样本都预测成Positive,因此TN=PN=0,因此$FPR=\frac{FP}{FP+TN}=1$,类似的TPR也是1。
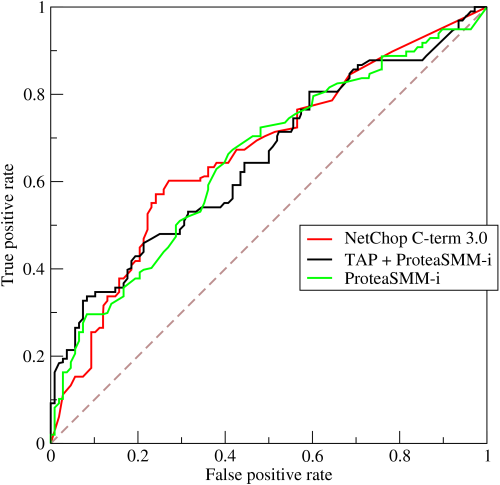
如果我们把阈值从1调整到0,FPR也会从0增加到1,TPR也会从0变到1,以FPR做横坐标、TPR做纵坐标,则可以画出一条ROC(receiver operating characteristic)曲线。ROC翻译成中文就是受试者工作特征,这个名字听起来有点奇怪。ROC曲线通常是直线y=x之上的一个上凸函数,并且经过(0,0)和(1,1)点,如下图所示:
AUC的英文全称是Area Under Curve,意思是曲线(Curve)下的面积,曲线指的就是ROC曲线。因此AUC更加准确的说法应该是AU-ROC(Area Under ROC Curve),也就是ROC曲线下的面积。显然ROC曲线越往上凸,则AUC越大,那么在曲线的中间我们可以找到FPR尽可能小而TPR尽可能大的点(阈值)。
另外一个值得注意的点:AUC评价的是模型的排序能力而不是ctr预估的偏差。举个例子,假设有3个测试样本,真实分类是[1,1,0,1],而模型1预测的ctr分别是[0.9, 0.7, 0.65, 0.55],而模型2预测的ctr是[0.8, 0.7, 0.65, 0.55]。如果从logloss来说显然是第一个模型要好,因为后面3个结果一样但是第一个0.9跟真实的1更加接近。但是他们的AUC是一样的,我们可以简单的手动计算一下:
| 阈值 | FPR | TPR |
|---|---|---|
| 1 | 0 | 0 |
| 0.899 | 0 | 0.33(TP=1,FN=2) |
| 0.699 | 0 | 0.66(TP=2,FN=1) |
| 0.649 | 1(FP=1,TN=0) | 0.66(TP=2,FN=1) |
| 0 | 1 | 1 |
| 阈值 | FPR | TPR |
|---|---|---|
| 1 | 0 | 0 |
| 0.799 | 0 | 0.33(TP=1,FN=2) |
| 0.699 | 0 | 0.66(TP=2,FN=1) |
| 0.649 | 1(FP=1,TN=0) | 0.66(TP=2,FN=1) |
| 0 | 1 | 1 |
数据特点
CTR数据的特征一般可以分为三大类:用户的特征、广告的特征和上下文特征。用户的特征包括用户性别、年龄、职业、教育水平等等;创意的特征包括广告的行业(旅游、电商,……)、标签等等;上下文的特征包括广告的位置、用户使用的设备、浏览器、时间、地点等。这些特征有一部分是连续的值,比如年龄;而更多的特征是Category(类别)的特征,比如性别为两类的男女,职业可以是销售、产品经理、……。对于Category的特征,我们通常使用one-hot的编码把它变成一个高纬的稀疏向量,比如职业细分的话可能几十上百种,地域按照城市分可能成千上万。另外为了提高模型的泛化能力我们可能把连续的特征进行离散化,比如把年龄分为18岁以下、18-29、30-40,……。这样的每一个输入特征向量可能是非常高维的一个稀疏的向量。
FM(Factorization Machines)
在FM模型之前,CTR预估最常用的模型是SVM和LR(包括用GBDT给它们提取非线性特征)。SVM和LR都是线性的模型(SVM理论上可以引入核函数从而引入非线性,但是由于非常高维的稀疏特征向量使得它很容易过拟合,因此实际很少用),但是实际的这些特征是有相关性的。比如根据论文DeepFM: A Factorization-Machine based Neural Network for CTR Prediction的调研,在主流的app应用市场里,在吃饭的时间点食谱类app的下载量明显会比平时更大,因此app的类别和时间会存在二阶的关系。另外一个例子是年轻男性更喜欢射击类游戏,这是年龄、性别和游戏类别的三阶关系。因此怎么建模二阶、三阶甚至更高阶的非线性的关系是预估能够更加准确的关键点。
下文参考了深入FFM原理与实践。
我们可以直接建模二阶关系:
\[y(\mathbf{x}) = w_0+ \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n w_{ij} x_i x_j\]其中,n是特征向量的维度,$x_i$是第i维特征,$w_0$、$w_i$、$w_{ij}$是模型参数。这种方法的问题是二阶关系的参数个数是$\frac{n(n-1)}{2}$,这样会导致模型的参数很多,另外因为特征向量非常稀疏,二次项参数的训练是很困难的。其原因是,每个参数 $w_{ij}$的训练需要大量$x_i$和$x_j$都非零的样本;由于样本数据本来就比较稀疏,满足“$x_i$和$x_j$都非零”的样本将会非常少。训练样本的不足,很容易导致参数 $w_{ij}$ 不准确,最终将严重影响模型的性能。
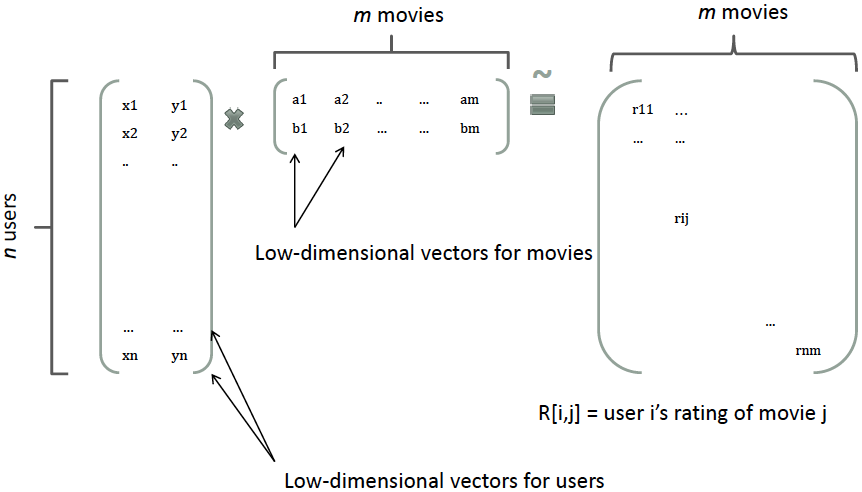
那么,如何解决二次项参数的训练问题呢?矩阵分解提供了一种解决思路。根据《Factorization Machines的一个talk》在model-based的协同过滤中,一个rating矩阵可以分解为user矩阵和item矩阵,每个user和item都可以采用一个隐向量表示。比如在下图中的例子中,我们把每个user表示成一个二维向量,同时把每个item表示成一个二维向量,两个向量的点积就是矩阵中user对item的打分。
类似地,所有二次项参数 $w_{ij}$ 可以组成一个对称阵$\mathbf{W}$(为了方便说明FM的由来,对角元素可以设置为正实数),那么这个矩阵就可以分解为 $\mathbf{W} = \mathbf{V}^T \mathbf{V}$,$\mathbf{V}$ 的第j列便是第j维特征的隐向量。换句话说,每个参数 $w_{ij} = \langle \mathbf{v}_i, \mathbf{v}_j \rangle$,这就是FM模型的核心思想。因此,FM的模型方程为(本文不讨论FM的高阶形式)
\[y(\mathbf{x}) = w_0+ \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j\]其中,$v_i$ 是第 i 维特征的隐向量,$\langle\cdot, \cdot\rangle$ 代表向量点积。隐向量的长度为 $k(k«n)$,包含 k 个描述特征的因子。根据公式(2),二次项的参数数量减少为 $kn$个,远少于多项式模型的参数数量。另外,参数因子化使得 $x_hx_i$ 的参数和 $x_ix_j$ 的参数不再是相互独立的,因此我们可以在样本稀疏的情况下相对合理地估计FM的二次项参数。具体来说,$x_hx_i$ 和 $x_ix_j$ 的系数分别为 \(\langle \mathbf{v}_h, \mathbf{v}_i \rangle\) 和 \(\langle \mathbf{v}_i, \mathbf{v}_j \rangle\),它们之间有共同项 $v_i$。也就是说,所有包含“$x_i$ 的非零组合特征”(存在某个 $j\neq i$,使得 $x_i x_j \neq 0$)的样本都可以用来学习隐向量 \(\mathbf{v}_i\),这很大程度上避免了数据稀疏性造成的影响。而在多项式模型中,$w_{hi}$ 和 $w_{ij}$ 是相互独立的。
直观上看,FM的复杂度是 $O(kn^2)$。但是,通过下式,FM的二次项可以化简,其复杂度可以优化到 $O(kn)$。由此可见,FM可以在线性时间对新样本作出预测。
\[\sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j = \frac{1}{2} \sum_{f=1}^k \left(\left( \sum_{i=1}^n v_{i, f} x_i \right)^2 - \sum_{i=1}^n v_{i, f}^2 x_i^2 \right)\]下面是上式的推导过程,不感兴趣的读者可以跳过。
\[\begin{split} & \sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j \\ = & \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j - \frac{1}{2} \sum_{i=1}^n \langle \mathbf{v}_i, \mathbf{v}_i \rangle x_i x_i \\ = & \frac{1}{2} \left( \sum_{i=1}^n \sum_{j=1}^n \sum_{f=1}^k v_{if}v_{jf} x_i x_j - \sum_{i=1}^n \sum_{f=1}^k v_{if}v_{if} x_i x_i \right) \\ = & \frac{1}{2} \sum_{f=1}^k \left( \left(\sum_{i=1}^n v_{if}x_i \right) \left( \sum_{j=1}^n v_{jf}x_j \right) -\sum_{i=1}^n v_{i,f}^2x_i^2 \right) \\ = & \frac{1}{2} \sum_{f=1}^k \left( \left(\sum_{i=1}^n v_{if}x_i \right)^2 -\sum_{i=1}^n v_{i,f}^2x_i^2\right) \end{split}\]训练的时候可以使用随机梯度下降算法,梯度计算公式为:
\[\frac{\partial}{\partial\theta} \hat{y} (\mathbf{x}) = \begin{cases} 1, & \text{if }\theta \text{ is }w_0 \\ x_i, & \text{if } \theta \text{ is } x_i \\ x_i \sum_{j=1}^nv_{j,f}x_j-v_{i,f}x_i^2 , & \text{if } \theta \text{ is } v_{i,f} \end{cases}\]其中,$v_{j,f}$ 是隐向量 \(\mathbf{v}_j\) 的第 $f$ 个元素。由于 $\sum_{j=1}^n v_{j, f} x_j$ 只与 f 有关,而与 i 无关,在每次迭代过程中,只需计算一次所有 f 的 $\sum_{j=1}^n v_{j, f} x_j$,就能够方便地得到所有 $v_{i,f}$ 的梯度。显然,计算所有 f 的$\sum_{j=1}^n v_{j, f} x_j$的复杂度是 $O(kn)$;已知 $\sum_{j=1}^n v_{j, f} x_j$ 时,计算每个参数梯度的复杂度是 $O(1)$;得到梯度后,更新每个参数的复杂度是 $O(1)$;模型参数一共有 $nk+n+1$ 个。因此,FM参数训练的复杂度也是 $O(kn)$。
DeepFM
概述
像LR/SVM这样的模型无法建模非线性的特征交互(interaction),我们只能人工组特征的交叉或者组合,比如通过数据分析发现时间和食谱类的app存在比较强的关联关系,然后把这个特征加到线性模型里去。这种方法的确定是需要人工做特征工程,成本很高,而且很多复杂的特征交互很难发现,就像啤酒和纸尿布这样的关系,我们只能做事后诸葛亮这样的分析:啊哈,确实很有道理,但是不做大量的数据分析想提前发现就比较困难。
FM通过给每个特征引入一个低维稠密的隐向量来减少二阶特征交互的参数个数,同时实现信息共享,使得在非常稀疏的特征向量上的学习更加容易泛化。理论上FM可以建模二阶以上的特征交互,但是由于计算量急剧增加,实际一般只用二阶的模型。
而(深度)神经网络的优势就是可以多层的网络结构更好的进行特征表示,从而学习高阶的非线性关系。DeepFM的思想就是结合FM在一阶和二阶特征的简洁高效和深度学习在高阶特征交互上的优势,同时通过共享FM和DNN的Embedding来减少参数量和共享信息,从而得到更好的模型。
方法简介
假设训练数据的个数为n,每一个训练样本为$(\mathcal{X},y)$,其中$(\mathcal{X}$由m个field组成,而$y \in {0,1}$表示用户是否点击。$(\mathcal{X}$的field可以是category的field,比如性别和地域等;也可以是连续的field,比如年龄。总的field个数可能只有几百个,但是如果用one-hot编码展开的话,这个特征向量会非常高维并且稀疏。我们把每一个$x_i$记为$x_i=[x_{field_1},x_{field_2},…,x_{field_m}]$,其中每一个$x_{field_i}$是其向量表示(连续的field就是1维的,而Category的field则用one-hot展开)。
DeepFM包括FM和DNN两个部分,最终的预测由两部分输出的相加得到:
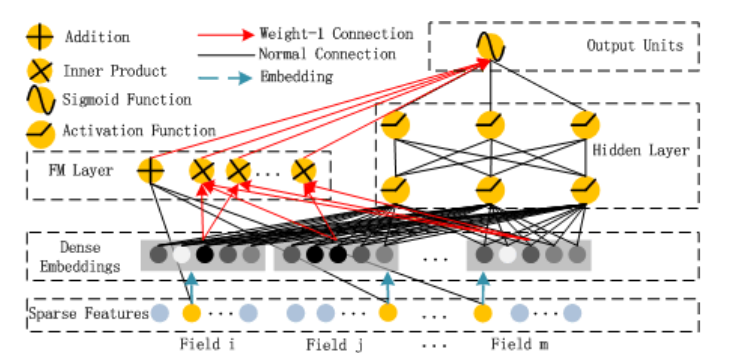
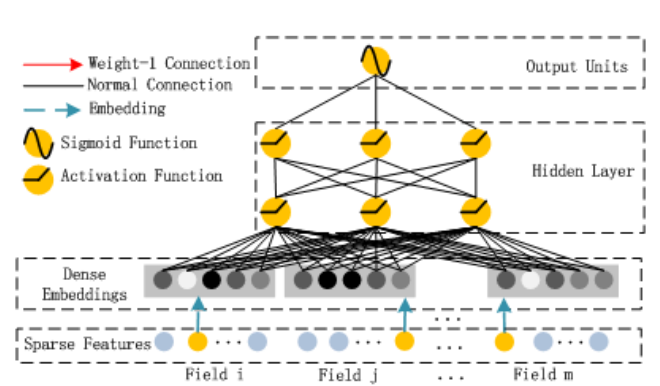
\[\hat{y}=sigmoid(y_{FM}+y_{DNN})\]其中$y_{FM}$是FM模型的输出,而$y_{DNN}$是DNN的输出。模型的结构如下图所示,它包含FM和DNN两个组件。
下面我们分别来看这两个组件。
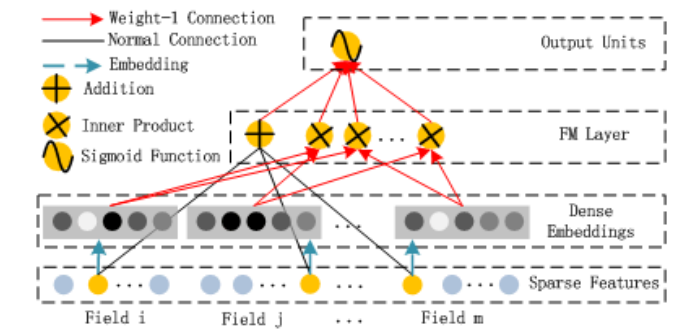
上图是FM组件,它实现的就是:
\[y_{FM}=\langle w, x \rangle + \sum_{i=1}^d \sum_{j=i+1}^d \langle V_i, V_j \rangle x_i \cdot x_j\]这个公式非常简单,但是如果用代码实现的话有一些技巧,比如怎么不用for循环(在Tensorflow这样的框架里循环是很麻烦而且很低效的)。后面的代码分析会介绍怎么用Embedding和矩阵运算不用for循环实现上面的计算。
上图就是DNN组件,也非常简单,不过我们需要记得它的Embedding要和前面的FM共享,后面的代码部分也会详细介绍怎么实现。对于深度学习不了解的读者可以参考《深度学习理论与实战:基础篇》。
代码实战
数据集
在介绍代码之前我们先准备一下实验的数据,这里使用了学术界常用的Criteo数据集,这是一个展示广告的数据集,有Criteo提供,曾经是Kaggle的一个比赛。Kaggle提供的链接已经失效,读者可以在这里下载。
下载的dac.tar.gz大概4.3G,解压后包含train.txt、test.txt和readme.txt三个文件。其中test.txt没有真实标签,因此不能用于真实的测试。train.txt大概有4500万行,我把这个文件用sample.py随机抽取90%作为训练集ctr-train.txt,剩下的10%作为验证集ctr-dev.txt。这些文件的每一行是一个训练数据,格式为:
$ head -n 1 ctr-train.txt
0 1 1 5 0 1382 4 15 2 181 1 2 2 68fd1e64 80e26c9b fb936136 7b4723c4 25c83c98 7e0ccccf de7995b8 1f89b562 a73ee510 a8cd5504 b2cb9c98 37c9c164 2824a5f6 1adce6ef 8ba8b39a 891b62e7 e5ba7672 f54016b9 21ddcdc9 b1252a9d 07b5194c 3a171ecb c5c50484 e8b83407 9727dd16
其中第1列是真实的标签,0表示没有点击而1表示点击。第2-14列是13个连续的特征,第15-40列是26个Category的特征。
DeepCTR简介
我们后面的实验和代码分析使用开源的DeepCTR,这里首先介绍DeepCTR的基本用法。
根据其文档的说明,DeepCTR是一个易于使用、模块化和可扩展的深度学习CTR模型库,它内置了很多核心的组件从而便于我们自定义模型,它兼容tensorflow 1.4+和2.0+。
除了DeepFM,DeepCTR还包括更多更新的模型,本篇文章只介绍DeepFM,下面是完整的模型列表:
DeepCTR快速上手
安装
最简单的方法是使用pip安装,CPU的版本使用如下的命令安装:
pip install deepctr[cpu]
GPU版本的安装方法为:
pip install deepctr[gpu]
四步实现训练
第一步:导入模型
import pandas as pd
from sklearn.preprocessing import LabelEncoder, MinMaxScaler
from sklearn.model_selection import train_test_split
from deepctr.models import DeepFM
from deepctr.inputs import SparseFeat, DenseFeat,get_feature_names
data = pd.read_csv('./criteo_sample.txt')
sparse_features = ['C' + str(i) for i in range(1, 27)]
dense_features = ['I'+str(i) for i in range(1, 14)]
data[sparse_features] = data[sparse_features].fillna('-1', )
data[dense_features] = data[dense_features].fillna(0,)
target = ['label']
这一步import依赖的模块,第一行使用pandas读取csv文件criteo_sample.txt,这个文件头几行为:
$ head -n 3 /home/lili/data/criteo_sample.txt
label,I1,I2,I3,I4,I5,I6,I7,I8,I9,I10,I11,I12,I13,C1,C2,C3,C4,C5,C6,C7,C8,C9,C10,C11,C12,C13,C14,C15,C16,C17,C18,C19,C20,C21,C22,C23,C24,C25,C26
0,,3,260.0,,17668.0,,,33.0,,,,0.0,,05db9164,08d6d899,9143c832,f56b7dd5,25c83c98,7e0ccccf,df5c2d18,0b153874,a73ee510,8f48ce11,a7b606c4,ae1bb660,eae197fd,b28479f6,bfef54b3,bad5ee18,e5ba7672,87c6f83c,,,0429f84b,,3a171ecb,c0d61a5c,,
0,,-1,19.0,35.0,30251.0,247.0,1.0,35.0,160.0,,1.0,,35.0,68fd1e64,04e09220,95e13fd4,a1e6a194,25c83c98,fe6b92e5,f819e175,062b5529,a73ee510,ab9456b4,6153cf57,8882c6cd,769a1844,b28479f6,69f825dd,23056e4f,d4bb7bd8,6fc84bfb,,,5155d8a3,,be7c41b4,ded4aac9,,
这是一个带表头的csv文件,通过pandas读取成列(features),其中C1-C26是Category的特征(sparse_features),而I1-I13是连续的特征(dense_features)。因为有缺失的值,我们把Category的缺失值设置为”-1”,而把连续的缺失值设置为0。
第二步:简单预处理
对于Category的特征,我们通常有两种方法把它变成一个数字:Label编码和hash编码。
Label编码就是把每一个Category变成0 ~ len(#unique) - 1之间的一个整数:
for feat in sparse_features:
lbe = LabelEncoder()
data[feat] = lbe.fit_transform(data[feat])
使用sklearn的LabelEncoder可以实现把Label编码成数字。LabelEncoder不能处理训练数据中没有出现过的Label,如果测试数据包含训练数据中没有的Label,则会出现问题。一种解决办法是引入特殊的”unknown”,但是由于没有训练数据,它的Embedding也是没有意义的。解决办法和NLP的词典类似——统计训练数据的词频,把低频的词都转换成”unknown”,这样一方面可以减小词典的大小,另一方面也可以提高模型的泛化能力(因为如果一个词/Label只出现很少次数,则它学到的特征通常是很不稳定的)。后面我们自己实现LabelEncoder时会看到这个技巧。
fit_transform等价于先调用fit()函数,然后调用transform()函数。fit()函数的作用是使用训练数据来统计一些信息,比如统计Label所有的词典,而transform()对数据进行预处理。
而hash编码是把每一个Category的字符串通过hash函数映射为0~一个固定的范围。它的优点是不用提前知道Category的所有可能值。
for feat in sparse_features:
lbe = HashEncoder()
data[feat] = lbe.transform(data[feat])
使用hash编码不需要fit(这个学习/统计过程),所以直接使用transform函数,另外在后面的训练过程中,需要第3步的SparseFeat或者VarlenSparseFeat的构造函数里设置use_hash=True。
对于连续的特征,我们通常需要把它的范围归一化到[0-1]这间,这样不同特征的权重才比较好学习。我们可以使用sklearn的MinMaxScaler来做这个预处理:
mms = MinMaxScaler(feature_range=(0,1))
data[dense_features] = mms.fit_transform(data[dense_features])
参数feature_range=(0,1)告诉MinMaxScaler我们期望归一化的范围是[0-1]。
第三步:生成feature column
对于稀疏的特征,我们可以使用Embedding把它变成低维稠密的向量,对于离散的特征,我们可以直接输入神经网络。
如果使用LabelEncoder来编码Category特征,则代码为:
sparse_feature_columns = [SparseFeat(feat, vocabulary_size=data[feat].nunique(),embedding_dim=4)
for i,feat in enumerate(sparse_features)]
dense_feature_columns = [DenseFeat(feat, 1)
for feat in dense_features]
SparseFeat就是用来定义Embedding,需要传入的参数除了名字之外,最重要的是vocabulary_size和embedding_dim,vocabulary_size是词典的大小(不同label的个数),而embedding_dim是Embedding后的维度。
连续的特征使用DenseFeat就可以了,我们这里的连续特征都是一维的。
如果使用HashEncoder,则代码为:
sparse_feature_columns = [SparseFeat(feat, vocabulary_size=1e6,embedding_dim=4,use_hash=True)
for i,feat in enumerate(sparse_features)]#The dimension can be set according to data
dense_feature_columns = [DenseFeat(feat, 1)
for feat in dense_features]
使用HashEncoder也是SparseFeat,只不过需要传入use_hash=True。另外vocabulary_size通常要大一些,以避免hash冲突太多(当然是不可能完全避免的,两个词映射为一个id后对于模型来说就不可分了,它的Embedding可能是两个词的平均)。
对于多值(multi-valued)稀疏特征,比如兴趣标签可能是多选,一种方法是变成二值的:是否喜欢汽车、是否喜欢军事、……。那还有一种就是多值的稀疏特征:兴趣=[6,8],6和8可能代表汽车和军事。对于多值的特征,比如上面的例子,我们可以把6和8都Embedding成一个长度为4的向量,那么怎么处理呢?除了RNN这样的模型可以处理变长输入,普通的DNN和CNN都无法处理。一种简单的方法就是把它们Pooling起来,比如加起来求平均或者取最大的。
varlen_feature_columns = [VarLenSparseFeat('genres', maxlen=max_len,vocabulary_size= len(
key2index) + 1,embedding_dim=4, combiner='mean',weight_name=None)]
VarLenSparseFeat就可以定义变长的SparseFeat,除了vocabulary_size和embedding_dim,需要指定最大的长度maxlen和combiner,这个例子的combiner是求平均。我们的Criteo数据集没有这种多值特征,因此不做深入介绍,感兴趣的读者可以参考示例Multi-value Input : Movielens。
接下来就是生成feature column:
dnn_feature_columns = sparse_feature_columns + dense_feature_columns
linear_feature_columns = sparse_feature_columns + dense_feature_columns
feature_names = get_feature_names(linear_feature_columns + dnn_feature_columns)
这里的sparse特征和dense特征都会输入DNN和线性层(二阶的FM组件会复用DNN的Embedding,后面代码分析会介绍)。
第四步:训练模型
train, test = train_test_split(data, test_size=0.2)
train_model_input = {name:train[name].values for name in feature_names}
test_model_input = {name:test[name].values for name in feature_names}
model = DeepFM(linear_feature_columns,dnn_feature_columns,task='binary')
model.compile("adam", "binary_crossentropy",
metrics=['binary_crossentropy'], )
history = model.fit(train_model_input, train[target].values,
batch_size=256, epochs=10, verbose=2, validation_split=0.2, )
pred_ans = model.predict(test_model_input, batch_size=256)
我们首先用sklearn的train_test_split把数据切分成训练集和测试集。然后定义train_model_input,它是一个dict,key是feature的名字,比如”C1”、”I1”,value是这一列的值。
然后用DeepFM类定义一个deepfm模型,需要传入的参数是linear_feature_columns和dnn_feature_columns。还有一个参数task=’binary’表明这是一个二分类的问题。
接下来是Keras的标准流程:compile、fit和predict。
DeepCTR代码分析
DeepFM函数
DeepFM函数构建一个Keras的Model对象,完整代码为:
def DeepFM(linear_feature_columns, dnn_feature_columns, fm_group=[DEFAULT_GROUP_NAME], dnn_hidden_units=(128, 128),
l2_reg_linear=0.00001, l2_reg_embedding=0.00001, l2_reg_dnn=0, init_std=0.0001, seed=1024, dnn_dropout=0,
dnn_activation='relu', dnn_use_bn=False, task='binary'):
构造DeepFM网络结构
:参数 linear_feature_columns: 线性部分使用的所有特征
:参数 dnn_feature_columns: DNN使用的所有特征
:参数 fm_group: list, 特征的分组,我们这里默认所有的特征都在一个组里
:参数 dnn_hidden_units: list, DNN的隐单元个数,默认是(128,128)表示3层的网络,隐单元个数都是128
:参数 l2_reg_linear: float. 线性模型的L2正则化参数
:参数 l2_reg_embedding: float. Embedding向量的L2正则化参数
:参数 l2_reg_dnn: float. DNN的L2正则化参数
:参数 init_std: float, Embedding向量的随机初始化标准差
:参数 seed: integer ,随机数种子
:参数 dnn_dropout: float,在[0,1)范围内,表示DNN的dropout的概率
:参数 dnn_activation: DNN的激活函数
:参数 dnn_use_bn: bool. DNN是否使用BatchNorm
:参数 task: str, ``"binary"``表示二分类的logloss,``"regression"``表示回归的loss
:返回: 一个Keras Model示例
features = build_input_features(
linear_feature_columns + dnn_feature_columns)
inputs_list = list(features.values())
group_embedding_dict, dense_value_list = input_from_feature_columns(features, dnn_feature_columns, l2_reg_embedding,
init_std, seed, support_group=True)
linear_logit = get_linear_logit(features, linear_feature_columns, init_std=init_std, seed=seed, prefix='linear',
l2_reg=l2_reg_linear)
fm_logit = add_func([FM()(concat_func(v, axis=1))
for k, v in group_embedding_dict.items() if k in fm_group])
dnn_input = combined_dnn_input(list(chain.from_iterable(
group_embedding_dict.values())), dense_value_list)
dnn_output = DNN(dnn_hidden_units, dnn_activation, l2_reg_dnn, dnn_dropout,
dnn_use_bn, seed)(dnn_input)
dnn_logit = tf.keras.layers.Dense(
1, use_bias=False, activation=None)(dnn_output)
final_logit = add_func([linear_logit, fm_logit, dnn_logit])
output = PredictionLayer(task)(final_logit)
model = tf.keras.models.Model(inputs=inputs_list, outputs=output)
return model
下面我们来分析其中重要的函数。
build_input_features
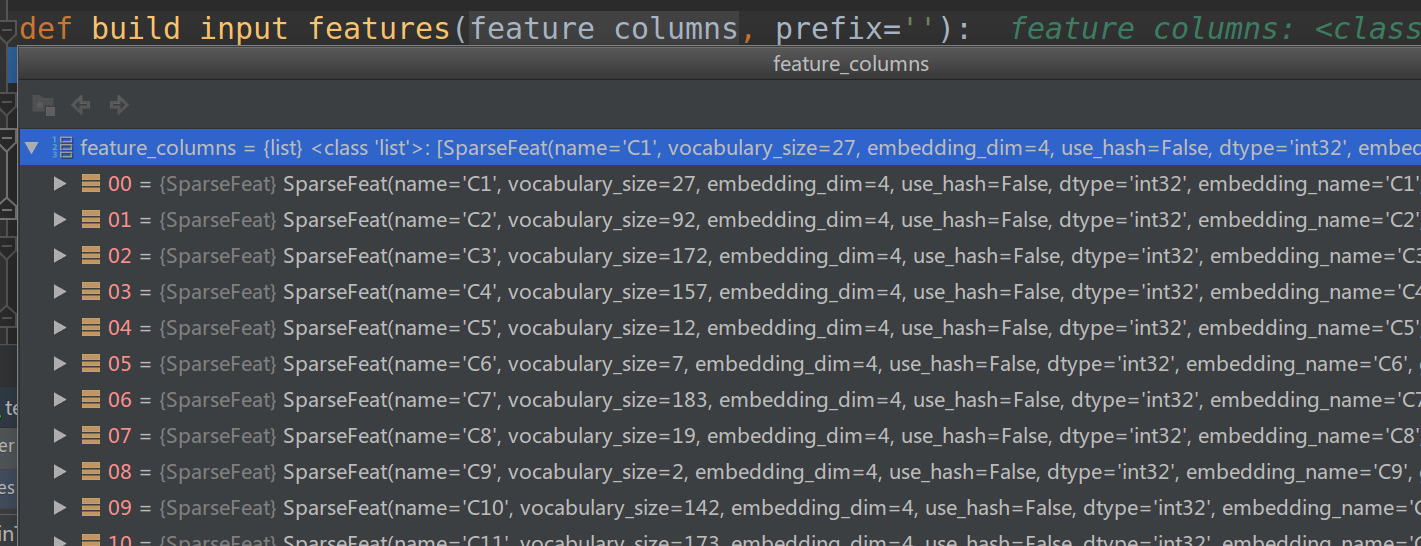
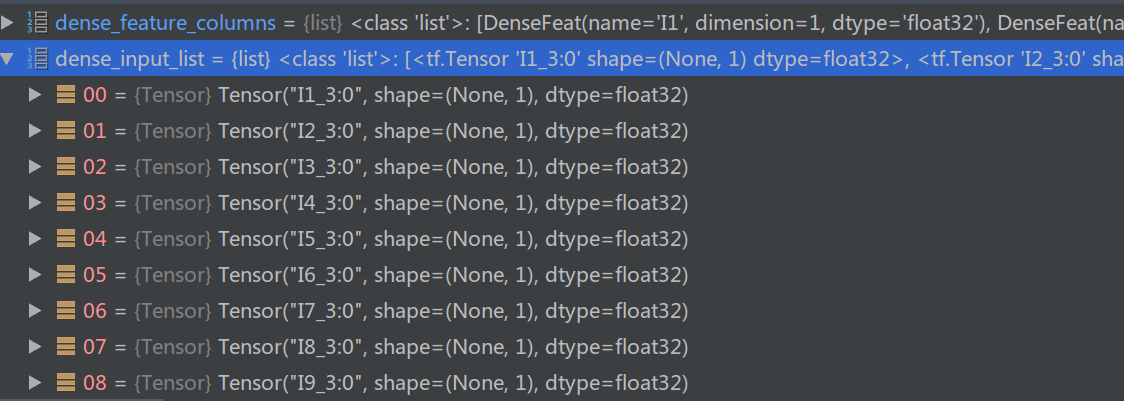
build_input_features函数的输入feature_columns是特征的list,每一个元素是SparseFeat或者DenseFeat。如下图所示
def build_input_features(feature_columns, prefix=''):
input_features = OrderedDict()
for fc in feature_columns:
if isinstance(fc, SparseFeat):
input_features[fc.name] = Input(
shape=(1,), name=prefix + fc.name, dtype=fc.dtype)
elif isinstance(fc, DenseFeat):
input_features[fc.name] = Input(
shape=(fc.dimension,), name=prefix + fc.name, dtype=fc.dtype)
elif isinstance(fc, VarLenSparseFeat):
input_features[fc.name] = Input(shape=(fc.maxlen,), name=prefix + fc.name,
dtype=fc.dtype)
if fc.weight_name is not None:
input_features[fc.weight_name] = Input(shape=(fc.maxlen, 1), name=prefix + fc.weight_name,
dtype="float32")
if fc.length_name is not None:
input_features[fc.length_name] = Input((1,),name=prefix+fc.length_name,dtype='int32')
else:
raise TypeError("Invalid feature column type,got", type(fc))
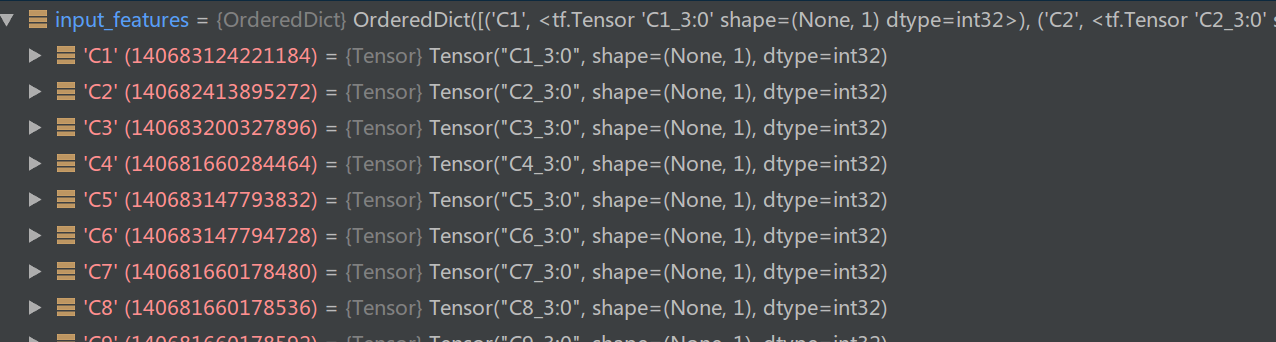
return input_features
返回值是一个OrderedDict,key是feature的名字比如”C1”,value是Keras的Input。对于Category的feature,Input的shape是1,对于Dense的feature,Input是其维度,这里都是1,这些都是Keras模型的输入。因此对于criteo.sample,输入是39个field。这和我们平时些Keras可能有一些不同,平时我通常把输入的所有field都拼接成一个大的向量。但是这里实现的是一个通用的CTR框架,它需要灵活的处理所有的数据集而不只是criteo,因此它把每一个field都作为一个单独的输入。下图是这个函数的输出。
input_from_feature_columns
def input_from_feature_columns(features, feature_columns, l2_reg, init_std, seed, prefix='', seq_mask_zero=True,
support_dense=True, support_group=False):
sparse_feature_columns = list(
filter(lambda x: isinstance(x, SparseFeat), feature_columns)) if feature_columns else []
varlen_sparse_feature_columns = list(
filter(lambda x: isinstance(x, VarLenSparseFeat), feature_columns)) if feature_columns else []
embedding_matrix_dict = create_embedding_matrix(feature_columns, l2_reg, init_std, seed, prefix=prefix,
seq_mask_zero=seq_mask_zero)
group_sparse_embedding_dict = embedding_lookup(embedding_matrix_dict, features, sparse_feature_columns)
dense_value_list = get_dense_input(features, feature_columns)
if not support_dense and len(dense_value_list) > 0:
raise ValueError("DenseFeat is not supported in dnn_feature_columns")
sequence_embed_dict = varlen_embedding_lookup(embedding_matrix_dict, features, varlen_sparse_feature_columns)
group_varlen_sparse_embedding_dict = get_varlen_pooling_list(sequence_embed_dict, features,
varlen_sparse_feature_columns)
group_embedding_dict = mergeDict(group_sparse_embedding_dict, group_varlen_sparse_embedding_dict)
if not support_group:
group_embedding_dict = list(chain.from_iterable(group_embedding_dict.values()))
return group_embedding_dict, dense_value_list
前两行从输入的feature_columns里滤出SparseFeat和VarLenSparseFeat放到sparse_feature_columns和varlen_sparse_feature_columns。我们这里的varlen_sparse_feature_columns为空;而sparse_feature_columns是C1-C26。
第三行用create_embedding_matrix函数构建每个field的Embedding矩阵。
def create_embedding_matrix(feature_columns, l2_reg, init_std, seed, prefix="", seq_mask_zero=True):
sparse_feature_columns = list(
filter(lambda x: isinstance(x, SparseFeat) , feature_columns)) if feature_columns else []
varlen_sparse_feature_columns = list(
filter(lambda x: isinstance(x, VarLenSparseFeat), feature_columns)) if feature_columns else []
sparse_emb_dict = create_embedding_dict(sparse_feature_columns, varlen_sparse_feature_columns, init_std, seed,
l2_reg, prefix=prefix + 'sparse', seq_mask_zero=seq_mask_zero)
return sparse_emb_dict
这个函数实际是调用create_embedding_dict来创建每个field的Embedding矩阵:
def create_embedding_dict(sparse_feature_columns, varlen_sparse_feature_columns, init_std, seed, l2_reg,
prefix='sparse_', seq_mask_zero=True):
sparse_embedding = {feat.embedding_name:Embedding(feat.vocabulary_size, feat.embedding_dim,
embeddings_initializer=RandomNormal(
mean=0.0, stddev=init_std, seed=seed),
embeddings_regularizer=l2(l2_reg),
name=prefix + '_emb_' + feat.embedding_name) for feat in sparse_feature_columns}
if varlen_sparse_feature_columns and len(varlen_sparse_feature_columns) > 0:
for feat in varlen_sparse_feature_columns:
# if feat.name not in sparse_embedding:
sparse_embedding[feat.embedding_name] = Embedding(feat.vocabulary_size, feat.embedding_dim,
embeddings_initializer=RandomNormal(
mean=0.0, stddev=init_std, seed=seed),
embeddings_regularizer=l2(
l2_reg),
name=prefix + '_seq_emb_' + feat.name,
mask_zero=seq_mask_zero)
return sparse_embedding
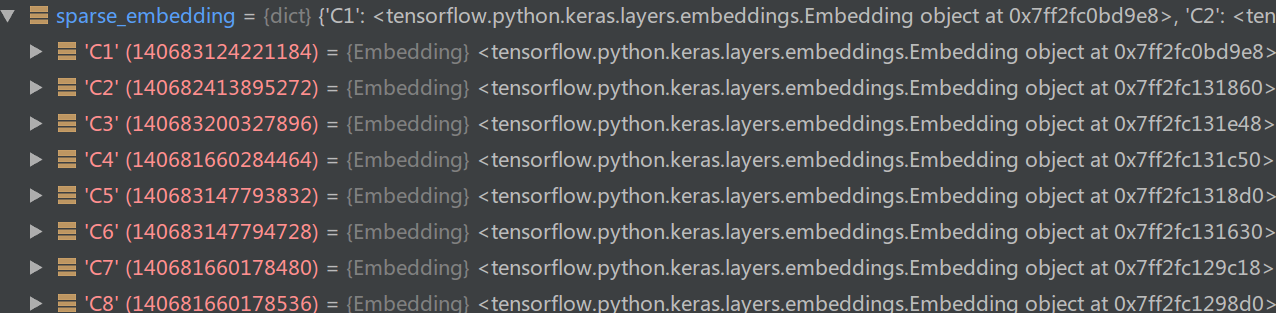
我们这里varlen_sparse_feature_columns是空,所以其实只执行了第一行,也就是遍历sparse_feature_columns中的C1-C26,然后为每一个field构建Embedding(feat.vocabulary_size, feat.embedding_dim…)。每一个Embedding的输入大小是C1-C26的词典大小,但是它们Embedding后都是相同的大小(这里是4)。
接着我们返回函数input_from_feature_columns,下一行是调用embedding_lookup函数,把输入的C1-C26对于的26个1维的Input Embedding成26个shape为4的向量:
def embedding_lookup(sparse_embedding_dict, sparse_input_dict, sparse_feature_columns, return_feat_list=(),
mask_feat_list=(), to_list=False):
group_embedding_dict = defaultdict(list)
for fc in sparse_feature_columns:
feature_name = fc.name
embedding_name = fc.embedding_name
if (len(return_feat_list) == 0 or feature_name in return_feat_list):
if fc.use_hash:
lookup_idx = Hash(fc.vocabulary_size, mask_zero=(feature_name in mask_feat_list))(
sparse_input_dict[feature_name])
else:
lookup_idx = sparse_input_dict[feature_name]
group_embedding_dict[fc.group_name].append(sparse_embedding_dict[embedding_name](lookup_idx))
if to_list:
return list(chain.from_iterable(group_embedding_dict.values()))
return group_embedding_dict
这个函数遍历sparse_feature_columns(C1-C26),根据feature_name找到对应的Input(lookup_idx = sparse_input_dict[feature_name]),然后用sparse_embedding_dictembedding_name把输入进行Embedding。
代码阅读起来可能会有一些难懂,原因是为了通用性,只能通过dict的名字来关联Input和Embedding。如果不考虑通用性,那么代码可能会非常简单:
input1 = Input((1,))
embedding1 = Embedding(feat1.vocab_size, 4)
output1 = embedding1(input1)
input2 = Input((1,))
embedding2 = Embedding(feat2.vocab_size, 4)
output2 = embedding1(input2)
....
input26 = .....
但是为了通用性,我们需要把所有的Input都放到sparse_input_dict里,把所有的Embedding都放到sparse_embedding_dict,把所有的output都放到group_embedding_dict,然后通过feature的name来关联。
group_embedding_dict会把同一个group里的特征放到一起,我们这里没有分组,因此默认的C1-C26都是在default_group里。
接着回到input_from_feature_columns执行下一行get_dense_input,这个函数把所有的DenseFeat拼起来:
def get_dense_input(features, feature_columns):
dense_feature_columns = list(filter(lambda x: isinstance(x, DenseFeat), feature_columns)) if feature_columns else []
dense_input_list = []
for fc in dense_feature_columns:
dense_input_list.append(features[fc.name])
return dense_input_list
这个函数很简单,就是把所有的Dense feature的输入向量放到一个list里,如下图所示:
接下来返回input_from_feature_columns会处理varlen_sparse_feature_columns,我们这里没有多值的特征,因此就不详细介绍了,它和普通的sparse_feature_columns的区别在于多了一个Pooling的步骤。
最后input_from_feature_columns函数返回的是group_embedding_dict和dense_value_list。分别表示Category Embedding后的list和Dense field的输入。
最后我们返回的DeepFM函数,进入get_linear_logit函数。
get_linear_logit函数
这个函数的作用其实就是线性部分,也就是$\langle W,x \rangle$,这本来很简单,但是我们需要把输入的C1-C26用one-hot进行编码,然后拼接起来,再把I1-I13也拼接起来,长度为vocab_1+…+vocab_26+13的输入向量,然后再乘以W。不过这里使用了Embedding实现了类似的效果,用Embedding Matrix实现了同样的效果,我猜测这是这是为了复用其他的代码。但是Embedding后的大小没有必要是4,其实是1就够了。
比如举个例子,假设Category为C1和C2,词典大小分别是3和2。假设当前的输入C1=2,C2=2(下标1开始),则one-hot后的向量为<0,1,0>拼接<0,1>,则 $\langle W,x \rangle=w_2 \times 1 + w_5 \times 1$。现在我们用Embedding,假设Embedding Matrix为:
e11 e12 e13 e14
e21 e22 e23 e24
e31 e32 e33 e34
e41 e42 e43 e44
e51 e52 e53 e54
则<0,1,0>会Embedding成向量[e21 e22 e23 e24],<0,1>会变成[e51 e52 e53 e54],最终得到的是(e21+e22+e23+e24) + (e51+e52+e53+e54),因此e21+e22+e23+e24等价于原来的$w_2$,e51+e52+e53+e54等价于$w_5$。
那么其实我们把每一个field Embedding成长度为4的向量是没有必要的,只需要Embedding成长度为1的就行了。
接下来是FM部分。
FM Layer
类FM基础了Keras的Layer,它的完整代码为:
class FM(Layer):
def __init__(self, **kwargs):
super(FM, self).__init__(**kwargs)
def build(self, input_shape):
if len(input_shape) != 3:
raise ValueError("Unexpected inputs dimensions % d,\
expect to be 3 dimensions" % (len(input_shape)))
super(FM, self).build(input_shape) # Be sure to call this somewhere!
def call(self, inputs, **kwargs):
if K.ndim(inputs) != 3:
raise ValueError(
"Unexpected inputs dimensions %d, expect to be 3 dimensions"
% (K.ndim(inputs)))
concated_embeds_value = inputs
square_of_sum = tf.square(reduce_sum(
concated_embeds_value, axis=1, keep_dims=True))
sum_of_square = reduce_sum(
concated_embeds_value * concated_embeds_value, axis=1, keep_dims=True)
cross_term = square_of_sum - sum_of_square
cross_term = 0.5 * reduce_sum(cross_term, axis=2, keep_dims=False)
return cross_term
def compute_output_shape(self, input_shape):
return (None, 1)
它的核心逻辑在call函数里实现。前面我们介绍了FM二阶特征交互的计算公式为:
\[\sum_{i=1}^d \sum_{j=i+1}^d \langle V_i, V_j \rangle x_i \cdot x_j\]难点是怎么不要for循环实现上面的计算。为了获得一些感觉,我们先看一个简单的例子。假设只有前面的C1和C2两个Category的特征,词典大小还是3和2。假设输入还是C1=2,C2=2(下标从1开始),则Embedding之后为$V_2=[e_{21}, e_{22}, e_{23}, e_{24}]$和$V_5=[e_{51}, e_{52}, e_{53}, e_{54}]$。
因为$x_i$和$x_j$同时不为零才需要计算,所以\(\sum_{i=1}^d \sum_{j=i+1}^d \langle V_i, V_j \rangle x_i \cdot x_j\)里需要计算的只有i=2和j=5的情况。因此
\[\sum_{i=1}^d \sum_{j=i+1}^d \langle V_i, V_j \rangle x_i \cdot x_j = \langle V_2, V_5 \rangle\]如果是C1,C2和C3呢?则需要把c1的Embedding向量$V_{c_1}$、$V_{c_2}$和$V_{c_3}$的两两内积:
\[\sum_{i=1}^d \sum_{j=i+1}^d \langle V_i, V_j \rangle x_i \cdot x_j = \langle V_{c_1}, V_{c_2} \rangle \ +\langle V_{c_1}, V_{c_3} \rangle + \langle V_{c_2}, V_{c_3} \rangle\]但是这怎么用矩阵乘法一次计算出来呢?我们可以看看这个:
\[x_1x_2 + x_1x_3 + x_2x_3 = \frac{1}{2}[(x_1+x_2+x_3)^2 -(x_1^2+x_2^2+x_3^2) ]\]因此我们可以把Embedding后的向量加起来,然后平方然后减去每一个向量的平方(内积),再除以2。对应到代码就是:
square_of_sum = tf.square(reduce_sum(
concated_embeds_value, axis=1, keep_dims=True))
sum_of_square = reduce_sum(
concated_embeds_value * concated_embeds_value, axis=1, keep_dims=True)
cross_term = square_of_sum - sum_of_square
cross_term = 0.5 * reduce_sum(cross_term, axis=2, keep_dims=False)
第一行是计算 $(V_{c_1}+…+V_{c_m})^2$。第二行是计算$V_{c_1}^2+…+V_{c_m}^2$。第三行是相减除以2。
接下来是DNN,这个就不介绍了,但是我们需要注意FM的输入和DNN的输入都是同一个group_embedding_dict:
fm_logit = add_func([FM()(concat_func(v, axis=1))
for k, v in group_embedding_dict.items() if k in fm_group])
dnn_input = combined_dnn_input(list(chain.from_iterable(
group_embedding_dict.values())), dense_value_list)
dnn_output = DNN(dnn_hidden_units, dnn_activation, l2_reg_dnn, dnn_dropout,
dnn_use_bn, seed)(dnn_input)
这样就实现了FM和DNN的Embedding的共享。注意:线性组件我们虽然也使用了Embedding来替代$\langle W,x \rangle$,但是这个Embedding并不是真正意义的Embedding,只是为了复用代码避免再次one-hot自己展开而已,所有不能共享。
最后是把linear_logit、fm_logit和dnn_logit加起来输入最后的sigmoid函数,然后用输入和输出构建Keras的Model:
final_logit = add_func([linear_logit, fm_logit, dnn_logit])
output = PredictionLayer(task)(final_logit)
model = tf.keras.models.Model(inputs=inputs_list, outputs=output)
PredictionLayer也是一个自定义的Layer,其实非常简单:
class PredictionLayer(Layer):
def __init__(self, task='binary', use_bias=True, **kwargs):
if task not in ["binary", "multiclass", "regression"]:
raise ValueError("task must be binary,multiclass or regression")
self.task = task
self.use_bias = use_bias
super(PredictionLayer, self).__init__(**kwargs)
def build(self, input_shape):
if self.use_bias:
self.global_bias = self.add_weight(
shape=(1,), initializer=Zeros(), name="global_bias")
# Be sure to call this somewhere!
super(PredictionLayer, self).build(input_shape)
def call(self, inputs, **kwargs):
x = inputs
if self.use_bias:
x = tf.nn.bias_add(x, self.global_bias, data_format='NHWC')
if self.task == "binary":
x = tf.sigmoid(x)
output = tf.reshape(x, (-1, 1))
return output
def compute_output_shape(self, input_shape):
return (None, 1)
def get_config(self, ):
config = {'task': self.task, 'use_bias': self.use_bias}
base_config = super(PredictionLayer, self).get_config()
return dict(list(base_config.items()) + list(config.items()))
只需要看一下call函数就行,如果是binary就使用sigmoid激活,否则(回归)直接输出。
大规模训练数据的支持
上面的代码使用起来非常简单,但是它使用Pandas来读取csv数据,对于总共4500万行的全量的训练数据,如果直接用Pandas读取到内存的话,可能需要几十GB的内存,而且实际的系统的训练数据量可能远远大于千万级别。
最简单的办法当然是把大的数据集拆分成很多小的数据,然后逐个训练。比如把4500万行拆分成10个450万行的小文件,然后逐个训练。但是这样做的缺点是每次需要手动拆分,每个小文件只能训练一个Epoch,然后再训练另外一个文件,对于超参数的条件、Learning rate的scheduler都会带来很大的问题。因此作者自己实现了一个Sequence,同时由于sklearn的LabelEncoder和MinMaxScaler只能读取内存中的数据,所以作者也实现了自己版本的CtrLabelEncoder和CtrMinMaxScaler,代码在preprocessor.py。
运行代码
首先需要预处理,用CtrLabelEncoder和CtrMinMaxScaler从训练数据进行fit:
python preprocessor.py /home/lili/data/ctr-train.txt /home/lili/data/train-label-encoder.pkl /home/lili/data/train-minmax-scaler.pkl
输出两个pickle的文件,分别把CtrLabelEncoder和CtrMinMaxScaler对象用pickle保持下来。后面的testctr2.py会用到这两个文件。
接着就是训练了:
python testctr2.py
由于时间关系,代码里都是绝对路径,读者要运行的话需要修改相应的文件路径。
实现原理和代码简介
对于大数据,Keras提供了fit_generator,我们先来看一下它的文档。
fit_generator(generator, steps_per_epoch=None, epochs=1, verbose=1, callbacks=None, validation_data=None, validation_steps=None, validation_freq=1, class_weight=None, max_queue_size=10, workers=1, use_multiprocessing=False, shuffle=True, initial_epoch=0)
[TODO]
实验结果
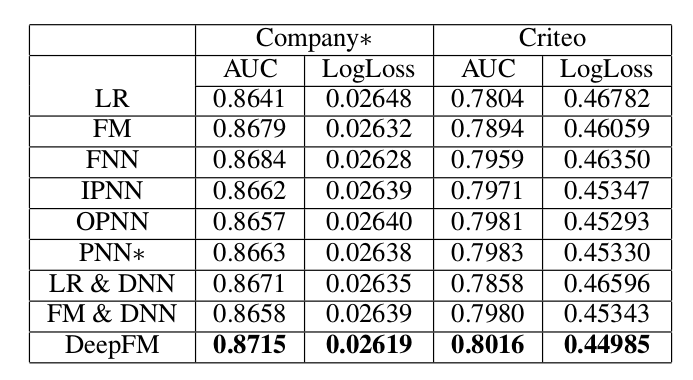
作者使用了默认的超参数,在4100万的训练数据上训练了10个epoch,在450万左右的验证集上的auc大概是0.795,logloss大概是0.46,比论文0.805的auc和0.45的logloss稍差一下,可能还需要调一调超参数多训练一些时间。
训练10个epoch大概花了16个小时。这和PaddlePaddle示例的结果是大致一致的。不过我发现训练DeepCTR时GPU的利用率很低,一般在30%下。这可能是因为特征都是Embedding后的稀疏矩阵导致的,PaddlePaddle用CPU训练一个epoch的时间也是1.8个小时,说明GPU的效率没有发挥出来。
- 显示Disqus评论(需要科学上网)