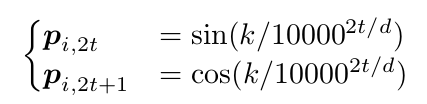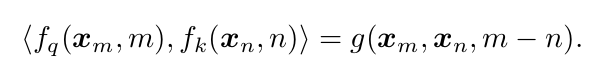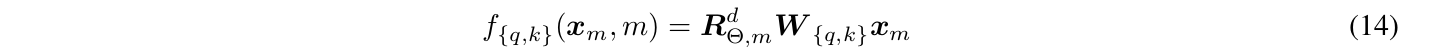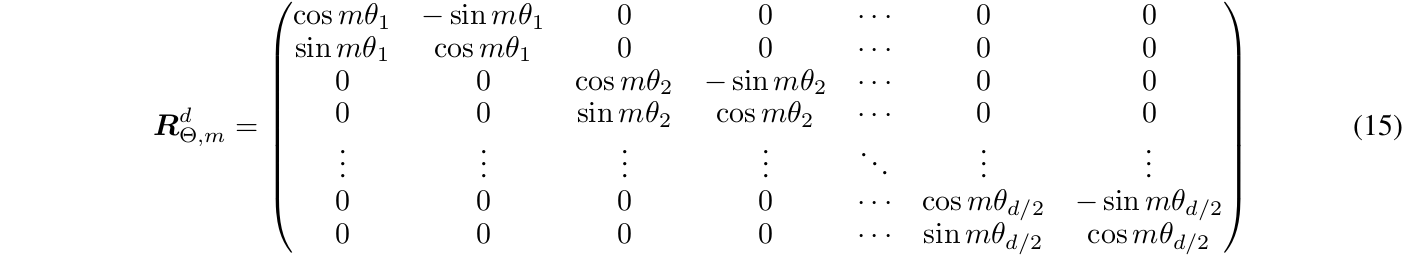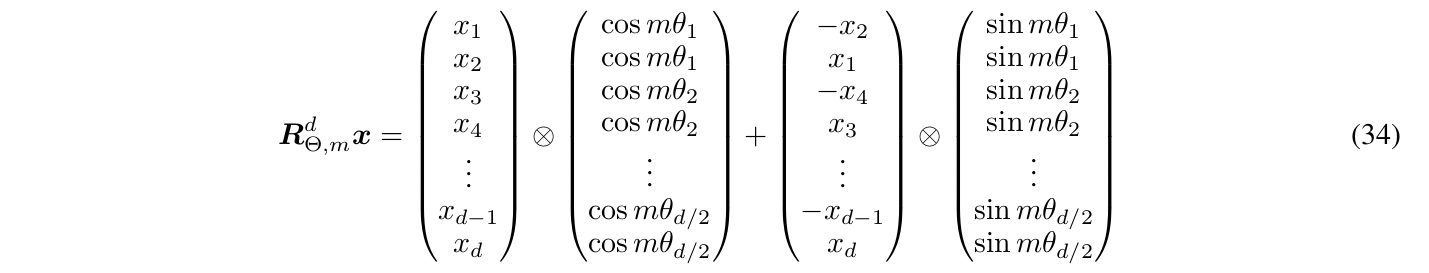RoPE论文解读

本文是对论文RoFormer: Enhanced Transformer with Rotary Position Embedding的解读。

背景和相关工作
本文的方法
参考文献

背景和相关工作

Preliminary

假设输入为N个token：$\mathcal{S}_N=\{w_i\}_{i=1}^N$。它们对应的word embedding为$E_N=\{x_i\}_{i=1}^N$。$x_i \in R^d$是d维的向量，它不包含位置信息。self-attention首先在word embedding上加入位置信息，然后把它们变成query，key和value向量：

query是第m个词，key和value是第n个词，通过函数$f_q,f_k\text{和}f_v$，把它们变成了向量。这三个f函数的第一个参数是word embedding，与位置无关，第二个参数是位置。有了q，k和v之后，就可以计算第m个query对第n个key的attention了，最简单的方法是计算q和k的内积，然后用softmax归一化：

绝对位置编码

最简单的是每个位置有一个embedding向量，类似与word embedding，然后直接把word embedding加到position embedding里。只不过index不是word的id，而是位置：

另外一种绝对位置编码是Transformer原始论文提出的正余弦函数：

注：上面公式有误，k应该改成i。

我们来看一下它的计算的例子：

def get_angles(pos, i, d_model):
  angle_rates = 1 / np.power(10000, (2 * (i//2)) / np.float32(d_model))
  return pos * angle_rates

def positional_encoding(position, d_model):
  angle_rads = get_angles(np.arange(position)[:, np.newaxis],
                          np.arange(d_model)[np.newaxis, :],
                          d_model)

  ar = np.array(angle_rads)
  
  # apply sin to even indices in the array; 2i
  angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])
  
  # apply cos to odd indices in the array; 2i+1
  angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])
    
  pos_encoding = angle_rads[np.newaxis, ...]
    
  return pos_encoding, ar
  
pe, ar = positional_encoding(64, 128)
print(pe[0][0][:10])
print(pe[0][1][:10])
print(pe[0][2][:10])
print(pe[0][3][:10])
print("###")
print(ar[0][:10])
print(ar[1][:10])
print(ar[2][:10])
print(ar[3][:10])

我们先看一下调用sin和cos之前和之后的值：

[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[1.         1.         0.86596432 0.86596432 0.74989421 0.74989421
 0.64938163 0.64938163 0.56234133 0.56234133]
[2.         2.         1.73192865 1.73192865 1.49978842 1.49978842
 1.29876326 1.29876326 1.12468265 1.12468265]
[3.         3.         2.59789297 2.59789297 2.24968263 2.24968263
 1.94814489 1.94814489 1.68702398 1.68702398]
 
 ### 调用sin和cos后：
 [0. 1. 0. 1. 0. 1. 0. 1. 0. 1.]
[0.84147098 0.54030231 0.76172041 0.64790587 0.68156135 0.73176098
 0.60469402 0.79645787 0.53316844 0.84600911]
[ 0.90929743 -0.41614684  0.98704625 -0.16043596  0.99748     0.07094825
  0.96322662  0.26869029  0.90213071  0.43146283]
[ 0.14112001 -0.9899925   0.51730572 -0.85580068  0.77827252 -0.62792665
  0.92964484 -0.36845688  0.99325317 -0.11596614]

常见的embedding大小是128，所以每一行为128个数值，因为太多，我们显示了前10列。第一行是第一个位置(0)的位置编码，它全是0，所以应用分别对偶数位和奇数位调用sin和cos得到[0, 1, 0, 1…..]。第二行是第二个位置(1)的位置编码，它的值为[1, 1, 0.86596432, 0.86596432, …]。分别应用sin和cos之后得到[0.84147098 0.54030231 0.76172041 0.64790587,…]。这样好像看不出什么规律，我们来看第一列：[1,2,3,4,….]，第三列[0.86, 1.73,…]。我们看到每一列的规律是[1,2,3,4,…]乘以一个固定的值。所以它是有明显的规律的。如果把弧度变成角度的话，那么每一列都是一个固定的角度值不断的旋转，只不过每一列的初始角度是不同，具体来讲是从1逐渐等比的方式逐渐减少的，比如上面的例子，第2行为：

[1.       0.865964 0.749894 0.649382 0.562341 0.486968 0.421697 0.365174
316228 0.273842 0.237137 0.205353 0.177828 0.153993 0.133352 0.115478
1      0.086596 0.074989 0.064938 0.056234 0.048697 0.04217  0.036517
031623 0.027384 0.023714 0.020535 0.017783 0.015399 0.013335 0.011548
01     0.00866  0.007499 0.006494 0.005623 0.00487  0.004217 0.003652
003162 0.002738 0.002371 0.002054 0.001778 0.00154  0.001334 0.001155
001    0.000866 0.00075  0.000649 0.000562 0.000487 0.000422 0.000365
000316 0.000274 0.000237 0.000205 0.000178 0.000154 0.000133 0.000115]

也就是ar[1][2]/ar[1][0]=0.865964, ar[1][4]/ar[1][2]=0.865964，….，这个比例0.865964是固定的，它等于 $10000^{-2/d}$。所以我们总结一下，位置编码的第一行都是0，这没啥。第二行是一个逐渐缩写的等比数列，分别是1,0.86,0.86^2，…。如果从列的角度，每一列都是一个等差数列，第一列是0,1,2,3,….，第三列是0,1*0.86,2*0.86，第5列是0, 1*0.86*0.86,2*0.86*0.86，…。

我们可以画图来看一下有没有什么规律。下图是d=64，并且画出了前10个位置的编码：

我们看前几列，它是有不同的变化的。但是当i>10之后，尤其是到30以后，我们看到每一列都是一样。为什么这样呢？因为我们只显示了前10个位置，因为比如第30列，它的第2行是0.0177，第3行是0.0177*2，第4行是0.0177*3，这些值的都非常小，所以应用cos之后都是1。从列的角度来看，越是前面的维度，它随位置的变化越快；越是后面的维度，它的变化就越慢。所以前面的维度能够区别很短的距离，而后面的维度只能能识别远距离的关系。

为什么要用这种三角函数呢？原文的解释是：We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset k, $\text{PE}_{pos+k}$ can be represented as a linear function of$\text{PE}_{pos}$. 具体的证明是：

关于旋转的性质，请参考[7]。这里我就不复制粘贴了。请仔细理解这个blog，后面的RoPE就比较好理解了。注：这两种绝对位置编码是不同的，第一种严格来说不能叫编码，应该叫位置embedding，它是学出来的；后者才能叫编码，它是一组固定的值。

相对位置编码

绝对位置编码的问题是，如果两个词的相对位置不变，但是绝对位置变了，那么它们的编码肯定变了。但是对于NLP任务来说，我们并不希望这样。比如”I like”的语义和它在句子中的绝对位置没有太大关系。为了解决这个问题，很多人提出了各种相对位置编码的方法。下面我们看几个比较典型的方法。

在[8]里，作者提出了如下的编码方法：

其中$\tilde{p}^k_r\text{和}\tilde{p}^k_r \in R^d$是可以训练的相对位置编码向量。$r=clip(m-n, r_{min}, r_{max})$表示query的位置m和key的位置n的差值，使用clip是为了避免参数过多，设定一个最小和最大的距离。注意：r可以是小于零的，表示query在key的左边。我们简单解读一下这个公式，query $x_m$的编码是和位置m无关的，它就是简单的用$W_q$相乘，所以函数$f_q(x_m)$是和m无关的，它只有一个参数，而函数$f_k(x_n,n)\text{和}f_v(x_n,n)$有两个参数，第二个是位置。不过我觉得更准确的写法应该是$f_k(x,r)$，它与m和n都没有直接关系，只与它们的差有关。

在[9]里，作者认为query和key还是可以用word embedding加上位置编码，也就是$q_m=f_q(x_m)=W_q(x_m+p_m)\text{以及}k_n=f_k(x_n)=W_k(x_n+p_n)$，然后求它们的内积，接着把它展开：

但是这里的$p_m和p_n$还是query和key的绝对位置编码。为了解决这个问题，作者把上式修改为：

第1项不变，它是内容和内容的attention计算。第2项是query对key的位置的attention，把绝对的编码$p_n$换成了新的相对位置的$\tilde{p}_{m-n}$，对应的变化矩阵也从$W_k$变成了$\tilde{W}_k$。第3项是query的位置对key的内容的attention，这是一个绝对位置，没有意义，所以作者直接把它改成了一个与位置无关的向量u。第4项是query的位置对key的位置的attention，后一个位置$p_n$可以改成相对的位置$\tilde{p}_{m-n}$，而第一个绝对的位置也是没有意义的，把它也改成一个与位置无关的向量v。这里面的向量和矩阵都是可以学习的。另外作者认为value的位置也是没有意义的，所以 $f_v(x_j)=W_vx_j$

在[10]里，作者认为内容和位置之间的attention是没有意义的，因此值保留第1和4项，只不过用来不同的参数矩阵U，另外增加了一个bias：

在[11]里，作者认为位置对位置的attention可以去掉，但是query的内容对key的位置以及query的位置对key的内容的attention是需要保留的，只不过它的第3项可以理解为key的内容对query的位置的attention，因此不需要引入一个u，而直接用$\tilde{p}_{m-n}$替代$p_{m}$：

本文的方法

目标

为了表示相对位置关系，我们期望$q_m和k_n$的内积可以表示成如下的形式：它只依赖于$q_m与k_n$的embedding，以及它们的相对位置$m-n$。

因此，我们的目标是寻找到一个合适的$f_q(x_m,m)$与$f_k(x_n,n)$，使得它们的内积只与相对位置$m-n$相关，而与$m和n$的绝对值无关。

Rotary position embedding

2D的情况

如果按照下面的方式定义$f_q(x_m,m)$与$f_k(x_n,n)$，则g是满足上述目标的。

其中，$Re[\cdot]$表示复数的实部，$(W_kx_n)^*$表示$W_kx_n$的共轭。$\theta \in R$是一个非零常数。我们对比一下，之前的方法都是在Word Embedding上加一个位置编码(比如$W_k(x_n+\tilde{p}_n$))，而本文的方法是对query和key乘以一个$e^{im\theta}$，也就是对原理的query和key做一个$m\theta$的旋转。因此这里的向量都是复向量，这可能让人困惑。其实我们把复数看成复平面上的二维向量就可以了，使用复数主要是方便计算旋转。我们用欧拉公式($e^{ix}=\cos x+i \sin x$)把前面两个式子展开，就可以得到没有复数的式子：

由于$f_q和f_k$只是下标不同，形式完全是一样的，所以上面合并成立一个公式。$f_{\{q,k\}}$的意思就是$f_k或者f_q$。上式看起来有点复杂，其实只是把$W_q$展开成2x2矩阵，$x_m$展开成二维向量，同时利用了欧拉公式表示旋转矩阵而已。如果不用欧拉公式和复数，我们看$f_q$的输入是二维向量$x_m=\begin{pmatrix} x_m^{(1)}\\ x_m^{(2)} \end{pmatrix}$和m，输出是(2x2)(2x2)(21)=21的向量。这个向量如果用复数表示就是前面形式更简单的$（W_kx_n)e^{im\theta}$。对于这个还是不太清楚的读者可以参考[12]，重点是理解用一个复数乘以另一个复数可以看成：把第二个复数旋转第一个复数的幅角，并且模乘以第二个复数的模；如果把复数看成向量，那么它等价于对这个向量左乘一个旋转矩阵$\begin{pmatrix} \cos \theta & - \sin \theta\\ \sin \theta & \cos \theta \end{pmatrix}$。现在的问题就是：为什么把$f_q和f_k$写出上面的形式之后，它们的内积就是那么复杂的一个g，并且g是和绝对位置m和n无关，但是与$m-n$有关呢？原论文把这个证明放到了后面。不过我觉得有必要在这里一起讲清楚了，否则读者可能还是比较困惑。注意：下一节的内容数学公式比较多，读者最好抽出几张草稿纸跟着抄写一遍。如果实在不能理解，那么至少要接受(承认)其结论——如果把$f_q和f_k$写成上面的公式后，它们的内积就是第三个公式的那种形式。

RoPE在2D时的推导

这里说的是推导，其实应该说是寻找。也就是说，为了找到满足目标的内积公式，$f_q和f_k$必须满足什么形式的约束，找来找去发现$f_q和f_k$必须满足的就是上面的公式。首先我们从$q_m和k_n$开始：

我们要求$q_m$是$x_m$和$m$的函数，$k_n$是$x_n$和n的函数。接着我们定义$q_m$和$k_n$的内积，希望它的形式是g，也就是它依赖$x_m、x_n和n-m$。

接着我们定义f的初始条件，也就是m=n=0的情况：

q和k可以看出还没有对key和query加入位置信息(没有旋转)时的情况。给定上面的内积和初始化约束，我们希望寻找满足它的$f_q和f_k$。我们首先利用复数及其乘法的几何意义(参考上一节)，我们可以把二维向量用复数来表示，并且复数可以用欧拉公式表示成模和幅角的函数：

看起来很复杂？不要被吓到了。$f_q(x_q,m)$就是一个二维向量，我们可以把它看出一个复数。既然是复数，那么就可以用欧拉公式表示。因此$R_q(x_q,m)$表示这个复数的模，$\mathcal{\Theta}_q(x_q,m)$表示这个复数的幅角。第二和第三个公式也是类似的。根据(21)，$f_q和f_k$的内积等于$g_(x_q,x_k,n-m)$，经过简单的复数计算可以得到：

上式推导的重点是：两个向量(复数表示)的内积等于第一个复数的共轭乘以第二个复数。注意：这只是一种定义方式。两个向量的传统内积是投影，而且维度是1。这里把两个向量的内积定义为第一个的共轭乘以第二个，也就是它们的模的乘积，第二个的幅角减去第一个。这样的结果还是一个复数！因此我们可以得到(24)。利用初始化条件(22)，也就是m和n等于零的情况：

(25)的第二个等号就是把(23)的m或者n设置为零。第一个等式就是复数的定义，q(k)可以表示为它的模和幅角的旋转表示。令m=n，以及m=n=0，代入(24)，可以得到：

具体来说，对于(24)，我们令m=n，则可以得到(26a)的第一个等式$R_q(x_q,m)R_k(x_k,m)=R_g(x_q,x_k,m-m)=R_g(x_q,x_k,0)$，接着，令m=n=0，则可以得到$R_q(x_q,0)R_k(x_k,0)=R_g(x_q,x_k,0)$，因此可以得到(26a)的第二个等号。注意：原论文的(26a)有一个错误，它写成$R_k(x_q,0)R_k(x_k,0)$了。最后利用(25)，$R_q(x_q,0)$是q的实部，$R_k(x_k,0)$是k的实部。 (26b)与前面类似，令(24)的第二个式子中m=n，则可以得到$\mathcal{\Theta}_k(x_k,m)-\mathcal{\Theta}_q(x_q,m)=\mathcal{\Theta}_g(x_q,x_k,0)$，这是(26b)的第一个等号，接着令m=n=0，则可以得到$\mathcal{\Theta}_k(x_k,0)-\mathcal{\Theta}_q(x_q,0)=\mathcal{\Theta}_g(x_q,x_k,0)$，最后利用(25)，可以得到最后一个等号。注意：原文最后两个式子加了模运算的符号，我的理解是不对的，应该就是两个幅角的相减。

(26a)就是$R_q(x_q,m)，R_k(x_k,m)，\Theta_k(x_k,m)和\Theta_q(x_q,m)$需要满足的约束，那么我们可以用下式定义这4个函数，从而保证可以满足约束：

注意上面的逻辑：我们的目标是寻找$f_q(x_q,m)，f_k(x_k,n)和g(x_q,x_k,n-m)$以便满足约束，而它们又可以分解为模和幅角。所以也许有很多种$R_q(x_q,m)，R_k(x_k,m)，\Theta_k(x_k,m)和\Theta_q(x_q,m)$的定义方式可以满足(26a)的约束。不过我们不需要找到所有的方式，只需要找到一种就可以。我们先看实部的约束，式(27)是满足约束的最简单的一种定义方式。这个式子定义的模与位置m或者n无关。下面我们来验证一下。我们首先来看(26a)关于实部的约束是否满足，我们把(27)的第一个和第二个式子代入，很容易发现$R_q(x_q,m)R_k(x_k,n)=\|q\|\|k\|$。利用(24)，我们可以得到$R_g(x_q,x_k,n-m)=R_q(x_q,m)R_k(x_k,n)=\|q\|\|k\|$。很好！我们这样定义的模既简单(与位置无关)，又满足约束。那么幅角呢？把(26b)调整一下顺序可以得到$\mathcal{\Theta}_k(x_k,m)-\theta_k=\mathcal{\Theta}_q(x_q,m)-\theta_q$。我们可以定义幅角$\mathcal{\Theta}_k(x_k,m)$使得它与query $x_k$无关，而且它还满足(26b)的约束。定义方法为：

也就是说，我们把$\mathcal{\Theta}_k(x_k,m)$定义为与m相关的函数$\phi(m)$加上常数$\theta_k$，即$\mathcal{\Theta}_k(x_k,m)=\phi(m)+\theta_k$。$\mathcal{\Theta}_q(x_q,m)$的定义也是类似的，$\mathcal{\Theta}_q(x_q,m)=\phi(m)+\theta_q$。显然这样定义的$\mathcal{\Theta}_k(x_k,m)$和$\mathcal{\Theta}_q(x_q,m)$满足$\mathcal{\Theta}_k(x_k,m)-\theta_k=\mathcal{\Theta}_q(x_q,m)-\theta_q$。而且$\mathcal{\Theta}_q(x_q,m)$只与位置m相关，而与$x_q$无关。为了确定$\phi(m)$，我们对(24)式的第二个式子取n=m+1，并且把(28)式代入就可以得到：

(29)式的右边与m无关，所以我们可以定义$\phi(m)$为m的线性函数：

我们可以验证一下(30)是否满足(29)：$\phi(m+1)-\phi(m)=(m+1)\theta+\gamma -m\theta-\gamma=\theta$，所以只需要令$\theta$等于(29)式右边那一堆就行了，当然这里要求$\theta$不等于零，否则$\phi(m)$就与m也无关了。总结一下，通过上面的过程，我们定义了$f_q(x_q,m)和f_k(x_k,n)$的模和幅角，当然也就定义了它们：

注：原文的公式(31)的第二项少了括号，应该是$\|q\|e^{i(\theta_q+m\theta+\gamma)}$。在(22)中，我们对于$f_q和f_k$没有要求任何约束，因此$f_q(x_q,m)和f_k(x_k,n)$可以自由选择任何形式。为了和普通的位置编码对比，我们定义它们为：

注：上式中第一个式子应该是$W_qx_m$。也就是说q和k是没有旋转的情况。另外为了简化，我们令$\gamma$为零，则(31)可以进一步化简为：

而(33)就是前一节定义的(12)的前两个公式。那么(12)的第3个公式呢？注意：我们在这一节定义的$g(x_q,x_k,n-m)$是一个复数，它当然是满足我们的目标——函数值只与query，key和相对位置n-m相关，而与绝对位置无关。但是我们想要定义的内积只是一个标量值，那怎么办呢？很简单，我们定义$q_m^Tk_n$取$g(x_q,x_k,n-m)$的实部就行了，因为一个复函数$g(x_q,x_k,n-m)$满足我们的目标——函数值只与query，key和相对位置n-m相关，那么它的实部显然也是满足的。那么$g(x_q,x_k,n-m)$是什么呢？根据我们的定义，它是$f_k(x_n,n)$乘以$f_q(x_m,m)$的共轭，因此： $g(x_q,x_k,n-m)=(W_qx_m)(W_kx_n)^*e^{i(n-m)\theta}$。取其实部就得到(12)的第3个式子。

从2D推广到高维

为了推广到高维d，思路是把d维空间划分成d/2个独立的2维子空间，不同的子空间有各自的旋转矩阵。因此$f_q(x_m,m)$还是一个旋转矩阵乘以$W_q$再乘以$x_m$：

唯一的区别就是旋转矩阵$R_{\Theta,m}^d$从2x2的旋转矩阵变成了dxd的更复杂的形式：

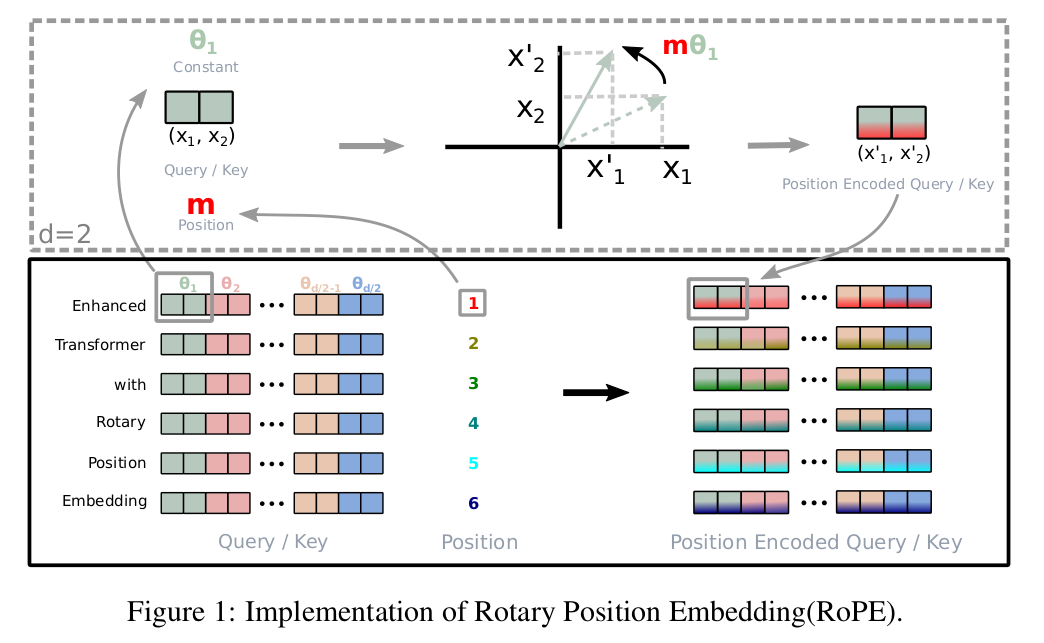
看起来很复杂，其实很简单：就是2x2的旋转矩阵(旋转的$\theta$不同)放到对角线上。其中$\theta_i=10000^{-2(i-1)/d},i\in[1,2,...,d/2]$。$\theta_i$这么定义是参考Transformer原始论文的形式，这样不同维度的旋转的尺度是不同的，从而不同的维度可以表现不同的位置变化模式。 RoPE的计算过程如下图所示：

上图的例子是对输入”Enhanced Transformer with Rotary Postion Embedding”进行第一层self-attention的计算。以计算第一个token为例，如果按照原来的位置编码方法，则是用”Enhanced”的word embedding加上位置编码作为输入，然后用$W_q$和$W_k$乘得到query和key向量。而现在的方法有所不同，”Enhanced”的word embedding先乘以$W_q$和$W_k$得到query和key，这两个向量都是d维的。然后把它切分成d/2个二维向量，比如图中最前面绿色的$(x_1,x_2)$。然后用旋转矩阵$\begin{pmatrix} \cos m\theta_1 & - \sin m\theta_1\\ \sin m\theta_1 & \cos m\theta_1 \end{pmatrix}$得到$(x_1',x_2')$，这里Enhanced是第一个token，所以m=1。用类似的方法可以得到query和key的第3~4，第5~6，…，第d/2-1~d/2维的向量。也就是图中右边的Position Encoded Query/Key。

有了Position Encoded Query和Key，我们就可以计算它们的内积：

注意：上式最右边我认为应该是$x^TW_q^T$，不过从实现的角度来说$W_q$是学习的参数，直接定义它的转置也是一样的。而$R_{\Theta,n-m}^d=(R_{\Theta,m}^d)^TR_{\Theta,n}^d$，这个读者可以自行验证。它的关键点在于q和k的内积只依赖其相对位置，这正是前面我们这么定义它们的目的。和前面的位置编码方法不同，RoPE并不是把位置编码加到Word Embedding里。它是对query和key的d/2个子空间分别进行了不同的旋转，直接把位置信息通过乘法的方式嵌入进去，这种方法更加自然的解决了相对位置编码的问题。

RoPE的性质

Long-term decay

这个性质指的是随着相对位置的增大，query和key的内积会逐渐衰减。这对于NLP任务来说是很有用的，详细的证明放在后面。

RoPE with linear attention

self-attention更通用的形式是：

在原始论文中$sim(q_m,k_n)=exp(q_m^Tk_n/\sqrt{d})$，因为需要计算每一对$q_m和k_n$的内积，所以时间复杂度是$\mathcal{O}(N^2)$。在[13]里，作者提出线性(linear)attention，把公式(17)改成了：

其中$\phi(\cdot)和\varphi(\cdot)$是非负函数。我们这里不详细介绍，感兴趣的读者可以参考[13]。这里需要指出的是：(18)式中，$\phi(q_m)$在求和公式里是不变的，因此可以提取到求和公式外面，所以我们只需要计算一次$\sum_{n=1}^N\varphi(k_n)$和$\sum_{n=1}^N\varphi(k_n)v_n$并且保存下来就行了，不同的query(m)可以复用计算结果，这样时间复杂度就变成了$\mathcal{O}(N)$。基于(18)，我们可以很容易位置信息通过旋转加入进去：

先看分子，我们对$\phi(q_m)$用$R_{\Theta,m}^d$对它进行了旋转，$\varphi(k_n)$也是类似的。而分母保持不变，这是为了防止分母旋转后为零。

理论解释

Derivation of RoPE under 2D

这部分内容已经放到前面了。

旋转矩阵的快速计算

计算$W_qx_m$之后需要乘以旋转矩阵$R_{\Theta,m}^d$，这是一个dxd的矩阵，看起来计算量不小。但是仔细观察我们会发现这是一个非常稀疏的矩阵，它只有在对角线以及它的带状区域非零，因此可以用下面的公式快速计算：

这个公式我们前面其实讲过，也就是把$(x_1,x_2)$乘以旋转矩阵$\begin{pmatrix} \cos m\theta_1 & - \sin m\theta_1\\ \sin m\theta_1 & \cos m\theta_1 \end{pmatrix}$，把$(x_3,x_4)$乘以旋转矩阵$\begin{pmatrix} \cos m\theta_2 & - \sin m\theta_2\\ \sin m\theta_2 & \cos m\theta_2 \end{pmatrix}$，…。只不过写成了向量的逐点相乘(pointwise product)而已。

Long-term decay of RoPE

$q=W_qx_m$和$k=W_kx_n$经过旋转后的内积可以写出分块的形式：

这个公式其实就是(12)的第3个式子，不过分成了d/2个块而已。$q_{[2i:2i+1]}$是取向量q的第2i和第2i+1个组成一个二维向量。记$h_i=q_{[2i:2i+1]}k^*_{[2i:2i+1]}$，$S_j=\sum_{i=0}^{j-1}e^{i(m-n)\theta_i}$，同时令$S_0=0,h_{d/2}=0$。使用Abel变换我们可以得到：

我不太了解Abel变换，不过(36)的第一个等式就是(35)，只不过用$h_i和S_{i+1}-S_i$替代(35)的项而已。(36)的第二个等号可以这样验证：

$\sum_{i=0}^{d/2-1}h_i(S_{i+1}-S_i)=h_0(S_1-S_0)+h_1(S_2-S_1)+...+h_{d/2-1}(S_{d/2}-S_{d/2-1})$ $-\sum_{i=0}^{d/2-1}S_{i+1}(h_{i+1}-h_i)=S_1(h_0-h_1)+S_2(h_1-h_2)+...+S_{d/2}(h_{d/2-1}-h_{d/2})$

再利用$S_0=0,h_{d/2}=0$，我们可以验证它们是完全相同的。我这里就不展开了，读者可以自行验证。接下来我们可以估算：

这个式子估计了(35)的上界，这个上界是随着m-n的增大而快速下界的，这说明随着相对位置的增大，query和key的内积会逐渐衰减，这就是所谓的Long-term decay。上界随相对位置m-n的变化如下图所示：