Direct Preference Optimization: Your Language Model is Secretly a Reward Model论文解读

本文是论文Direct Preference Optimization: Your Language Model is Secretly a Reward Model的解读。

目录

• Abstract
• 1 Introduction
• 2 Related Work
• 3 Preliminaries
• 4 Direct Preference Optimization
• 5 Theoretical Analysis of DPO
  • 5.1 你的语言模型实际上是一个奖励模型
  • 5.2 Actor-Critic算法的不稳定性
• 6 实验
  • 6.1 DPO如何有效地优化RLHF目标？
  • 6.2 DPO在真实偏好数据集上的扩展性如何？
  • 6.3 对新输入分布的泛化
  • 6.4 验证GPT-4评估与人类评估的一致性
• 7 讨论

Abstract

尽管大规模无监督语言模型（LMs）能够学习广泛的世界知识和一些推理技能，但由于其完全无监督的训练性质，实现对其行为的精确控制仍然是困难的。现有的获取这种可操纵性的方法是收集相对于模型生成的质量的人类标签，并使用强化学习从人类反馈中进行微调，通常使用强化学习来进行人类反馈（RLHF）。然而，RLHF是一个复杂且经常不稳定的过程，首先拟合一个反映人类偏好的奖励模型，然后使用强化学习微调大型无监督LM，以最大化这个估计的奖励，同时又不能偏离原始模型太远。在本文中，我们介绍了一种新的RLHF奖励模型的参数化，该参数化允许以闭合形式提取相应的最优策略，使我们能够仅使用简单的分类损失解决标准的RLHF问题。由此产生的算法，我们称之为直接偏好优化（DPO），稳定、性能良好且计算轻量，消除了在微调过程中对LM进行采样或进行大量超参数调整的需要。我们的实验证明，DPO能够以与现有方法相当或更好的方式微调LM，以与人类偏好一致。值得注意的是，使用DPO进行微调在控制生成物的情感方面超过了基于PPO的RLHF，在总结和单轮对话中匹配或改善了响应质量，同时实施和训练要简单得多。

1 Introduction

大规模无监督语言模型（LMs）在非常大的数据集上训练，获得了令人惊讶的能力[11, 7, 40, 8]。然而，这些模型是在由具有各种目标、优先级和技能集的人生成的数据上训练的。其中一些目标和技能可能不值得模仿；例如，虽然我们希望我们的AI编码助手能够理解常见的编程错误以便纠正它们，但在生成代码时，我们希望将模型偏向于其训练数据中存在的（潜在的罕见的）高质量编码能力。同样，我们可能希望我们的语言模型了解到50%的人信奉的一个常见误解，但我们绝对不希望模型在50%的查询中声称这个误解是真实的！换句话说，从模型极为广泛的知识和能力中选择出其期望的响应和行为对于构建安全、高性能和可控的AI系统至关重要[26]。虽然现有的方法通常使用强化学习（RL）来引导LMs以匹配人类偏好，但我们将展示现有方法使用的基于RL的目标可以通过一个简单的二元交叉熵目标进行精确优化，极大简化了偏好学习流程。

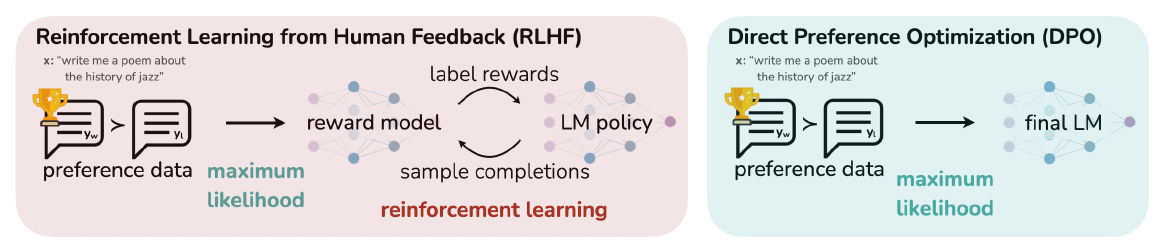图1：DPO在避免强化学习的同时优化人类偏好。现有的使用人类反馈微调语言模型的方法首先适应一个奖励模型，该模型基于提示和对响应对的人类偏好数据，然后使用强化学习找到一个最大化学得奖励的策略。相比之下，DPO直接通过简单的分类目标对最能满足偏好的策略进行优化，拟合一个隐式奖励模型，其相应的最优策略可以以闭合形式提取。

在高层次上，现有的方法通过人类偏好的数据集来灌输期望的行为到语言模型中，这些偏好代表了人类认为安全和有用的行为类型。这个偏好学习阶段发生在大规模无监督预训练的初始阶段，该预训练使用大型文本数据集。虽然偏好学习的最直接方法是在高质量响应的人类演示上进行监督微调，但最成功的一类方法是从人类（或AI）反馈中进行强化学习（RLHF/RLAIF; [12, 2]）。RLHF方法适应一个人类偏好数据集的奖励模型，然后使用RL优化语言模型策略，以产生被赋予高奖励的响应，同时不过度偏离原始模型。虽然RLHF可以生成具有令人印象深刻的对话和编码能力的模型，但RLHF流程比监督学习复杂得多，涉及训练多个LMs和在训练循环中从LM策略中采样，带来了显著的计算成本。

在本文中，我们展示了如何直接优化语言模型以符合人类偏好，而无需显式奖励建模或强化学习。我们提出了直接偏好优化（DPO），这是一种隐式优化与现有RLHF算法相同目标的算法（最大化奖励并带有KL散度约束），但实现简单且容易训练。从直觉上讲，DPO更新增加了更好响应相对于较差响应的相对对数概率，但它包含了一个动态的、每个示例的重要性权重，防止了我们发现的使用朴素概率比率目标引起的模型退化。与现有算法类似，DPO依赖于一个理论上的偏好模型（例如Bradley-Terry模型; [5]），该模型衡量了给定奖励函数与经验偏好数据的一致性。然而，尽管现有方法使用偏好模型来定义一个偏好损失以训练奖励模型，然后训练一个优化学习的策略，但DPO使用变量的变化来直接定义策略的偏好损失。鉴于具有模型响应的人类偏好数据集，DPO因此可以使用简单的二元交叉熵目标优化策略，产生最优策略以适应偏好数据拟合的隐式奖励函数。我们的主要贡献是直接偏好优化（DPO），这是一种从偏好中训练语言模型的简单无强化学习算法。我们的实验证明，DPO至少与现有方法一样有效，包括基于PPO的RLHF，在情感调制、总结和对话等任务中学习偏好，使用具有最多6B参数的语言模型。

2 Related Work

逐渐增加规模的自监督语言模型学会在零-shot[31]或使用少量提示[6, 25, 11]的情况下完成某些任务。然而，通过在指令和人类编写的补全数据集上进行微调，它们在下游任务上的性能和与用户意图的一致性可以显著提高[23, 36, 13, 39]。这种“指令微调”过程使LLMs能够推广到指令微调集之外的指令，并通常提高其可用性[13]。尽管指令微调取得了成功，但相对于专家演示，响应质量的相对人类判断通常更容易收集，因此随后的研究使用人类偏好数据集对LLMs进行微调，以提高在翻译[18]、总结[38, 49]、讲故事[49]和遵循指令[26, 32]等任务中的熟练程度。这些方法首先优化神经网络奖励函数，使其与Bradley-Terry模型[5]等偏好模型下的偏好数据兼容，然后使用强化学习算法，通常是REINFORCE [45]、近端策略优化（PPO; [37]）或其变体[32]，对语言模型进行微调，以最大化给定的奖励。与之密切相关的研究线借助使用人类反馈进行指令遵循微调的LLMs，生成针对安全性或无害性等目标属性的额外合成偏好数据，仅使用人类提供的弱监督，以LLM注释的文本规范形式。这些方法代表了两个工作领域的融合：一个是使用强化学习训练语言模型以实现各种目标[33, 27, 46]的工作，另一个是从人类偏好中学习的一般方法的工作[12, 19]。尽管使用相对人类偏好的吸引力很大，但使用强化学习对大型语言模型进行微调仍然是一个主要的实际挑战；这项工作提供了一种在没有强化学习的情况下优化相对偏好的理论上合理的方法。

在语言之外的环境中，从偏好中学习策略已经在bandit和强化学习环境中研究，并提出了几种方法。使用动作的偏好或排名，而不是奖励，进行上下文bandit学习被称为上下文对决bandit（CDB; [48, 14]）。在缺乏绝对奖励的情况下，CDB的理论分析将最优策略的概念替代为冯·诺伊曼获胜者，即其预期在与任何其他策略的比赛中获胜的率至少为50%[14]。然而，在CDB设置中，偏好标签是在线给定的，而在从人类偏好中学习的情况下，我们通常是从固定的离线偏好注释的动作对中学习的[47]。类似地，基于偏好的强化学习（PbRL）是根据未知“评分”函数生成的二元偏好而不是奖励来学习[9, 35]。存在各种PbRL算法，包括可以重复使用离线偏好数据的方法，但通常首先明确估计潜在评分函数（即奖励模型），然后对其进行优化[16, 9, 12, 34, 19]。相比之下，我们提出了一种单阶段策略学习方法，直接优化策略以满足偏好。

3 Preliminaries

我们回顾了Ziegler等人在RLHF流程中的工作（以及后续的[38, 1, 26]）。通常，该流程包括三个阶段：

1); 监督微调（SFT）; 2) 偏好采样和奖励学习; 3) 强化学习优化。

SFT：RLHF通常从对感兴趣的下游任务（对话、总结等）使用监督学习对预训练LM进行微调开始，以获得模型$\pi^{\text{SFT}}$。

奖励建模阶段：在第二阶段，使用SFT模型提示一些提示x，产生答案对$(y_1,y_2) \sim \pi^{\text{SFT}}$。然后，这些答案对被呈现给人类标注者，他们对一个答案表达偏好，表示为$y_w \succ y_l \vert x$，其中$y_w$和$y_l$分别表示$(y_1, y_2)$中的较好和较差响应。假设这些偏好是由一些潜在的奖励模型$r^∗(x, y)$生成的，而我们无法访问该模型。有许多用于建模偏好的方法，Bradley-Terry（BT）[5]模型是一个流行的选择（尽管更通用的Plackett-Luce排名模型[30, 21]也与该框架兼容，如果我们可以访问多个排名的答案）。BT模型规定人类偏好分布$p^∗$可以写成：

假设我们可以访问从\(p^∗\)中采样的一组静态对比数据\(\mathcal{D}=\{x^{(i)}, y_w^{(i)}, y_l^{(i)}\}_{i=1}^n\)，我们可以对奖励模型$r_{\phi}(x, y)$进行参数化，并通过最大似然估计来估计参数。将问题框定为二元分类，我们有负对数似然损失：

其中$\sigma$是逻辑函数。在LM的上下文中，网络$r_{\phi}(x, y)$通常从SFT模型$\pi^{\text{SFT}}(y | x)$初始化，其中在最终变换器层之上添加了一个线性层，用于生成奖励值的单一标量预测[49]。为确保具有较低方差的奖励函数，先前的工作对奖励进行了归一化，使得对所有x，$E_{x,y \sim \mathcal{D}} [r_{\phi}(x, y)] = 0$。

RL微调阶段：在RL阶段，我们使用学到的奖励函数向语言模型提供反馈。特别是，我们制定以下优化问题，

其中$\beta$是一个参数，用于控制与基准参考策略$\pi_{\text{ref}}$（即初始SFT模型$\pi^{\text{SFT}}$）的偏差。在实践中，语言模型策略$\pi_\theta$也初始化为$\pi^{\text{SFT}}$。添加的约束非常重要，因为它防止模型偏离奖励模型准确的分布，同时保持生成的多样性并防止单一高奖励答案的模式崩溃。由于语言生成的离散性质，这个目标是不可微的，通常使用强化学习进行优化。标准方法[49, 38, 1, 26]是构建奖励函数$r(x, y) = r_\phi(x, y) - \beta(log \pi_\theta(y | x) - log \pi_{\text{ref}}(y | x))$，并使用PPO[37]进行最大化。

4 Direct Preference Optimization

受到在大规模问题上应用强化学习算法的挑战的启发，例如对语言模型进行微调，我们的目标是提出一种直接使用偏好进行策略优化的简单方法。与先前的强化学习从人类反馈中微调（RLHF）方法不同，这些方法学习奖励然后通过强化学习进行优化，我们的方法利用了一种特定的奖励模型参数化选择，使其最优策略能够以封闭形式提取，而无需进行强化学习的训练循环。正如我们接下来将详细描述的，我们的关键洞察是利用从奖励函数到最优策略的解析映射，这使我们能够将对奖励函数的损失转化为对策略的损失。这种变量转换方法避免了拟合显式的、独立的奖励模型，同时仍然在现有的人类偏好模型下进行优化，例如Bradley-Terry模型。实质上，策略网络同时表示语言模型和（隐式的）奖励。

DPO目标函数的推导 我们从与先前工作相同的强化学习目标开始，即Eq. 3，使用一个通用的奖励函数 r。根据先前的工作[29, 28, 17, 15]，可以直观地证明在Eq. 3中KL受限奖励最大化目标的最优解具有以下形式：

其中 \(Z(x)=\sum_y\pi_{\text{ref}}(y \vert x) \exp(\frac{1}{\beta}r(x,y))\)是分区函数。详细的推导请参见附录 A.1。即使我们使用ground truth奖励函数\(r^*\)的MLE估计 $r_\phi$，估计分区函数Z(x) 仍然昂贵[17, 15]，这使得这种表示在实践中难以利用。然而，我们可以重新排列 Eq. 4，将奖励函数表达为其相应的最优策略

我们可以将这种重新参数化应用于ground truth奖励\(r^*\)和相应的最优模型 \(\pi^*\)。幸运的是，Bradley-Terry 模型仅取决于两个完成之间的奖励差异，即 \(p^*(y_1 \succ y_2) \vert x) = \sigma(r^*(x, y_1) - r^*(x, y_2))\)。将在 Eq. 5 中对\(r^*(x,y)\)的重新参数化代入偏好模型 Eq. 1 中，分区函数被消除，我们可以用最优策略\(\pi^*\)和参考策略$\pi_{\text{ref}}$来表达人类偏好的概率。因此，Bradley-Terry 模型下的最优 RLHF 策略\(\pi^*\)满足偏好模型：

推导见附录 A.2。虽然 Eq. 6 使用了 Bradley-Terry 模型，但我们同样可以在更一般的 Plackett-Luce 模型[30, 21]下进行推导，具体见附录 A.3。现在我们已经用最优策略而不是奖励模型表示人类偏好数据的概率，我们可以为参数化策略 $\pi_\theta$ 制定一个最大似然目标。与奖励建模方法类似（即 Eq. 2），我们的策略目标变为：

通过这种方式，我们使用一种替代参数化来拟合一个隐式奖励，其最优策略简单地是 $\pi_\theta$。此外，由于我们的方法等同于拟合重新参数化的 Bradley-Terry 模型，因此具有一些理论性质，如在合适的假设下对偏好数据分布的一致性[4]。在第5节中，我们将进一步讨论DPO的理论性质与其他工作的关系。

【译注，上面是理解DPO的关键，我这里简单的解释一下，感兴趣的读者还是需要阅读附录里的推导过程。

1.公式(1)

假设我们(人)有一个打分/reward函数r(x,y)，也就是给定一个输入x和一个输出y，我们会打一个分数/reward。当然我们假设这个函数是”好的”。什么叫好？直觉上它应该满足，如果$y_1$比$y_2$好，那么$r(x,y_1) > r(x,y_2) $。好的越多，分大的也越多。

我们假设每个标注人员都有这样一个隐含的reward函数在它的脑子里，但问题在于为了成本和一致性，我们让标注人员比较$r(x,y_1),r(x,y_2)$。我们看到是$r(x,y_1) > r(x,y_2)$，但在标注人员脑子里的可能值$r(x,y_1)=3,r(x,y_2)=1$我们并不知道。

但是我们假设公式(1)的\(p^*(y_1 \succ y_2)\)函数，这个函数是说标注人员打分是一个随机的函数，给定$r(x,y_1),r(x,y_2)$，我就可以计算出标注人员认为$y_1$比$y_2$好的概率。这个假设的形式是合理的——如果$r(x,y_1) == r(x,y_2)$，则概率是0.5，如果$r(x,y_1) > r(x,y_2)$，则概率大于0.5并且它们的差距越大，概率也越大。当$r(x,y_1) \gg r(x,y_2)$时，概率趋近于1。如果$r(x,y_1) < r(x,y_2)$则概率小于0.5。

细心的读者可以发现(1)式其实就是logistic函数，我们把分子变成1，则(1)可以写成logistic函数的形式：

2.公式(2)

就像前面说过的，我们看到的是概率\(p^*(y_1 \succ y_2)\)的采样(比如$y_1$比$y_2$好)。我们可以根据观察最大似然估计r(x,y)。如果进行推导的话，可以得出最大似然估计等价于最小化公式(2)的loss。这个公式也比较复合直觉：如果$r(x,y_w)$比$r(x,y_l)$好，则$\sigma(r(x,y_w)-r(x,y_l))$较大，则loss(负log)较小。

3.公式(3)

我们有了reward模型之后，就需要用PPO等算法对llm进行强化学习了。学习的目标是调整策略(llm模型)使得reward最大化，当然为了防止模型作弊过拟合reward模型，我们还需要增加一个KL loss，使得llm和参考的llm(通常是ppo之前的版本)不要偏离太远。

4.公式(4)

给定一个reward模型r(x,y)，一个参考llm $\pi_{\text{ref}}(y \vert x)$，对应它们的最优策略可以写成公式(4)的形式，这个的详细证明过程参考附录A.1。如果对证明不感兴趣，至少也应该承认这是可以做到的。因为后面的定理1需要这个公式。

5.公式(5)

把公式(4)左右取log，然后整理一下就行了，读者可以自己拿笔写一下。

6.公式(6)

公式(5)对所有的r(x,y)和对应的$pi_r$都成立，那么对于人脑子里真实的\(r^*(x,y)\)和对应的最优策略\(\pi^*\)当然也成立。把(5)式中的$r(x,y),\pi_r$用\(r^*(x,y),\pi^*\)替换，然后代入(1)式(或者我前面化简的logistic形式)，则公共的$\beta \log Z(x)$被减去了，整理一下就是公式(6)。

7.公式(7)

仔细观察公式(6)，这个函数的输入是策略\(\pi^*\)，输出是偏好概率函数\(p^*(y_1 \succ y_2 \vert x)\)。和(2)进行类比，我们就可以定义(注意是定义不是推导，推导参考附录A.3)DPO的loss——它为什么是合理的前面论文也解释过了，包括对它的梯度的分析，这里就不赘述了。

】

DPO更新的作用是什么？ 为了对DPO有一个机械的理解，分析损失函数 \(\mathcal{L}_{\text{DPO}}\) 的梯度是有用的。相对于参数 $\theta$的梯度可以写为：

\(\hat{r}_\theta(x,y)=\beta \log \frac{\pi_\theta(y \vert x)}{\pi_{\text{ref}}(y \vert x)}\) 表示语言模型 $\pi_\theta$ 和$\pi_{\text{ref}}$隐含定义的奖励。直观地说，损失函数\({L}_{\text{DPO}}\)的梯度增加了首选响应 $y_w$ 的可能性，并减少了 $y_l$ 的可能性。重要的是，示例的权重取决于隐含奖励模型 \(\hat{r}_\theta\) 如何错误的评价分差，乘以β进行缩放，即，隐含奖励模型对完成的排序有多不正确，考虑到 KL 约束的强度。我们的实验表明这种加权的重要性，因为没有权重系数的这种方法的朴素版本可能导致语言模型退化（附录表格3）。

DPO 概要。通常的 DPO 流程如下：1) 对于每个提示 x，从参考模型 $\pi_{\text{ref}}(· \vert x)$ 中抽样完成 $y_1, y_2$，并用人类偏好进行标记，构建离线偏好数据集 \(\mathcal{D}=\{x^{(i)}, y_w^{(i)}, y_l^{(i)}\}_{i=1}^N\)；2) 针对给定的 $\pi_{\text{ref}}$、$\mathcal{D}$ 和所需的 $\beta$，优化语言模型 $\pi_\theta$ 以最小化 \(\mathcal{L}_{\text{DPO}}\)。在实践中，人们希望重复使用公开可用的偏好数据集，而不是生成样本并收集人类偏好。由于偏好数据集是使用 $\pi^{\text{SFT}}$ 进行抽样的，我们在可能的情况下初始化 $\pi_{\text{ref}}=\pi^{\text{SFT}}$。然而，当 $\pi^{\text{SFT}}$ 不可用时，我们通过最大化首选完成 $(x, y_w)$ 的似然度来初始化 $\pi_{\text{ref}}$，即，\(\pi_{\text{ref}} = \arg \max_\pi \mathbb{E}_{x,y_w \sim \mathcal{D}} [log \pi(y_w \vert x)]\)。这个过程有助于减轻真实参考分布不可用和 DPO 使用的 $\pi_{\text{ref}}$ 之间的分布偏移。有关实现和超参数的更多详细信息可在附录 B 中找到。

5 Theoretical Analysis of DPO

在这一部分，我们对DPO方法进行了进一步解释，提供了理论支持，并将DPO的优势与用于RLHF（如PPO [37]）的actor critic算法的问题联系起来。

5.1 你的语言模型实际上是一个奖励模型

DPO能够绕过显式的拟合奖励模型和执行RL来学习策略这两步，仅使用单一的最大似然目标。请注意，优化目标Eq. 5等效于具有奖励参数化\(r^*(x,y)=\beta \log \frac{\pi_\theta^*(y \vert x)}{\pi_{\text{ref}}^*(y \vert x)}\)的Bradley-Terry模型，我们优化我们的参数化模型$\pi_\theta$，类似于在变量变换下的Eq. 2中的奖励模型优化。在本节中，我们将建立这种重新参数化背后的理论，展示它不限制学到的奖励模型的类别，并允许精确恢复最优策略。我们首先定义了奖励函数之间的等价关系。

定义1：我们称两个奖励函数r（x，y）和r’（x，y）等价，当且仅当r（x，y） - r’（x，y） = f（x）对于某个函数f成立。

【上面的定义需要简单解释一下，对于同一个x，假设有两个response：y1和y2，我们代入：

两个式子左右相减得到：

这说明对于同一个输入x的不同输出，两个奖励函数对于它们的打分分差是一致的，那么这两个奖励函数就是等价的。比如x表示一道题1+1=?，y1表示1+1=2，y2表示1+1=3。 两个奖励函数打分的绝对值不重要，但只有它们打分的分差一致就行。比如r给两者的打分是1和0，r’的打分是100和99。那么就是等价的。

】

很容易看出这确实是一个等价关系，将奖励函数集合划分为不同的类别。我们可以陈述以下两个引理：

引理1：在Plackett-Luce，特别是Bradley-Terry的偏好框架下，来自相同类别的两个奖励函数引起相同的偏好分布。

引理2：来自相同等价类的两个奖励函数在受限RL问题下引起相同的最优策略。

【需要用自然语言(人话)解释一下上面的数学语言。 前面我们定义了两个奖励函数什么情况下等价，那么因为等价关系满足自反，对称和传递（reflexive, symmetric, and transitive)，因此这种关系形成等价类(Equivalence Classes)。等价类是对讨论集合的一个划分(Partition)。还是太数学语言？我们举个例子：我们定义两个人居住在同一个国家的关系叫做同居关系(好奇怪的关系！)。那么它是满足自反对称和传递的，为什么？因为一个人x和它自己是居住在同一个国家(我们不允许一个人有两国身份)；如果x和y居住在同一个国家，那么y和x居住在同一个国家(这不废话吗)；如果x和y居住在同一个国家，y和z居住在同一个国家，那么x和z也居住在同一个国家。我们把有同居关系的所有人都可以放到一起，他们就形成了一个集合(国家)，全世界所有的人都会被包含在一个国家里(也许鲁滨逊那个国家只有一个人)，而且不可能被超过一个国家包含。用数学语言就是一个人有且仅有一个国家。

第一个引理说的是对于偏好分布来说同一个类别的奖励函数是没有区别的。这个证明比较简单，如果我们仔细观察前面公式(1)定义的偏好分布概率，会发现它对两个输出$y_1$和$y_2$的偏好只依赖与奖励函数的差，也与奖励函数的绝对值无关，这正是奖励函数等价的定义。

第二个引理说的是：如果两个奖励函数是等价的，那么用它来做强化学习，学习到的最优策略(模型)也是等价的。这两个引理合在一起的意思就是：我们寻找奖励函数时只需要寻找等价类就行了。就好像全世界有70多亿人，从同居关系的角度来说，我们只需要研究100多个国家就行了。 】

证明是直接的，我们将它们推迟到附录A.5中。第一个引理是Plackett-Luce模型族的一个众所周知的欠规范问题[30]。由于这种欠规范，我们通常必须加入额外的可辨认性约束，以确保从Eq. 2中获得MLE估计[4]。第二个引理陈述了来自同一类的所有奖励函数产生相同的最优策略，因此对于我们的最终目标，我们只关心从最优类别中恢复任意奖励函数。我们在附录A.6中证明了以下定理：

定理1：在温和的假设下，与Plackett-Luce（特别是Bradley-Terry）模型一致的所有奖励类别都可以用重新参数化\(r(x,y)=\beta \log \frac{\pi(y \vert x)}{\pi_{\text{ref}}(y \vert x)}\)表示，其中\(\pi_{\text{ref}}(y \vert x)\)是指定的参考模型，而$\pi(y \vert x)$是存在的。

证明概要：考虑任何奖励函数r(x，y)，存在由Eq. 4指定的相应最优模型$\pi_r(y \vert x)$。我们将展示，来自r等价类的奖励函数可以使用上述重新参数化表示。我们将投影f定义为

操作符f简单地使用$\pi_r$的分区函数的对数对奖励函数进行归一化。由于添加的归一化项仅是前缀x的函数，$f(r; \pi_{\text{ref}} , \beta)(x, y)$是r(x, y)等价类中的奖励函数。最后，将r替换为Eq. 5的RHS（对于任何奖励函数都成立），我们有\(f(r; \pi_{\text{ref}} , \beta)(x, y)=\beta \log \frac{\pi(y \vert x)}{\pi_{\text{ref}}(y \vert x)}\)。也就是说，投影f生成r等价类中具有所需形式的奖励函数，我们在所提出的重新参数化的奖励模型中没有失去任何一般性。

我们可以将定理1视为准确说明DPO重新参数化选择了每个等价类中的哪个奖励函数，即满足以下条件的奖励函数：

$\pi(y \vert x)$是一个有效的分布（概率为正且总和为1）。然而，根据Eq. 4，我们可以看出Eq. 9是由奖励函数r(x, y)引起的最优策略的分区函数。DPO算法的关键洞见是，我们可以对Plackett-Luce（特别是Bradley-Terry）偏好模型的欠规范进行一定的约束，以保留可表示的奖励模型类别，但同时使得Eq. 4中的最优策略在所有提示x上都变得解析可处理。

【译注：公式(8)看起来很复杂，但是我们不用关心，只需要知道一个(x,y)的函数h(x,y)对所有的y求和/积分后就没有y了，也就是变成了一个x的函数。因此f(x,y)=r(x,y) + h(x)，所以根据上面的定义它们是等价的。把(5)的右边代入(8)就可以得到\(f(x,y)=\beta \log \frac{\pi(y \vert x)}{\pi_{\text{ref}}(y \vert x)}\)。

公式(9)是怎么来的呢？加入我们想找到满足定理1的r(x,y)，那么我们令h(x)=0就可以了。因为这个时候r(x,y)=f(x,y)。logX=0，则X=1，这就是公式(9)。

再复述一下这个定理：你给我一个$r(x,y)$和\(\pi_{\text{ref}}(y \vert x)\)，我就能找到一个$\pi(y \vert x)$，使得你给我的$r(x,y)$可以写成\(r(x,y)=\beta \log \frac{\pi(y \vert x)}{\pi_{\text{ref}}(y \vert x)}\)这种形式。 】

5.2 Actor-Critic算法的不稳定性

我们还可以利用我们的框架来诊断用于RLHF的标准Actor-Critic算法的不稳定性，例如PPO。我们按照RLHF流程，专注于第3节中概述的RL微调步骤。我们可以将其与控制即推理框架[20]联系起来，该框架用于第3节中概述的受限RL问题。我们假设有一个参数化模型$\pi_\theta(y \vert x)$，并最小化\(\mathbb{D}_{\text{KL}}[\pi_\theta(y \vert x) \vert\vert \pi^*(y \vert x)]\) ，其中\(\pi^*\)是由奖励函数$r_\phi(x,y)$ 用Eq. 7得到的最优策略。通过一些代数运算，这推导出了优化目标：

这与之前的工作[49, 38, 1, 26]中使用DPO等效奖励优化的相同目标，适用于$r_\phi$奖励类别。在这种设置中，我们可以将$f (r_\phi ,\pi_{\text{ref}} ,\beta)$中的标准化项解释为参考策略$\pi_{\text{ref}}$的软值函数。虽然这个项不影响最优解，但是如果没有它，目标的策略梯度可能具有较大的方差，使学习变得不稳定。我们可以通过使用一个学习的值函数来适应标准化项，但这也可能难以优化。作为替代，先前的研究使用了人类完成基线来对奖励进行标准化，本质上是对标准化项的单一样本蒙特卡洛估计。与之相反，DPO重新参数化产生的奖励函数不需要任何基线。

【关于Actor-Critic算法稳定性可以参考强化学习简介】

6 实验

在本节中，我们从经验上评估DPO直接从偏好中训练策略的能力。首先，在一个良好控制的文本生成环境中，我们问：相比于常见的偏好学习算法如PPO，DPO在最大化奖励和最小化与参考策略的KL散度之间的权衡效率如何？接下来，我们评估DPO在更大的模型和更困难的RLHF任务上的性能，包括摘要生成和对话。我们发现，几乎不需要调整超参数，DPO的性能通常与或优于强基线，如使用PPO的RLHF，以及在学习奖励函数下返回N个采样轨迹中的最佳轨迹。在呈现这些结果之前，我们描述了实验设置；附录C中提供了额外的细节。

任务。我们的实验探索了三种不同的开放式文本生成任务。对于所有实验，算法从偏好数据集\(D = \{(x^{(i)}, y_w^{(i)}, y_l^{i)}\}_{i=1}^N\)，学习策略。在 受控情感生成 中，x是来自IMDb数据集[22]的电影评论的前缀，策略必须生成带有积极情感的y。为了进行受控评估，对于这个实验，我们使用预训练的情感分类器生成对生成的偏好对，其中$p(\text{positive} \vert x, y_w) > p(\text{positive} \vert x, y_l)$。对于SFT，我们在IMDB数据集的训练集上微调GPT-2-large直到收敛（详细信息见App C.1）。在摘要生成中，x是来自Reddit的一个论坛帖子；策略必须生成帖子中主要观点的摘要y。遵循之前的工作，我们使用Reddit TL;DR摘要数据集[41]以及由Stiennon等人收集的人类偏好。我们使用SFT模型在由Stiennon等人采样的人类撰写的论坛帖子摘要的基础上，使用TRLX [42]框架进行RLHF。人类偏好数据集是由Stiennon等人在一个不同但类似训练的SFT模型的样本上收集的。最后，在单轮对话中，x是一个人类查询，可能是关于天体物理的问题或关于关系建议的请求。策略必须对用户的查询生成引人入胜且有帮助的响应y；我们使用Anthropic Helpful and Harmless对话数据集[1]，其中包含17万个人类与自动助手之间的对话。每个对话都以一个由大型（尽管未知）语言模型生成的一对响应结束，以及一个表示人类首选响应的偏好标签。在这种情况下，没有可用的预训练SFT模型；因此，我们在仅对首选完成进行微调的情况下，对一个现成的语言模型进行微调，以形成SFT模型。

评估。我们的实验使用两种不同的评估方法。为了分析每个算法在优化受限奖励最大化目标方面的效果，在受控情感生成设置中，我们通过其实现的奖励和与参考策略的KL散度的frontier来评估每个算法；由于我们可以访问地面真实奖励函数（情感分类器），因此这个frontier是可计算的。然而，在现实世界中，地面真实奖励函数是未知的；因此，我们评估算法与基线策略的胜率，使用GPT-4作为人类对摘要质量和对话有用性进行评估的代理，在摘要和单轮对话设置中分别进行。对于摘要，我们使用测试集中的参考摘要作为基线；对于对话，我们使用测试数据集中的首选响应作为基线。尽管现有研究表明语言模型可能是比现有指标更好的自动评估者[10]，我们进行了一项人类研究，以证明我们使用GPT-4进行评估的合理性，详见第6.4节。我们发现GPT-4的判断与人类强烈相关，与人类评估者之间的一致性通常类似或更高。

方法。除了DPO之外，我们评估了几种现有方法来训练语言模型以符合人类偏好。最简单的方法是使用GPT-J [43]进行零次提示在摘要任务中，以及使用Pythia-2.8B [3]在对话任务中进行2次提示。此外，我们评估了SFT模型以及Preferred-FT，这是一个使用受控情感和摘要中的SFT模型（或单轮对话中的通用LM）的选择完成yw进行监督学习微调的模型。另一种伪监督方法是Unlikelihood [44]，简单地优化策略，以最大化分配给yw的概率并最小化分配给yl的概率；我们在“不可能性”项上使用一个可选系数α ∈ [0, 1]。我们还考虑了使用从偏好数据中学到的奖励函数的PPO [37]以及PPO-GT，后者是从控制情感设置中可用的地面真实奖励函数学到的神经网络。在我们的情感实验中，我们使用了PPO-GT的两个实现，一个是现成的版本[42]，另一个是归一化奖励并进一步调整超参数以提高性能的修改版本（我们在运行“正常”的PPO时也使用这些修改）。最后，我们考虑了N次采样中的最佳基线，从SFT模型（或对话中的Preferred-FT）中采样N个响应，并根据从偏好数据集学到的奖励函数返回得分最高的响应。这种高效的方法将奖励模型的质量与PPO优化解耦，但在测试时对每个查询进行N次完成采样在计算上是不切实际的，即使对于中等的N也需要。

6.1 DPO如何有效地优化RLHF目标？

典型的RLHF算法中使用的KL受限奖励最大化目标在平衡奖励的同时限制策略不偏离参考策略太远。因此，在比较算法时，我们必须考虑到实现的奖励以及KL差异；即使稍微提高奖励，但KL差异较大，也未必是可取的。图2显示了在情感生成设置中各种算法的奖励-KL frontier。我们对每个算法执行多次训练运行，在每次运行中使用不同的策略保守性超参数（对于PPO，目标KL ∈ {3, 6, 9, 12}，对于不可能性，β ∈ {0.05, 0.1, 1, 5}，对于Preferred-FT，α ∈ {0.05, 0.1, 0.5, 1}，对于随机种子）。此扫描总共包括22次运行。在每次训练步骤达到收敛之后的100个步骤，我们评估每个策略在一组测试提示上，计算在真实奖励函数下的平均奖励，以及与参考策略的\(\text{KL}(\pi\vert \vert \pi_{\text{ref}})\)下的平均序列级KL。我们发现DPO产生了迄今为止最有效的frontier，实现了最高的奖励，同时仍然保持较低的KL。这个结果特别显着，有多个原因。首先，DPO和PPO优化相同的目标，但DPO明显更高效；DPO的奖励/KL权衡严格优于PPO。其次，即使PPO可以访问地面真实奖励（PPO-GT），DPO仍然实现了比PPO更好的frontier。

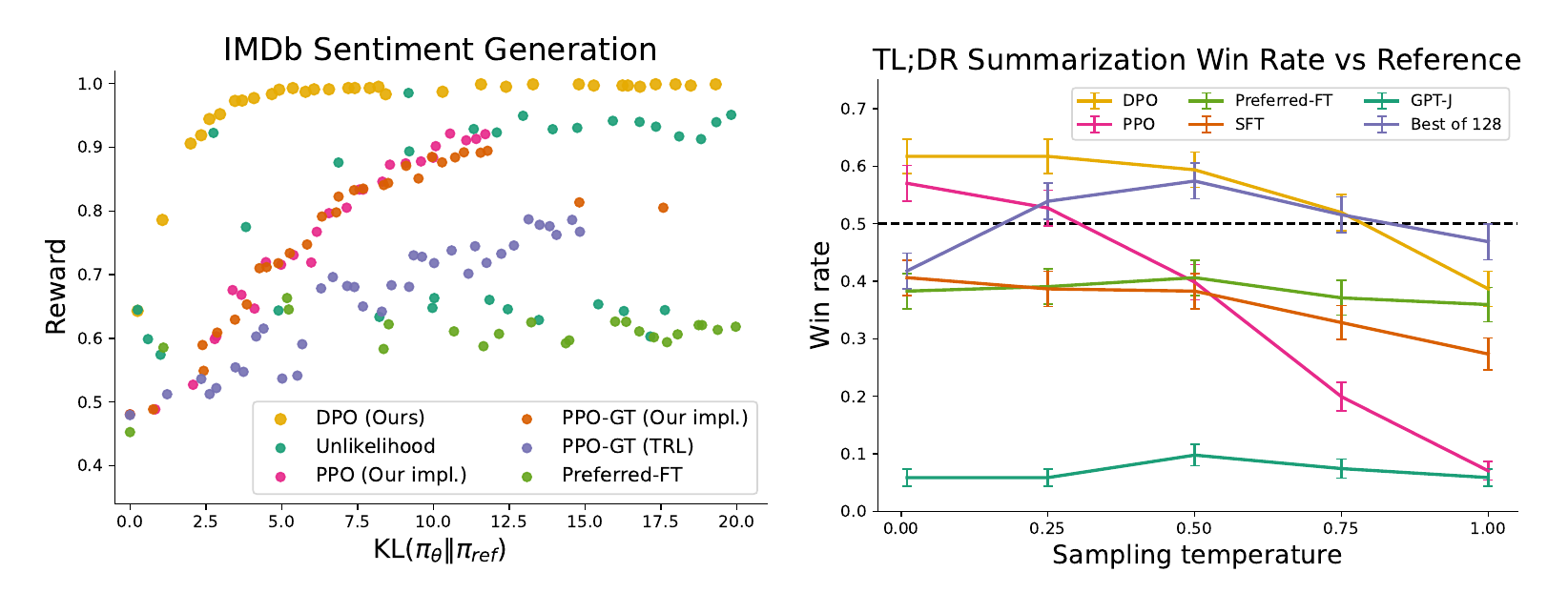图2：左图。预期奖励与与参考策略的KL之间的frontier。DPO在所有KL值上提供了最高的预期奖励，显示了优化的质量。右图。TL;DR摘要的胜率与人类撰写的摘要相对比，使用GPT-4作为评估器。在摘要生成方面，DPO超过了PPO的最佳性能，同时对采样温度的变化更具鲁棒性。

6.2 DPO在真实偏好数据集上的扩展性如何？

接下来，我们评估DPO在摘要生成和单轮对话中的微调性能。对于摘要生成，自动评估指标如ROUGE可能与人类偏好的相关性较差[38]，先前的研究发现使用PPO在人类偏好上微调LM可以提供更有效的摘要。我们通过在TL;DR摘要生成数据集的测试集上对完成进行采样，并计算与测试集中参考完成的平均胜率来评估不同的方法。所有方法的完成都以从0.0到1.0变化的温度进行采样，胜率显示在图2（右图）中。DPO、PPO和Preferred-FT都微调相同的GPT-J SFT模型[4]。我们发现在温度为0.0时，DPO的胜率约为61%，超过了PPO在其最佳采样温度为0.0时的57%的性能。与Best of N基线相比，DPO还实现了更高的最大胜率。我们注意到我们没有对DPO的β超参数进行实质性调整，因此这些结果可能低估了DPO的潜力。此外，我们发现DPO对于采样温度比PPO更具鲁棒性，而PPO的性能在高温下可能降至基础GPT-J模型的水平。Preferred-FT在SFT模型上并没有显著改进。我们还在第6.4节中直接比较了DPO和PPO的人类评估，在那里发现DPO在温度为0.25时的采样次数比PPO在温度为0时的采样次数高出58%。

在单轮对话中，我们在Anthropic HH数据集的测试子集上评估了不同方法，该子集包含一步人-助手交互。GPT-4评估使用测试中的首选完成作为参考来计算不同方法的胜率。由于此任务没有标准的SFT模型，我们从一个预训练的Pythia-2.8B开始，使用Preferred-FT在所选完成上训练一个参考模型，使完成处于模型的分布内，然后使用DPO进行训练。我们还与Best of 128 Preferred-FT完成（我们发现Best of N基线在这个任务中在128次完成时达到平稳状态；详见附录图4）和Pythia-2.8B基础模型的2次提示版本进行比较，发现DPO在每种方法的最佳性能温度下表现得相当好甚至更好。我们还评估了使用PPO在Anthropic HH数据集上从一个知名来源[6]进行训练的RLHF模型[5]，但无法找到比基础Pythia-2.8B模型性能更好的提示或采样温度。根据我们在TL;DR的结果以及两种方法都优化相同奖励函数的事实，我们认为Best of 128是PPO级别性能的粗略代理。总体而言，DPO是唯一在Anthropic HH数据集上比首选完成性能更好的计算效率高的方法，并且与计算要求高的Best of 128基线提供类似或更好的性能。最后，图3显示DPO相对迅速地收敛到其最佳性能。

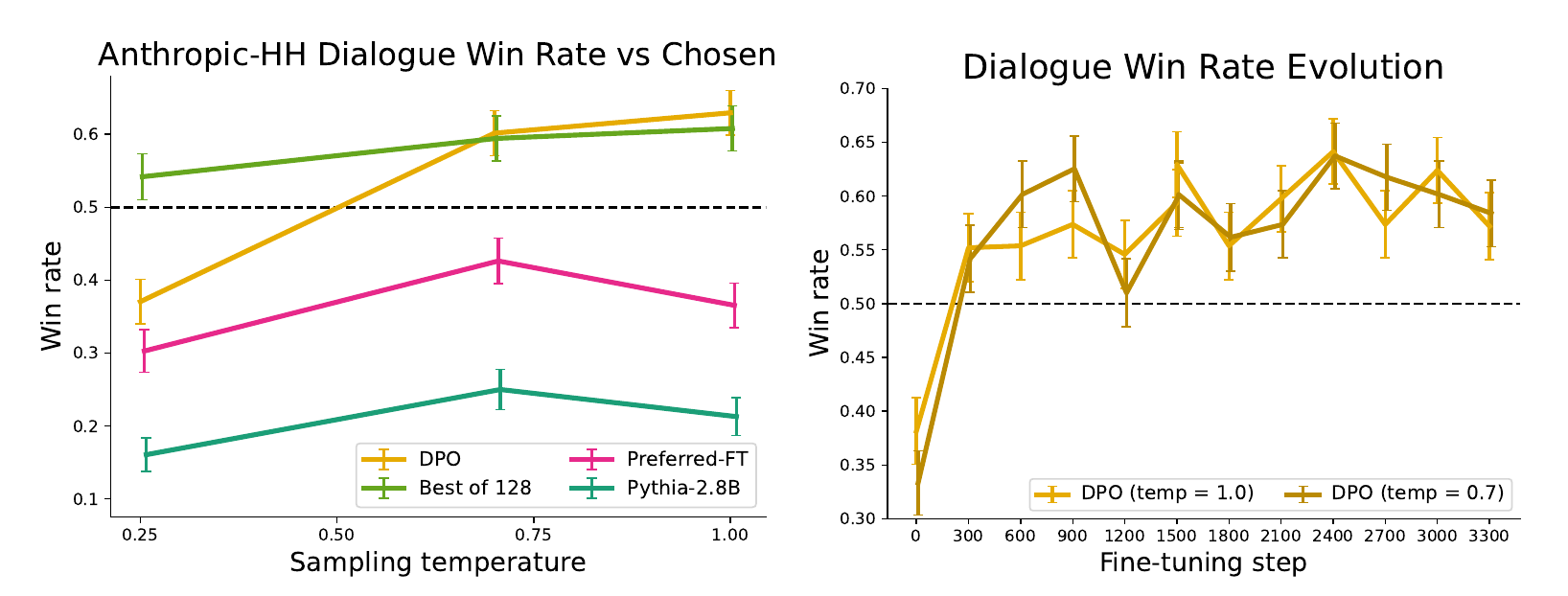图3：左图。由GPT-4计算的Anthropic-HH单步对话的胜率；DPO是唯一一个在Anthropic-HH测试集中超越所选摘要的方法。右图。在训练过程中不同采样温度的胜率。DPO在整个训练过程中对数据集标签的改进在不同采样温度下相对稳定。

6.3 对新输入分布的泛化

为了进一步比较PPO和DPO在分布转移下的性能，我们评估了来自我们Reddit TL;DR摘要实验的PPO和DPO策略在不同分布（CNN/DailyMail数据集[24]中的新闻文章）上的性能，使用TL;DR的最佳采样温度（0和0.25）。结果如表1所示。我们使用相同的GPT-4（C）提示计算了针对数据集中CNN/DailyMail的ground-truth摘要的GPT-4胜率，但将“forum post”替换为“news article”。对于这个新的分布，DPO继续以显著的优势胜过PPO策略。这个实验初步证明了DPO策略能够类似地泛化到PPO策略，尽管DPO没有使用PPO使用的额外的未标记的Reddit TL;DR提示。

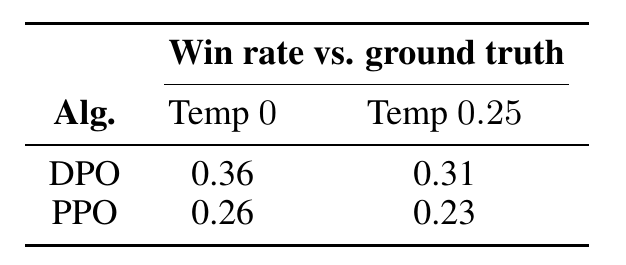表1：GPT-4在分布之外的CNN/DailyMail输入文章中与ground-truth摘要的胜率。

6.4 验证GPT-4评估与人类评估的一致性

我们进行了一项人类研究，以验证GPT-4的评估的可靠性，使用TL;DR摘要实验的结果和两个不同的GPT-4提示。GPT-4（S）（简单）提示简单地询问哪个摘要更好地总结了帖子中的重要信息。GPT-4（C）（简洁）提示还询问哪个摘要更为简洁；我们评估这个提示是因为我们发现与GPT-4（S）提示相比，GPT-4更喜欢更长、更重复的摘要。有关完整提示，请参见附录C.2。我们进行了三个比较，使用最高（DPO，温度0.25）、最低（PPO，温度1.0）和中等表现（SFT，温度0.25）的方法，以覆盖各种样本质量；所有三种方法都与贪婪采样的PPO（其性能最佳的温度）进行比较。我们发现，无论使用哪个提示，GPT-4都倾向于与人类一样经常达成一致，这表明GPT-4是人类评估的一个合理代理（由于人类评分者有限，我们只收集了DPO和PPO-1比较的多个人类判断）。总体而言，GPT-4（C）提示通常提供更符合人类的胜率；因此，我们在第6.2节的主要结果中使用此提示。有关人类研究的其他详细信息，包括呈现给评分者的Web界面和人类志愿者名单，请参见附录D.3。

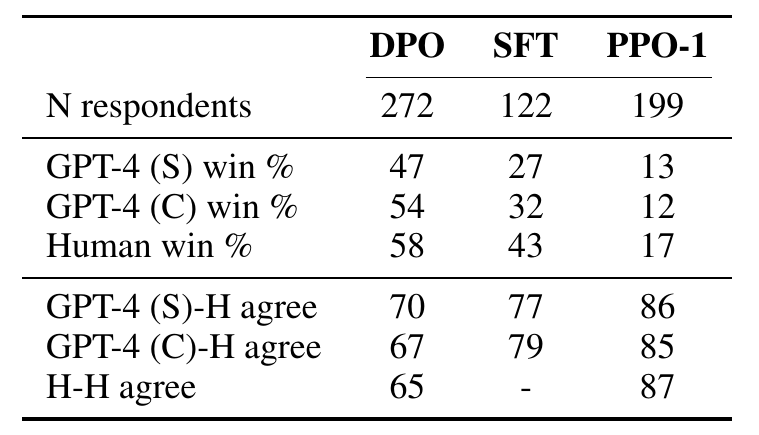表2：比较人类和GPT-4在TL;DR摘要样本上的胜率以及每个判断的一致性。人类与GPT-4的一致性与人类之间的一致性差不多。每个实验将来自所述方法的摘要与温度为0的PPO的摘要进行比较。

7 讨论

从偏好中学习是一种强大、可扩展的框架，用于训练具备能力和对齐的语言模型。我们引入了DPO，这是一种简单的训练范式，用于从偏好中训练语言模型，而无需使用强化学习。与强迫偏好学习问题适应标准强化学习设置以使用现成的强化学习算法不同，DPO确定了语言模型策略和奖励函数之间的映射，使得可以通过简单的交叉熵损失直接训练语言模型以满足人类偏好，而无需强化学习或丧失通用性。几乎没有超参数调整，DPO的性能与现有的RLHF算法相当或更好，包括基于PPO的算法；因此，DPO在从人类偏好中训练更多语言模型方面有着实质性的降低难度。

局限性和未来工作。我们的结果提出了未来工作的一些重要问题。与从显式奖励函数学习相比，DPO策略在分布之外的泛化能力如何？我们的初步结果表明，DPO策略可以类似于基于PPO的模型进行泛化，但需要进行更全面的研究。例如，使用来自DPO策略的自我标记进行训练是否同样能有效利用未标记的提示？在另一个方面，奖励过度优化在直接偏好优化设置中如何表现，图3右侧性能的轻微下降是否是其一个实例？此外，虽然我们评估了具有60亿参数的模型，但将DPO扩展到规模更大的最新模型是未来工作的一个激动人心的方向。关于评估，我们发现GPT-4计算的胜率受提示的影响；未来的工作可能会研究从自动化系统中引导高质量判断的最佳方法。最后，DPO存在许多可能的应用，超出了从人类偏好中训练语言模型的范围，包括在其他模态中训练生成模型。

• ← Previous Post
• Next Post →