本文介绍基于HMM模型的语音识别系统。更多文章请点击深度学习理论与实战:提高篇。
目录
HMM模型自从1980年代被用于语音识别以来,一直都是实际语音识别系统的主流方法。即使到了今天,End-to-End的语音识别系统不断出现,在工业界很多主流的系统仍然还是在使用基于HMM模型的方法,当然很多情况引入了深度神经网络用来替代传统的GMM模型。因此我们首先来了解一些经典的基于HMM模型的语音识别系统。
语音产生过程
语音的激励来自于肺呼出的气体,声门的不断开启和闭合会产生周期的信号,这个信号的频率就叫基音频率(fundamental frequency F0),如下图所示,这个信号的基频是150Hz。
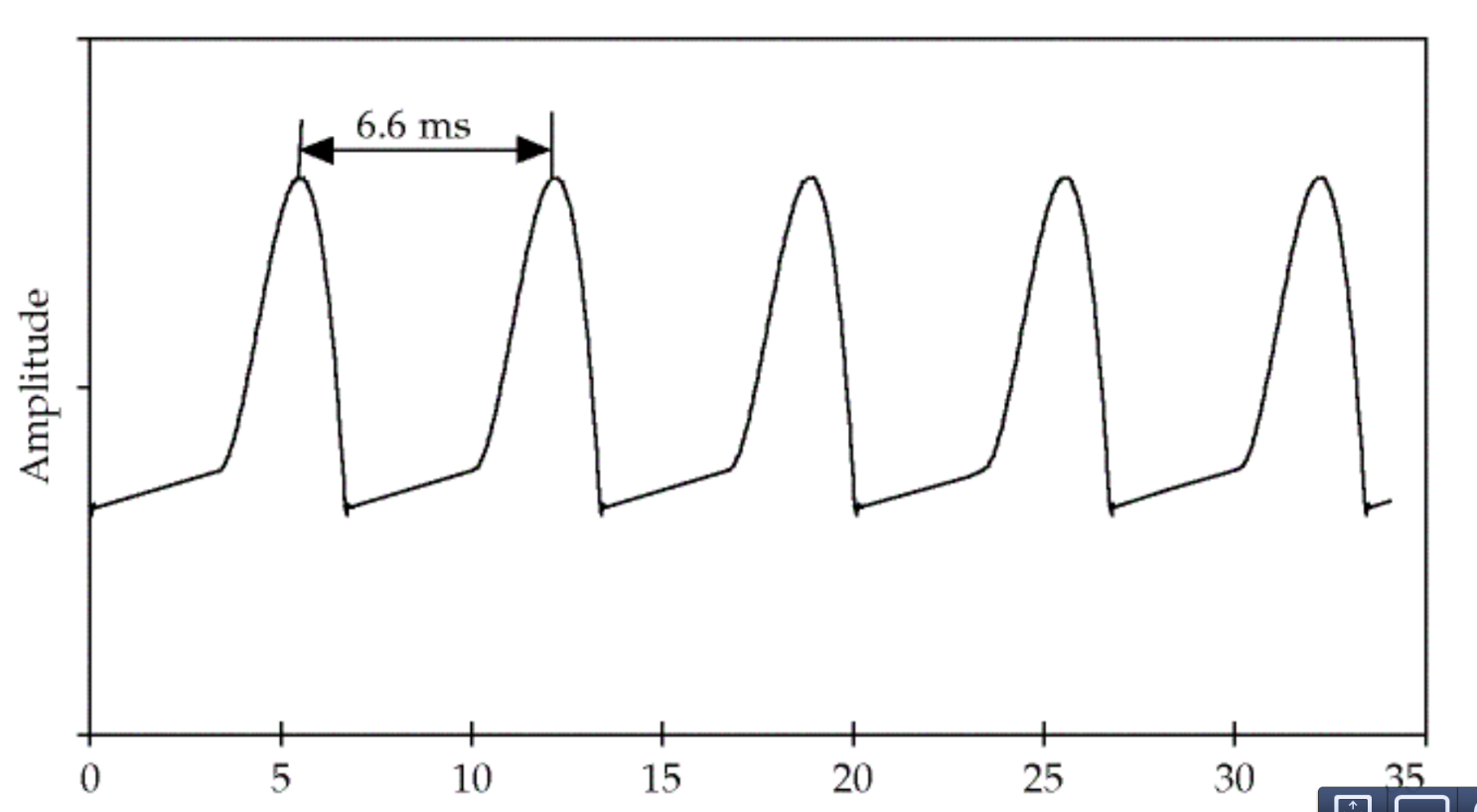 图:基音频率 图片来自课程cs224
图:基音频率 图片来自课程cs224
除了150HZ的基音频率,它也会产生300Hz、450Hz…的信号,这些叫做泛音(harmonics),最终得到的信号的频谱如下图所示。
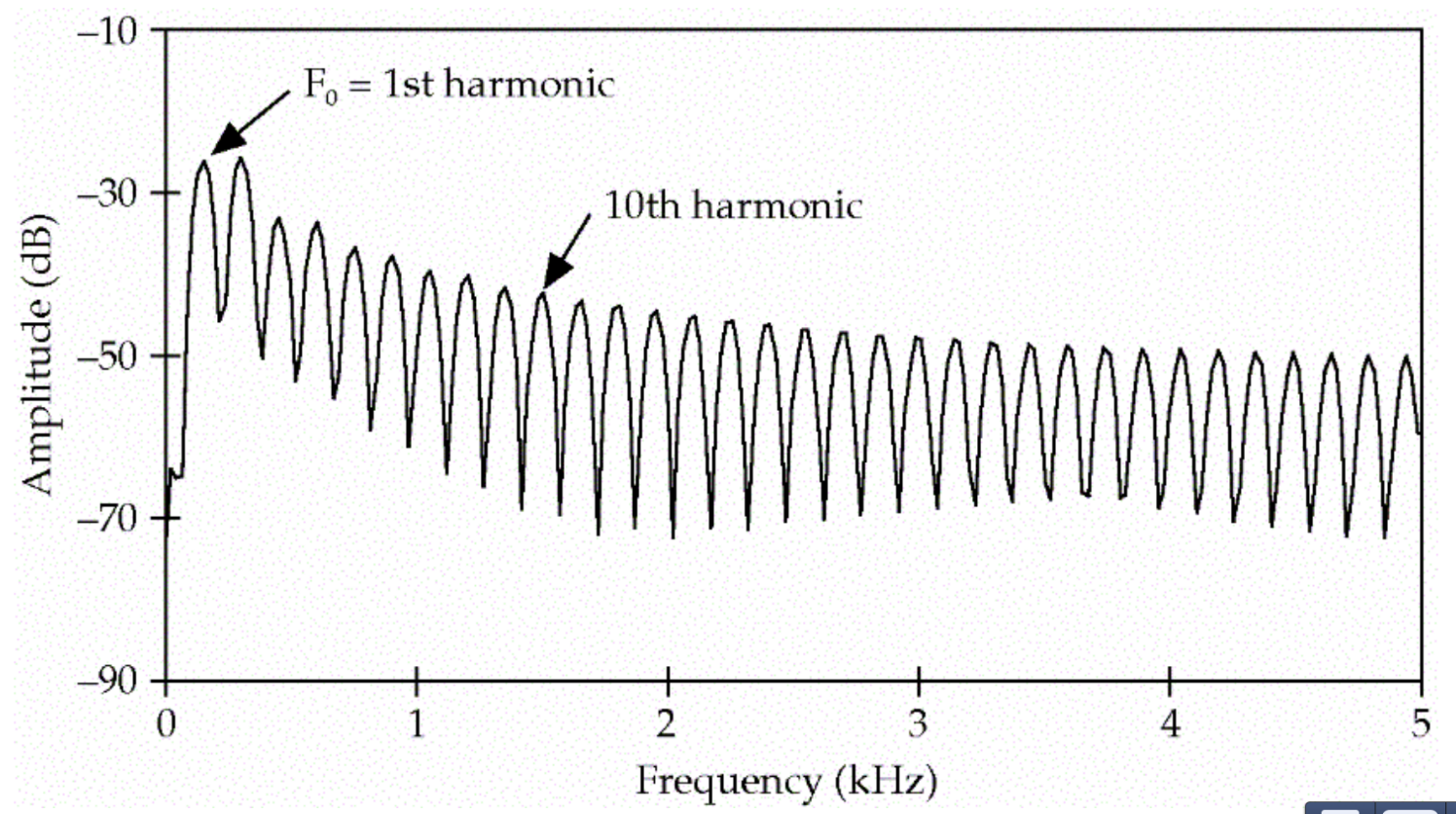 图:Harmonics 图片来自课程cs224
图:Harmonics 图片来自课程cs224
每个人的基音频率都是不同的,同时一个人也要发出各种不同的声音,这是怎么实现的呢?原理人在发不同音的时候声道、口腔、舌头、牙齿和鼻腔等发音器官会处于不同的开合状态,比如发a的时候口长得比较开,发s的时候我们让舌头和上牙之间有一个很小的缝隙,从而产生摩擦的声音。从信号处理的角度来说,这些发音器官的不同状态就产生了不同的滤波器。
我们每个人的基频虽然不同,但是在发相同的音的时候产生的滤波器都是类似的,因此我们每个人说”你好”的最终信号虽然不同,但是我们的口腔等发音器官的状态是类似的。因此我们也可以把发声看做如下图所示的过程。
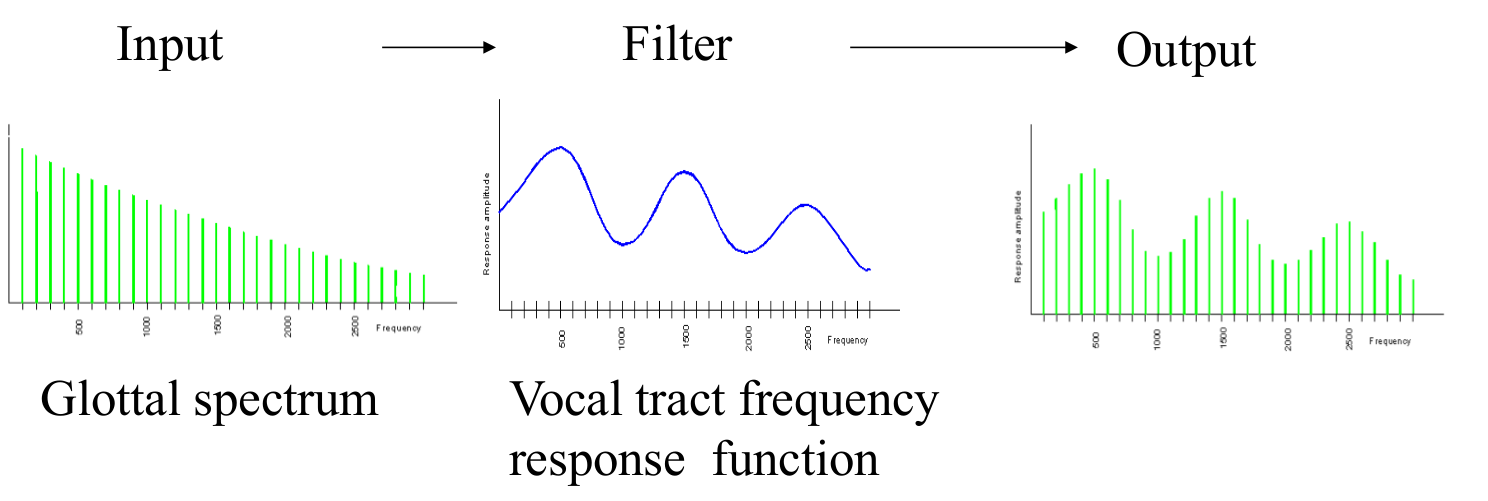 图:source-filter模型 图片来自课程cs224
图:source-filter模型 图片来自课程cs224
我们的呼吸带动声门的开闭产生的信号叫源(source),我们的声道等发声器官是滤波器(filter),它们作用的结果就是最终的语音信号。
听觉感知过程
说话产生的声波在空气中的震动,然后会传到耳朵里。人的耳蜗在接收到声音信号时,不同的频率会引起耳蜗不同部位的震动。高频声波是使耳蜗底部基底膜振动;低频声波使耳蜗顶部基底膜振动;中频声波使基底膜中部发生振动。我们大致可以认为不同部位的纤毛会接收不同频率的声波,因此耳蜗就像一个频谱仪,虽然它没有学习过傅里叶变换,但是它知道怎么进行傅里叶分析。因此为了模拟人类的听觉,我们通常需要把时域的信号变换成频域的信号。关于傅里叶分析,这个教程非常直观,建议读者阅读。
信号处理
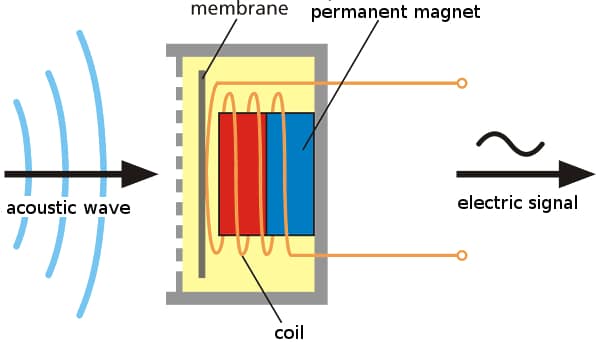
为了能让计算机处理,我们首先会使用麦克风把声压转换成电信号,如下图所示。工作的时候麦克风的膜片(membrane)会随着声波振动,从而把声波转换成不断变化强度的电信号。
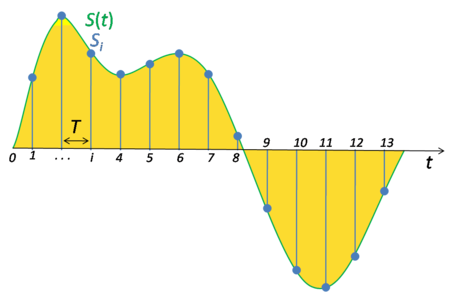
为了便于计算机处理,我们需要把模拟的电信号转换成数字信号。这就需要ADC(Analog-to-Digital Conversion)把模拟信号转换成数字信号,它包括采样和量化两个步骤。因为人类的语音来说,我们说话产生的声音的频率范围是小于8KHz的,根据奈奎斯特和香农采样定理,我们的采样频率只要达到16KHz(采样频率指的是每秒钟从模拟信号抽样的点的个数),那么就可以完全通过采样点恢复出原始信号。人类的听觉极限一般是20Hz-20KHz,因此CD一般使用44.1KHz的采样频率。采样过程如下图所示,因此采样把一个时间轴连续的信号变成离散的信号。
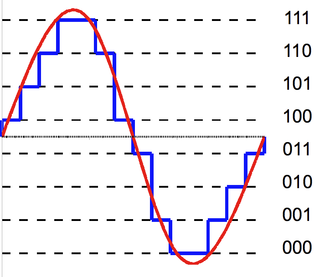
采样之后,我们的信号点由无穷个变成了有限个,但是信号的值还是一个连续的实数,所以我们需要使用量化技术把它离散化。
比如上图使用的3bit的量化,那么总共有8种可能的取值,我们把任意一个实数值”量化”到最接近的那个值。对于语音信号来说,我们通常使用16bit的量化,也就是有$2^{16}=64K$种不同的取值。
在实际的电话系统中,为了减少传输的数据量,通常会使用A律(A-Law)或者μ律(μ-Law)把16bit的信号压缩成8bit,中国和欧洲采用的是A律,美国和日本采用的是μ律。
上面描述的采样和量化过程通常也叫脉冲编码调制(Pulse Code Modulation, PCM),这是个通信的术语,我们知道就行了。
特征提取
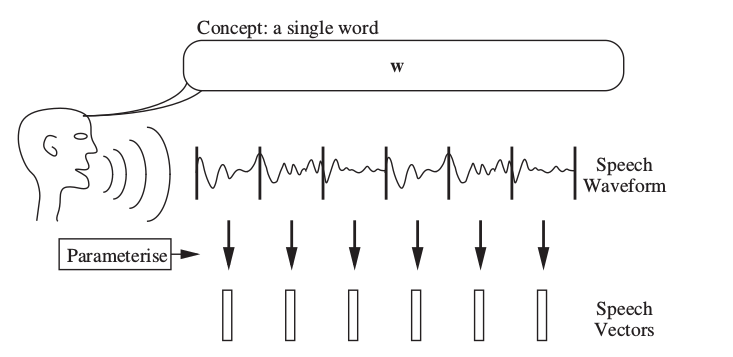
前面我们分析了人耳的听觉其实是频谱的分析,因此计算机也要模拟这个过程。上述得到的是时域的信号(信号岁时间的变化),但是语音信号是个时变信号,直接对很长时间的语音做傅里叶变换并无意义,因此我们通常先需要把语音信号切分成很短的窗口(通常是25ms的时长),然后通过特征提取从这个窗口提取一个特征向量。因此一个时域信号在特征提取之后就变成了特征向量的序列,如下图所示。
对于语音识别来说,最常见特征提取方法是MFCC。因为细节比较多,所以MFCC特征提取放到单独的一篇文章,请阅读MFCC特征提取教程。
HMM模型简介
通过特征提取之后,输入的一段语音信号就变成了特征向量的序列。语音识别系统需要根据特征向量序列来识别对应的词序列,这是一个序列标注的问题。Hidden Markov Mode(HMM)是一种解决序列标注问题的模型,在语音识别领域得到广泛应用。它一直是语音识别的主流框架,即使到了深度学习时代,不断的出现End-to-end的模型,但到目前为止还是有很多系统使用HMM(不过也加入了很多深度学习的模型)。
为了便于理解,我们首先通过一个假想的例子来说明什么是HMM。假设我们是来自2799年的气候学家,我们想知道2007年夏天的气温。我们找不到气象局的数据,但是发现了Jason的日志,他每天会记录吃了几个雪糕。一般来说天气越热,他吃的雪糕数量就越多,因此我们可能根据这个信息猜测某天的气温。为了简化问题,我们假设气温只分为热(Hot)和冷(Cold)两个取值。因此我们的问题为:给定观察序列O(每天吃雪糕的个数),猜测出最“可能”的状态序列(每天到底是冷是热)。
我们这里有两个重要信息:不同天气吃雪糕的概率是不同的;连续两天的天气的变化是有规律的。我们可以使用Hidden Markov Mode(HMM)来建模这个问题,HMM是一个生成模型,我们假设模型有一个隐状态的序列(天气序列),但是看不到;我们看到的是一个观察序列(吃雪糕数的序列)。HMM会有两个概率来利用前面说的两个重要信息:隐状态的跳转概率和发射概率。状态的跳转概率指的是从一个隐状态跳转到另一个隐状态的概率,比如今天是H,那么明天是H还是C的概率是不同的。而发射概率指的是如果天气是H(或者C),Jason吃雪糕数量的概率分布。
HMM模型的目的就是根据观察的序列,估计“最可能”的模型(就是这两个概率)。那什么叫最可能的模型呢?这两个概率都有无穷(或者只是很多)种可能,假设Jason吃雪糕的数量只能是$O={1,2,3}$,$p(O=1|H),p(O=2|H),p(O=3|H)$表示热天吃一、二和三支雪糕的概率,那么可能的一种概率分布是(0.1,0.2,0.7),也可能是(0.1,0.3,0.6),…,理论上有无穷种可能。但是模型一旦确定,我们可以计算在这个模型下看到某个序列的概率(计算方法后面会介绍)。存在一个(或者多个)模型使得这个概率最大,那么我们就可以认为这个模型是“最优”的。理论上我们可以“遍历”所有可能的模型,然后找到“最优”的模型,但实际上可能的模型参数是无穷的,因此我们需要更聪明的办法来找到这个最优的模型。下面我们先形式化的定义HMM以及HMM模型的三个问题。
定义
HMM包括如下部分:
-
$Q=\{Q_1,Q_2,…,Q_N\}$
包含N个状态的状态集合Q
-
$A=\{a_{11},a_{12},…,a_{1N},…,a_{N1},a_{N2},…,a_{NN}\}$
状态转移概率矩阵,要求$\sum_{j=1}^Na_{ij}=1$
-
$O=o_1o_2…o_T$
观察序列,也就是前面提取的特征,为了简单,我们这里先假设观察是离散(有限)的。这里每个$o_t$属于字典集合$\mathcal{V}=\{v_1,v_2,…,v_V\}$。
-
$B=b_i(o_t)$
观察似然(observation likelihoods),也叫发射概率(emission probabilities),表示在状态i看到观察$o_t$的概率
-
$q_0, q_F$
初始和结束状态,同时还包括初始状态到N个状态的跳转概率$q_{01},..,q_{0N}$和N个状态到结束状态的跳转概率$q_{1F},..,q_{NF}$,注意其它状态是不能跳到初始状态的,结束状态也不能跳到其它状态。
这里我们先假设是离散的(有限的),后面我们会把它推广到连续分布的情况。在有的书籍里,HMM可能没有特殊的初始状态和结束状态,那种HMM里除了状态跳转概率之外,还需要一个初始状态的概率分布。这两种方式本质上是等价的,但是使用初始状态和结束状态可以更方便的把多个HMM拼接成一个更大的HMM,这在语音识别中是非常有用的。模型一开始就处于初始状态,因此$P(Q_0=q_0)=1$,另外比较特殊的一点就是在HMM在这两个状态是不会生成观察数据的。
一阶HMM(这里只介绍一阶的HMM)有两个基本假设。第一个假设是当前状态只依赖于上一个状态,而与更早的状态无关。用数学语言描述就是:
\[P(q_i|q_1,...,q_{i-1})=P(q_i|q_{i-1})\]第二个假设就是当前的观察值只依赖于当前的状态,而与之前的状态无关,与其它的观察也无关。
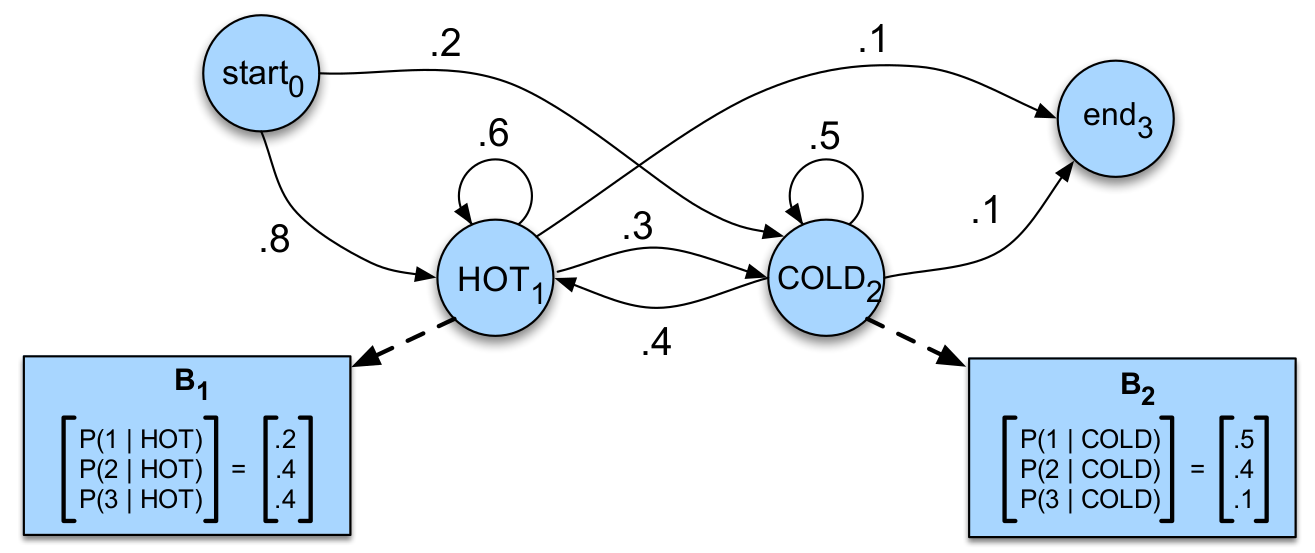
\[P(o_i|q_1,...,q_T,o_1,...,o_T)=P(o_i|q_i)\]比如上面的例子,下图是对应的HMM,这里的参数表示了一种可能的模型(不同的参数组合代表不同的模型,在机器学习里,我们通常研究某种形式的模型,它们的函数形式是类似的,只是参数不同)。有了模型,任意给定一个观察序列,我们就有办法(后面会介绍计算方法)计算这个模型产生(这就是所谓的生成式(generative)模型)这个序列的概率。
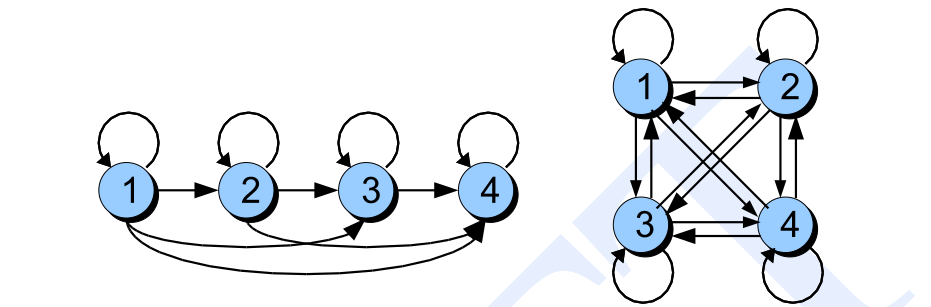
上面的HMM,每个状态(初始和结束状态不算)之间的跳转概率都是大于零的,这种HMM叫作各态历经的(ergodic)HMM。在语音识别中,我们通常使用自左向右的Bakis类型的HMM,如下图左所示。我们用一个HMM来建模一个单词,我们可以把发音分成3个阶段——开始阶段,中间阶段和收尾阶段。比如单词one的发音是/wʌn/,那么在/w/的状态只能跳到自己或者下一个状态/ʌ/(当然有的模型可以跳过下一个状态跳到下下个状态,用来表示非常快速的发音或者忽略某个发音),跳到自己表示当前时刻仍然还是在发/w/的音,而跳到下一个状态/ʌ/就表示/w/发音结束了。它只能从左往右跳转,而不能发完/ʌ/之后又来发/w/的音。
HMM有三个基本问题:
- 似然(Likelihood) 给定HMM$\lambda=(A,B)$和观察序列O,计算似然$P(O |\lambda)$
- 解码(Decoding) 给定HMM$\lambda=(A,B)$和观察序列O,寻找最优的状态序列Q
- 学习(Learning) 给定观察序列,寻找最优的模型参数$\lambda=(A,B)$
下面我们分别介绍怎么解决这三个问题。
似然:前向算法(forward algorithm)
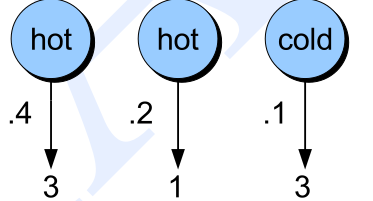
比如前面的例子,我们怎么计算$P(3,1,3|\lambda)$呢?这似乎有些困难,但是如果我们知道这三天的天气是(hot,hot,cold),那么就很容易计算条件概率$P(3,1,3|hot,hot,cold)$。因为根据假设2,我们很容易计算:
\[P(3,1,3|hot,hot,cold)=P(3|hot)P(1|hot)P(3|cold)\]如图下图所示,我们可以很容易的计算:
\[P(3|hot)P(1|hot)P(3|cold)=0.4*0.2*0.1=0.008\]我们想求的概率是$P(O)$。现在可以求出$P(O|Q)$,那么可以先求联合概率分布$P(O,Q)$,然后用联合概率分布对Q求和(如果是连续变量就变成积分)就可以得到边缘分布$P(O)$。我们首先来求联合分布:
\[\begin{split} P(O,Q) & =P(O|Q)P(Q) \\ & = P(q_0,q_1,q_2,...,q_T,q_F) P(o_1,o_2,...,o_T|q_0,q_1,q_2,...,q_T,q_F) \\ & = P(q_0) \prod_{i=1}^{T}P(q_i|q_0,...q_{i-1}) \prod_{i=1}^{T}P(o_i|q_0,...,q_F,o_1,...,o_{i-1}) \\ & = 1 \times \prod_{i=1}^{T}P(q_i|q_{i-1}) P(q_F|q_T) \prod_{i=1}^{T}P(o_i|q_i) \end{split}\]第三行的推导使用了前面的两个假设:当前状态只依赖前一个状态;当前观察值依赖当前状态。有了P(O,Q),我们就可以求P(O):
\[P(O)=\sum_QP(O,Q)\]但是上式需要遍历所有可能的状态序列$q_0, q_1, …, q_T,q_F$,如果HMM模型是各态历经的,那么每个$q_i,i=1,2,…,T$都有N种可能,那么总共有$N^T$种状态序列,即使HMM是Bakis类型的,可以去掉很多理论上不可能的序列,但复杂度仍然还是也是$O(N^T)$的。
但如果我们仔细分析,我们会发现很多重复计算。比如假设T=3,共有三种状态$Q=\{q_1,q_2,q_3\}$,我们考虑3个状态序列
\[\begin{split} q_1,q_2,q_1 \\ q_1,q_2,q_2 \\ q_1,q_2,q_3 \end{split}\]我们会计算:
\[\begin{split} P(o_1,o_2,o_3|q_1,q_2,q_1) =P(q_1|q_0)P(q_2|q_1)P(q_1|q_2)P(q_F|q_1) P(o_1|q_1)P(o_2|q_2)P(o_3|q_1) \\ P(o_1,o_2,o_3|q_1,q_2,q_2) =P(q_1|q_0)P(q_2|q_1)P(q_2|q_2)P(q_F|q_2) P(o_1|q_1)P(o_2|q_2)P(o_3|q_2) \\ P(o_1,o_2,o_3|q_1,q_2,q_3) =P(q_1|q_0)P(q_2|q_1)P(q_3|q_2)P(q_F|q_3) P(o_1|q_1)P(o_2|q_2)P(o_3|q_3) \end{split}\]我们会发现$=P(q_1|q_0)P(q_2|q_1)$和$P(o_1|q_1)P(o_2|q_2)$是重复计算。因此我们可以使用动态规划算法,长度为k的路径的概率可以复用长度为k-1的路径的概率计算结果。为了实现动态规划算法,我们首先定义前向(forward)概率$\alpha_t(j)$为:
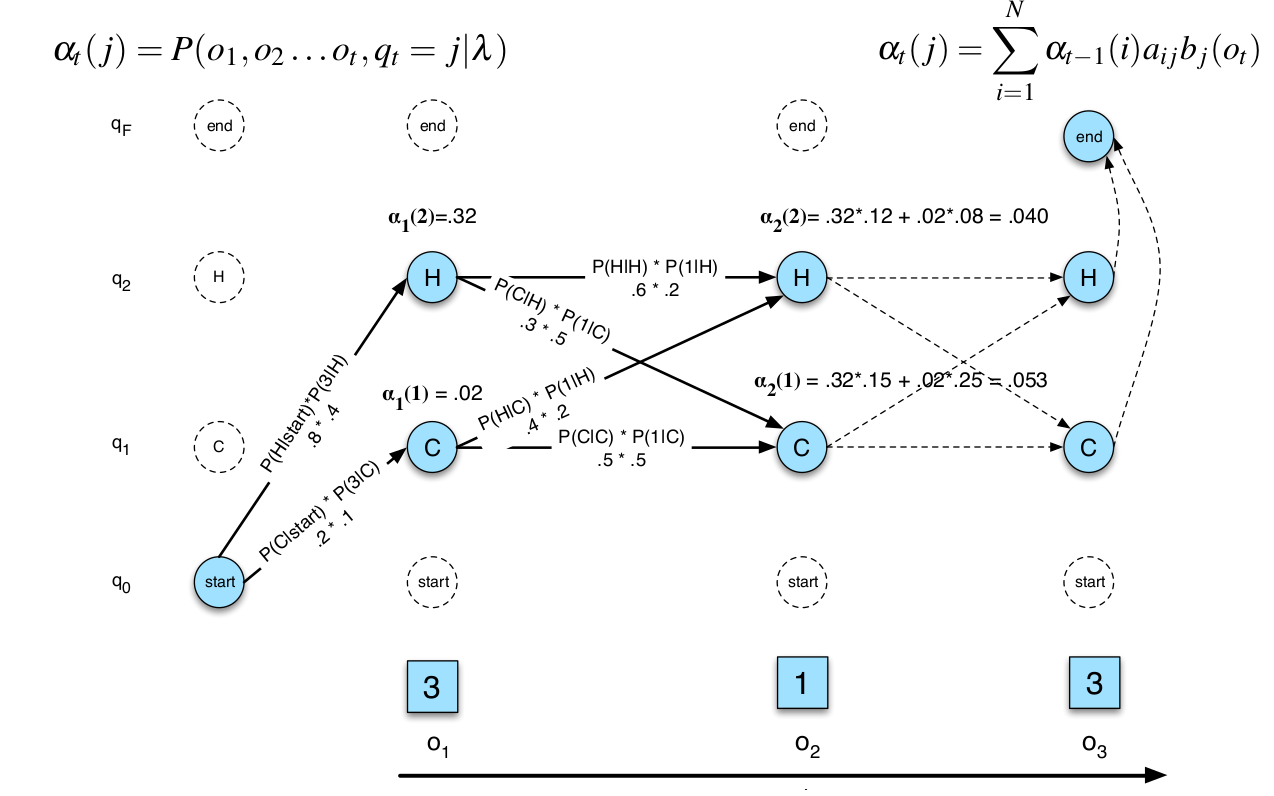
\[\alpha_t(j)=P(o_1,o_2,...,o_t,q_t=j|\lambda)\]前向概率$\alpha_t(j)$的意思是观察$o_1,o_2,…,o_t$并且t时刻的状态是j(更加准确的说法是$Q_j$)的联合概率分布。它可以由t-1时刻的前向概率递推得到:
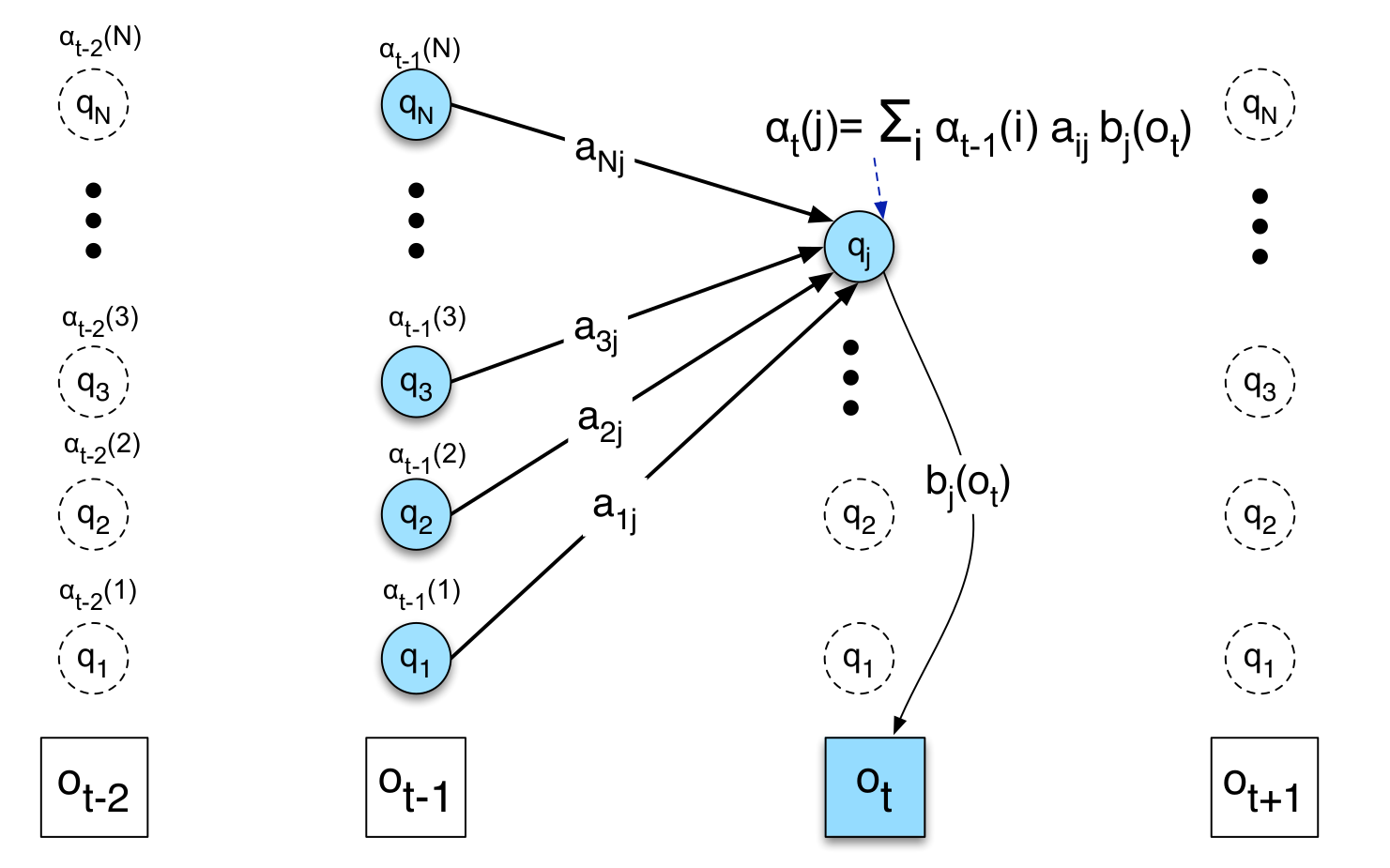
\[\alpha_t(j)=\sum_{i=1}^{N}\alpha_{t-1}(i)a_{ij}b_j(o_t)\]上面的递推公式可以用下图来解释:我们要计算t时刻处于状态j并且观察到$o_1,…,o_t$的概率,那么有N种可能:t-1时刻处于状态1并且观察到$o_1,…,o_{t-1}$并且从t-1时刻的状态1跳转到t时刻的状态j并且t时刻通过状态j发射$o_t$;t-1时刻处于状态2并且观察到$o_1,…,o_{t-1}$并且从t-1时刻的状态2跳转到t时刻的状态j并且t时刻通过状态j发射$o_t$,…。
t-1时刻处于状态1并且观察到$o_1,…,o_{t-1}$的概率就是$\alpha_{t-1}(1)$,而t-1时刻处于状态2并且观察到$o_1,…,o_{t-1}$的概率就是$\alpha_{t-1}(2)$,…。因此:
\[\alpha_t(j)=\alpha_{t-1}(1)a_{1j}b_j(o_t) + ...+ \alpha_{t-1}(N)a_{Nj}b_j(o_t)=\sum_{i=1}^{N}\alpha_{t-1}(i)a_{ij}b_j(o_t)\]根据定义,递推的初始条件为:
\[\alpha_1(j)=a_{0j}b_j(o_1), 1 \le j \le N\]这样我们可以一直递推得到$\alpha_T(1),…,\alpha_T(N)$,但是我们需要求的是$P(O|\lambda)$,怎么求这个概率呢?
\[P(O|\lambda)=\alpha_T(q_F)=\sum_{i=1}^{N}\alpha_T(i)a_{iF}\]Forward Trellis展示了前向算法的计算过程,比如预测天气的例子,如下图所示。
图中有两个状态$q_1,q_2$,观察序列为$o_1,o_2\text{和}o_3$。总共有$2^3=8$条不同的路径,我们首先计算$\alpha_1(1)$和$\alpha_1(2)$,接着计算$\alpha_2(1)$和$\alpha_2(2)$,然后是$\alpha_3(1)$和$\alpha_3(2)$,最后计算P(O)。读者可以对照前面的跳转概率自己计算一下。下面是前向算法的伪代码:
解码:Viterbi算法
解码问题是在给定观察和模型的条件下寻找一条“最优”的路径(状态序列Q),使得P(O,Q)的概率最大。当然我们也可以遍历所有路径然后选择最大概率的那条,但是这个时间复杂度太高。我们可以用和前向算法类似的动态规划算法来加快速度,这就是Viterbi算法。为了使用Viterbi算法,我们需要定义$v_t(j)$为:
\[v_t(j)=\underset{q_1...q_{t-1}}{max}P(q_0,q_1,...,q_{t-1},o_1,...,o_t, q_t=j|\lambda)\]$P(q_0,q_1,…,q_{t-1},o_1,…,o_t, q_t=j|\lambda)$是观察为$o_1,…,o_t$,状态为$q_0,…,q_{t-1},j$的联合概率。$v_t(j)$它要求在所有长度为t的路径中寻找最大的联合概率(当然也需要找到这条路径),要求是t时刻的状态是一定为j。
和前向算法类似,我们也可以用递推公式来计算。t时刻的最优路径一定是基于t-1时刻的最优路径的,这满足动态规划的最优子结构性质,从而可以使用动态规划算法。
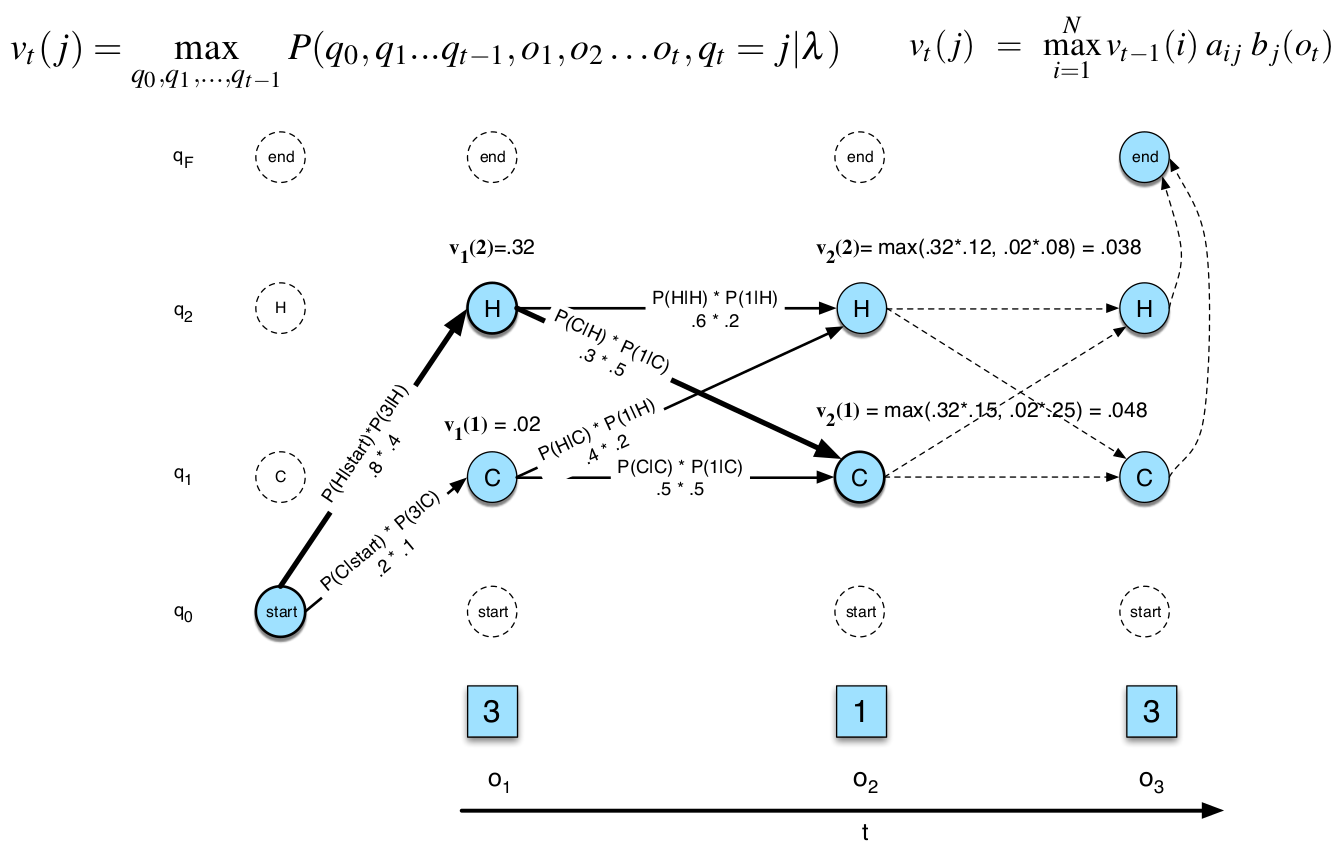
\[v_t(j)=max_{i=1}^N v_{t-1}(i)a_{ij}b_j(o_t)\]另外为了回溯,我们需要记下当前最优路径的上一个状态,我们可以使用数组$bt_t(j)$来保存它。下面我们把Viterbi算法的递推过程,首先初始条件可以更加定义直接得出:
\[\begin{split} v_1(j) & =a_{0j}b_j(o_1),\text{其中} 1 \le j \le N \\ bt_1(j) &=0 \end{split}\]然后是递推公式:
\[\begin{split} v_t(j)=max_{i=1}^N v_{t-1}(i)a_{ij}b_j(o_t), \text{其中} 1 \le j \le N , 1 \le t \le T \\ bt_t(j)=argmax_{i=1}^N v_{t-1}(i)a_{ij}b_j(o_t), \text{其中} 1 \le j \le N , 1 \le t \le T \end{split}\]最后步骤:
\[\begin{split} \text{最优路径的概率:} P*=v_T(q_F)=max_{i=1}^Nv_T(i)a_{iF} \\ \text{最优路径在T时刻的状态:} q_T*=bt_T(q_F)=argmax_{i=1}^Nv_T(i)a_{iF} \end{split}\]和前向算法类似,我们也可以使用Viterbi Trellis来展示计算过程,如下图所示。
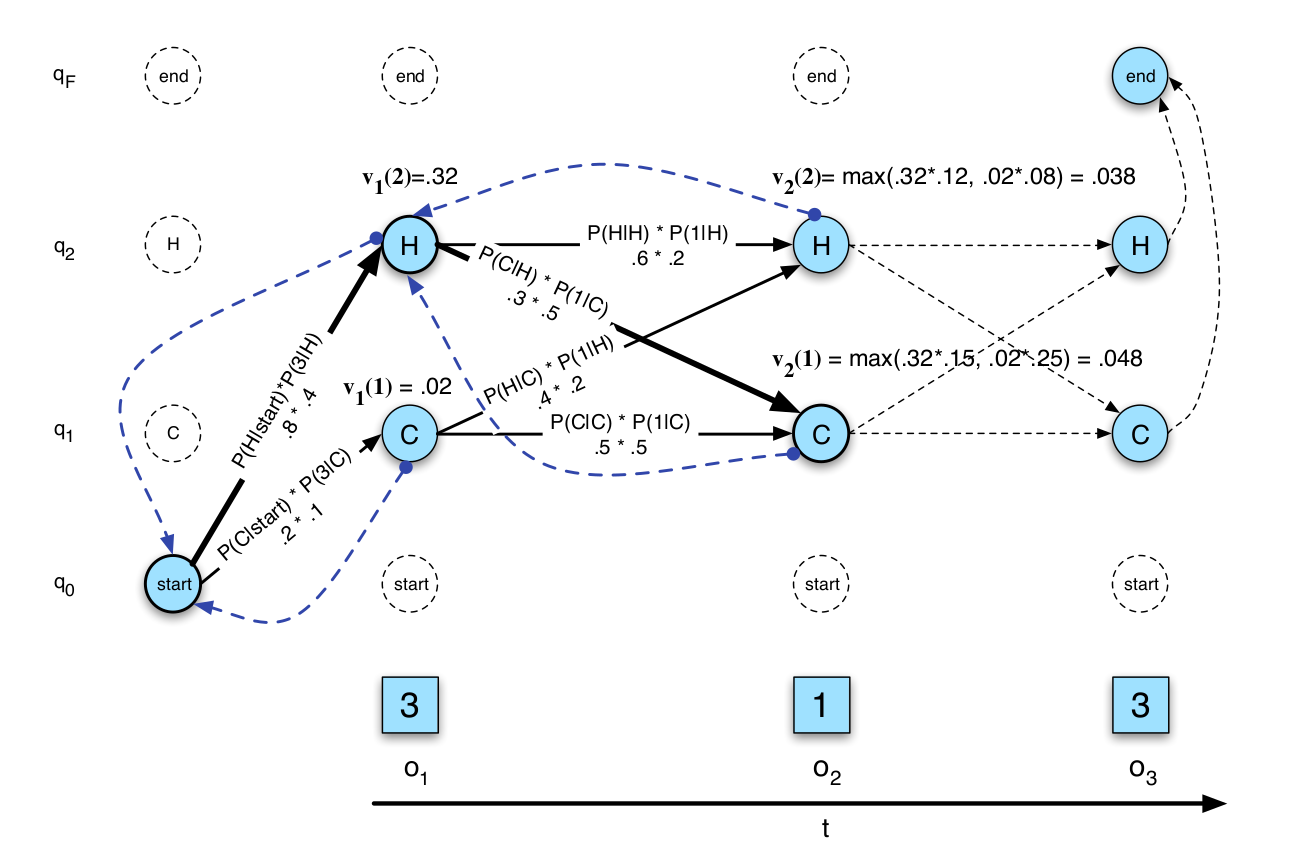
因为$bt_t(j)$记录了当前最优路径上一个时刻的状态,所以我们可以通过回溯的方法找到最优路径,如下图所示。
完整的算法伪代码如下:
学习:前向后向(forward-backward)算法
学习问题是:给定一些(我们先考虑一个)观察序列O,选择最优的模型参数(A,B)使得$P(O|\lambda)$的概率最大。我们可以使用前向后向算法,或者也叫Baum-Welch算法来解决学习问题。前向后向算法是EM(Expectation Maximization)算法的一个例子,我们这里先不介绍EM算法,而是通过更加直觉的方式来理解前向后向算法。
直接找到最优的参数使得$P(O|\lambda)$最大比较困难,但是如果我们知道观察序列O对应的状态序列Q的话,问题就容易很多了。比如我们需要估计跳转概率$a_{ij}$,它的最大似然估计就是:
\[\hat{a}_{ij}=\frac{C(i \rightarrow j)}{\sum_{q \in Q} C(i \rightarrow q)}\]这个公式很符合直觉:要知道从状态i跳转到j的概率,首先数一下从i到j跳转的次数,然后再除以所有i出发的跳转,从而使得$\sum_ja_{ij}=1$。类似的我们可以估计发射概率:
\[\hat{b}_j(v_k)=\frac{\sum_{t=1}^T 1_{[o_t=v_k and s_t=j]} }{\sum_{t=1}^T 1_{[s_t=j]} }\]其中函数\(1_{[s_t=j]}\)是indicator函数,如果t时刻的状态为j,它的值为1,否则为0。因此分母就是状态j出现的次数。类似的,\(1_{[o_t=v_k and s_t=j]}\)是t时刻的状态为j并且观察是$v_k$,因此分子就是状态为j并且观察是$v_k$出现的次数。
现在的问题是我们并不知道观察O对应的状态序列。回忆一下前面的解码问题:如果我们知道模型的最优参数,那么我们可以使用Viterbi算法找到“最优”的状态序列,假如有了这个状态序列,我们就可以估计模型的最优参数。这似乎是一个鸡生蛋蛋生鸡的问题——知道模型参数就可以通过Viterbi算法找到隐状态,知道隐状态就可以学习模型参数。
现在两者都不知道怎么办?我们可以先随机初始化一组模型参数,根据这组模型参数估计最优的状态序列;有了状态序列,我们又可以最大似然估计模型的参数。可以证明(但这里不会证明)新的模型参数要比之前的更好,这样我们就可以不断的循环这个过程——用新的模型参数再去求最优序列,然后再用新的状态序列估计更新的参数。直到新参数和旧参数一样才停止,实际的停止条件是超过一定迭代次数或者新旧参数差不多。这个时候可以证明我们找到了局部最优的解(但不是全局最优解)。
注意:上面描述的算法通常叫作Viterbi训练算法。那什么是前向后向算法?它和Viterbi算法有什么区别?
Viterbi训练算法的问题在于它会为每一个时刻找一个固定的“最优”的状态,但很多时候某个观察到底是属于哪个状态是很难确定的。尤其在迭代的早期,本来模型就不好,用它来找到的“最优”状态序列就不准,然后用不准的状态来估计模型参数就更不准了。所以更好的办法是用当前的模型计算每个时刻的状态的概率分布,这样可以避免前面的问题。那怎么计算每个隐状态的概率分布呢?这就需要用到前向后向算法了。
我们首先定义$\gamma_t(j)$为t时刻处于状态j的概率:
\[\label{eq:fb-gamma} \gamma_t(j)=P(q_t=j|O,\lambda)\]根据概率的定义,需要$\sum_j\gamma_t(j)=1$。有了这个概率之后,我们就可以计算:
\[\hat{b}_j(v_k)=\frac{\sum_{t=1}^T 1_{[o_t=v_k]} \gamma_t(j) }{\sum_{t=1}^T \gamma_t(j)}\]我们首先来看这个公式的分母,分母可以认为是状态j出现的次数,不过t时刻j可能出现0.5次,表示t时刻状态为j的概率是0.5。而之前t时刻要么状态为j,要么不为j,也就是概率要么是1,要么是0。类似的,分子是状态为j并且观察为$v_k$的次数。和分母一样,分子可以可能在t时刻出现0.5次的情况。$\gamma_t(j)$也叫作状态占有(State Occupation)概率,表示某个时刻被某个状态“占有”的概率。除了$\gamma_t(j)$,我们还需要定义一个跳转的概率$\epsilon_t(i,j)$,它表示t时刻状态为i并且t+1时刻状态为j的概率。
\[\epsilon_t(i,j)=P(q_t=i,q_{t+1}=j|O,\lambda)\]有了它之后我们可以估计$\hat{a}$:
\[\begin{split} \hat{a_{ij}} & =\frac{\sum_{t=1}^{T-1} \epsilon_t(i,j) }{\sum_{t=1}^{T-1}\sum_{k=1}^{N}\epsilon_t(i,k)} \\ & =\frac{\sum_{t=1}^{T-1} \epsilon_t(i,j) } {\sum_{t=1}^T \gamma_t(i)} \end{split}\]分子可以看作从i跳到j的次数(当然和前面一样,可能出现0.5次);而分母是状态i出现的次数。注意:
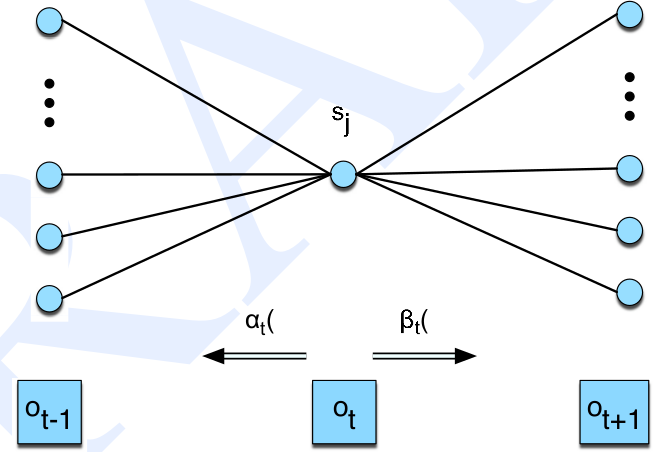
\[\gamma_t(i)=\sum_{k=1}^{N}\epsilon_t(i,k)\]接下来的问题就是怎么用前向后向算法计算$\gamma_t(j)$和$\epsilon_t(j,k)$,我们之前定义了前向概率$\alpha_t(j)$,我们还需要定义后向概率$\beta_t(i)$:
\[\beta_t(i)=P(o_{t+1}, ..., o_T|q_t=i,\lambda)\]前向概率是看到$o_1,…,o_t$,而后向概率是看到$o_{t+1},…,o_T$。还有一点就是:前向概率是观察和状态的联合概率分布;而后向概率$q_t=i$是条件。
后向概率也可以类似前向概率那样通过递推来计算。初始条件可以根据定义直接计算:
\[\beta_T(i)=a_{iF}, 1 \le i \le N\]递推公式:
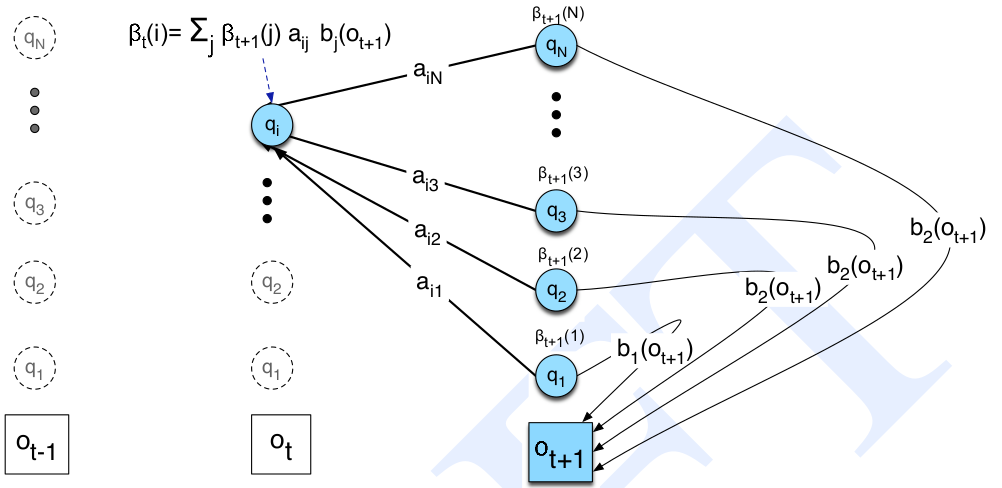
\[\beta_t(i)=\sum_{j=1}^{N}a_{ij}b_j(o_{t+1})\beta_{t+1}(j), 1 \le i \le N, 1 \le t < T\]最后的计算:
\[P(O|\lambda)=\beta_1(0)=\alpha_T(q_F)=\sum_{j=1}^{N}a_{0j}b_j(o_1)\beta_1(j)\]后向概率的递推公式可以参考下图。最后我们发现,后向概率也可以用来计算似然概率$P(O|\lambda)$,它们的方向是相反的。前向概率是联合概率而后向概率是条件概率。
这里读者可能会有疑问,前向概率已经能计算似然概率了,我们再计算一个后向概率有什么用处?回顾一下,我们这里的目的并不是计算似然概率,而是计算$\gamma_t(j)$和$\epsilon_t(i,j)$。有了前向和后向概率之后,我们就可以计算这两个概率:
\[\begin{split} \gamma_t(j) & =P(q_t=j|O,\lambda) \\ & = \frac{P(q_t=j,O|\lambda)}{P(O|\lambda)} \\ & = \frac{P(o_1,...,o_t,o_{t+1},...,o_T, q_t=j|\lambda)}{P(O|\lambda)} \\ & = \frac{P(o_1,...,o_t,q_t=j|\lambda) P(o_{t+1},...,o_T|q_t=j,\lambda)}{P(O|\lambda)} \\ & = \frac{\alpha_t(j)\beta_t(j)}{P(O|\lambda)} \end{split}\]大部分推导过程只是用到概率的定义,在第三步用到了公式:
\[\begin{split} P(X,Y|Z) & =P(X|Y,Z)P(Y|Z) \\ P(X|Y,Z) & =\frac{P(X,Y|Z)}{P(Y|Z)} \end{split}\]读者可以根据条件概率的定义推导这两个公式,后面的推导也会反复用到这两个公式,请读者熟悉它们。一种记忆方法就是把Z去掉,它们就变成了:
\[\begin{split} P(X,Y) & =P(X|Y)P(Y) \\ P(X|Y) & =\frac{P(X,Y)}{P(Y)} \end{split}\]这两个公式读者应该非常熟悉,因此可以对比记忆。从上式中,分子是t时刻的前向概率乘以后向概率,分母是似然概率。从这里读者也可以明白为什么后向概率要定义成条件概率了,因为这样定义就可以很容易的计算状态占有概率$\gamma_t(j)$。类似的,我们也可以参考下图来解释怎么根据前向和后向概率来计算状态占有概率。
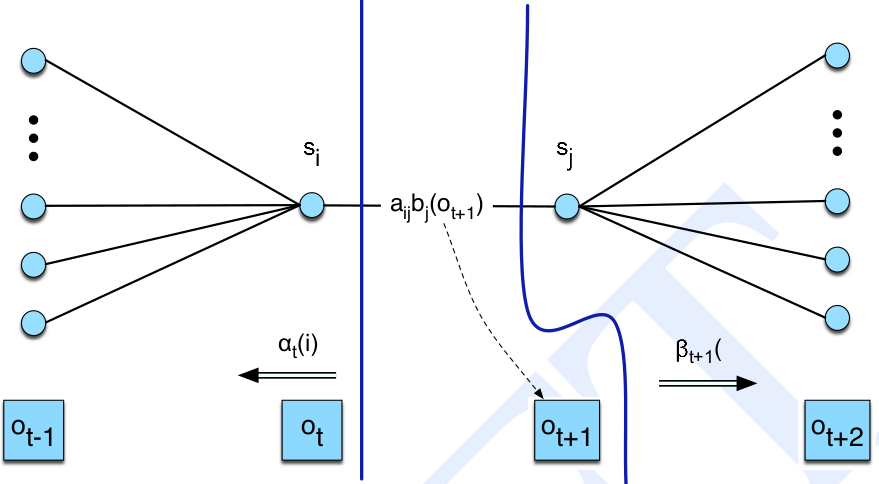
\[\begin{split} \epsilon_t(i,j) & = P(q_t=i, q_{t+1}=j|O,\lambda) \\ & = \frac{P(q_t=i, q_{t+1}=j, O|\lambda)}{P(O|\lambda)} \\ & = \frac{P(q_t=i, q_{t+1}=j, o_1,...,o_t,o_{t+1},..,o_T|\lambda)}{P(O|\lambda)} \\ & = \frac{P(o_1,...,o_t, q_t=i, q_{t+1}=j, o_{t+1},..,o_T|\lambda)}{P(O|\lambda)} \\ & = \frac{P(o_1,...,o_t, q_t=i|\lambda)P(q_{t+1}=j, o_{t+1},..,o_T|o_1,...,o_t, q_t=i,\lambda)}{P(O|\lambda)} \\ & = \frac{\alpha_t(i)}{P(O|\lambda)} P(q_{t+1}=j, o_{t+1},..,o_T|o_1,...,o_t, q_t=i,\lambda) \\ & = \frac{\alpha_t(i)}{P(O|\lambda)} P(o_{t+1},..,o_T|q_{t+1}=j, o_1,...,o_t, q_t=i,\lambda)P(q_{t+1}=j|o_1,...,o_t, q_t=i,\lambda) \\ & = \frac{\alpha_t(i)}{P(O|\lambda)} P(o_{t+1},..,o_T|q_{t+1}=j,\lambda)P(q_{t+1}=j|q_t=i,\lambda) \\ & = \frac{\alpha_t(i)}{P(O|\lambda)} P(o_{t+1}|q_{t+1}=j,\lambda)P(o_{t+2},...,o_T|q_{t+1}=j,\lambda) a_{ij} \\ & = \frac{\alpha_t(i)}{P(O|\lambda)}a_{ij}b_j(o_{t+1})\beta_{t+1}(j) \\ & = \frac{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}{P(O|\lambda)} \end{split}\]上面的推导反复使用了条件概率的定义,此外也用到HMM的两个假设。读者可以参考下图来理解推导过程。
- 显示Disqus评论(需要科学上网)