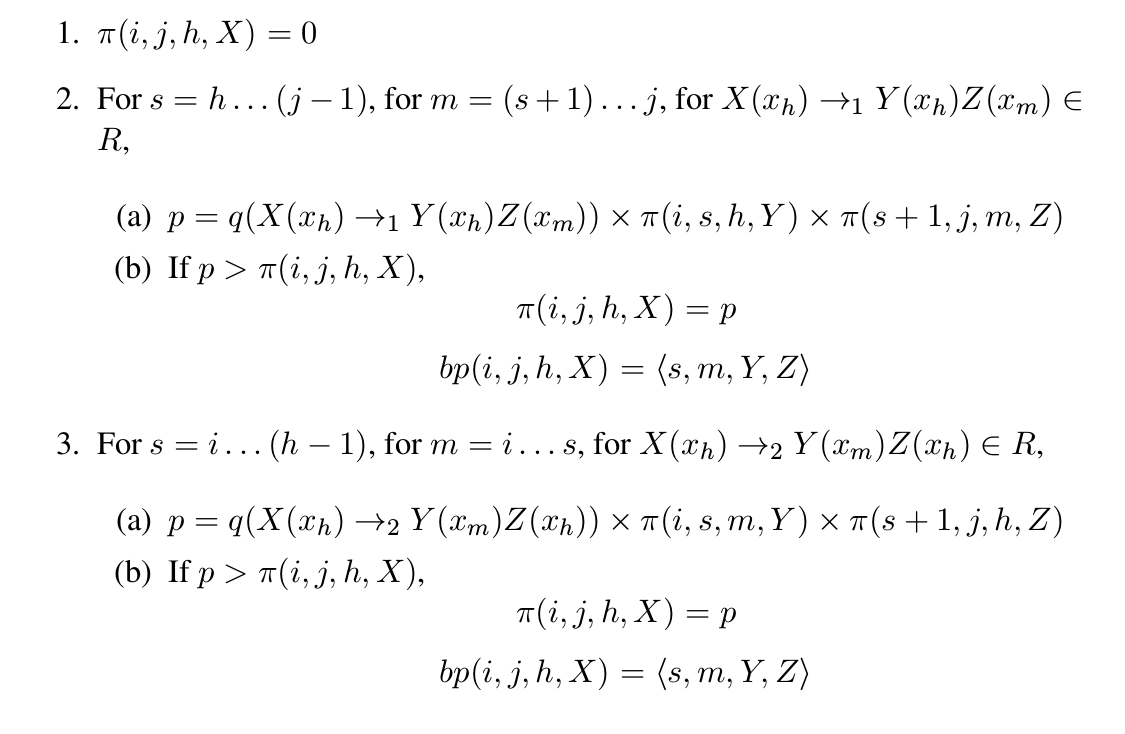本文介绍成分句法分析。更多文章请点击深度学习理论与实战：提高篇。
目录
- 简介
- 上下文无关文法(Context-Free Grammars/PCFGs)
- CFG的歧义
- PCFGs的定义
- PCFGs的参数估计
- PCFGs的Parsing
- 词汇化的(Lexicalized)PCFGs
- 成分句法分析的效果评估
简介
英语的语法分析很早就有，我们(中国人)现在学习英语非常重要的部分依然是学习语法(Grammar)。我们这里研究的是句法(Syntax)分析，语法(Grammar)和句法(Syntax)的区别是什么呢？语法(grammar)包括句法(Syntax)、词法(morphology)和音韵学(phonology)。因此语法是一个比句法更大的概念，音韵学是研究发音的学科，更多的是和语音识别与语音合成有关。句法是研究词和词如何组合成正确的句子，而词法则主要研究词的变形。举个例子：「主语是第三人称单数时，谓语动词要用第三人称单数形式」，这是一条语法规则。其中的第三人称（人称）、单数（数）是词法的范畴，主语、谓语动词、主谓一致则是句法的范畴。
句法(Syntax)的英语单词来源于希腊单词sýntaxis，它的意思是布置(arrangement)和放在一起(setting out together)，也就是研究怎么样把词汇组织成句子。 语言学中有很多种句法分析的理论和方法，最常见的一种就是成分(Constituency)分析，这也是本节的内容，后面我们会介绍另外一种句法分析——依存句法分析。
成分(Constituency)是一种抽象，它把(语法)作用相同(相似)的一些词组合成一个单元。比如名词短语(Noun Phrase)，它的语法作用和名词类似，可以在句子中充当主语或者宾语等成分。因此成分句法分析就是分析怎么由词构成短语，有简单短语构成复杂短语，最终构成句子的过程。下面我们来介绍用于成分句法分析的最常见PCFGs。
上下文无关文法(Context-Free Grammars/PCFGs)
上下文无关文法是一个4元组$G=(N,\Sigma,R,S)$，其中：
- N是一个有限的非终结符集合
- $\Sigma$是一个有限的终结符集合(字母表)
- R是一个有限的产生式规则集合，每一个产生式规则的形式为$X \rightarrow Y_1Y_2…Y_n$，其中$X \in N$，$Y_i \in N \cup \Sigma$。
- $S \in N$是一个特殊的开始符号
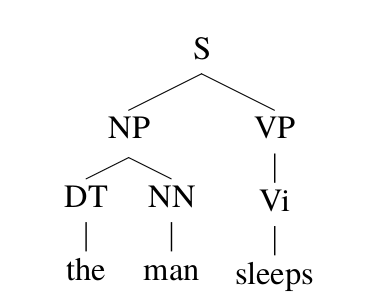
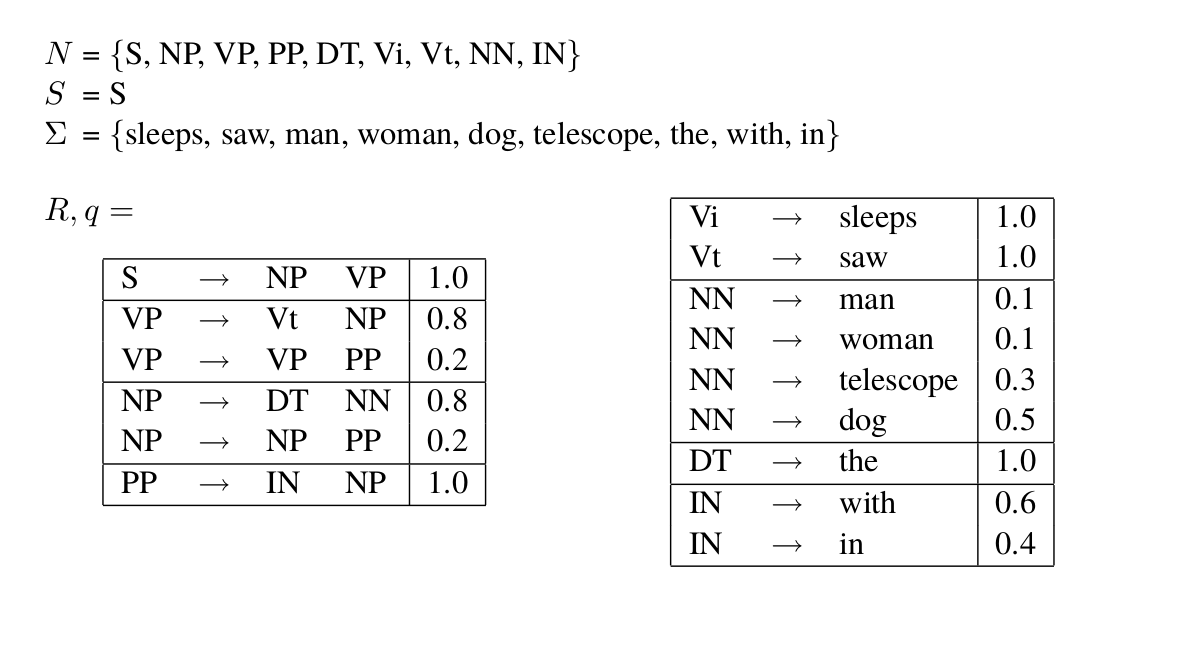
下图是一个简单的CFG，它是英语语法的一部分。N是基本的句法类别(Syntax Categories)，比如开始符号S代表句子(Sentence)，NP代表名词短语(Noun Phrase)，VP代表动词短语(Verb Phrase)。$\Sigma$代表词典。产生式规则：
\[\begin{split} S \rightarrow \text{NP VP} \\ \text{NN} \rightarrow man \end{split}\]第一个规则表示一个句子可以由一个名词短语和一个动词短语组合而成。而第二个规则表明一个单数名词(NN)可以是单词”man”。产生式规则$X \rightarrow Y_1Y_2…Y_n$非常灵活，只要满足$X \in N$和$Y_i \in N \cup \Sigma$就行。比如我们可以有一元(unary)的产生式规则：
\[\begin{split} \text{NN} \rightarrow man \\ S \rightarrow \text{NP} \end{split}\]产生式规则的右边也可以同时有终结符和非终结符，比如：
\[\begin{split} \text{VP} \rightarrow \text{John Vt Mary} \\ \text{NP} \rightarrow \text{the NN} \end{split}\]产生式规则的右边甚至可以是空，比如：
\[\begin{split} \text{VP} \rightarrow \epsilon \\ \text{VP} \rightarrow \epsilon \end{split}\]这里用$\epsilon$表示空字符串。
图：CFG的示例
接下来我们介绍一下CFG的最左(left-most)推导(Derivations)。给定一个CFG，一个最左推导是字符串的序列$s_1…s_n$，其中：
- $s_1=S$，也就是说$s_1$是只包含开始符号的字符串
- $s_n \in \Sigma^*$，即最后一个字符串只包含终结符号
- $s_i$是这么从$s_{i-1}$推导出来的——把$s_i$的右边的第一个非终结符号用一个产生式规则的右边替换得到，要求这个产生式规则的左边就是$s_i$的第一个非终结符号
第三条看起来有点复杂，但其实很简单，下面我们通过一个例子来说明。还是以上图的CFG为例。下面是一个推导过程：
\[\begin{split} & s_1=S \\ & s_2= \text{NP VP} (S \rightarrow \text{NP VP}) \\ & s_3=\text{DT NN VP} (\text{NP} \rightarrow \text{DT NN})\\ & s_4=\text{the NN VP}(\text{DT} \rightarrow the) \\ & s_5=\text{the man VP}(\text{NN} \rightarrow man) \\ & s_6=\text{the man Vi}(\text{VP} \rightarrow \text{Vi}) \\ & s_7=\text{the man sleeps}(\text{Vi} \rightarrow sleeps) \end{split}\]最左推导的每一步都使用了一个产生式规则($s_1=S$除外)，因此推导过程也可以用产生式规则的序列来表示。用parse tree来表示推导会更加直观，上面的推导过程可以用下图所示的parse tree来表示。
图：Parse Tree
这棵树的根是$S$，表明$s_1=S$。接着看S的子树，我们可以得到$s_2=\text{NP VP}$，。。。有了最左推导的定义，我们下面可以定义一个CFG的语言：\(L(\text{CFG})=\{s \vert s \in \Sigma^* \text{并且s可以由CFG的一个最左推导推出} \}\)。比如上面的”the man sleeps”就是上面的CFG的语言中的一个字符串(句子)。
CFG的歧义
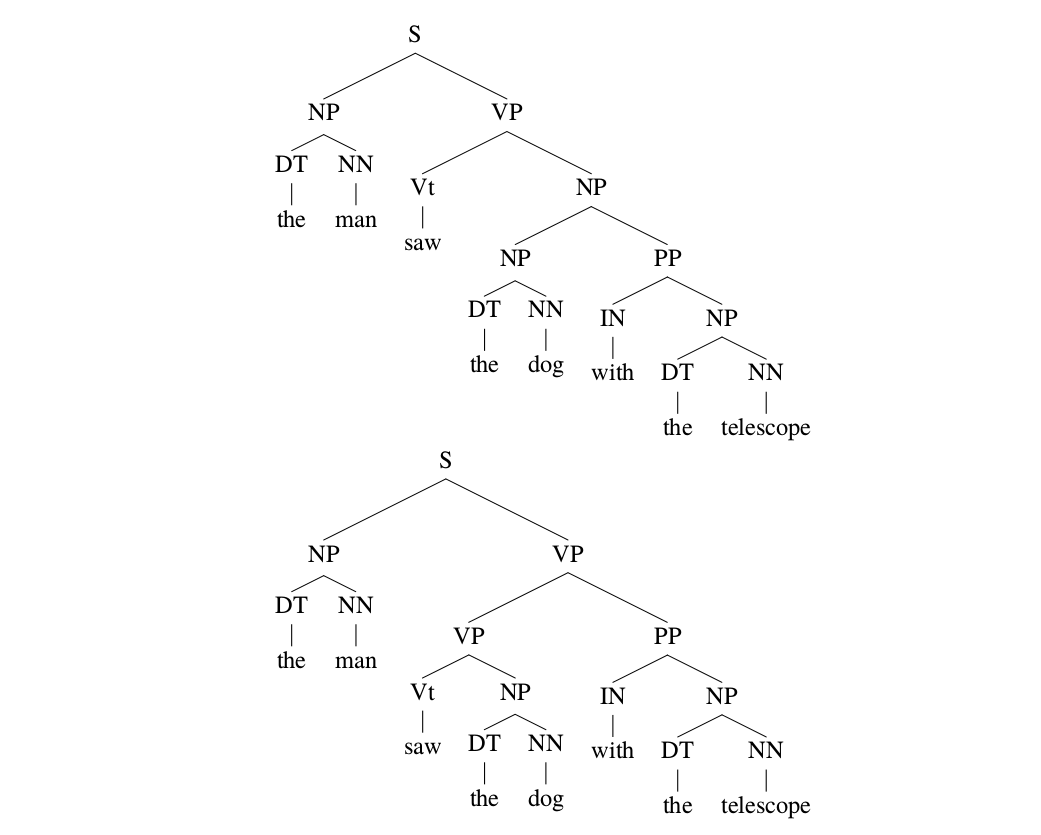
有的时候CFG里的一个字符串s可能有多种不同的推导方法，我们称在这个CFG里s是有歧义的。比如下图所示，字符串”the man saw the dog with the telescope”有两种推导方法。一种语义是”这人用望远镜看到这只狗”；另外一种语义是”这个人看到了带着望远镜的狗”。这两种推导都是合法CFG的语法的，当然从语义的角度来说第一种更合理(概率更大)一些，但是也不能说第二种推导完全没有道理，因为完全有可能狗的主人把望远镜套在狗的身上，然后被另外一个人看到了。
图：CFG有歧义
为了解决歧义问题，我们可以引入概率，这就是概率上下文无关文法(PCFGs)。
PCFGs的定义
在介绍PCFGs的定义前需要介绍一些记号。给定一个CFG G，我们定义$\mathcal{T}_G$为文法G的所有最左推导的集合。对于任意的$t \in \mathcal{T}_G$，yield(t)是推导t产生的字符串，比如上图的推导产生的字符串是”the man sleeps”。
因为歧义，一个字符串可能有多种推导方法，我们把所有能够推导字符串s的推导方法集合记为$\mathcal{T}_G(s)$：
\[\mathcal{T}_G(s)=\{t: t \in \mathcal{T}_G, yield(t)=s \}\]如果一个句子(字符串)是有歧义的，那么$\vert \mathcal{T}_G(s) \vert >1$；如果一个句子是符号语法的，那么至少有一个推导能产生这个句子，$\vert \mathcal{T}_G(s) \vert >0$。而PCFG的核心思想是对于G的所有推导t，我们定义一个概率分布，使得：
\[\begin{split} p(t) \ge 0 \\ \sum_{t \in \mathcal{T}_G}p(t)=1 \end{split}\]这个任务看起来很困难，因为一个文法G的推导可能有无穷多个，它产生的句子可能也有无穷多个。但是通过下面的介绍，我们会发现这个概率很容易定义。这样的概率又有什么作用呢？我们可以用它来消除歧义，比如一个句子s有多种推导，那么我们可以选择概率最大的那个作为s的推导。
\[\underset{t \in \mathcal{T}_G(s)}{argmax}p(t)\]现在有三个问题：
- 怎么定义概率p(t)
- 怎么根据数据学习出概率p(t)的参数
- 根据句子s，怎么快速的计算$\underset{t \in \mathcal{T}_G(s)}{argmax}p(t)$
下面我们先来定义PCFG，一个PCFG定义为：
- 一个CFG $G=(N, \Sigma, S, R)$
- 对于R中的每一个产生式规则$\alpha \rightarrow \beta$，有对应的$q(\alpha \rightarrow \beta)$。它可以认为是在进行最左推导是把$\alpha$替换成$\beta$的概率。
根据概率的定义，它需要满足如下的约束：
\[\begin{split} \underset{\alpha \rightarrow \beta \in R: \alpha=X}{\Sigma}q(\alpha \rightarrow \beta)=1 \\ q(\alpha \rightarrow \beta) \ge 0 \end{split}\]有了上面的定义，一种推导的概率p(t)可以简单的有这个推导用到的所有产生式规则的概率相乘得到：
\[p(t)=\prod_{i=1}^{n}q(\alpha_i \rightarrow \beta_i),\text{ 其中}\alpha_i \rightarrow \beta_i \text{是最左推导第i步用到的产生式规则}\]读者可以验证(证明)一下p(t)确实是$t \in \mathcal{T}_G$上的概率分布。
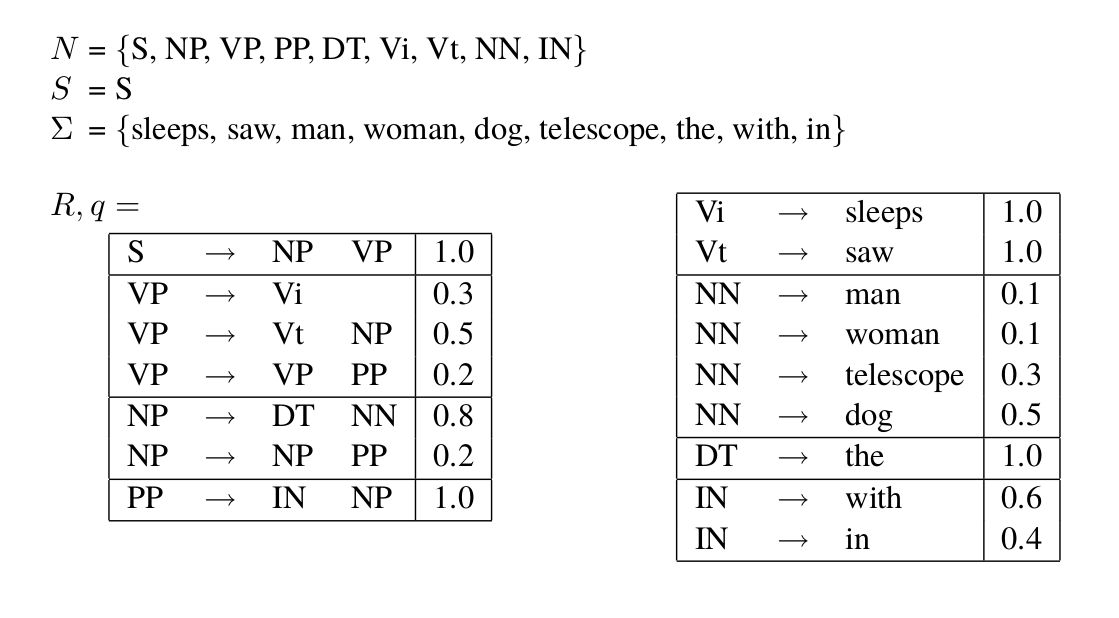
下图是一个PCFG，根据图中的定义，很显然它满足$q(\alpha \rightarrow \beta) \ge 0$。我们下面验证一下$\underset{\alpha \rightarrow \beta \in R: \alpha=X}{\Sigma}q(\alpha \rightarrow \beta)=1$是否满足，我们用$X=\text{VP}$来验证一下：
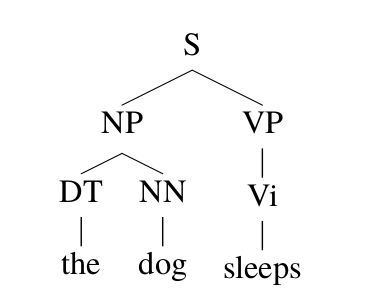
\[\begin{split} \underset{\alpha \rightarrow \beta \in R: \alpha=VP}{\Sigma}q(\alpha \rightarrow \beta) & = q(\text{VP} \rightarrow \text{Vi}) + q(\text{VP} \rightarrow \text{Vt NP}) + q(\text{VP} \rightarrow \text{VP PP}) \\ & = 0.3 + 0.5 + 0.2 \\ & = 1.0 \end{split}\]
图：PCFG的例子
下面我们来看一个计算p(t)的例子，比如下图所示的推导，我们可以这样计算其概率：
\[\begin{split} p(t) = & q(S \rightarrow \text{NP VP}) \times q(\text{NP} \rightarrow \text{DT NN}) \\ & \times q(\text{DT} \rightarrow the) \times q(\text{NN} \rightarrow dog) \times q(\text{VP} \rightarrow \text{Vi}) \times q(\text{Vi} \rightarrow sleeps) \end{split}\]
图：一个最左推导对应的parse tree
PCFGs是一个产生式模型，它可以如下的产生一个句子：
- 当i=1的时候，$s_1=S$
- 如果$s_i$全是终结符号，那么过程结束，并且得到一个句子，否则：
- 找到$s_i$最左边的非终结符号，假设是X
- 根据概率分布$q(X \rightarrow \beta)$选择产生式规则$X \rightarrow \beta$
- 替换$s_i$的X为$\beta$得到$s_{i+1}$
- $i=i+1$
PCFGs的参数估计
假设我们有一些“训练”数据，所谓的训练数据就是一个句子和它的parse tree。我们通常把这样的标注数据成为树库(TreeBank)，最常见的英文树库是LDC标注的Penn Treebank (PTB)，它来自华尔街日报(WSJ)句子，并通过人工进行标注。有兴趣的读者可以参考Treebank-3s、Penn Tree Bank (PTB) dataset introduction和NLTK Data。常见的中文树库也是LDC标注的，读者可以参考Chinese Treebank 9.0。
假设parse tree为$t_1,…,t_m$，要求所有$t_i$的开始符号是S，它们对应的句子就是$yield(t_1),…,yield(t_m)$。我们可以通过如下的方法得到一个PCFG $G=(N, \Sigma, S, R, q)$。
- N是$t_1,…,t_m$里出现过的非终结符号的集合
- $\Sigma$是$t_1,…,t_m$中出现过的终结符号的集合
- S是开始符号
- R是所有在$t_1,…,t_m$中出现过的产生式规则的集合
-
q使用最大似然估计得到：
\[q_{ML}(\alpha \rightarrow \beta)=\frac{Count(\alpha \rightarrow \beta)}{Count(\alpha)}\]上式中$Count(\alpha \rightarrow \beta)$是$t_1,…,t_m$里这个规则使用的次数，而$Count(\alpha)$是非终极符号$\alpha$出现的次数。
比如，规则$\text{VP} \rightarrow \text{Vt NP}$在我们的训练数据里出现了105次，而VP出现了1000次，则$q(\text{VP} \rightarrow \text{Vt NP})=\frac{105}{1000}$。
PCFGs的Parsing
接下来要解决的问题就是：给定PCFG和句子s，怎么快速的找到概率最大的parse tree？或者更加形式化的描述：
\[\underset{t \in \mathcal{T}_G(s)}{argmax}p(t)\]我们可以使用CYK算法来对PCFG进行parsing，这是一种动态规划算法。不过CYK算法要求CFG(PCFG)是乔姆斯基范式(Chomsky Normal Form)的，因此我们先介绍乔姆斯基范式的定义。
乔姆斯基范式(Chomsky Normal Form/CNF)
对于一个CFG $G=(N,\Sigma, S, R)$，如果它的任意一个产生式规则是下面的两种形式之一，那么它就是乔姆斯基范式的。
\[\begin{split} X \rightarrow Y_1Y_2, \text{ 其中}X,Y_1,Y_2 \in N \\ X \rightarrow a, \text{其中} X \in N a \in \Sigma \end{split}\]也就是说乔姆斯基范式的产生式要么右边是一个终结字符(单词)，要么是两个非终结符。任何一个CFG都可以转化成与之等价的乔姆斯基范式，有兴趣的读者可以参考相关资料，本书不介绍具体算法。
下图是与上图的PCFG等价的乔姆斯基范式。
图：乔姆斯基范式的CFG
CKY算法
下面我们介绍parse乔姆斯基范式的PCFG的CKY算法。它的输入是一个乔姆斯基范式的PCFG和一个句子$s=x_1…x_n$，它的输出是：
\[\underset{t \in \mathcal{T}_G(s)}{argmax}p(t)\]为了使用CKY算法，我们首先需要定义一些记号：
-
给定句子$x_1…x_n$，$X \in N$，$1 \le i \le j \le n$，我们定义$\mathcal{T}(i,j,X)$为所有通过X推导出$x_i…x_j$ parse tree的集合
-
$\pi(i,j,X)=\underset{t \in \mathcal{T}(i,j,X)}{max}p(t)$，如果$\mathcal{T}(i,j,X)$是空集，我们定义$\pi(i,j,X)=0$
因此$\pi(i,j,X)$是所有从X推导出$x_i…x_j$的集合中概率最大的那个推导(parse tree)。我们可以发现：
\[\underset{t \in \mathcal{T}_G(s)}{max}p(t)=\pi(1,n,S)\]因为根据定义$\pi(1,n,S)$是S推导出$x_1…x_n=s$的集合中概率最大的那个。CKY算法的关键是使用递归(递推)公式来计算$\pi(i,j,X)$，我们先看递归的出口：
\[\pi(i,i,X)=\begin{cases} q(X \rightarrow x_i) \text{ if }X \rightarrow x_i \in R \\ 0 \text{ 否则} \end{cases}\]上式是比较明显的，要从X推导出$x_i$，因为$x_i$是终结符，乔姆斯基范式里要么一个非终极符产生一个终结符，要么非一个终结符产生两个非终结符。显然如果是第二种情况，那么最终产生的非终极符一定大于1，因此只能是第一种情况。当$1 \le i < j \le n$时，递归公式为：
\[\pi(i,j,X)=\underset{\underset{s \in \{i,...,j-1\} }{X \rightarrow \text{YZ} \in R,}}{max}(q(X \rightarrow \text{YZ}) \times \pi(i,s,Y) \times \pi(s+1,j,Z))\]我们可以这样解读上面的递归公式：因为X产生的字符串大于1个符号，因此一定使用了某个产生式规则$X \rightarrow \text{YZ}$，那么肯定存在一个$s \in {i,…,j-1}$使得Y产生$x_i…x_s$并且Z产生$x_{s+1}…s_j$。因此为了求X产生$x_i…x_j$的最大概率，我们需要遍历所有的左边是X右边是两个非终结符号的产生式规则，并且要变量所有的切分方式s，然后从这里面挑选概率最大的一个。如果给定了$X \rightarrow YZ$和s，那么最大概率的parse tree显然是$q(X \rightarrow YZ) \times \pi(i,s,Y) \times \pi(s+1,j,Z)$。
为了找到最优的parse tree，我们不但需要记录$\pi(i,j,X)$的值，还需要记录对应的规则$X\rightarrow YZ$和切分点s，这样便于以后回溯。完整的伪代码下图所示。
图：CKY算法伪代码
词汇化的(Lexicalized)PCFGs
PCFGs的问题
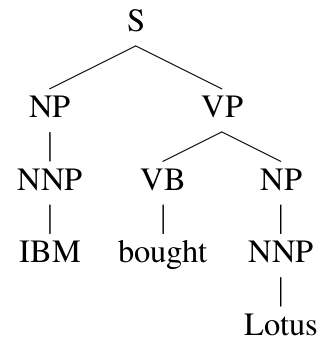
PCFGs有两个问题：模型忽略了词汇的(lexcial)信息；忽略句法结构信息。词汇化的PCFGs用于解决第一个问题，而第二个问题我们尝试通过扩展词汇化的PCFGs来解决。比如下图的parsing tree，它的概率为：
\[q(S \rightarrow \text{NP VP}) \times q(\text{VP} \rightarrow \text{VB NP}) \times q(\text{NP} \rightarrow \text{NNP}) \times q(\text{NP} \rightarrow \text{NNP}) \\ \times q(\text{NNP} \rightarrow IBM ) \times q(\text{VB} \rightarrow bought) \times q(NNP \rightarrow Lotus)\]
图：PCFGs的问题
如果我们仔细分析这个parse tree，我们会发现PCFGs有很多很强的独立性假设。比如叶子节点的词汇只依赖于它的词性(它的父亲节点)，比如”IBM”只依赖于词性NNP，而与整棵树的结构无关。一个词只要它的词性确定了，那么它的概率就与这棵树的其它部分没有任何关系了。这显然不是一个合理的假设，在有parsing的歧义的时候，这个假设就会带来问题，下面我们通过一个例子来看这个问题。
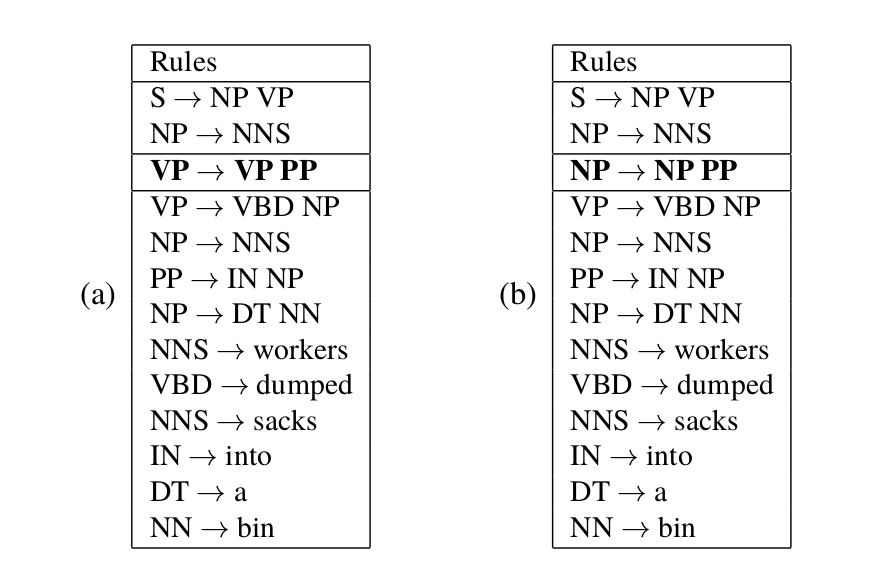
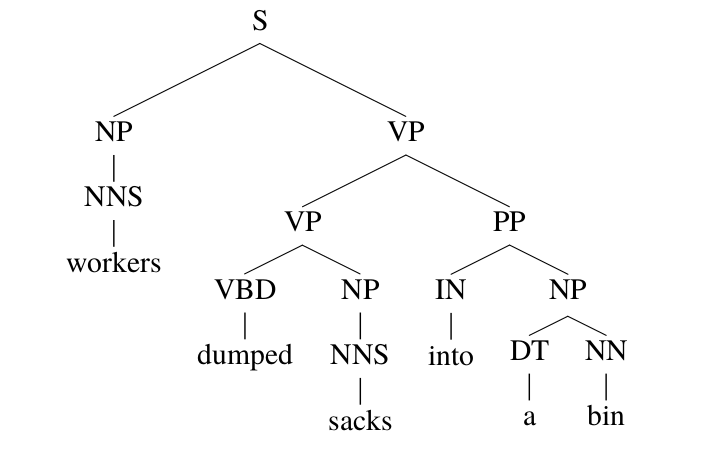
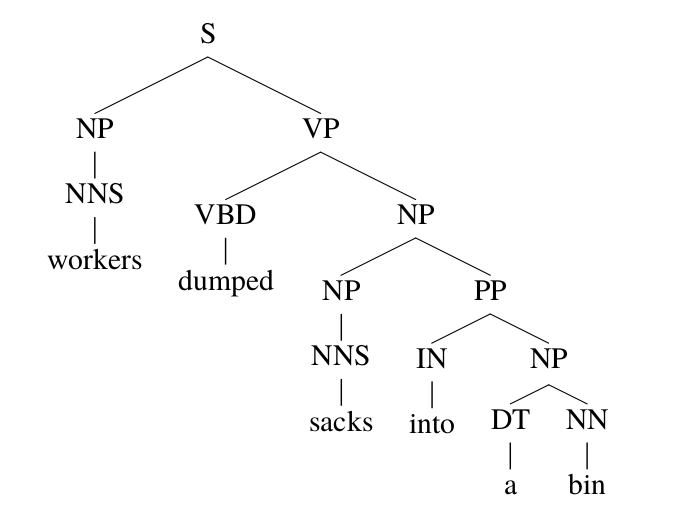
比如”the worker dumped the sacks into the bin”这个句子，有两种parsing方法，如下图所示，它们使用的产生式规则序列如下图所示，请读者验证这两种parsing是合法的。
 |
 |
|---|---|
| 第一种parse方法 | 第一种parse方法 |
图：两种parsing使用的产生式规则序列
这中歧义在英语中非常常见，叫作prepositional-phrase (PP) attachment歧义。但是对于这个句子，从语义上分析，第一种是合理的，而第二种是不合理的。通过上图，我们发现这两棵parsing tree只有一个产生式规则是不同的，前者是”VP -> VP PP”而后者是”NP -> NP PP”，其余的都是相同的。如果$q(VP \rightarrow \text{VP PP}) > q(NP \rightarrow \text{NP pp})$，那么CYK算法会选择第一种parsing方法；而如果$q(VP \rightarrow \text{VP PP}) < q(NP \rightarrow \text{NP pp})$，则会选择第二种parsing方法。
在这里，词汇的信息是不起任何作用的，但实际这并不合理。因为人在理解这个句子是，会利用词汇的信息。即使最简单的统计，我们也能发现，into这个词更倾向于into XX是介词短语(PP)而不是动词短语的附着成分(Attachment)。而在这个例子里，PCFGs完全不考虑词汇的信息，从而很难处理这种歧义。
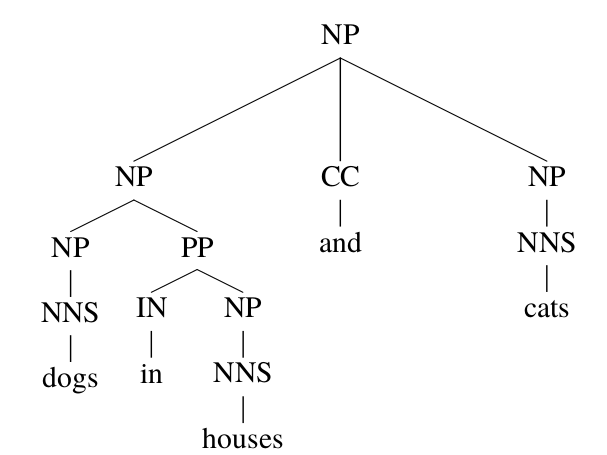
我们再来看一个并列歧义的问题，这也是英语中非常常见的一种歧义。如下图所示，有两种parsing方法。
 |
|
这两种parsing使用的产生式规则完全一样，因此不过PCFGs的概率q怎么取值，它们的概率都是一样的，完全无法判断。但是从词汇的角度，显然第一种更加可能，因为”dog”和”cat”都是动物，因此可以并列；而”house”和”cat”显然不太可能并列。另外”in”可以和”house”搭配而显然不能和”cat”搭配。
PCFGs除了忽略词汇的信息之外，它也忽略树的结构信息，这类信息对于人来parsing也是很有用的。如下图所示，句子”president of a company in Africa”有两种parsing方法，这里显然是第一种更加合理——非洲某个公司的总裁。从词汇的角度，in Africa更时候修饰company和不是president。但是即使不看词汇信息，利用句子结构信息，我们也可以判断第一种的可能性更大。
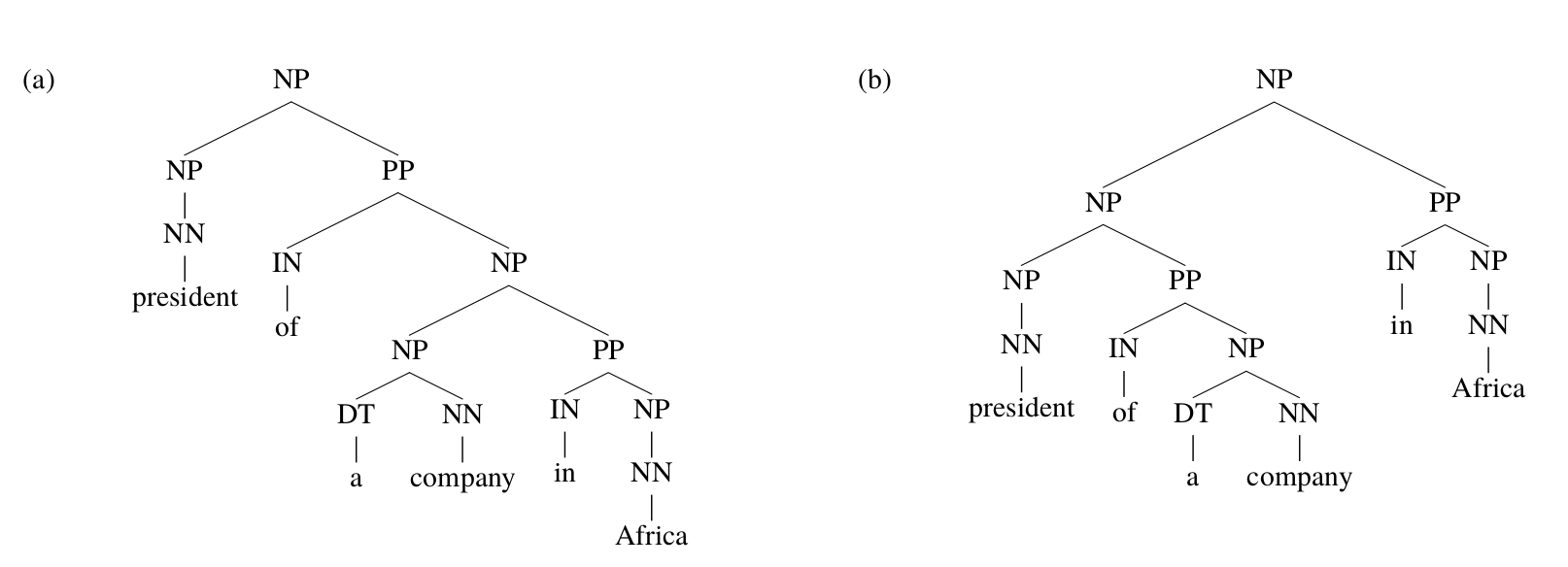图：”president of a company in Africa”的两种parsing方法
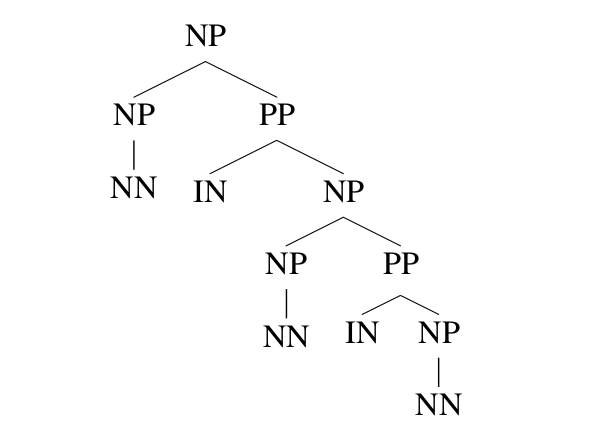
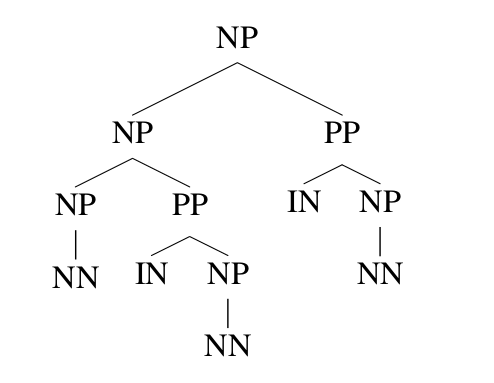
如果忽略掉词汇信息，两种parsing tree的结构如下图所示。如果看不到词汇，我们会倾向于选择哪种结构呢？根据训练数据的统计，我们可以发现第一种结构出现的次数更多。而从语言学分析，介词短语(PP)倾向于修饰离自己比较近的名词短语(NP)。因此如果其它概率都一样的情况下，我们根据这个信息也会正确的做出判断。
 |
 |
这种语法现象叫作close attachment，除了名词短语，动词短语(VP)也会影响PP到底attach到哪里，比如句子”John was believed to have been shot by Bill”。一种是parsing是”(人们)相信John是被Bill枪击了”；另外一种是”Bill相信John被(他人)枪击了”。根据close attachment原则，我们会选择第一种parsing方法，这显然也更加合理。
TreeBank的词汇化(Lexicalization)
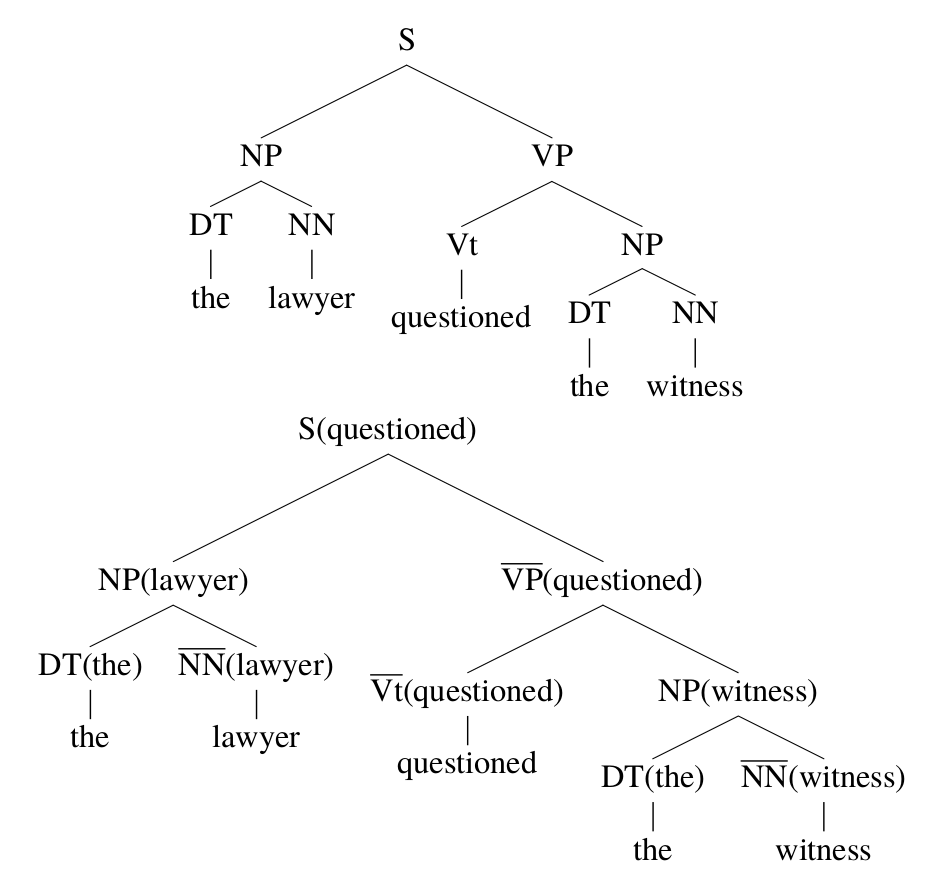
前面介绍了PCFGs的缺陷，其中之一是没有考虑词汇的信息。因此我们可以扩展PCFGs变成词汇化(Lexicalized)PCFGs。在扩展之前我们首先需要把训练数据树库变成词汇化的。如下图所示，图的上边是普通的parsing tree，而下边是词汇化后的parsing tree。
图：Parsing Tree的词汇化
词汇化的parsing tree的每一个非终结符号多了一个括号括起来的词。比如原来的
\[S \rightarrow \text{NP VP}\]变成了
\[S(questioned) \rightarrow \text{NP(lawyer) VP(questioned)}\]在词汇化的PCFGs里，非终结符号是类似NP(lawyer)，它附加了词汇信息。注意：NP(lawyer)和NP(man)是两个完全不同的符号。从某种意义上讲，词汇化的PCFGs还是一个PCFGs，只不过非终结符号变得非常多了，原来的一个NP现在可能变成几千个NP(xx)。
这可能会带来数据稀疏的问题，后面我们会简要的讨论怎么解决这个问题，但是现在我们暂且不考虑它。现在的问题是我们怎么把普通的parsing tree变成词汇化的parsing tree，也就是怎么给每个非终结符号加上括号里的词汇。如上图所示，为什么是S(questioned)而不是S(the)？
比较直接的想法是这个词汇是这棵子树最”重要”的词汇，比如S代表整个句子，句子最重要的成分就是谓词。而”the witness”这个子树最重要的是名词witness而不是定冠词the。当然我们可以让人工来挑选每棵子树最重要的词，但是这个标注成本非常高。更加可行的方法是制定一些规则，用来判断一个产生式规则最重要的部分，也就是所谓的”head”。
比如规则$S \rightarrow \text{NP VP}$，我们一般认为动词短语比名词短语重要，因此我们把VP标注为head。又比如$NP \rightarrow \text{ DT NN}$，我们可以规定NN是head。有了这些规则和parsing tree，我们可以自底向上自动的标注出所有子树的head。
比如上图的例子，$DT \rightarrow the$，只有一个词，那么显然the就是head，类似的witness是NN的head词。接着根据产生式规则$NP \rightarrow \text{DT NN}$，我们把NN的head设置为NP的head。。。。
而每种产生式规则怎么确定head部分呢？这通常更加人类的经验编制的一些规则，比如下图所示的规则。 这些规则用于确定$NP \rightarrow \text{XXXX}$的head。我们简单的解读一下：如果右边包含”NN, NNS或者NNP”，那么选择最右边的NN，NNS或者NNP。否则如果有NP，那么选择最右边的NP。再否则如果包含JJ那么选择最右边的JJ，。。。。
比如有一个规则$NP \rightarrow \text{DT JJ NP NP}$，根据前面的规则，我们应该选择最后一个NP。
图：确定产生式规则的head的一些规则示例
词汇化PCFGs的定义
词汇化PCFGs的关键就是把PCFGs的规则
\[S \rightarrow \text{NP VP}\]变成
\[S(examined) \rightarrow \text{NP(lawyer) VP(examined)}\]但是上述表示方法可能有歧义，原因是可能右边的两个非终结符号完全一样，因此我们在箭头的后面加上数字1或者2来表示左边的head来自于右边的第一个部分还是第二个部分。比如前面的例子，我们可以记为： \(S(examined) \rightarrow_2 \text{NP(lawyer) VP(examined)}\)
下面我们来形式化的定义词汇化的PCFGs，这里我们假设它是符合乔姆斯基范式的。符合乔姆斯基范式的词汇化的PCFGs是一个六元组$G = (N, \Sigma, R, S, q, \gamma)$，其中：
- N是一个有限的非终结符号的集合
- $\Sigma$是一个有限的终结符号集合
-
R是一个有限的产生式规则集合，规则只能是如下3种形式之一
\[\begin{split} X(h) \rightarrow_1 Y_1 (h) Y_2 (m) \text{，其中 } X, Y_1 , Y_2 \in N , h, m \in \Sigma \\ X(h) \rightarrow_2 Y_1 (m) Y_2 (h) \text{，其中 } X, Y_1 , Y_2 \in N , h, m \in \Sigma \\ X(h) \rightarrow h \text{，其中 } X \in N , h \in \Sigma \end{split}\] -
对于任何的$r \in R$，有$q(r) \ge 0$，并且对于任何的$X \in N, h \in \Sigma$，有：
\[\underset{r \in R:\text{LHS}(R)=X(h)}{\Sigma}q(r)=1\]上式中$\text{LHS}(R)$表示产生规则的左边部分，也就是$\rightarrow$左边的非终结符号X(h)
-
对于任何的$X \in N, h \in \Sigma$，有一个对应的$\gamma(X, h) \ge 0$，并且满足：
\[\underset{X \in N, h \in \Sigma}{\Sigma}\gamma(X,h)=1\]
和PCFGs对比，词汇化的PCFGs多了一个$\gamma(X,h)$，它可以理解为某棵子树的根为X(h)的概率。假设词汇化PCFGs的一个parsing tree的最左推导是$r_1…,r_N$，那么这个parsing tree的概率为：
\[\gamma(LHS(r_1))\prod_{i=1}^{N}q(r_i)\]还是拿上图b为例，最左推导使用的规则为：
\[\begin{split} & \text{S(questioned)} \rightarrow_2 \text{NP(lawyer) VP(questioned)} \\ & \text{NP(lawyer)} \rightarrow_2 \text{DT(the) NN(lawyer)} \\ & \text{DT(the)} \rightarrow the \\ & \text{NN(lawyer)} \rightarrow lawyer \\ & \text{VP(questioned)} \rightarrow_1 \text{Vt(questioned) NP(witness)} \\ & \text{NP(witness)} \rightarrow_2 \text{DT(the) NN(witness)} \\ & \text{DT(the)} \rightarrow the \\ & \text{NN(witness)} \rightarrow witness \\ \end{split}\]因此这棵parsing tree的概率为：
\[\begin{split} & \gamma(S, questioned) \\ & q(\text{S(questioned)} \rightarrow_2 \text{NP(lawyer) VP(questioned)}) \\ & q(\text{NP(lawyer)} \rightarrow_2 \text{DT(the) NN(lawyer)}) \\ & q(\text{DT(the)} \rightarrow the) \\ & q(\text{NN(lawyer)} \rightarrow lawyer) \\ & q(\text{VP(questioned)} \rightarrow_1 \text{Vt(questioned) NP(witness)}) \\ & q(\text{NP(witness)} \rightarrow_2 \text{DT(the) NN(witness)}) \\ & q(\text{DT(the)} \rightarrow the) \\ & q(\text{NN(witness)} \rightarrow witness) \\ \end{split}\]我们可以发现词汇化的PCFGs和PCFGs非常相似，只是多了一个概率$\gamma(S, questioned) $，它可以看成是questioned作为句子head的概率。而PCFGs里树根总是S，因此$\gamma(S)=1$，而词汇化的PCFGs里树根是很多不同的非终结符号$S(word)$。
词汇化PCFGs的参数估计
词汇化PCFGs的参数估计和PCFGs类似，只不过它的规则更多，因此需要用平滑的技巧来解决数据稀疏的问题。就像语言模型，如果我们把一个句子当成一个整天，那么它在训练数据里出现的可能性是非常小的，但是我们可以通过一些假设，把一个句子的概率分解成更小的N-gram。词汇化的PCFGs的参数估计也可以采取类似的方法来分解。
给定一个规则$X(h) \rightarrow_1 Y_1 (h) \; Y_2 (m)$，我们定义如下的记号：X是左边的非终结符号，H是head词，M是修饰词(modifier)，R表示去掉词汇后的规则。比如规则$S(examined) \rightarrow_2 \text{NP(lawyer) VP(examined)}$，我们可以得到如下记号：
\[\begin{split} & X=S \\ & H=examined \\ & M=lawyer \\ & R=S \rightarrow_2 \text{NP VP} \end{split}\]有了上面的记号，我们可以这样来计算q： \(\begin{split} & q(S(examined) \rightarrow_2 \text{NP(lawyer) VP(examined)}) \\ = & P (R=S \rightarrow_2 \text{NP VP}, M = lawyer|X = S, H = examined) \end{split}\)
我们可以这样来解读上式：S(examined) 产生NP(lawyer) VP(examined)的概率等于X=S并且head词是examined的条件下使用规则$R=S \rightarrow_2 \text{NP VP}$并且修饰词是lawyer的概率。通过链式法则，我们可以把上面的概率分解为两部分：
\[\begin{split} & P (R=S \rightarrow_2 \text{NP VP}, M = lawyer|X = S, H = examined) \\ = & P (R=S \rightarrow_2 \text{NP VP}|X = S, H = examined) \\ & \times P (M = lawyer|R=S \rightarrow_2 \text{NP VP}, X = S, H = examined) \end{split}\]我们可以使用最大似然估计分布估计这两部分。比如我们可以估计：
\[\begin{split} q_{ML} (S \rightarrow_2 \text{NP VP}|S, examined)=\frac{count(R = S \rightarrow_2 \text{NP VP}, X = S, H = examined)}{count(X = S, H = examined)} \end{split}\]我们可以得到：
\[P (R=S \rightarrow_2 \text{NP VP}|X = S, H = examined)=q_{ML} (S \rightarrow_2 \text{NP VP}|S, examined)\]但是有可能训练数据中S(examined)没有出现过甚至examined这个词都没有出现过，那么$q_{ML}$就是零，因此我们可以采取语言模型回退的方法——如果trigram没有出现过，那么用bigram来估计；如果bigram没有出现，那么用unigram来估计。我们这里可以估计：
\[q_{ML}(S \rightarrow_2 \text{NP VP}|S)=\frac{count(R = S \rightarrow_2 \text{NP VP}, X = S)}{count(X = S)}\]然后把它们线性加权得到：
\[\begin{split} & P (R=S \rightarrow_2 \text{NP VP}|X = S, H = examined)\\ & = \lambda_1 \times q_{ML} (S \rightarrow_2 \text{NP VP}|S, examined) +(1-\lambda_1) \times q_{ML}(S \rightarrow_2 \text{NP VP}|S) \end{split}\]类似的，对于上面的等式的第二部分，我们可以如下估计：
\[\begin{split} q_{ML}(lawyer|S \rightarrow_2 \text{NP VP}, examined) & = \frac{count(M = lawyer, R = \rightarrow_2 \text{NP VP}, H = examined)}{count(R = \rightarrow_2 \text{NP VP}, H = examined)} \\ q_{ML} (lawyer|S \rightarrow_2 \text{NP VP}) & = \frac{count(M = lawyer, R = \rightarrow_2 \text{NP VP})}{count(R = S \rightarrow_2 \text{NP VP})} \end{split}\]然后得到：
\[\begin{split} & P (M = lawyer|R \rightarrow_2 \text{NP VP}, X = S, H = examined) \\ & = \lambda_2 \times q_{ML}(lawyer|S \rightarrow_2 \text{NP VP}, examined) + (1-\lambda_2) \times q_{ML} (lawyer|S \rightarrow_2 \text{NP VP}) \end{split}\]把它们放到一起，我们就可以得到：
\[\begin{split} & q(S(examined) \rightarrow_2 \text{NP(lawyer) VP(examined)}) \\ = & (\lambda_1 \times q_{ML} (S \rightarrow_2 \text{NP VP}|S, examined) + (1 − \lambda_1 ) \times q_{ML}(S \rightarrow_2 \text{NP VP}|S)) \\ & \times (\lambda_2 × q_{ML}(lawyer|S \rightarrow_2 \text{NP VP}, examined) + (1 − \lambda_2 ) \times q_{ML} (lawyer|S \rightarrow_2 \text{NP VP})) \end{split}\]词汇化PCFGs的Parsing算法
我们可以采取类似PCFGs的CYK算法，这里我们首先需要定义一个记号$\pi(i,j,h,X)$，它表示所有这样的parsing tree——它的树根是$X(x_h)$，它推导出的句子是$x_i…x_j$的集合中概率最大的那个。这个定义有些绕口，我们通过一个例子来说明它。
比如前面的一个句子”workers dumped the sacks into a bin”，这是一个长度(n)为7的句子，我们看看$\pi(2,7,2,VP)$是什么意思。它表示的是所有根为VP(dumped)并且推导出”dumped the sacks into a bin”字符串的子树中概率的最大值。我们可以用递归的方法来计算$\pi$，其中递归的出口是：
\[\pi(i,i,i,X)=q(X(x_i) \rightarrow x_i)\]如果没有规则$X(x_i) \rightarrow x_i$，那么$q(X(x_i) \rightarrow x_i)=0$。比如前面的例子：
\[\pi(1, 1, 1, \text{NNS}) = q(\text{NNS(workers)} \rightarrow workers)\]对于$\pi(i,j,h,X)$，我们可以使用规则$X(x_h) \rightarrow_1 Y_1(x_h)Y_2(x_m)$或者$X(x_h) \rightarrow_2 Y_1(x_m)Y_2(x_h)$，并且可以选择i到j直接的所有切分点s，其中让$Y_1$产生$x_i…x_s$以及$Y_2$产生$x_{s+1}…s_j$。然后从中选择最大的概率值。注意：如果使用$X(x_h) \rightarrow_1 Y_1(x_h)Y_2(x_m)$，则head词在$Y_1$子树参数，因此切分点s一定在h+1到j之间；而如果是$X(x_h) \rightarrow_2 Y_1(x_m)Y_2(x_h)$，则切分点s一定在i到h-1之间。
计算$\pi(i,j,k,X)$完整的伪代码如下图所示。
图：$\pi(i,j,k,X)$的计算
有了上面的算法，我们就可以得到词汇化的PCFGs的parsing算法，如下图所示。
图：词汇化PCFGs的CKY算法
成分句法分析的效果评估
我们通常使用F1来衡量成分句法分析的效果。它的定义是：
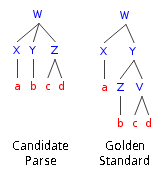
\[F_1=\frac{1}{\frac{1}{precision}+\frac{1}{recall}}=\frac{2 \cdot precision \cdot recall}{precision+recall}\]其中精度(precision)的定义为：正确的成分(constituency)个数/模型输出的成分总数；而召回率(recall)的定义为：正确的成分个数/正确parse树成分的总数。比如下图所示的例子，左边是模型输出的parse tree，右边是正确的parse tree。我们首先列举出所有的成分：
候选(candidate) 正确(gold)
X:a X:a
Y:b Z:b
Z:cd V:cd
-- Y:bcd
W:abcd W:abcd
有两种计算精度和召回的方法——LAS(labeled attachment score)和UAS(unlabeled attachment score )。UAS只要求成分的非终极符匹配；而LAS要求非终极符和词序列(label)同时正确。
比如上面的例子，先考虑UAS，匹配的成分为X、Y、Z、W，因此精度为1，召回为4/5，F1为0.89。如果考虑LAS，那么匹配的只有X:a和W:abcd，因此精度为2/4，召回为2/5，F1为0.44。
图：模型的parse树和正确(参考)的parse树
- 显示Disqus评论(需要科学上网)