本文介绍时间差分(Temporal Difference)方法。会分别介绍On-Policy的SARSA算法和Off-Policy的Q-Learning算法。因为Off-Policy可以高效的利用以前的Episode数据,所以后者在深度强化学习中被得到广泛使用。我们会通过一个Windy GridWorld的简单游戏介绍这两种算法的实现。
更多本系列文章请点击强化学习简介系列文章。更多内容请点击深度学习理论与实战:提高篇。
目录
- 时间差分预测(TD Prediction)
- Driving Home例子
- TD和MC的比较
- SARSA
- Windy Gridworld环境介绍
- SARSA代码
- Q-学习(Q-Learning)
- Q-Learning代码
时间差分是一种非常重要的强化学习方法,它结合了动态规划和蒙特卡罗方法的优点。
时间差分预测(TD Prediction)
我们首先回顾一下MC的增量更新公式:
\[V(S_t) \leftarrow V(S_t)+\alpha [G_t-V(S_t)]\]这个和之前Q(s,a)的更新公式稍微有一些区别,这里的$\alpha$是个常量,而在之前的更新公式是一个不断变化的量。但其基本思路是一致的,我们“期望”的$V(S_t)$是$G_t$,因此$[G_t-V(S_t)]$可以认为是现在“估计”和实际值的“误差”,再乘以一个较小的数字$\alpha$。这有点像梯度下降,如果误差为零,那么就没有变化,如果误差越大,则V的更新也越多。这个算法就叫constant-α MC。
前面也讨论过了,蒙特卡罗方法的缺点是$G_t$只有在Episode结束后才能计算出来。接下来我们介绍的TD(0)方法能够解决这个问题,首先我们来看它的更新公式:
\[V(S_t) \leftarrow V(S_t)+\alpha [R_{t+1}+\gamma V(S_{t+1})-V(S_t)]\]从公式来看,时刻t的状态$S_t$的更新不需要等到Episode结束,只需要等到下一个时刻t+1。蒙特卡罗方法的更新目标(Update Target)是$G_t$,而TD(0)的目标是$R_{t+1}+\gamma V(S_{t+1})$。因为TD(0)更新一个状态的价值函数时需要依赖另外一个状态的价值,所以它是bootstrapping的方法。
\[\begin{split} v_\pi(s) & \equiv \mathbb{E}_\pi[G_t|S_t=s] \\ & =\mathbb{E}_\pi[R_{t+1}+\gamma G_{t+1}|S_t=s] \\ & =\mathbb{E}_\pi[R_{t+1}+\gamma v_\pi{S_{t+1}}|S_t=s] \end{split}\]大体来说,蒙特卡罗方法使用第一个等式的估计(采样平均)作为更新目标,而动态规划使用第三个公式作为更新目标。而TD(0)使用第三个公式的估计(采样),同时还用当前的$V(S_{t+1})$来近似$v_\pi{S_{t+1}}$。因此TD(0)可以认为是结合了蒙特卡罗采样和bootstrapping,bootstrapping是用估计来更新估计。根据前面的分析,TD(0)的误差为:
\[\delta_t \equiv R_{t+1}+\gamma V(S_{t+1}) -V(S_t)\]我们来看一下TD(0)和MC的关系,MC方法在Episode结束之前是不会改变V(s)的,但是 TD(0)会在t+1时刻更新$S_t$。为了便于分析,我们暂时假设直到Episode结束才统一更新。
\[\begin{split} G_t-V(S_t) & =R_{t+1}+\gamma G_{t+1}-V(S_t) +\gamma V(S_{t+1}) -\gamma V(S_{t+1}) \\ & =\delta_t+\gamma(G_{t+1}-V(S_{t+1}))\\ & =\delta_t+\gamma \delta_{t+1}+\gamma^2(G_{t+2}-V(S_{t+2}))\\ & =\delta_t+\gamma \delta_{t+1}+\gamma^2 \delta_{t+2} + ... +\gamma^{T-t-1}\delta_{T-1}+\gamma^{T-t}(G_T-V(S_t))\\ & =\delta_t+\gamma \delta_{t+1}+\gamma^2 \delta_{t+2} + ... +\gamma^{T-t-1}\delta_{T-1}+\gamma^{T-t}(0-0))\\ & =\sum_{k=t}^{T-1}\gamma^{k-t}\delta_k \end{split}\]Driving Home例子
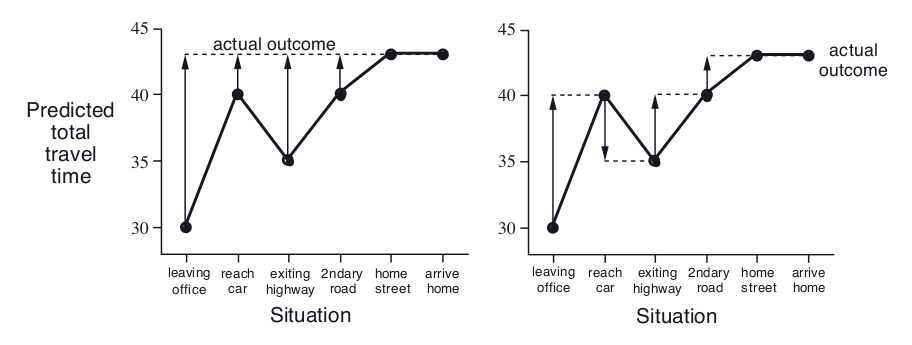
为了比较MC和TD方法,我来看一个例子。我们需要估计开车回家要花的时间,当离开办公室的时候,我们会注意现在的时间,今天是星期几,今天的天气怎么样,综合考虑所有可能影响交通的因素。比如今天是星期五,现在是下午6点,根据以往的经验,我们估计可能需要花30分钟。当走到车前时已经是6:05了,我们发现开始下雨了,因为下雨天交通会变坏,我们重新估计的结果是我们还需要35分钟才能到家,因此此时估计总的到家时间是40分钟。15分钟后我们下了高速,这比预计的时间要短,因此我们重新估计总的时间为35分钟。不过很不幸,前面有个大货车,路又很窄超不了车,6:40才到底小区的路口。这已经花了40分钟了,根据经验,3分钟后就可以到家了,因此我们重新估计总的时间是43分钟后。而3分钟后,果然我们如期到家。
假设状态就是每一段路的起始和结束,然后我们需要估计的是从当前状态(点)到家的时间(如果是为了找到回家最快的策略,我们可以把Reward定义为花费时间的负值,不过这里我们只考虑预测,因此我们用正值,这样看起来简单)。我们把每个状态(一段路的开始点)开始的时间点,这段路估计要花的时间,总的估计的(从办公室)到家的时间用表格画出来:
| 状态 | 已用时间 | 估计剩余时间 | 估计到家总时间 |
|---|---|---|---|
| 周五下午六点办公室 | 0 | 30 | 30 |
| 走到车旁,开始下雨 | 5 | 35 | 40 |
| 下高速 | 20 | 15 | 35 |
| 第二段路,在火车后 | 30 | 10 | 40 |
| 走到小区街道 | 40 | 3 | 43 |
| 到家 | 43 | 0 | 43 |
我们可以把每个状态估计总的到家时间(表格的最后一列)画出来,如下图所示。我们先看左图,这是MC方法的情况,虚线表示每个状态的估计值和真实值的差$\delta$。在Episode结束之前,我们不知道真实值是多少,只有到家之后,我们知道总共花费了43分钟,那么我们知道了误差$\delta$,从而可以更新每个状态的V(s)。而右边是TD的情况,我们不需要等到家,而只需要在下一个状态结束,我们就能更新前一个状态。比如最初我们估计要花30分钟,但到了第二个状态来到车前时,我们发现情况有变,我们重新估计可能要花40分钟,其实这个时候TD就可以用40-30作为$\delta$来更新$V(S_1)$了。
TD和MC的比较
TD相对于MC最大的优点当然就是它是online的算法,不用等到Episode结束就可以更新,因此也就可以用于连续的任务。此外,TD通常收敛的更快,当然这只是经验,并没有理论的证明。$G_t=R_{t+1}+\gamma R_{t+2}+…+\gamma^{T-1}R_T$是$v_\pi(S_t)$的无偏估计,而”真实“的TD更新目标$R_{t+1}+\gamma v_\pi(S_{t+1})$也是无偏估计,但是因为我们并不知道$v_\pi(S_{t+1})$而是用$V(S_{t+1})$来近似的,也就是我们实际用的TD更新目标是$R_{t+1}+\gamma V(S_{t+1})$。这个目标是有偏的估计。因为MC依赖很多随机的Action、随机的状态跳转和随机的reward,所以它的估计方差较大,而TD值有一次随机的Action、随机的状态跳转和随机的reward,因此方差较小。此外MC因为有bootstrapping,因此它的收敛也依赖于初始值。
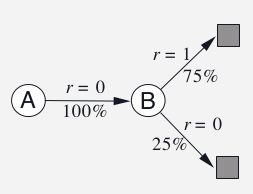
接下来我们分析一下MC和TD优化的“目标”分别是什么?首先我们来看一个例子。假设这个MRP(我们不考虑Action)有两个状态A和B,我们有如下8个Episode:
A,0,B,0
B,1 6次
B,0
(A,0,B,0)表示初始化状态A,进入B,reward是0,然后进入B,reward是0,结束。
对于上面的数据,我们计算\(V(B)=\frac{6*1+2*0}{8}=0.75\),那么V(A)呢?我们可能有两种算法,第一种算法如上图所示:A不是终止状态,A跳转到B的概率是100%,因此V(A)和V(B相同)。而第二种算法是$V(A)=\frac{0*1}{1}=0$,也就是出现A的Episode一次,最终的Reward是0,因此计算平均值就是0。第二种方法是MC,它不考虑A和B的关系,只是看最终的回报。而第一种是TD,它会用B的值来计算A的值。MC的目标函数是最小均方误差:
\[L=\sum_{k=1}^K\sum_t^{T_k}(G_t^k-V(S_t^k)^2)\]因此对于上面的例子只有一个Episode,G=0,所有V(A)=0时损失是最小0。似乎看起来最小均方误差是不错的目标函数,那还有没有更好的呢?它的问题是没有利用环境的马尔科夫属性,而TD的目标函数就利用了这个特性,它是从所有的MDP里选择似然(likelihood)最大的那个MDP,然后根据这个MDP来计算最优的V(s),也就是它先根据数据估计出MDP的参数,对于上面的AB问题,它的MDP动力系统是:
\[\begin{split} \hat{P}_{s,s'}^a & =\frac{}{N(s,a)}\sum_{k=1}^K\sum_{t=1}^{T_k}1(s_t^k,a_t^k,s_{t+1}^k=s,a,s') \\ \hat{R}_s^a & =\frac{1}{N(s,a)}\sum_{k=1}^K\sum_{t=1}^{T_k}1(s_t^k,a_t^k=s,a)R_t^k \end{split}\]然后根据这个MDP计算出V(A)=V(B)=0.75。从上面的分析来说,如果环境是MDP的,那么TD会好一些。
SARSA
有了TD(0)来进行策略评估(预测问题),接下来我们就可以用它来找最优策略(控制问题)。我们首先介绍On-Policy的算法SARSA。之前我们的TD(0)的更新公式是关于V(s)的,现在我们首先把它改成Q(s,a)的:
\[Q(S_t,A_t) \leftarrow Q(S_t,A_t)+\alpha [R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t)]\]这个公式更新是需要下一个t+1时刻d的$S_{t+1}$和$A_{t+1}$,再加上t时刻的$S_t$和$A_t$,以及$R_{t+1}$。这五个字母拼起来就是SARSA,因此这个算法就叫SARSA算法。伪代码如下:
Windy Gridworld环境介绍
在介绍实现SARSA的代码之前,我们先来构建一个Windy Gridworld的环境,并且会说明为什么这个问题很难用MC来解决而很容易用TD来解决。
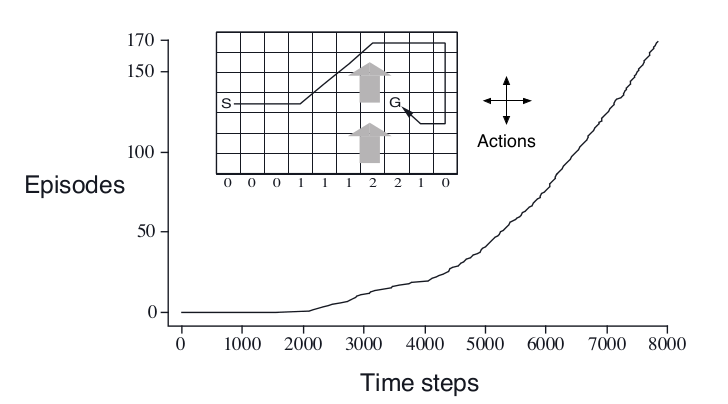
如下图所示,和普通的Gridworld不同,每一列的点都有风,比如第7列和第8列的风速都是2,如果我们从第7列采取向右的Action,则它会向右走一格并且被风吹得往上走两格。图中的路径是最优的路径。 这个环境用MC方法效果就不好,因为很多Episode很长甚至如果某个策略不好的话,可能永远到底不了终点。而TD方法就能解决这个问题,因为它不用等到结束就可以根据Reward更新了。
我们先看WindyGridworldEnv,完整代码在这里。
对于二维网格这样的环境,我们的类可以继承discrete.DiscreteEnv,然后实现render方法就行。那step呢?我们需要实现环境的动力学$P(s’|s,a)$。对于Windy GridWorld来说状态是(7,10)的数组,总共有70个状态。每种状态有4个Action,表示我们让Agent向上下左右4个方向移动。这个环境是确定的,因此对于每一个(s,a)的组合,只有一个s’的概率是1,其余的是0。除了$P(s’|s,a)$,我们还需要知道初始状态的概率分布,我们这里很简单,它的初始状态也是固定的在(3,0),因此在这点的概率是1,而其余点的概率都是0。
这些信息需要通过调用父类的构造函数告诉OpenAI Gym,如下所示:
super(WindyGridworldEnv, self).__init__(nS, nA, P, isd)
这里nS=70,告诉DiscreteEnv这个环境有70个状态。nA=4,表示每个状态都有4种可能的Action——上下左右。
P是一个dict,key是(0-69),表示每个状态的转移概率。注意:我们用二维数组表示状态,但是DiscreteEnv要求状态是一维的。我们需要在二维和一维之间进行转换,这里会用到numpy.ravel_multi_index函数。我们通过几个例子来学习这个函数:
>>> arr = np.array([[3,6,6],[4,5,1]])
>>> np.ravel_multi_index(arr, (7,6))
array([22, 41, 37])
我们先看第二个参数(7,6),它的意思是二维数组的大小是(7,6)。而输入是3组二维坐标(3,4)、(6,5)和(6,1),默认把二维变成一维是类似与C语言的二维数组——首先是第一行的6个数,然后是第二行。因此(3,4)对应的一维下标是3*6+4=22。
除了C语言的行优先(默认),还可以类似Fortran语言的列优先:
>>> arr = np.array([[3,6,6],[4,5,1]])
>>> np.ravel_multi_index(arr, (7,6), order='F')
array([31, 41, 13])
(3,4)表示第3行第4列,因为是列优先,所以4*7+3=31。
两者的区别如下:
# C风格的顺序
0 1 2
3 4 5
# Fortrain风格的顺序
0 2 4
1 3 5
我们以第二行第七列为例,它的二维坐标是(1, 6),对应的一维坐标是1*10+6=16。P[16]的内容为:
{
0: [(1.0, 6, -1.0, False)],
1: [(1.0, 7, -1.0, False)],
2: [(1.0, 6, -1.0, False)],
3: [(1.0, 5, -1.0, False)]
}
这又是一个dict,key是4个Action,0表示UP、1表示RIGHT、2表示DOWN、3表示LEFT。因此上面的例子表示P[16]往上走的概率分布是[(1.0, 6, -1.0, False)],这是一个数组。通常$P(s’|s,a)$是一个概率,s’可以取很多可能值,但是我们这里只有一个s’的概率不是零(是1),因此我们的这个数组只有一个元素。1.0表示概率$P(6|16,UP)=1$,状态6转换成二维左边是(0,6),确实是在(1,6)的上方。-1.0表示Reward,False表示这个状态不是结束状态。
另外如果走一步可能越界,那么就保持原地不动,比如我们来看P[0]:
{
0: [(1.0, 0, -1.0, False)],
1: [(1.0, 1, -1.0, False)],
2: [(1.0, 10, -1.0, False)],
3: [(1.0, 0, -1.0, False)]
}
(0, 0)是最左上的点,它往上(0)和往左(3)都越界(碰墙),因此还是呆在原地不到。
我们的目标点是第四行第八列,坐标是(3,7),因此P[48]为:
{
0: [(1.0, 28, -1.0, False)],
1: [(1.0, 39, -1.0, False)],
2: [(1.0, 48, -1.0, False)],
3: [(1.0, 37, -1.0, True)]
}
它表示第五行第九列(状态48)往左走一步就进入目标点,因为它除了往左走,还会被风上吹一步。这是如上图所示的最右一步。注意:风力是离开某点起作用的。比如现在在(4, 8),它的风力是往上的1;它往左一步就进入(4, 7),然后被风吹上一格变成(3, 7)。这里的风力是(4, 8)点也就是起点的风力。有的读者可能会以为先走的(4,7)点,然后用这点风力来吹,但是这点的风力是往上的2,那就会变成(2, 7),这样理解是不对的。
isd(Initial State Distribution)表示初始状态的分布,这是一个长度为70的数组,表示初始处于这个状态的概率,我们这里返回的isd只有在下标30(对应的二维下标是(3,0))是1,其余都是零,也就是初始状态总是在第四行第一列。
理解了这些,代码就很好理解了,render函数就是把它用图形(ascii art)的方式展现出来,这里就不赘述了,完整代码如下:
UP = 0
RIGHT = 1
DOWN = 2
LEFT = 3
class WindyGridworldEnv(discrete.DiscreteEnv):
metadata = {'render.modes': ['human', 'ansi']}
# 把范围限定为(0, shape[0]-1)和(0, shape[1]-1)内。
def _limit_coordinates(self, coord):
coord[0] = min(coord[0], self.shape[0] - 1)
coord[0] = max(coord[0], 0)
coord[1] = min(coord[1], self.shape[1] - 1)
coord[1] = max(coord[1], 0)
return coord
# 计算P(s'|s,a)
def _calculate_transition_prob(self, current, delta, winds):
# current是2-tuple,分别表示横纵轴坐标
# delta是移动方向,比如向右异地是(0,1),向上是(-1,0)
# 计算方法是把current和delta的对应坐标相加,同时在加上往上(-1,0)的风乘以风力。
# 风力存在winds数组里,winds[1,2]表示下标为(1,2)点的风力
new_position = np.array(current) + np.array(delta) + np.array([-1, 0]) * winds[tuple(current)]
new_position = self._limit_coordinates(new_position).astype(int)
new_state = np.ravel_multi_index(tuple(new_position), self.shape)
is_done = tuple(new_position) == (3, 7)
return [(1.0, new_state, -1.0, is_done)]
def __init__(self):
self.shape = (7, 10)
nS = np.prod(self.shape)
nA = 4
# 风力
winds = np.zeros(self.shape)
# 第4,5,6,9列的风力为1
winds[:,[3,4,5,8]] = 1
# 第7和8列的风力为2
winds[:,[6,7]] = 2
# 计算P(s'|s,a)
P = {}
for s in range(nS):
position = np.unravel_index(s, self.shape)
P[s] = { a : [] for a in range(nA) }
P[s][UP] = self._calculate_transition_prob(position, [-1, 0], winds)
P[s][RIGHT] = self._calculate_transition_prob(position, [0, 1], winds)
P[s][DOWN] = self._calculate_transition_prob(position, [1, 0], winds)
P[s][LEFT] = self._calculate_transition_prob(position, [0, -1], winds)
# 初始状态在 (3, 0)
isd = np.zeros(nS)
isd[np.ravel_multi_index((3,0), self.shape)] = 1.0
super(WindyGridworldEnv, self).__init__(nS, nA, P, isd)
def render(self, mode='human', close=False):
if close:
return
outfile = StringIO() if mode == 'ansi' else sys.stdout
for s in range(self.nS):
position = np.unravel_index(s, self.shape)
# print(self.s)
if self.s == s:
output = " x "
elif position == (3,7):
output = " T "
else:
output = " o "
if position[1] == 0:
output = output.lstrip()
if position[1] == self.shape[1] - 1:
output = output.rstrip()
output += "\n"
outfile.write(output)
outfile.write("\n")
我们来尝试一下这个环境,代码在Windy Gridworld.ipynb。
env = WindyGridworldEnv()
print(env.reset())
env.render()
print(env.step(1))
env.render()
print(env.step(1))
env.render()
print(env.step(1))
env.render()
print(env.step(1))
env.render()
输出为:
30
o o o o o o o o o o
o o o o o o o o o o
o o o o o o o o o o
x o o o o o o T o o
o o o o o o o o o o
o o o o o o o o o o
o o o o o o o o o o
(31, -1.0, False, {'prob': 1.0})
o o o o o o o o o o
o o o o o o o o o o
o o o o o o o o o o
o x o o o o o T o o
o o o o o o o o o o
o o o o o o o o o o
o o o o o o o o o o
(32, -1.0, False, {'prob': 1.0})
o o o o o o o o o o
o o o o o o o o o o
o o o o o o o o o o
o o x o o o o T o o
o o o o o o o o o o
o o o o o o o o o o
o o o o o o o o o o
(33, -1.0, False, {'prob': 1.0})
o o o o o o o o o o
o o o o o o o o o o
o o o o o o o o o o
o o o x o o o T o o
o o o o o o o o o o
o o o o o o o o o o
o o o o o o o o o o
(24, -1.0, False, {'prob': 1.0})
o o o o o o o o o o
o o o o o o o o o o
o o o o x o o o o o
o o o o o o o T o o
o o o o o o o o o o
o o o o o o o o o o
o o o o o o o o o o
它对应的就是上图所示的前4步。
SARSA代码
代码在SARSA.ipynb,非常简单,基本和伪代码一样:
def sarsa(env, num_episodes, discount_factor=1.0, alpha=0.5, epsilon=0.1):
"""
SARSA 算法: On-policy TD控制。找到最优的ε-greedy 策略。
参数:
env: OpenAI 环境。
num_episodes: 采样的episodes次数。
discount_factor: 打折因子。
alpha: TD学习率(learning rate)。
epsilon: ε-贪婪的ε,随机行为的概率
返回值:
二元组(Q, stats).
Q 是最优行为价值函数,一个dictionary state -> action values.
stats是一个EpisodeStats对象,这个对象有两个numpy数值,分别是
episode_lengths和episode_rewards,存储每个Episode的长度和奖励,用于绘图。
"""
# 最终返回的Q(s,a)函数The final action-value function。
# 它是一个嵌套的dictionary state -> (action -> action-value)。
Q = defaultdict(lambda: np.zeros(env.action_space.n))
# 参考返回值的注释。
stats = plotting.EpisodeStats(
episode_lengths=np.zeros(num_episodes),
episode_rewards=np.zeros(num_episodes))
# 通过Q(s,a)得到ε-贪婪的策略,注意Q变化后策略就随着改变了。
policy = make_epsilon_greedy_policy(Q, epsilon, env.action_space.n)
for i_episode in range(num_episodes):
if (i_episode + 1) % 100 == 0:
print("\rEpisode {}/{}.".format(i_episode + 1, num_episodes), end="")
sys.stdout.flush()
# 重置环境并且采样第一个Action
state = env.reset()
action_probs = policy(state)
action = np.random.choice(np.arange(len(action_probs)), p=action_probs)
for t in itertools.count():
# 采取行为A
next_state, reward, done, _ = env.step(action)
# 选择下一个行为A'
next_action_probs = policy(next_state)
next_action = np.random.choice(np.arange(len(next_action_probs)), p=next_action_probs)
# 更新统计信息
stats.episode_rewards[i_episode] += reward
stats.episode_lengths[i_episode] = t
# TD Update
td_target = reward + discount_factor * Q[next_state][next_action]
td_delta = td_target - Q[state][action]
Q[state][action] += alpha * td_delta
if done:
break
action = next_action
state = next_state
return Q, stats
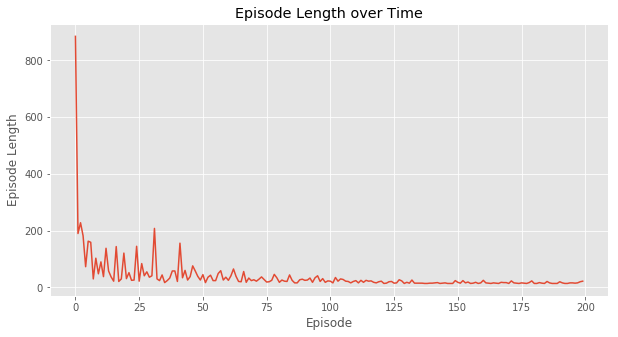
对于windy gridworld任务,我们的超参数ε=0.1,TD(0)收敛后的策略平均需要17步,比最优的15步多2步,原因是它有0.1的概率会随机采取行为。下图我们绘制是Episode长度的变化,可以看出,刚开始一个episode很长(斜率很低),然后随着迭代快速收敛到一个最优这(斜率不再变化)。
Q-学习(Q-Learning)
接下来我们讨论一种Off-Policy的TD学习算法Q-Learning,这是非常流行的一种算法,后面我们介绍深度学习和强化学习的结合时就会介绍Deep Q-Learning。我们知道Off-Policy有两个策略——目标策略和行为策略。对于Q-Learning来说也是有两个策略的,但是和之前的Off-Policy不同,Q-Learning的两个策略都是依赖与同一个Q函数,因此叫做Q-Learning。首先我们看一下怎么把基于重要性采样的Off-Policy MC算法推广到基于重要性采样的Off-Policy TD算法,然后再分析Q-Learning是怎么来的。
回顾一下前面的内容,Off-Policy的MC算法的核心点是用行为策略采样Episode,但是更新V(s)或者Q(s,a)时回报要乘以重要性比例:
\[\rho_{t:T+1}=\prod_{k=t}^{T}\frac{\pi(A_k|S_k)}{b(A_k|S_k)}\]V(s)的更新公式是:
\[V(S_t) \leftarrow V(S_t)+\alpha(\rho_{t:T+1}G_t-V(S_t))\]如果我们用TD来代替MC,那么更新公式是:
\[V(S_t) \leftarrow V(S_t)+\alpha(\rho_{t:T+1}(R_{t+1}+\gamma V(S_{t+1}))-V(S_t))\]Q-Learning有两个策略,基于Q(s,a)的贪心策略,这是目标策略;基于Q(s,a)的ε-贪婪策略,这是行为策略。此外Q-Learning不使用重要性采样,因此$\rho$是1。因此Q-Learning的更新公式是:
\[Q(S_t,A_t) \leftarrow Q(S_t,A_t)+\alpha(R_{t+1}+\gamma V(S_{t+1},A')-Q(S_t,A_t))\]在状态$S_t$是的Action使用ε-贪婪的策略,采取行为$A_t$之后进入状态$S_{t+1}$,这个时候的A’使用目标策略:
\[\pi(S_{t+1})=arg\max_{a'} Q(S_{t+1},a')\]把这个式子代入上式得到Q-Learning的更新目标:
\[\begin{split} & R_{t+1}+\gamma V(S_{t+1},A')-Q(S_t,A_t) \\ & =R_{t+1}+\gamma V(S_{t+1},arg\max_{a'} Q(S_{t+1},a'))-Q(S_t,A_t) \\ & =R_{t+1}+\gamma \max_aV(S_{t+1},a)-Q(S_t,A_t) \end{split}\]和SARSA不同,前者两次行为$A_t$和$A_{t+1}$都由ε-贪婪的策略生成,而Q-Learning中,我们用行为策略(ε-贪婪的策略)生成了$A_t$,用目标策略来“模拟生成”$A_{t+1}$。
假设初始化状态是$S_0$,SARSA是如下更新的:根据行为策略生成$A_0$,执行此Action,进入状态$S_1$,然后再更加相同的行为策略生成$A_1$,注意此时还没有执行$A_1$,此时就可以更加SARSA公式更新Q从而更新行为策略了。而如果是Q-Learning,更加行为策略生成$A_0$,执行词Action,进入$S_1$,此时就可以更新Q从更新行为策略了。接着用新的行为策略选择$A_1$并进入$S_2$。
从上面的比较可以看出,对于SARSA,$A_0$和$A_1$都是有初始化的Q对于的ε-贪婪策略生成的行为;而对于Q-Learning,$A_0$是用初始化的策略,而$A_1$已经是一个新的行为策略了。了解了他们的区别之后,Q-Learning的伪代码就很简单了:
Q-Learning代码
完整代码在Q-Learning.ipynb。
def q_learning(env, num_episodes, discount_factor=1.0, alpha=0.5, epsilon=0.1):
"""
Q-Learning 算法: Off-policy TD控制,它会采样ε-贪婪的策略来生成行为,并且使用贪婪的策略找到最优策略
参数:
env: OpenAI 环境。
num_episodes: 采样的episode次数
discount_factor: 打折因子。
alpha: TD学习率
epsilon: ε
返回值:
二元组(Q, stats).
Q 是最优行为价值函数,一个dictionary state -> action values.
stats是一个EpisodeStats对象,这个对象有两个numpy数值,
分别是episode_lengths和episode_rewards,存储每个Episode的长度和奖励,用于绘图。
"""
# 最终返回的Q(s,a)函数The final action-value function。
# 它是一个嵌套的dictionary state -> (action -> action-value)。
Q = defaultdict(lambda: np.zeros(env.action_space.n))
# 参考返回值的注释。
stats = plotting.EpisodeStats(
episode_lengths=np.zeros(num_episodes),
episode_rewards=np.zeros(num_episodes))
# 通过Q(s,a)得到ε-贪婪的策略,注意Q变化后策略就随着改变了。
policy = make_epsilon_greedy_policy(Q, epsilon, env.action_space.n)
for i_episode in range(num_episodes):
if (i_episode + 1) % 100 == 0:
print("\rEpisode {}/{}.".format(i_episode + 1, num_episodes), end="")
sys.stdout.flush()
# 重置环境
state = env.reset()
for t in itertools.count():
# 使用ε-贪婪的策略采样一个Action
action_probs = policy(state)
action = np.random.choice(np.arange(len(action_probs)), p=action_probs)
next_state, reward, done, _ = env.step(action)
# 更新统计信息
stats.episode_rewards[i_episode] += reward
stats.episode_lengths[i_episode] = t
# TD Update
best_next_action = np.argmax(Q[next_state])
td_target = reward + discount_factor * Q[next_state][best_next_action]
td_delta = td_target - Q[state][action]
Q[state][action] += alpha * td_delta
if done:
break
state = next_state
return Q, stats
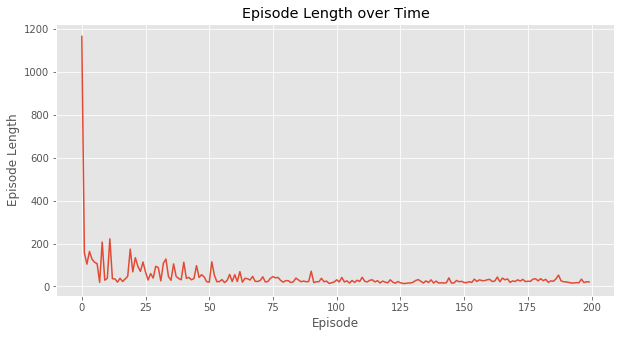
如下图所示,运行之后我们发现Q-Learning最后学到了最优的策略——最优的步数15。和On-line的SARSA对比,Off-Policy策略的Q-Learning能够学到最优的策略。
- 显示Disqus评论(需要科学上网)