本文是对Very Little Evolutionary Game Theory的翻译。
目录
Portuguese man o’war(僧帽水母,学名Physalia physalis)既不是葡萄牙人也不是军舰。它看起来像水母,其实并不是水母。它甚至不是一个动物。它是不同动物的集合体。每个个体做自己的事情,它们彼此合作联合一起(fusing togethoer)在海洋里一路驰骋,就像是一艘胶状(jelly)的海盗船。
每个僧帽水母战舰可能持续一年或者更长时间。所以进化生物学家会问:它们之间的合作是怎么进化而来的,它们有怎么防止搭顺风车的骗子?同样的问题我们也会去问我们更熟悉的动物之间的关系,比如合作的狮群和喂养后代的企鹅,或者真正的海盗。
在上面的这些例子里,它和前面章节的博弈游戏有一个很大的区别。前面章节的游戏相互博弈的双方见过一次之后就再也不会相见(或者即使再相见也不会记得彼此,所以相当于每次都是新的博弈对手)。存在这样的一次性交往的社会。但是灵长类群体和僧帽水母不是这样的。相同的个体在生命周期内会多次交往(博弈)。
为了建模这些关系的进化,我们需要学习可重复的游戏(repeated games)。在可重复的游戏里,个体形成群组(group),它们会多次互动(iteract),并且使用过去的经验来改变群组或者改变自己的策略。对于这个框架,我们的问题是:什么样的策略能够进化出持久的合作关系?
几乎所有重要的博弈论,尤其是应用到人类和其它动物社会时,都需要考虑可重复的游戏。不幸的是,即使是简单的博弈游戏,一旦可重复之后,都会变得很复杂。个体的交互次数越多,可能采取的策略也就越多。而且执行或者对于行为理解的细小错误都会导致巨大的差异。不过我们还是和之前一样,先分析和理解简单的问题,然后再逐渐加大难度。
迭代的(iterated)囚徒困境
在一个不确定结束的(uncertain end)重复博弈游戏里,互惠(reciprocity)策略相对不合作是稳定的。但它相对其它合作的策略是不稳定的。
被研究的最多的重复游戏就是迭代囚徒困境。这个简单的游戏就是普通的囚徒困境的可加性(addictive)版本。假设两个博弈者,他们可以互相帮助对方。帮助对方需要消耗c,而被帮助者获得收益b。我们假设b>c。下面是这个游戏的payoff矩阵:
| 合作 | 不合作 | |
| 合作 | b-c | -c |
| 不合作 | b | 0 |
我们可以发现,从个体的角度来看。最安全的策略就是不合作,这是个人最优策略。因为不管对方采取什么策略,我采取不合作都比合作强。我们具体来看一下:比如对方合作,我如果合作收益是b-c,这是小于不合作的b;如果对方不合作,我不合作的0也是大于合作的-c的。所以从这个角度来看,不合作是最优策略。当然从全局整体来看,如果双方能够合作,那么大家的收益b-c是大于0的。甚至极端一点,如果有一方合作,另一方不合作,从整体来看一个b加上一个-c也比两个零强。
现在我们把这个游戏嵌入到一个重复的结构里,这样两个相同的个体会多次玩这个博弈游戏。重复的结构有很多种可能,它会影响到进化行为的最终结果。一个确定次数的重复是无效的。比如一个游戏重复10次,这和不重复的游戏没有区别。因为不管前面9次采取什么样的策略,第10次游戏的时候大家都知道后面不会再见面了,所以这一次它们不用考虑后面的事情了,因此这一次游戏的策略和玩一次时没有区别的。类似的,既然第10次的策略和前面9次没有关系,那么第9次也不用考虑后面的事情了,因此也是和玩一次的策略是一样的。……
如果游戏的次数是不确定的,那么事情就完全不同了。我们假设两个个体首先会玩一局游戏,然后有w的概率继续玩下一场(当然有1-w的概率不再继续)。w是一个常数,而且每次游戏结束后都是相同的概率w来继续下一场。
所以有的时候博弈的一对只会玩一次游戏就结束了,这种情况的概率是(1-w);也有出现两次游戏的情况,其概率是w(1-w);也有三次的,概率是$w^2(1-w)$;……。个体会因为自然原因而死亡,但是除非w特别接近1或者两次游戏的间隔非常短(1秒钟玩一次?),通常情况我们不用考虑个体死亡的问题。如果自然选择非常强,游戏次数的分布细节是很重要的;而如果自然选择不是那么强,则我们只需要考虑平均游戏次数就可以给我们足够精确的近似了。我们后面只考虑平均的简单情况(再复杂数学知识就可能不够用了,^_^)。
平均的游戏次数是$1/(1-w)$。有两种方法来计算(证明)这个结果。首先我们考虑常规方法。假设R是平均游戏次数,那么更加前面的定义,它的计算公式为:
\[R = \sum_{i=1}^{\infty}w^{i-1}(1-w)(i)\]不要被公式吓得,仔细多读几次就能用自然语言理解它。这个公式的意思是,游戏的次数只是是一次,最多是无穷次。那么游戏玩i次的概率是多少呢?如果两者玩i次,那么说明什么呢?说明前面i-1次结束后都接着玩,所以概率是$ww \cdots w=w^{i-1}$,最后一次结束,其概率是(1-w)。所以玩i次的概率是$w^{i-1}(1-w)$,然后用这个概率乘以i并且累加起来就是平均次数。
但是这个公式又是怎么变成$1/(1-w)$的呢?下面会进行推导,对于数学实在头疼的读者可以跳过【不过译者还是强烈建议尝试一下,数学没有那么复杂,理解了它的逻辑之后会发现它甚至是美的,跳过去虽然不用费脑子,但是也错失了很多东西】。
\(R = \sum_{i=1}^{\infty}w^{i-1}(1-w)(i) = (1-w)(1)+w(1-w)(2)+w^2(1-w)(3)+ w^3(1-w)(4) + \cdots\) 这里的tricky之处是上面的几何无穷级数有一种循环的结构。我们可以把从第二项开始的项提取一个w,然后合并起来:
\[R=(1-w) + w \underbrace{((1-w)2 + w(1-w)3 + w^2(1-w)4 + \cdots)}_{Q}\]通过观察,我们发现Q和R很相似,只是第二个乘数比Q大1,我们把Q的第二项拆分出一个1来:
\[R=(1-w) + w \underbrace{((1-w)(1+1) + w(1-w)(2+1) + w^2(1-w)(3+1) + \cdots)}_{Q}\]这些拆分出来的1的相关项是$(1-w)1+w(1-w)1+w^2(1-w)1+\cdots$,这个无穷级数的和是1。为什么?因为它是全概率分布。【译注:如果读者不能理解这个,也可以利用等比数列求和公式计算。$1+w+w^2+w^3+\cdots = \lim_{n \to \infty} \frac{1-w^n}{1-w} = \frac{1}{1-w}$,所以前面的等式可以提取(1-w)。$(1-w)1+w(1-w)1+w^2(1-w)1+\cdots=(1-w)(1+w+w^2+w^3+\cdots)=(1-w)\frac{1}{1-w}=1$。】
所以代入之后可以继续化简:
\[R=(1-w) + w(1 + \underbrace{((1-w)1 + w(1-w)2 + w^2(1-w)3 + \cdots)}_{R}\] \[R = (1-w)+w(1+R)\]化简之后得到$R=1/(1-w)$。
除了上面的常规方法,这里还有一种更简单(译注:只是过程简单,但是需要脑筋转弯的更为tricky方法)的方法。这个方法的核心是:不管之前两人玩了多少次游戏,未来的期望游戏次数是不变的。所以可以得到$R=1+wR$,从而得出$R=1/(1-w)$。
为什么?我们可以这样来看。两个人平均的合作次数R,他们首先至少合作一次,这就是右式的1,接着他们有w的概率继续下去。而继续下去和从新开始游戏其实没有区别,也是至少先玩一次,然后有w的概率继续玩。【译注:有没有联想到前面无穷级数的Q和R?期望读者两种方法都能理解,尤其第一种是非常简单的,只是比较繁琐而已。第二种比较tricky,需要多想想】
如果我们不引入之前游戏的信息,那么重复游戏和一次性的游戏并无区别。比如一种策略是总是合作(ALLC)的策略。当群体都是ALLC的策略者时,每次的fitness是(b-c),然后平均的游戏次数是R,所以期望的fitness是$R(b-c)$。另外一种策略是总是不合作(NO-C),当少量NO-C变异出现时,它们碰到的总是ALLC,它们的fitness是b,所以期望的fitness是$Rb$。所以ALLC的策略会被NO-C入侵,最终群体都不合作,这和一次性的囚徒困境是一样的。
现在看一种根据过去行为随机应变的简单策略。这种策略在第一次总是合作,而后面的策略是复制对手上一次的策略。这种策略有一个名字叫Tit-for-Tat(TFT)【译注:有些中文文献把它翻译成以牙还牙策略,类似朋友来了有好酒,敌人来了有猎枪】。TFT能够抵挡NO-C这种”坏人”的入侵吗?TFT直接总是会合作,因为第一次双方都合作,接着后面大家都复制对方的策略,因此也都是合作。所以TFT占据主流时其平均fitness是$R(b-c)$。如果少量的NO-C出现,它碰到的都是TFT,它们在第一次时TFT会合作,但是NO-C不合作,然后第二次TFT复制NO-C的策略,从第二次开始一直都是不合作了。因此NO-C只能在第一次占便宜,得到b的收益,后面大家都不合作了。如果TFT想要能抵制NO-C的入侵,需要满足:
\[R(b-c)>b\]这个条件其实是很容易满足的。比如w=0.9,则R=10,即使b-c比较小,乘以10之后也可能比b大。我们把$R=1/(1-w)$代入:
\[wb>c\]因此,如果b/c=2,那么只需要w>0.5就行了。这并不是苛刻的要求,因此即使关系不会持续太久,互利合作也是可以建立起来的。【译注:这里的核心点在于,因为要考虑到后面的收益,所以我们不能把事情做得太绝,不能做一锤子买卖】
TFT策略非常出名,Robert Axelrod为此写过一本《合作的进化》来介绍它。它揭示了互利共赢基本逻辑和为什么这种策略能够促成合作。但是TFT策略是不稳定的,ALLC策略可以入侵TFT,因为群体里只有TFT和ALLC时,他们的行为是相同的——他们总是合作,所以其fitness是一样的。但是如果ALLC变多之后,搭便车的NO-C就可能入侵了。这有点像老鹰-鸽子-报复者的情况。
微小的错误,巨大的差异
在重复游戏中错误是很关键的。如果游戏重复的次数足够多,即使少量的错误也会改变关系的动力学。
考虑一个个体在选择合作策略的时候可能会失败。这是因为要合作就必须采取行动,采取行动就有可能失败,即使个体主观上是想合作的。假设一个个体打算合作但是最终没有采取合作行为的概率是x。在博弈论里,这个错误叫做实现错误(Implementation Error)。实现错误可以区分出ALLC和TFT两种策略。这个错误会同时影响这两种策略,但是TFT会进行报复——即使对方主观上是想合作的,而ALLC不会采取报复行动。
要在存在错误的情况下计算期望的收益(payoff),我们需要计算在各种可能的关系持续次数和各种可能的错误路径。这看起来非常困难。我们可以把这个问题表示为意图状态(intention state)的跳转,这会使得问题变得简单。【译注:熟悉数学的读者可能会联想到马尔科夫链】
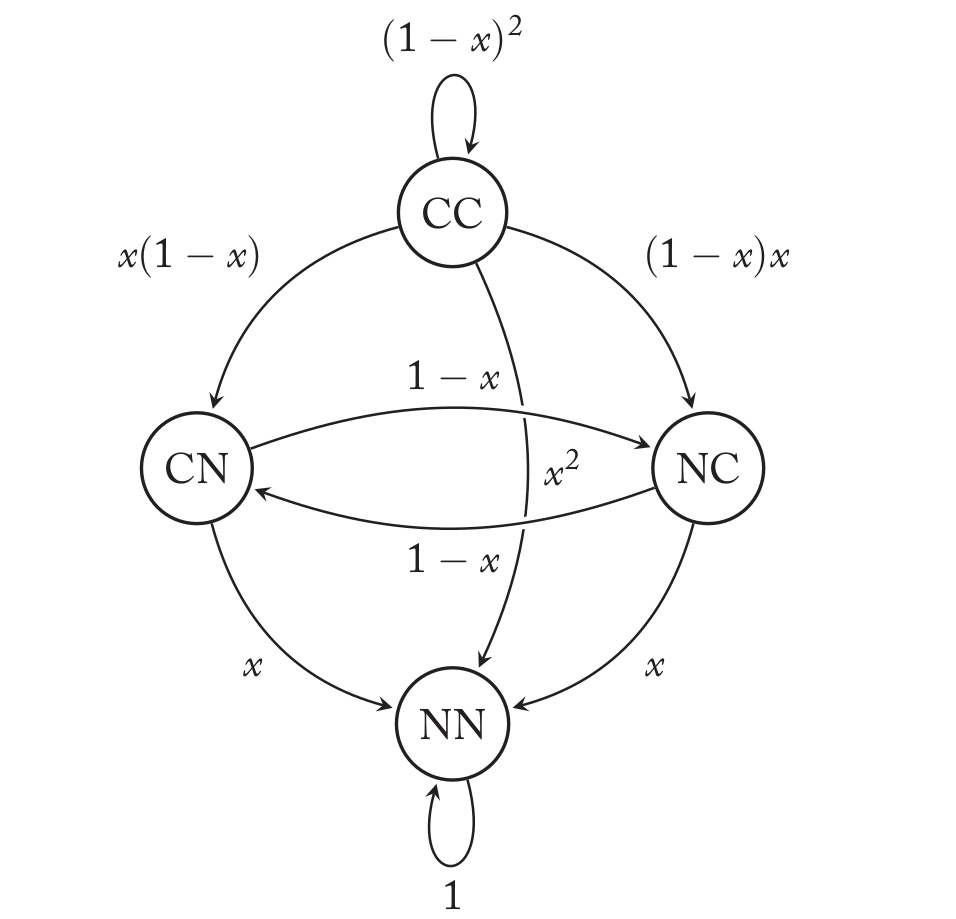
对于两个TFT的情况,总共有四种可能:它们都想(【译注:只是想,实际可能会出错】)合作,记为CC;我方(focal)不想合作但是对方想合作,记为NC;我方想合作但对方不想合作,记为CN;双方都不想合作,记为NN。实现错误会影响这些状态的跳转,这些跳转可以用下图来表示。
上图中圆圈代表状态,也就是双方的意图,边代表了状态之间的跳转,边上的值代表了跳转的概率。一开始的状态是CC,如果两种都没有实现错误,那么最终的动作就是和意图一样,双方都合作。既然双方的实际动作都是合作,而TFT的策略是复制对方的策略,所以下一次的意图(注意不是实际动作)仍然都是合作,所以这条边的起点和终点都是CC,也就是图中CC上的那个环。那么都不错误的概率是多少呢?显然是$(1-x)^2$。类似的,如果状态CC的时候双方都发生了实现错误,所以双方的意图虽然都是CC,但是时间的动作确实不合作,而下一次双方的策略都是复制对方的策略,所以会跳转到NN的状态,这种情况发生的概率是$x^2$,这就是从CC到NN的那条边。
【译注:原文只分析了上面的两条边,我们再来多看几个边。比如CC到CN的边。注意:这里的CN指的是下一轮focal的意图是合作(C),对手的意图是不合作(N)。这是什么意思呢?因为两者都是TFT,这说明上一轮对手是合作,而focal不合作,从而说明对手没有实现错误,而focal出现了实现错误,因此这条边的概率是x(1-x)。类似的,CC到NC的边是(1-x)x。注意:我们这里的概率乘法第一个是focal的概率,第二个是对手的概率,所以CC到NC的概率写成了(1-x)x,而CC到CN的概率是x(1-x)。请读者仔细思考确保理解了这一点。NN状态下只能跳转到NN,因为不合作是不会有实现错误的,所以双方以1的概率正确的实现意图,也就是不合作。最后我们再来看一个从CN到NC的跳转,CN状态说明我方想合作对方不想合作,而NC表示我方不想合作而对方想合作,因为是TFT,所以NC的意图表明上一轮实际发生的动作是CN,而上一轮的意图也是CN,这说明我方意图是C最后实现也是C,对方意图是N最后实现动作也是N,我们知道C到C正确执行的概率是(1-x),而N到N总是会正确执行(或者说以概率1执行),所以这条边的概率是(1-x)*1。】
我们可以使用上图来计算TFT遇到另外一个TFT时的期望的收益。这里使用的方法是对每一个状态的收益写出一个方程式来,这样4个状态有4个方程式和4个未知数,可以通过解方程得到每个状态的收益。【译注:这听起来有一些难以理解,请读者先耐心看完之后再多思考一下】我们首先来考虑状态CC的期望收益,我们把它记为$V_{CC}$。如果双方都不犯错,那么实际的动作都是合作,这样双方的收益都是b-c,并且下一轮双方的意图还是CC。这种情况方式的概率是$(1-x)^2$,所以如果局势这样发展,我们的收益是$(b-c)+(1-x)^2V_{CC}$。【译注:这里有点类似前面平均次数的方法,$V_{CC}$的计算会递归依赖$V_{CC}$】。CC除了跳转到CC,还有可能跳转到其它3个状态。详细的公式我们下面再讨论。按照这个方法,我们可以列出4个方程式,里面有4个未知数(其实NN状态的收益明显是0,可以去掉,不过其它一些情况下所有状态都不是0的收益,所以我们还是保留NN状态,这样的话我们的方法更有普适性)。最终我们可以解出:
\[V(TFT | TFT)=\frac{(1-x)(b-c)}{1-w(1-x)}\]我们可以拿这个式子和没有错误的情况$\frac{b-c}{1-w}$对比一下。在错误可能发生的情况下,单次游戏的收益变少了【从b-c变成了(1-x)(b-c)】,游戏的平均次数也变少了【从1/(1-w)变成了1/(1-w(1-x))】。原因之一就是一旦双方发生误会,进入NN状态就再也无法跳出这个状态了。【双方都太记仇了!】另外如果x=0,也就是没有实现错误,这个公式就退化成(b-c)/(1-w)了,这也能验证我们的推导应该是正确的。
下面我们就详细的说明一下这4个方程是怎么列举出来的。【译注:虽然解方程的过程非常复杂和繁琐,但是我们可以借助一些数学工具软件。我们唯一要理解的是为什么能得出这4个方程式,这是重中之重,理解了这4个方程式,就理解了整个逻辑。虽然跳过这部分不影响阅读,但是强烈建议读者跟着推导一下。我也会尽量准确翻译并且补充一下说明。】
为了计算人口中大部分是TFT时,$V(TFT | TFT)$,我们需要为跳转图中的每一个状态写出一个方程式,我们首先来看意图状态是CC的情况。
\[V_{CC} = (1-x)^2(b-c+wV_{CC}) +x(1-x)(b+wV_{CN})+(1-x)x(-c+wV_{NC})+x^2(0)\]【译注:我们来理解一下这个式子,第一项是意图是CC,并且双方都没有错误的情况。这种情况的收益是(b-c),概率是$(1-x)^2$,并且下一个状态也是CC,所以还要递归加上下一次游戏的收益。下一次游戏继续的概率是w,而初始状态是CC,所以是需要加上$wV_{CC}$。第二项是我方实现错误,从而最终的动作是不合作(N),而对方正确,最终的动作是合作(C),这种情况发生的概率是x(1-x)。这种情况下我方的收益是b,并且新的状态是CN,所以还要加上$wV_{CN}$。第三项和第二项是类似的,最后一项是双方都实现错误,因此收益是0。】
接下来我们看$V_{CN}$:
\[V_{CN}=(1-x)(-c + wV_{NC}) + x(0)\]【译注:CN状态如果正确实现,那么实际的行为就是合作/不合作,TFT复制对方的策略,因此下一轮的意图是NC。双方都正确的概率是(1-x)*1(不合作不会发生错误)。我方合作但是对方不合作,所以我方的收益是-c,并且继续游戏的概率是w,然后再乘以未来继续游戏的收益$V_{NC}$。如果我方实现错误(对方不合作是不会出错的),那么就变成了NN。】
最后是$V_{NC}$:
\[V_{NC}=(1-x)(b + wV_{CN}) + x(0)\]【译注:NC如果正确实现,那么就变成CN,这个基本和上式类似的,只不过收益是b】
现在我们有三个方程和三个未知量$V_{CC},V_{CN},V_{NC}$,我们可以用Mathematica之类的软件来帮助我们求解。如果我们想自己手动求解的话,我们可以根据第2和第3个方程先把$V_{CN}和V_{NC}$解出来,因为这两个方程式里没有$V_{CC}$。然后代入进第一个方程可以解出$V_{CC}$。
解出来的结果是:
\[V_{CN}=(1-x)\frac{w(1-x)b-c}{(1-w(1-x))(1+w(1-x))} \\ V_{NC}=(1-x)\frac{b-w(1-x)c}{(1-w(1-x))(1+w(1-x))} \\ V_{CC}=\frac{(1-x)(b-c)}{1-w(1-x)}\]因为一对TFT的初始状态是CC(双方都想合作),所以$V(TFT | TFT)=V_{CC}$。到此为止,我就已经计算好了$V(TFT | TFT)$。为了分析NO-C和ALLC能否入侵,我们还需要计算$V(NO-C | TFT)$和$V(ALLC | TFT)$。首先我们来计算前者:
\[V(NO-C | TFT) = (1-x)b + x(0) + w(0)\]上面式子的含义是:NO-C当然是永远不合作,而且也不存在实现错误。TFT第一次是想合作的,但是有x的概率实现错误不合作,(1-x)的概率合作。第一次的期望收益是(1-x)b+x(0)。不管哪种情况,第二次TFT都不会合作,所以w乘以0表示有w的概率进入下一轮,但是没有收益了。
TFT要想抵御NO-C的入侵,需要满足$V(TFT | TFT) > V(NO-C | TFT)$,化简之后的条件是$(1-x)wb>c$。
接下来我们计算$V(ALLC | TFT)$,它的方法和前面计算$V(TFT | TFT)$类似,我们来分析它的状态跳转。由于ALLC的意图总是合作(当然可能会实现错误导致实际不合作,但意图还是合作),所以只有两种意图状态CC和CN。我们先来看CC状态,如果双方都是没有实现错误,那么实际的动作都是合作,这种情况发生的概率是$(1-x)^2$。另外一种情况是对方发生实现错误,那么实际的动作是CN,而第二轮我方(ALLC)总是C,对方复制我方的动作C,所以还是跳到C,因此这种情况还是会跳到CC状态。这种情况的概率是(1-x)x。如果我方实现错误,对方正确,那么实际发生的是NC,第二轮对方复制我方策略,这样会跳到CN状态,这种情况的概率是x(1-x)。最后一种情况是双方实现错误,实际发生的是NN,第二轮变成CN,概率为$x^2$。
把这四种情况的概率和收益都累加起来就得到第一个方程:
\[V_{CC}=\underbrace{(1-x)^2(b-c+wV_{CC})}_{\text{no mistake}} + \underbrace{(1-x)x(-c+wV_{CC})}_{\text{partner(TFT) error}} + \\ \underbrace{x(1-x)(b+wV_{CN})}_{\text{focal(ALLC) error}} + \underbrace{x^2(0+wV_{CN})}_{\text{both error}}\]【译注:我们再来复述一下上面的式子。CC状态如果双方都不犯错,那么概率是$(1-x)^2$,下一次的状态是CC,收益是$b-c+wV_{CC}$。 如果我方正确对方错误,那么发生的概率是(1-x)x,并且下一个状态是CC,因此收益是$-c+wV_{CC}$。如果我方错误对方正确,那么发生的概率是x(1-x),并且下一个状态是CN,因此收益是$b+wV_{CN}$。最后一种情况就是双方都发生错误,概率是$x^2$,下一个状态是CN,收益是0。】
接下来我们看CN状态,它只有两种情况:我方按意图正确执行和实现错误(因为对方的意图是N,这是不可能实现错误的!)。如果我方没有实现错误,那么最终的动作是CN,下一轮我方(ALLC)是C,而TFT复制我方上一轮的策略也是C,因此它会跳到CC状态,这个发生的概率是(1-x)。如果我方发生实现错误,那么最终的动作是NN,下一轮我方是C,而对方复制我方策略N,因此跳转到CN自己,这个情况的概率是x。
\[V_{CN}=\underbrace{(1-x)(-c+wV_{CC})}_{\text{focal no mistake}} + \underbrace{x(0+wV_{CN})}_{\text{focal error}}\]通过这两个方程可以解出:
\[V_{CC}=(1-x)\frac{(1-xw)b-c}{1-w}=V(ALLC | TFT)\]如果我们希望TFT可以抵御ALLC,那么就要求$V(TFT | TFT) > V(ALLC | TFT)$。经过化简后的条件是$(1-x)wb<c$。我们把这个条件与TFT抵御NO-C($(1-x)wb>c$)相比,可以发现这两个条件正好相反。所以TFT是无法同时抵御NO-C和ALLC的侵入的!
我们把这三个放到一起来比较一下:
\[V(TFT | TFT) = \frac{(1-x)(b-c)}{1-w(1-x)} \\ V(NO-C | TFT) = (1-x)b \\ V(ALLC | TFT) = (1-x)\frac{(1-xw)b-c}{1-w}\]我们先来看$V(TFT | TFT)$和$V(ALLC | TFT)$。在TFT和TFT的配对下,错误会减小分子和增大分母,也就是说每次游戏的收益因为错误变小而游戏的平均次数也会变少。而TFT和ALLC的情况有所不同,因为ALLC总是会合作,所以不会出现双方都陷入报复从而导致游戏提前结束。对于NO-C来说,虽然它的收益也会因为错误而从b变成了(1-x)b,但是相对TFT来说它的损失没有那么大,因为在没有错误的情况下它也只能玩一局,所以它的(有效)游戏次数并没有变化。
这里需要注意,我们假设只有合作才会出错,而不合作是永远不会出错的。我们的理由是合作需要做一些事情,做事情就可能出错,而不合作就是什么也不干,所以不出错。但是有的时候合作是什么也不干,而不合作需要做事情。比如有一个公共的鱼塘,大家都打渔,则把小鱼苗都打光了,这是不利于群体的事情。在这种情况下,合作就是不打渔,不合作就是打渔。不打渔就是什么也不干,而打渔是做事情。在这种情况下合作是不会出错,但是不合作可能出错,比如我本来想打渔,但是因为我水平太差没打着。
另外我们这里的收益是加性的(additive),也就是说如果只有一方合作,那么合作方是-c,不合作方是b,两个人的总体收益是b-c,如果两方都合作,那么两人的收益都是b-c。如果收益是synergistic,那么两人合作的话,双方的收益是B-c,其中B>b。举个例子,比如两个猴子,合作就是给对方挠痒痒,不合作就是什么也不干。如果只有一只猴子给另一种猴子挠痒痒,那么合作的一方的成本是-c,另一种猴子的收益是b。如果双方都给对方挠痒痒,那么双方的收益不仅仅是b-c,而是B-c,这个额外的B-b可能是因为它们除了被挠痒痒的收益之外还会建立良好的友谊带来的额外收益。
学习和错误
有些策略学习合作或者不合作这两种选择哪种的收益大,这种学习策略在有实现错误的情况下比TFT更优。
前面的例子里的策略都是固定的策略(即使TFT是根据对手进行调整,但是这个策略本身是固定的),除此之外还有一些策略是学习而来的。下面我考虑一种叫做Pavlov的策略。这个策略有一个期望的收益值,如果采取某种行为(不论是合作还是不合作)的收益达到了预期,它就持续采用这种行为。我们假设预期的收益是b-c,也就是双方合作的收益。【译注:我不想占便宜(b),也不想吃亏(-c)】在这个游戏里只有3中收益,b(我方占便宜),-c(我方吃亏),b-c(正常合作)。如果收益大于等于b-c,也就是b-c或者b,我就保持当前的行为;如果收益小于b-c,也就是-c,我就改变行为。从这里我们可以看出,Pavlov并不是一个像TFT那么”道德的”的策略——能够占便宜也行,反正不能吃亏。
首先考虑没有实现错误的情况。如果两个Pavlov相遇,初始化的行为是合作,那么他们的收益是b-c,所以他们都会保持之前的行为,从而一直合作下去。如果一上来双方都不合作,那么第一轮游戏的收益是0,没有达到预期的b-c,所以双方都切换到合作然后一直合作下去。【译注:如果一方合作另一方不合作,那么游戏的行为序列是NC->NN->CC->CC】 Pavlov占据主导时会采取相互合作的行为,所以是一个不错的策略。
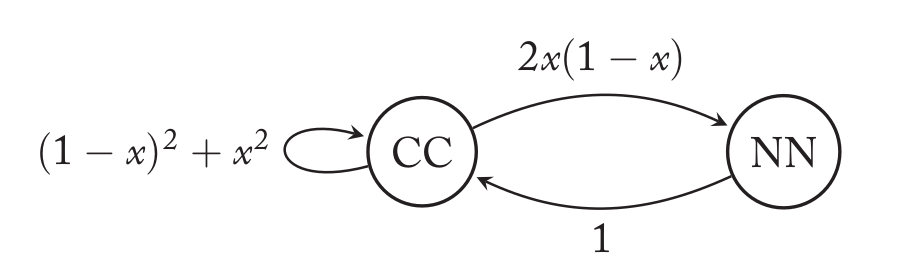
接下来看看Pavlov策略发生错误的情况。和前面一样,假设意图是合作但是由于实现错误导致不合作的概率是x。和前面一样,我们画出其状态转移图:
从CC到CC有两种情况:一种是双方都没有错误,这种情况的概率是$(1-x)^2$;另一种情况是双方都出错,实际执行的动作是NN,双方的收益都是0,因此下一轮双方的意图都是CC【译注:Pavlov是改变上一轮的行为而不是意图!】。当只有一方出错的时候,对方的收益是0,从而会改变其行为。比如我方出错,实际执行是NC,我方收益b对方-c,因此我方保持对方改变,从而下一轮的意图是NN。类似的,对方出错,实际执行的是CN,我方收益-c对方b,因此我方改变对方保持,从而下一轮也是NN。这两种情况的概率都是x(1-x)。最后一种情况是NN,因为NN不会有实现错误,所以实际发生的也是NN,双方的收益都是0,所以双方都改变行为变成CC,其概率是1。
下面我们来计算$P(Pavlov | Pavlov)$,这和前面一样,我们需要根据状态转移图列出方程式,首先看$V_{CC}$:
\[V_{CC}=(1-x)^2(b-c+wV_{CC}) + x(1-x)(b+wV_{NN}) + (1-x)x(-c+wV_{NN}) + x^2(0+wV_{NN})\]上式的解读:(1)从CC跳转到CC,概率是$(1-x)^2$,收益是(b-c)和未来的预期收益$V_{CC}$乘以继续游戏的概率w。(2)我方出错对方不出错,概率是x(1-x),收益是b和未来的预期收益$V_{NN}$乘以w。(3)我方不出错对方出错,概率是x(1-x),收益是-c和未来的预期收益。(4)双方出错,概率是$x^2$,收益是0和未来的预期收益。
接下来是$V_{NN}$:
\[V_{NN}=1(0+wV_{CC})\]NN到CC的概率是1,并且当前收益是0,未来预期收益是$V_{CC}$乘以w。
通过这两个方程解出$V_{CC}$:
\[V_{CC}=\frac{(1-x)(b-c)}{(1-w)(1+2wx(1-x))}=P(Pavlov | Pavlov)\]接下来我们看少量ALLC能否入侵。我们可以用类似的方法计算,这里只有两种情况CC和CN,因为ALLC总是合作。我们还是先看$V_{CC}$
\[V_{CC}=(1-x)^2(b-c+wV_{CC}) + x(1-x)(b+wV_{CN}) + (1-x)x(-c+wV_{CN}) + x^2(0+wV_{CC})\]解读:(1)双方都正确,概率是$(1-x)^2$,实际动作是CC,我方(ALLC)下一轮C,对方到达预期保持C。(2)我方出错对方正确,概率是x(1-x),实际动作是NC,我方下一轮是C,对方收益-c未达预期变成N,因此下一轮的意图是CN。(3)我方正确对方出错,概率是(1-x)x,实际动作是CN,我方下一轮总是C,对方收益达到预期保持N,所以下一轮是CN。(4)双方出错,概率是$x^2$,实际动作是NN,我方下一轮C,对方下一轮C。
接下来是$V_{CN}$:
\[V_{CN}=(1-x)(-c+wV_{CN})+x(0+wV_{CC})\]因为只有我方意图是C可能出错,所以只有两种情况:(1)我方正确,概率是(1-x),实际动作是CN,我方下一轮还是C,对方收益b达到预期保持N,所以下一轮还是CN。(2)我方出错,概率是x,实际动作是NN,我方下一轮还是C,对方收益0未达预期,下一轮改成C,所以最终是CC。
通过这两个方程我们可以解出$V_{CC}$:
\[V_{CC}=\frac{(1-x)(b( 1- w(1-x) ) - c( 1 - w( 1-(3-x)x) ))}{(1-w) (1-w( 1-(3-x)x))}=P(ALLC | Pavlov)\]这两个公式看起来都很复杂,不过我们的问题是Pavlov是否能抵挡ALLC的入侵,也就是什么时候$P(Pavlov | Pavlov) > P(ALLC | Pavlov)$,经过化简后的条件是$b>c$。这个条件总是满足的,所以ALLC不能入侵Pavlov。
接下来我们看看NO-C是否可以入侵Pavlov。方法是类似的,这个状态图只有NC和NN两种状态。
\[V_{NC}=(1-x)(b+wV_{NN}) +x(0+wV_{NC})\]解读:(1)对方正确,概率是(1-x),实际动作是NC,我方下一轮总是N,对方收益-c所以改变为N,因此下一轮NN。(2)对方实现错误,概率x,时间动作是NN,下一轮变成NC。
\[V_{NN}=1(0+wV_{NC})\]解读:NN总是会正确,所以概率是1,实际动作是NN,下一轮变成NC。
通过上面的方程解出:
\[V_{NC}=\frac{(1-x)b}{(1-w)(1+w(1-x))}=P(NO-C | Pavlov)\]要分析$P(NO-C | Pavlov)$和$P(Pavlov | Pavlov)$哪个大比较复杂,我们可以画两条曲线,横轴是x,纵轴分别是这两个值。
下面我们来分析一下Pavlov能否抵挡ALLC和NO-C的入侵。回顾一下,TFT的主要问题是不能同时抵挡ALLC和NO-C的入侵,实现错误也不能改变这一事实。前面分析过了,少量的ALLC不能入侵Pavlov,原因是Pavlov会利用ALLC总是合作的弱点,从而停留在CN状态。因为在CN状态,Pavlov的收益是b,ALLC是-c,Pavlov是在占便宜,但是ALLC不会改变策略,而Pavlov也不是”道德的君子”,它只要收益大于预期的b-c就不会改变行为。除非发生了实现错误,然后跳到NN状态。然后Pavlov决定改变策略回到CC状态。从这里可以看出,Pavlov并不是一种”合作的”策略,它只想要b-c或者更好的收益。如果对方有便宜给它占它是不会犹豫的。
Pavlov的弱点是NO-C,因为一开始NC,如果Pavlov没有出错,则跳到NN,如果出错,Pavlov还会尝试合作跳到NC。而且即使在NN状态,双方都不合作了,Pavlov还是会尝试去和NO-C合作,跳到NC状态。因此和TFT相比,Pavlov好像更”宽恕”一点。当然我们知道它内心并没有宽恕对方,只是想改变大家都不好的困境而已。而TFT则强硬的多:你不合作我就不跟你合作,咱俩死磕!Pavlov在条件满足的情况下也是能够抵御少量NO-C的入侵的,不过抵抗能力没有TFT强。
伙伴选择(Partner Choice)
离开不合作的伙伴而去搜寻新的合作伙伴的策略需要考虑搜索的代价以及市场上可以获得的伙伴。
重复的囚徒困境可以有很多不同的方式来解读。我们可以认为每个个体都有一个固定的伙伴并且平均玩$R=\frac{1}{1-w}$次,我们也可以认为每个个体有多个伙伴。比如在狒狒群里,每个成年狒狒都会不断和其它狒狒交互。某些伙伴会保持合作,而另一些不会。当不合作的动作是不互动,就像默认的囚徒困境游戏,那么结果就像伙伴选择:个体只会和群体的一部分成员合作。
作为一个通用的伙伴选择模型,重复的囚徒困境有明显的缺陷。首先,个体不可能与其他每个人结伴。关系是特殊的并且能帮的伙伴也是有限的,所以个体必须决定去帮助谁。其次,维持关系的伙伴们之间可能会想要进行更多次数的互动,以便最大化合作的益处。为了解决这些问题,我们需要新的方法来建模动态伙伴选择。
现在假设一个个体一次只和一个(固定的)伙伴玩重复的囚徒困境游戏。每次游戏,个体都可以选择继续维持和当前伙伴的关系,但也可以和当前伙伴解除关系并且搜寻一个新的合作伙伴。关系有各种各样结束的原因,我们不去探究,只是假设维持关系的概率是w。不过是什么原因解除了关系,寻找新的伙伴都是需要时间的(有代价)。一次游戏的时间内找到新伙伴的概率是s。那么和前面类似,平均找到新伙伴的时间是$S=1/(1-s)$(【译注:用游戏的次数来计时,这里假设每次游戏的时间是固定的,而且个体一生中就不停玩这个游戏】)。假设搜寻新伙伴概率s是一个常数,这似乎有些不合理——比如如果在我们周围没有配对的个体比较少,那么显然搜寻时间会更长,不过我们现在先使用这个简单的假设从而让问题变得简单一点。
生命不是无限的,从而搜索是有成本的。搜索的时候不能获得收益,时间也是有限的。假设每个个体玩了一局游戏还能继续存活的概率是$\lambda$,那么个体的平均寿命(以游戏的次数来计算)是$1/(1-\lambda)$。
下一步是计算fitness。在个体一生中基于这种伙伴关系他的期望收益是多少?假设群体中TFT是占大多数的。两个TFT组成的伙伴时他们期望的fitness是$R(b-c)$,然后他们的关系破裂,所以他们需要花S轮游戏时间来寻找新的伙伴。然后平均玩R轮游戏后又关系破裂。所以一个个体一生的时间被划分成R+S长度的片段。在每个片段中平均的fitness是$R(b-c)$。因此他们一生期望的fitness是:
\[V(TFT | TFT) = \frac{L}{R+S}R(b-c)\]伙伴选择能够帮助TFT抵御NO-C的侵入吗?少量NO-C出现时,他和TFT只玩一局游戏就关系破裂,然后话S轮的时间找新的牺牲者(【原文为Victim,这里有一种隐喻:NO-C不是好人,TFT是被他占便宜的对象】),因此它一生的fitness是:
\[V(NO-C | TFT) = \frac{L}{1+S}b\]如果TFT要想抵御NO-C的入侵,需要满足:
\[\frac{L}{R+S}R(b-c) > \frac{L}{1+S}b\]这个条件不太好解释,它依赖与R和S的具体值,后面会画图来帮助理解。这里会对它进行一些变换,从而让我们可以获得一些洞见。
回忆一下,在没有伙伴选择(也就是游戏结束后就没有新的伙伴了)时TFT稳定的条件是$R(b-c)>b$。这等价于$R>b/(b-c)$。让我们把有伙伴选择的新条件也写出R的式子:
\[R>\frac{Sb}{(1+S)(b-c)-b}\]这个两个条件哪个更容易满足?更容易满足对于R>x来说x越小越容易满足。因此如果伙伴选择更容易满足,那么条件是:
\[\frac{b}{b-c} > \frac{Sb}{(1+S)(b-c)-b}\]化简后变成$c<0$,这显然是永远不可能成立的。所以伙伴选择并不能让TFT更加稳定(面对NO-C的入侵)。
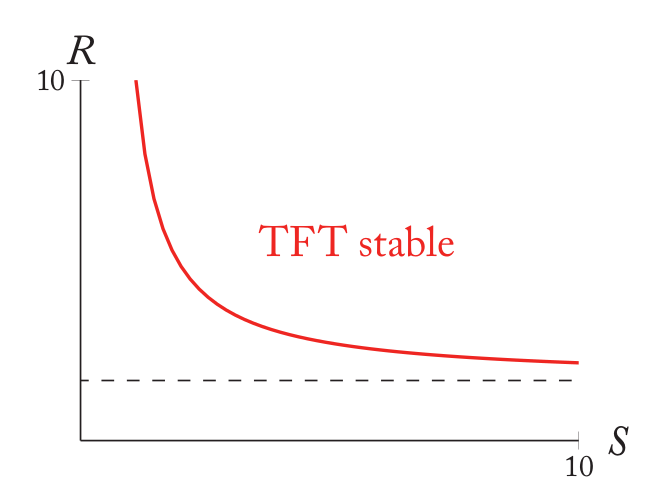
把R的临界值(TFT更稳定)和S的关系用图画出来会更加直观。这个曲线是$R=\frac{Sb}{(1+S)(b-c)-b}$,如果$b/(b-c)$在这个曲线之上,那么TFT会变得更稳定。
上图是b=2以及c=1.2的情况。虚线是$b/(b-c)$。在红色曲线之上,TFT会因为伙伴选择而更稳定。但是我们看到在这里,虚线总是在红色曲线之下,所以在这里,伙伴选择反而变得更加糟糕。这似乎是违背我们直觉的,但是仔细想一下其实很合理。原来少量的NO-C出现时,当然和他合作的那个TFT很倒霉,但是至少后面关系破裂时就不会再让NO-C占便宜了。而在这种伙伴选择的假设下,这个NO-C有可以去”祸害”其他TFT。
不要因此得出伙伴选择是一个坏的规则,因为这个模型中缺失了很多动态信息。不过这个模型也给我们提了一个醒:我们必须小心的进行假设的验证而不能太靠直觉。
【译注:在人类这样的社会里,NO-C可能会被打上”不是好的合作伙伴”这样的标签,从而使得他想找新伙伴的难度加大,这也是除了固定的一个TFT跟它死磕的更好的一种”惩罚”。】
- 显示Disqus评论(需要科学上网)