WFST介绍

本文会形式化的定义WFST和基于自动机理论介绍它的基本属性。然后会介绍一些用于构建和优化语音识别网络的重要操作(operation)。读者也可以参考深度学习理论与实战提高篇·WFST简介和深度学习理论与实战提高篇·HMM和WFST代码示例

目录

• 有穷自动机(Finite Automata)
• FA的基本属性
• 半环(semi-ring)
• 基本运算
• 转换机(transducer)的复合
• 优化运算
  • 确定化
  • Weight Pushing
  • 最小化(Minimization)
  • 消除ε跳转

有穷自动机(Finite Automata)

WFST是一种有穷自动机(FA)。一个有穷自动机有一个有限的状态集合以及状态之间的跳转，其中每个跳转至少有一个标签(label)。最基本的FA是有限状态接收机(finite state acceptor/FSA)。giddy一个输入符号序列，FSA返回”接受”或者”不接受”，它的判断条件是：如果存在一条从初始状态到终止状态的路径，使得路径上的标签序列正好等于输入符号序列，那么就是”接受”，否则就是”不接受”。

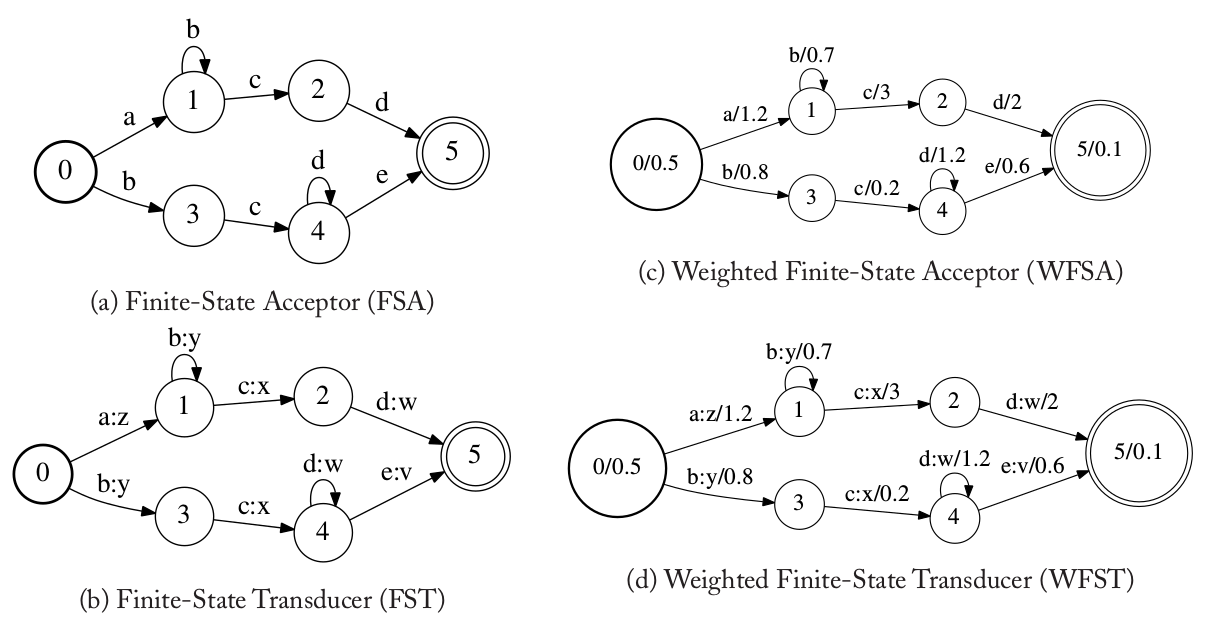
下图(a)是一个FSA的例子，图中的节点和边分布代表状态和状态之间的跳转。比如这个FSA接受在符号序列”a,b,c,d”，因为状态跳转序列”0,1,1,2,5”是从初始状态到最终状态的路径，它的边对应的符号序列正好是”a,b,c,d”。但是它不能接受”a,b,d”，因为无法找到满足条件的状态序列。因此，一个FSA代表了它能接受的符号序列的集合。符号序列也被成为字符串。图(a)的FSA代表的字符串集合等价于正则表达式”ab∗cd|bcd∗e”。我们这里假设状态0是初始状态而5是终止状态。如果没有特殊说明，我们用加粗的圆圈表示初始状态，用两个圈表示终止状态。

图：有穷自动机示例

接下来我们介绍几种FSA的扩展，这里我们之后介绍有限状态转录机(Finite-State Transducer/FST)，加权有限状态接收机(Weighted Finite-State Acceptor/WFSA)和加权有限状态转录机(Weighted Finite-State Transducer/WFST)。这些FA继承了FSA的基本特性，但是它们的输出不只是一个二值的”接受/不接受”，而是会输出另一个符号序列(FST)，一个权值(WFSA)或者同时输出一个新的符号序列和权值(WFST)。

FST的每个跳转(边)上都有一个输出符号，因此它的边上是一个输入标签和输出标签的pair。上图(b)中就是一个FST的例子。在图中用”输入符号:输出符号”来表示。通过这个扩展，FST描述了把一个输入符号序列转换为另一个输出符号的转换规则。例子中的FST可以把输入符号序列”a,b,c,d”转换成”z,y,x,w”。

WFSA的每个跳转除了输入符号还有一个weight，此外初始状态和终止状态也有对应的初始weight和终止weight。weight通常代码跳转的概率或者代价，不同的路径上的weight会通过”乘法”来累计。因此，WFSA提供了一种比较不同路径的度量(measure)。上图(c)是一个WFSA的例子。在上图中，每条边为”输入标签/weight”，并且初始状态表示为”初始状态ID/weight”；终止状态表示为”终止状态ID/weight”。对于这个WFSA，它接受序列”a,b,c,d”并且累计的weight是0.252：路径是0,1,1,2,5，weight为0.5 × 1.2 × 0.7 × 3 × 2 × 0.1。

WFST的跳转上同时包括输出标签和weight，因此WFST可以认为是FST和WFSA的组合。上图(d)是一个WFST的例子，图中的边上为”输入符号:输出符号/weight”。初始和终止的weight也在对应的状态上标识出来。这这个WFST里，它可以把输入符号序列”a,b,c,d”变成”z,y,x,w”，并且weight是0.252。

weight元素的集合$\mathbb{K}$上的一个WFST由下面的8-tuple $(\Sigma, \Delta, Q, I, F, E, \lambda, \rho)$来定义：

• $\Sigma$是一个有限的输入符号集合
• $\Delta$是一个有限的输出符号集合
• Q是一个有限的状态集合
• $I \subseteq Q$是初始状态集合
• $F \subseteq Q$是终止状态集合
• $E \subseteq Q \times (\Sigma \cup { \epsilon }) \times (\Delta \cup { \epsilon }) \times \mathbb{K} \times Q$ 跳转的多重集合。
• $\lambda : I \rightarrow \mathbb{K}$ 是初始状态weight的函数
• $\rho : F \rightarrow \mathbb{K}$ 是终止状态weight的函数

$\epsilon$是一个特殊的(输入和输出)符号，它代表空，没有输入/输出。上图(d)的WFST为：

• $\Sigma = \{a,b,c,d,e\}$
• $\Delta = \{v,x,y,w,z\}$
• $Q=\{0,1,2,3,4,5\}$
• $I=\{0\}$
• $F=\{5\}$
• $E=${(0,a,z,1.2,1), (0,b,y,0.8,3), (1,b,y,0.7,1), (1,c,x,3,2), (2,d,w,2,5), (3,c,x,0.2,4), (4,d,w,1.2,4), (4,e,v,0.6,5)}
• $\lambda(0)=0.5$
• $\rho(5)=0.1$

E中的每一个跳转为(源状态, 输入符号, 输出符号, weight, 目标状态)。其它的FA，包括FSA、FST和WFSA，都可以看成WFST的特殊情况。

另外一种FA的扩展方式是把跳转的输入/输出符号变成一个输入/输出字符串(一个字符串是多个符号)。不过本文不会考虑这种情况。事实上，基于字符串的FA可以转换成与之等价的基于单个符号的FA。

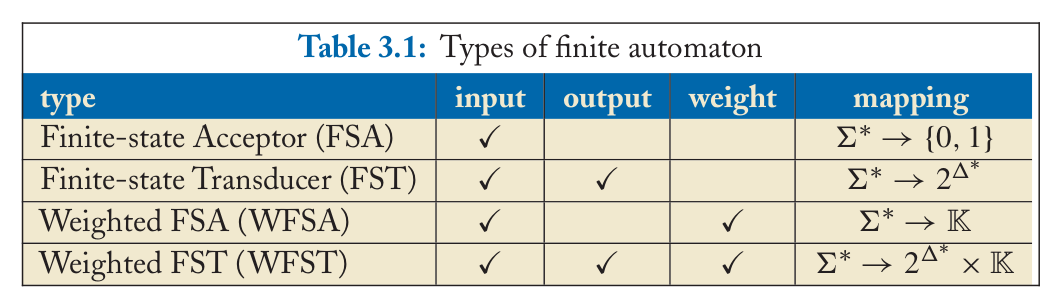
最后，我们用下表来总结4种类型的FA。如上面提到过的，FSA的跳转上只有一个输入符号并且最终返回是否接受某个输入符号序列。在下表里，”function”表示这个FA表示的映射(mapping)。对于FSA来说，\(\Sigma^*\)里的一个输入符号序列被映射为二值${0,1}$，其中0表示接受1表示拒绝。FST的跳转上同时有输入和输出符号，它表示的映射是一个函数\(f: \Sigma^* \rightarrow 2^{\Delta^*}\)，这里\(2^{\Delta^*}\)表示\(\Delta^*\)的幂集。它表示FST可以把同一个输入字符串(符号序列)映射为多个(当然也包括零个)输出符号序列。WFSA的跳转上有一个weight，它表示的映射为\(f:\Sigma^* \rightarrow \mathbb{K}\)，也就是把一个输入字符串映射为$\mathbb{K}$里的一个元素(数)。而WFST是WFSA和FST的组合，它把一个输入字符串映射为一个集合，集合中的每个元素包括一个输出字符串和一个weight。

图：4种FA的对比

请读者注意这几个缩写：FA指的是Finite Automata，它是一个最大的概念，它包括下面的所有自动机；FSA，Finite State Acceptor；WFSA，Weighted FSA；FST，有限状态转换机；WFST，Weighted FST。另外我们有时会用缩写DFA和NFA，它指的是确定的FA和不确定的FA，一般如果不做明确说明分别指的是确定的FSA和不确定的FSA。

FA的基本属性

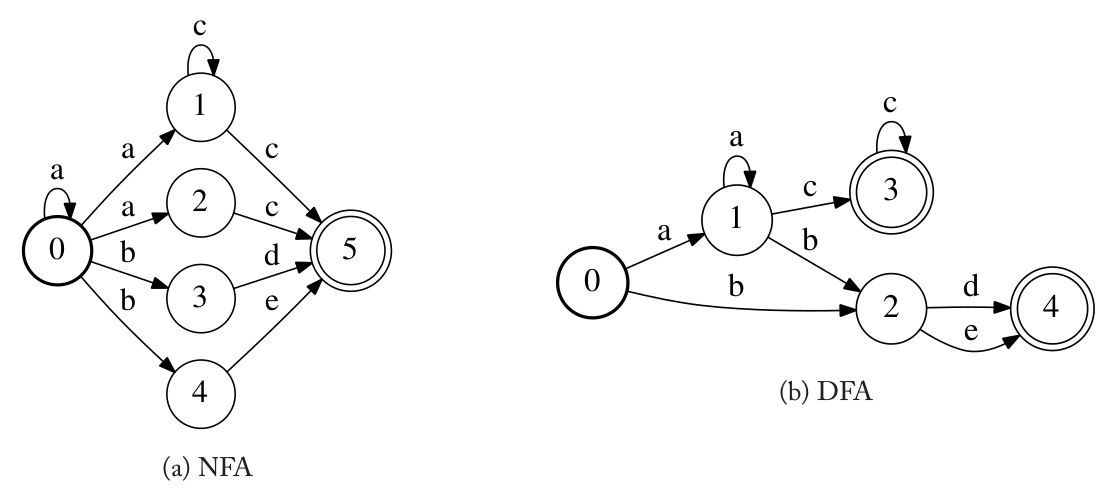
FA的一个重要性质是它是确定的(deterministic)还是非确定的(non-deterministic)。一个确定的FA(DFA)只有一个初始状态，并且对于每个状态如果给定了一个输入符号，最多有一条边。因此如果某个输入符号序列是被它接受的，也只有一条对应的从初始状态到终止状态的路径。DFA的优点是给定输入符号序列，判断它是否被接受的计算是比较快的(相对于非确定的NFA来说)。如果我们使用二分查找来获得一个输入符号的边的话，DFA的计算复杂度是$O(L log_2 \hat{D})$。这里L是输入符号序列的长度，D是从一个状态跳出的边的最大数量。这个计算复杂度适合长度L成线性比例关系的，但是和$\hat{D}$对数的关系，也就是说$\hat{D}$的成倍增长不会引起复杂度的成倍增长。

而NFA给定一个状态和一个输入符号，它可以有多条跳转的边。因此，我们需要考虑多种可能的路径。虽然NFA的计算复杂度依赖于它的结构，在最坏的情况下的复杂度是$O(L \times \vert Q \vert \times \vert E \vert$。不过存在一个算法把NFA转换成与之等价的DFA。这叫做确定化(determinization)算法。确定化之后，NFA的功能可以由与之等价的计算量更少的DFA来实现。下图的NFA和DFA是等价的。注意：虽然所有的FSA可以确定化，但是对于其它的FA，比如FST、WFSA和WFST不一定存在与之等价的确定化的FA。

图：NFA和等价的DFA

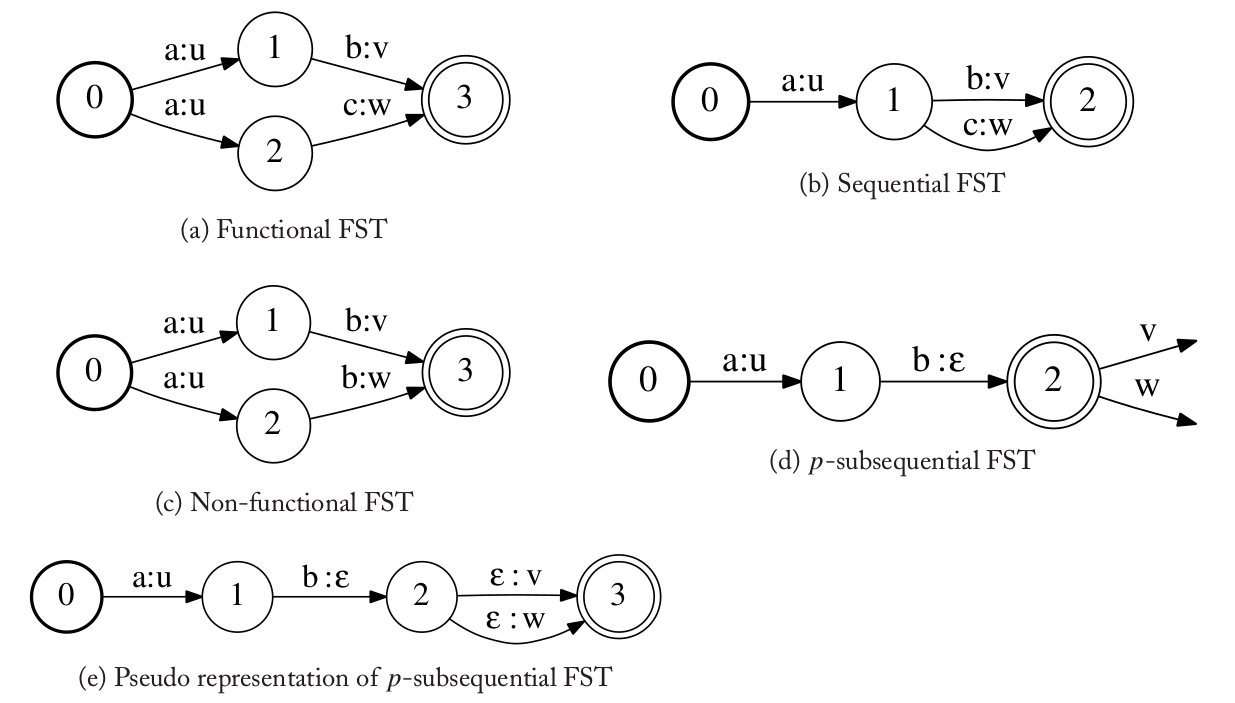
转换机(FST和WFST)是sequential当且仅当在我们只考虑输入符号的时候它是确定的。另外，转换机是函数的(functional)当且仅当对于任意一个输入符号序列，最多有一个输出符号序列(当然可以没有)与之对应。函数的转换机是可以确定化的，这里我们不做证明。下图展示了一些FST。

图：不同属性的FST

图(a)是函数的FST；图(b)是它确定化后的等价的sequential的FST。注意：图(a)不是sequential的，因为在状态1的时候输入符号是a的边有两条；但是它是函数的，因为对于任何一个输入字符串，最多有一个输出字符串。

图(c)是非函数的FST，因为给定输入字符串”ab”，输出有两个字符串”uv”和”uw”。如果只考虑输入符号，它是可以确定化的；但是如果考虑输出符号，则它因为输出符号的歧义而不能确定化。在这种情况下，它的确定化会得到p-subsequential的FST，如图(d)所示，这是一种更加一般的sequential FST。p-subsequential的FST允许它的终止状态有p个带标签的跳转(这些边只有起点没有终点)。不过本文不讨论这种定义，它可以表示为等价的FST，如图(e)所示。通过在原来的终止状态后面引入$\epsilon$的跳转和新的终止状态来实现。

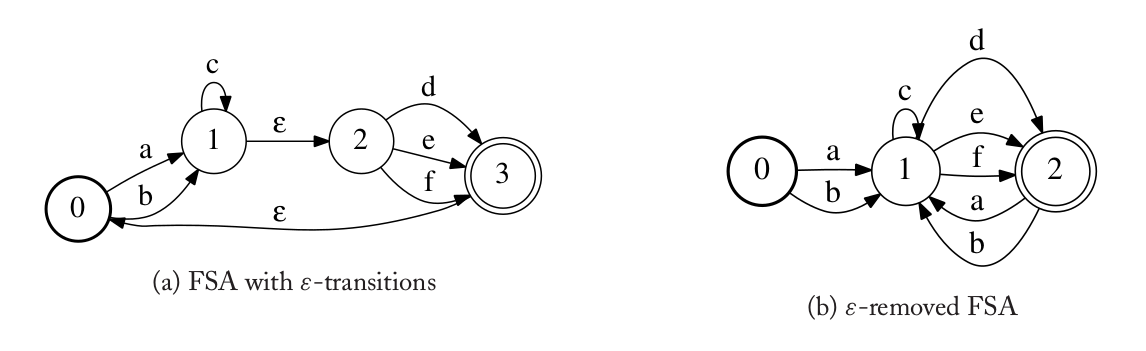
FA的另外一个重要属性就是它的输入标签里是否有特殊的ε。输入符号为ε的跳转叫做ε-跳转，这个状态的跳转不需要任何输入符号就可以进行。下图(a)是一个包含ε-跳转的FSA。这个FSA首先在状态0通过输入符号”a”或者”b”跳转到状态1。因为状态1和2之间有一个ε-跳转，因此它可以在不读入任何输入符号的条件下跳转到状态2，当然在没有任何输入的时候它也可以还是呆在状态1。因此这FSA可以同时呆在状态1和2。因此有ε-跳转的FSA是非确定的，我们把它叫做ε-NFA。

存在一个算法(ε-消除算法)把一个ε-NFA转换成与之等价的没有ε-跳转的NFA。下图(b)是与(a)等价的没有ε-跳转的NFA。

图：ε-NFA和没有ε的NFA

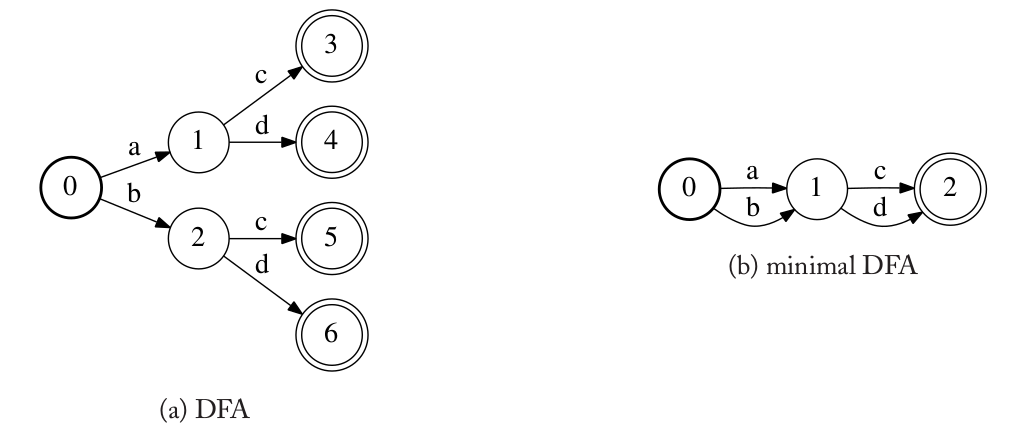
最后，给定一个FA，我们把所有与之等价的DFA组成的集合里状态数最小的DFA叫做最小DFA。下图(a)是一个DFA，图(b)是与之等价的最小DFA。最小DFA也可以用于检查不同的FA是否等价，因为两个FA通过消除ε跳转、确定化和最小化之后，如果它们是等价的，则经过上述3个操作之后得到的最小DFA是完全一样的(状态和跳转完全一样，当然可能是状态的命名不一样)。

图：DFA和与之等价的最小DFA

半环(semi-ring)

对于加权的(weighted)FA，weight以及其上的二元运算”加法”和”乘法”需要更加形式化的定义用于使得FA和相关的算法更加一般化。在理论上，weight和其上的运算是使用半环来定义的，这是一种抽象代数的代数结构。这意味着任何类型的weight都可以把FA的算法处理，当然前提是需要用这个weight的集合来定义一个半环。

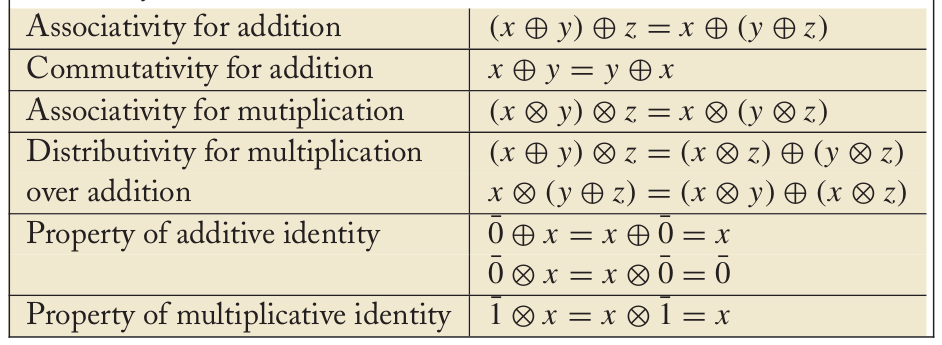
半环类似于环(群、环、域是抽象代数的基本研究对象，计算机专业的读者可能学过的离散数学也会有部分介绍)，这是一种代数结构，但是半环并不像环那样要求加法逆元的存在。一个半环定义为$(\mathbb{K}, \bigoplus, \bigotimes, \bar{0}, \bar{1})$，其中$\mathbb{K}$是一个集合，$\bigoplus$和$\bigotimes$是$\mathbb{K}$上的两个二元运算，分别叫做”加法”和”乘法”。$\bar{0}$和$\bar{1}$是属于$\mathbb{K}$的两个特殊元素，分别叫做加法单位元和乘法单位元，因为它们和实数中的0和1有类似的性质，因此也叫零元和幺元。半环必须满足下表的性质。

图：半环的性质

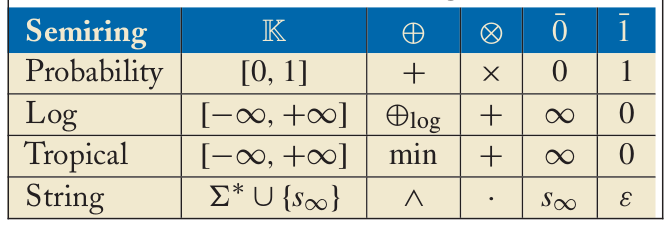
下表是一些常见半环，其中$x \bigoplus_{log} y \equiv -log(e^{-x}+e^{-y})$。

图：常见的半环

在基于WFST的语音识别系统了，热带半环(tropical semiring)是最常用的一个半环，它的weight集合是实数集合，而”加法”和”乘法”被定义为min和普通的加法。在WFST的优化时也会用到log半环。当对一个加权的FA执行某个运算的时候，考虑我们用到的半环的某些性质会有帮助，因为我们可能利用这些形状简化算法的计算。下面我们介绍一些常见的性质。

• 交换的(commutative)

一个半环$(\mathbb{K}, \bigoplus, \bigotimes, \bar{0}, \bar{1})$是交换的，则其”乘法”是遵循交换律，也就是：

热带半环和log半环是交换的半环。

• 幂等的(idempotent)

一个半环$(\mathbb{K}, \bigoplus, \bigotimes, \bar{0}, \bar{1})$是幂等的，则其”加法”满足：

热带半环是幂等的，因为$min(x,x)=x$。但是log半环不是，因为$x \ne x \bigoplus_{log} x$。

• k-closed

假设$k \le 0$，一个半环$(\mathbb{K}, \bigoplus, \bigotimes, \bar{0}, \bar{1})$是k-closed，则它满足：

使用数学归纳法，还可以推广到所有的$l>k$的情况：

热带半环是0-closed，而log半环如果忽略很小的误差也可以认为是k-closed。

• weakly left-divisible

一个半环$(\mathbb{K}, \bigoplus, \bigotimes, \bar{0}, \bar{1})$是weakly left-divisible，则其”加法”满足这样的性质：如果$x \bigoplus y \ne \bar{0}$，则至少存在一个z使得$x=(x \bigoplus y) \bigotimes z$。

热带半环和log半环都是weakly left-divisible的半环。

• zero-sum free

一个半环$(\mathbb{K}, \bigoplus, \bigotimes, \bar{0}, \bar{1})$是zero-sum free的，则它满足：如果$x \bigoplus y=\bar{0}$，则$x=y=\bar{0}$。

基本运算

这里，我们回顾一些FA(而不仅仅是WFST)上的一些一元和二元操作。我们已经介绍过一个FA代表了从一个输入符号序列到weight或/和一个输出符号序列的映射。这些基本的操作是通过增加或者删除跳转并且和其它的FA的组合(combining)来扩展实现的。

在自动机理论里，Kleene闭包(closure)、并(union)和连接(concatenation)是所有的FA都有的三种常见运算。Kleene闭包让一个FA接受的字符串是原来自动机接受的字符串的零次或者多次重复。给定一个自动机A，它的Kleene闭包被记作\(A^*\)。两个FA的并是它们能接受的字符串集合的并集。而两个FA的连接则是这样的字符串集合：它是两个字符串的连接，并且第一个字符串来自第一个FA；第二个字符串来自第二个FA。

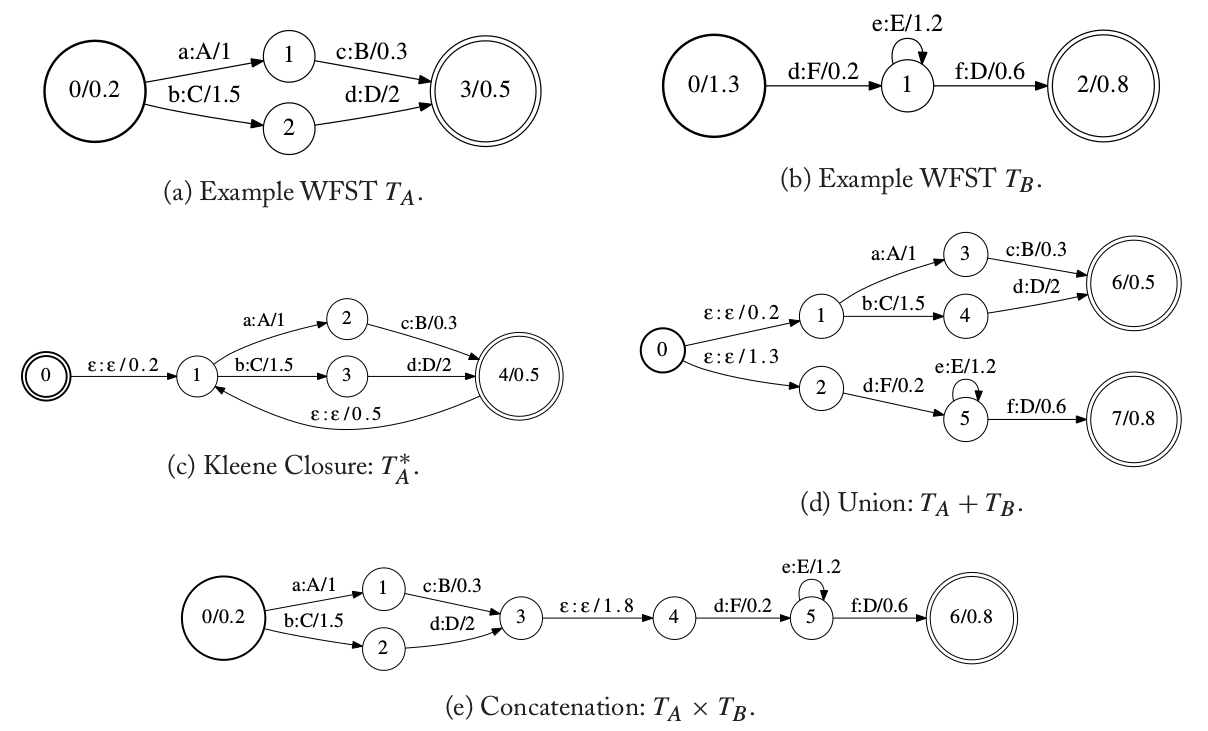
给定两个自动机$A_1$和$A_2$，它们的并记作$A_1 \cup A_2$或者$A_1 + A_2$，它们的连接记作$A_1 \cdot A_2$或者$A_1 \times A_2$。下图(a)和(b)分别是两个WFST $T_A$和$T_B$。图(c)是WFST $T_A$的Kleene闭包\(T_A^*\)，要实现Kleene闭包，我们首先增加一个新的初始状态，然后让它以一个ε-跳转到原来的初始状态(原来的初始状态现在就不是初始状态了)并且把原来的初始weight移到这条边上，然后在原来的终止状态增加一个空的跳转到原来的初始状态(注意不是新的初始状态，否则weight会有问题)。图(d)是$T_A \cup T_B$，实现的的方法为：新建一个新的初始状态，然后用ε-跳转分别跳到原来$T_A$和$T_B$的初始状态(在$T_A \cup T_B$里原来$T_A$和$T_B$的初始状态不再是初始状态，并且它们的初始weight移到这条边上了)。图(e)是$A_1 \cdot A_2$，实现的方法为：在$T_A$的每一个终止状态都新加一个ε-跳转到$T_B$的每一个初始状态，并且把$T_B$的终止状态的weight和$T_A$的初始状态的weight都移到这条边上，然后把$T_A$的终止状态变成普通的状态，把$T_B$的初始状态变成普通的状态。

图：自动机的基本运算

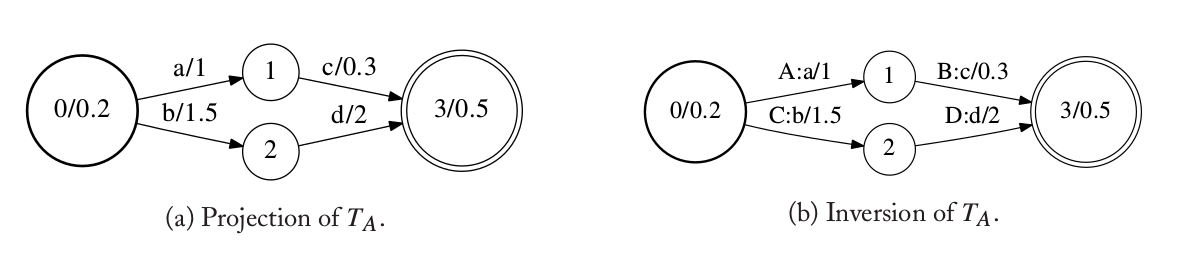
对于转换机(FST和WFST)，投影(projection)、反转(inversion)和复合(composition)是比较重要的运算。投影是通过去掉输出符号把一个转换机变成一个接收机。反转是把转换机的输入和输出反过来。下图是对WFST $T_A$的投影和反转。投影时直接把输出符号去掉就行；而反转则是把边的输入和输出符号交换一下，其余的都不变。

图：投影和反转

转换机(transducer)的复合

在介绍复合之前我们先介绍几个术语。

给定一个WFST $T=(\Sigma, \Delta, Q, I, F, E, \lambda, \rho)$，对于任何的$q \in Q$，我们把从q出去的边组成的多重集合(所谓多重集合指的是其元素可以重复)记作$E[q]$。对于任意的$e \in E$，我们把跳转的输入符号记作$i[e]$，输出符号记作$o[e]$，起点(边的出发状态)记作$p[e]$，终点记作$n[e]$，weight记作$w[e]$。一条路径可以用跳转的序列来表示为$\pi=e_1,…,e_k$，其中满足后一条边的起点是前一条边的终点，亦即$n[e_{j-1}]=p[e_j], j=2,…,k$。此外我们把这些记号扩展到路径，把路径的起点记为$p[\pi]$，路径的终点记为$n[\pi]$。路径的输入字符串记为$i[\pi]$，其中$i[\pi]=i[e_1] \cdot \cdot \cdot i[e_k]$。类似的输出字符串记为$o[\pi]$，其中$o[\pi]=o[e_1] \cdot \cdot \cdot o[e_k]$。$w[\pi]=w[e_1] \bigotimes \cdot \cdot \cdot \bigotimes w[e_k]$。如果$p[e_1] \in I$(路径的起点是初始状态)并且$n[e_k] \in F$，则这条路径叫做一条成功的路径。如果一个状态(点)可以从(某个)初始状态走到这里并且也可以从这个点走到(某个)终止状态，则这个状态成为coaccessible。coaccessible的状态至少在一条成功的路径上(因为可以从初始状态走到它然后又可以从它走到终止状态，显然只是一条成功的路径)。非coaccessible的状态被成为死(dead)状态。类似的，跳转(边)也分为coaccessible和非coaccessible。删除一个FA的非coaccessible的点和边的操作叫做trimming，没有死状态和死跳转的FA叫做trimmed的FA。一个FA进行trimming之后得到的FA就是trimmed的FA。

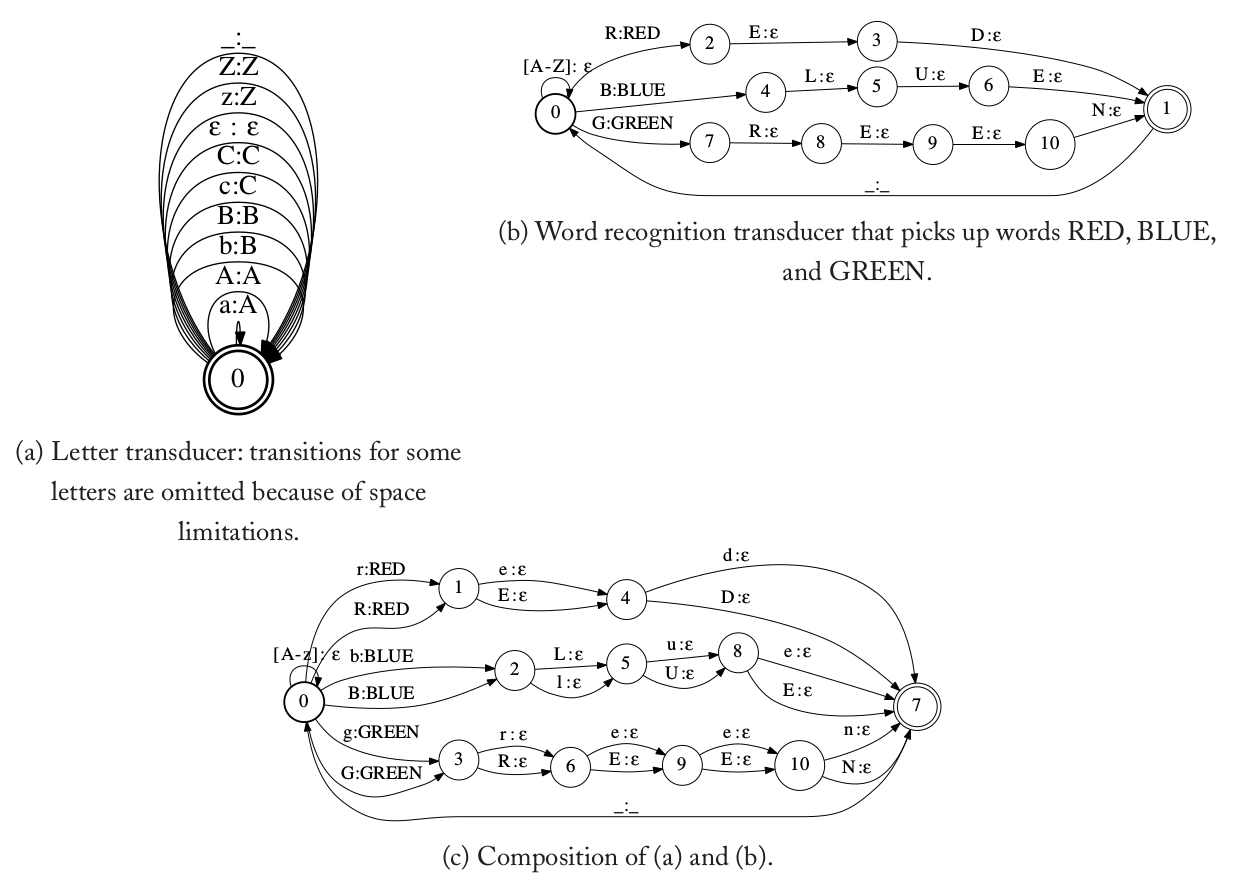
下面我们来介绍复合算法的基本原理。下图(a)是一个转换机，它的作用是把输入字符串所有的字符都变成大写；图(b)只识别(接受)”RED”、”BLUE”和”GREEN”三个词(字符串)。它们复合后的结果如图(c)所示，这个复合后的FST的作用是识别各种大小写组合的这3个词(比如”REd”、”BluE”)。有的时候设计一个FST是比较复杂的，但是通过把它分解为多个FST的复合会变得容易得多。

图：复合操作

下面的算法10是没有ε的WFST复合算法，它要求第一个转换机的输出符号不包含ε并且第二个转换机的输入符号也不包含ε。等下我们会介绍更加通用的能处理ε的算法。

图：没有ε的复合算法

在上面的算法里，$T_1=(\Sigma_1, \Delta_1, Q_1, I_1, F_1, E_1, \lambda_1, \rho_1)$，$T_2=(\Sigma_2, \Delta_2, Q_2, I_2, F_2, E_2, \lambda_2, \rho_2)$。复合后的WFST的状态是$T_1$和$T_2$的状态对组成。因此复活后的状态用原来状态对$(q_1,q_2)$来表示，其中$q_1 \in Q_1$并且$q_2 \in Q_2$。从复合状态$(q_1,q_2)$出去的跳转也是$e_1$和$e_2$的组合，其中$e_1 \in E[q_1]$、$e_2 \in E[q_2]$并且$o[e_1]=i[e_2] \ne \epsilon$。这会产生一个复合后的WFST的一个跳转，这条边的起点是$(q_1,q_2)$，终点是$(n[e_1],n[e_2])$，输入符号是$i[e_1]$，输出符号是$o[e_2]$，weight是$w[e_1] \bigotimes w[e_2]$。这样的话，T相对于是$T_1$和$T_2$的级联。这个算法的复杂度是$O(\vert T_1 \vert \vert T_2 \vert)$，其中$\vert T_1 \vert = \vert Q_1 \vert + \vert E_1 \vert $，也就是点的个数加边的条数。

在上面的算法里，第1-4行是处理复合后的初始状态，它是直接通过$I_1$和$I_2$的笛卡尔积计算得到。初始状态$(i_1,i_2)$的weight是$\lambda(i_1) \bigotimes \lambda(i_2)$。然后在第5行把所有的初始状态都插入到状态队列Q和未处理(待处理)队列S里。接下来就是一个大的循环处理S中的状态$(q_1,q_2)$直到S为空。在第9-12行，如果$q_1$和$q_2$分别是$T_1$和$T_2$的终止状态，则$(q_1,q_2)$是复合后的终止状态，需要把它加到F，而它的weight为$\rho(q_1) \bigotimes \rho(q_2)$。第13-19行，我们遍历$q_1$的出边$e_1$和$q_2$的出边$e_2$的所有组合，如果$e_1$的输出符号$o[e_1]$等于$e_2$的输入符号$i[e_2]$，则它们可以产生一条新的边。这条新边的起点是$(q_1,q_2)$、终点是$(n[e_1],n[e_2])$(n[e_1]是边$e_1$指向的状态)、输入符号是$i[e_1]$、输出符号是$o[e_2]$、weight是$w[e_1] \bigotimes w[e_2]$。我们需要把这条边加到复合后的WFST的跳转集合E里。如果新的状态$(n[e_1],n[e_2])$之前没有处理过，也需要加到S和Q里。因为E是一个多重集合(multi-set)，相同的跳转(起点和终点相同并且输入和输出符号也相同，weight可以不同)可以会出现多次。

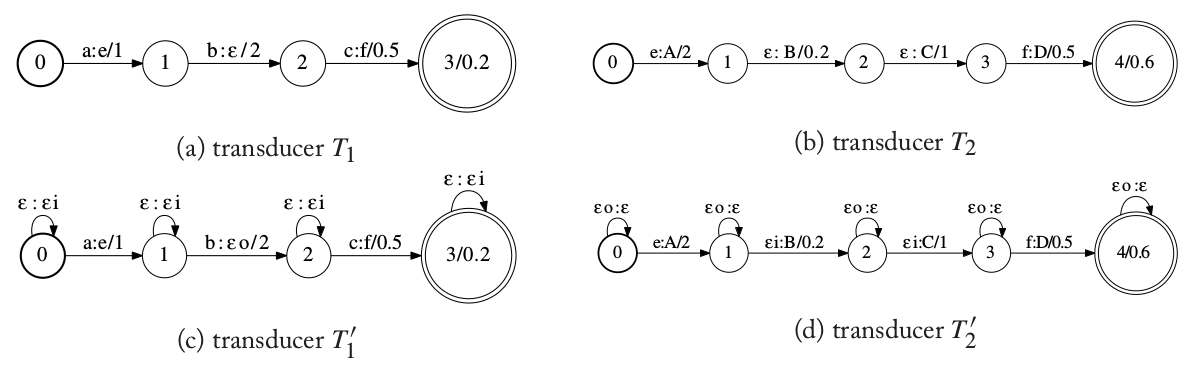
上面的算法假设$T_1$的边输出符号不是ε并且$T_2$的输入符号也不是ε。对于更通用的复合算法，我们需要小心的处理ε，从而通过模拟ε-跳转得到扩展的算法。这个扩展算法可以使用FST的操作来解释。如下图所示，图(a)和(b)是待复合的WFST，其中图(a)的输出符号包含ε，图(b)的输入符号包含ε。图(a)把输入字符串”abc”转换成”ef”；而图(b)把输入字符串”ef”转换成”ABCD”。所以复合后的WFST应该是把”abc”转换成”ABCD”。

图：有ε的WFST以及对它进行修改以便复合操作

为了进行复合，我们对$T_1$和$T_2$进行扩展。ε-跳转指定是自动机在没有输入的情况下就进行跳转。为了复合，我们需要考虑两种情况：$T_1$的输出为ε；$T_2$的输入为ε。

在第一种情况下，$T_1$没有输出，因此只是$T_1$发生了ε-跳转而$T_2$的状态没有变化。而第二种情况下，$T_2$在不需要输入的情况下发生跳转，因此$T_1$不需要产生任何输出也就是$T_1$的状态不发生变化。为了模拟这些跳转，我们在上图(c)和(d)中分别对$T_1$和$T_2$进行扩展。

做法是对于$T_1$的每一个状态都增加输入是ε输出是εi的自跳转，它表示$T_1$的状态不变，只是$T_2$发生自跳转(自跳转的输入是εi)，另外需要把原来的输出从ε变成εo，以示区别。对于$T_2$需要把原来的输入为ε的边改成输入为εi的边，这是和前面配合的，它表示$T_2$进行空跳转，而$T_1$不动；类似的需要给$T_2$的每一状态都增加自跳转，输入为εo输出为ε。

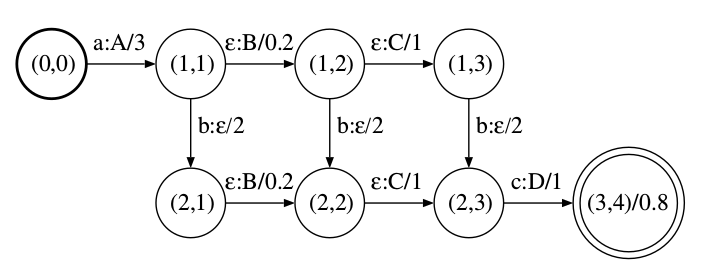
把扩展后的$T_1’$和$T_2’$用前面的算法进行复合，就可以得到有ε的WFST的复合结果，如下图所示。

图：$T_1 \circ T_2$

我们来看(1,1)->(1,2)，$T_1$的状态是从1->1，所以是经过边1-ε:εi->1；而$T_2$的状态是从1-εi:B->2，所以复合后的边为(1,1)-ε:B->(1,2)。这是我们说的第一种情况：$T_1$的状态不变而$T_2$发生ε-跳转。类似的从(1,1)->(2,1)是第二种情况，请读者自己分析。

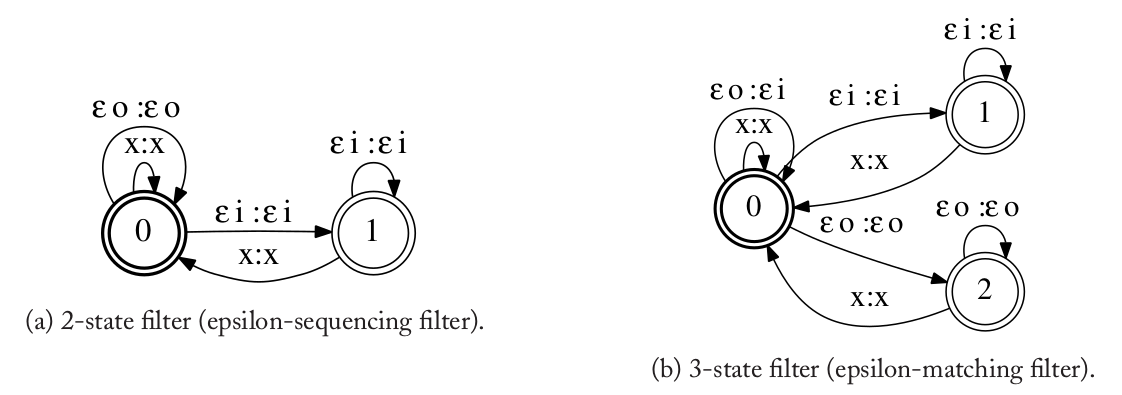
但是上图的WFST存在冗余的路径。此外，对于非幂等(non-idempotent)的半环比如概率和log半环，因为存在冗余路径，对于一个输入字符串：输出字符串对累加的weight也是不对的。为了解决这个问题，一种叫做filter的WFST被引入复合运算。假设F是一个filter，我们复合时计算的是$T_1’ \circ F \circ T_2’$而不是$T_1’ \circ T_2’$。比如下图(a)是一个两状态(也叫epsilon-sequencing)的filter，图中”x”表示$\Sigma_2 \cap \Delta_1$中的任一符号。

图：复合用的filter

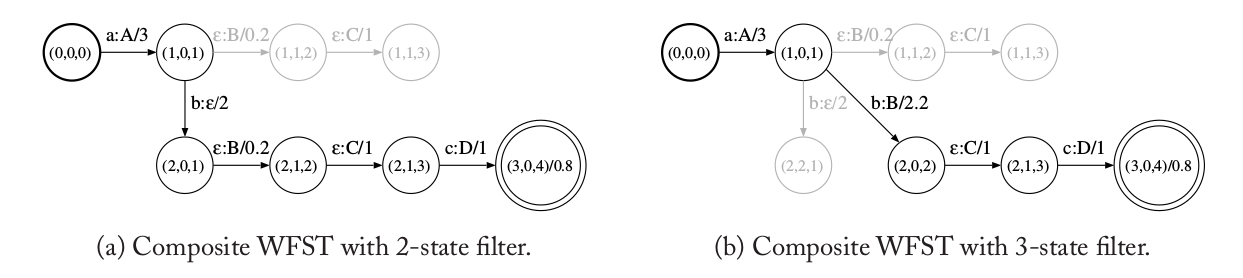
我们可以这样来理解图(a)的这个filter，如果输入是普通的符号x，则输出x；假设当前在状态0，如果输入是εo，则输出也是εo，表示$T_1$发生ε-跳转而$T_2$状态不变；如果输入是εi，则输出是εi，并且跳到状态2，这个状态表示$T_2$发生ε跳转而$T_1$不动。这个filter会优先考虑$T_1$状态变化的情况。$T_1’ \circ F \circ T_2’$得到的WFST如下图(a)所示，图中灰色的路径死掉的路径。在上面的复合中，类似于(1,1)->(1,2)->(2,2)这样的路径是不允许的。因为这条路径首先是$T_2$发生εi的跳转($T_1$不动)，然后立刻是$T_1$发生εo的跳转($T_2$不动)，而在这个filter里，经过εi之后状态跳到了1，而状态1是不允许εo的跳转的。通过这样的方法，我们可以去掉冗余的路径。当然图(a)复合的结果还有死掉的状态和跳转，我们需要去掉。

图：$T_1’ \circ F \circ T_2’$

另外，我们可以使用3-状态的filter(epsilon-matching filter)，如上图(b)所示，使用它计算$T_1’ \circ F \circ T_2’$的结果如上图(b)所示。3-状态的filter会尽量优先走εo:εi的边，也就是用$T_1$的ε输出来驱动$T_2$的ε输入。所以我们看到有从(1,0,1)->(2,0,2)的跳转，它不允许εi之后马上是εo的跳转(和前面的2-状态filter一样)，而且它也不允许εo之后马上是εi的跳转。因此我们看到(1,0,1)->(2,2,1)之后不能在跳到(2,0,2)，同样的(1,0,1)->(1,1,2)之后也不能跳到(2,0,2)。如果我们希望保留相同数目的ε，则应该使用2-状态的filter。否则应该使用3-状态的filter，因为它得到的WFST更加紧凑。

当然，上面是从原理上介绍WFST的复合时使用了filter来进行3个WFST的复合，但是在实际的WFST的实现代码里，filter的逻辑是用代码来实现的，这样实现的复合速度会更快并且使用更少的内存。

优化运算

下面简要的介绍一些重要的优化运算，包括确定化(determinization)、weight pushing和最小化(minimization)。这些运算会把一个WFST转换成等价的WFST，但是这些优化后的WFST的执行速度更快并且运行时使用的内存也更少。

确定化

确定化是FA最重要的优化运算。确定化是使用FA来解决序列识别和转换问题的重要优势，因为与原始FA等价的确定化的DFA的速度要比非确定的NFA要快得多。在设计一个FA来解决问题的时候，使用NFA通常更便于人理解(参考WFST简介·非确定有穷自动机)。但是从计算机运行的效率来说NFA通常比不上DFA。因此确定化在加速FA的执行方面是非常有用的。

前面提到过，给定一个状态和一个输入符号，DFA有且仅有一条跳出的边(有时为了简化会省略跳到死状态的边，但实际上DFA对于任何输入都是有边的)，因此如果DFA接受某个输入符号序列，则存在唯一的成功路径与之对应。寻找这条成功路径的时间复杂度是与序列的长度成正比，假设通过二叉树来存储每个状态的跳转，则每一步的复杂度是$log_2 \vert E(q) \vert$。

确定化的代码如下所示，它基本是和经典的FSA的确定化算法是一样的(参考WFST简介·通过子集构造把NFA转换成DFA)。在这个算法里，如果从一个状态遇到某一个输入符号有多条跳转，那么它们会被合并成一个跳转。多个跳转的终点状态也会被合并成一个新的状态。因此，在这个确定化后的FA里的一个状态是原来FA的状态的集合。当已经确定化的新状态给定一个输入符号时，这个状态对应的老状态的集合中的每一个都会尝试处理这个输入符号，然后把这些终点状态组成一个新的集合(新的状态)。通过这种方法，一开始的时候把所有原来FA的初始状态的集合当作新FA的初始状态，然后用上面的方法不断扩展得到新的状态，直到所有的新状态都处理完成为止。上面介绍的是NFA(非确定的有限状态接收机，其实应该简写为NFSA，但是很少有人这么简写)转换成DFA(确定的有限状态接收机)的算法。对于WFST，算法需要做一点扩展来支持输出符号和weight。粗略来讲，经典的确定化算法会使用输入符号来绑定跳转和终点状态。但是WFST的边上还有输出符号和weight。即使两个跳转的输入符号是相同的，它们的输出符号和weight也可能不相同。不同的输出符号和weight不能合并到通一个跳转上。因此在WFST的确定化算法里，不同跳转的输出字符串的公共前缀以及weight的和会放到新的跳转里。余下的输出字符和余下的weight会放到新状态里。因此，确定化的WFST的状态是一个三元组的集合，\(\{(p, z, v) \vert p \in Q, z \in \Delta^* , v \in K\}\)，这里p是原始WFST的状态，z是余下的输出符号，v是余下的weight。为了能够确定化，半环需要是weakly left-divisible的，这样可以把weight的和除以每个跳转的weight。

上面的算法会从原始的WFST $T=(\Sigma, \Delta, Q, I, F, E, \lambda, \rho)$生成确定化的WFST $T’=(\Sigma, \Delta, Q’, I’, F’, E’, \lambda’, \rho’)$。第1行代码生成T’的初始状态i’，i’是一个集合，这个集合的每一个元素都是三元组，$(i, \epsilon, \lambda(i))$。前面我们介绍过了T’的每一个状态都是(p, z, v)这样的三元组，其中p是T里的状态，z是余下的输出符号，v是余下的weight。对于初始状态，p是T里的初始状态i，z是空，而v是初始状态的weight $\lambda(i)$。第2行把i’的weight设置为半环的幺元$\bar{1}$。第3行把初始状态加到集合Q’和S里，其中Q’是确定化后的WFST的状态集合，而S是待处理的新状态。

然后代码是一个大的while循环，处理S中的所有未处理状态，直到S为空。第5和6行从S里弹出一个带处理的新状态p’。

第7行遍历p’能处理的所有输入x。这一行有一些复杂，我们来详细阅读它。这一行为：$\text{for each } x \in \{ x \vert i[e]=x, e=E[p], p \in Q[p’] \}$。用自然语言来描述就是：对于p’这个集合里的每一个原始状态p，我们遍历它的每一条边E[p]，然后找到这条边的输入符号i[e]为x。$Q[p’]$这个记号之前好像没有介绍过，我们来看一个例子。比如下图(b)的第二个状态$p’=\{(1,X,0),(2,Y,0.7) \}$，则$Q[p’]$是p’中每个元素(是一个三元组)的第一个元素(来自T的状态)组成的集合。因此对于这个p’，$Q[p’]=\{1, 2\}$。而对于$p \in \{1,2\}$，我们可以遍历原始WFST的边(图a里)1-b:ε->4、1-c:Z->5、2-b:ε->6和2-d:Z->6。然后得到这4条边的所有输入符号组成的集合，也就是$\{b,c,d\}$。

第8行是计算从p出发输入符号为x的所有的边的输出符号(实际是(p,z,v)里的$z \cdot y$)的最长公共子串，因为我们这里介绍的WFST的输入是一个符号(而不是一个字符串)，因此最长公共子串最长就是一个字符，如果相同输入的输出不同，那么最长公共子串就是ε。这一行代码也有点复杂，我们来仔细阅读它：

我们先看$(p,z,v) \in p’$，它先遍历p’的所有元素，根据p在原始WFST里找输入符号为x的所有边$(p,x,y,w,q) \in E$，然后把两个字符串z和y连接起来。其中z是(p,z,v)里余下的输出字符串，而y是边$(p,x,y,w,q) \in E$里的输出符号。这样对于每一条边$(p,x,y,w,q) \in E$，都可以计算一个$z \cdot y$，最后符号$\land$表示求这些字符串的最长公共子串。这个计算结果是新的WFST里的边的输出符号。

读懂了第8行，第9行就非常类似了，只不过它是计算的是新的WFST里的边的weight。v是(p,z,v)里余下来的weight，而w是边$(p,x,y,w,q) \in E$里的weight，把它们用$\bigotimes$乘起来，最后用$\bigoplus$求和。

接下来第10行构造一个新的状态q’，这个状态也是一个集合，集合的每个元素依然是一个三元组(状态,余下的输出字符串,余下的weight)。其中状态是q。余下的输出字符串是$y’^{-1} \cdot z \cdot y$，因为$y’$的字符串放到新的边里了，所以这条边余下的输出字符串是$z \cdot y$乘以y’的逆，因此这里要求半环是weakly left-divisible的。余下的weight也类似，是$w’^{-1} \bigotimes v \bigotimes w$，然后用$\bigoplus$加起来。

这样就构造出T’的一条边：(p’, x, y’,w’,q’)，在第11行把它加到E’里。

如果新的状态q’之前没有出现过，那么需要把它加到Q’里。如果q’的某个状态是原始WFST的终止状态，则q’就是新的WFST的一个终止状态。它的终止weight $\rho(q’)$的计算是在第16行：$\rho(q’)=\{(z, \bigoplus\{ v \bigotimes \rho(q) \vert (q,z,v) \in q’, q \in F \}) \}$，它是把剩余的输出字符串和weight都放到$\rho(q’)$里。

第18行把这个新的状态加入到待处理新状态集合S里，等待后续的处理。

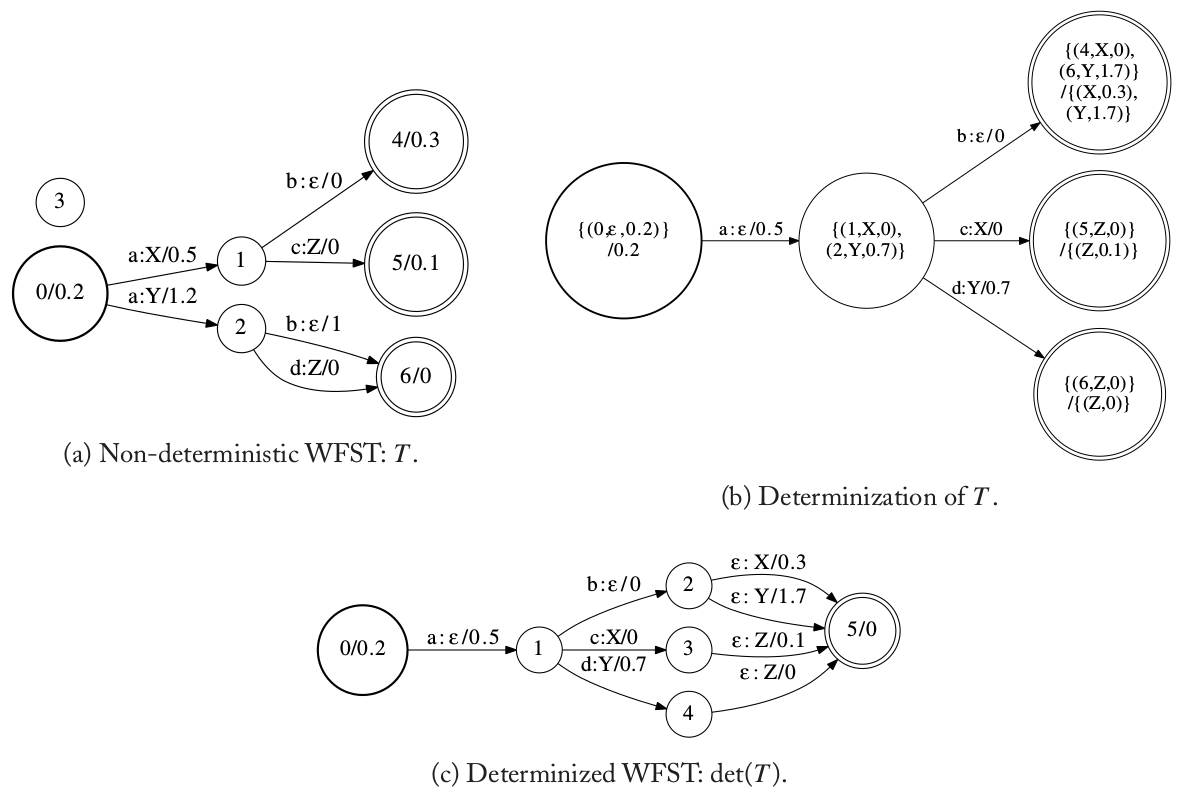
下图是一个确定化的示例。图(a)是一个非确定的WFST T，而确定化算法生成的状态如图(b)所示。在这个例子里，T’的初始状态是$\{ (0, \epsilon, 0.2) \}$，它的weight是\bar{1}(注：原文为0.2，我理解应该是$\bar{1}$)。从这个初始状态跳出的边是由原始WFST的两条边0-a:X->1和0-a:Y->2合并而成的，输出符号的公共前缀为$(\epsilon \cdot X) \land (\epsilon \cdot Y)=\epsilon$。如果是热带半环，则新边的weight为$(\bar{1} \bigotimes 0.5) \bigoplus (\bar{1} \bigotimes 1.2)=0.5 \bigoplus 1.2=0.5$。而终点状态变成$\{ (1, X, 0),(2, Y, 0.7) \}$，这个0.7是$0.5^{-1} \bigotimes 1.2=0.7$。这里原始WFST的状态1和2被合并成新WFST里的一个状态。

图：WFST确定化的例子

接着，原始WFST里的状态4和6被输入符号”b”合并成新的状态$q’=\{(4, X, 0), (6, Y, 1.7)\}$，因为状态4和6都是原始WFST的终止状态，所以这个新状态也是T’的终止状态，剩下的输出字符串和weight被放到$\rho(q’)=\{(X, 0.3), (Y, 1.7)\}$里。图(b)中的其它状态也是通过类似的方法计算得到。最后我们把状态起一个新的名字(编号)，并且创建一个新的终止状态，让原来那些终止状态通过边”ε:余下的输出字符串/余下的weight”跳到这个新的终止状态。这样得到的WFST只有一个终止状态，如图(c)所示。

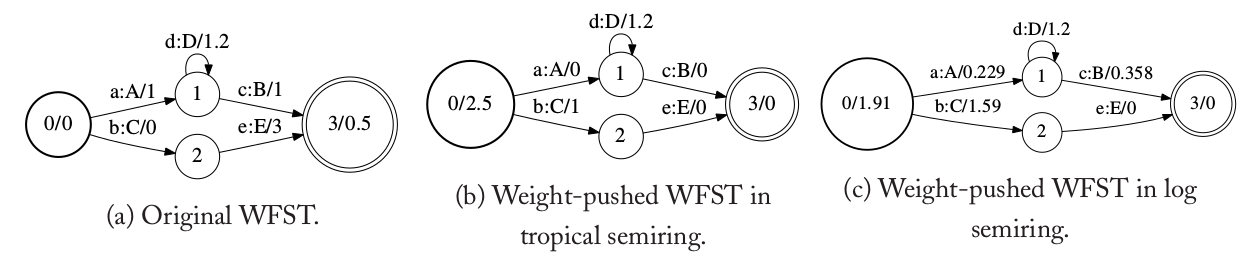
Weight Pushing

Weight Pushing运算的作用是把一个WFST所有路径的weight分布往初始状态push，但是不改变任何成功路径的weight。在许多序列识别和转换问题里，寻找最可能或者最小代价是WFST需要解决的最重要的问题。当我们使用一个weighted的FA时，这个问题就变成FA搜索weight最大或者最小的成功路径的问题。Weight Pushing因为把路径的weight推到前面，因此对于那种look-ahead的算法(比如Beam搜索)，它能更快的滤掉早期不太有希望的路径，从而减少搜索时间。

图：Weight Pushing的例子

上图(a)是一个WFST，图(b)是在热带半环上的Weight Pushing的结果，图(c)是在log半环上的结果。在图(a)中，成功路径0->1->3的weight为$0 \bigotimes 1 \bigotimes 1 \bigotimes 0.5=2.5$。在图(b)中，weight被尽量往前面push，成功路径0->1->3的weight变为$2.5 \bigotimes 0 \bigotimes 0 \bigotimes 0$。而另一条成功路径0->2->3的weight从$0 \bigotimes 0 \bigotimes 3 \bigotimes 0.5=3.5$变成了$2.5 \bigotimes 1 \bigotimes 0 \bigotimes 0$。通过上面的分析，我们验证了Weight Pushing后的WFST确实没有改变成功路径的weight。

通用的Weight Pushing算法分为两步。第一步：计算每个状态的势(potential)，它是从这个状态到某个终止状态的所有路径的weight的和。第二步：把边的weight修改成起点和终点的势的差。这样就会让weight移到初始状态。注意每个跳转的weight是基于势的差，因此bias项会被消除掉并且移到初始状态。所有状态的势可以通过一个通用的从终止状态开始的最短路径算法得到，如下所示。

在这个算法了，在q的势$V[q]$的计算公式为：

上式中$\Pi(q,F)$是从q出发到底终止状态的所有路径的集合。$w[\pi]$是路径$\pi$的weight的乘积。但是如果从q到某个终止状态的路径存在环(loop)的话，这个集合是无穷的。因为无法处理无穷的情况，这个算法假设半环是k-closed。因此，对于回路c，下面的等式：

在$l>k$时成立。因此如果一个回路的环(loop)重复k次以上，我们可以忽略k次以后的部分。

算法12的第1-7行是初始化状态q的势$V[q]$，对于终止状态，它的势为$\rho(q)；而其它状态为$$\bar{0}$。第8行把终止状态放到待处理队列S中，接下来的9-23行是一个大的循环，处理S中的所有状态直到它为空。

在第10-13行，状态q从S中弹出，r[q]暂存在R中，然后把r[q]设置为$\bar{0}$。这里的r[q]代表从上次q被弹出之后累加的路径weight。

第14-22行，对于状态q的每一条入边e，路径的weight被传递到之前的状态p[e] (入边的起点)，这里$E^{-1}[q]$代表进入q的跳转(多重)集合。在第15行，p[e]的当前计算的势会和新的势——$V[p[e]] \bigoplus (R \bigotimes w[e])$进行比较。如果它们相同，则不做任何操作。否则需要更新p[e]的势并且把状态p[e]入队以便下一步累计路径的weight。$V[p[e]] \ne V[p[e]] \bigoplus (R \bigotimes w[e])$是什么意思呢？我们假设这里是热带半环，则乘法$\bigoplus$是min，因此$V[p[e]] \bigoplus (R \bigotimes w[e])$是找出(-log概率)最小的路径，其实也就是概率最大的路径。如果通过q<-e-p[e]有一条概率更大的路径，那么就应该更新p[e]的势。当S是空的时候，所有的势都不再发生变换，循环也就停止了。

上面的算法对于k-closed的半环肯定能循环终止。热带半环是0-closed。而log半环如果忽略很小的weight是k-closed。对于k-closed的半环，第15行判断x=y要改成”如果$\vert x-y \vert < \delta$则认为x=y”。上面的算法队列可以是任何弹出的策略，实际通常使用优先队列，优先弹出势最大的状态，这样循环会更快的终止。

计算了状态的势之后，第二步就非常简单了，算法如下：

对于初始状态，它的weight $\rho(q)$要乘以V[q]。对于每一条边，它的weight要加上前后两个状态的差，也就是$V[q]^{-1} \bigotimes w[e] \bigotimes V[n[e]]$。最后对于终止状态，它的weight要”除以”(就是乘以逆)V[q]，也就是$V[q]^{-1}\rho(q)$。

最小化(Minimization)

最小化是在所有与原始FA等价的DFA(不包括NFA)里寻找状态数最小的那个DFA。WFST的最小化算法包含两个步骤：

• 把WFST的weight和输出标签往初始状态push
• 使用经典的最小化算法，这里需要把”输入:输出/weight”看成一个标签

有很多最小化的算法。这些算法基本都是获取原来状态机状态集合的一个划分(partition)，所谓的划分(动词)是把一个集合切分成几个非空集合，这些集合的交集为空，并集为原始集合。每一个分块(partition)中的状态是等价的或者说不可区分的(not distinguished)，所谓不可区分指的是两个状态如该状态1有一条从它出发到某个终止状态的路径，它接受某个字符串，则状态2也一定存在到终止状态的路径也接受这个字符串；反之亦然。对于WFST来说，两个状态$q_1, q_2 \in Q$是等价的充要条件是：

其中，

用自然语言来描述$L(q,x)$就是：存在一条路径$\pi$，它的起点是q，终点是终止状态，并且路径打输入字符串是x；则$L(q,x)$的值是这条路径的输出字符串和weight。如果从q出发输入字符串x无法走到终止状态呢？那就没有定义(意义)。因此充要条件的含义是：对于任何一个字符串x，如果能从$q_1$走到终止状态，则x也能使得$q_2$走到终止状态，而且这两条路径的输出字符串和weight也要完全相同。这里我们假设WFST是确定的，因此路径是唯一的。

得到状态集合的划分之后，同一个划分的所有状态被替换成一个新的状态。原来状态的所有跳转都要迁移到这个新的状态里，同一个输入符号的多个跳转需要合并。

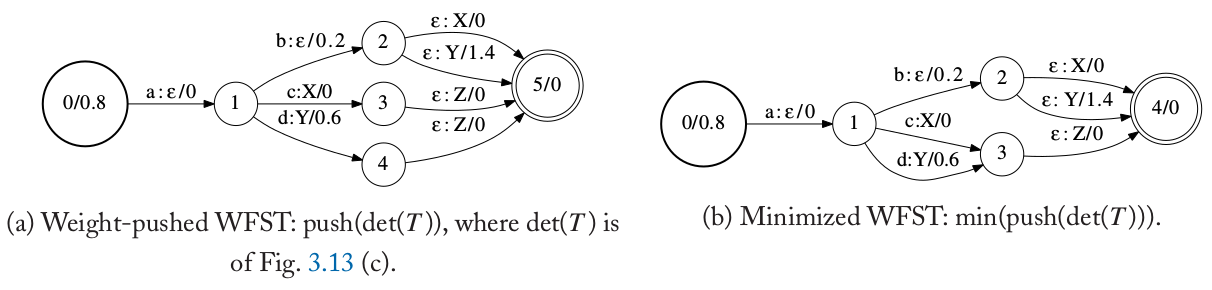
下图(a)是对原始WFST T(原始的T在上图(c))进行push(det(T))之后的结果，首先进行确定化，然后进行weight pushing。我们发现状态3和4是等价的，因此最小化后它们被合并成一个状态。注意，在weight pushing之前，状态3和4并不是等价的，所以则最小化前需要先做weight pushing。label pushing也可能是需要的。比如我们可以把输出符号也看成一个字符串半环上的weight，然后进行weight pushing(把公共的前缀往前push)。

图：最小化的例子

Hopcroft算法是非常流行的最小化DFA的有效算法，它的计算复杂度是$O(\vert E \vert log \vert Q \vert)$。这个算法会遍历目前的每一个块(block，一开始只有一个块)，然后不断的切分(split)这些块直到它里面的状态都是等价的。为了切分当前划分的每一个块，首先会选择一个块为splitter，然后其他块被切分。在切分的每一步里，如果一个块的部分状态组成的集合会被移出这个块——条件是这些状态在给定输入符号时会跳到splitter的某个状态里。然后原来的块会被切分成两个：被移出的状态集合以及剩下的状态集合。通过上面的步骤，每个块被逐渐提炼(refine)成等价状态的集合。这里不做证明，很多文献都有详细的介绍。下面是针对WFST做了微小修改的Hopcroft最小化算法。

在第1行，当前划分P和队列W初始化为空集$\emptyset$。队列W是一个等待列表，它包含用于切分P中块的切分块(splitter)。第2-7行进行初始划分，所有的非终止状态是一个集合，而终止状态根据其weight是否相同划分成不同的集合。在第5行，终止状态组成的块会放到W里作为splitter。

原始的Hopcroft算法把状态集合划分成两个块F和Q-F。对于WFST，我们进一步把F根据终止weight划分成不同的集合，因为相同的weight的终止状态才是等价的。此外，我们还可以利用每个状态的跳出边的信息来进一步细粒度的初始划分，因为如果两个状态的出边的输入符号、输出符号和wegiht有任何一个不同，则这两个状态就是可以区分的(不等价)。这样初始化的话我们可以把状态切分到更多更细粒度的块。这样的初始化可以加速算法。不过这里由于篇幅的限制我们不详细介绍。

第8-27行迭代的切分块。第9行，从队列W里弹出一个切分块(splitter)S。第10行遍历跳进S的所有三元组(i/输入符号，o/输出符号，w/weight)，这里$E^{-1}[S]$表示这样的边——这条边的终点包含在S里，用数学语言来描述就是$\{e \in E \vert n[e] \in S \}$。我们把跳入S并且三元组是(i,o,w)的边的起点(状态)组成的集合记作$R_{i,o,w}。$根据三元组(i,o,w)，如果一个块B的边包含$E^{-1}[S]$里的一条边(也就是块B可以跳到S)并且$B \not\subseteq R_{i,o,w}$(也就是至少还有一条状态不是跳到S的)，则我们可以把B切分成两个子集：$B_1=B \cap R_{i,o,w}$(跳到S的状态集合)和$B-B_1$(不跳到S的状态集合)。如果B属于splitter集合W，第15行把B从划分中去掉，替换成两个子集$B_1$和$B_2$。然后把$B_1$和$B_2$加到W里作为splitter。否在如果B不属于W，则把$B_1$和$B_2$中元素个数较少的放到W里。

等价状态的集合划分完成后，第28-35行利用划分来重新构建一个最小化的WFST。第28行用划分P得到新的状态集合$Q’$。第29-31行，对于原始WFST的每一个条边$e \in E$，找到边e的起点(p[e])对应的划分，作为新边的起点，类似的方法出来终点。这里B(s)表示得到状态s所在的划分(的ID)。新边的输入符号、输出符号和weight保持不变。

第32-35行处理新状态的终止状态和weight：如果某个划分里的所有状态都是原始WFST的终止状态，则这个划分S构成的新状态就是新WFST里的一个终止状态，并且它的weight是S里某个状态的weight(所有状态的weight应该是相同的，否则就不等价里)，也就是$\rho’(S)=\rho(p), p \in S$。

因为Hopcroft算法是通用的算法，所以它也可以用于任何确定的WFST，这也包括有环的确定的WFST。如果WFST是无环的，则可以使用更加高效的Revuz算法，其计算复杂度是$O(\vert E \vert)$。在这个算法里，初始划分是通过从终止状态开始用深度优先搜索得到的一个最大高度(height)的划分。每个块根据输入符号基于最大的高度来进行切分。详细介绍可以参考Minimisation of acyclic deterministic automata in linear time。

消除ε跳转

ε消除算法是把一个ε-NFA转换成等价的没有ε的NFA。前面提到过，ε的存在使得FA不确定。虽然前面介绍的FA的确定化算法可以应用与ε-NFA——我们需要把ε看成一个普通的输入符号，但是这样得到的FA还是包含ε的。因此最终的FA看起来像DFA，但是实际还是个NFA。如果我们在确定化算法使用之前先消除ε，则这个FA就可以完全的(真正的)被确定化。

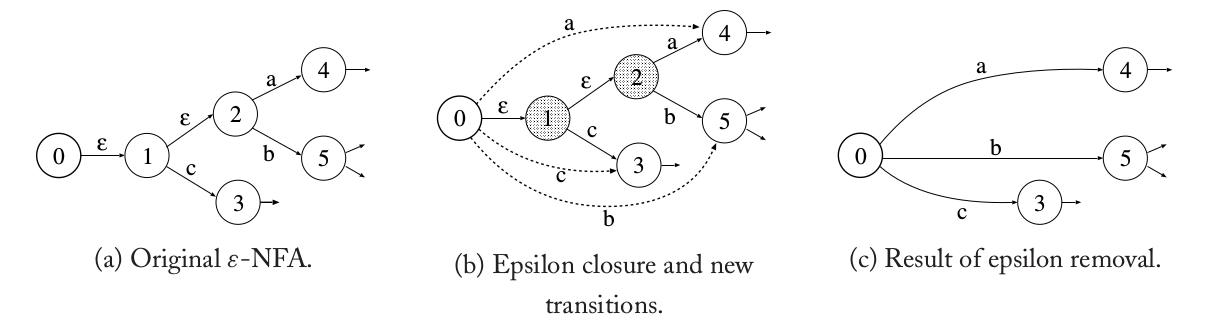
ε消除算法的基本思路是删除ε-跳转，然后把它替换成新的非ε-跳转，这些新跳转是原来的跳转里的一个或者多个ε-跳转加上一个非ε-跳转得到。新跳转的输入符号还原来的非ε-跳转的一样。如果有一个非终止状态能通过ε-跳转到某个终止状态，则在消除里ε跳转的FA里这个非终止状态也变成终止状态。下图展示里ε消除的基本概念。

图：ε消除的基本概念

图(a)是一个ε-NFA的一部分。ε消除算法首先找到每个状态的ε闭包(closure)。一个状态的ε闭包是这个状态可以通过一个或者多个ε-跳转到达的所有状态组成的集合。图(b)中的灰色背景的状态1和2说明它们属于状态0的ε闭包。同时则图(b)中ε闭包里的状态1和2出去的非ε跳转”2-a->4”、”2-b->5”和”1-c->3”会产生新的”0-a->4”、”0-b->5”和”0-c->3”。最后ε闭包只保留一个状态0，其余的状态2和3以及它们的边都删除掉，就打得到图(c)里的没有ε的NFA。

前面介绍的是NFA(接收机)的ε消除算法，但是WFST还有输出符号和weight，因此还需要进行扩展。这里介绍Generic ε-Removal and Input ε-Normalization Algorithms for Weighted Transducers里的算法。首先，这个算法把输入和输出符号都是ε的边ε:ε当成一个ε来处理。其次，给定一个状态，需要计算这个状态和它的ε闭包里的每一个状态的距离，并且乘以最后一个非ε跳转的weight来得到新跳转的weight。闭包里两个状态的路径可以使用标准的单元最大路径算法来实现(只走ε的边)。下面是WFST的ε消除算法代码。

这个算法遍历WFST状态集合Q里的每一个状态p，ε:ε这样的跳转会被丢弃然后替换成和原来等价的非ε跳转。在第2行，非ε的跳转直接保留下来复制到$E’$。在第3行，对于状态p的ε闭包里的每一个(q, w’)(w’是p通过ε跳转到q的距离)，q出发的某个非ε跳转(q,x,y,w,r)会被替换成从p出发的新跳转，这个新跳转的输入和输出符号不变，weight是$w’ \bigotimes w$，这里要求(x,y)不等于(ε,ε)。第5-14行检查p是否能够通过ε跳转到达终止状态，如果是的话，需要把p也加到终止状态集合里，并且计算相应的$\rho’$。具体来说，如果p属于终止状态，那么$\rho’(p)=\rho(p)$；如果p通过ε跳转到达终止状态q，则$\rho’(p) \leftarrow \rho’(p) \bigoplus (w’ \bigotimes \rho(q))$。

注意：上面的算法只消除ε:ε这样的边，而ε:x或者x:ε仍然会保留下来。为了尽可能多的消除ε，我们可以在使用上面的算法前先进行同步(synchronization)。同步算法会把一个WFST转换成等价的并且对于成功的路径他会尽量同步的消费输入和输出符号的WFST。因此同步后的WFST会增加(x:x)和(ε:ε)这样的边而减少(x:ε)和(ε:x)这样的边。同步之后，ε消除算法能够更多的消除ε跳转。关于同步算法，感兴趣的读者可以参考Mehryar Mohri的Weighted automata algorithms。

• ← Previous Post