本文介绍Transformer的代码。
目录
- 运行代码
- 背景介绍
- 模型结构
- Encoder和Decoder Stack
- MultiHeadedAttention
- MultiHeadedAttention的应用
- 全连接SubLayer
- Embedding和Softmax
- 位置编码
- 完整模型
- 训练
本文内容参考了The Annotated Transformer。读者可以从这里下载代码。这篇文章是原始论文的读书笔记，它除了详细的解释论文的原理，还用代码实现了论文的模型。
注意：这里并不是完全翻译这篇文章，而是根据作者自己的理解来分析和阅读其源代码。Transformer的原理在前面的图解部分已经分析的很详细了，因此这里关注的重点是代码。网上有很多Transformer的源代码，也有一些比较大的库包含了Transformer的实现，比如Tensor2Tensor和OpenNMT等等。作者选择这个实现的原因是因为它是一个单独的ipynb文件，如果我们要实际使用非常简单，复制粘贴代码就行了。而Tensor2Tensor或者OpenNMT包含了太多其它的东西，做了过多的抽象。虽然代码质量和重用性更好，但是对于理解论文来说这是不必要的，并且增加了理解的难度。
运行代码
这里的代码需要PyTorch-0.3.0(高版本的0.4.0+都不行)，所以建议读者使用virtualenv安装。为了在Jupyter notebook里使用这个virtualenv，需要执行如下命令：
source /path/to/virtualenv/bin/activate
pip install ipykernel
python -m ipykernel install --user --name=pytorch-0.3.0
jupyter notebook
点击kernel菜单->select kernel -> pytorch-0.3.0
背景介绍
前面提到过RNN等模型的缺点是需要顺序计算，从而很难并行。因此出现了Extended Neural GPU、ByteNet和ConvS2S等网络模型。这些模型都是以CNN为基础，这比较容易并行。但是和RNN相比，它较难学习到长距离的依赖关系。
本文的Transformer使用了Self-Attention机制，它在编码每一词的时候都能够注意(attend to)整个句子，从而可以解决长距离依赖的问题，同时计算Self-Attention可以用矩阵乘法一次计算所有的时刻，因此可以充分利用计算资源(CPU/GPU上的矩阵运算都是充分优化和高度并行的)。
模型结构
目前的主流神经序列转换(neural sequence transduction)模型都是基于Encoder-Decoder结构的。所谓的序列转换模型就是把一个输入序列转换成另外一个输出序列，它们的长度很可能是不同的。比如基于神经网络的机器翻译，输入是法语句子，输出是英语句子，这就是一个序列转换模型。类似的包括文本摘要、对话等问题都可以看成序列转换问题。我们这里主要关注机器翻译，但是任何输入是一个序列输出是另外一个序列的问题都可以考虑使用Encoder-Decoder模型。
Encoder讲输入序列$(x_1,…,x_n)$映射(编码)成一个连续的序列$z=(z_1,…,z_n)$。而Decoder根据z来解码得到输出序列$y_1,…,y_m$。Decoder是自回归的(auto-regressive)——它会把前一个时刻的输出作为当前时刻的输入。Encoder-Decoder结构模型的代码如下：
class EncoderDecoder(nn.Module):
"""
标准的Encoder-Decoder架构。这是很多模型的基础
"""
def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
super(EncoderDecoder, self).__init__()
# encoder和decoder都是构造的时候传入的，这样会非常灵活
self.encoder = encoder
self.decoder = decoder
# 源语言和目标语言的embedding
self.src_embed = src_embed
self.tgt_embed = tgt_embed
# generator后面会讲到，就是根据Decoder的隐状态输出当前时刻的词
# 基本的实现就是隐状态输入一个全连接层，全连接层的输出大小是词的个数
# 然后接一个softmax变成概率。
self.generator = generator
def forward(self, src, tgt, src_mask, tgt_mask):
# 首先调用encode方法对输入进行编码，然后调用decode方法解码
return self.decode(self.encode(src, src_mask), src_mask,
tgt, tgt_mask)
def encode(self, src, src_mask):
# 调用encoder来进行编码，传入的参数embedding的src和src_mask
return self.encoder(self.src_embed(src), src_mask)
def decode(self, memory, src_mask, tgt, tgt_mask):
# 调用decoder
return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)
EncoderDecoder定义了一种通用的Encoder-Decoder架构，具体的Encoder、Decoder、src_embed、target_embed和generator都是构造函数传入的参数。这样我们做实验更换不同的组件就会更加方便。
class Generator(nn.Module):
# 根据Decoder的隐状态输出一个词
# d_model是Decoder输出的大小，vocab是词典大小
def __init__(self, d_model, vocab):
super(Generator, self).__init__()
self.proj = nn.Linear(d_model, vocab)
# 全连接再加上一个softmax
def forward(self, x):
return F.log_softmax(self.proj(x), dim=-1)
注意：Generator返回的是softmax的log值。在PyTorch里为了计算交叉熵损失，有两种方法。第一种方法是使用nn.CrossEntropyLoss()，一种是使用NLLLoss()。第一种方法更加容易懂，但是在很多开源代码里第二种更常见，原因可能是它后来才有，大家都习惯了使用NLLLoss。我们先看CrossEntropyLoss，它就是计算交叉熵损失函数，比如：
criterion = nn.CrossEntropyLoss()
x = torch.randn(1, 5)
y = torch.empty(1, dtype=torch.long).random_(5)
loss = criterion(x, y)
比如上面的代码，假设是5分类问题，x表示模型的输出logits(batch=1)，而y是真实分类的下标(0-4)。实际的计算过程为：\(loss = - \sum_{i=1}^5y_i log (softmax(x)_i)\)。
比如logits是[0,1,2,3,4]，真实分类是3，那么上式就是：
\[loss = - \sum_{i=1}^5y_i log (softmax(x)_i)= - log (softmax(x)_3)=-log\frac{e^3}{e^0+e^1+e^2+e^3+e^4}\]因此我们也可以使用NLLLoss()配合F.log_softmax函数(或者nn.LogSoftmax，这不是一个函数而是一个Module了)来实现一样的效果：
m = nn.LogSoftmax(dim=1)
criterion = nn.NLLLoss()
x = torch.randn(1, 5)
y = torch.empty(1, dtype=torch.long).random_(5)
loss = criterion(m(x), y)
NLLLoss(Negative Log Likelihood Loss)是计算负log似然损失。它输入的x是log_softmax之后的结果(长度为5的数组)，y是真实分类(0-4)，输出就是x[y]。因此上面的代码为：
criterion(m(x), y)=m(x)[y]
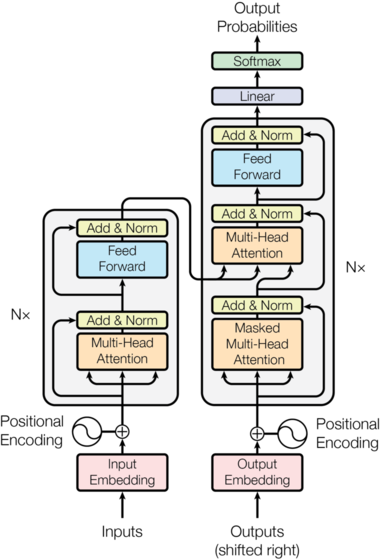
Transformer模型也是遵循上面的架构，只不过它的Encoder是N(6)个EncoderLayer组成，每个EncoderLayer包含一个Self-Attention SubLayer层和一个全连接SubLayer层。而它的Decoder也是N(6)个DecoderLayer组成，每个DecoderLayer包含一个Self-Attention SubLayer层、Attention SubLayer层和全连接SubLayer层。如下图所示。
图：Transformer的结构
Encoder和Decoder Stack
前面说了Encoder和Decoder都是由N个相同结构的Layer堆积(stack)而成。因此我们首先定义clones函数，用于克隆相同的SubLayer。
def clones(module, N):
# 克隆N个完全相同的SubLayer，使用了copy.deepcopy
return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
这里使用了nn.ModuleList，ModuleList就像一个普通的Python的List，我们可以使用下标来访问它，它的好处是传入的ModuleList的所有Module都会注册的PyTorch里，这样Optimizer就能找到这里面的参数，从而能够用梯度下降更新这些参数。但是nn.ModuleList并不是Module(的子类)，因此它没有forward等方法，我们通常把它放到某个Module里。接下来我们定义Encoder：
class Encoder(nn.Module):
"Encoder是N个EncoderLayer的stack"
def __init__(self, layer, N):
super(Encoder, self).__init__()
# layer是一个SubLayer，我们clone N个
self.layers = clones(layer, N)
# 再加一个LayerNorm层
self.norm = LayerNorm(layer.size)
def forward(self, x, mask):
"逐层进行处理"
for layer in self.layers:
x = layer(x, mask)
# 最后进行LayerNorm，后面会解释为什么最后还有一个LayerNorm。
return self.norm(x)
Encoder就是N个SubLayer的stack，最后加上一个LayerNorm。我们来看LayerNorm：
class LayerNorm(nn.Module):
def __init__(self, features, eps=1e-6):
super(LayerNorm, self).__init__()
self.a_2 = nn.Parameter(torch.ones(features))
self.b_2 = nn.Parameter(torch.zeros(features))
self.eps = eps
def forward(self, x):
mean = x.mean(-1, keepdim=True)
std = x.std(-1, keepdim=True)
return self.a_2 * (x - mean) / (std + self.eps) + self.b_2
LayerNorm我们以前介绍过，代码也很简单，这里就不详细介绍了。注意Layer Normalization不是Batch Normalization。如上图所示，原始论文的模型为：
x -> attention(x) -> x+self-attention(x) -> layernorm(x+self-attention(x)) => y
y -> dense(y) -> y+dense(y) -> layernorm(y+dense(y)) => z(输入下一层)
这里稍微做了一点修改，在self-attention和dense之后加了一个dropout层。另外一个不同支持就是把layernorm层放到前面了。这里的模型为：
x -> layernorm(x) -> attention(layernorm(x)) -> x + attention(layernorm(x)) => y
y -> layernorm(y) -> dense(layernorm(y)) -> y+dense(layernorm(y))
原始论文的layernorm放在最后；而这里把它放在最前面并且在Encoder的最后一层再加了一个layernorm。这里的实现和论文的实现基本是一致的，只是给最底层的输入x多做了一个layernorm，而原始论文是没有的。下面是Encoder的forward方法，这样对比读者可能会比较清楚为什么N个EncoderLayer处理完成之后还需要一个LayerNorm
def forward(self, x, mask):
"逐层进行处理"
for layer in self.layers:
x = layer(x, mask)
return self.norm(x)
不管是Self-Attention还是全连接层，都首先是LayerNorm，然后是Self-Attention/Dense，然后是Dropout，最好是残差连接。这里面有很多可以重用的代码，我们把它封装成SublayerConnection。
class SublayerConnection(nn.Module):
"""
LayerNorm + sublayer(Self-Attenion/Dense) + dropout + 残差连接
为了简单，把LayerNorm放到了前面，这和原始论文稍有不同，原始论文LayerNorm在最后。
"""
def __init__(self, size, dropout):
super(SublayerConnection, self).__init__()
self.norm = LayerNorm(size)
self.dropout = nn.Dropout(dropout)
def forward(self, x, sublayer):
"sublayer是传入的参数，参考DecoderLayer，它可以当成函数调用，这个函数的有一个输入参数"
return x + self.dropout(sublayer(self.norm(x)))
这个类会构造LayerNorm和Dropout，但是Self-Attention或者Dense并不在这里构造，还是放在了EncoderLayer里，在forward的时候由EncoderLayer传入。这样的好处是更加通用，比如Decoder也是类似的需要在Self-Attention、Attention或者Dense前面后加上LayerNorm和Dropout以及残差连接，我们就可以复用代码。但是这里要求传入的sublayer可以使用一个参数来调用的函数(或者有__call__)。
有了这些代码之后，EncoderLayer就很简单了：
class EncoderLayer(nn.Module):
"EncoderLayer由self-attn和feed forward组成"
def __init__(self, size, self_attn, feed_forward, dropout):
super(EncoderLayer, self).__init__()
self.self_attn = self_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 2)
self.size = size
def forward(self, x, mask):
"Follow Figure 1 (left) for connections."
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
return self.sublayer[1](x, self.feed_forward)
为了复用，这里的self_attn层和feed_forward层也是传入的参数，这里只构造两个SublayerConnection。forward调用sublayer[0] (这是SublayerConnection对象)的__call__方法，最终会调到它的forward方法，而这个方法需要两个参数，一个是输入Tensor，一个是一个callable，并且这个callable可以用一个参数来调用。而self_attn函数需要4个参数(Query的输入,Key的输入,Value的输入和Mask)，因此这里我们使用lambda的技巧把它变成一个参数x的函数(mask可以看成已知的数)。因为lambda的形参也叫x，读者可能难以理解，我们改写一下：
def forward(self, x, mask):
z = lambda y: self.self_attn(y, y, y, mask)
x = self.sublayer[0](x, z)
return self.sublayer[1](x, self.feed_forward)
self_attn有4个参数，但是我们知道在Encoder里，前三个参数都是输入y，第四个参数是mask。这里mask是已知的，因此我们可以用lambda的技巧它变成一个参数的函数z = lambda y: self.self_attn(y, y, y, mask)，这个函数的输入是y。
self.sublayer[0]是个callable，self.sublayer[0] (x, z)会调用self.sublayer[0].call(x, z)，然后会调用SublayerConnection.forward(x, z)，然后会调用sublayer(self.norm(x))，sublayer就是传入的参数z，因此就是z(self.norm(x))。z是一个lambda，我们可以先简单的看成一个函数，显然这里要求函数z的输入是一个参数。理解了Encoder之后，Decoder就很简单了。
class Decoder(nn.Module):
def __init__(self, layer, N):
super(Decoder, self).__init__()
self.layers = clones(layer, N)
self.norm = LayerNorm(layer.size)
def forward(self, x, memory, src_mask, tgt_mask):
for layer in self.layers:
x = layer(x, memory, src_mask, tgt_mask)
return self.norm(x)
Decoder也是N个DecoderLayer的stack，参数layer是DecoderLayer，它也是一个callable，最终__call__会调用DecoderLayer.forward方法，这个方法(后面会介绍)需要4个参数，输入x，Encoder层的输出memory，输入Encoder的Mask(src_mask)和输入Decoder的Mask(tgt_mask)。所有这里的Decoder的forward也需要这4个参数。
class DecoderLayer(nn.Module):
"Decoder包括self-attn, src-attn, 和feed forward "
def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
super(DecoderLayer, self).__init__()
self.size = size
self.self_attn = self_attn
self.src_attn = src_attn
self.feed_forward = feed_forward
self.sublayer = clones(SublayerConnection(size, dropout), 3)
def forward(self, x, memory, src_mask, tgt_mask):
m = memory
x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
return self.sublayer[2](x, self.feed_forward)
DecoderLayer比EncoderLayer多了一个src-attn层，这是Decoder时attend to Encoder的输出(memory)。src-attn和self-attn的实现是一样的，只不过使用的Query，Key和Value的输入不同。普通的Attention(src-attn)的Query是下层输入进来的(来自self-attn的输出)，Key和Value是Encoder最后一层的输出memory；而Self-Attention的Query，Key和Value都是来自下层输入进来的。
Decoder和Encoder有一个关键的不同：Decoder在解码第t个时刻的时候只能使用1…t时刻的输入，而不能使用t+1时刻及其之后的输入。因此我们需要一个函数来产生一个Mask矩阵，代码如下：
def subsequent_mask(size):
"Mask out subsequent positions."
attn_shape = (1, size, size)
subsequent_mask = np.triu(np.ones(attn_shape), k=1).astype('uint8')
return torch.from_numpy(subsequent_mask) == 0
我们阅读代码之前先看它的输出：
print(subsequent_mask(5))
# 输出
1 0 0 0 0
1 1 0 0 0
1 1 1 0 0
1 1 1 1 0
1 1 1 1 1
我们发现它输出的是一个方阵，对角线和下面都是1。第一行只有第一列是1，它的意思是时刻1只能attend to输入1，第三行说明时刻3可以attend to {1,2,3}而不能attend to{4,5}的输入，因为在真正Decoder的时候这是属于Future的信息。知道了这个函数的用途之后，上面的代码就很容易理解了。代码首先使用triu产生一个上三角阵：
0 1 1 1 1
0 0 1 1 1
0 0 0 1 1
0 0 0 0 1
0 0 0 0 0
然后需要把0变成1，把1变成0，这可以使用 matrix == 0来实现。
MultiHeadedAttention
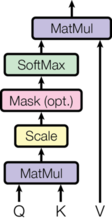
Attention(包括Self-Attention和普通的Attention)可以看成一个函数，它的输入是Query,Key,Value和Mask，输出是一个Tensor。其中输出是Value的加权平均，而权重来自Query和Key的计算。具体的计算如下图所示，计算公式为：
\[\mathrm{Attention}(Q, K, V) = \mathrm{softmax}(\frac{QK^T}{\sqrt{d_k}})V\]
图：Attention的计算
代码为：
def attention(query, key, value, mask=None, dropout=None):
d_k = query.size(-1)
scores = torch.matmul(query, key.transpose(-2, -1)) \
/ math.sqrt(d_k)
if mask is not None:
scores = scores.masked_fill(mask == 0, -1e9)
p_attn = F.softmax(scores, dim = -1)
if dropout is not None:
p_attn = dropout(p_attn)
return torch.matmul(p_attn, value), p_attn
我们使用一个实际的例子跟踪一些不同Tensor的shape，然后对照公式就很容易理解。比如Q是(30,8,33,64)，其中30是batch，8是head个数，33是序列长度，64是每个时刻的特征数。K和Q的shape必须相同的，而V可以不同，但是这里的实现shape也是相同的。
scores = torch.matmul(query, key.transpose(-2, -1)) \
/ math.sqrt(d_k)
上面的代码实现$\frac{QK^T}{\sqrt{d_k}}$，和公式里稍微不同的是，这里的Q和K都是4d的Tensor，包括batch和head维度。matmul会把query和key的最后两维进行矩阵乘法，这样效率更高，如果我们要用标准的矩阵(二维Tensor)乘法来实现，那么需要遍历batch维和head维：
batch_num = query.size(0)
head_num = query.size(1)
for i in range(batch_num):
for j in range(head_num):
scores[i,j] = torch.matmul(query[i,j], key[i,j].transpose())
而上面的写法一次完成所有这些循环，效率更高。输出的score是(30, 8, 33, 33)，前面两维不看，那么是一个(33, 33)的attention矩阵a，$a_{ij}$表示时刻i attend to j的得分(还没有经过softmax变成概率)。
接下来是scores.masked_fill(mask == 0, -1e9)，用于把mask是0的变成一个很小的数，这样后面经过softmax之后的概率就很接近零(但是理论上还是用来很少一点点未来的信息)。
这里mask是(30, 1, 1, 33)的tensor，因为8个head的mask都是一样的，所有第二维是1，masked_fill时使用broadcasting就可以了。这里是self-attention的mask，所以每个时刻都可以attend到所有其它时刻，所有第三维也是1，也使用broadcasting。如果是普通的mask，那么mask的shape是(30, 1, 33, 33)。
这样讲有点抽象，我们可以举一个例子，为了简单，我们假设batch=2, head=8。第一个序列长度为3，第二个为4，那么self-attention的mask为(2, 1, 1, 4)，我们可以用两个向量表示：
1 1 1 0
1 1 1 1
它的意思是在self-attention里，第一个序列的任一时刻可以attend to 前3个时刻(因为第4个时刻是padding的)；而第二个序列的可以attend to所有时刻的输入。而Decoder的src-attention的mask为(2, 1, 4, 4)，我们需要用2个矩阵表示：
第一个序列的mask矩阵
1 0 0 0
1 1 0 0
1 1 1 0
1 1 1 0
第二个序列的mask矩阵
1 0 0 0
1 1 0 0
1 1 1 0
1 1 1 1
接下来对score求softmax，把得分变成概率p_attn，如果有dropout还对p_attn进行Dropout(这也是原始论文没有的)。最后把p_attn和value相乘。p_attn是(30, 8, 33, 33)，value是(30, 8, 33, 64)，我们只看后两维，(33x33) x (33x64)最终得到33x64。
接下来就是输入怎么变成Q,K和V了，我们之前介绍过，对于每一个Head，都使用三个矩阵$W^Q, W^K, W^V$把输入转换成Q，K和V。然后分别用每一个Head进行Self-Attention的计算，最后把N个Head的输出拼接起来，最后用一个矩阵$W^O$把输出压缩一下。具体计算过程为：
\[\mathrm{MultiHead}(Q, K, V) = \mathrm{Concat}(\mathrm{head_1}, ..., \mathrm{head_h})W^O \\ \text{where}~\mathrm{head_i} = \mathrm{Attention}(QW^Q_i, KW^K_i, VW^V_i)\]其中，$W^Q_i \in \mathbb{R}^{d_{\text{model}} \times d_k}$，$W^K_i \in \mathbb{R}^{d_{\text{model}} \times d_k}$, $W^V_i \in \mathbb{R}^{d_{\text{model}} \times d_v}$ ， $W^O \in \mathbb{R}^{hd_v \times d_{\text{model}}}$。
在这里，我们的Head个数h=8，$d_k=d_v=d_{\text{model}}/h=64$。
详细结构如下图所示，输入Q，K和V经过多个线性变换后得到N(8)组Query，Key和Value，然后使用Self-Attention计算得到N个向量，然后拼接起来，最后使用一个线性变换进行降维。
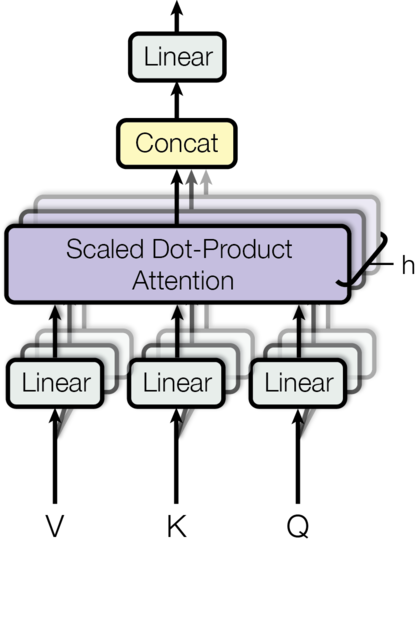图：Multi-Head Self-Attention详细结构图
代码如下：
class MultiHeadedAttention(nn.Module):
def __init__(self, h, d_model, dropout=0.1):
super(MultiHeadedAttention, self).__init__()
assert d_model % h == 0
# We assume d_v always equals d_k
self.d_k = d_model // h
self.h = h
self.linears = clones(nn.Linear(d_model, d_model), 4)
self.attn = None
self.dropout = nn.Dropout(p=dropout)
def forward(self, query, key, value, mask=None):
if mask is not None:
# 所有h个head的mask都是相同的
mask = mask.unsqueeze(1)
nbatches = query.size(0)
# 1) 首先使用线性变换，然后把d_model分配给h个Head，每个head为d_k=d_model/h
query, key, value = \
[l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for l, x in zip(self.linears, (query, key, value))]
# 2) 使用attention函数计算
x, self.attn = attention(query, key, value, mask=mask,
dropout=self.dropout)
# 3) 把8个head的64维向量拼接成一个512的向量。然后再使用一个线性变换(512,521)，shape不变。
x = x.transpose(1, 2).contiguous() \
.view(nbatches, -1, self.h * self.d_k)
return self.linears[-1](x)
我们先看构造函数，这里d_model(512)是Multi-Head的输出大小，因为有h(8)个head，因此每个head的d_k=512/8=64。接着我们构造4个(d_model x d_model)的矩阵，后面我们会看到它的用处。最后是构造一个Dropout层。
然后我们来看forward方法。输入的mask是(batch, 1, time)的，因为每个head的mask都是一样的，所以先用unsqueeze(1)变成(batch, 1, 1, time)，mask我们前面已经详细分析过了。
接下来是根据输入query，key和value计算变换后的Multi-Head的query，key和value。这是通过下面的语句来实现的：
query, key, value = \
[l(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
for l, x in zip(self.linears, (query, key, value))]
zip(self.linears, (query, key, value))是把(self.linears[0],self.linears[1],self.linears[2])和(query, key, value)放到一起然后遍历。我们只看一个self.linears[0] (query)。根据构造函数的定义，self.linears[0]是一个(512, 512)的矩阵，而query是(batch, time, 512)，相乘之后得到的新query还是512(d_model)维的向量，然后用view把它变成(batch, time, 8, 64)。然后transponse成(batch, 8,time,64)，这是attention函数要求的shape。分别对应8个Head，每个Head的Query都是64维。
Key和Value的运算完全相同，因此我们也分别得到8个Head的64维的Key和64维的Value。接下来调用attention函数，得到x和self.attn。其中x的shape是(batch, 8, time, 64)，而attn是(batch, 8, time, time)。
x.transpose(1, 2)把x变成(batch, time, 8, 64)，然后把它view成(batch, time, 512)，其实就是把最后8个64维的向量拼接成512的向量。最后使用self.linears[-1]对x进行线性变换，self.linears[-1]是(512, 512)的，因此最终的输出还是(batch, time, 512)。我们最初构造了4个(512, 512)的矩阵，前3个用于对query，key和value进行变换，而最后一个对8个head拼接后的向量再做一次变换。
MultiHeadedAttention的应用
在Transformer里，有3个地方用到了MultiHeadedAttention：
-
Encoder的Self-Attention层
query，key和value都是相同的值，来自下层的输入。Mask都是1(当然padding的不算)。
-
Decoder的Self-Attention层
query，key和value都是相同的值，来自下层的输入。但是Mask使得它不能访问未来的输入。
-
Encoder-Decoder的普通Attention
query来自下层的输入，而key和value相同，是Encoder最后一层的输出，而Mask都是1。
全连接SubLayer
除了Attention这个SubLayer之外，我们还有全连接的SubLayer，每个时刻的全连接层是可以独立并行计算的(当然参数是共享的)。全连接层有两个线性变换以及它们之间的ReLU激活组成：
\[\mathrm{FFN}(x)=\max(0, xW_1 + b_1) W_2 + b_2\]全连接层的输入和输出都是d_model(512)维的，中间隐单元的个数是d_{ff}(2048)。代码实现非常简单：
class PositionwiseFeedForward(nn.Module):
def __init__(self, d_model, d_ff, dropout=0.1):
super(PositionwiseFeedForward, self).__init__()
self.w_1 = nn.Linear(d_model, d_ff)
self.w_2 = nn.Linear(d_ff, d_model)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
return self.w_2(self.dropout(F.relu(self.w_1(x))))
在两个线性变换之间除了ReLu还使用了一个Dropout。
Embedding和Softmax
输入的词序列都是ID序列，我们需要Embedding。源语言和目标语言都需要Embedding，此外我们需要一个线性变换把隐变量变成输出概率，这可以通过前面的类Generator来实现。我们这里实现Embedding：
class Embeddings(nn.Module):
def __init__(self, d_model, vocab):
super(Embeddings, self).__init__()
self.lut = nn.Embedding(vocab, d_model)
self.d_model = d_model
def forward(self, x):
return self.lut(x) * math.sqrt(self.d_model)
代码非常简单，唯一需要注意的就是forward处理使用nn.Embedding对输入x进行Embedding之外，还除以了$\sqrt{d\_model}$。
位置编码
位置编码的公式为：
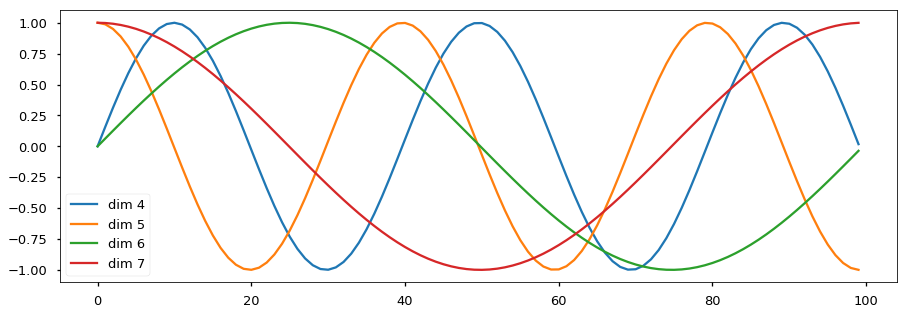
\[\begin{split} PE_{(pos,2i)} = sin(pos / 10000^{2i/d_{\text{model}}}) \\ PE_{(pos,2i+1)} = cos(pos / 10000^{2i/d_{\text{model}}}) \end{split}\]假设输入是ID序列长度为10，如果输入Embedding之后是(10, 512)，那么位置编码的输出也是(10, 512)。上式中pos就是位置(0-9)，512维的偶数维使用sin函数，而奇数维使用cos函数。这种位置编码的好处是：$PE_{pos+k}$ 可以表示成 $PE_{pos}$的线性函数，这样网络就能容易的学到相对位置的关系。下图是一个示例，向量的大小d_model=20，我们这里画出来第4、5、6和7维(下标从零开始)维的图像，最大的位置是100。我们可以看到它们都是正弦(余弦)函数，而且周期越来越长。
图：位置编码向量示例图
前面我们提到位置编码的好处是$PE_{pos+k}$ 可以表示成 $PE_{pos}$的线性函数，我们下面简单的验证一下。我们以第i维为例，为了简单，我们把$10000^{2i/d_{\text{model}}}$记作$W_i$，这是一个常量。
\[\begin{split} PE_{pos+k} &= sin(\frac{pos+k}{W_i}) = sin(\frac{pos}{W_i})cos(\frac{(k}{W_i}) + cos(\frac{pos}{W_i})sin(\frac{(k}{W_i}) \\ & = sin(\frac{pos}{W_i}) \times \text{与k有关的量} + cos(\frac{pos}{W_i}) \times \text{与k有关的量} \end{split}\]我们发现$PE_{pos+k}$ 确实可以表示成 $PE_{pos}$的线性函数。
这个Module的完整代码为：
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout, max_len=5000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(p=dropout)
# Compute the positional encodings once in log space.
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2) *
-(math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0)
self.register_buffer('pe', pe)
def forward(self, x):
x = x + Variable(self.pe[:, :x.size(1)], requires_grad=False)
return self.dropout(x)
代码细节请读者对照公式，这里值得注意的是调用了Module.register_buffer函数。这个函数的作用是创建一个buffer，比如这里把pi保存下来。register_buffer通常用于保存一些模型参数之外的值，比如在BatchNorm中，我们需要保存running_mean(Moving Average)，它不是模型的参数(不用梯度下降)，但是模型会修改它，而且在预测的时候也要使用它。这里也是类似的，pe是一个提前计算好的常量，我们在forward要用到它。我们在构造函数里并没有把pe保存到self里，但是在forward的时候我们却可以直接使用它(self.pe)。如果我们保存(序列化)模型到磁盘的话，PyTorch框架也会帮我们保存buffer里的数据到磁盘，这样反序列化的时候能恢复它们。
完整模型
构造完整模型的函数代码如下：
def make_model(src_vocab, tgt_vocab, N=6,
d_model=512, d_ff=2048, h=8, dropout=0.1):
c = copy.deepcopy
attn = MultiHeadedAttention(h, d_model)
ff = PositionwiseFeedForward(d_model, d_ff, dropout)
position = PositionalEncoding(d_model, dropout)
model = EncoderDecoder(
Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N),
nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
Generator(d_model, tgt_vocab))
# 随机初始化参数，这非常重要
for p in model.parameters():
if p.dim() > 1:
nn.init.xavier_uniform(p)
return model
首先把copy.deepcopy命名为c，这样使下面的代码简洁一点。然后构造MultiHeadedAttention，PositionwiseFeedForward和PositionalEncoding对象。接着就是构造EncoderDecoder对象。它需要5个参数：Encoder、Decoder、src-embed、tgt-embed和Generator。
我们先看后面三个简单的参数，Generator直接构造就行了，它的作用是把模型的隐单元变成输出词的概率。而src-embed是一个Embeddings层和一个位置编码层c(position)，tgt-embed也是类似的。
最后我们来看Decoder(Encoder和Decoder类似的)。Decoder由N个DecoderLayer组成，而DecoderLayer需要传入self-attn, src-attn，全连接层和Dropout。因为所有的MultiHeadedAttention都是一样的，因此我们直接deepcopy就行；同理所有的PositionwiseFeedForward也是一样的网络结果，我们可以deepcopy而不要再构造一个。
训练
在介绍训练代码前我们介绍一些Batch类。
class Batch:
def __init__(self, src, trg=None, pad=0):
self.src = src
self.src_mask = (src != pad).unsqueeze(-2)
if trg is not None:
self.trg = trg[:, :-1]
self.trg_y = trg[:, 1:]
self.trg_mask = \
self.make_std_mask(self.trg, pad)
self.ntokens = (self.trg_y != pad).data.sum()
@staticmethod
def make_std_mask(tgt, pad):
"创建Mask，使得我们不能attend to未来的词"
tgt_mask = (tgt != pad).unsqueeze(-2)
tgt_mask = tgt_mask & Variable(subsequent_mask(tgt.size(-1)).type_as(tgt_mask.data))
return tgt_mask
Batch构造函数的输入是src和trg，后者可以为None，因为再预测的时候是没有tgt的。我们用一个例子来说明Batch的代码，这是训练阶段的一个Batch，src是(48, 20)，48是batch大小，而20是最长的句子长度，其它的不够长的都padding成20了。而trg是(48, 25)，表示翻译后的最长句子是25个词，不足的也padding过了。
我们首先看src_mask怎么得到，(src != pad)把src中大于0的时刻置为1，这样表示它可以attend to的范围。然后unsqueeze(-2)把把src_mask变成(48/batch, 1, 20/time)。它的用法参考前面的attention函数。
对于训练来说(Teaching Forcing模式)，Decoder有一个输入和一个输出。比如句子”<sos> it is a good day <eos>”，输入会变成”<sos> it is a good day”，而输出为”it is a good day <eos>”。对应到代码里，self.trg就是输入，而self.trg_y就是输出。接着对输入self.trg进行mask，使得Self-Attention不能访问未来的输入。这是通过make_std_mask函数实现的，这个函数会调用我们之前详细介绍过的subsequent_mask函数。最终得到的trg_mask的shape是(48/batch, 24, 24)，表示24个时刻的Mask矩阵，这是一个对角线以及之下都是1的矩阵，前面已经介绍过了。
注意src_mask的shape是(batch, 1, time)，而trg_mask是(batch, time, time)。因为src_mask的每一个时刻都能attend to所有时刻(padding的除外)，一次只需要一个向量就行了，而trg_mask需要一个矩阵。
训练的代码就非常简单了，下面是训练一个Epoch的代码：
def run_epoch(data_iter, model, loss_compute):
start = time.time()
total_tokens = 0
total_loss = 0
tokens = 0
for i, batch in enumerate(data_iter):
out = model.forward(batch.src, batch.trg, batch.src_mask, batch.trg_mask)
loss = loss_compute(out, batch.trg_y, batch.ntokens)
total_loss += loss
total_tokens += batch.ntokens
tokens += batch.ntokens
if i % 50 == 1:
elapsed = time.time() - start
print("Epoch Step: %d Loss: %f Tokens per Sec: %f" %
(i, loss / batch.ntokens, tokens / elapsed))
start = time.time()
tokens = 0
return total_loss / total_tokens
它遍历一个epoch的数据，然后调用forward，接着用loss_compute函数计算梯度，更新参数并且返回loss。这里的loss_compute是一个函数，它的输入是模型的预测out，真实的标签序列batch.trg_y和batch的词个数。实际的实现是MultiGPULossCompute类，这是一个callable。本来计算损失和更新参数比较简单，但是这里为了实现多GPU的训练，这个类就比较复杂了。
到此我们介绍了Transformer最核心的算法，这个代码还包含了Label Smoothing，BPE等技巧，有兴趣的读者可以自行阅读，本书就不介绍了。
- 显示Disqus评论(需要科学上网)