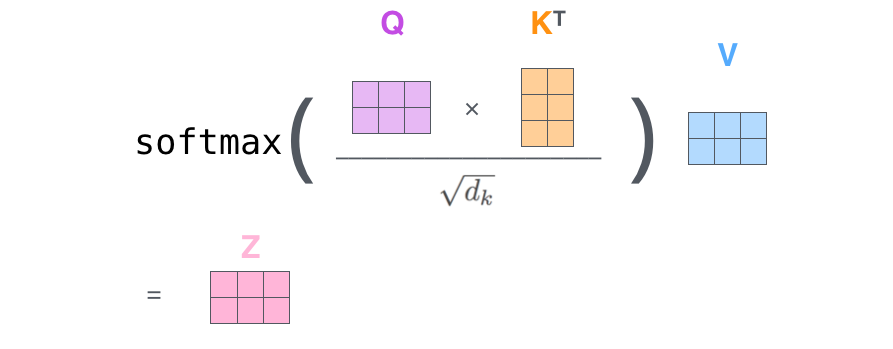本文用图解的方式介绍Transformer模型的基本原理。
目录
概述
Transformer模型来自论文Attention Is All You Need。这个模型最初是为了提高机器翻译的效率，它的Self-Attention机制和Position Encoding可以替代RNN。因为RNN是顺序执行的，t时刻没有完成就不能处理t+1时刻，因此很难并行。但是后来发现Self-Attention效果很好，在很多其它的地方也可以使用Transformer模型。这包括著名的OpenAI GPT和BERT模型，都是以Transformer为基础的。当然它们只使用了Transformer的Decoder部分，由于没有了Encoder，所以Decoder只有Self-Attention而没有普通的Attention。
我们通过图解的方式来直观的理解Transformer模型的基本原理，这部分内容主要参考了文章The Illustrated Transformer。
模型概览
我们首先把模型看成一个黑盒子，如下图所示，对于机器翻译来说，它的输入是源语言(法语)的句子，输出是目标语言(英语)的句子。
图：Transformer的输入和输出
把黑盒子稍微打开一点，Transformer(或者任何的NMT系统)都可以分成Encoder和Decoder两个部分，如下图所示。
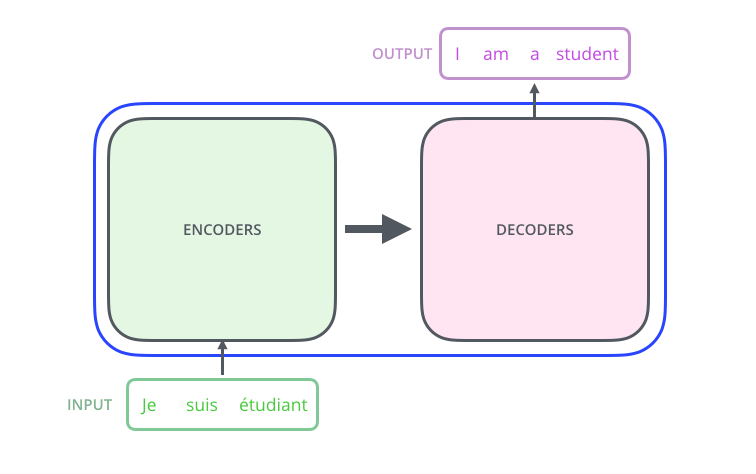图：Transformer的Encoder-Decoder结构
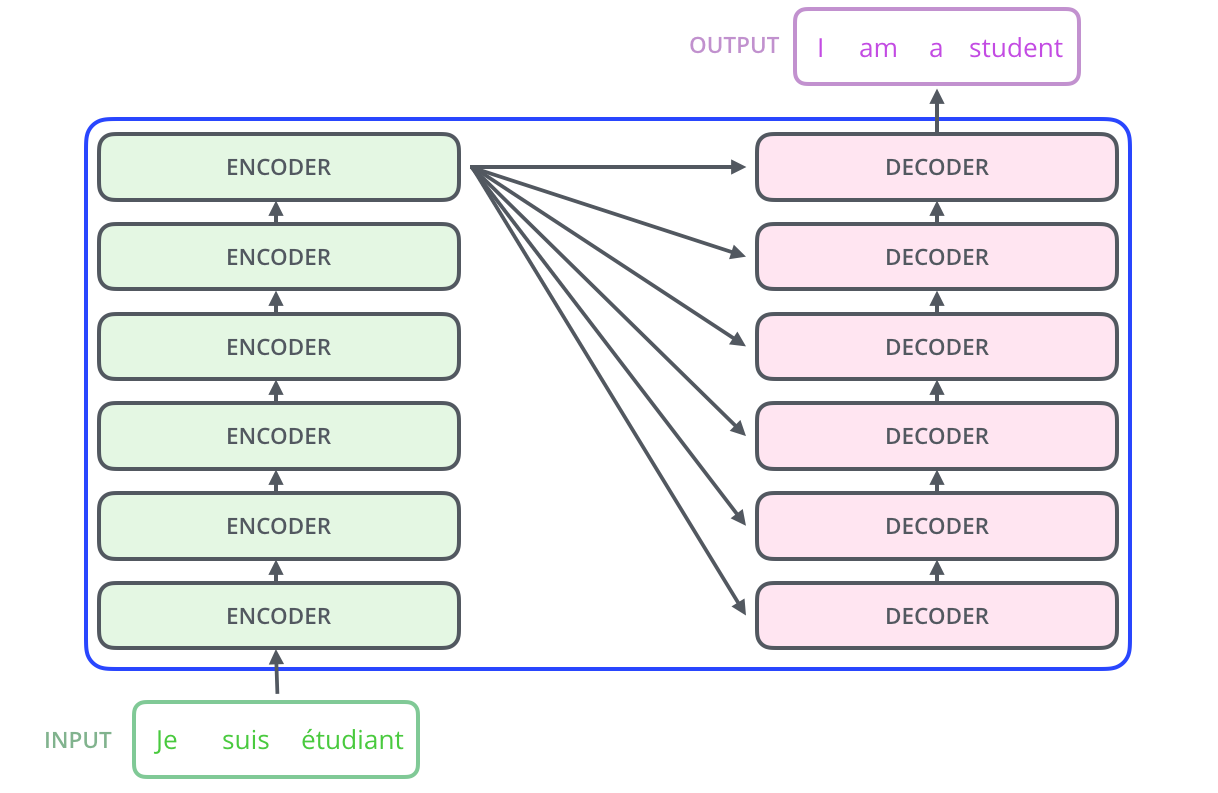
再展开一点，Encoder由很多(6个)结构一样的Encoder堆叠(stack)而成，Decoder也是一样。如下图所示。注意：每一个Encoder的输入是下一层Encoder输出，最底层Encoder的输入是原始的输入(法语句子)；Decoder也是类似，但是最后一层Encoder的输出会输入给每一个Decoder层，这是Attention机制的要求。
图：Stacked Encoder and Decoder
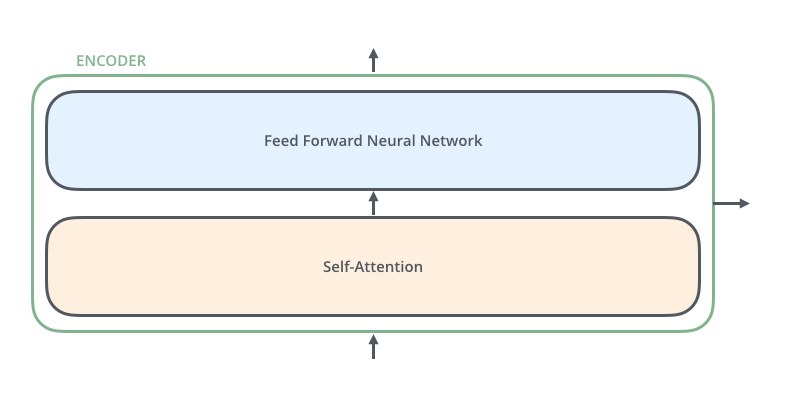
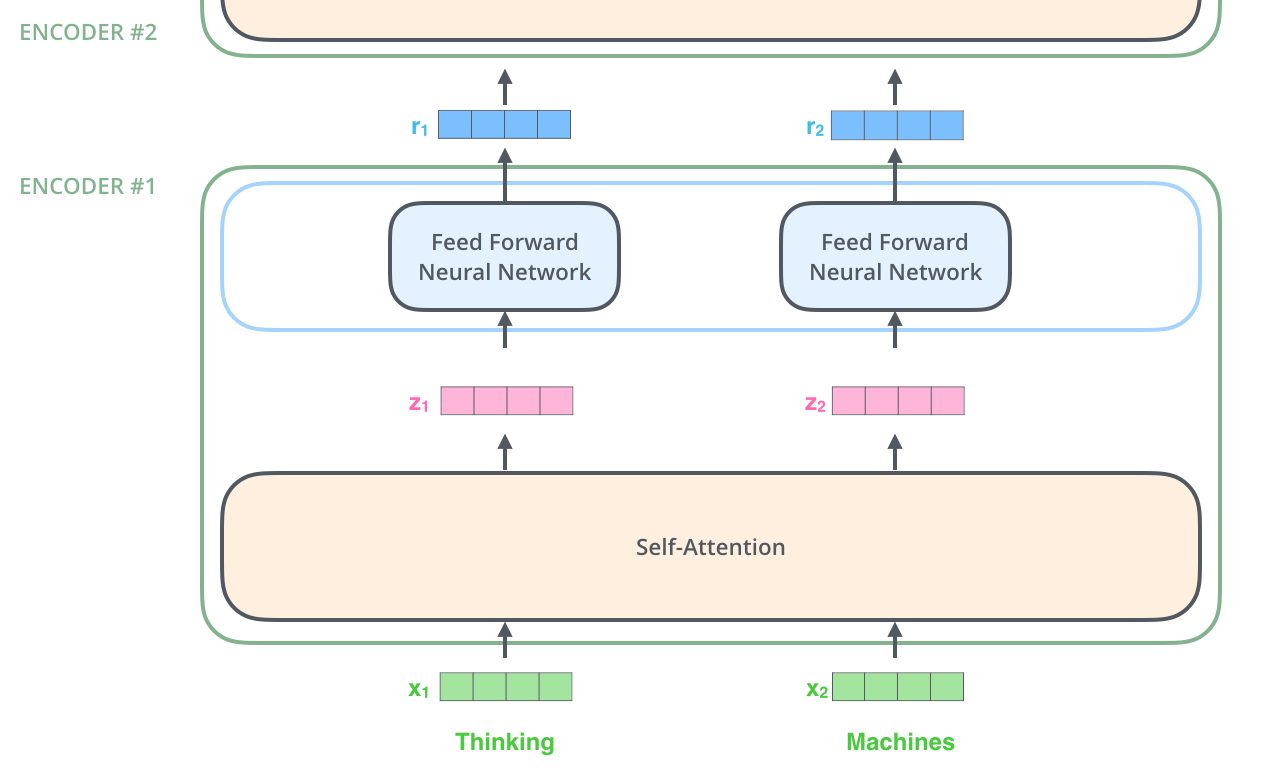
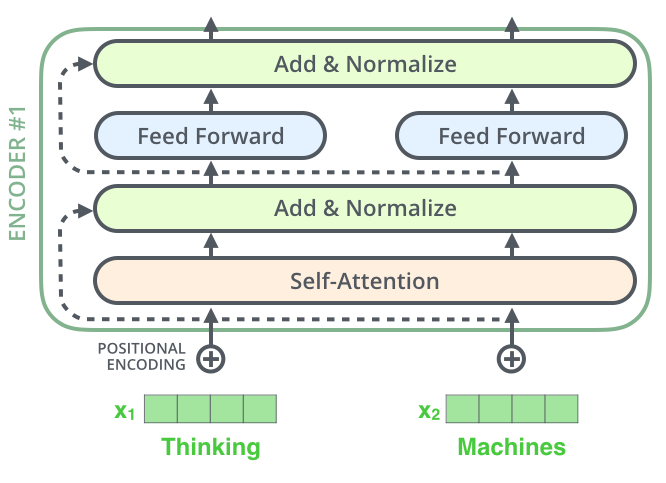
每一层的Encoder都是相同的结构，它由一个Self-Attention层和一个前馈网络(全连接网络)组成，如下图所示。
图：Transformer的一个Encoder层
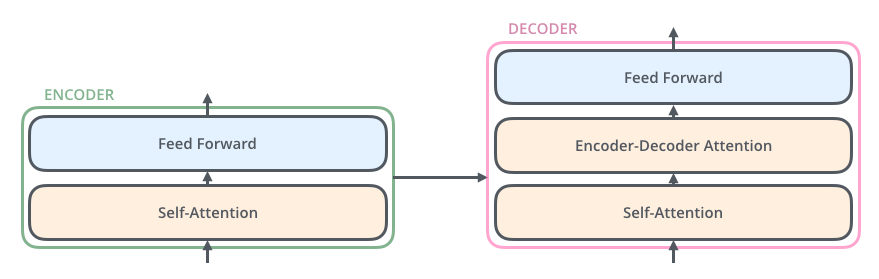
每一层的Decoder也是相同的结构，它除了Self-Attention层和全连接层之外还多了一个普通的Attention层，这个Attention层使得Decoder在解码时会考虑最后一层Encoder所有时刻的输出。它的结构如下图所示。
图：Transformer的一个Decoder层
加入Tensor
前面的图示只是说明了Transformer的模块，接下来我们加入Tensor，了解这些模块是怎么串联起来的。输入的句子是一个词(ID)的序列，我们首先通过Embedding把它变成一个连续稠密的向量，如下图所示。
图：Emebdding层
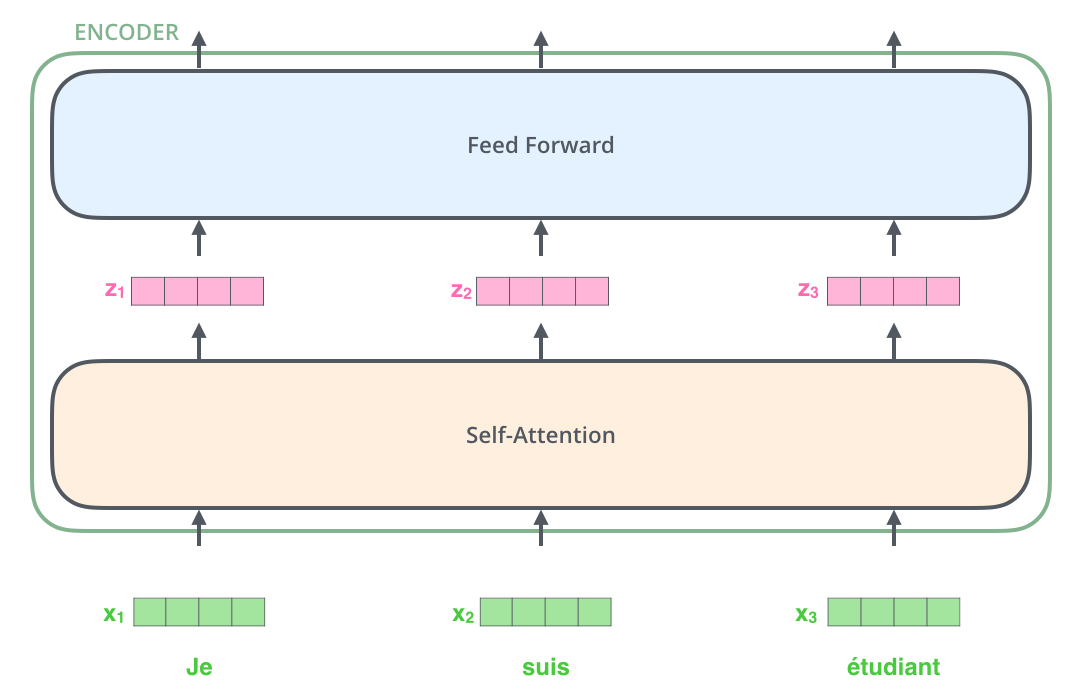
Embedding之后的序列会输入Encoder，首先经过Self-Attention层然后再经过全连接层，如下图所示。
图：带Tensor的Emebdding层
我们在计算$z_i$时需要依赖所有时刻的输入$x_1,…,x_n$，不过我们可以用矩阵运算一下子把所有的$z_i$计算出来(后面介绍)。而全连接网络的计算则完全是独立的，计算i时刻的输出只需要输入$z_i$就足够了，因此很容易并行计算。下图更加明确的表达了这一点。图中Self-Attention层是一个大的方框，表示它的输入是所有的$x_1,…,x_n$，输出是$z_1,…,z_n$。而全连接层每个时刻是一个方框(但不同时刻的参数是共享的)，表示计算$r_i$只需要$z_i$。此外，前一层的输出$r_1,…,r_n$直接输入到下一层。
图：带Tensor的Emebdding层2
Self-Attention简介
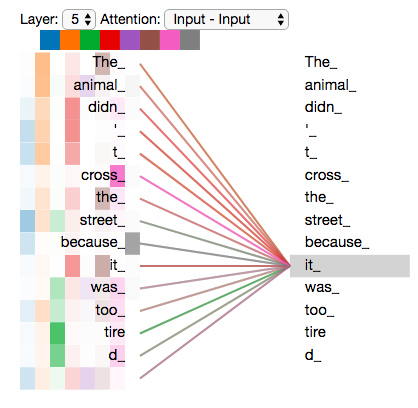
比如我们要翻译如下句子”The animal didn’t cross the street because it was too tired”(这个动物无法穿越马路，因为它太累了)。这里的it到底指代什么呢，是animal还是street？要知道具体的指代，我们需要在理解it的时候同时关注所有的单词，重点是animal、street和tired，然后根据知识(常识)我们知道只有animal才能tired，而street是不能tired的。Self-Attention用Encoder在编码一个词的时候会考虑句子中所有其它的词，从而确定怎么编码当前词。如果把tired换成narrow，那么it就指代的是street了。
而LSTM(即使是双向的)是无法实现上面的逻辑的。为什么呢？比如前向的LSTM，我们在编码it的时候根本没有看到后面是tired还是narrow，所有它无法把it编码成哪个词。而后向的LSTM呢？当然它看到了tired，但是到it的时候它还没有看到animal和street这两个单词，当然就更无法编码it的内容了。
当然多层的LSTM理论上是可以编码这个语义的，它需要下层的LSTM同时编码了animal和street以及tired三个词的语义，然后由更高层的LSTM来把it编码成animal的语义。但是这样模型更加复杂。
下图是模型的最上一层(下标0是第一层，5是第六层)Encoder的Attention可视化图。这是tensor2tensor这个工具输出的内容。我们可以看到，在编码it的时候有一个Attention Head(后面会讲到)注意到了Animal，因此编码后的it有Animal的语义。
图：Self-Attention的可视化
Self-Attention详细介绍
下面我们详细的介绍Self-Attention是怎么计算的，首先介绍向量的形式逐个时刻计算，这便于理解，接下来我们把它写出矩阵的形式一次计算所有时刻的结果。
对于输入的每一个向量(第一层是词的Embedding，其它层是前一层的输出)，我们首先需要生成3个新的向量Q、K和V，分别代表查询(Query)向量、Key向量和Value向量。Q表示为了编码当前词，需要去注意(attend to)其它(其实也包括它自己)的词，我们需要有一个查询向量。而Key向量可以认为是这个词的关键的用于被检索的信息，而Value向量是真正的内容。
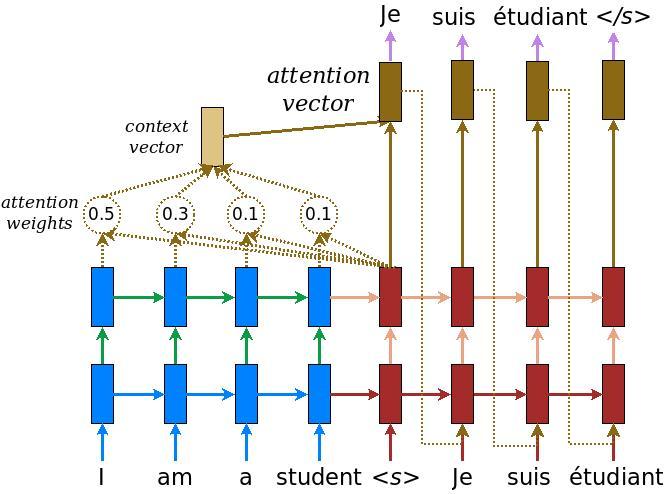
我们对比一下普通的Attention(Luong 2015)，使用内积计算energy的情况。如下图所示，在这里，每个向量的Key和Value向量都是它本身，而Q是当前隐状态$h_t$，计算energy $e_tj$的时候我们计算Q($h_t$)和Key($\bar{h}_j$)。然后用softmax变成概率，最后把所有的$\bar{h}_j$加权平均得到context向量。
而Self-Attention里的Query不是隐状态，并且来自当前输入向量本身，因此叫作Self-Attention。另外Key和Value都不是输入向量，而是输入向量做了一下线性变换。当然理论上这个线性变换矩阵可以是Identity矩阵，也就是使得Key=Value=输入向量。因此可以认为普通的Attention是这里的特例。这样做的好处是模型可以根据数据从输入向量中提取最适合作为Key(可以看成一种索引)和Value的部分。类似的，Query也是对输入向量做一下线性变换，它让系统可以根据任务学习出最适合的Query，从而可以注意到(attend to)特定的内容。
图：普通的Attention机制
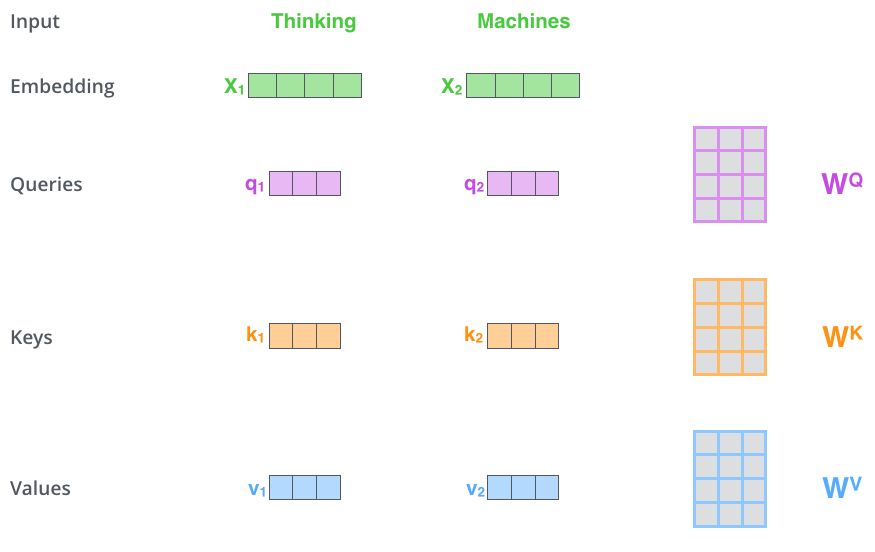
具体的计算过程如下图所示。比如图中的输入是两个词”thinking”和”machines”，我们对它们进行Embedding(这是第一层，如果是后面的层，直接输入就是向量了)，得到向量$x_1,x_2$。接着我们用3个矩阵分别对它们进行变换，得到向量$q_1,k_1,v_1$和$q_2,k_2,v_2$。比如$q_1=x_1 W^Q$，图中$x_1$的shape是1x4，$W^Q$是4x3，得到的$q_1$是1x3。其它的计算也是类似的，为了能够使得Key和Query可以内积，我们要求$W^K$和$W^Q$的shape是一样的，但是并不要求$W^V$和它们一定一样(虽然实际论文实现是一样的)。
图：K、V和Q的计算过程
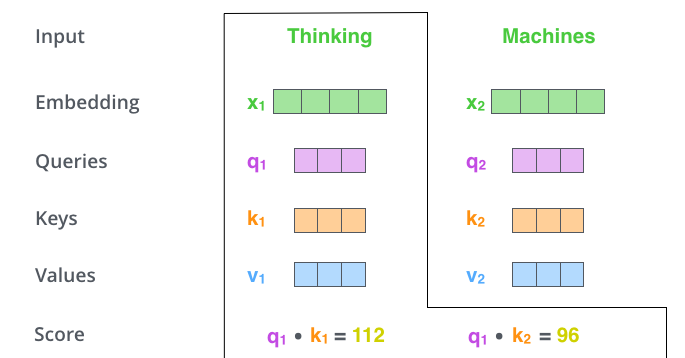
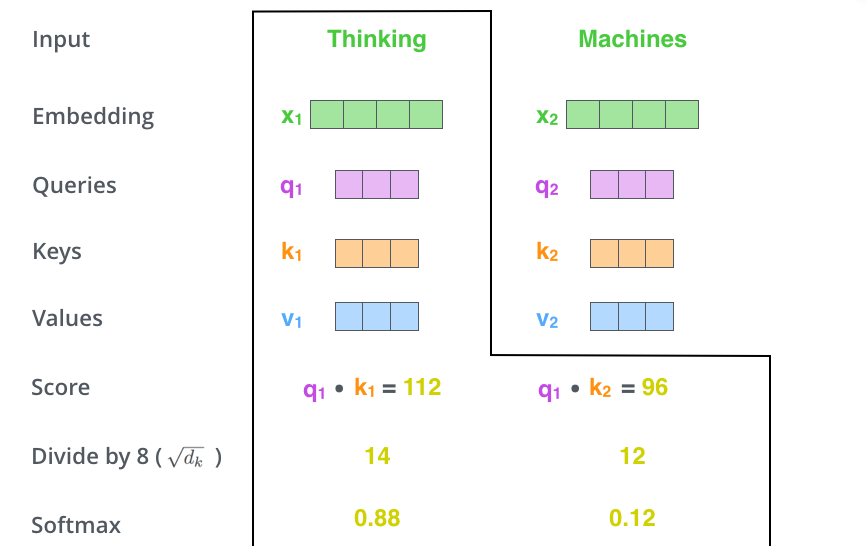
每个时刻t都计算出$Q_t,K_t,V_t$之后，我们就可以来计算Self-Attention了。以第一个时刻为例，我们首先计算$q_1$和$k_1,k_2$的内积，得到score，过程如下图所示。
图：Self-Attention的向量计算步骤一
接下来使用softmax把得分变成概率，注意这里把得分除以8$(\sqrt{d_k})$之后再计算的softmax，根据论文的说法，这样计算梯度时会更加稳定(stable)。计算过程如下图所示。
图：Self-Attention的向量计算步骤二
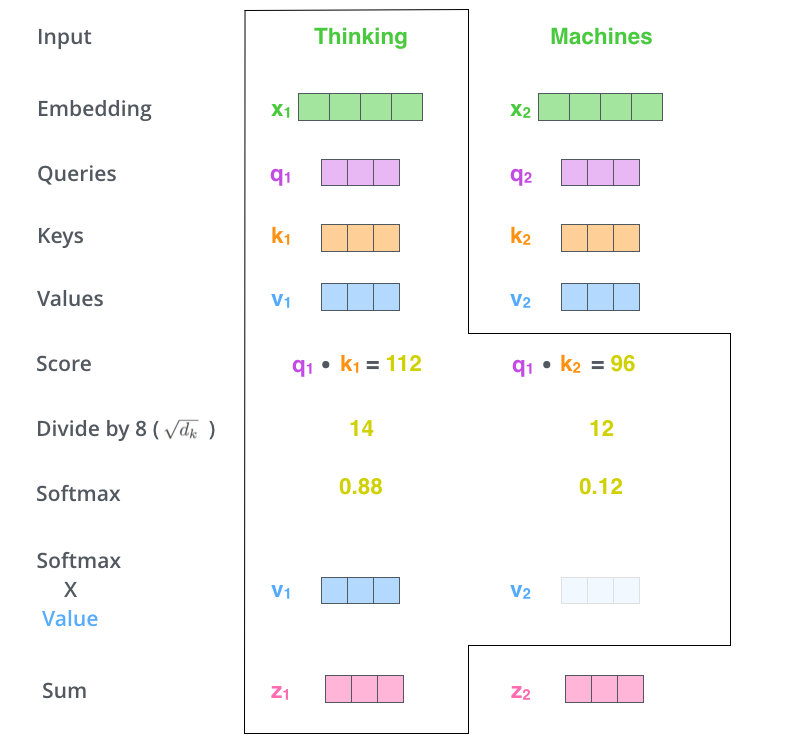
接下来用softmax得到的概率对所有时刻的V求加权平均，这样就可以认为得到的向量根据Self-Attention的概率综合考虑了所有时刻的输入信息，计算过程如下图所示。
图：Self-Attention的向量计算步骤三
这里只是演示了计算第一个时刻的过程，计算其它时刻的过程是完全一样的。
矩阵计算
前面介绍的方法需要一个循环遍历所有的时刻t计算得到$z_t$，我们可以把上面的向量计算变成矩阵的形式，从而一次计算出所有时刻的输出，这样的矩阵运算可以充分利用硬件资源(包括一些软件的优化)，从而效率更高。
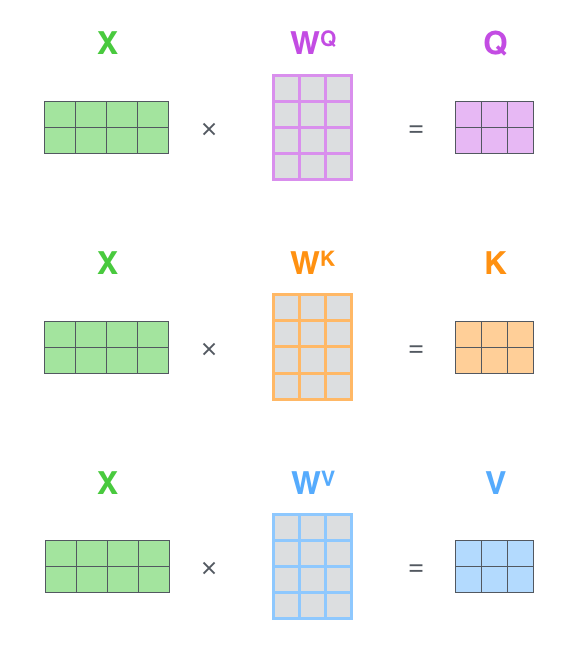
第一步还是计算Q、K和V，不过不是计算某个时刻的$q_t,k_t,v_t$了，而是一次计算所有时刻的Q、K和V。计算过程如下图所示。这里的输入是一个矩阵，矩阵的第i行表示第i个时刻的输入$x_i$。
图：Self-Attention的矩阵计算步骤一
接下来就是计算Q和K得到score，然后除以$(\sqrt{d_k})$，然后再softmax，最后加权平均得到输出。全过程如下图所示。
图：Self-Attention的矩阵计算步骤二
Multi-Head Attention
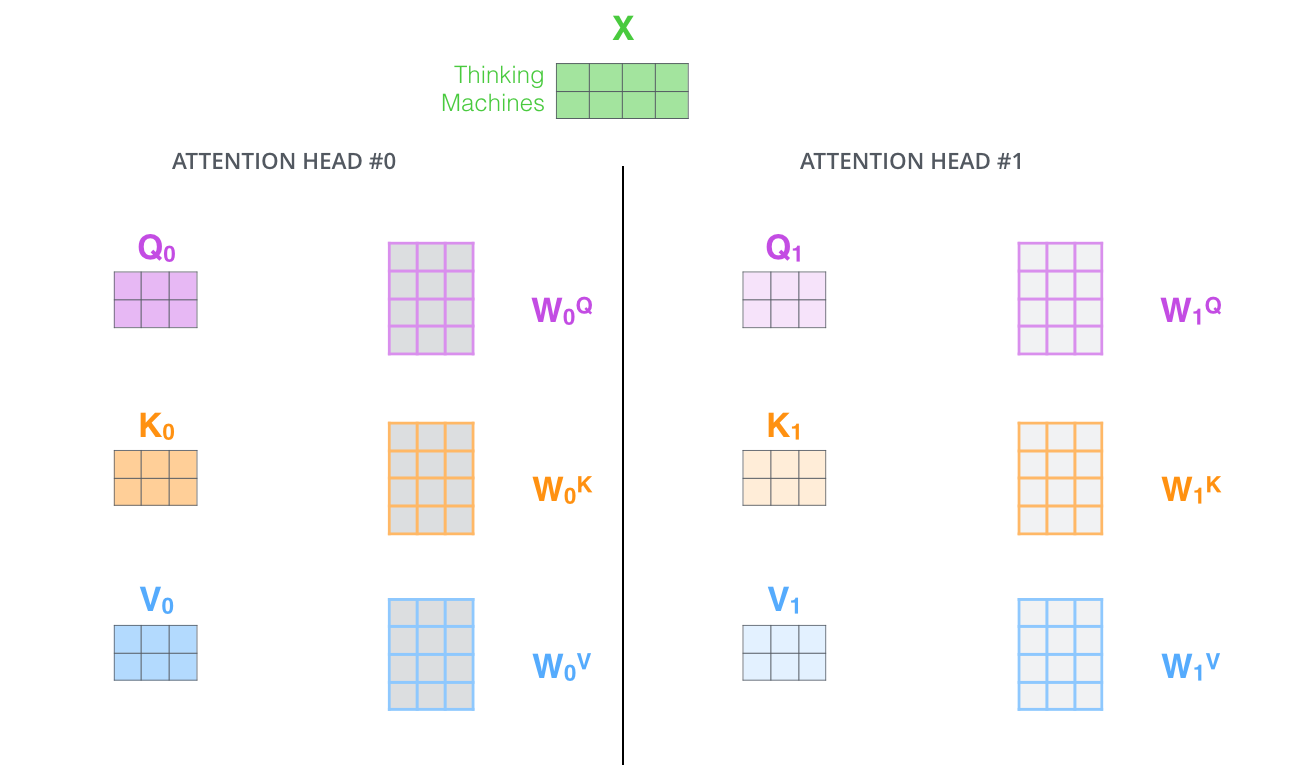
这篇论文还提出了Multi-Head Attention的概念。其实很简单，前面定义的一组Q、K和V可以让一个词attend to相关的词，我们可以定义多组Q、K和V，它们分别可以关注不同的上下文。计算Q、K和V的过程还是一样，这不过现在变换矩阵从一组$(W^Q,W^K,W^V)$变成了多组$(W^Q_0,W^K_0,W^V_0)$ ，$(W^Q_1,W^K_1,W^V_1)$，…。如下图所示。
图：Multi-Head计算多组Q、K和V
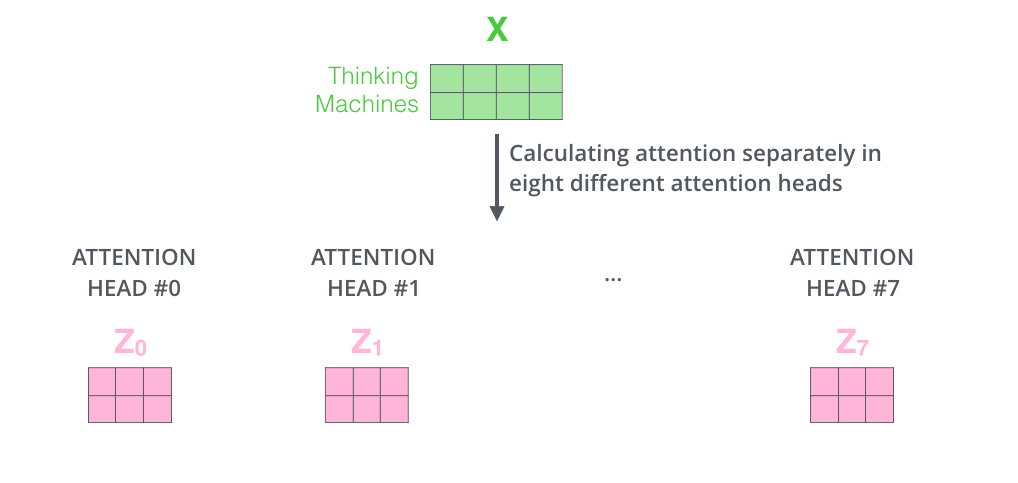
对于输入矩阵(time_step, num_input)，每一组Q、K和V都可以得到一个输出矩阵Z(time_step, num_features)。如下图所示。
图：Multi-Head计算输出多个Z
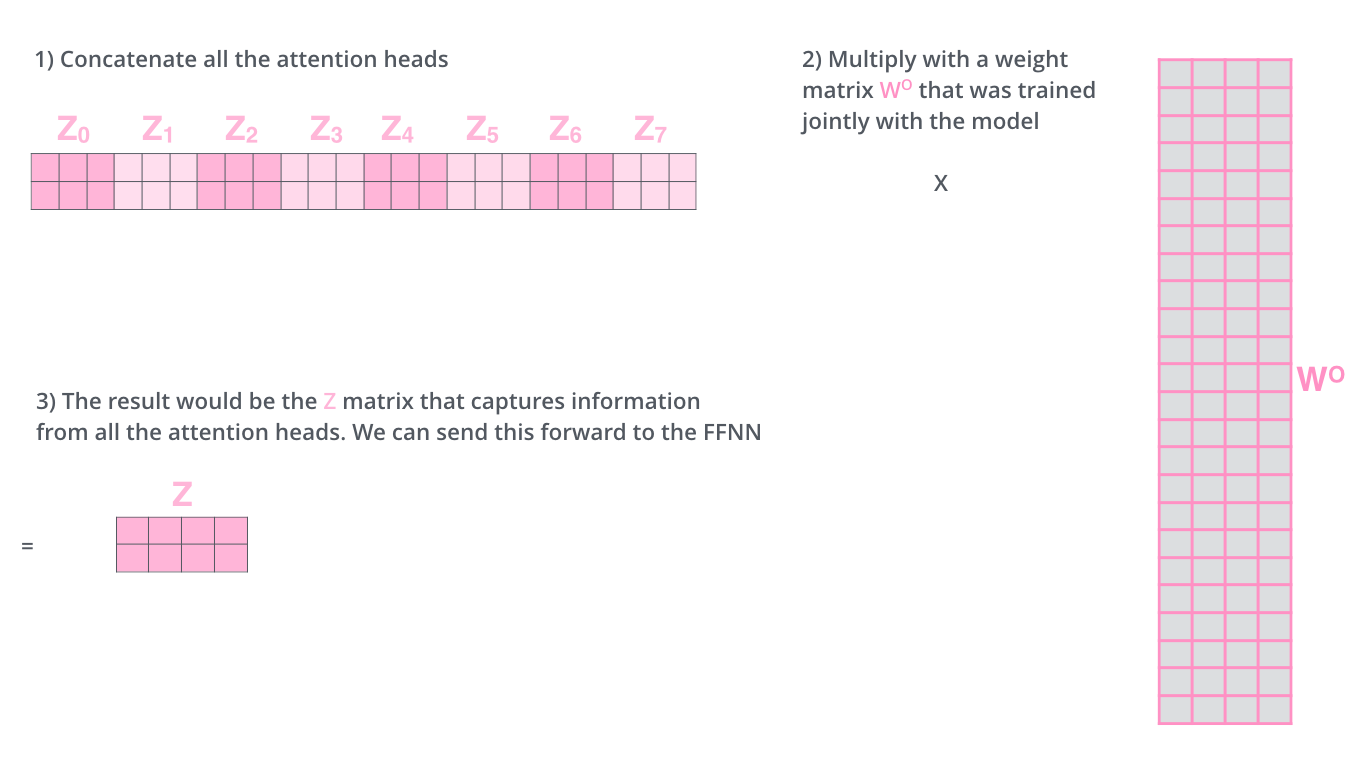
但是后面的全连接网络需要的输入是一个矩阵而不是多个矩阵，因此我们可以把多个head输出的Z按照第二个维度拼接起来，但是这样的特征有一些多，因此Transformer又用了一个线性变换(矩阵$W^O$)对它进行了压缩。这个过程如下图所示。
图：Multi-Head输出的拼接压缩
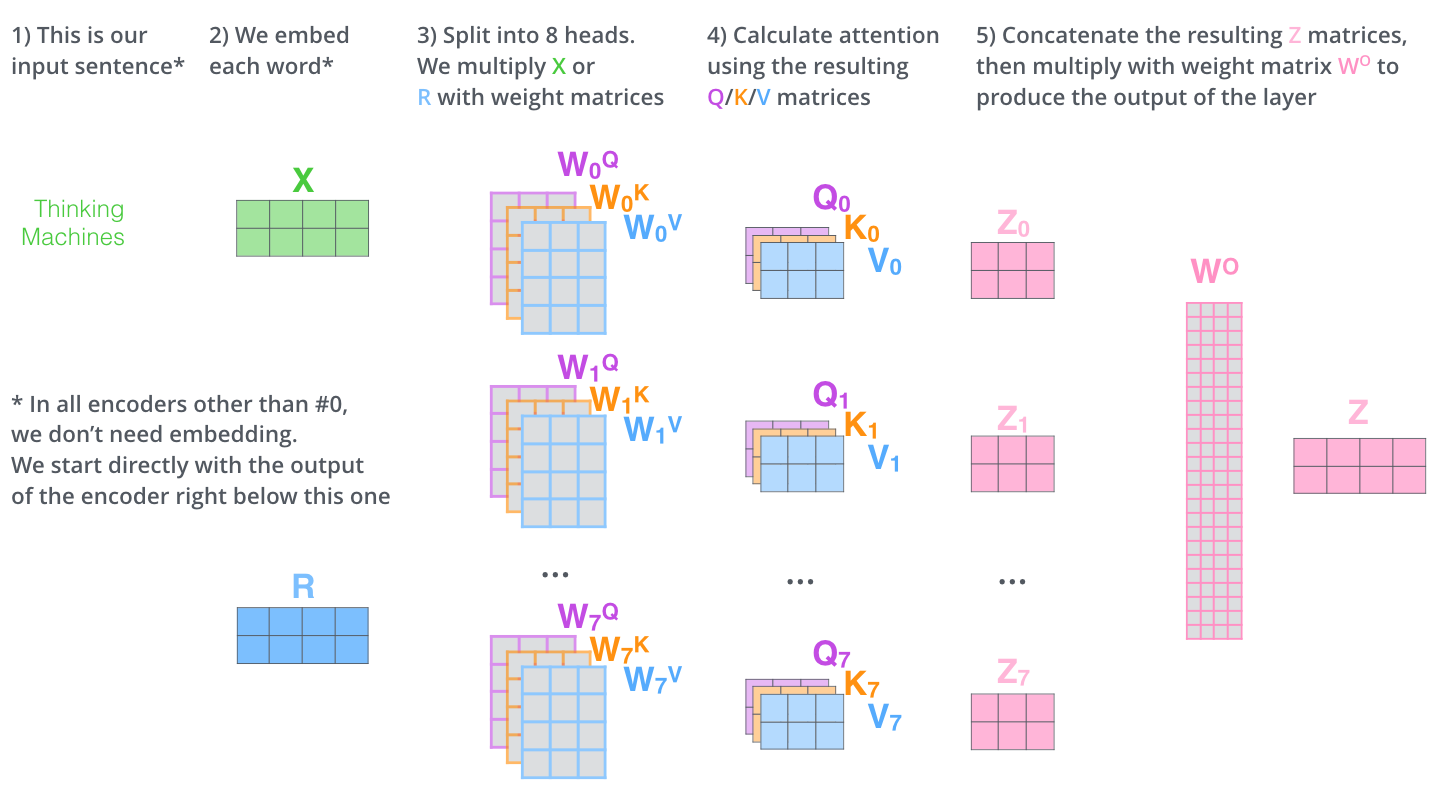
上面的步骤涉及很多步骤和矩阵运算，我们用一张大图把整个过程表示出来，如下图所示。
图：Multi-Head计算完整过程
我们已经学习了Transformer的Self-Attention机制，下面我们通过一个具体的例子来看看不同的Attention Head到底学习到了什么样的语义。
下图所示，那么就很难理解它到底注意的是什么内容。从上面两图的对比也能看出使用多个Head的好处——每个Head(在数据的驱动下)学习到不同的语义。
图：一个Head的语义
图：另一个Head的语义
位置编码(Positional Encoding)
注意：这是Transformer原始论文使用的位置编码方法，而在BERT模型里，使用的是简单的可以学习的Embedding，和Word Embedding一样，只不过输入是位置而不是词而已。
我们的目的是用Self-Attention替代RNN，RNN能够记住过去的信息，这可以通过Self-Attention“实时”的注意相关的任何词来实现等价(甚至更好)的效果。RNN还有一个特定就是能考虑词的顺序(位置)关系，一个句子即使词完全是相同的但是语义可能完全不同，比如”北京到上海的机票”与”上海到北京的机票”，它们的语义就有很大的差别。我们上面的介绍的Self-Attention是不考虑词的顺序的，如果模型参数固定了，上面两个句子的北京都会被编码成相同的向量。但是实际上我们可以期望这两个北京编码的结果不同，前者可能需要编码出发城市的语义，而后者需要包含目的城市的语义。而RNN是可以(至少是可能)学到这一点的。当然RNN为了实现这一点的代价就是顺序处理，很难并行。
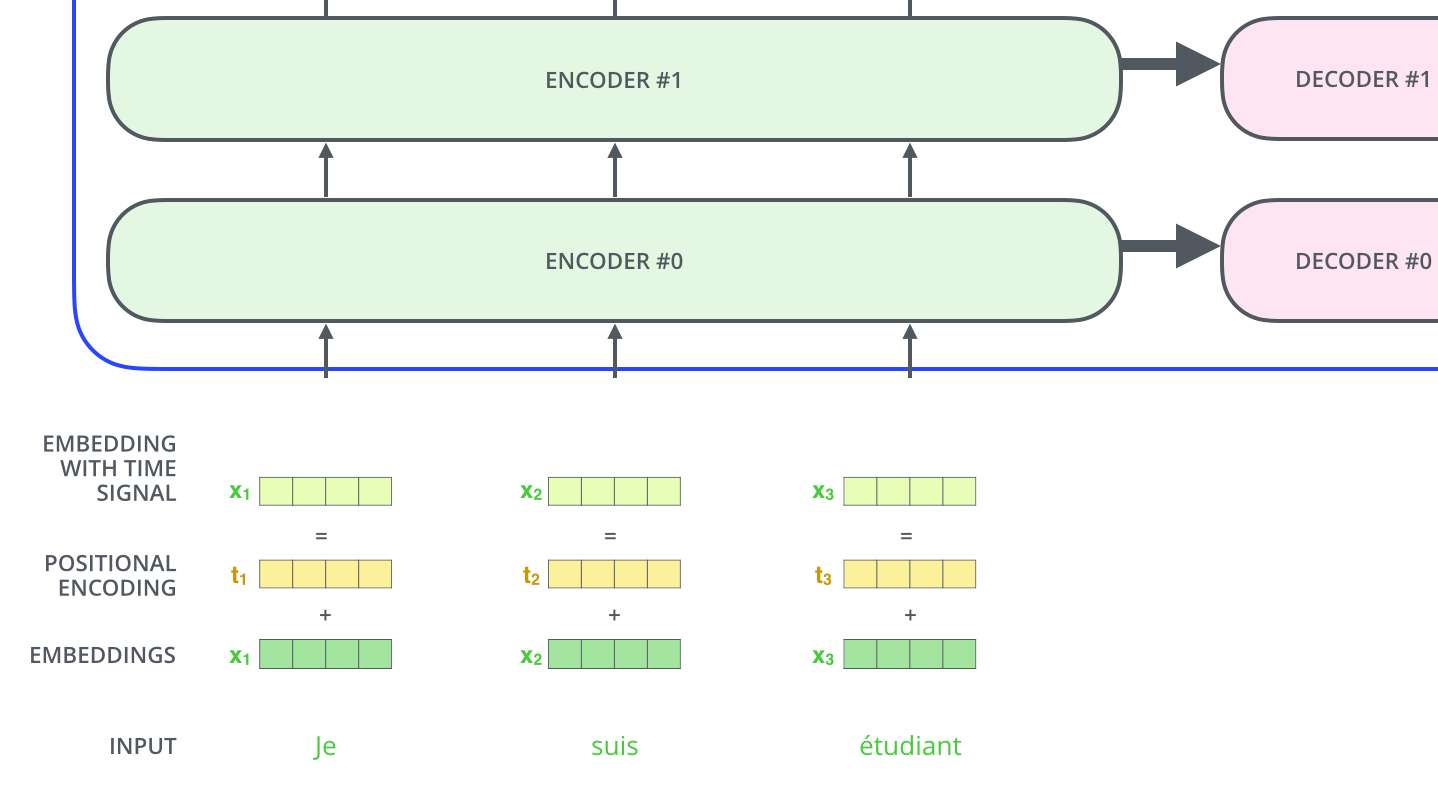
为了解决这个问题，我们需要引入位置编码，也就是t时刻的输入，除了Embedding之外(这是与位置无关的)，我们还引入一个向量，这个向量是与t有关的，我们把Embedding和位置编码向量加起来作为模型的输入。这样的话如果两个词在不同的位置出现了，虽然它们的Embedding是相同的，但是由于位置编码不同，最终得到的向量也是不同的。
位置编码有很多方法，其中需要考虑的一个重要因素就是需要它编码的是相对位置的关系。比如两个句子：”北京到上海的机票”和”你好，我们要一张北京到上海的机票”。显然加入位置编码之后，两个北京的向量是不同的了，两个上海的向量也是不同的了，但是我们期望Query(北京1)Key(上海1)却是等于Query(北京2)Key(上海2)的。具体的编码算法我们在代码部分再介绍。位置编码加入后的模型如下图所示。
图：位置编码
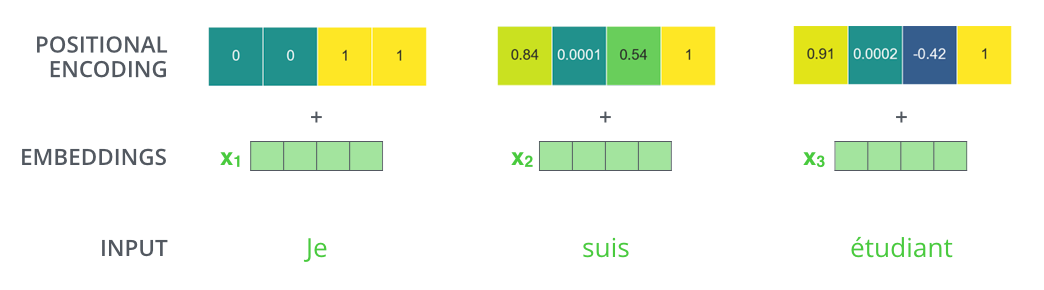
一个具体的位置编码的例子如下图所示。
图：位置编码的具体例子
后面在代码部分，我们还会详细介绍这种编码的特点。
LayerNorm
前面我们介绍过Batch Normalization，这个技巧能够让模型收敛的更快。但是Batch Normalization有一个问题——它需要一个minibatch的数据，而且这个minibatch不能太小(比如1)。另外一个问题就是它不能用于RNN，因为同样一个节点在不同时刻的分布是明显不同的。当然有一些改进的方法使得可以对RNN进行Batch Normalization，比如论文Recurrent Batch Normalization，有兴趣的读者可以自行阅读 。
Transformer里使用了另外一种Normalization技巧，叫做Layer Normalization。我们可以通过对比Layer Normalization和Batch Normalization来学习。
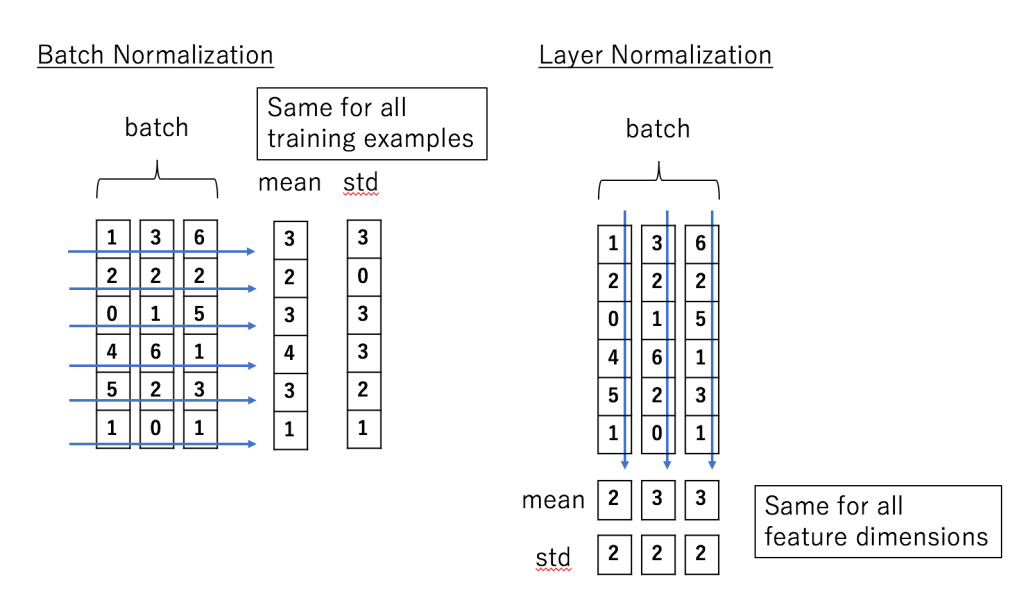
假设我们的输入是一个minibatch的数据，我们再假设每一个数据都是一个向量，则输入是一个矩阵，每一行是一个训练数据，每一列都是一个特征。BatchNorm是对每个特征进行Normalization，而LayerNorm是对每个样本的不同特征进行Normalization，因此LayerNorm的输入可以是一行(一个样本)。
如下图所示，输入是(3,6)的矩阵，minibatch的大小是3，每个样本有6个特征。BatchNorm会对6个特征维度分别计算出6个均值和方差，然后用这两个均值和方差来分别对6个特征进行Normalization，计算公式如下：
\[\begin{split} \mu_j &=\frac{1}{m}\sum_{i=1}^{m}x_{ij} \\ \sigma_j^2 & = \frac{1}{m}\sum_{i=1}^{m}(x_{ij}-\mu_j)^2 \\ \hat{x}_{ij} & =\frac{x_{ij}-\mu_j}{\sqrt{\sigma_j^2+\epsilon}} \end{split}\]而LayerNorm是分别对3个样本的6个特征求均值和方差，因此可以得到3个均值和方差，然后用这3个均值和方差对3个样本来做Normalization，计算公式如下：
\[\begin{split} \mu_i &=\frac{1}{n}\sum_{j=1}^{n}x_{ij} \\ \sigma_i^2 & = \frac{1}{m}\sum_{j=1}^{m}(x_{ij}-\mu_i)^2 \\ \hat{x}_{ij} & =\frac{x_{ij}-\mu_i}{\sqrt{\sigma_i^2+\epsilon}} \end{split}\]
图：BatchNorm vs LayerNorm
因为LayerNorm的每个样本都是独立计算的，因此minibatch可以很小甚至可以是1。实验证明LayerNorm不仅在普通的神经网络中有效，而且对于RNN也非常有效。
BatchNorm看起来比较直观，我们在数据预处理也经常会把输入Normalize成均值为0，方差为1的数据，只不过它引入了可以学习的参数使得模型可以更加需要重新缓慢(不能剧烈)的调整均值和方差。而LayerNorm似乎有效奇怪，比如第一个特征是年龄，第二个特征是身高，把一个人的这两个特征求均值和方差似乎没有什么意义。论文里有一些讨论，都比较抽象。当然把身高和年龄平均并没有什么意义，但是对于其它层的特征，我们通过平均”期望”它们的取值范围大体一致，也可能使得神经网络调整参数更加容易，如果这两个特征实在有很大的差异，模型也可以学习出合适的参数让它来把取值范围缩放到更合适的区间。
残差连接
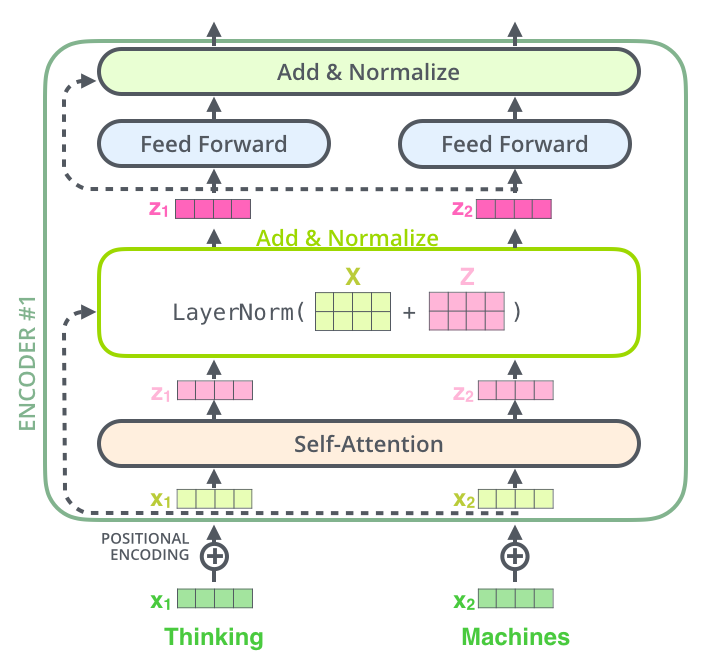
每个Self-Attention层都会加一个残差连接，然后是一个LayerNorm层，如下图所示。
图：残差和Layer Normalization
下图展示了更多细节：输入$x_1,x_2$经self-attention层之后变成$z_1,z_2$，然后和残差连接的输入$x_1,x_2$加起来，然后经过LayerNorm层输出给全连接层。全连接层也是有一个残差连接和一个LayerNorm层，最后再输出给上一层。
图：残差和Layer Normalization细节
Decoder和Encoder是类似的，如下图所示，区别在于它多了一个Encoder-Decoder Attention层，这个层的输入除了来自Self-Attention之外还有Encoder最后一层的所有时刻的输出。Encoder-Decoder Attention层的Query来自下一层，而Key和Value则来自Encoder的输出。
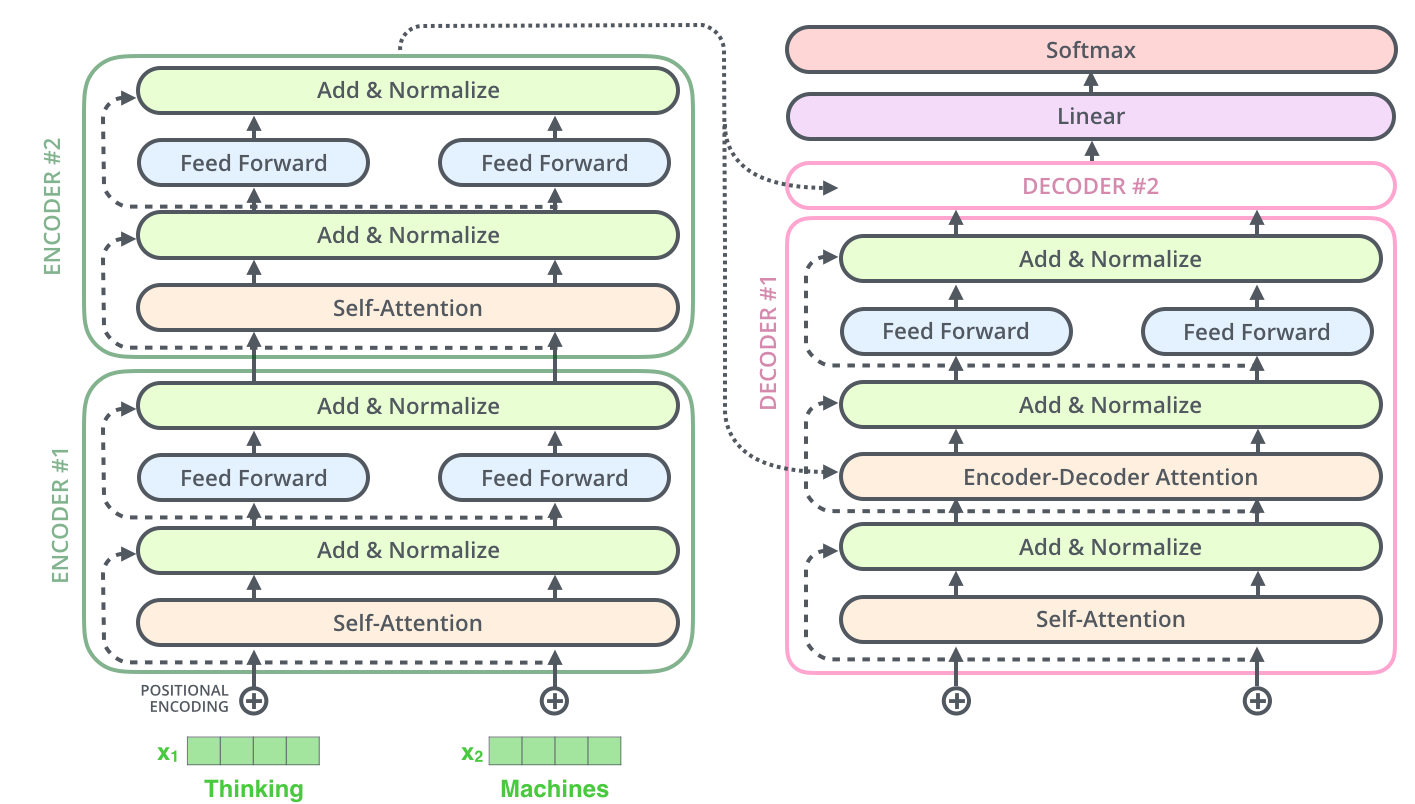图：Decoder的残差和Layer Normalization
- 显示Disqus评论(需要科学上网)