GraphCast: Learning skillful medium-range global weather forecasting

本文是论文GraphCast: Learning skillful medium-range global weather forecasting的解读。

目录

• Abstract
• Introduction
• GraphCast
• 验证方法
• 预测验证结果
• 严重天气事件预测结果
• 严重天气事件预测结果
  • 热带气旋轨迹
  • 大气河流
  • 极端高温和低温
• 训练数据新旧的影响
• 结论
• 数据和材料可用性
• 补充材料
• 1. 数据集
  • 1.1. ERA5
  • 1.2. HRES
  • 1.3. 热带气旋数据集
• 2 符号和问题陈述
  • 2.1. 时间符号
  • 2.2. 一般预测问题陈述
  • 2.3. 建模ECMWF天气数据
• 3 GraphCast模型
  • 3.1. 生成预测
  • 3.2. 架构概述
  • 3.3. GraphCast的图
  • 3.4. 编码器
  • 3.5. 处理器
  • 3.6. 解码器
  • 3.7. 标准化和网络参数化
• 4 训练细节
  • 4.1. 训练拆分
  • 4.2. 训练目标
  • 4.3. 自回归目标训练
  • 4.4. 优化
  • 4.5. 课程训练计划
  • 4.6. 减小内存占用
  • 4.7. 训练时间
  • 4.8. 软件和硬件堆栈
• 5 验证方法
  • 5.1. 训练、验证和测试拆分
  • 5.2. 将GraphCast与HRES进行比较
    • 5.2.1. Ground True数据集的选择
    • 5.2.2. 确保同化窗口具有相等的前瞻
    • 5.2.3. 初始化时间和有效时间的对齐
    • 5.2.4. 评估时期
  • 5.3. 评估指标
  • 5.4. 统计方法学
    • 5.4.1. 均值差异的显著性检验
• 6 与先前的机器学习基线比较

Abstract

全球中期天气预报对许多社会和经济领域的决策至关重要。传统的数值天气预测利用增加的计算资源来提高预测准确性，但无法直接利用历史天气数据来改进基础模型。我们引入了一种基于机器学习的方法，称为“GraphCast”，它可以直接从再分析数据中进行训练。该方法在全球范围内以0.25°分辨率在不到一分钟内预测了数百个天气变量，持续10天。我们展示了GraphCast在1380个验证目标中在90%的情况下明显优于最准确的操作性确定性系统，并且其预测支持更好的严重事件预测，包括热带气旋(tropical cyclones)、大气河流(atmospheric rivers)和极端温度。GraphCast是准确和高效的天气预测的重要进展，有助于实现机器学习在建模复杂动态系统方面的潜力。

Introduction

在2022年10月中旬，意大利博洛尼亚的时间是05:45 UTC，欧洲中期天气预报中心（ECMWF）的新高性能计算设施刚刚开始运行。在过去的几个小时里，集成预报系统（IFS）一直在运行复杂的计算，以预测未来几天甚至几周的地球天气，其第一批预测结果刚刚开始向用户传播。这个过程每六个小时重复一次，每天都会为世界提供最准确的天气预报。

IFS和现代天气预报总体上是科学和工程的胜利。天气系统的动力学是地球上最复杂的物理现象之一，每天个人、产业和决策者做出无数决策都取决于准确的天气预报，从是否穿夹克到是否逃离危险的风暴。如今，天气预报的主导方法是“数值天气预测”（NWP），涉及使用超级计算机解决天气的控制方程。NWP的成功在于通过严格而持续的研究实践提供对天气现象的日益详细的描述，以及NWP在更大的计算资源下实现更高准确性的能力。结果，天气预报的准确性年复一年地提高，以至于可以提前多天预测表面温度(surface temperature)或飓风路径，这在几十年前是不可想象的。

然而，尽管传统的NWP在计算方面扩展得很好，但其准确性并不随着历史数据的增加而提高。有大量的天气和气候(climatological)数据档案，例如ECMWF的MARS，但直到最近，很少有实际手段可以利用这些数据直接提高预测模型的质量。相反，NWP方法是通过高度训练有素的专业人员创新更好的模型、算法和近似值来改进的，这可能是一个耗时且昂贵的过程。

基于机器学习的天气预测（MLWP）提供了一种替代传统NWP的方法，其中预测模型直接从历史数据中进行训练。这有望通过捕捉数据中难以用明确方程表示的模式和尺度来提高预测准确性。MLWP还通过利用现代深度学习硬件而不是超级计算机，以及在速度和准确性之间取得更有利的平衡，提供了更高效的机会。最近，MLWP在传统NWP相对较弱的领域，例如亚季节性热浪(sub-seasonal heat wave)预测和从雷达(radar)图像进行的降水即时(precipitation nowcasting)预测方面取得了进展。在这些领域，准确的方程和稳健的数值方法并不容易获得。

在中期天气预报领域，即对未来10天内的大气(atmospheric)变量进行预测，像IFS这样基于NWP的系统仍然是最准确的。世界上最顶尖的确定性操作系统是ECMWF的High RESolution forecast（HRES），它是IFS的组成部分，以大约一个小时的时间生成全球10天的预报，分辨率为0.1°纬度/经度[27]。然而，在过去的几年里，基于MLWP的中期预测方法一直在稳步进步，得益于WeatherBench等基准。基于卷积神经网络[35, 36, 28]和Transformers[24]的深度学习架构在粗于1.0°的纬度/经度分辨率上已经显示出有希望的结果，而最近的研究则使用图神经网络（GNN）[11]、傅里叶神经算子[25, 14]和Transformers[4]，在1.0°和0.25°的分辨率下对一些变量和达到七天的前瞻期表现出接近IFS的性能。

表格1 GraphCast建模的天气变量和层次。列标题中括号中的数字表示该列中的条目数量。粗体的变量和层次表示这些变量和层次已包含在评分卡评估中。

GraphCast

在这里，我们介绍一种新的全球中期天气预测的机器学习方法，名为“GraphCast”。该方法在单个Google Cloud TPU v4设备上能够在不到一分钟内生成准确的10天预报，并支持诸如预测热带气旋路径、大气河流和极端温度等应用。

GraphCast的输入是地球天气的最近两个状态——当前时间和六小时之前的状态，并预测未来六小时的天气状态。一个天气状态由一个0.25°纬度/经度网格（721 × 1440）表示，在赤道大约对应于28 × 28千米的分辨率（图1a），其中每个网格点表示一组表面和大气变量（列在表1中）。与传统的数值天气预测系统一样，GraphCast是自回归的：可以通过将其自己的预测反馈为输入来“滚动”，生成任意长的天气状态轨迹（图1b–c）。

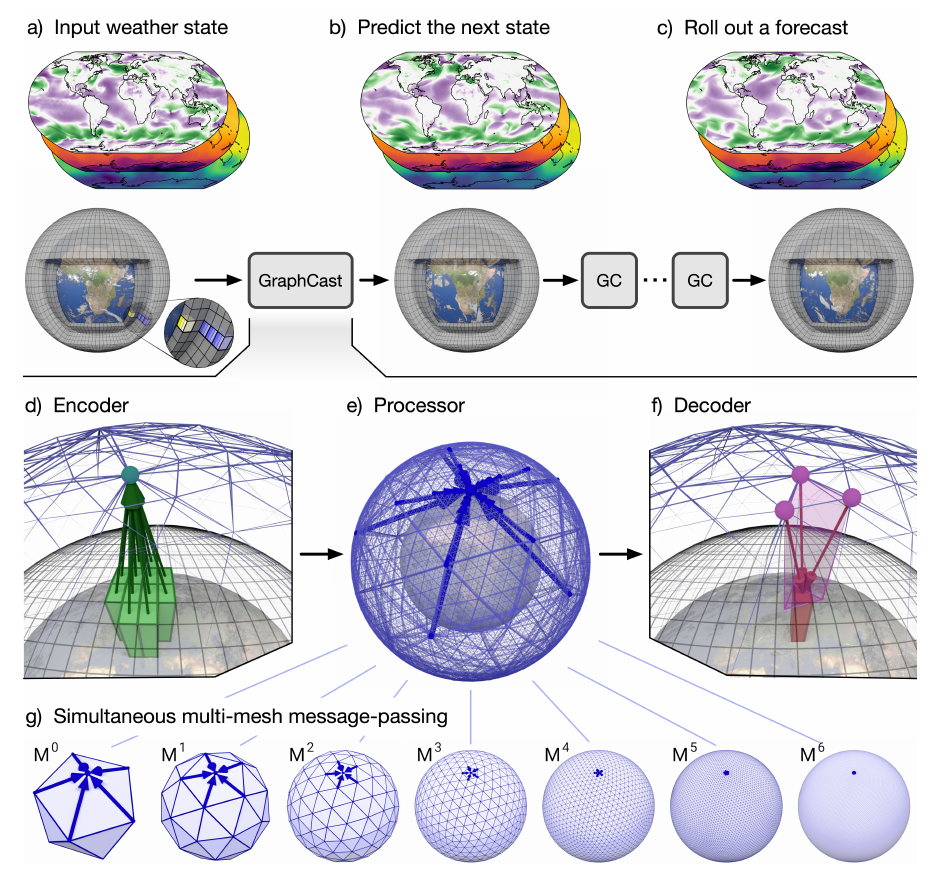图1 模型示意图。 (a) 输入的天气状态定义在一个0.25°纬度-经度网格上，总共包括721 × 1440 = 1,038,240个点。放大的弹出窗口中的黄色层表示5个表面变量，蓝色层表示在37个压力层重复的6个大气变量（每个点总共有5 + 6 × 37 = 227个变量），导致状态表示为235,680,480个值。 (b) GraphCast预测网格上的下一个天气状态。 (c) 通过迭代地将GraphCast应用于每个先前预测的状态，生成表示不同前瞻时段的状态序列，从而进行预测。 (d) GraphCast架构的编码器组件将输入的局部区域（绿色框）映射到多重网格(multi-mesh)图表示的节点（绿色，朝上的箭头终止在绿蓝色的节点上）。 (e) 处理器组件使用学到的消息传递（终止在节点上的重型蓝色箭头）更新每个多重网格节点。 (f) 解码器组件将处理后的多重网格特征（紫色节点）映射回网格表示（红色，朝下的箭头终止在红色框上）。 (g) 多重网格是从增加分辨率的正二十面体网格(icosahedral meshes)中导出的，从基础网格（$M^0$，12个节点）到最细分辨率（$M^6$，40,962个节点），其在全球范围内具有均匀分辨率。它包含来自$M^6$的节点集，以及从$M^0$到$M^6$的所有边。对不同网格边的学习消息传递同时发生，以便每个节点都由其所有传入的边更新。

GraphCast采用基于图神经网络（GNNs）的神经网络架构，采用“编码-处理-解码”配置[1]，总共包含3670万个参数。先前基于GNN的学习模拟器[31, 26]在学习由偏微分方程建模的流体和其他系统的复杂动态方面非常有效，这支持它们用于建模天气动力学的适用性。

编码器（图1d）使用单个GNN层将表示为节点属性的变量（标准化为零均值单位方差）映射为“多重网格”的内部表征——它们也用节点属性来表示。

多重网格（图1g）是一个具有高空间分辨率的空间均匀的图形。它是通过迭代六次细化正二十面体（12个节点，20个面，30条边）定义的，其中每次细化将每个三角形分成四个较小的三角形（导致四倍的面和边），然后将节点重新投影到球面上。多重网格包含来自最高分辨率网格的40,962个节点，以及在中间图形中创建的所有边的并集，形成具有不同长度的边的平坦层次结构。

处理器（图1e）使用16个不共享的GNN层在多重网格上执行学习的消息传递，实现了少量消息传递步骤的高效局部和长程信息传播。

解码器（图1f）将多重网格表示中最终处理器层的学习特征映射回纬度-经度网格。它使用单个GNN层，并将输出预测为相对于最近的输入状态的残差更新（通过输出标准化以实现目标残差的单位方差）。有关更多架构细节，请参见附录第3节。

在模型开发期间，我们使用了ECMWF的ERA5 [10]再分析存档中的39年（1979年至2017年）历史数据。作为训练目标，我们通过垂直层加权平均均方误差（MSE）。误差是在GraphCast的预测状态和相应的ERA5状态之间在N个自回归步骤上计算的。N的值逐渐从1增加到12（即，从六小时到三天）在训练过程中。GraphCast经过梯度下降和反向传播训练以最小化训练目标。在32个Cloud TPU v4设备上使用批并行处理，训练GraphCast大约花费了四周。有关更多培训细节，请参见附录第4节。

与实际部署场景一致，模型开发时未提供未来信息，我们在从2018年开始的保留数据上评估了GraphCast（请参见附录第5.1节）。

验证方法

我们通过将GraphCast的准确性与HRES在大量变量、层次和前瞻时段上的准确性进行全面比较来全面验证其预测技能。我们使用两个技能指标来量化GraphCast、HRES和机器学习基线的各自技能水平：均方根误差（RMSE）和异常相关系数（ACC）。

在GraphCast每个网格点预测的227个变量和层次组合中，我们评估了其在其中的69个【5+13层*5变量/层】上对HRES的技能，对应于WeatherBench [27]的13个层次和ECMWF Scorecard [9]的变量；请参见表1中的粗体变量和层次，以及附录第1.2节，其中HRES周期在评估期间处于运行状态。请注意，我们在评估中排除了总降水，因为ERA5降水数据存在已知偏差 [15]。除了主文中报告的总体性能外，附录第7节提供了进一步的详细评估，包括其他变量、区域性能、纬度和压力层影响、谱特性(spectral properties)、模糊效应(blurring)、与其他基于机器学习的预测的比较以及模型设计选择的影响。

在进行这些比较时，建立技能的两个关键选择包括：（1）用于比较的基准真值的选择，以及（2）对用于将数据与观测数据进行匹配的数据同化窗口(data assimilation windows)的仔细核算。我们使用ERA5作为评估GraphCast的基准真值，因为它是经过训练的，以将ERA5数据作为输入并预测ERA5数据作为输出。然而，评估HRES的预报是否与ERA5的预报相符会导致初始预报步骤上的非零误差。相反，我们构建了一个“HRES在步骤0的预报”（HRES-fc0）数据集，用作HRES的基准真值。HRES-fc0包含了HRES预报在未来初始化时的输入（请参见附录第1.2节），确保每个数据点都通过最近的观测数据进行匹配，并且HRES预报的零步骤将具有零误差。

方法之间的公平比较要求任何一种方法都不应具有其他方法无法获得的特权信息。由于天气预报数据的性质，这需要仔细控制ERA5和HRES数据同化窗口之间的差异。每天，HRES使用以00z、06z、12z和18z为中心的四个+/-3小时的窗口同化观测数据（其中18z表示18:00 UTC），而ERA5使用以00z和12z为中心的两个+9小时/-3小时的窗口，或等效地使用以06z和18z为中心的两个+3小时/-9小时的窗口。我们选择评估GraphCast的预报是从06z和18z的初始化开始的，确保其输入携带来自未来观测的+3小时的信息，与HRES的输入相匹配。我们没有评估GraphCast从00z和12z的初始化开始，以避免ERA5输入具有+9小时的先行步骤，而HRES输入具有+3小时的先行步骤。在选择目标前瞻时段并仅每12小时评估目标时，我们应用了相同的逻辑，以确保基准真值ERA5和HRES具有相同的+3小时的先行步骤（请参见附录第5.2节）。

HRES的预报在06z和18z初始化时仅运行3.75天（HRES的00z和12z初始化运行10天）。因此，我们的图表将显示一个虚线过渡线，过渡线之前是与06z和18z初始化的HRES进行比较的3.5天，之后是与00z和12z初始化进行比较的。附录第5节包含更多的验证细节。

预测验证结果

我们发现，在以0.25°的纬度/经度级别分辨率和13个垂直层次进行评估的10天预测中，GraphCast在天气预报技能方面优于HRES。

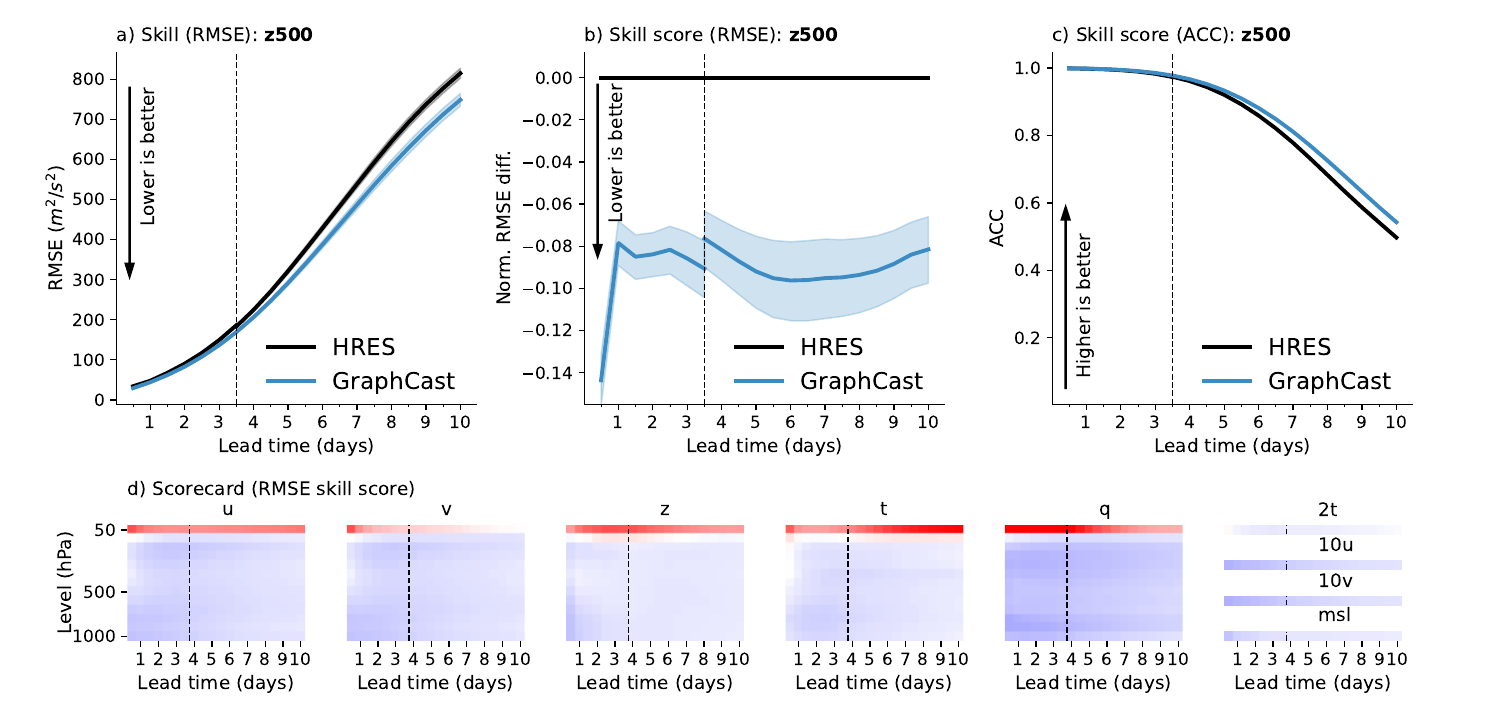图2 2018年GraphCast和HRES的技能和技能分数。 (a) 在z500上，GraphCast（蓝线）和HRES（黑线）的RMSE技能（y轴）随前瞻时段的变化（x轴）。误差条代表95%的置信区间。垂直虚线表示3.5天，即HRES 06z/18z预测的最后12小时增量。黑线代表HRES，其中早于和晚于3.5天的前瞻时段分别来自06z/18z和00z/12z的初始化。 (b) 在z500上，GraphCast与HRES之间的RMSE技能分数（y轴）随前瞻时段的变化（x轴）。技能分数的95%置信区间用误差条表示。我们观察到GraphCast曲线上的不连续，因为3.5天之前的技能分数是在GraphCast（在06z/18z初始化）和HRES的06z/18z初始化之间计算的，而3.5天之后的技能分数是相对于HRES的00z/12z初始化计算的。 (c) 在z500上，GraphCast（蓝线）和HRES（黑线）的ACC技能（y轴）随前瞻时段的变化（x轴）。 (d) 针对HRES的GraphCast的RMSE技能分数的记分卡。每个子图对应一个变量：u，v，z，t，q，2t，10u，10v，m sl，分别是风速u，风速v，位势高度z，温度t，比湿q，两米温度2t，10米风速10u，10米风速10v，平均海平面气压m sl。每个热图的行对应于13个压力层次（对于大气变量），从顶部的50 hPa到底部的1000 hPa。每个热图的列对应于20个前瞻时段，间隔为12小时，从左侧的12小时到右侧的10天。每个单元格的颜色代表技能分数，如(b)所示，其中蓝色表示负值（GraphCast的技能更好），红色表示正值（HRES的技能更好）。

严重天气事件预测结果

除了评估GraphCast在各种变量和前瞻时段上对HRES的预测技能之外，我们还评估了其预测如热带气旋、大气河流和极端温度等严重天气事件的支持能力。这些是GraphCast虽然没有专门训练，但对人类活动非常重要的关键下游应用。

热带气旋轨迹 提高热带气旋预测的准确性有助于避免伤害和生命损失，同时减少经济损失 [21]。通过将跟踪算法应用于位势高度（z）、水平风（10u/10v、u/v）和平均海平面气压（msl）的预测，可以预测气旋的存在、强度和轨迹。我们实施了基于ECMWF发布的协议的跟踪算法，并将其应用于GraphCast的预测，以生成气旋轨迹预测（详见附录第8.1节）。作为比较的基线，我们使用了从HRES的0.1°预测中获取的操作轨迹，存储在TIGGE存档中 [5, 34]，并对两个模型相对于IBTrACS [13, 12]的轨迹进行了测量，后者是从各种分析和观测来源汇总的气旋轨迹的单独再分析数据集。与已建立的热带气旋预测评估 [20] 一致，我们在GraphCast和HRES都检测到气旋时评估所有轨迹，确保两个模型在相同的事件上进行评估，并验证每个模型的真正阳性率相似。

图3a显示，GraphCast在2018年至2021年期间的中位轨迹误差低于HRES。由于HRES和GraphCast的每个轨迹的误差是相关的，我们还测量了两个模型之间每个轨迹的配对误差差异，并发现在18小时到4.75天的前瞻时段内，GraphCast明显优于HRES，如图3b所示。误差条显示了中位数的自举95%置信区间（详见附录第8.1节以获取详细信息）。

图2a–c显示了GraphCast（蓝线）在RMSE技能、RMSE技能分数（即，模型A与基线B之间的标准化RMSE差异，定义为(RMSEA − RMSEB )/RMSEB）和ACC技能方面优于HRES（黑线）的情况下，在z 5 0 0（500 hPa处的位势高度）“头条”场上的表现。使用z500，它编码了大气的天气尺度的压力分布，是文献中常见的，因为它具有很强的气象重要性 [27]。这些图表显示，GraphCast在所有前瞻时段上的技能分数更好，技能分数提高了约7%–14%。附录第7.1节中提供了其他头条变量的图表。

图2d总结了对所有1380个评估变量和压力层的RMSE技能分数，跨足迹10天的预测，以与ECMWF Scorecard类似的格式呈现。单元格的颜色与技能分数成比例，其中蓝色表示GraphCast的技能更好，红色表示HRES的技能更高。GraphCast在1380个目标中优于HRES的比例为90.3%，并在89.9%的目标上显著优于HRES（p ≤ 0 . 05，名义样本大小 n ∈ {729, 730}）。有关方法的详细信息，请参见附录第5.4节，有关p值、检验统计量和有效样本大小的信息，请参见附录表5。

HRES表现优于GraphCast的大气层区域（在记分卡中以红色显示的顶行），在平流层中局部地占有不成比例的位置，并具有最低的训练损失权重（请参见附录第7.2.2节）。在排除50 hPa层时，GraphCast在其余1280个目标上显著优于HRES，比例为96.9%。在排除50和100 hPa层时，GraphCast在其余1180个目标上显著优于HRES，比例为99.7%。在进行按区域评估时，我们发现先前的结果在全球范围内通常成立，详细信息请参见附录图16至18。

我们发现增加MSE损失中的自回归步数可提高GraphCast在较长前瞻时段的性能（请参见附录第7.3.2节），并鼓励它通过预测空间平滑输出来表达其不确定性，导致在较长前瞻时段的预测更模糊（请参见附录第7.5.3节）。然而，HRES的基础物理方程不会导致模糊的预测。为了评估GraphCast相对于HRES在RMSE技能上的相对优势是否在HRES也允许模糊其预测的情况下保持，我们对GraphCast和HRES进行了模糊滤波，通过最小化与模型各自基准真值的RMSE。我们发现，优化模糊的GraphCast在1380个验证目标中比优化模糊的HRES更具技能，这与我们上述的结论基本一致（请参见附录第7.4节）。 我们还将GraphCast的表现与顶尖的基于机器学习的天气模型Pangu-Weather [4]进行了比较，并发现GraphCast在他们提出的252个目标中优于Pangu-Weather的99.2%（详见附录第6节）。

严重天气事件预测结果

除了评估GraphCast在各种变量和前瞻时段上对HRES的预测技能之外，我们还评估了其预测如热带气旋、大气河流和极端温度等严重天气事件的支持能力。这些是GraphCast虽然没有专门训练，但对人类活动非常重要的关键下游应用。

热带气旋轨迹

提高热带气旋预测的准确性有助于避免伤害和生命损失，同时减少经济损失 [21]。通过将跟踪算法应用于位势高度（z）、水平风（10u/10v、u/v）和平均海平面气压（msl）的预测，可以预测气旋的存在、强度和轨迹。我们实施了基于ECMWF发布的协议的跟踪算法，并将其应用于GraphCast的预测，以生成气旋轨迹预测（详见附录第8.1节）。作为比较的基线，我们使用了从HRES的0.1°预测中获取的操作轨迹，存储在TIGGE存档中 [5, 34]，并对两个模型相对于IBTrACS [13, 12]的轨迹进行了测量，后者是从各种分析和观测来源汇总的气旋轨迹的单独再分析数据集。与已建立的热带气旋预测评估 [20] 一致，我们在GraphCast和HRES都检测到气旋时评估所有轨迹，确保两个模型在相同的事件上进行评估，并验证每个模型的真正阳性率相似。

图3a显示，GraphCast在2018年至2021年期间的中位轨迹误差低于HRES。由于HRES和GraphCast的每个轨迹的误差是相关的，我们还测量了两个模型之间每个轨迹的配对误差差异，并发现在18小时到4.75天的前瞻时段内，GraphCast明显优于HRES，如图3b所示。误差条显示了中位数的自举95%置信区间（详见附录第8.1节以获取详细信息）。

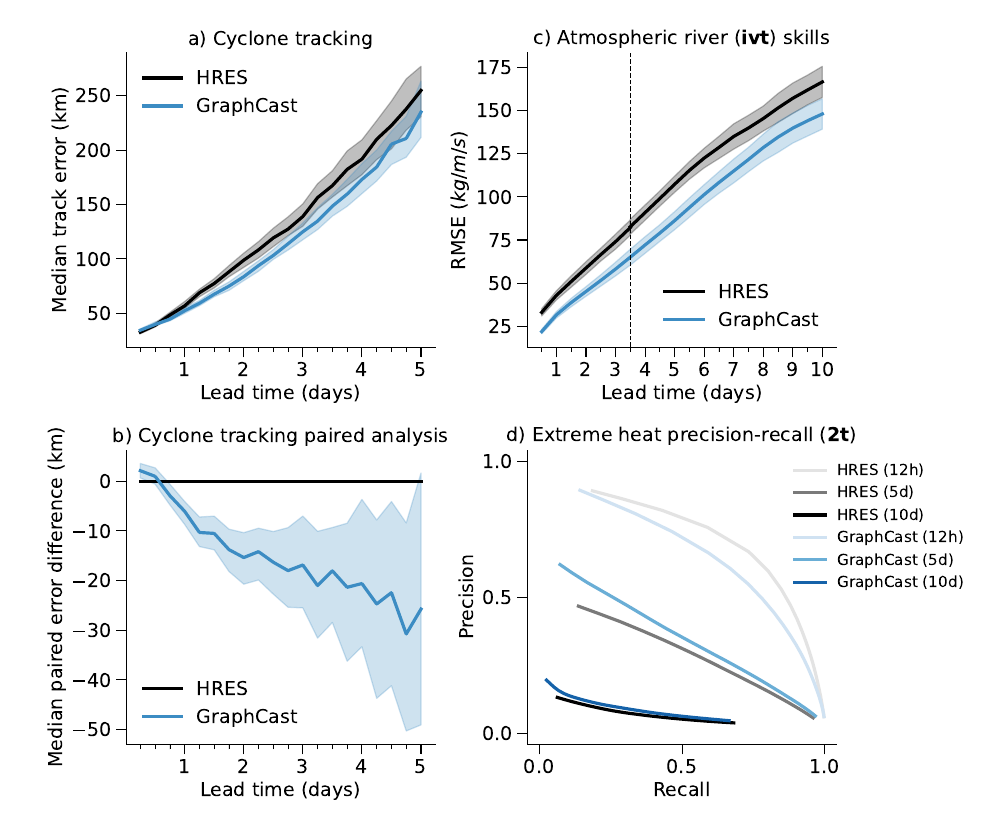图3 严重天气事件预测。 (a) GraphCast和HRES的气旋预测表现。x轴表示前瞻时段（以天为单位），y轴表示中位轨迹误差（以千米为单位）。误差条代表中位数的自举95%置信区间。 (b) GraphCast和HRES之间的气旋预测配对误差差异。x轴表示前瞻时段（以天为单位），y轴表示中位配对误差差异（以千米为单位）。误差条代表中位数差异的自举95%置信区间（详见附录第8.1节）。 (c) GraphCast和HRES的大气河流预测（i v t）技能。x轴表示前瞻时段（以天为单位），y轴表示RMSE。误差条为95%的置信区间。 (d) GraphCast和HRES的极端高温预测精度-召回。x轴表示召回，y轴表示精度。曲线表示在扫过应用于预测信号的增益时，不同的精度-召回折衷（详见附录第8.3节）。

大气河流

大气河流是大气中狭窄的区域，负责在中纬度地区极向输送大部分水汽，并在美国西海岸生成30%-65%的年降水 [6]。它们的强度可以通过垂直积分的水汽输送ivt [23, 22]来表征，该指标表明一个事件是否将提供有益的降水或与灾难性损害有关 [7]。ivt可以从水平风速（u和v）和比湿（q）的非线性组合计算，而GraphCast可以预测这些变量。我们在大气河流最为频繁的寒冷月份（10月至4月）评估GraphCast对北美沿海和东太平洋地区的预测。尽管GraphCast没有专门训练来表征大气河流，图3c显示GraphCast相较于HRES在i v t的预测上有所改善，从短期到长期的前瞻时段，改善程度从25%逐渐提高到10%（详见附录第8.2节）。

极端高温和低温

极端高温和低温以相对于典型气候学的大幅度异常为特征 [19, 16, 18]，可能对人类活动造成危险和干扰。我们评估了HRES和GraphCast在预测在北半球和南半球的夏季地区、每天的不同时段以及每年的不同月份中，距离典型气候学顶部2%的事件的技能，对应于12小时、5天和10天的前瞻时段。我们绘制了精度-召回曲线 [30]，以反映在减少假阳性（高精度）和减少假阴性（高召回）之间的不同可能的折衷。对于每个预测，我们通过变化“增益”参数，该参数将2t预测的偏离相对于中位气候学进行缩放，来获取曲线。

图3d显示，相较于HRES，GraphCast在5天和10天的前瞻时段的精度-召回曲线均优于HRES，这表明GraphCast在更长的时间范围内在极端分类方面的预测通常优于HRES。相比之下，HRES在12小时的前瞻时段具有更好的精度-召回，这与图2d所示的GraphCast对HRES的2t技能分数接近零是一致的。我们通常发现这些结果在其他与极端高温相关的变量（如t850和z500 [18]）、其他极端阈值（5%、2%和0.5%）以及冬季的极端寒冷预测中是一致的。详见附录第8.3节以获取详细信息。

训练数据新旧的影响

GraphCast 可以定期使用最新数据进行重新训练，从而原则上允许其捕捉随时间变化的天气模式，例如 ENSO 周期和其他振荡，以及气候变化的影响。我们使用始于 1979 年，但分别在 2017 年、2018 年、2019 年和 2020 年结束的数据训练了四个不同版本的 GraphCast 模型（我们将在 2017 年结束的变体标记为 “GraphCast:<2018”，依此类推）。我们将它们与 HRES 在 2021 年的测试数据上的性能进行了比较。

图4显示了这四个变体和 HRES 的技能得分（由 GraphCast:<2018 标准化）对于 z500。我们发现，尽管 GraphCast 在 2018 年之前的训练性能仍然与 2021 年的 HRES 相竞争，但将其训练至 2021 年之前进一步提高了其技能得分（详见附录第7.1.3节）。我们推测这种最新性效应使得能够捕捉到最近的天气趋势，从而提高了准确性。这表明 GraphCast 的性能可以通过使用更近期的数据进行重新训练而得到提升。

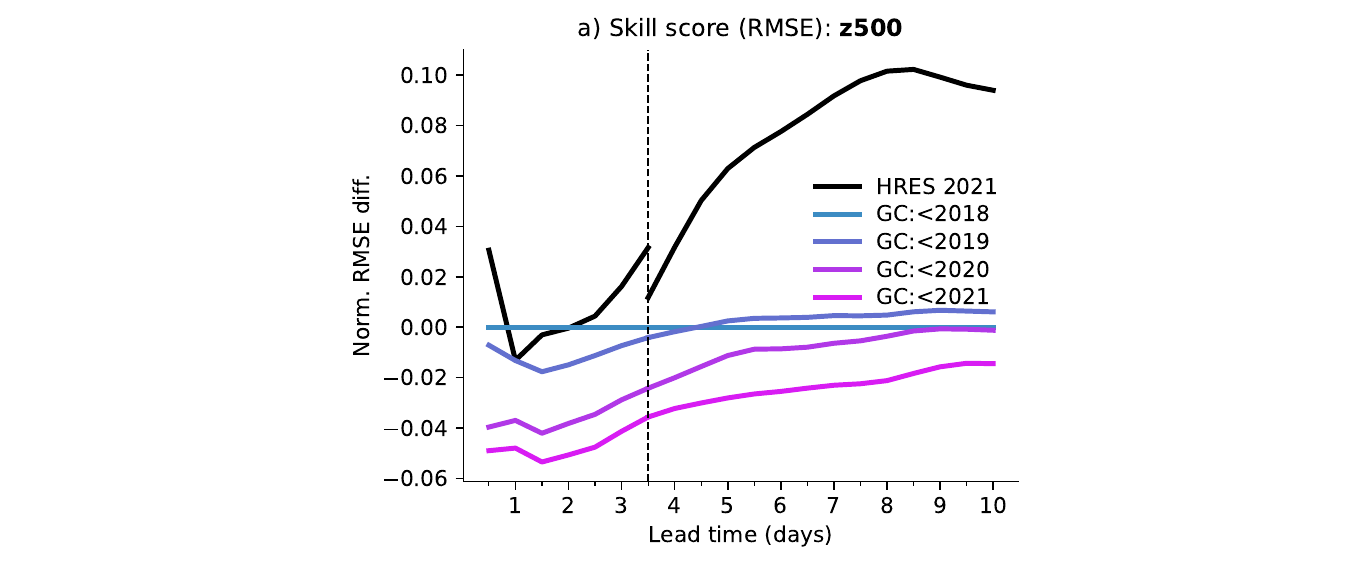图4 使用更近期数据训练GraphCast。每条有颜色的线代表使用不同年份结束的数据训练的GraphCast，从2018年（蓝色）到2021年（紫色）。y轴表示对于z500，相对于在2018年之前训练的GraphCast，在2021年测试数据上的RMSE技能得分，而x轴表示时程。垂直虚线表示3.5天，即HRES的06z/18z预报结束的地方。黑线表示HRES，其中早于和晚于3.5天的时程分别来自于06z/18z和00z/12z的初始化。

结论

GraphCast相对于HRES的预测技能和效率表明，机器学习天气预测（MLWP）方法现在与传统的天气预测方法相媲美。此外，GraphCast在严重事件预测方面的性能，尽管它并非直接针对这些事件进行训练，显示了其稳健性和在下游价值方面的潜力。我们认为这标志着天气预测的一个转折点，有助于通过使廉价的预测更准确、更易获得，并适用于特定应用，加强个人和行业的基于天气的决策制定。

GraphCast拥有3670万个参数，按照现代机器学习的标准来说是一个相对较小的模型，选择这个规模是为了保持内存占用的可控性。虽然HRES的分辨率达到了0.1°，包括137个垂直层和高达1小时的时间步长，但GraphCast的运行分辨率为0.25°纬度/经度，包括37个垂直层和6小时的时间步长，这是由于ERA5训练数据的本地0.25°分辨率以及在硬件上适应更高分辨率数据的工程挑战。总体而言，GraphCast应被视为一个模型家族，当前版本是我们在当前工程约束下能够实际适应的最大版本，但在未来随着更大的计算资源和更高分辨率的数据，其规模可能会进一步扩大。

我们方法的一个关键局限性在于不确定性的处理方式。我们专注于确定性预测并与HRES进行比较，但ECMWF的IFS的另一支柱，即集合预测系统ENS，在10天以上的预测中尤为重要。由于天气动力学的非线性性，随着时程的增长，不确定性逐渐增加，而这并不能被单一确定性预测很好地捕捉。ENS通过生成多个随机预测来解决这个问题，这些预测模拟了未来天气的经验分布，但生成多个预测是昂贵的。相比之下，GraphCast的MSE训练目标鼓励它通过对其预测进行空间平滑来表达其不确定性，这可能会限制其在某些应用中的价值。建立更明确地模拟不确定性的系统是下一步中的关键一步。

重要的是要强调，依赖于大量高质量数据的MLWP在NWP的支持下才能实现，并且像ECMWF的MARS档案这样的丰富数据源是非常宝贵的。因此，我们的方法不应被视为传统天气预测方法的替代品，后者已经在几十年的时间里得到了发展，并在许多实际场景中进行了严格测试，提供了许多我们尚未探索的功能。相反，我们的工作应被解释为MLWP能够应对现实中的预测问题的证据，并具有潜力作为当前最佳方法的补充和改进。

在天气预测之外，GraphCast还可以为其他重要的地理时空预测问题开辟新的方向，包括气候和生态、能源、农业以及人类和生物活动，以及其他复杂的动力学系统。我们相信，基于丰富的真实数据训练的学习模拟器将在推动机器学习在物理科学中的作用方面发挥关键作用。

数据和材料可用性

GraphCast的代码和训练权重公开可在GitHub上获取 https://github.com/deepmind/graphcast。本研究使用了欧洲中期气象预报中心（ECMWF）的公开数据。我们使用了ECMWF档案（已过期的实时数据）中的ERA5、HRES和TIGGE产品，其使用受到知识共享署名4.0国际许可协议（CC BY 4.0）的约束。我们使用了来自 https://www.ncei.noaa.gov/products/international-best-track-archive 的IBTrACS版本4，并参考了文献[13, 12]。图1中的地球纹理是在CC BY 4.0下使用的，来源于 https://www.solarsystemscope.com/textures/。

补充材料

1. 数据集

在本节中，我们概述了我们用于训练和评估GraphCast（补充部分1.1）的数据，定义NWP基线HRES的预测的数据，以及我们用作HRES的基准的HRES-fc0的数据（补充部分1.2）。最后，我们描述了用于热带气旋分析的数据（第1.3节）。

我们构建了多个用于训练和评估的数据集，由ECMWF的数据档案和IBTrACS [29, 28]的子集组成。通常，我们区分源数据，我们称之为“存档”或“已存档数据(“archive” or “archived data”)，与我们从这些存档构建的数据集，我们称之为“数据集”(dataset)。

1.1. ERA5

为了训练和评估GraphCast，我们从ECMWF的ERA5 [24]档案的子集中构建了我们的数据集。ERA5是一个庞大的数据集，代表了从1959年到现在的全球天气情况，分辨率为0.25°纬度/经度，时间间隔为1小时，包括数百个静态、地表和大气变量。ERA5档案基于再分析，使用ECMWF的HRES模型（第42r1周期），该模型在2016年的大部分时间内处于运行状态（见表3），在ECMWF的4D-Var数据同化系统中。ERA5同化了观测的12小时窗口，从21z-09z和09z-21z，以及先前的预测，形成了每个历史日期和时间的天气状态的密集表示。

我们的ERA5数据集包含ECMWF的ERA5档案中可用变量的子集（表2），在37个压力层上：1, 2, 3, 5, 7, 10, 20, 30, 50, 70, 100, 125, 150, 175, 200, 225, 250, 300, 350,400, 450, 500, 550, 600, 650, 700, 750, 775, 800, 825, 850, 875, 900, 925, 950, 975, 1000 hPa。所包含的年份范围是1979-01-01至2022-01-10，这些年份被降采样为6小时的时间间隔（对应每天的00z、06z、12z和18z）。降采样是通过子采样完成的，除了总降水量，该量是对应降采样时间之前6小时累积的。

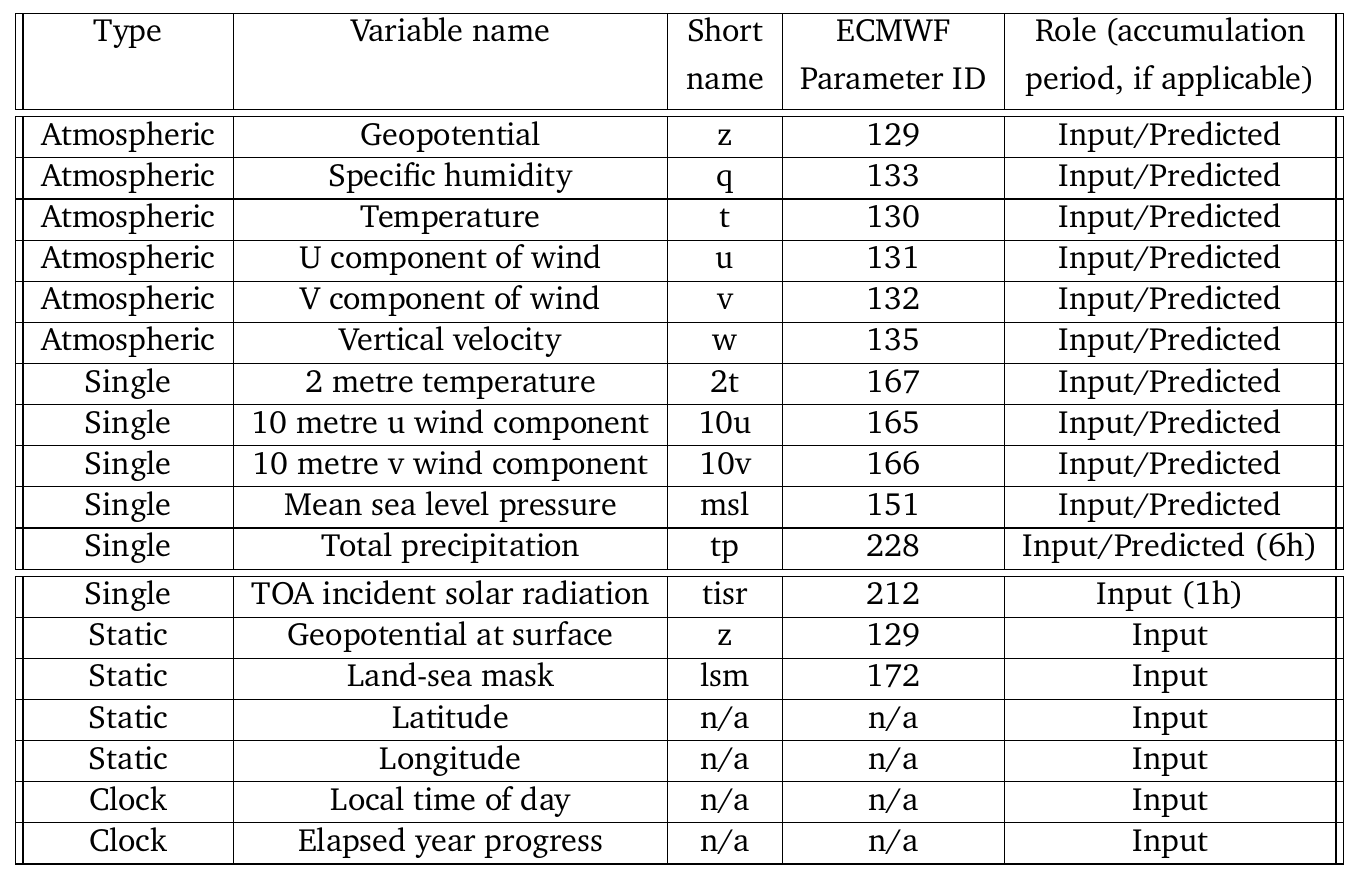表2 我们数据集中使用的ECMWF变量。 “Type”列指示变量是表示静态属性、时变的单层属性（例如，包括地表变量）还是时变的大气属性。 “Variable name”和“Short name”列是ECMWF的标签。 “ECMWF Parameter ID”列是ECMWF的数值标签，可以用于构造ECMWF变量描述的URL，将其附加为后缀到以下前缀，将“ID”替换为数值代码：https://apps.ecmwf.int/codes/grib/param-db/?id=ID。 “Role”列指示变量是我们的模型作为输入并进行预测的内容，还是仅作为输入上下文使用的内容（双横线将预测变量与仅输入变量分隔开来，以使划分更可见）。

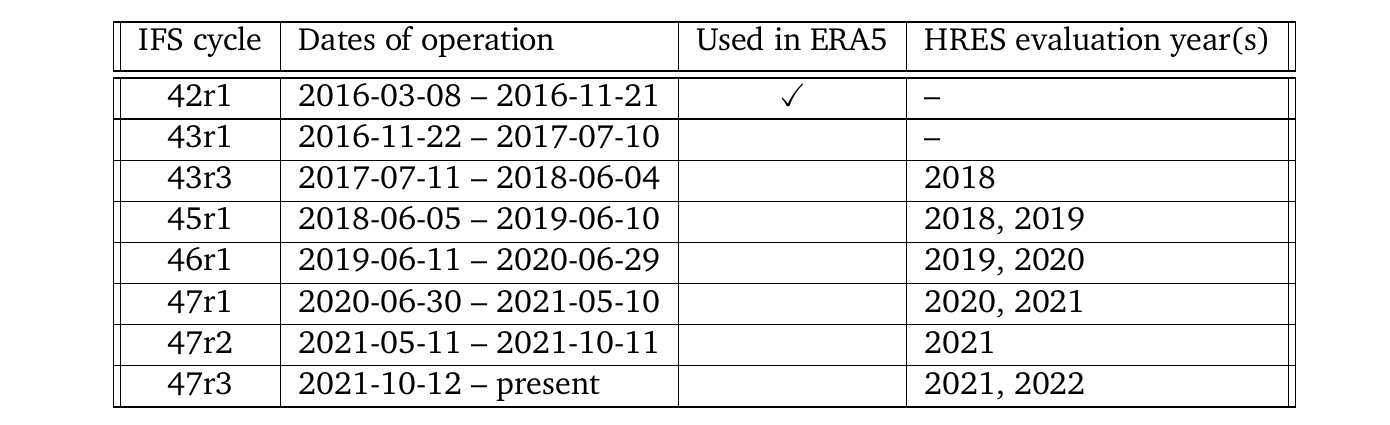表3 自2016年以来的0.1°分辨率IFS周期。表格显示了每个在0.1°纬度/经度分辨率下运行的IFS周期。列代表IFS周期版本，其运行日期，是否用于ERA5的数据同化，以及在我们的结果评估中将其用作与GraphCast比较的基准的年份。有关完整的周期发布时间表，请参见https://www.ecmwf.int/en/forecasts/documentation-and-support/changes-ecmwf-model。

1.2. HRES

对HRES模型基线的评估需要两组不同的数据，即预报数据和实况数据，这些数据在随后的小节中进行了总结。在我们的测试年份期间运行的HRES版本显示在表3中。

HRES操作性预报 HRES通常被认为是全球最准确的确定性基于数值天气预报的模型，因此为了评估HRES基线，我们构建了HRES的存档历史预报数据集。由于ECMWF定期更新HRES，因此这些预报代表了当时制作预报时的最新HRES模型。这些预报以其本地表示形式下载（使用球谐函数和八面体简化的高斯网格(spherical harmonics and an octahedral reduced Gaussian grid)，TCo1279 [36]），大致相当于0.1°纬度/经度分辨率。然后，我们使用ECMWF的Metview库将预报在空间上下采样到0.25°纬度/经度网格（以匹配ERA5的分辨率），采用默认的regrid参数。我们将其在时间上下采样到6小时间隔。有两组HRES预报：在00z/12z初始化的预报，发布为10天的时间跨度；在06z/18z初始化的预报，发布为3.75天的时间跨度。

HRES-fc0 为了评估HRES操作性预报的技能，我们基于ECMWF的HRES操作性预报存档构建了一个地面实况数据集“HRES-fc0”。该数据集包括每个HRES预报的初始时间步，初始化时间为00z、06z、12z和18z（参见图5）。HRES-fc0数据与ERA5数据相似，但在预报时间使用最新的ECMWF NWP模型进行同化，并同化与相应日期和时间前后±3小时的观测。请注意，ECMWF还提供“HRES Analysis”数据的存档，该数据与我们的HRES-fc0数据集不同。HRES分析数据集包括大气和地表分析数据，但它不是提供给HRES预报的输入，因此我们不使用它作为地面实况数据，因为这会在HRES预报和地面实况之间引入差异，仅仅是因为HRES使用不同的输入，这在短期内尤为显著。

HRES NaN处理 ECMWF HRES存档中变量850hPa（z850）和925hPa（z925）的极小子集的值不是数字（NaN）。这些NaN似乎均匀分布在2016-2021年的范围内和在预报时间上。这大约占z850的像素的0.00001%（每十个1440 x 721纬度/经度帧中的一个像素），z925的像素的0.00000001%（每一万个1440 x 721纬度/经度帧中的一个像素），对性能没有可测量的影响。为了更容易比较，我们用邻近像素的加权平均值填充了这些极少数的缺失值。我们使用侧邻居的权重为1，对角邻居的权重为0.5。

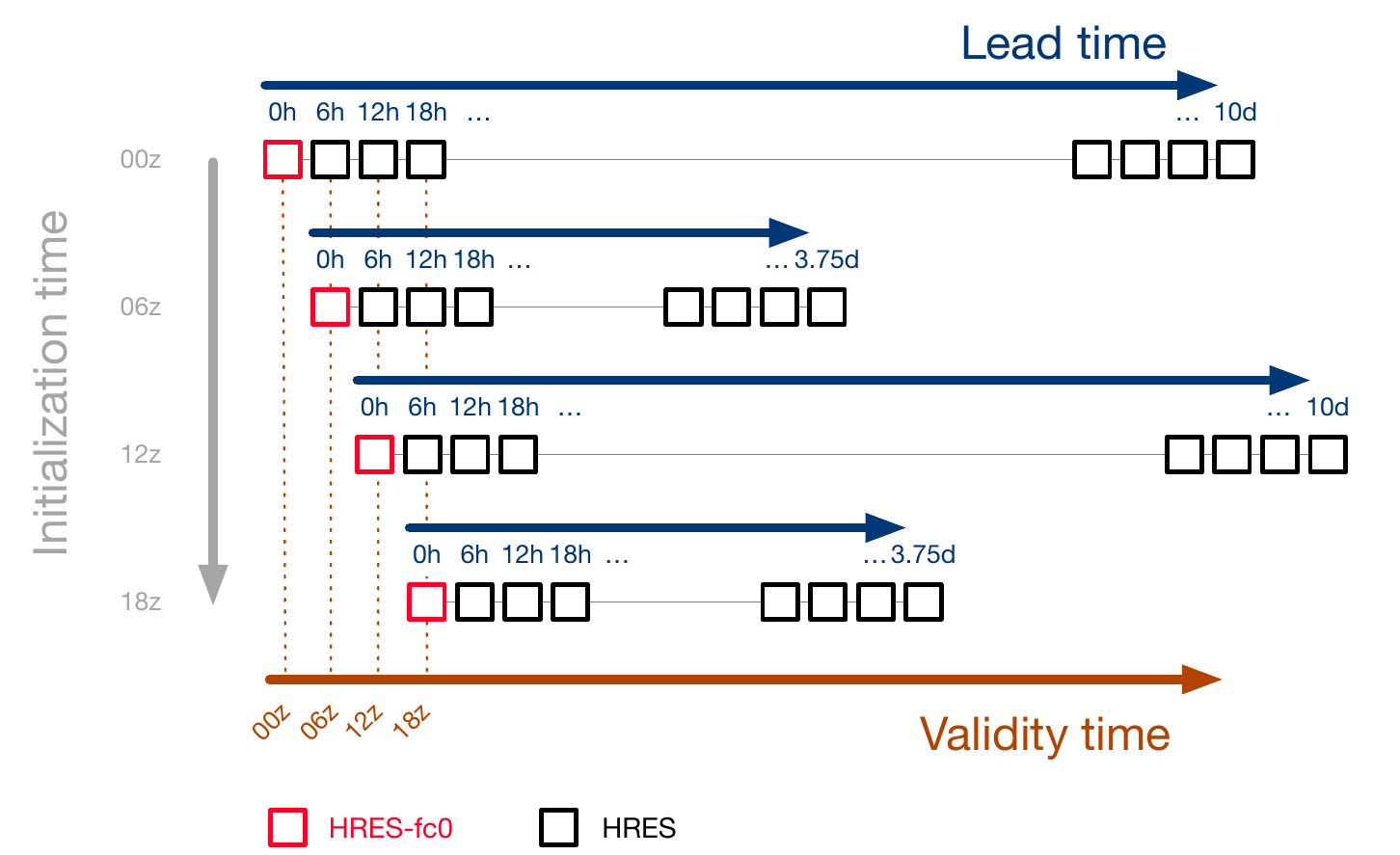图5 HRES-fc0示意图。每条水平线代表HRES进行的一次预测，初始化时间不同（灰色轴）。从00z和12z初始化的HRES预测可进行长达10天的预测（蓝色轴），而从06z和18z初始化的HRES预测则可进行长达3.75天的预测。每个正方形代表HRES预测的状态，以6小时为间隔（示意图中省略了较小的时间步长以及在预测轨迹中间的状态）。红色正方形代表每个HRES预测在时间0的预测，并定义了包含在HRES-fc0中的数据点。棕色轴表示有效时间，并允许可视化来自不同初始化时间的预测的对齐。例如，HRES在06z初始化的预测（从顶部的第二行正方形开始）在12小时的前瞻时间，即18z的有效时间（从左边数的第3个正方形），将与在18z初始化的HRES预测的第一步（最后一行正方形的红色正方形）进行比较。

1.3. 热带气旋数据集

在我们对热带气旋预测的分析中，我们使用了IBTrACS [28, 29, 31, 30] 存档来构建地面实况数据集。这包括来自约十几个权威来源的历史气旋路径。每条路径是一个时间序列，以6小时为间隔（00z、06z、12z、18z），其中每个时间步代表气旋眼在纬度/经度坐标上的位置，以及该时刻的Saffir-Simpson等级和其他相关的气象特征。

对于HRES基线，我们使用了TIGGE存档，该存档提供了在0.1°分辨率下，使用操作跟踪器估算的HRES预测的气旋路径 [8, 46]。这些数据以XML文件的形式存储，可通过 https://confluence.ecmwf.int/display/TIGGE/Tools 下载。为了将数据转换为适用于进一步后处理和分析的格式，我们实施了一个解析器，用于提取感兴趣年份的气旋路径。XML文件中相关的部分（标签）是“forecast”类型的，通常包含与不同初始预测时间对应的多条路径。在这些标签中，我们提取气旋名称（标签“cycloneName”）、纬度（标签“latitude”）和经度（标签“longitude”）值以及有效时间（标签“validTime”）。 有关跟踪算法和结果的详细信息，请参见第8.1节。

2 符号和问题陈述

在本节中，我们定义了在全文中使用的有用的时间符号（第2.1节），形式化了我们解决的一般预测问题（第2.2节），并详细说明了我们如何建模天气的状态（第2.3节）。

2.1. 时间符号

在预测中使用的时间符号可能令人困惑，涉及到一些不同的时间符号，例如，用于表示初始预测时间(initial forecast time)、有效时间(validity time)、预测时限(forecast horizon)等。因此，为了明确和简化，我们引入了一些标准化的术语和符号。我们将特定的时间点称为“日期-时间”，由日历日期和UTC时间指示。例如，2018-06-21_18:00:00 表示2018年6月21日UTC时间18:00。为了简便，我们有时还使用Zulu约定，即00z、06z、12z、18z分别表示00:00、06:00、12:00、18:00的UTC时间。我们进一步定义以下符号：

• t：预测时间步骤索引，表示从预测初始化以来的步数。
• T：预测时限，表示预测中的总步数。
• d：有效时间，表示特定天气状态的日期-时间。
• $d_0$：预测初始化时间，表示预测初始输入的有效时间。
• Δd：预测步长，表示一个预测步骤中经过的时间。
• τ：预测提前时间，表示预测中的经过时间（即τ = tΔd）。

2.2. 一般预测问题陈述

设 $Z^d$ 表示全球天气在时间 d 的真实状态。真实天气的时间演变可以用一个基础的离散时间动力学函数 $\Phi$ 来表示，该函数生成下一个时间步骤（$\Delta d$ 后的未来）的状态，即 $Z^{d+\Delta d} = \Phi(Z^d)$。然后，通过对 $\Phi$ 进行 T 次自回归，我们得到 T 未来天气状态的轨迹：

我们的目标是找到真实动力学函数$\Phi$ 的准确且高效的模型$\phi$，该模型可以有效地预测未来某个预测时限 $T\Delta d$ 内的天气状态。我们假设不能直接观测 $Z^d$，而是只有一些部分观测 $X^d$，它是对完美预测天气所需的状态信息的不完整表示。由于 $X^d$ 只是瞬时状态 $Z^d$ 的近似，我们还为$\phi$提供了一个或多个过去的状态 $X^{d−\Delta d}，X^{d−2\Delta d},…$(除了$X^d$之外)。然后，该模型可以原则上利用这些附加上下文信息更准确地逼近 $Z^d$。因此，$\phi$ 预测未来的天气状态为：

类似于方程(1)，预测 $\hat{X}^{d+\Delta d}$可以被反馈到 $\phi$ 中，以自回归地产生完整的预测：

我们通过量化$\phi$预测的轨迹 $\hat{X}^{d+\Delta d:d+T\Delta d}$ 与地面实况轨迹 $X^{d+\Delta d:d+T\Delta d}$ 之间的匹配程度来评估$\phi$的预测质量或技能。然而，重要的是要强调，$\hat{X}^{d+\Delta d:d+T\Delta d}$ 只包括我们对 $Z^{d+\Delta d:d+T\Delta d}$ 的观测，而 $Z^{d+\Delta d:d+T\Delta d}$ 本身是未观测到的。我们使用一个目标函数来衡量预测与实况之间的一致性，

该函数在第5节中有明确描述。 在我们的工作中，数据和预测的时间分辨率始终为 Δd = 6 小时，最大预测时限为 10 天，对应总步数 T = 40。由于 Δd 在本文中是一个常数，我们可以使用 $(X^t, X^{t+1}, …, X^{t+T})$ 而不是 $X^d, X^{d+\Delta d}, …, X^{d+T \Delta d}$，通过使用整数而不是具体的日期-时间来索引时间，从而简化表示法。

2.3. 建模ECMWF天气数据

在训练和评估模型时，我们将我们的ERA5数据集视为表面和大气天气状态的地面真实表示。正如第1.2节所述，我们使用HRES-fc0数据集作为评估HRES技能的地面真实。

在我们的数据集中，ERA5天气状态 $X^t$ 包括表2中的所有变量，水平纬度-经度分辨率为0.25°，共有721 × 1440 = 1,038,240个网格点和37个垂直压力层。大气变量在所有压力层定义，(水平)网格点的集合为 $G_{0.25°} = \{−90.0, −89.75, . . . , 90.0\} \times \{−179.75, −179.5, . . . , 180.0\}$。这些变量通过它们的短名称唯一标识（对于大气变量，还有压力层）。例如，表面变量“2米温度”表示为2t；压力层为500 hPa的大气变量“高度位势”表示为z500。请注意，我们的模型仅输出“预测”变量，因为”input-only”变量是先验已知的强迫项，只是在每个时间步上附加到状态上。由于简化起见，我们在描述中忽略了它们，因此总共有5个表面变量和6个大气变量。

从所有这些变量中，我们的模型为总共227个目标变量预测了5个表面变量和6个大气变量。还提供了几个静态和/或外部变量作为我们模型的输入上下文。这些变量显示在表1和表2中。静态/外部变量包括网格/网格的几何形状、地形（地表高势）、陆海遮罩和大气顶部辐射等信息。

我们将对应于特定网格点i（总共1,038,240个）的变量子集称为$x^t_i$，将227个目标变量中的每个变量j称为$x^t_{i,j}$。因此，完整的状态表示$X^t$ 包含总共721 × 1440 × (5 + 6 × 37) = 235,680,480个值。请注意，在极点，1440个经度点是相等的，因此实际的不同网格点数量略小。

3 GraphCast模型

本节详细描述了GraphCast，从生成预测的自回归过程开始（第3.1节），然后以通俗的语言概述架构（第3.2节），接着是定义GraphCast的所有图的技术描述（第3.3节），包括其编码器（第3.4节），处理器（第3.5节）和解码器（第3.6节），以及所有归一化和参数化细节（第3.7节）。

3.1. 生成预测

我们的GraphCast模型被定义为一个单步学习的模拟器，扮演方程（2）中的φ的角色，并基于两个相邻的输入状态预测下一步，

如同方程（3），我们可以迭代应用GraphCast来产生一个预测，

这在图1b、c中有所说明。在早期的实验中，我们发现两个输入状态的性能要优于一个，而三个并没有足够的帮助来证明增加的内存占用是合理的。

3.2. 架构概述

GraphCast的核心架构采用了图神经网络（GNNs）的“编码-处理-解码”配置[6]，如图1d、e、f所示。基于GNN的学习模拟器在学习流体和其他材料的复杂物理动力学方面非常有效[43, 39]，因为它们的表示和计算结构类似于学习的有限元求解器[1]。 GNN的一个关键优势是输入图的结构决定了表示中的哪些部分通过学到的消息传递相互作用，从而允许在任何范围内进行任意模式的空间相互作用。相比之下，卷积神经网络（CNN）限制在局部区域内计算相互作用（或者，在稀疏卷积的情况下，可以在正则分布的更长范围内进行计算）。而Transformer[48]虽然也能计算任意长程计算，但由于计算所有对所有的相互作用引起的二次内存复杂度，它在处理非常大的输入时（例如GraphCast的全球输入中的100多万个网格点）不会很好地扩展。Transformer的现代扩展通常会使可能的相互作用稀疏化以减少复杂性，实际上使它们类似于GNNs（例如，图注意力网络[49]）。

我们利用GNN模型能够建模任意稀疏相互作用的能力，引入了GraphCast的内部“多网格”表示，它允许在少数消息传递步骤内进行长距离相互作用，并且在全球范围内具有一般均匀的空间分辨率。这与经度-纬度网格形成对比，后者导致网格点的非均匀分布。由于极点的高分辨率需要不成比例的计算资源，使用经度-纬度网格并不是一种明智的表示方法。

我们的多网格是通过首先将正20面体（12个节点和20个面）迭代6次，以获得具有40962个节点和81920个面的正20面体网格层次结构构建的。我们利用了粗网格节点是细网格节点的子集这一事实，这使我们能够将来自网格层次结构的所有级别的边叠加到最高分辨率的网格上。这个过程产生了一个多尺度的网格集合，其中粗糙的边在多个尺度上跨越长距离，而细边捕获本地相互作用。图1g显示了每个单独的精化网格，图1e显示了完整的多网格。

GraphCast的编码器（图1d）首先使用具有从网格点到多网格的有向边的GNN将原始的纬度-经度网格的输入数据映射到多网格上的学习特征。处理器（图1e）然后使用16层深度的GNN在多网格上执行学习消息传递，通过长距离的边实现了信息的有效传播。解码器（图1f）然后使用具有有向边的GNN将最终的多网格表示映射回纬度-经度网格，并将该网格表示$Y^{t+k}$与输入状态$X^{t+k}$结合起来形成输出预测，$X^{t+k+1} = X^{t+k} + Y^{t+k}$。

编码器和解码器不需要将原始数据排列成规则的直角网格，并且也可以应用于任意类似网格的状态离散化[1]。这一通用架构基于在许多复杂流体系统和其他物理领域中取得成功的各种基于GNN的学习模拟器[43, 39, 15]。类似的方法在天气预报中也取得了有希望的结果[26]。

在单个Cloud TPU v4设备上，GraphCast可以在不到60秒的时间内生成0.25°分辨率的10天预测（每6小时一步）。作为对比，ECMWF的IFS系统在一个11664核集群上运行，生成0.1°分辨率的10天预报（在前90小时以1小时间隔发布，从第93-144小时以3小时间隔，从150-240小时以6小时间隔发布，大约需要一个小时的计算时间[41]）。请参阅HRES的发布详情：https://www.ecmwf.int/en/forecasts/datasets/set-i…。

3.3. GraphCast的图

GraphCast是使用图神经网络（GNNs）以“编码-处理-解码”配置实现的，其中编码器将输入纬度-经度网格上的（表面和大气）特征映射到多网格，处理器在多网格上执行多轮消息传递，解码器将多网格特征映射回输出纬度-经度网格（参见图1）。

该模型在图$\mathcal{G}(\mathcal{V}^G ，\mathcal{V}^M ，\mathcal{E}^M，\mathcal{E}^{\text{G2M}}，\mathcal{E}^{\text{M2G}})$上操作，详细定义如下几段所述。

Grid节点 $\mathcal{V}^\mathcal{G}$表示包含每个Grid节点 $\mathcal{v}^G_i$ 的集合。每个Grid节点表示在给定的纬度-经度点i处大气的垂直切片。与每个Grid节点 $\mathcal{v}^G_i$关联的特征为 $\boldsymbol{v}_i^{G,\text{features}}= [\boldsymbol{x}^{t-1}_i , \boldsymbol{x}^t_i , \boldsymbol{f}^{t-1}_i , \boldsymbol{f}^{t}_i , \boldsymbol{f}^{t+1}_i , \boldsymbol{c}_i ]$，其中 $\boldsymbol{x}^t_i$ 是与Grid节点 $\mathcal{v}^G_i$ 相对应的时变气象状态$X^t$，包含所有37个大气层次的所有预测数据变量以及表面变量。强迫(forcing)项$\boldsymbol{f}^{t}$由可以通过解析计算得到的时变特征组成，不需要由GraphCast进行预测。它们包括在大气顶部累积的总太阳辐射，每小时累积一次，当地时间的正弦和余弦（归一化为[0,1))，年进度的正弦和余弦（归一化为[0,1))。常数 $\boldsymbol{c}_i$ 是静态特征：二进制的陆地-海洋掩膜，地表的位势高度，纬度的余弦，以及经度的正弦和余弦。在0.25°分辨率下，共有721×1440 = 1,038,240个网格节点，每个节点具有(5个表面变量 + 6个大气变量 × 37层次) × 2步 + 5个强迫项 × 3步 + 5个常数 = 474个输入特征。

Mesh节点 $\mathcal{V}^M$表示包含每个Mesh节点 $\mathcal{v}_i^M$ 的集合。Mesh节点均匀分布在球面上，形成一个R-refined的正20面体网格 $M^R$。$M^0$ 对应于一个单位半径的正20面体（12个节点和20个三角形面），其面与极点平行（见图1g）。通过将每个三角面分成4个较小的面，将新节点投影回单位球上，每个边的中点处产生一个额外的节点，将网格迭代地细化$M^r \rightarrow M^{r+1}$，从而获得更高的分辨率。与每个Mesh节点$\mathcal{v}_i^M$关联的特征$\boldsymbol{v}_i^{M,\text{features}}$包括纬度的余弦，以及经度的正弦和余弦。GraphCast使用经过R = 6次细化的Mesh$M^6$，得到40,962个Mesh节点（见补充表4），每个节点具有3个输入特征。

表4 多网格统计信息。多级细化的正20面体网格的统计数据，其中统计数据与细化级别 R 相关。边被视为双向的，因此我们计算网格中每条边两次（分别为每个方向一次）。

Mesh边 $\mathcal{E}^M$ 是在Mesh中连接的Mesh节点之间添加的双向边。至关重要的是，对于所有的细化级别，即最细的网格 $M^6$，以及 $M^5$、$M^4$、$M^3$、$M^2$、$M^1$ 和 $M^0$，都会向 $\mathcal{E}^M$ 中添加Mesh边。这是因为细化过程的工作方式：$M^{r −1}$ 的节点始终是 $M^r$ 中节点的子集。因此，引入在较低细化级别的节点充当更长距离通信的枢纽，与最大细化级别无关。包含所有细化级别的边的联合集的结果图被称为“多网格”(multi-mesh)。请参见图1e、g，其中显示了细化层次中所有单个网格以及完整的多网格。

对于连接发送Mesh节点 $v_s^M$ 到接收网格节点 $v_r^M$ 的每条边 $e^M_{v_s^M \rightarrow v_r^M}$，我们使用Mesh节点在单位球上的位置构建边特征 $\boldsymbol{e}^M_{v_s^{M,\text{features}} \rightarrow v_r^M}$，包括边的长度以及在接收节点的局部坐标系中计算的发送节点和接收节点的 3D 位置的矢量差异。接收者的局部坐标系是通过应用旋转来计算的，该旋转改变方位角(azimuthal)，直到接收者节点位于经度 0 处，然后通过改变极角(polar angle)的旋转，直到接收者也位于纬度 0 处。这导致总共有 327,660 条网格边（参见表4），每条边都有4个输入特征。

Grid2Mesh 边 $\mathcal{E}^{\text{G2M}}$ 是将发送Grid节点连接到接收Mesh节点的单向边。如果Grid节点与Mesh节点之间的距离小于或等于Mesh $M^6$ 中边的长度的0.6倍（参见图1），则添加边 \(e^{\text{G2M}}_{v_s^G \rightarrow v_r^M}\)，这确保每个Grid节点都连接到至少一个Mesh节点。特征\(\boldsymbol{e}^{\text{G2M, features}}_{v_s^G \rightarrow v_r^M}\)的构建方式与Mesh边相同。这导致总共有1,618,746条Grid2Mesh边，每条边都有4个输入特征。

Mesh2Grid 边 $\mathcal{E}^{\text{M2G}}$是将发送网格节点连接到接收网格节点的单向边。对于每个网格点，我们找到包含它的网格 $M^6$ 中的三角形面，并添加三条形式为 \(e^{\text{M2G}}_{v_s^M \rightarrow v_r^G}\) 的边，将网格节点连接到与该面相邻的三个网格节点（参见图1）。特征\(\boldsymbol{e}^{\text{M2G, features}}_{v_s^M \rightarrow v_r^G}\)的构建方式与Mesh边相同。这导致总共有3,114,720条Mesh2Grid边（3个网格节点连接到每个721×1440纬度-经度网格点），每条边都有四个输入特征。

3.4. 编码器

编码器的目的是将数据准备成潜在(latent)表示，以供处理器专门在多网格上运行。

嵌入输入特征 作为编码器的一部分，我们首先使用五个多层感知机（MLP）将grid节点、mesh节点、mesh边、grid到mesh边以及mesh到grid边的特征嵌入到固定大小的潜在空间中。

Grid2Mesh GNN 接下来，为了将大气状态的信息从grid节点传输到mesh节点，我们在连接grid节点和mesh节点的Grid2Mesh二分图$\mathcal{G}_{\text{G2M}}(\mathcal{V}^G ，\mathcal{V}^M ，\mathcal{E}^{\text{G2M}})$上执行单一消息传递步骤。此更新使用增强为能够处理多个节点类型的交互网络[5, 6]进行。首先，使用相邻节点的信息更新每个Grid2Mesh边，

然后，通过汇总到达该网格节点的所有边的信息来更新每个网格节点：

每个网格节点也会进行更新，但不进行聚合，因为网格节点不是Grid2Mesh子图中任何边的接收者，

在更新了所有三个元素之后，模型包括一个残差连接，并为简化表示法，重新分配变量，

3.5. 处理器

处理器是一个深度的图神经网络（GNN），在仅包含Mesh节点和Mesh边的Mesh子图$\mathcal{G}^M(\mathcal{V}^M, \mathcal{E}^M)$上运行。请注意，Mesh边包含完整的多网格，不仅包括$M^6$的边，还包括$M^5$、$M^4$、$M^3$、$M^2$、$M^1$和$M^0$的所有边，这将实现长距离通信。

多网格GNN Mesh GNN的单个层是一个标准的交互网络[5, 6]，首先使用相邻节点的信息更新每个Mesh边：

然后，通过汇总到达该网格节点的所有边的信息来更新每个网格节点：

在更新了这两者之后，通过一个残差连接更新表示，并为简化表示法，也重新分配给输入变量：

前面的段落描述了单个消息传递层，但按照类似[43, 39]的方法，我们迭代地应用了这一层16次，对每一层中的MLP使用了不共享的神经网络权重。

3.6. 解码器

解码器的作用是将信息带回到网格并提取输出。

Mesh2Grid GNN 与Grid2Mesh GNN类似，Mesh2Grid GNN在Mesh2Grid二分图$\mathcal{G}_{\text{M2G}}(\mathcal{V}^G ，\mathcal{V}^M ，\mathcal{E}^{\text{M2G}})$上执行单次消息传递。Grid2Mesh GNN在功能上等效于Mesh2Grid GNN，但使用Mesh2Grid边将信息沿相反方向发送。GNN首先使用相邻节点的信息更新每个Grid2Mesh边：

然后，通过汇总到达该网格节点的所有边的信息来更新每个网格节点：

在这种情况下，我们不更新Mesh节点，因为从这一点开始它们将不再发挥任何作用。 同样，我们在这里添加了一个残差连接，并为了简化表示法，只重新分配了网格节点的变量：

输出函数 最后，使用另一个MLP为每个网格节点产生预测$\hat{\boldsymbol{y}}_i$，

其中包含该网格节点的所有227个预测变量。类似于[43, 39]，下一个天气状态$\hat{X}^{t+1}$通过将每个网格节点的节点预测$\hat{Y}^t$添加到所有网格节点的输入状态来计算。

3.7. 标准化和网络参数化

输入标准化 与[43, 39]类似，我们对所有输入进行了标准化。对于每个物理变量，我们计算了在1979年至2015年期间每个气压级别的均值和标准差，并使用这些值将它们标准化为零均值和单位方差。对于相对边距和长度，我们将特征标准化为最长边的长度。为简单起见，我们在符号中省略了这个输出标准化。

输出标准化 因为我们的模型输出一个差异$\hat{Y}^t$，在推断期间，它会被加到$X^t$以产生$\hat{X}^{t+1}$，所以我们通过计算每个变量的时间差$Y^t = X^{t+1}−X^t$的每个气压级别的标准差统计数据来标准化模型的输出。当GNN产生输出时，我们将该输出乘以这个标准差，以在计算$\hat{X}^{t+1}$之前得到$\hat{Y}^t$，如方程（18）中所示。为简单起见，我们在符号中省略了这个输出标准化。

神经网络参数化 GraphCast中的神经网络都是MLP，具有一个隐藏层，隐藏层和输出层的大小均为512（除了解码器MLP的最终层，其输出大小为227，与每个网格节点的预测变量数量相匹配）。我们选择了所有MLP的“swish”[40]激活函数。所有MLP之后都跟有一个LayerNorm [3]层（解码器的MLP除外）。

4 训练细节

本节提供有关GraphCast训练的详细信息，包括用于开发模型的数据拆分（第4.1节），目标函数的完整定义以及与每个变量和垂直层面相关的权重（第4.2节），自回归训练方法（第4.3节），优化设置（第4.4节），用于减少训练成本的课程训练（第4.5节），用于减少GraphCast内存占用的技术细节（第4.6节），训练时间（第4.7节）以及我们使用的软件堆栈（第4.8节）。

4.1. 训练拆分

为了模拟实际的部署条件，其中预测不能依赖于未来的信息，我们将用于开发GraphCast的数据和用于测试其性能的数据“因果地”拆分，即“开发集”仅包含早于“测试集”中的日期。开发集包括1979年至2017年的时期，测试集包含2018年至2021年的年份。在完成开发阶段之前，研究人员和模型训练软件都不被允许查看测试集的数据。这防止了我们对模型架构和训练协议的选择能够利用未来的任何信息。

在我们的开发集中，我们进一步将数据拆分为包括1979年至2015年的训练集和包括2016年至2017年的验证集。我们将训练集用作模型的训练数据，将验证集用于超参数优化和模型选择，即选择表现最佳的模型架构。然后，我们冻结了模型架构和所有训练选择，并进入测试阶段。在初步工作中，我们还探讨了对1959年至1978年的较早数据进行训练，但发现它对性能的改善有限，因此在我们的工作的最后阶段，我们简化起见排除了1959年至1978年的数据。

4.2. 训练目标

GraphCast被训练以在12步（3天）的预测期内针对ERA5目标最小化目标函数，使用梯度下降。训练目标定义为目标输出X与预测输出$\hat{X}$之间的均方误差（MSE），

其中

• $\tau \in 1:T_{\text{train}}$: 是对应于 $T_{\text{train}}$ 自回归步骤的lead时间。
• $d_0 \in D_{\text{batch}}$ 代表训练集中一批预测的预测初始化日期和时间，
• $j \in J$ 索引变量，对于大气变量，还包括气压级别。例如，J = {z1000, z850，…，2t, msl}，
• $i \in G_{0.25°}$ 是网格中的位置（纬度和经度）坐标，
• \(\hat{x}_{ij}^{d_0+\tau}\)和\(x_{ij}^{d_0+\tau}\)是某个变量级别、位置和lead时间的预测和目标值，
• $s_j$ 是每个变量级别的时间差的逆方差，
• $w_j$ 是每个变量级别的损失权重，
• $a_i$ 是纬度-经度网格单元的面积，随纬度变化，并标准化为网格上的单位均值。

为了构建单一标量损失，我们在纬度-经度、气压级别、变量、lead时间和批次大小上取平均值。我们在纬度-经度轴上进行加权平均，权重与纬度-经度单元的大小成比例（标准化为均值1）。我们在时间和批次上应用均匀平均。

\(s_j=\mathbb{V}_{i,t}[x_{i,j}^{t+1} - x_{i,j}^{t}]^{-1}\)是每个变量级别的时间差的逆方差估计，目的是将目标（在连续步骤中）标准化为单位方差。这些估计是从训练数据中得出的。然后，我们应用了每个变量级别的损失权重 $w_j$。对于大气变量，我们在各个级别上进行加权平均，权重与该级别的气压成比例（标准化为单位均值），如图6a所示。我们在这里使用气压作为密度的代理[26]。请注意，应用于50 hPa或以下的气压级别的损失权重，HRES性能较GraphCast好，仅占所有变量和级别的总损失权重的0.66%。在模型开发中，我们调整了表面变量的损失权重，以使所有变量在验证性能上大致相当：2 t的权重为1.0，而10u、10v、msl和tp的权重分别为0.1，如图6b所示。所有变量的损失权重总和为7.4，即（大气变量的6 × 1.0，加上表面变量的（1.0 + 0.1 + 0.1 + 0.1 + 0.1））。

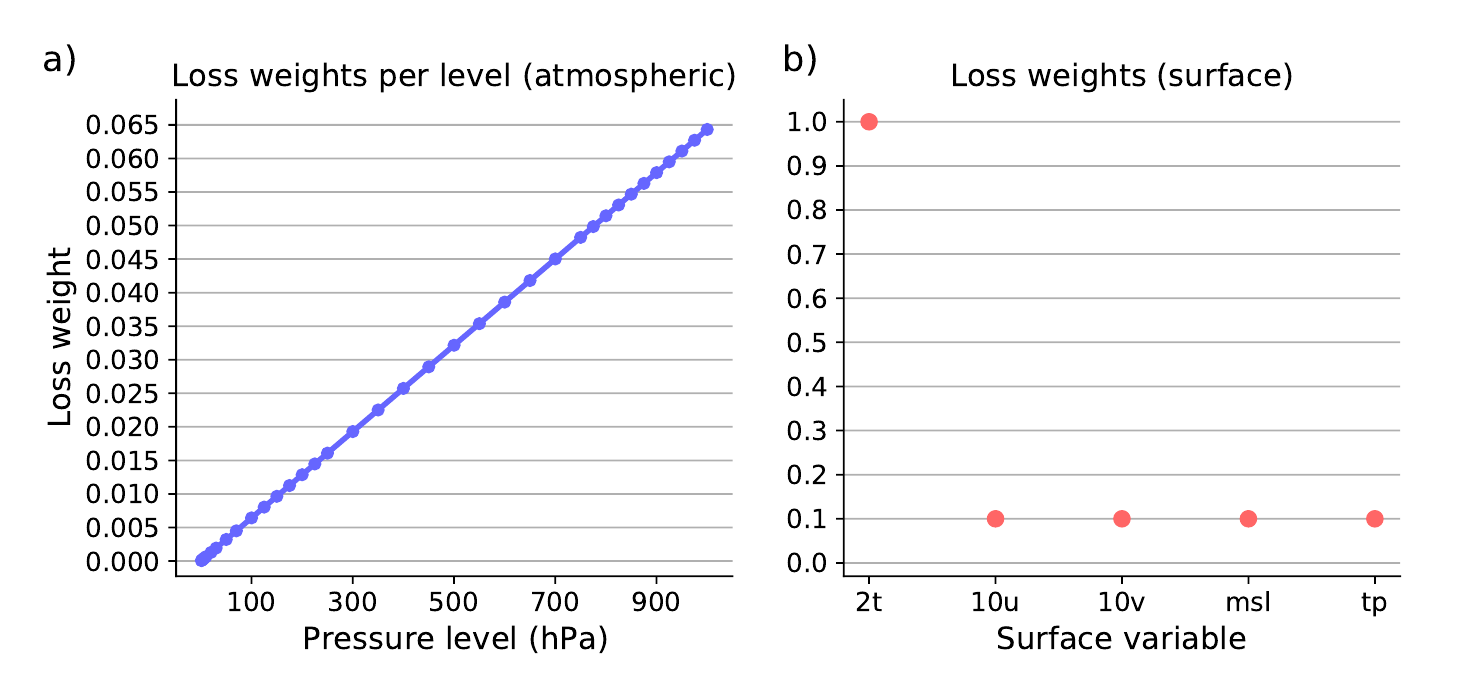图6 训练损失权重。 (a) 大气变量的每个气压级别的损失权重。 (b) 表面变量的损失权重。

4.3. 自回归目标训练

为了提高我们模型在多个步骤上进行准确预测的能力，我们采用了自回归训练机制，其中模型的预测下一步被反馈为预测下一步的输入。最终版本的GraphCast是在12个自回归步骤上进行训练的，遵循下面描述的课程训练计划。优化过程计算了每个预测步骤的损失，相对于相应的实际步骤，使用反向传播通过完整展开的模型迭代序列进行了模型参数的误差梯度反向传播（即通过时间的反向传播）。

4.4. 优化

使用梯度下降和小批量样本最小化训练目标函数。我们从ERA5训练数据集中有放回地抽样32个数据点的批次。我们使用AdamW优化器[33, 27]，其参数为（beta1 = 0.9，beta2 = 0.95）。我们对权重矩阵使用了0.1的权重衰减。我们使用梯度（范数）裁剪，最大范数值为32。

4.5. 课程训练计划

模型的训练通过三个阶段的课程进行，其中学习率和自回归步骤的数量有所变化。第一阶段包括1000次梯度下降更新，其中有一个自回归步骤，并且学习率的计划从0线性增加到1e−3（图7a）。第二阶段包括299,000次梯度下降更新，还是一个自回归步骤，并且学习率的计划使用半余弦衰减函数回到0（图7b）。第三阶段包括11,000次梯度下降更新，其中自回归步骤的数量从2增加到12，每1000次更新增加1，并且学习率固定为3e−7（图7c）。

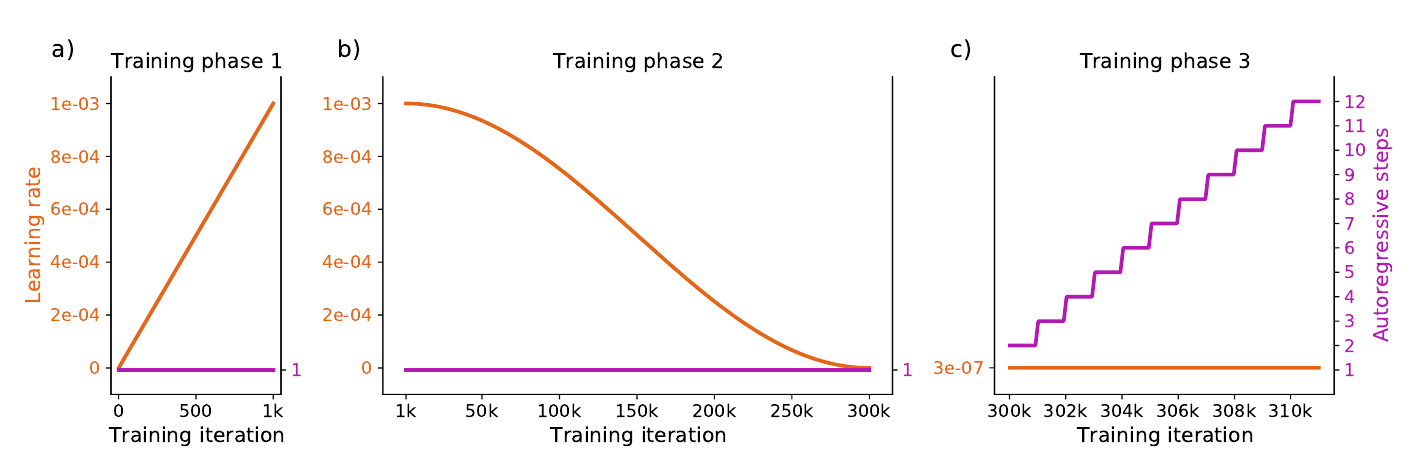图7 训练计划。 (a) 训练的第一阶段。 (b) 训练的第二阶段。 (c) 训练的第三阶段。

4.6. 减小内存占用

为了将长轨迹（12个自回归步骤）适应Cloud TPU v4设备的32GB内存，我们采用了几种策略来减小模型的内存占用。首先，我们使用批量并行性将数据分布到32个TPU设备上（即每个设备一个数据点）。其次，我们使用bfloat16浮点精度来减小激活所占内存的大小（注意，我们在评估时使用全精度数字（即float32）来计算性能指标）。最后，我们使用梯度检查点[11]来进一步减小内存占用，以降低训练速度的代价。

4.7. 训练时间

按照上述逐步增加自回归步骤的训练计划，GraphCast在32个TPU设备上训练大约需要四周时间。

4.8. 软件和硬件堆栈

我们使用JAX [9]、Haiku [23]、Jraph [17]、Optax、Jaxline [4]和xarray [25]来构建和训练我们的模型。

5 验证方法

本节详细介绍了我们的评估协议。第5.1节详细介绍了我们在因果方式下拆分数据的方法，确保我们的评估测试具有有意义的泛化性，即不利用未来信息。第5.2节更详细地解释了我们选择评估HRES技能并将其与GraphCast进行比较的方法，从需要与HRES特定的基准相对应开始以避免在短领先时间内对其进行惩罚（第5.2.1节），ERA5和HRES使用不同同化窗口对每个状态的前瞻(lookahead)产生的影响（第5.2.2节），选择GraphCast和HRES的初始化时间，以确保所有方法在输入和目标中都受益于相同的前瞻（第5.2.3节），以及我们用于报告2018年性能的评估期间（第5.2.4节）。第5.3节提供了我们主要结果中用于衡量技能的指标的定义，以及在补充结果中使用的指标。最后，第5.4节详细介绍了我们的统计测试方法。

5.1. 训练、验证和测试拆分

在测试阶段，使用在开发阶段结束时冻结的协议（第4.1节），我们训练了四个不同时期的GraphCast版本。这些模型分别在1979-2017、1979-2018、1979-2019和1979-2020的数据上进行了训练，以用于评估期间2018-2021、2019-2021、2020-2021和2021。同样，这些拆分保持了模型的训练版本和用于评估其性能的数据之间的因果分离（见图8）。我们的大多数结果是在2018年进行评估的（即使用在1979-2017年训练的模型），但也有几个例外情况。对于气旋追踪实验，我们报告了2018-2021的结果，因为气旋不太常见，因此包括更多年份可以增加样本量。我们使用最新版本的GraphCast对特定年份进行预测：GraphCast<2018对于2018年的预测，GraphCast<2019对于2019年的预测，依此类推。对于训练数据的最新性实验，我们评估了截至不同年份的不同模型在2021年测试性能上的比较。

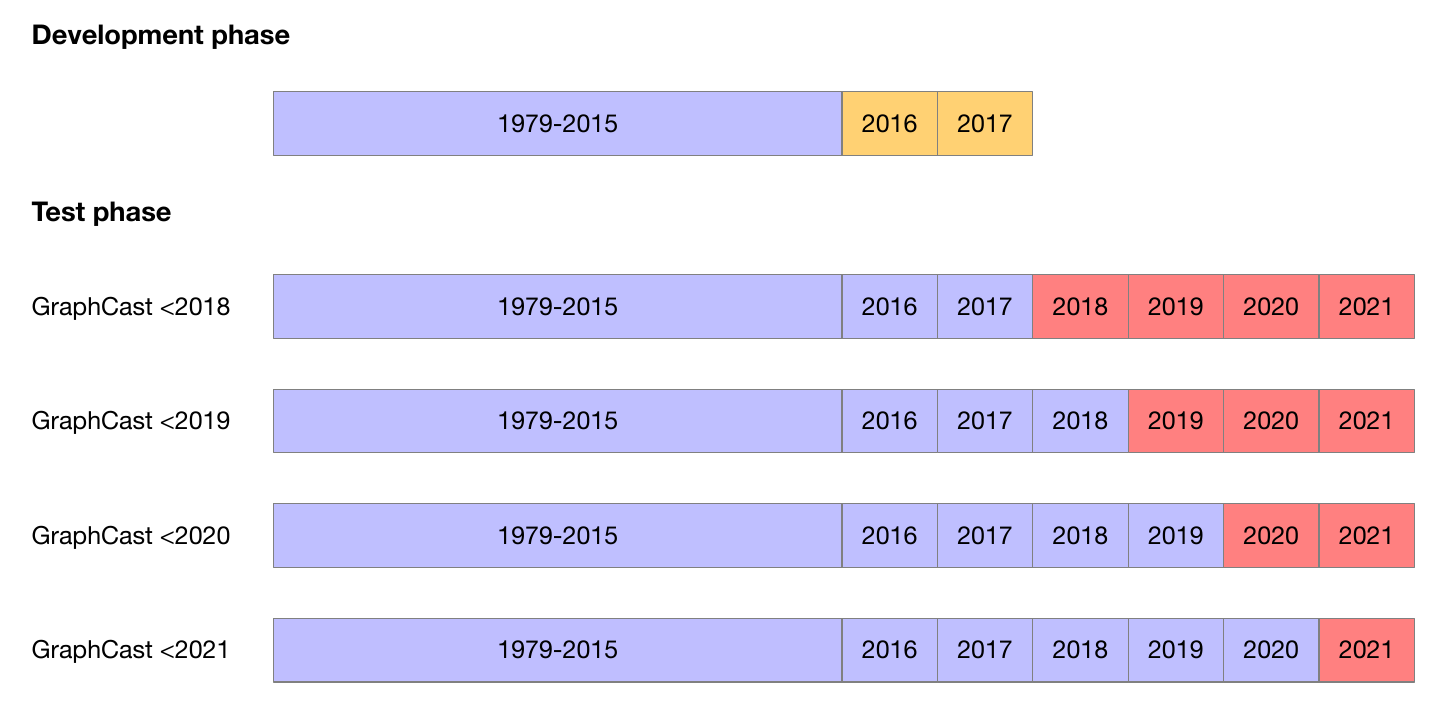图8 数据拆分摘要。在开发阶段，GraphCast在1979-2015年进行训练（蓝色）并在2016-2017年进行验证（黄色），直到训练协议被冻结。在测试阶段，GraphCast的四个版本在更大且更近期的训练集上进行了训练。蓝色年份表示给定版本的GraphCast的训练年份，红色年份表示在测试时可用的数据，同时满足拆分因果关系。

5.2. 将GraphCast与HRES进行比较

5.2.1. Ground True数据集的选择

GraphCast被训练以预测ERA5数据，并将ERA5数据作为输入；我们还使用ERA5作为评估我们模型的Ground True数据。然而，HRES预报是基于HRES分析初始化的。通常，将模型与其自身的分析进行验证会提供最佳的技能估计[45]。因此，我们构建了一个“HRES预报步骤0”（HRES-fc0）数据集，其中包含HRES预报的未来初始化的初始时间步（见表3）。我们使用HRES-fc0作为评估HRES预报的Ground True数据。

5.2.2. 确保同化窗口具有相等的前瞻

在比较GraphCast和HRES的技能时，我们做出了几个选择，以控制ERA5和HRES-fc0数据同化窗口之间的差异。如第1节所述，每天HRES使用以00z、06z、12z和18z为中心的四个+/-3h窗口同化观测数据（其中18z表示Zulu约定的18:00 UTC），而ERA5使用以00z和12z为中心的两个+9h/-3h窗口，或等效地，以06z和18z为中心的两个+3h/-9h窗口。请参见图9以进行说明。我们选择评估GraphCast从06z和18z初始化的预测，确保其输入携带来自未来+3h观测的信息，与HRES的输入相匹配。我们没有评估GraphCast从00z和12z初始化的情况，以避免ERA5输入具有+9h前瞻而HRES输入具有+3h前瞻的不匹配。图10展示了从06z/18z和00z/12z初始化的GraphCast性能。当从具有更大前瞻的状态初始化时，GraphCast显示出明显的改善，并且在较长的前瞻时间内持续存在，支持我们从06z/18z初始化进行评估的选择。在选择要评估的目标时，我们采用了相同的逻辑：我们仅评估那些对HRES和ERA5都具有+3h前瞻的目标。鉴于我们选择在06z和18z进行初始化，这相当于每12小时评估一次，即在未来的06z和18z分析时间。作为一个实际例子，如果我们要评估从06z初始化的GraphCast和HRES，在领先时间6h（即12z），GraphCast的目标将整合+9h前瞻，而HRES的目标仅会融合+3h前瞻。在相等的领先时间下，这可能使GraphCast的任务更加困难。

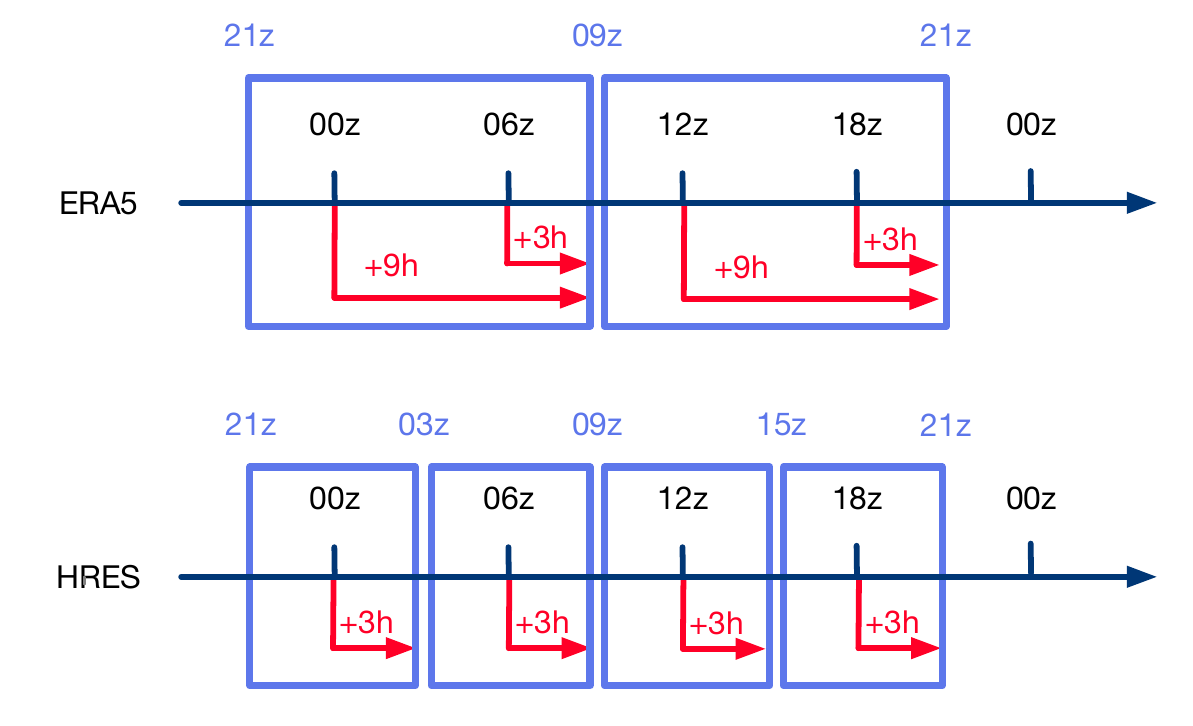图9 ERA5和HRES同化窗口的示意图。数据同化窗口以蓝色矩形标记，对于ERA5为12小时，对于HRES为6小时。红色箭头表示相应状态中包含的有效前瞻的持续时间。

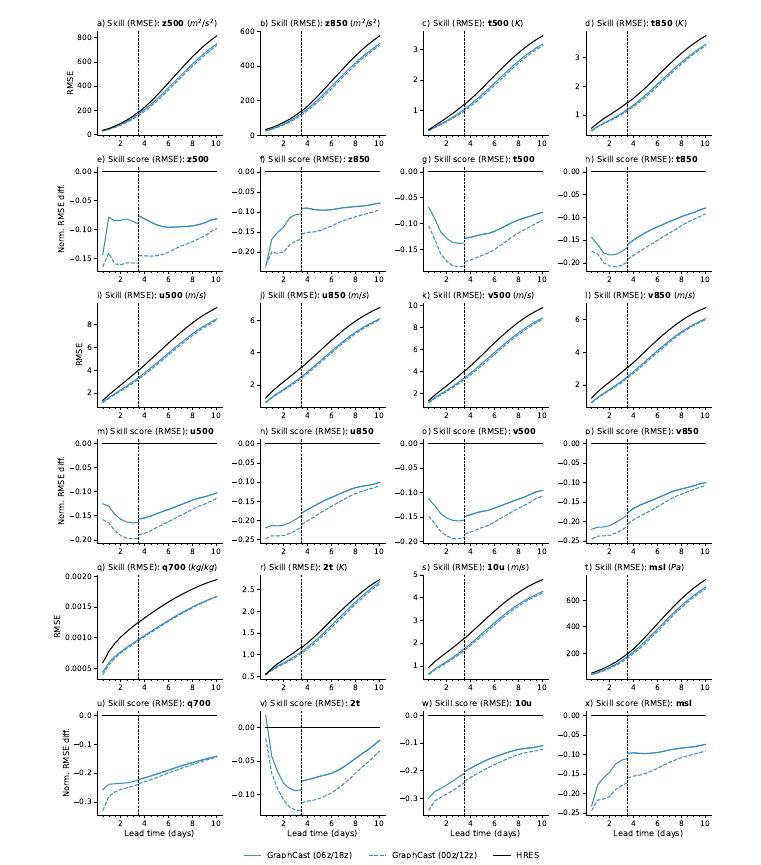图10 初始化时间的影响。当从具有更长前瞻的ERA5状态（00z/12z）初始化时，GraphCast的性能优于从具有较短前瞻的ERA5状态（06z/18z）初始化时。这种改善在短到长的预测领先时间内都可以测量到。这支持我们选择从06z/18z评估所有模型，以避免给GraphCast带来优势。x轴表示领先时间，在10天内以12小时为步长。y轴表示RMSE技能或技能得分。

5.2.3. 初始化时间和有效时间的对齐

如上所述，与HRES进行公正比较要求我们使用06z和18z初始化时进行GraphCast的评估，并且领先时间是12小时的倍数，这意味着有效时间也是06z和18z。

对于领先时间长达3.75天，存档中有使用06z和18z初始化和有效时间的HRES预报，我们使用这些数据在这些领先时间进行与GraphCast的类似比较。请注意，因为我们仅在12小时的领先时间增量上进行评估，这意味着最终领先时间为3.5天。

对于4天及以上的领先时间，存档中只有00z和12z初始化的HRES预报，这意味着我们只能将GraphCast与06z和18z进行比较，并将HRES与00z和12z进行比较。

在这些全球RMSE的比较中，我们预期时间差异会给HRES带来轻微的优势。在图11中，我们可以看到在3.5天的领先时间之内，HRES的RMSE通常在00z和12z初始化/有效时间上平均较小，而在06z和18z时间上，GraphCast进行评估。我们还可以看到随着领先时间的增加，差异减小，而且06z/18z的RMSE通常似乎趋向于00z/12z的RMSE上方渐近线，但在其内2%。我们预计这些差异会在更长的领先时间继续有利于HRES，并且无论如何都会保持较小，因此我们认为它们不会影响我们在GraphCast具有更强技能的情况下的结论。

每当我们将RMSE和其他评估指标绘制为领先时间的函数时，我们用虚线表示切换点，即从在06z/18z上评估HRES切换到在00z/12z上评估的3.5天时刻。在这个切换点，我们清楚地绘制了06z/18z和00z/12z的指标，以显示不连续性。

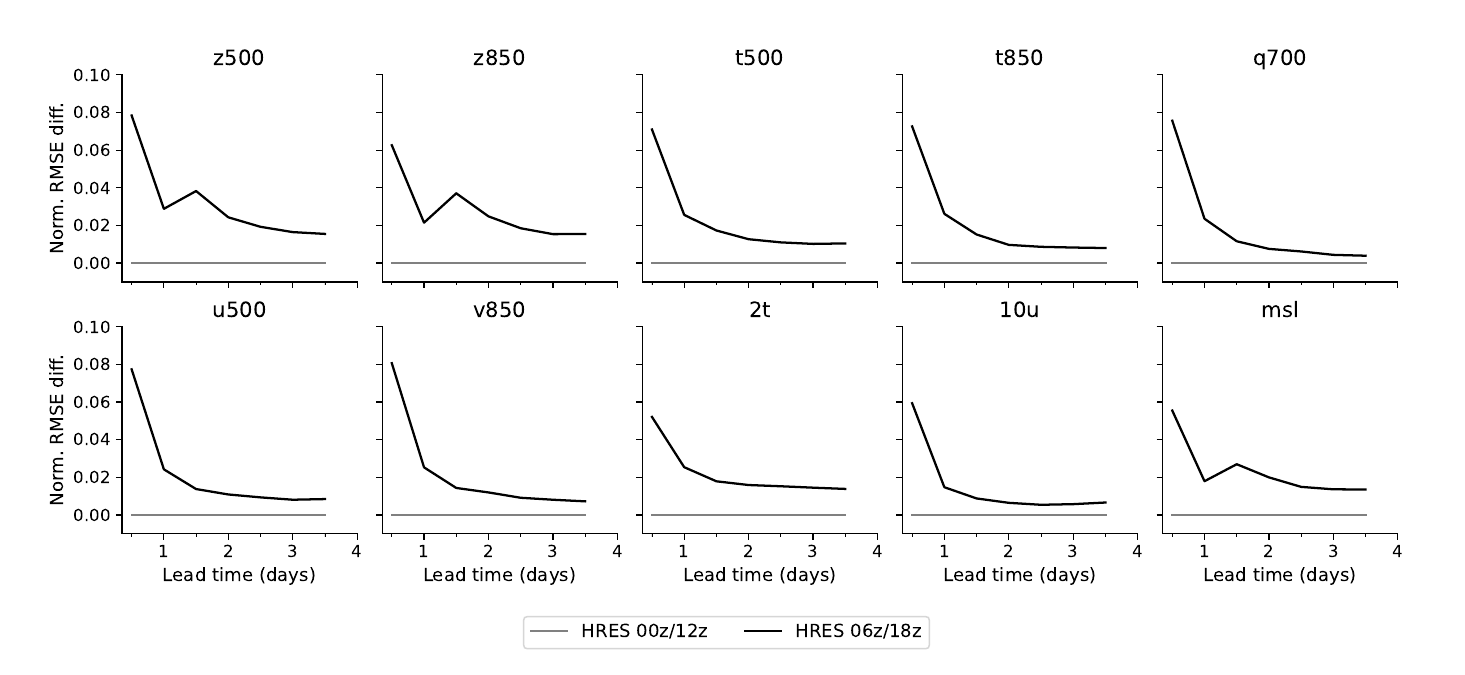图11 HRES在06z/18z和00z/12z初始化时的RMSE技能得分。图表显示HRES在06z/18z初始化时（黑线）相对于在00z/12z初始化时的RMSE技能得分（灰线）随领先时间的变化情况。我们绘制了长达3.5天的领先时间，这是HRES在06z/18z初始化时的预测可用的最长时间。y轴刻度是共享的。

5.2.4. 评估时期

我们的大部分主要结果是基于2018年的数据报告的（来自我们的测试集），其中第一个预报初始化时间为2018-01-01_06:00:00 UTC，最后一个为2018-12-31_18:00:00，或者在评估HRES的更长领先时间时为2018-01-01_00:00:00和2018-12-31_12:00:00。对于气旋追踪和数据新近性影响的其他结果分别使用了2018年至2021年和2021年的数据。

5.3. 评估指标

我们使用均方根误差（RMSE）和异常相关系数（ACC）来量化GraphCast、其他机器学习模型和HRES的技能水平，这两者都是相对各自地面真实数据计算的。RMSE度量了对于给定变量 j 和给定前导时间$\tau$见方程（20）），预测和地面真实之间的差异的幅度。ACC，$\mathcal{L}_{\text{ACC}}^{j,\tau}$，定义在方程（29）中，衡量了预测与气候学差异，即预测的平均天气与给定位置和日期的地面真实差异之间的相关性。对于技能评分，我们使用模型 A 与基线 B 之间的归一化 RMSE 差异$(\text{RMSE}_A − \text{RMSE}_B ）/\text{RMSE}_B$，以及归一化 ACC 差异$\text{ACC}_A − \text{ACC}_B/(1 − \text{ACC}_B )$。

所有指标均使用float32精度计算，并使用变量的本机动态范围报告，不进行规范化。

均方根误差（RMSE）。我们使用经纬度加权的均方根误差（RMSE）来量化给定变量 $x_j$ 和前导时间 $\tau = t\Delta d$的预测技能，具体计算如下：

其中

• $d_0 \in D_{\text{eval}}$ 代表评估数据集中的预报初始化日期和时间，
• $j \in J$ 索引变量和层次，例如，J = {z1000, z850，…，2t，msl}，
• $i \in G_{0.25°}$ 是网格中位置（纬度和经度）的坐标，
• \(\hat{x}_{j,i}^{d_0+\tau}\)和\(x_{j,i}^{d_0+\tau}\) 是某个变量级别、位置和前导时间的预测和目标值，
• $a_i$ 是纬度经度格网单元的面积（在整个网格上归一化为单位平均值），随纬度变化。

通过在预测初始化上的均值计算中采用平方根，我们遵循WeatherBench [41]的惯例。然而，我们注意到这与许多其他情境中定义RMSE的方式不同，其中平方根仅应用于最终均值，即

均方根误差（RMSE），球谐(spherical harmonic)域。在涉及到在球谐域中进行滤波、截断或分解的预测的所有比较中，为方便起见，我们直接在球谐域中计算RMSE，所有均值都在平方根内取，

其中\(\hat{f}_{j,l,m}^{d_0+\tau}\)和\(f_{j,l,m}^{d_0+\tau}\)是具有总波数 j，纬度波数(wavenumber )l 和经度波数m的球谐函数的预测和目标系数。我们使用离散球谐变换 [13] 从基于网格的数据中计算这些系数，其三角形截断波数为719，这是为了解决我们在赤道上0.25°（28km）分辨率的网格。这意味着l的范围从0到$l_{max} = 719$，m的范围从−l到l。

这个RMSE密切逼近Equation (21)中给出的基于网格的RMSE的定义，但并非完全可比，部分原因是在波数719处的三角形截断不能解决靠近极点的等角网格的额外分辨率。

均方根误差（RMSE），每个位置。这是根据Equation (21)中的RMSE定义计算的，但针对单个位置：

我们还按纬度将RMSE进行了细分：

其中 $|\text{lon}(G_{0.25°})|$ = 1440 是我们正规的0.25°网格中不同经度的数量。

均方根误差（RMSE），按地表高程。这是根据方程（21）的RMSE定义计算的，但限制在地表位势高度范围内，由表面位势的下限$z_l \le z_{\text{surface}} \lt z_u$给出：

其中$\mathbb{I}$表示指示函数。

平均偏差误差（MBE），按位置计算。此量的定义为：

每个位置的均方根平均偏差误差（RMS-MBE）。这量化了方程（26）中每个位置偏差的平均幅度，表示为：

每个位置平均偏差错误的相关性。这量化了两个不同模型A和B的每个位置偏差（Equation (26)）之间的相关性。我们使用未居中的相关系数，因为在偏差测量中原点零的显著性，根据以下公式计算这个数量：

异常相关系数（ACC）。我们还根据以下公式计算了给定变量$x_j$和前瞻时间$\tau = t\Delta d$的异常相关系数：

其中$C_{j,i}^{d_0+\tau}$，是给定变量、水平层、纬度和经度处的climatology平均值，C是包含验证时间$d_0+\tau$的一年中的日平均。气候平均值是使用1993年至2016年之间的ERA5数据计算的。其他变量的定义与上文相同。

5.4. 统计方法学

5.4.1. 均值差异的显著性检验

对于每个前瞻时间τ和变量层次j，我们测试GraphCast和HRES的每个初始化时间的RMSE均值之间是否存在差异（在公式（30）中定义）。我们使用带有自相关校正的成对双侧t检验，遵循[16]的方法学。该检验假设预测分数差异的时间序列适当地建模为平稳的Gaussian AR(2)过程。这个假设对于我们来说并不完全成立，但在[16]中被认为是适用于ECMWF对中程天气预报的验证的。

我们测试的名义样本大小是n = 730，在4天以下的前瞻时间，包括2018年365天中每天的两次预报初始化。 （对于超过4天的前瞻时间，我们有n = 729，请参见第5.4.2节）。然而，这些数据（RMSE预测差异）在时间上是自相关的。根据[16]的方法，我们估计了标准误差的膨胀因子k，该因子进行了校正。k的值在1.21到6.75之间，最高值通常出现在短前瞻时间和最低压力水平。这对应于在16到501范围内的降低有效样本大小$n_{\text{eff}}=n/k^2$。

请参见表5，其中包含我们显著性检验的详细结果，包括p值、t检验统计量的值和$n_{\text{eff}}$的值。

6 与先前的机器学习基线比较

为了确定GraphCast的性能与其他ML方法相比如何，我们关注Pangu-Weather [7]，这是一个在0.25°分辨率下运行的强大的MLWP基线。为了进行最直接的比较，我们偏离了我们的评估协议，并使用了[7]中描述的协议。由于已发布的Pangu-Weather结果是从00z/12z初始化获得的，我们使用相同的初始化时间进行GraphCast的评估，而不是使用06z/18z，就像本文的其余部分一样。这使得这两个模型都可以在相同的输入上初始化，这些输入包含相同数量的先行信息（+9小时，参见第5.2.2和5.2.3节）。由于HRES初始化最多包含+3小时的先行信息，即使从00z/12z初始化，我们也没有显示HRES（针对ERA5或HRES-fc0的对比），因为这会对其不利。我们协议的第二个不同之处是每6小时报告性能，而不是每12小时。由于两个模型都是针对ERA5进行评估，它们的目标是相同的，特别是对于给定的前瞻时间，目标对于GraphCast和Pangu-Weather都包含+3小时或+9小时的先行信息，从而实现了公平的比较。

Pangu-Weather [7]报告了其7天的预报准确性（RMSE和ACC）：z500、t500、t850、q500、u500、v500、2t、10u、10v和msl。

如图12所示，GraphCast（蓝线）在99.2%的目标上优于Pangu-Weather [7]（红线）。对于表面变量（2t、10u、10v、msl），GraphCast在前几天的误差约为10-20%较低，并且在较长的前瞻时间内趋于稳定，误差约为7-10%较低。Pangu-Weather唯一在252个总目标中优于GraphCast的两个度量标准是z500，在6和12小时的前瞻时间，其中GraphCast的平均RMSE较高1.7%（图12a、e）。

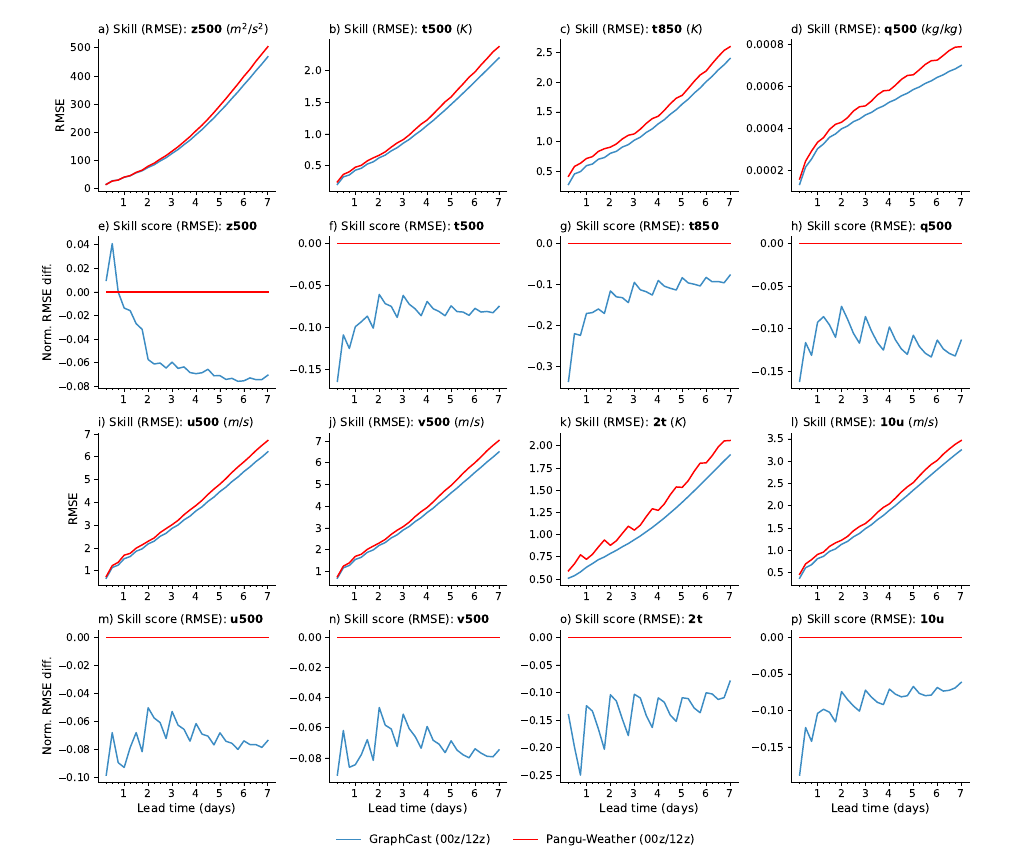图12 GraphCast与Pangu-Weather的RMSE技能比较。第1和第3行显示GraphCast（蓝线）和Pangu-Weather [7]（红线）的绝对RMSE；第2和第4行显示相对于Pangu-Weather的模型之间的标准化RMSE差异。每个子图表示一个单一变量（对于大气变量，还包括压力水平），如子图标题所示。x轴表示前瞻时间，在10天内以6小时的步幅。y轴表示（绝对或标准化的）RMSE。所选择的变量和层次是由[7]报告的。我们没有包含10v，因为已经包含了10u，而且这两者高度相关。

• ← Previous Post
• Next Post →