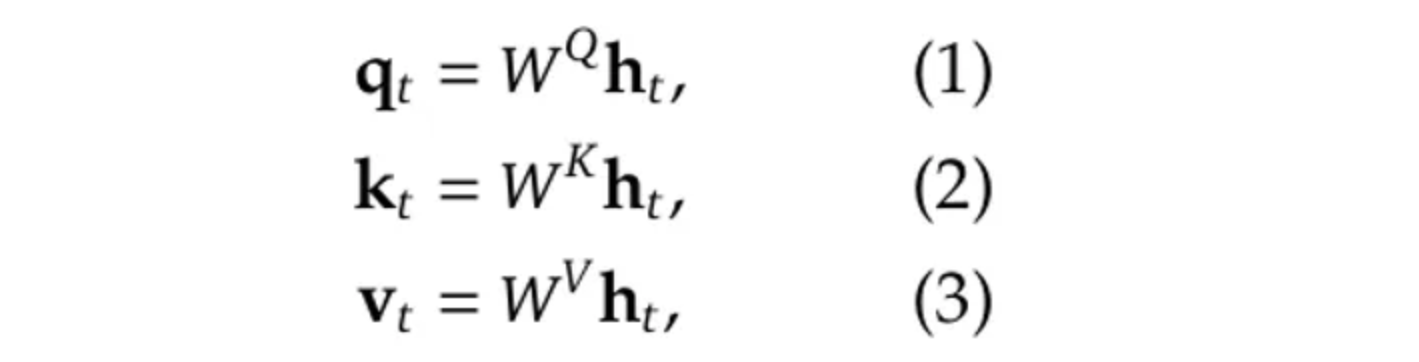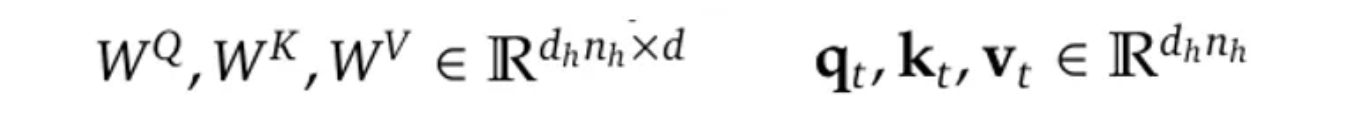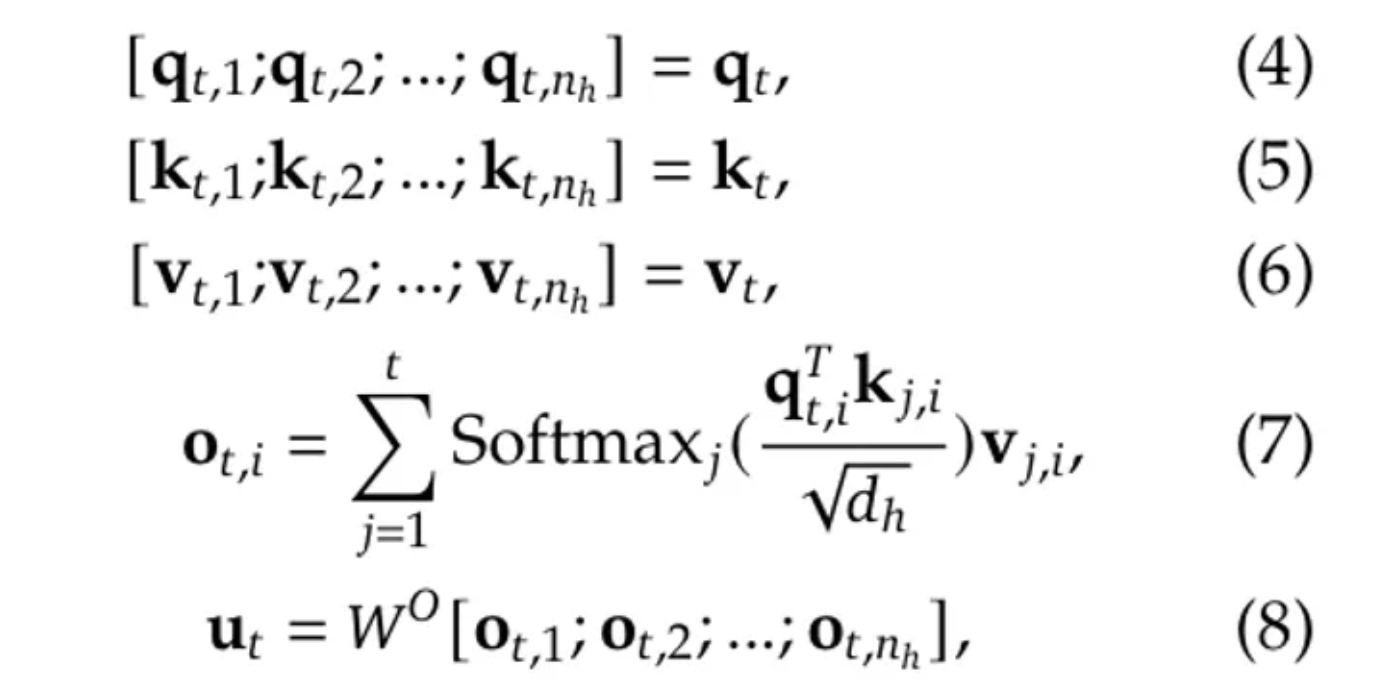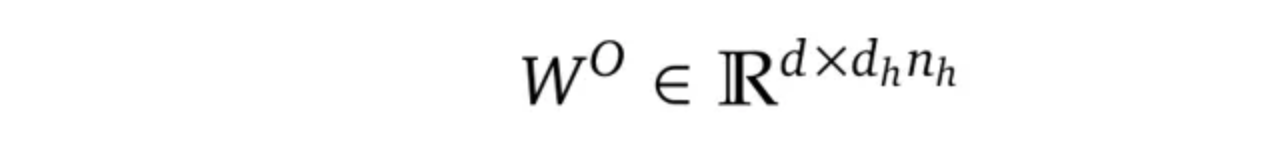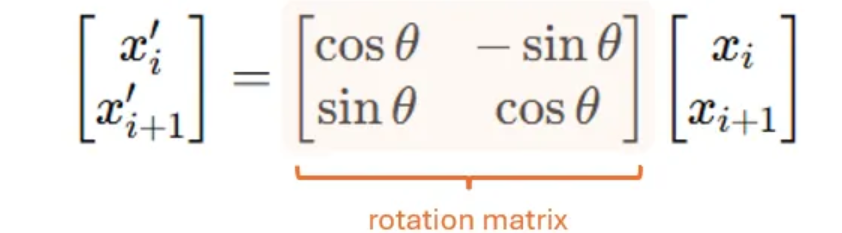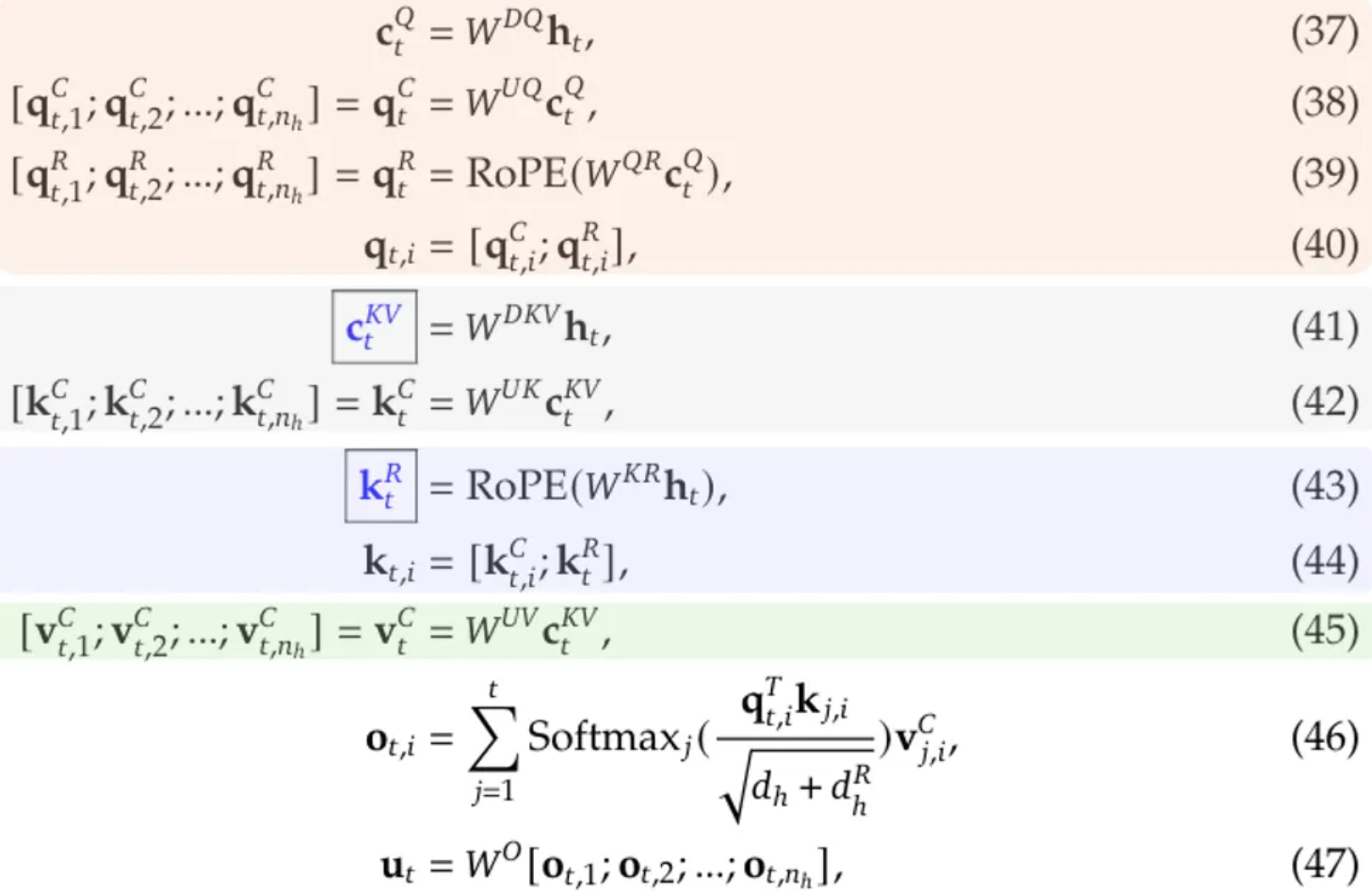翻译：DeepSeek-V3 Explained 1: Multi-head Latent Attention

本文翻译DeepSeek-V3 Explained 1: Multi-head Latent Attention。

这是我们的新系列文章《DeepSeek-V3 解析》的第一篇，我们将尝试揭开 DeepSeek-V3 [1], [2] 的神秘面纱，这是 DeepSeek 最新开源的模型。

在本系列中，我们计划涵盖两个主要主题：

DeepSeek-V3 的主要架构创新，包括多头潜在注意力（Multi-head Latent Attention, MLA）[[3]、DeepSeekMoE [4]、无辅助损失的负载均衡 [5] 和多标记预测训练。
DeepSeek-V3 的训练，包括预训练、微调和强化学习对齐阶段。

本文主要关注多头潜在注意力，这一技术最初是在 DeepSeek-V2 的开发中提出的，随后也被应用于 DeepSeek-V3。

背景
多头潜在注意力 (Multi-head Latent Attention, MLA)
参考文献

背景

为了更好地理解MLA，并使本文内容更加完整，我们将在深入探讨MLA的细节之前，重新回顾本节中几个相关的概念。

解码器专用Transformer中的MHA

请注意，MLA是为了加快自回归文本生成中的推理速度而开发的，因此我们在此背景下讨论的MHA是针对解码器专用Transformer的。

下图比较了用于解码的三种Transformer架构，其中（a）展示了在原始论文《Attention is All You Need》中提出的编码器和解码器。其解码器部分随后被文献[6]简化，形成了图（b）中所示的解码器专用Transformer模型，该模型后来被许多生成模型（如GPT[8]）采用。

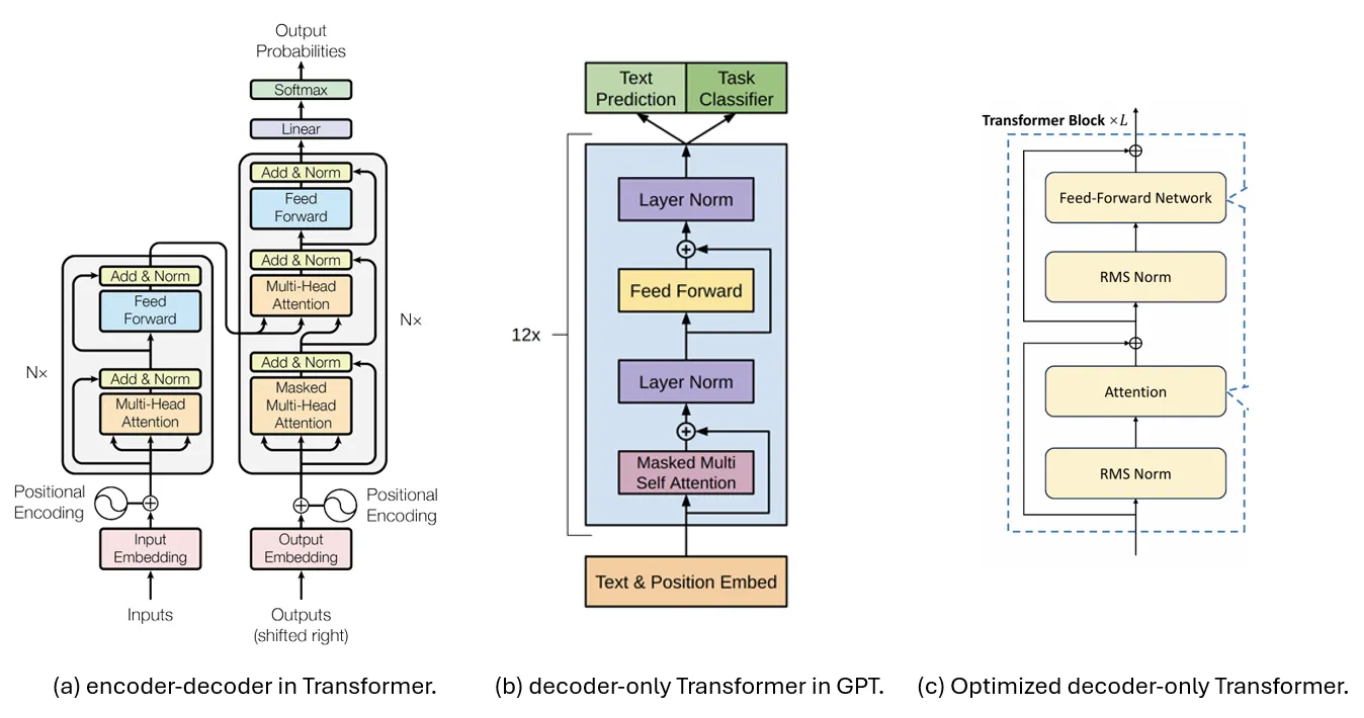图1.Transformer架构。（a）在[6]中提出的编码器-解码器。（b）在[7]中提出的解码器专用Transformer，并在GPT[8]中使用。（c）在注意力机制之前使用RMS Norm的（b）的优化版本。[3]

如今，大语言模型（LLMs）更倾向于选择图（c）中所示的结构，以实现更稳定的训练。这种结构在输入端而非输出端应用了归一化，并且将LayerNorm升级为RMS Norm。这将作为本文讨论的基准架构。

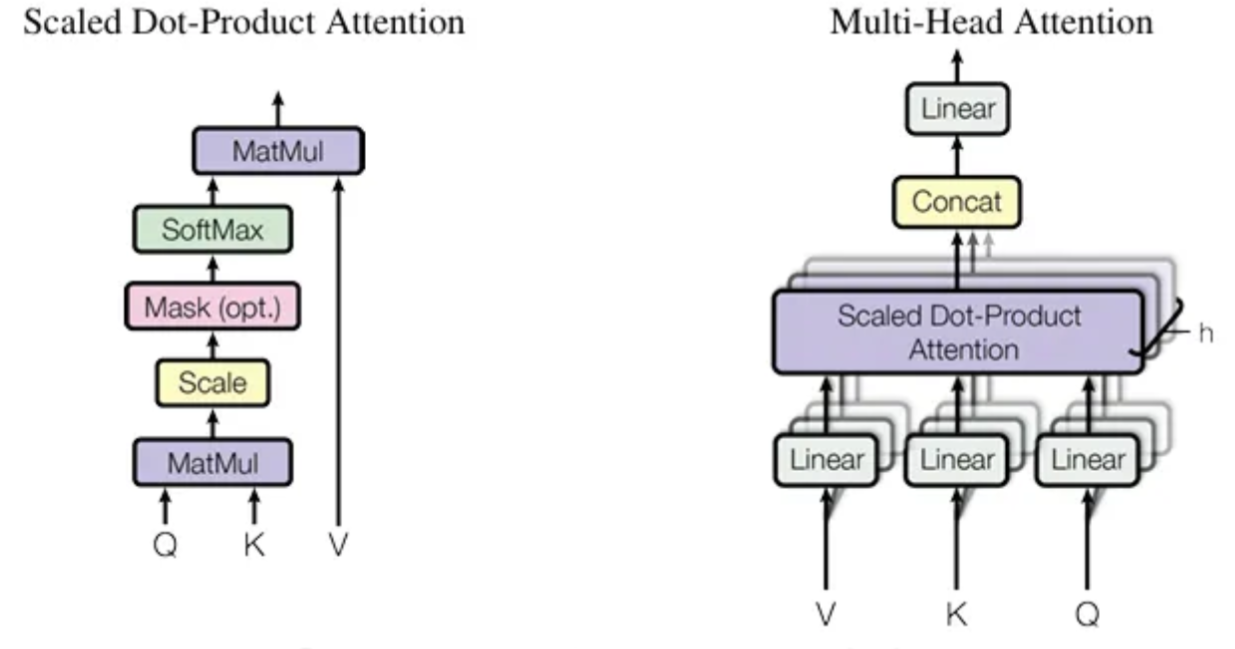
在这个背景下，多头注意力（MHA）的计算过程在很大程度上遵循了文献[6]中的描述，如下图所示：

假设我们有 $n_h$ 个注意力头，每个注意力头的维度表示为 $d_h$，那么拼接后的维度将是 $n_h \cdot d_h$。

对于一个有 $l$ 层的模型，如果我们用 $h_t$ 表示第 $t$ 个标记在该层的输入，其维度为 $d$，我们需要使用线性映射矩阵将 $h_t$ 的维度从 $d$ 映射到 $n_h \cdot d_h$。

更正式地，我们有（公式来自[3]）：

其中 $W^Q$, $W^K$和$W^V$是线性映射矩阵:

经过这样的映射后，$q_t$、$k_t$ 和 $v_t$ 将被拆分成 $n_h$ 个头，以计算缩放点积注意力：

其中 $W^O$ 是另一个投影矩阵，用于将维度从 $n_h \cdot d_h$ 映射回到 $d$：

请注意，上述由公式(1)到(8)描述的过程仅适用于单个标记。在推理过程中，我们需要对每个新生成的标记重复这一过程，这涉及大量的重复计算。这导致了一种称为键值缓存（Key-Value Cache）的技术。

键值缓存（Key-Value Cache）

顾名思义，键值缓存是一种旨在通过缓存和重用之前的键（Key）和值（Value），而不是在每个解码步骤中重新计算它们，从而加速自回归过程的技术。

需要注意的是，键值缓存通常仅在推理阶段使用，因为在训练阶段，我们仍然需要并行处理整个输入序列。

键值缓存通常以循环缓冲区的形式实现。在每个解码步骤中，仅计算新的查询（Query），而缓存中存储的键（K）和值（V）将被重用，因此注意力将使用新的查询（Q）和重用的键（K）和值（V）来计算。同时，新标记的键（K）和值（V）也会被追加到缓存中，以便后续使用。

然而，键值缓存带来的加速是以增加内存为代价的，因为键值缓存通常会随着批量大小 × 序列长度 × 隐藏层大小 × 注意头数量而扩展，这在我们有更大的批量大小或更长的序列时会导致内存瓶颈。

这进一步促使了两种旨在解决这一限制的技术的出现：多查询注意力（Multi-Query Attention）和分组查询注意力（Grouped-Query Attention）。

多查询注意力（MQA）与分组查询注意力（GQA）

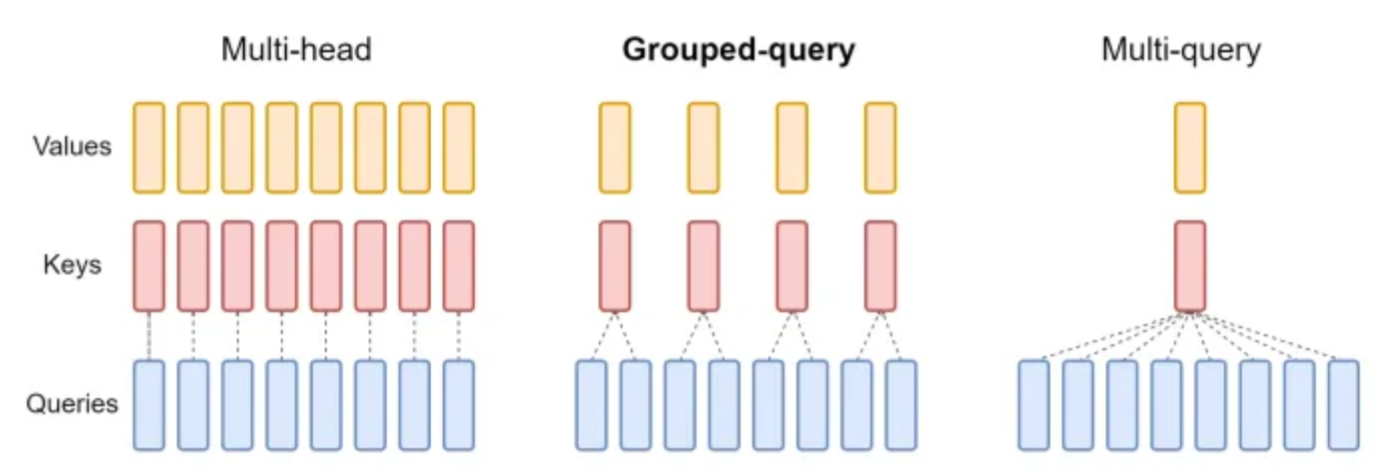
下图展示了原始多头注意力（MHA）、分组查询注意力（GQA）[10]和多查询注意力（MQA）[9]之间的比较。

MQA的基本思想是在所有查询头之间共享一个键（Key）和一个值（Value）头，这可以显著减少内存使用，但同时也会对注意力的准确性产生影响。

GQA可以被视为介于MHA和MQA之间的一种折中方法，其中一对键和值头仅由一组查询头共享，而不是所有查询头。然而，这仍然会导致与MHA相比结果略逊一筹。

在后续章节中，我们将看到MLA如何在内存效率和建模准确性之间寻求平衡。

RoPE（旋转位置嵌入）

我们需要提到的最后一个背景知识是RoPE [11]，它通过使用正弦函数在多头注意力中旋转查询（Query）和键（Key）向量，将位置信息直接编码到注意力机制中。

更具体地说，RoPE在每个标记的查询和键向量上应用一个位置相关的旋转矩阵，并以正弦和余弦函数为基础，但以一种独特的方式应用它们以实现旋转。

为了理解其位置相关性，考虑一个只有4个元素的玩具嵌入向量，即（$x_1$，$x_2$，$x_3$，$x_4$）。

要应用RoPE，我们首先将连续的维度配对：

（$x_1$，$x_2$）→位置1 （$x_3$，$x_4$）→位置2

然后，我们应用一个旋转矩阵来旋转每一对：

其中，$\theta = \theta(p) = p \cdot \theta_0$，而$\theta_0$是一个基础频率。在我们的4维玩具示例中，这意味着（$x_1$，$x_2$）将被旋转$\theta_0$，而（$x_3$，$x_4$）将被旋转$2 \cdot \theta_0$。

这就是为什么我们将这种旋转矩阵称为位置相关的：在每个位置（或每对位置），我们会应用一个不同的旋转矩阵，旋转角度由位置决定。

RoPE因其在编码长序列方面的高效性而被广泛应用于现代大型语言模型（LLMs）中，但从上述公式可以看出，它对查询（Q）和键（K）都是位置敏感的，这在某些方面使其与MLA不兼容。

多头潜在注意力 (Multi-head Latent Attention, MLA)

我们终于可以进入 MLA 部分了。在本节中，我们将首先概述 MLA 的核心思想，然后深入探讨它为何需要修改旋转位置编码 (RoPE)。最后，我们将详细介绍 MLA 的算法及其性能。

MLA：核心思想

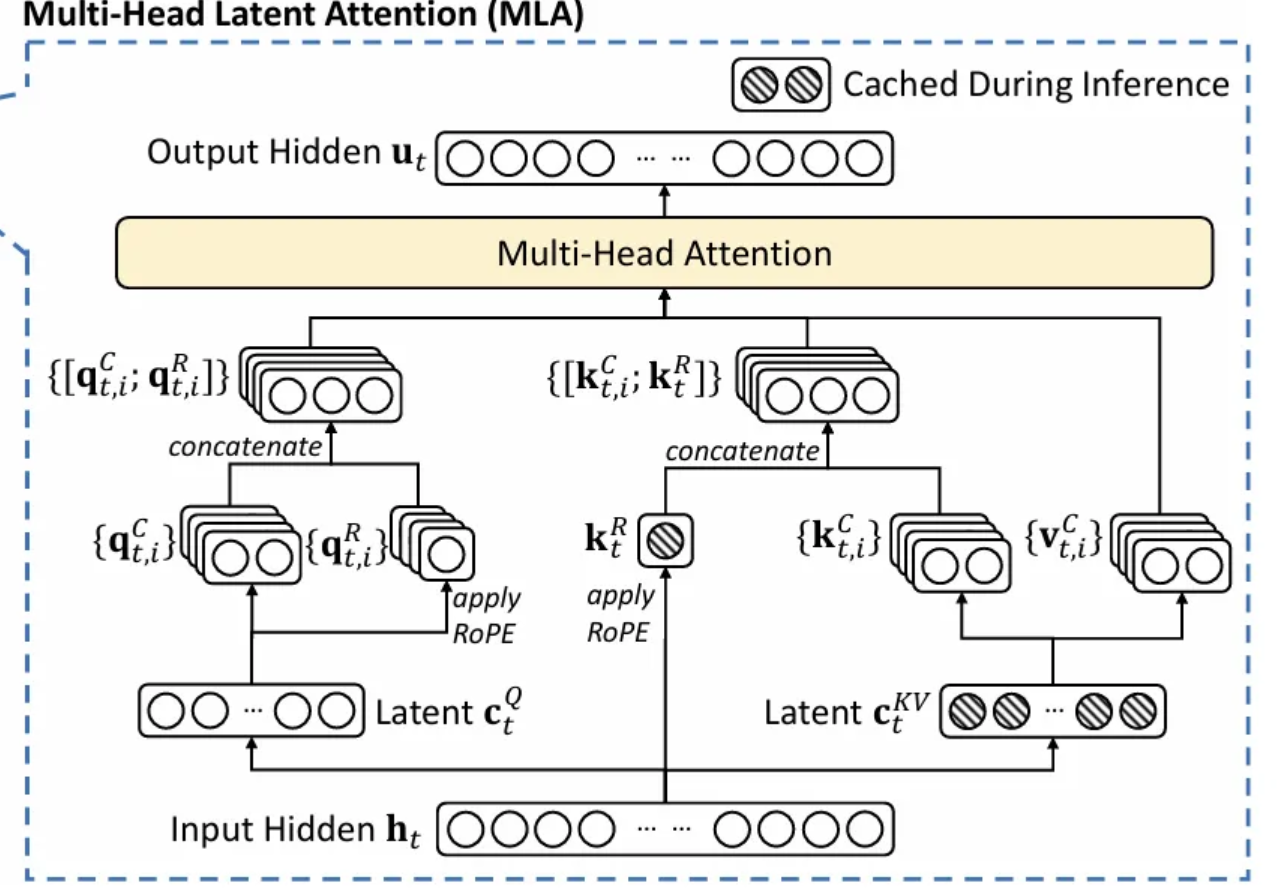
MLA 的基本思想是将注意力输入 $h_t$ 压缩成一个低维度的潜在向量，其维度为 $d_c$，其中 $d_c$ 远低于原始维度 ($n_h \cdot d_h$)。之后，当我们需要计算注意力时，我们可以将这个潜在向量映射回高维空间，以恢复键（keys）和值（values）。因此，只需要存储潜在向量，从而显著减少内存占用。

这个过程可以用以下方程更正式地描述：其中 $c^{KV}_t$ 是潜在向量，$W^{DKV}$ 是将 $h_t$ 的维度从 ($n_h \cdot d_h$) 映射到 $d_c$ 的压缩矩阵（这里上标中的 D 代表“下投影”，意味着压缩维度），而 $W^{UK}$ 和 $W^{UV}$ 都是上投影矩阵，它们将共享的潜在向量映射回高维空间。

类似地，我们也可以将查询（queries）映射到一个潜在的低维向量，然后将其再映射回原始的高维空间：

为什么需要解耦式 RoPE

正如我们之前提到的，RoPE 是训练生成模型处理长序列的常见选择。如果直接应用上述 MLA 策略，将与 RoPE 不兼容。

为了更清楚地说明这一点，考虑我们使用公式 (7) 计算注意力时会发生什么：当我们用转置的 q 乘以 k 时，矩阵 $W^Q$ 和 $W^{UK}$ 将出现在中间，它们的组合相当于一个将维度从 $d_c$ 映射到 $d$ 的单一映射。

在原始论文 [3] 中，作者将此描述为 $W^{UK}$ 可以被 $W^Q$ “吸收”，因此我们不需要在缓存中存储 $W^{UK}$，从而进一步减少了内存使用。

然而，当我们考虑图 (4) 中的旋转矩阵时，情况就不同了，因为 RoPE 会在 $W^{UK}$ 的左侧应用一个旋转矩阵，而这个旋转矩阵最终会出现在转置的 $W^Q$ 和 $W^{UK}$ 之间。

正如我们在背景部分解释的那样，这个旋转矩阵是位置依赖的，这意味着每个位置的旋转矩阵都不同。因此，$W^{UK}$ 不再能被 $W^Q$ 吸收。

为了解决这个冲突，作者提出了他们称之为“解耦式 RoPE”的方法，即引入额外的查询向量和共享的键向量，并且这些额外的向量只用于 RoPE 过程中，同时使原始的键与旋转矩阵保持某种隔离。

MLA 的整个过程可以总结如下（公式编号沿用 [3] 的附录 C）：

其中：

公式 (37) 至 (40) 描述了如何处理查询（query）token。
公式 (41) 和 (42) 描述了如何处理键（key）token。
公式 (43) 和 (44) 描述了如何使用额外的共享键进行 RoPE（旋转位置编码），请注意，公式 (42) 的输出不参与 RoPE。
公式 (45) 描述了如何处理值（value）token。

在此过程中，只有带有蓝色框的变量需要被缓存。以下流程图可以更清晰地展示这一过程：

MLA 的性能

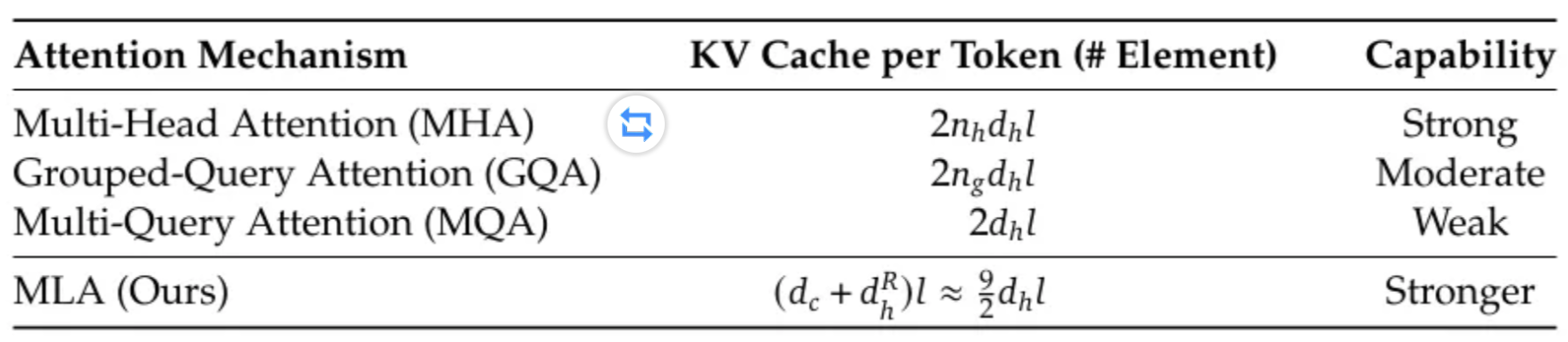
下表比较了多头注意力 (MHA)、分组查询注意力 (GQA)、多查询注意力 (MQA) 和多头潜在注意力 (MLA) 在每 token 所需的 KV 缓存元素数量以及建模能力方面的差异。这表明 MLA 确实能在内存效率和建模能力之间取得更好的平衡。

有趣的是，MLA 的建模能力甚至超越了原始的 MHA。

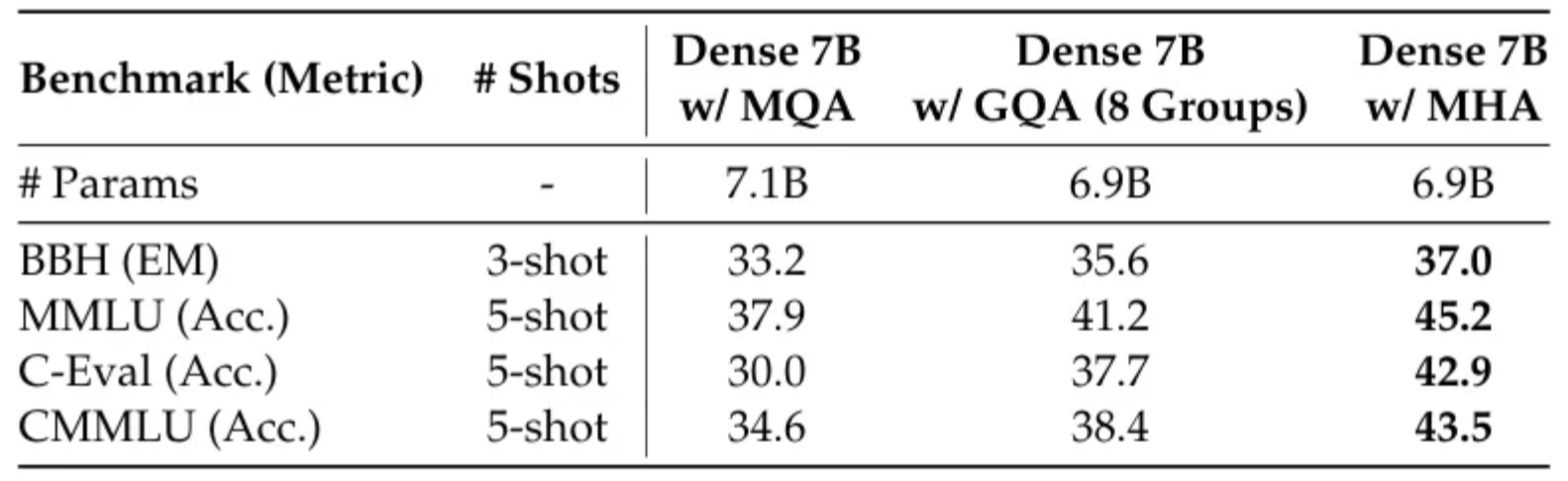
更具体地说，下表展示了 MHA、GQA 和 MQA 在 7B 模型上的性能，其中 MHA 的表现显著优于 MQA 和 GQA。

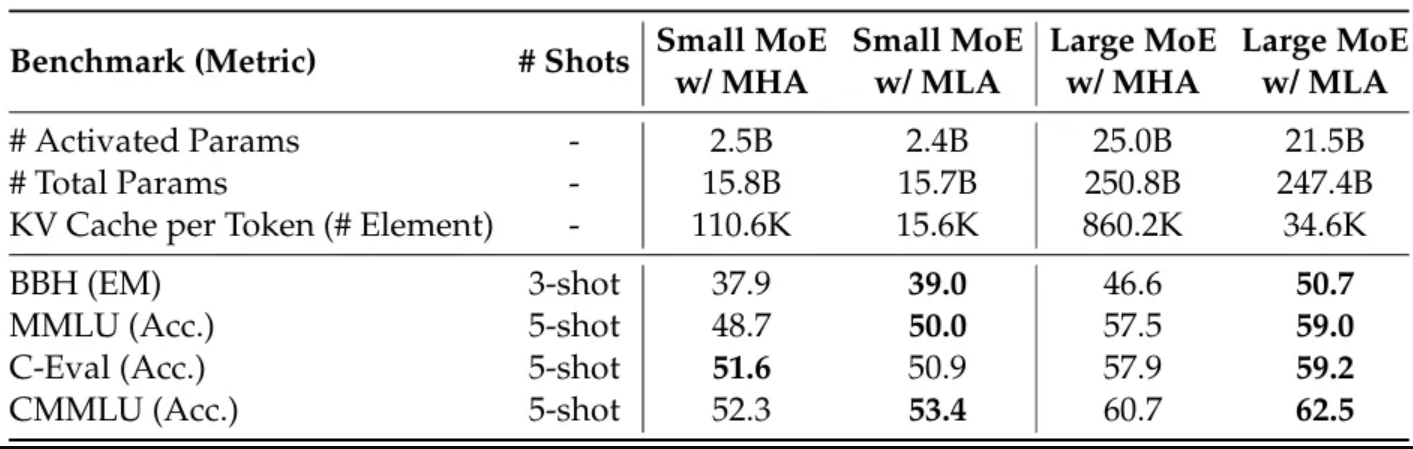
[3] 的作者还对 MHA 和 MLA 进行了分析，结果总结在下表中。从中可以看出，MLA 的总体表现更优。