本文翻译YaRN: Efficient Context Window Extension of Large Language Models。
目录
摘要
旋转位置嵌入（Rotary Position Embeddings, RoPE）已被证明能有效编码基于 Transformer 的语言模型中的位置信息。然而，这些模型未能泛化到其训练时的序列长度之外。我们提出了 YaRN (Yet another RoPE extensioN method)，这是一种计算高效的方法，用于扩展此类模型的上下文窗口，与现有方法相比，它所需的 token 数量减少 10 倍，训练步数减少 2.5 倍。使用 YaRN，我们展示了 LLaMA 模型可以有效地利用并外推到比其原始预训练允许的更长的上下文长度，同时在上下文窗口扩展方面超越了之前的最先进水平。此外，我们证明了 YaRN 具有外推超越微调数据集有限上下文的能力。使用 YaRN 微调的模型已在线提供并可复现，上下文长度可达 128k，网址为 https://github.com/jquesnelle/yarn。
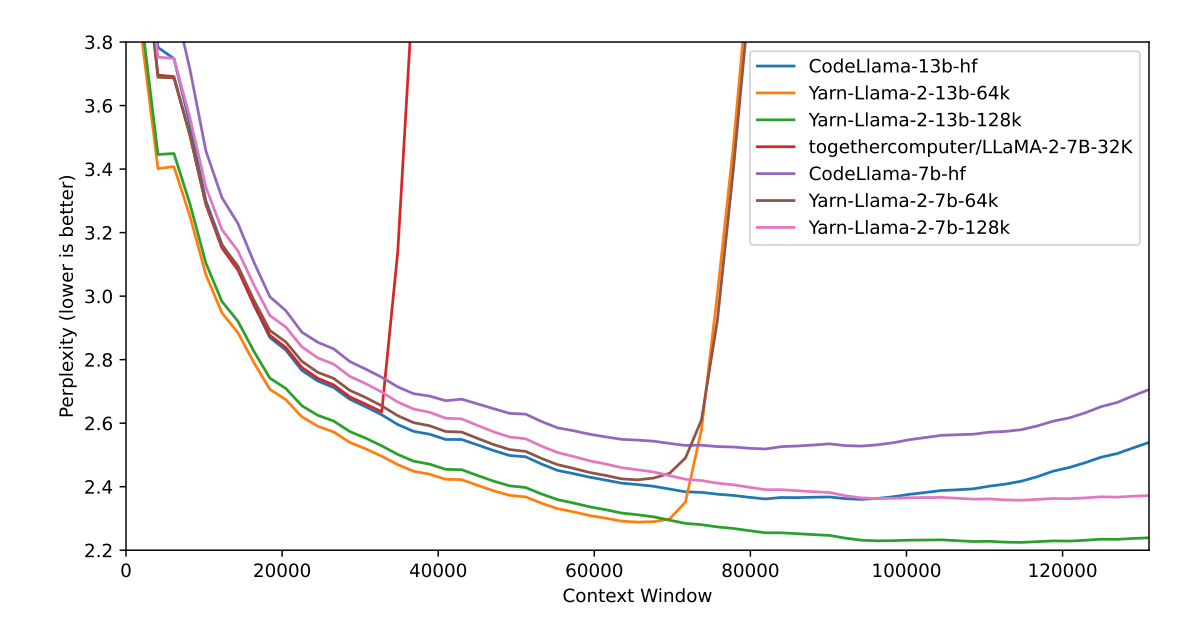图 1：十份 128k Proof-pile 文档（截断至评估上下文窗口大小）的滑动窗口困惑度 (S = 256)
1 引言
基于 Transformer 的大型语言模型（LLM） [40] 已成为许多自然语言处理（NLP）任务的普遍选择，尤其是在上下文学习（ICL）等长距离能力至关重要的场景。在执行 NLP 任务时，由训练过程决定的最大序列长度（上下文窗口）一直是预训练 LLM 的主要限制之一。能够通过少量微调（或不微调）动态扩展上下文窗口变得越来越受欢迎。为此，Transformer 的位置编码成为讨论的焦点。
最初的 Transformer 架构使用了绝对正弦位置编码，后来被改进为可学习的绝对位置编码 [15]。此后，相对位置编码方案 [32] 进一步提高了 Transformer 的性能。目前最流行的相对位置编码有 T5 Relative Bias [30]、RoPE [34]、XPos [35] 和 ALiBi [27]。
位置编码的一个反复出现的局限性是无法泛化到训练期间看到的上下文窗口之外。尽管 ALiBi 等一些方法能够进行有限的泛化，但没有一种方法能够泛化到比其预训练长度显著更长的序列 [22]。
已经有一些工作旨在克服这一限制。[9] 和同时期 [21] 提出通过位置插值（PI）和少量数据微调来稍微修改 RoPE，从而扩展上下文长度。作为替代，[6] 提出了“NTK-aware”插值，考虑了高频损失。此后，又提出了“NTK-aware”插值的两种改进方法，侧重点不同：
- “Dynamic NTK”插值方法 [14]，用于无需微调的预训练模型。
- “NTK-by-parts”插值方法 [7]，在对少量更长上下文数据进行微调时表现最佳。
“NTK-aware”插值和“Dynamic NTK”插值已经出现在 Code Llama [31]（使用“NTK-aware”插值）和 Qwen 7B [2]（使用“Dynamic NTK”）等开源模型中。
在本文中，除了完整阐述先前未发表的关于“NTK-aware”、“Dynamic NTK”和“NTK-by-part”插值的工作之外，我们还提出了 YaRN (Yet another RoPE extensioN method)，这是一种改进的方法，旨在高效扩展使用旋转位置嵌入 (RoPE) 训练的模型的上下文窗口，包括 LLaMA [38]、GPT-NeoX [5] 和 PaLM [10] 系列模型。
YaRN 在上下文窗口扩展方面达到了最先进的性能，其微调数据量不到原始预训练数据的 ~0.1%。同时，通过结合推理时技术——动态缩放 (Dynamic Scaling)，Dynamic-YaRN 可以在不进行任何微调的情况下将上下文窗口扩展两倍以上。
2 背景与相关工作
2.1 旋转位置嵌入 (Rotary Position Embeddings)
我们工作的基础是 [34] 中引入的旋转位置嵌入（Rotary Position Embedding, RoPE）。我们在一个隐藏层上进行操作，其中隐藏神经元的集合表示为 $D$。给定一个向量序列 $x_1, \dots, x_L \in \mathbb{R}^{|D|}$，根据 [34] 的符号，注意力层首先将这些向量转换为查询向量和键向量：
\[q_m = f_q(x_m, m) \in \mathbb{R}^{|D|}, \quad k_n = f_k(x_n, n) \in \mathbb{R}^{|D|}. \quad (1)\]接下来，注意力权重计算如下：
\[\text{softmax}\left(\frac{q_m^T k_n}{\sqrt{|D|}}\right), \quad (2)\]其中 $q_m, k_n$ 被视为列向量，因此 $q_m^T k_n$ 仅仅是欧几里得内积。
在 RoPE 中，我们首先假设 $|D|$ 是偶数，并将嵌入空间和隐藏状态识别为复向量空间：
\[\mathbb{R}^{|D|} \cong \mathbb{C}^{|D|/2}\]其中内积 $q^T k$ 变为标准 Hermitian 内积的实部 $\text{Re}(q^*k)$。更具体地说，同构交错实部和复部：
\[(x_m)_1, \dots,(x_m)_{|D|} \quad \mapsto \quad (x_m)_1 + i(x_m)_2, \dots,((x_m)_{|D|-1} + i(x_m)_{|D|}), \quad (3)\] \[(q_m)_1, \dots,(q_m)_{|D|} \quad \mapsto \quad (q_m)_1 + i(q_m)_2, \dots,((q_m)_{|D|-1} + i(q_m)_{|D|}). \quad (4)\]为了将嵌入 $x_m, x_n$ 转换为查询和键向量，我们首先给定 $\mathbb{R}$-线性算子 $W_q, W_k : \mathbb{R}^{|D|} \to \mathbb{R}^{|D|}$。
在复坐标中，函数 $f_q, f_k$ 由下式给出：
\[f_q(x_m, m) = e^{im\theta} W_q x_m, \quad f_k(x_n, n) = e^{in\theta} W_k x_n, \quad (5)\]其中 $\theta = \text{diag}(\theta_1, \dots, \theta_{|D|/2})$ 是对角矩阵，其中 $\theta_d = b^{-2d/|D|}$ 且 $b = 10000$。通过这种方式，RoPE 将每个（复值）隐藏神经元与一个单独的频率 $\theta_d$ 关联起来。这样做的好处是查询向量和键向量之间的点积仅依赖于相对距离 $m - n$，如下所示：
\[\langle f_q(x_m, m), f_k(x_n, n) \rangle_{\mathbb{R}} \quad (6)\] \[= \text{Re}(\langle f_q(x_m, m), f_k(x_n, n) \rangle_{\mathbb{C}}) \quad (7)\] \[= \text{Re}(x_m^* W_q^* W_k x_n e^{i\theta(m-n)}) \quad (8)\] \[= g(x_m, x_n, m - n). \quad (9)\]在实坐标中，RoPE 可以用以下函数表示：
\[f_W(x_m, m, \theta_d) = \begin{pmatrix} \cos m\theta_1 & -\sin m\theta_1 & 0 & 0 & \cdots & 0 & 0 \\ \sin m\theta_1 & \cos m\theta_1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m\theta_2 & -\sin m\theta_2 & \cdots & 0 & 0 \\ 0 & 0 & \sin m\theta_2 & \cos m\theta_2 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m\theta_l & -\sin m\theta_l \\ 0 & 0 & 0 & 0 & \cdots & \sin m\theta_l & \cos m\theta_l \end{pmatrix} W x_m,\]因此：
\[f_q = f_{W_q}, \quad f_k = f_{W_k}\]2.2 位置插值 (Position Interpolation)
由于语言模型通常是使用固定的上下文长度进行预训练的，因此很自然地会问，如何通过相对较少的数据微调来扩展上下文长度。对于使用 RoPE 作为位置嵌入的语言模型，Chen 等人 [9] 以及同时期的 kaiokendev [21] 提出了位置插值 (Position Interpolation, PI) 来将上下文长度扩展到预训练的限制之外。虽然直接的外推法在序列 $w_1, \dots, w_L$（其中 $L$ 大于预训练限制）上表现不佳，但他们发现，在预训练限制内插值位置索引在少量微调的帮助下效果良好。具体来说，对于一个带有 RoPE 的预训练语言模型，他们通过以下方式修改 RoPE：
\[f'_W (x_m, m, \theta_d) = f_W \left( x_m, \frac{mL}{L'}, \theta_d \right), \quad (10)\]其中 $L’ > L$ 是超出预训练限制的新上下文窗口。通过原始预训练模型加上修改后的 RoPE 公式，他们进一步在少几个数量级的 token 上（Chen 等人 [9] 中为几十亿个 token）对语言模型进行微调，并成功实现了上下文窗口扩展。
2.3 补充符号
扩展上下文长度与原始上下文长度之间的比率具有特殊重要性，我们引入符号 $s$ 定义为：
\[s = \frac{L'}{L}, \quad (11)\]我们将 $s$ 称为缩放因子（scale factor）。
我们还将公式 (10) 重写并简化为以下通用形式：
\[f'_W(x_m, m, \theta_d) = f_W(x_m, g(m), h(\theta_d)), \quad (12)\]其中 $g(m)$ 和 $h(\theta_d)$ 是依赖于方法的函数。对于 PI（位置插值），我们有 $g(m) = m/s$，$h(\theta_d) = \theta_d$。在后续章节中，当我们引入新的插值方法时，有时我们只指定函数 $g(m)$ 和 $h(\theta_d)$。
此外，我们将 $\lambda_d$ 定义为 RoPE 嵌入在第 $d$ 个隐藏维度上的波长（wavelength）：
\[\lambda_d = \frac{2\pi}{\theta_d} = 2\pi b^{\frac{2d}{|D|}}. \quad (13)\]波长描述了 RoPE 嵌入在维度 $d$ 上完成一次完整旋转 ($2\pi$) 所需的 token 长度。
鉴于某些插值方法（例如 PI）不关心维度的波长，我们将这些方法称为“盲”插值方法（”blind” interpolation methods），而其他方法（例如 YaRN）则关心波长，我们将它们归类为“目标”插值方法（”targeted” interpolation methods）。
2.4 相关工作
ReRoPE [33] 也旨在扩展使用 RoPE 预训练的现有模型的上下文大小，并声称无需任何微调即可实现“无限”上下文长度。这一说法得到了在 Llama 2 13B 模型上，损失随上下文长度增加到 16k 而单调递减的支持。它通过修改注意力机制来实现上下文扩展，因此并非纯粹的嵌入插值方法。由于它目前与 Flash Attention 2 [13] 不兼容，并且在推理过程中需要两次注意力通过，我们不将其纳入比较。
与我们的工作同时进行的 LM-Infinite [16] 提出了与 YaRN 类似的想法，但侧重于未经微调模型的“即时”长度泛化。由于它们也修改了模型的注意力机制，因此它不是一种嵌入插值方法，并且不能立即与 Flash Attention 2 兼容。
3 方法论
虽然 PI（位置插值）平等地拉伸所有 RoPE 维度，但我们发现 PI [9] 描述的理论插值界限不足以预测 RoPE 与 LLM 内部嵌入之间复杂的动态。在以下小节中，我们将描述我们单独识别并解决的 PI 的主要问题，以便为读者提供我们协同使用的每种方法（以获得完整的 YaRN 方法）的背景、起源和理由。
3.1 高频信息丢失 - “NTK-aware”插值
如果我们仅从信息编码的角度来看 RoPE，[36] 使用神经正切核（NTK）理论表明，如果输入维度较低且相应的嵌入缺乏高频分量，深度神经网络在学习高频信息方面存在困难。这里我们可以看到相似之处：token 的位置信息是一维的，而 RoPE 将其扩展为 $n$ 维复向量嵌入。
RoPE 在许多方面与傅里叶特征 [36] 非常相似，因为可以将 RoPE 定义为傅里叶特征的一种特殊的 1D 情况。不加区分地拉伸 RoPE 嵌入会导致重要的高频细节丢失，而网络需要这些细节来解析既非常相似又非常接近的 token（描述最小距离的旋转不能太小，以便网络能够检测到它）。
我们假设在 PI [9] 中观察到的在较大上下文尺寸上微调后，较短上下文尺寸的困惑度略有增加可能与此问题有关。在理想情况下，在较大上下文尺寸上进行微调不应该降低较小上下文尺寸的性能。
为了解决在插值 RoPE 嵌入时丢失高频信息的问题，[6] 开发了“NTK-aware”插值。它不是将 RoPE 的每个维度都等比例地缩放 $s$ 倍，而是通过减少高频缩放，增加低频缩放，将插值压力分散到多个维度上。可以通过多种方式实现这种转换，但最简单的方法是对 $\theta$ 的值进行基变换。
更准确地说，根据第 2.3 节中设定的符号，我们将“NTK-aware”插值方案定义如下（具体推导细节请参见附录 A.1）：
定义 1 “NTK-aware”插值是对 RoPE 的修改，使用公式 (12) 和以下函数。
\[g(m) = m \quad (14)\] \[h(\theta_d) = b'^{-2d/|D|} \quad (15)\]其中
\[b' = b \cdot s^{\frac{|D|}{|D|-2}}. \quad (16)\]根据 [6] 的结果，与 PI [9] 相比，该方法在扩展未经微调模型的上下文大小方面表现得更好。然而，该方法的一个主要缺点是，鉴于它不仅仅是一种插值方案，一些维度会稍微外推到“超出范围”的值，因此使用“NTK-aware”插值 [6] 进行微调会比 PI [9] 产生更差的结果。此外，由于“超出范围”的值，理论上的缩放因子 $s$ 不能准确描述真实的上下文扩展比例。实际上，对于给定的上下文长度扩展，缩放值 $s$ 必须设置得高于预期值。
我们注意到，在本文发布前不久，Code Llama [31] 发布了，并手动将基数 $b$ 缩放到 1M 来使用“NTK-aware”缩放。
3.2 相对局部距离的损失——“NTK-by-parts”插值
对于 PI（位置插值）和“NTK-aware”插值等盲插值方法，我们平等地处理所有 RoPE 隐藏维度（即它们对网络具有相同的影响）。然而，有强烈的线索表明我们需要目标插值方法。
在本节中，我们主要根据 RoPE 公式中定义的波长 $\lambda_d$（见公式 13）进行思考。为简单起见，我们省略了 $\lambda_d$ 中的下标 $d$，读者可以将 $\lambda$ 视为任意周期函数的波长。
RoPE 嵌入的一个有趣观察是，给定上下文大小 $L$，存在一些维度 $d$，其波长长于预训练期间看到的最大上下文长度（$\lambda > L$），这表明某些维度的嵌入可能未在旋转域中均匀分布。在这种情况下，我们假定拥有所有唯一位置对意味着绝对位置信息保持完整。相反，当波长较短时，网络只能访问相对位置信息。
此外，当我们通过缩放因子 $s$ 或使用基变换 $b’$ 来拉伸所有 RoPE 维度时，所有 token 都会彼此更接近，因为两个向量旋转较小的点积会更大。这种缩放严重损害了 LLM 理解其内部嵌入之间微小局部关系的能力。我们假设这种压缩会导致模型在相邻 token 的位置顺序上感到困惑，从而损害模型的能力。
为了弥补这个问题，鉴于我们发现的这两个先前的观察结果，我们选择根本不插值高频维度，而总是插值低频维度。具体来说：
- 如果波长 $\lambda$ 远小于上下文大小 $L$，我们不进行插值；
- 如果波长 $\lambda$ 等于或大于上下文大小 $L$，我们只进行插值并避免任何外推（与之前的“NTK-aware”方法不同）；
- 介于两者之间的维度可以兼具两者，类似于“NTK-aware”插值。
因此，引入原始上下文大小 $L$ 与波长 $\lambda$ 之间的比率 $r = \frac{L}{\lambda}$ 更为方便。在第 $d$ 个隐藏状态中，比率 $r$ 以以下方式依赖于 $d$：
\[r(d) = \frac{L}{\lambda_d} = \frac{L}{2\pi b'^{\frac{2d}{|D|}}}. \quad (17)\]为了定义上述不同插值策略的边界，我们引入了两个额外参数 $\alpha, \beta$。所有满足 $r(d) < \alpha$ 的隐藏维度 $d$ 是我们按缩放因子 $s$ 进行线性插值的维度（完全像 PI 一样，避免任何外推），而满足 $r(d) > \beta$ 的维度 $d$ 是我们根本不进行插值的维度。定义斜坡函数 $\gamma$ 为：
\[\gamma(r) = \begin{cases} 0, & \text{if } r < \alpha \\ 1, & \text{if } r > \beta \\ \frac{r - \alpha}{\beta - \alpha}, & \text{otherwise}. \end{cases} \quad (18)\]借助斜坡函数，“NTK-by-parts”方法可以描述如下：
定义 2 “NTK-by-parts”插值是对 RoPE 的修改，使用公式 (12) 和以下函数：
\[g(m) = m \quad (19)\] \[h(\theta_d) = \left( 1 - \gamma\left(r(d)\right) \right)\frac{\theta_d}{s} + \gamma\left(r(d)\right)\theta_d. \quad (20)\]$\alpha$ 和 $\beta$ 的值应根据具体情况进行调整。例如，我们通过实验发现，对于 Llama 系列模型，$\alpha = 1$ 和 $\beta = 32$ 是很好的值。
使用本节中描述的技术，所得方法的一个变体以“NTK-by-parts”插值 [7] 的名称发布。正如 [7] 所示，这种改进的方法在未经微调的模型和经过微调的模型上都优于之前的 PI [9] 和“NTK-aware”3.1 插值方法。
3.3 动态缩放——“Dynamic NTK”插值
在许多用例中，会执行多次前向传播，其序列长度从 1 到最大上下文大小不等。一个典型的例子是自回归生成，其中序列长度在每一步之后递增 1。有两种应用使用缩放因子 $s$ 的插值方法（包括 PI、“NTK-aware”和“NTK-by-parts”）：
- 在整个推理周期中，嵌入层是固定的，包括缩放因子 $s = L’/L$，其中 $L’$ 是扩展上下文大小的固定数量。
- 在每次前向传播中，位置嵌入更新缩放因子 $s = \max(1, l’/L)$，其中 $l’$ 是当前序列的序列长度。
问题 (1) 是模型在长度小于 $L$ 时可能会经历性能折扣，并且当序列长度长于 $L’$ 时会突然下降。但是，通过执行 (2) 中的动态缩放，它允许模型在达到训练上下文限制 $L’$ 时优雅地降级，而不是立即崩溃。我们将这种推理时方法称为动态缩放方法（Dynamic Scaling method）。当它与“NTK-aware”插值结合时，我们称之为“Dynamic NTK”插值（”Dynamic NTK” interpolation）。它首次公开出现在 [14] 的 Reddit 帖子中。
一个值得注意的事实是，“Dynamic NTK”插值在未进行任何微调的预训练模型 $L$ 上表现异常出色（$L’ = L$）。这得到了附录 B.3 中实验的支持。
通常在重复的前向传播中，会应用 kv-caching [8]，以便我们可以重用先前的键值向量并提高整体效率。我们指出，在某些实现中，当 RoPE 嵌入被缓存时，需要注意对其进行修改，以便与 kv-caching 的动态缩放兼容。正确的实现应该在应用 RoPE 之前缓存 kv-嵌入，因为每个 token 的 RoPE 嵌入都会随着 $s$ 的变化而变化。
3.4 YaRN
除了前面提到的插值技术外，我们还观察到在注意力 softmax 之前引入一个温度参数 $t$ 到 logits 上，对困惑度产生统一的影响，无论数据样本和扩展上下文窗口中的 token 位置如何（参见附录 A.2）。更准确地说，我们修改了注意力权重的计算方式，而不是公式 (2)：
\[\text{softmax}\left(\frac{q_m^T k_n}{t\sqrt{|D|}}\right). \quad (21)\]将 RoPE 重新参数化为一组 2D 矩阵对这种注意力缩放的实现具有明显的优势：我们可以转而使用一种“长度缩放”技巧，即通过简单地将复数 RoPE 嵌入按相同量缩放，从而将 $q_m$ 和 $k_n$ 都按常数因子 $\sqrt{1/t}$ 缩放。有了这个，YaRN 可以在不修改其代码的情况下有效地改变注意力机制。此外，它在推理和训练期间都零开销，因为 RoPE 嵌入是预先生成的，并可重复用于所有前向传播。将其与“NTK-by-parts”插值结合，我们就得到了 YaRN 方法。
定义 3 “YaRN 方法”是指公式 (21) 中的注意力缩放与第 3.2 节中引入的“NTK-by-parts”插值的结合。
对于 LLaMA 和 Llama 2 模型，我们推荐以下值：
\[\sqrt{\frac{1}{t}} = 0.1 \ln(s) + 1. \quad (22)\]上述方程是通过在 LLaMA 7b、13b、33b 和 65b 模型上，在不进行微调的情况下，使用“NTK-by-parts”方法（第 3.2 节）将 $\sqrt{1/t}$ 与不同因子 $s$ 扩展下的最低困惑度进行拟合得到的。我们注意到，相同的 $t$ 值也适用于 Llama 2 模型（7b、13b 和 70b）。这表明增加熵的特性和温度常数 $t$ 可能具有一定程度的“普适性”，并且可能在某些模型和训练数据之间具有泛化性。
YaRN 方法结合了我们所有的发现，并在微调和非微调场景中都超越了所有以前的方法。由于其低开销，YaRN 可以直接兼容修改注意力机制的库，例如 Flash Attention 2 [13]。
4 实验
我们展示了 YaRN 成功地扩展了使用 RoPE 作为位置嵌入的语言模型的上下文窗口。此外，这一结果仅通过 400 次训练步骤即可实现，约占模型原始预训练语料库的 0.1%，比 Rozière 等人 [31] 减少了 10 倍的 token，比 Chen 等人 [9] 减少了 2.5 倍的训练步骤，使其在训练过程中具有高度的计算效率，并且没有额外的推理成本。我们计算长文档的困惑度并在既定基准上进行评分，以评估所得模型，发现它们超越了所有其他上下文窗口扩展方法。
我们大致遵循了 [9] 中概述的训练和评估程序。
4.1 训练
为了进行训练，我们扩展了 Llama 2 [39] 的 7B 和 13B 参数模型。除了按照 3.4 节所述，将嵌入频率计算中的 $s$ 分别设置为 16 和 32 之外，LLaMA 模型架构没有进行任何更改。
我们使用 2 × 10⁻⁵ 的学习率，没有权重衰减，以及 20 步的线性预热，并结合 AdamW [24] 的 $\beta_1 = 0.9$ 和 $\beta_2 = 0.95$。对于 $s = 16$，我们使用 PyTorch [26] 的完全分片数据并行 [42] 和 Flash Attention 2 [13]，在全局批量大小为 64 的情况下，在 PG19 数据集 [29] 上微调了 400 步，该数据集被分块为 64k 的片段，并以 BOS 和 EOS 标记开头和结尾。对于 $s = 32$，我们遵循相同的程序，但从完成的 $s = 16$ 检查点开始，并额外训练了 200 步。
4.2 外推与迁移学习
在 Code Llama [31] 中，使用 16k 上下文的数据集，其缩放因子设置为 $s \approx 88.6$，对应于 355k 的上下文大小。他们表明，网络可以外推到 100k 上下文，而无需在训练期间见过这些上下文大小。类似于 3.1 节和 Rozière 等人 [31] 的工作，YaRN 也支持使用高于数据集长度的缩放因子 $s$ 进行训练。由于计算限制，我们仅通过使用相同的 64k 上下文数据集，对 $s = 16$ 模型进一步微调 200 步来测试 $s = 32$。
我们在 4.3.1 节中表明， $s = 32$ 模型在训练期间仅使用 64k 上下文，就成功外推到 128k 上下文。与之前的“盲”插值方法不同，YaRN 在增加缩放因子 $s$ 时，在迁移学习方面效率更高。这表明从 $s = 16$ 到 $s = 32$ 的成功迁移学习，无需网络重新学习插值嵌入，因为 $s = 32$ 模型在整个上下文大小上与 $s = 16$ 模型等效，尽管只在 $s = 32$ 上训练了 200 步。
4.3 评估
评估主要集中在三个方面：
- 微调模型在扩展上下文窗口下的困惑度分数，
- 微调模型上的 Passkey 检索任务，
- 微调模型的常见 LLM 基准测试结果。
4.3.1 长序列语言建模
为了评估长序列语言建模性能，我们使用了 GovReport [18] 和 Proof-pile [4] 数据集，两者都包含许多长序列样本。所有评估均专门使用这两个数据集的测试集。所有困惑度评估均使用 Press 等人 [27] 的滑动窗口方法计算，其中 $S = 256$。
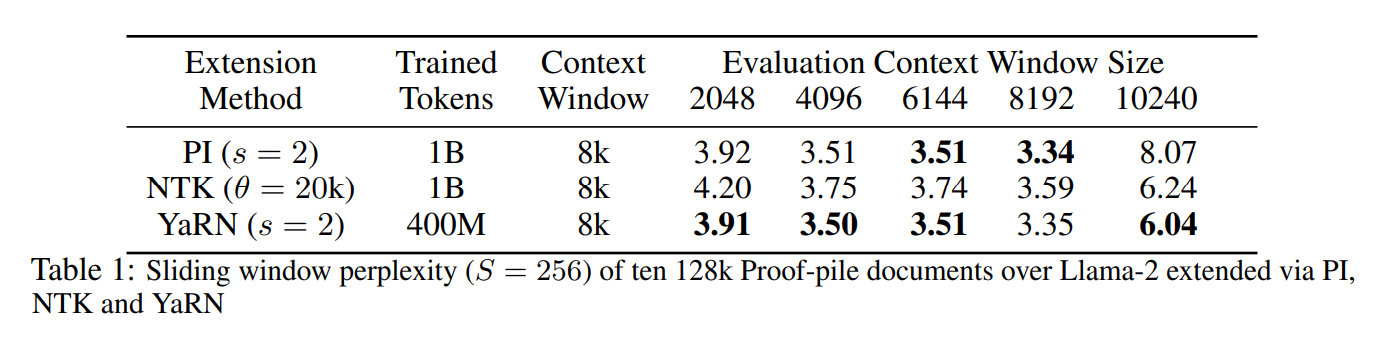
首先，我们评估了模型随着上下文窗口增加的表现。我们从 Proof-pile 中随机选择 10 个至少包含 128k token 的样本，并评估了这些样本在从 2k token 到 128k token 截断为 2k 步时的困惑度。表 1 显示了通过 PI (LLongMA-2 7b⁵)、”NTK-aware” 和 YaRN 将 Llama-2 模型从 4096 扩展到 8192 上下文长度的并排比较。请注意，PI 和 “NTK-aware” 模型是使用 Chen 等人 [9] 的方法进行训练的，而 YaRN 使用相同的方法，但训练步骤和数据量减少了 2.5 倍，如第 4 节所述。
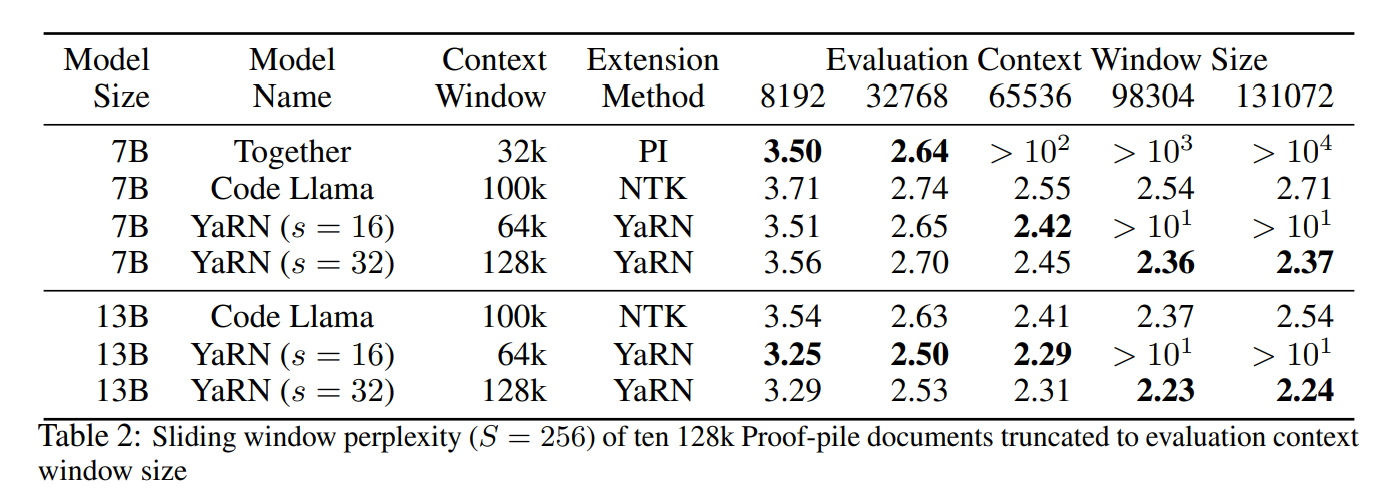
我们进一步评估了 YaRN 在缩放因子 $s = 16, 32$ 时的性能，并将其与一些从 Llama-2 微调并扩展到超过 32k 上下文窗口的开源模型（如 Together.ai [37] 和 “NTK-aware” Code Llama [31]）进行了比较。结果总结在表 2 中（更详细的图表在图 1 中）。
我们观察到模型在整个目标上下文大小范围内表现出强大的性能，YaRN 插值是第一个成功将 Llama 2 的有效上下文大小扩展到 128k 的方法。特别值得注意的是 YaRN ($s = 32$) 模型，尽管微调数据长度限制在 64k token，但其困惑度在 128k 范围内持续下降，这表明模型能够泛化到未见过的上下文长度。
此外，在附录 B.1 中，我们展示了表 4 中在 32k 最大上下文窗口设置下（不使用动态缩放）评估的 50 个未截断的 GovReport 文档的平均困惑度结果，每个样本至少包含 16k token。与 Proof-pile 结果类似，GovReport 结果表明使用 YaRN 进行微调在长序列上取得了良好的性能。
4.3.2 Passkey 检索
Passkey 检索任务 [25] 衡量模型从大量无意义文本中检索简单通行码（即五位数字）的能力。为了评估模型，我们对 Passkey 检索任务进行了 10 次迭代，Passkey 均匀分布在评估上下文窗口的随机位置上，上下文窗口大小从 8k 到 128k 不等。使用 YaRN 在 128k 上下文大小下微调的 7b 和 13b 模型在整个上下文窗口大小内以极高准确率（> 99%）通过了 Passkey 检索任务。详细结果见附录 B.2。
4.3.3 标准化基准测试
Hugging Face Open LLM Leaderboard [19] 对多种 LLM 在一组标准化的四个公共基准上进行了比较。具体来说，我们使用了 25-shot ARC-Challenge [11]、10-shot HellaSwag [41]、5-shot MMLU [17] 和 0-shot TruthfulQA [23]。
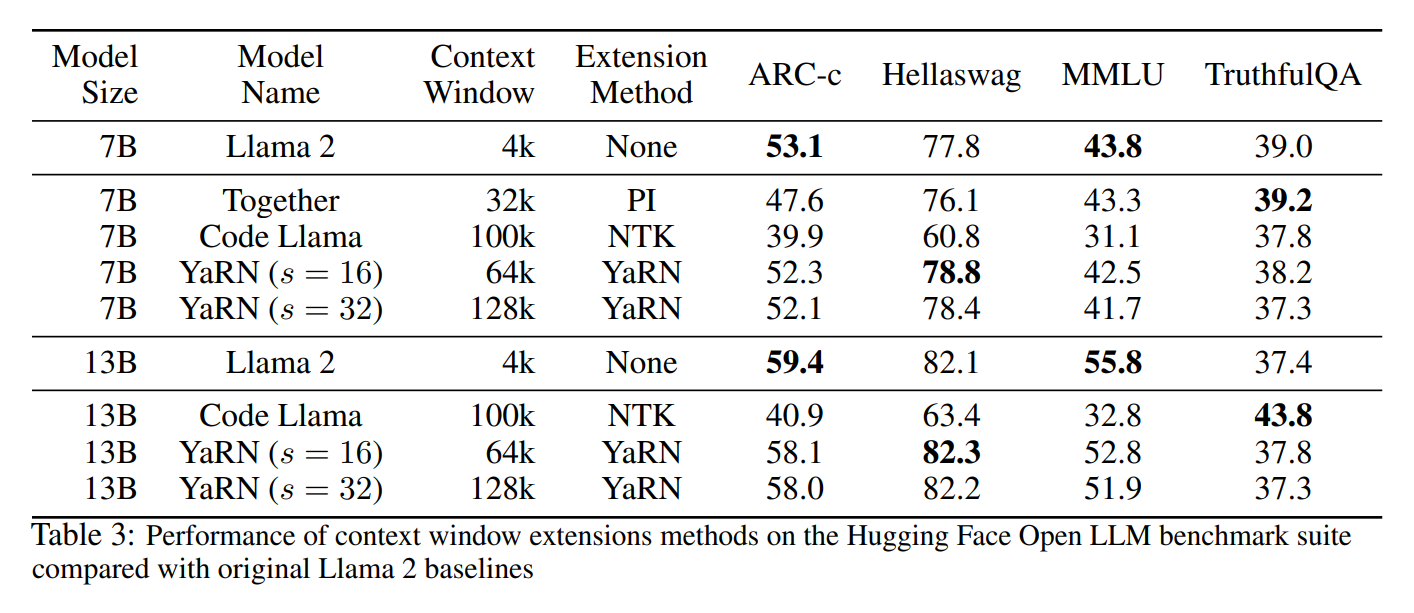
为了测试模型在上下文扩展下的性能下降，我们使用这套基准评估了我们的模型，并将其与 Llama 2 基线的既定分数以及公开可用的 PI 和“NTK-aware”模型进行了比较。结果总结在表 3 中。
我们观察到 YaRN 模型与其各自的 Llama 2 基线之间性能下降极小。我们还观察到 YaRN $s = 16$ 和 $s = 32$ 模型之间的分数平均下降了 0.49%。由此我们得出结论，从 64k 到 128k 的迭代扩展导致的性能损失可以忽略不计。
5 结论
总而言之，我们已经表明 YaRN 改进了所有现有的 RoPE 插值方法，并且可以作为 PI 的直接替代品，没有缺点且实现工作量极小。微调后的模型在多个基准测试中保持了其原始能力，同时能够处理非常大的上下文大小。此外，YaRN 允许在较短的数据集上通过微调进行高效外推，并且可以利用迁移学习实现更快的收敛，这两者在计算受限的情况下都至关重要。最后，我们展示了 YaRN 在外推方面的有效性，它能够“短时训练，长时间测试”。
- 显示Disqus评论(需要科学上网)