本文继续介绍基于HMM模型的语音识别系统。更多文章请点击深度学习理论与实战：提高篇。
目录
高斯分布和GMM
前面我们介绍HMM的时候假设发射概率$b_j(o_t)$是一个离散概率分布。在定义HMM的时候假设$o_t$属于字典集合$\mathcal{V}=\{v_1,v_2,…,v_V\}$。但前面特征提取部分得到的特征是一个连续的向量，比如MFCC得到39维的连续特征向量。那怎么解决这个问题呢？一种最简单的方法是矢量量化(Vector Quantization,VQ)，把连续的概率分布变成离散的概率分布。
矢量量化(Vector Quantization VQ)
VQ类似于聚类算法，它首先对训练数据中的所有特征向量进行聚类，比如聚类为256个类别，找出每个聚类的”代表”向量(prototype vector)，把这些类别编号成$v_1,…,v_{256}$。如果我们对于输入的观察特征向量，计算它和256个代表向量的“距离”，选择最近的那个类别输出。
VQ非常简单，但是用离散的分布来表示连续分布，效果并不好，因此通常我们直接用连续概率分布来建模$b_j(o_t)$。对于似然计算或者解码，它和离散的分布并没有区别，但是对于前向后向学习算法需要根据我们使用的连续概率分母做相应的改动。我们首先介绍最简单的(多变量)高斯分布，然后再把它推广到高斯混合模型。
高斯(Gaussian)分布
我们首先来回顾一下单变量高斯分布。高斯分布也叫正态(normal)分布，它的概率密度函数为：
\[f(x|\mu,\sigma)=\frac{1}{\sqrt{\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \equiv \mathcal{N}(\mu, \sigma^2)\]式中$\mu$是均值，$\sigma$是标准差。如下图所示，高斯分布是一个单峰的结构，离均值越近，概率就越大。而$\sigma$越小，均值附近的概率就越多。
图：高斯分布
假如观察$o_t$是一维(实际是39维)的连续变量，那么我们可以用高斯分布来建模$b_j(o_t)$：
\[b_j(o_t)=\frac{1}{\sqrt{2\pi \sigma_j^2}}e^{-\frac{(o_t-\mu_j)^2}{2\sigma_j^2}}\]每个状态j都有对应的$\mu_j$和$\sigma_j$。给定任意的$o_t$，根据上面的公式我们可以计算$b_j(o_t)$。需要注意的是：上式是概率密度函数(PDF)，一个区域的概率是PDF的积分，高斯分布在某个点的概率是零，PDF的值可能大于1，这显然是不符合概率的定义。但是我们可以取$o_t$附近一个很小的区域$\Delta$，那么这个区域的概率就是$\mathcal{N}(\mu_t,\sigma_t^2)\Delta$。因为我们不关心$b_j(o_t)$的具体值(0.1或者10)，而是关心$b_j(o_t)$和$b_k(o_t)$的比例(0.1 vs 0.2和10 vs 20是一样的)。所以我们实际计算的时候用PDF在某一点的值来替代实际的概率。
那怎么估计高斯分布的参数$\mu$和$\sigma$呢？假设我们知道每个观察属于哪个状态，也就是我们可以得到状态$Q_j$的所有观察$o_1,…,o_T$，那么我们可以用最大似然方法来估计它们：
\[\begin{split} \hat{\mu_j} & =\frac{1}{T}\sum_{i=1}^{T}o_i \\ \hat{\sigma_j^2} & =\frac{1}{T}\sum_{i=1}^{T}(o_t-\hat{\mu_j})^2 \end{split}\]我们并不知道每个观察对于的状态，但是我们可以使用前向后向算法计算状态占用概率$\gamma_t(j)$，因此和离散的分布类似，我们可以用下面的公式来用EM算法计算新的$\mu$和$\sigma$：
\[\begin{split} \hat{\mu_j} & =\frac{\sum_{t=1}^{T}\gamma_t(j) o_t}{\sum_{t=1}^{T}\gamma_t(j)} \\ \hat{\sigma^2} & =\frac{\sum_{t=1}^{T} \gamma_t(j)(o_t-\hat{\mu_j})^2}{\sum_{t=1}^{T} \gamma_t(j)} \end{split}\]实际的观察是多维(比如39维)的向量，因此我们需要多变量的高斯分布，它的PDF为：
\[\mathcal{N}(\boldsymbol{o}|\boldsymbol{\mu}, \boldsymbol{\Sigma})=\frac{1}{\sqrt{(2\pi)^n |\boldsymbol{\Sigma}|}}e^{-\frac{1}{2}(\boldsymbol(o)-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1}(\boldsymbol(o)-\boldsymbol{\mu}) }\]其中$\boldsymbol{\mu}$是均值向量，$\boldsymbol{\Sigma}$是协方差矩阵。指数中的$-\frac{1}{2}(\boldsymbol{o}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1}(\boldsymbol(o)-\boldsymbol{\mu})$叫作二次型(quadratic form)。
\[\begin{split} \boldsymbol{\mu}=(\mu_1, ..., \mu_D)^T \\ \boldsymbol{\Sigma}=\begin{pmatrix} \sigma_{11} & \dots & \sigma_{1D} \\ \vdots & \ddots & \vdots \\ \sigma_{D1} & \dots & \sigma_{DD} \end{pmatrix} \end{split}\]均值向量$\boldsymbol{\mu}$是随机变量$\boldsymbol{x}$的期望：$\boldsymbol{\mu}=\mathbb{E}(\boldsymbol{x})$。而协方差矩阵的定义为：
\[\boldsymbol{\Sigma}=\mathbb{E}[(x-\mu)(x-\mu)^T]\]$\boldsymbol{\Sigma}$是一个$D \times D$的对称矩阵：
\[\Sigma_{ij}=E[(x_i-\mu_i)(x_j-\mu_j)^T]=E[(x_j-\mu_j)(x_i-\mu_i)^T]=\Sigma_{ji}\]从协方差的符号可以两个分量之间的关系：如果$x_i$越大在$x_j$也越大，那么$(x_i-\mu_i)(x_j-\mu_j)^T$通常大于零，因此期望大于零，从而$\Sigma_{ij}>0$；如果$x_i$越大在$x_j$反而越小，那么$(x_i-\mu_i)(x_j-\mu_j)^T$小于零；而如果$x_i$的变化和$x_j$没有什么关系，$\Sigma_{ij}=0$。很显然$x_i$和$x_i$自己的变化趋势是一致的，因此对角线上的元素$\Sigma_{ii}>0$。
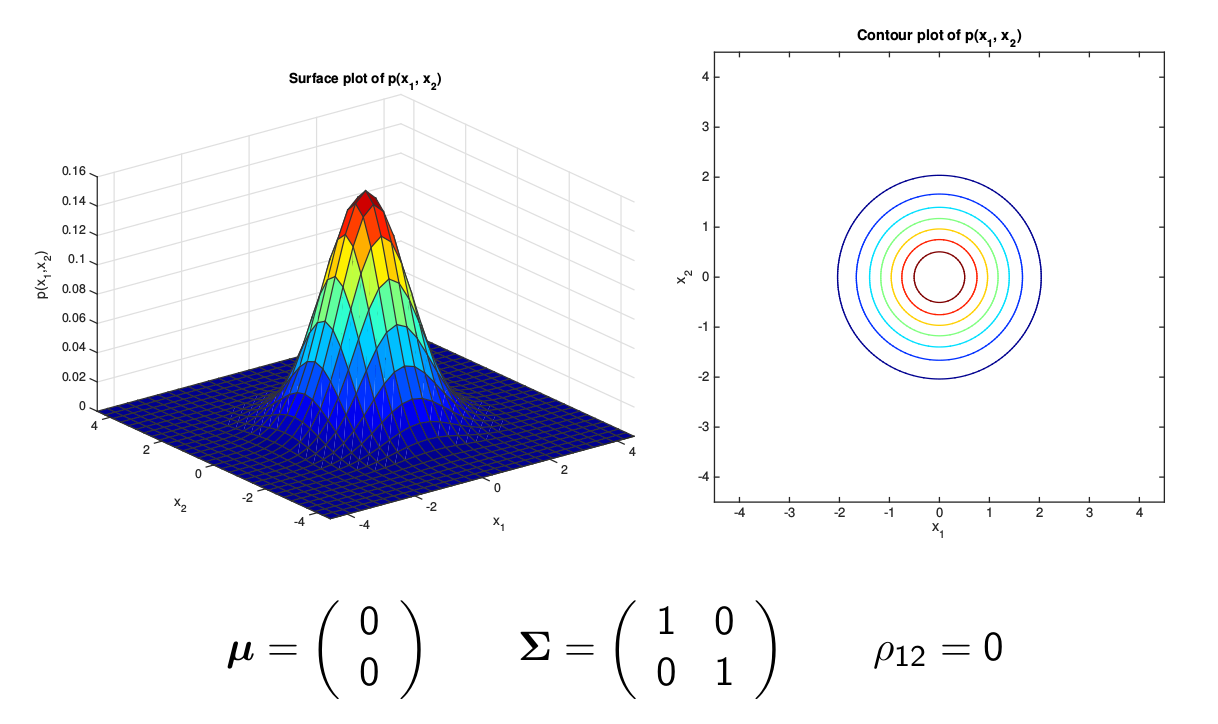
最简单的多变量(为了可视化这里使用两变量)高斯分布的协方差矩阵是单位矩阵(或者单位矩阵乘以一个常数)，如下图所示，它的等高线是一个圆形。
图：Spherical Gaussian
另外一种简单的情况就是协方差矩阵是一个对角矩阵，但是对角线上的元素不相等，如下图所示，它的等高线是一个椭圆，并且椭圆的轴是和坐标轴平行(垂直)的。
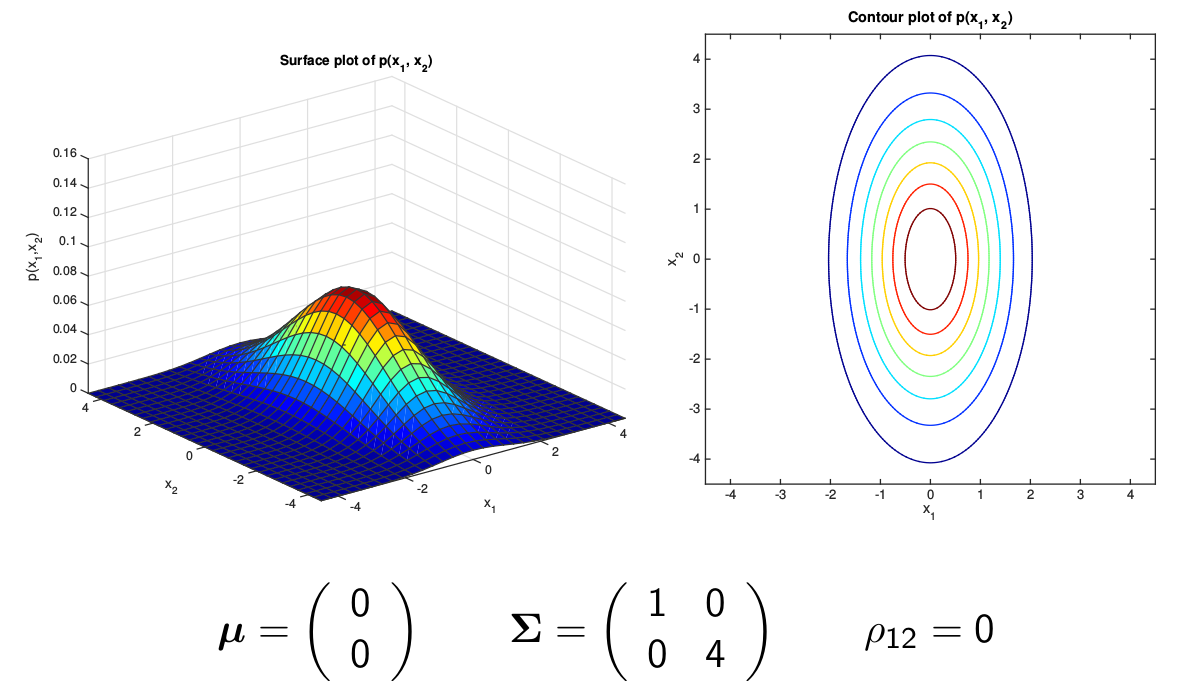图：Diagonal Covariance Gaussian
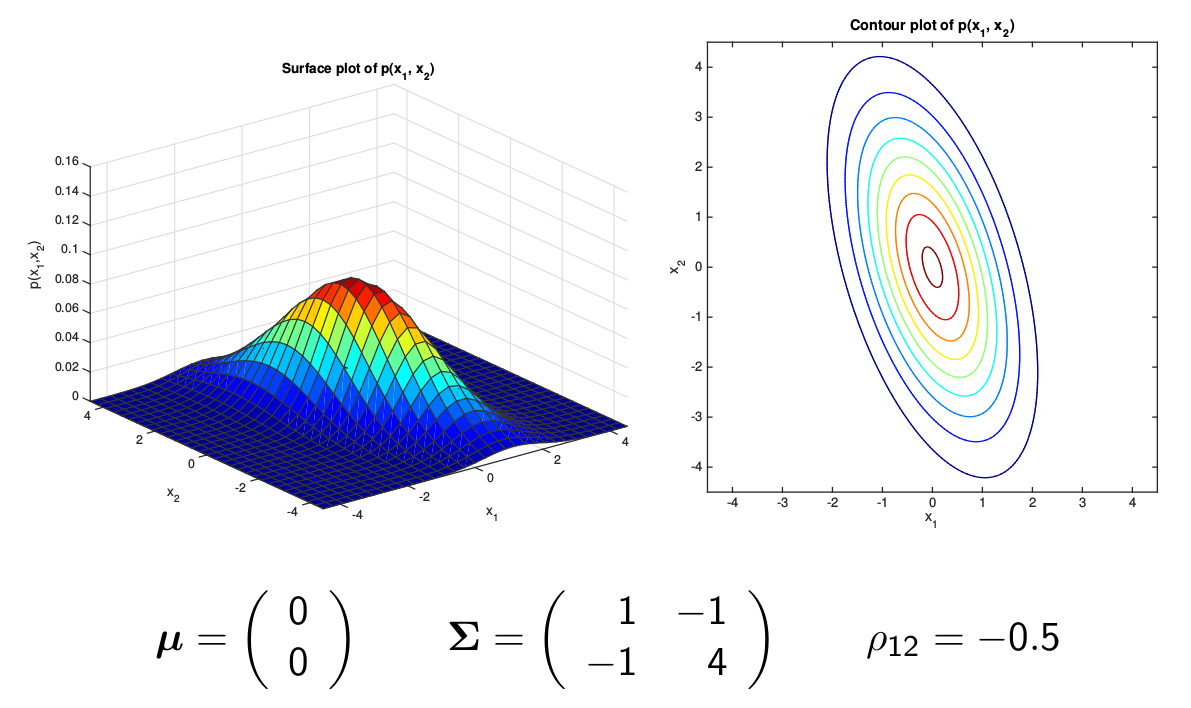
当然更复杂的协方差矩阵所有的元素都不为零，如下图所示，它的等高线是一个椭圆，轴和坐标轴不平行。
图：Full Covariance Gaussian
如果是对角的协方差矩阵，那么只有D个参数，而如果是普通的协方差矩阵，那么有D(D+1)/2个参数。为了简化计算，我们通常使用对角的协方差矩阵，但是它要求特征的各个维度是不相关的，前面我们介绍的MFCC有一步会进行DCT变换，它使得MFCC的各个维度是不相关的，从而可以使用对角的协方差矩阵。多变量高斯分布的参数估计和前面类似，如果知道每个观察对应的状态，那么可以用最大似然估计，计算公式是类似的，只是把标量变成了向量和矩阵：
\[\begin{split} \hat{\boldsymbol{\mu_j}} & =\frac{1}{T}\sum_{i=1}^{T}\boldsymbol{o_i} \\ \hat{\boldsymbol{\Sigma_j}} & =\frac{1}{T}\sum_{i=1}^{T}(\boldsymbol{o_t}-\boldsymbol{\hat{\mu_j}})(\boldsymbol{o_t}-\boldsymbol{\hat{\mu_j}})^T \end{split}\]实际在前向后向算法时我们知道时刻t属于状态j的概率$\gamma_t(j)$，那么我们可以用它来计算：
\[\begin{split} \hat{\boldsymbol{\mu_j}} & =\frac{\sum_{t=1}^{T}\gamma_t(j) \boldsymbol{o_t}}{\sum_{t=1}^{T}\gamma_t(j)} \\ \hat{\boldsymbol{\Sigma_j}} & =\frac{\sum_{t=1}^{T} \gamma_t(j)(\boldsymbol{o_t}-\hat{\boldsymbol{\mu_j}})(\boldsymbol{o_t}-\hat{\boldsymbol{\mu_j}})^T}{\sum_{t=1}^{T} \gamma_t(j)} \end{split}\]下图是用高斯分布拟合数据的一个例子。左图是待拟合的数据，而右图是拟合的结果。
图：左: 数据， 右：使用高斯分布拟合数据
高斯混合模型(Gaussian Mixture Model GMM)
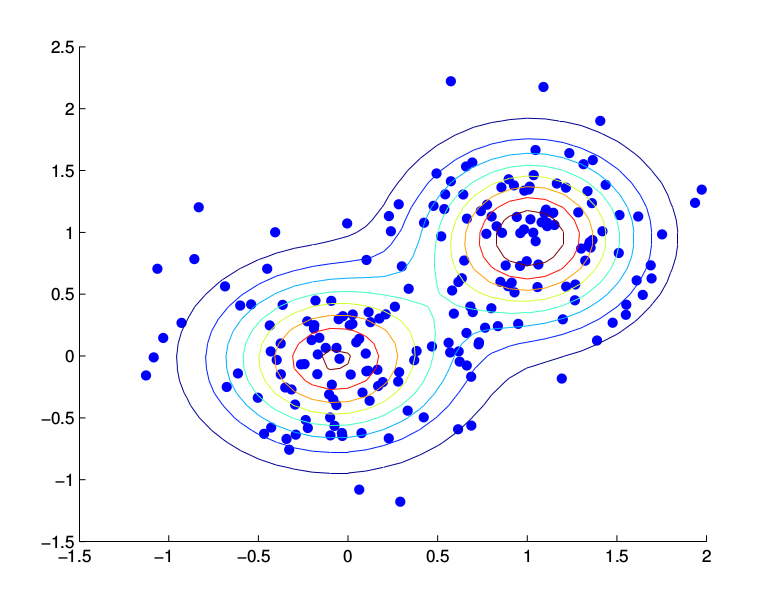
高斯分布适合数据只有单峰的情形，也就是数据集中分布在某个中心点(均值)的情形。但是很多数据不是单峰的，它的数据是分布在多个中心点，比如下图所示的例子，数据明显有两个中心[0,0]和[1,1]，这种数据就不适合使用高斯分布来拟合。这样的数据可以用本节介绍的高斯混合模型来建模。
图：多中心数据分布的例子
在介绍高斯混合模型之前我们先来介绍一些混合模型(Mixture Model)。混合(概率)模型是多个概率模型线性组合而成的模型，它的概率密度函数为：
\[p(x)=\sum_{m=1}^{M}P(m)P(x|m)\]其中$P(x|m)$是第m个分量(component)的概率密度函数，而$P(m)$是混合系数(mixing parameter)。和HMM类似，Mixture Model也是一个产生式模型，我们可以使用如下步骤来“生成”一个数据：
- 根据$P(m)$选择一个分量m
- 根据$P(x|m)$生成一个数据
最常见的一种混合模型就是高斯混合模型，它的每个分量的概率密度函数是高斯分布函数：
\[b_j(o_t)=\sum_{m=1}^{M}c_{jm}\mathcal{N}(x|\mu_{jm},\Sigma_{jm})\]这里的$c_{jm}$就是前面的$P(m)$，在GMM里我们通常用这个记号。比如上面的例子很难用高斯分布来建模，但是我们可以很容易的用高斯混合模型来建模，如下图所示。
图：高斯混合模型拟合多中心数据的例子
因此如果模型参数$c_{jm}$和$\mu_{jm},\Sigma_{jm}$已知，那么我们很容易计算$b_j(o_t)$。那么接下来的问题是参数学习的问题。和HMM类似，我们也可以用EM算法来估计GMM的参数。
现在最大的问题就是我们不知道某个数据点是由哪个分量产生的(就像我们不知道某个观察是由哪个状态发射一样)，假设我们知道问题就好办了。
为了简化问题，我们首先假设只有一个状态j。然后我们再假设知道某个观察$o_t$是由某个分类产生的，我们用向量$z_t$来表示，这个向量是一个one-hot的向量，如果观察有第m个分量产生，那么$z_{mt}=1$，而其它的$z_{nt}=0$。
很显然，在任意时刻t，有且仅有一个m使得$z_{mt}$不为零(为1)。知道$z_{mt}$之后我们就可以统计有多少个观察是由分量m产生的了：
\[N_m=\sum_{t=1}^{T}z_{mt}\]我们可以用这些属于分量m(有分量m产生)的数据来估计$\mu_m$和$\Sigma_m$以及$c_m$：
\[\begin{split} \hat{\boldsymbol{\mu}} & = \frac{\sum_t z_{mt}\boldsymbol{o_t}}{N_m} \\ \hat{\boldsymbol{\Sigma}} & = \frac{\sum_t z_{mt}(\boldsymbol{o_t}-\hat{\boldsymbol{\mu}})(\boldsymbol{o_t}-\hat{\boldsymbol{\mu}})^T}{N_m} \\ \hat{c_m} & =\frac{\sum_tZ_{mt}}{T}=\frac{N_m}{T} \end{split}\]但是我们并不知道$z_{mt}$，那怎么办呢？和HMM类似，我们先假设知道$\mu_m$和$\Sigma_m$以及$c_m$，那么就可以估计$P(m|o_t)$：
\[P(m|o_t)=\frac{P(o_t|m)P(m)}{P(o_t)}=\frac{P(o_t|m)P(m)}{\sum_{m=1}^{M}P(o_t|m)P(m)}\]类似于状态占有概率，我们可以把$P(m|o_t)$叫作分量占有概率(component occupation probabilities)。这个概率和状态占有概率类似，它是soft的，也就是对于$o_t$，任意分量m都有一些概率，而不是one-hot的。有了前面的分析，我们可以用类似的EM算法来估计GMM的参数：
- 随机初始化GMM的参数
- 根据现有参数计算$P(m|o_t)$ E-step
- 根据$P(m|o_t)$更新GMM参数 M-step
- 不断重复2和3步，直到收敛(参数不怎么变化)
根据$P(m|o_t)$更新GMM参数的公式为：
\[\begin{split} \hat{\boldsymbol{\mu}} & = \frac{\sum_t P(m|o_t)\boldsymbol{o_t}}{N_m} \\ \hat{\boldsymbol{\Sigma}} & = \frac{\sum_t P(m|o_t)(\boldsymbol{o_t}-\hat{\boldsymbol{\mu}})(\boldsymbol{o_t}-\hat{\boldsymbol{\mu}})^T}{N_m} \\ \hat{c_m} & =\frac{\sum_t P(m|o_t)}{T}=\frac{N_m}{T} \end{split}\]前面假设只有一个状态，也就是$o_1,…,o_T$都是属于状态j的，但是根据之前HMM的前向后向算法，$o_t$属于状态j的概率是状态占有概率$\gamma_t(j)$。那怎么把GMM的参数学习融入到HMM的前向后向算法里呢？首先我们需要稍微修改HMM的定义，原来我们定义的发射概率B要改成连续的GMM：
\[b_j(o_t)=\sum_{m=1}^{M}c_{jm}\mathcal{N}(o_t|\mu_{jm},\Sigma_{jm})\]有了初始的跳转概率A和发射概率B，我们就可以用前向后向算法计算$\gamma_t(j)$和$\epsilon_t(i,j)$。根据这两个概率就可以计算新的跳转概率A和B，然后不断的重复上面的过程直到收敛。这里计算新的B的时候有需要用EM算法估计GMM的参数。之前我们介绍GMM的参数估计时假设$o_1,…,o_t,…,o_T$都是属于状态j的，而这里我们认为观察$o_t$属于状态j的概率是$\gamma_t(j)$，因此我们需要稍微修改一些GMM的公式：
\[\begin{split} \hat{\boldsymbol{\mu}} & = \frac{\sum_t \gamma_t(j,m)\boldsymbol{o_t}}{N_m} \\ \hat{\boldsymbol{\Sigma}} & = \frac{\sum_t \gamma_t(j,m)(\boldsymbol{o_t}-\hat{\boldsymbol{\mu}})(\boldsymbol{o_t}-\hat{\boldsymbol{\mu}})^T}{N_m} \\ \hat{c_m} & =\frac{\sum_t \gamma_t(j,m)}{T} \end{split}\]其中$\gamma_t(j,m)=\gamma_t(j)P_j(m|o_t)$，$\gamma_t(j)$是观察$o_t$属于状态j的概率，而$P_j(m|o_t)$是在已知$o_t$是属于状态j的条件下分量占有概率。
- 显示Disqus评论(需要科学上网)