本文继续介绍基于HMM模型的语音识别系统。更多文章请点击深度学习理论与实战：提高篇。
目录
语音识别各模型的层次结构
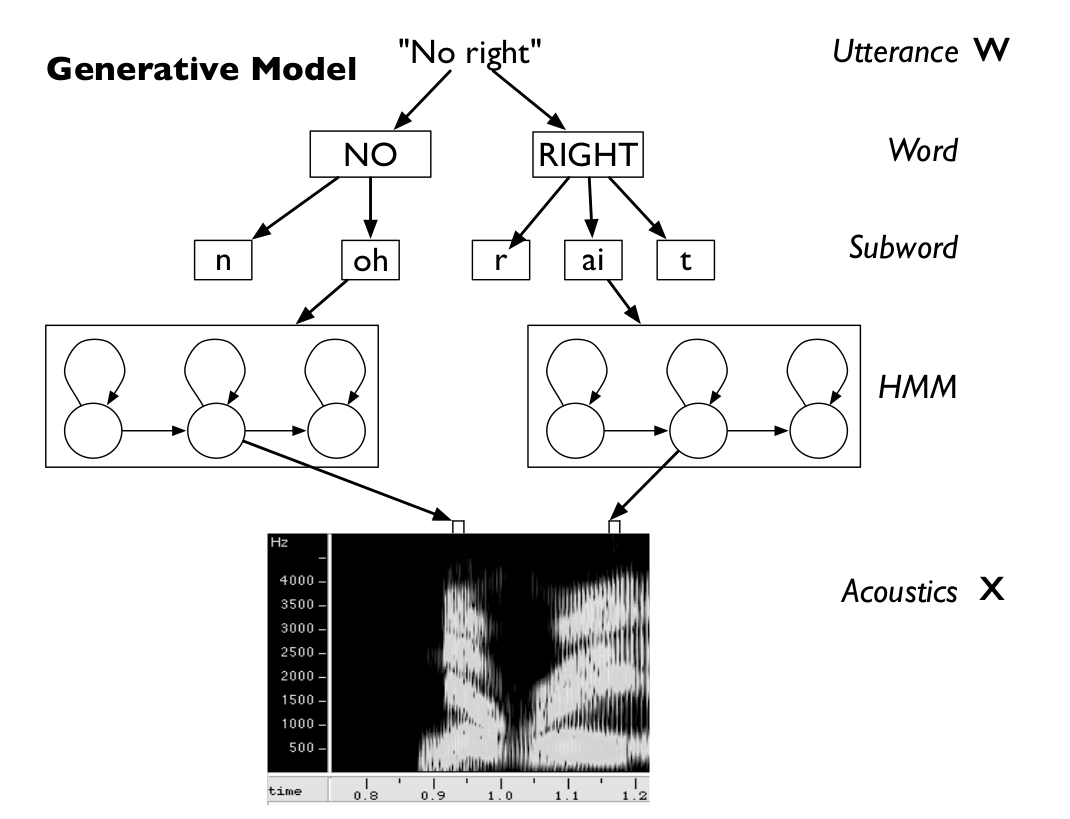
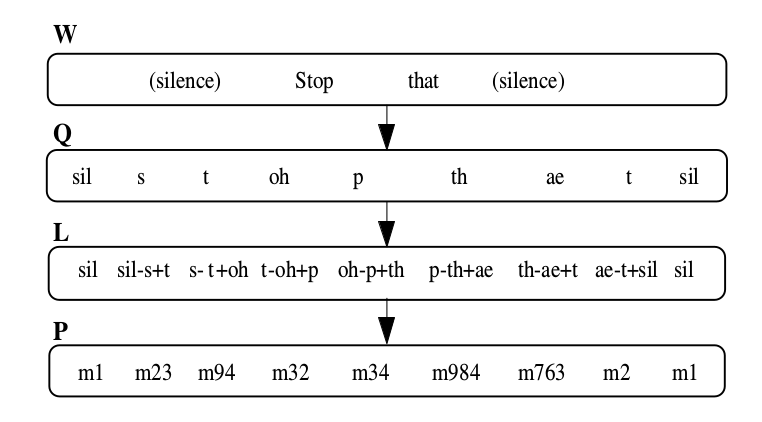
我们可以根据说话的过程把语音识别的各个单元(unit)分成如下图所示的层次结构。这是一个生成的过程。最上面是utterance，也就是一句话(不一定是语言学上的完整一句话)，比如这里的”No right”。往下一层是词(word)，比如这里是两个词”No”和”right”。再往下是subword(比如因子)，单词”No”根据发音词典可以分解为两个因子[“n”, “oh”]。再往下就是因子的HMM(比如用三状态的HMM来表示一个因子)。最后一层是声学模型，它根据状态生成观察。
发声过程从上到下输入是utterance W，输出是声学特征X。而识别的过程正好反过来，我们需要寻找：
\[\begin{split} W* & =\underset{W}{argmax}P(W|X) \\ & = \underset{W}{argmax} \frac{P(X|W)P(W)}{P(X)} \\ & = \underset{W}{argmax} P(X|W)P(W) \end{split}\]上式中$P(W)$就是语言模型，而$P(X|W)$就是声学模型，通常会包括发音模型，HMM-GMM模型，当然也可以用DNN来替代GMM变成HMM-DNN模型。
图：语音单元的层次结构
连续语音识别
简介
前面介绍的HMM和GMM可以用来做孤立词的识别，比如识别0-9十个数字，每个数字对应一个3状态的HMM，发射概率可以是GMM模型。通过训练数据我们可以使用前向后向算法训练HMM-GMM的参数，而预测的时候我们可以对十个模型分别计算后验概率：
\[P(M_i|O) \propto P(O|M_i)P(M_i), \; i=0,1,..,9\]其中$P(O|M_i)$可以通过前向算法计算出来，而$P(M_i)$就是10个数字的先验概率，可以简单的认为它们是等概率的。然后我们选择概率最大的i作为识别的结果。
那么怎么处理包含多个词的句子呢？当然最简单的是先进行词的切分，然后分别识别每一个词。但是这显然不好，首先我们说话不是一个词一个词来说的，要正确切分每一个词是很困难的；其次同音或者发音类似的词很多，我们需要考虑整个句子根据上下文才能正确的识别每一个词。
为了实现连续的识别，我们可以把每个词的HMM拼接成大的HMM，训练的时候我们是知道句子的每一个词的，因此我们可以用词的HMM拼接成句子的HMM。预测的时候也是类似的，根据语言模型，遍历所有可能的句子，拼接得到这些句子的HMM。然后用HMM-GMM计算声学模型概率，再加上语言模型的概率得到句子的最终概率，最后选择概率最大的那个句子。当然这个搜索空间是非常大的，我们需要近似的搜索算法，后面的解码器部分会介绍。这里我们先只考虑声学模型的训练部分。
但是每个词都使用一个HMM来建模有很多缺点：词很多，这需要很多个HMM模型；很多词在训练数据中出现很少，也就是数据稀疏的问题；为了识别一个新词需要重新训练声学模型，比如加入一个新的人名。
音子模型
为了解决上面的问题，我们通常对更细粒度的子词单元进行HMM建模。虽然词很多，但是组成词的因素是不多的，比如英语的音素也就是四五十个左右。因此我们可以对每一个phone建立一个HMM模型，而词的HMM就可以使用它的phone的HMM拼接起来。当然这就需要知道每个词由哪些phone组成，最常见的是人工来编纂发音词典，比如下面是CMU发音词典的两个词：
AQUIRE AE K W AY R
ABOUTS AH B AW T S
这样给定一个词，我们就知道它的音子序列，然后我们通过把每个音子的HMM拼接起来就可以得到这个词的HMM，类似的我们把很多词的HMM拼接起来就可以得到一个句子的HMM。
使用发音词典有新词的问题，比如词典里没有”balisong”这个词，那么我们无法识别这个词。但是对于表音的语言(比如英语)，我们是可以”猜测”出未知词的发音的。这个时候我们可以使用一个模型来学习怎么把词变成因子序列，这个模型通常被成为Grapheme-to-Phoneme (G2P)模型。我们可以根据发音词典来学习发音规律，这样新词来了之后就可以猜测可能的发音。这显然可以使用我们熟悉的Seq2seq模型来解决，有兴趣的读者可以试试g2p-seq2seq。
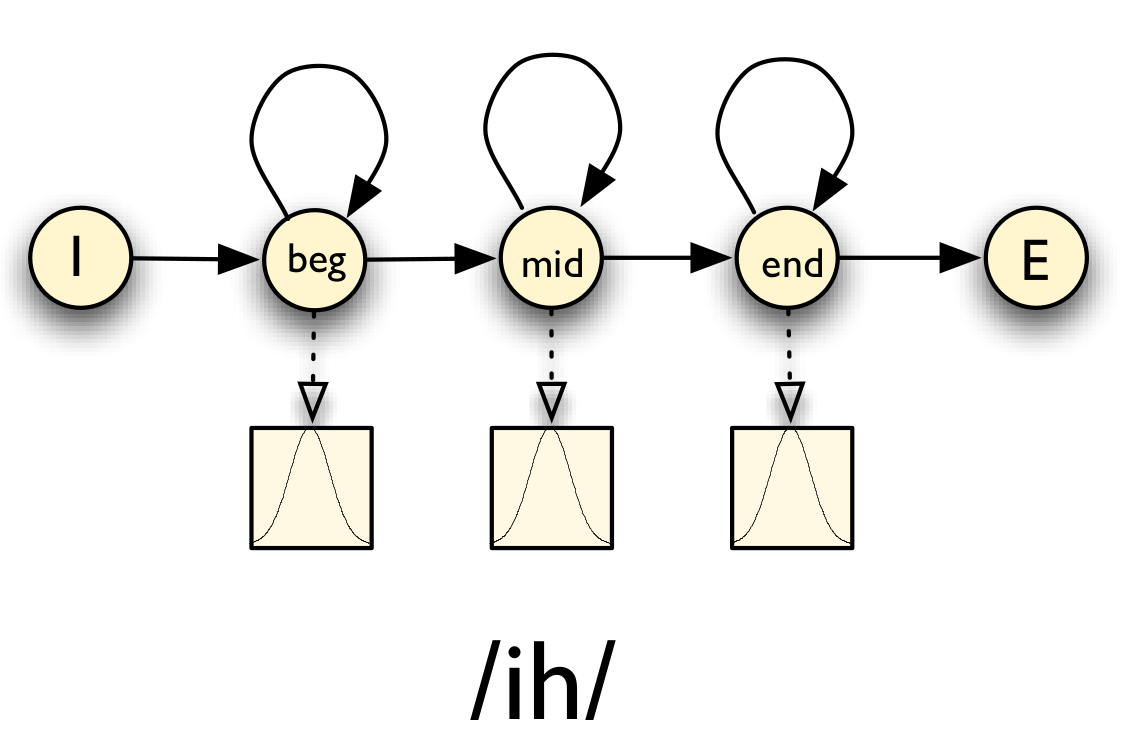
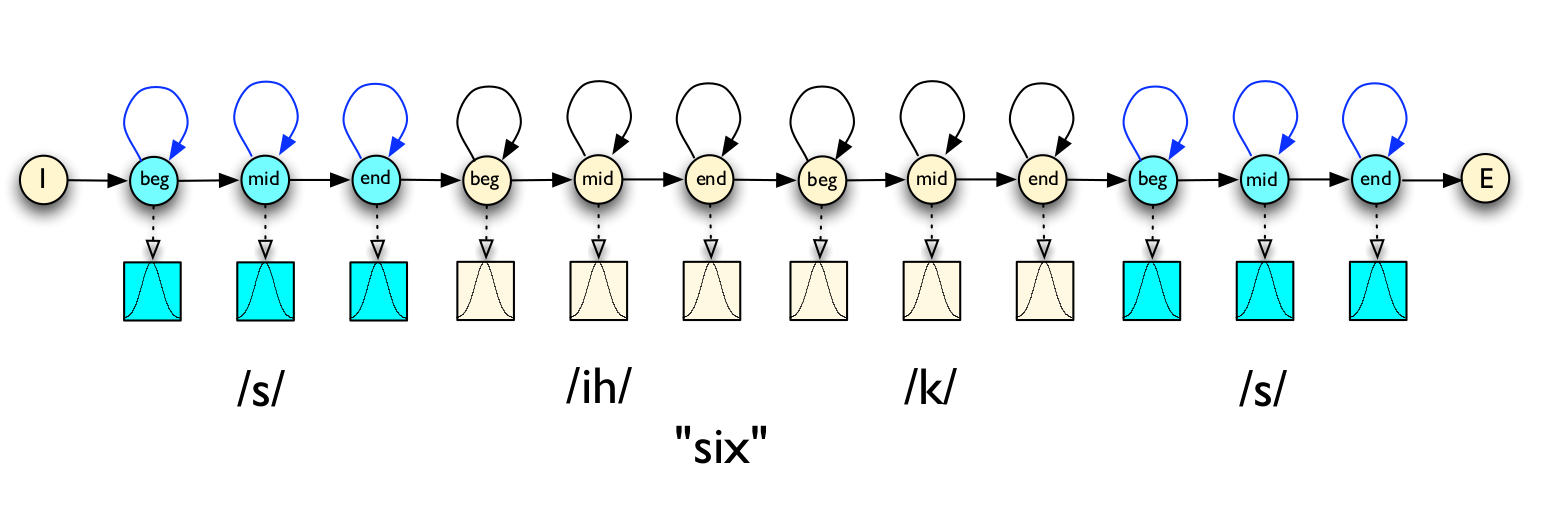
对于每个音子，我们通常使用三个状态的HMM来建模。如下图所示，音子/ih/可以用三状态的HMM建模。这样一个词，比如six，我们就可以把4个音素/s ih k s/拼接得到一个大的HMM，如下图所示。
图：音子ih的HMM模型
图：词six的HMM模型
上下文相关的(Context Dependency/CD)音子模型
但是一个音子在不同的上下文会有不同的发音，这就是所谓的协同发音(Coarticulation)。为了解决这个问题，我们通常建立上下文相关的音子模型，最常见的就是考虑一个音子的左右两个音子，这就是triphone模型。我们通常使用类似l-x+r来表示当前考虑的音子是x，它左边的音子是l而右边是r。根据triphone是否跨越词的边界又可以分类为词内的(word-internal) triphones和跨词的(cross-word) triphone。比如句子”don’t ask”，如果使用词内的triphone，则可以表示为：
sil d+oh d-oh+n oh-n+t n-t ah+s ah-s+k s-k sil
sil表示silence，我们可以理解为一个特殊的词，它不考虑上下文。n-t表示当前音子是t而左边是n，ah+s表示当前音子是ah而右边是s。
如果使用跨词的triphone，则应该可以表示：
sil sil-d+oh d-oh+n oh-n+t n-t+ah t-ah+s ah-s+k s-k+sil sil
那么有多少个triphone呢？假设音子有40个，那么理论上可能有$40^3=64, 000$，实际上英语可能出现的triphone会有50,000左右。假设我们使用3状态的HMM，每个状态使用10个分量的GMM模型，那么总共有1.5M个高斯分布。再假设我们使用39维的MFCC特征，高斯分布的协方差矩阵是对角阵，那么每个高斯有39(均值)+39(协方差矩阵)=78个参数。78 * 10+10(GMM的混合参数)=790个参数。那么总共有50,000 * 3 * 790=118M参数。
我们的训练数据很难覆盖这么多的参数，很多参数对应的训练数据没有或者很少，因此很难准确的估计其参数。为了解决这个问题，我们会使用参数共享(Parameter Sharing)的方法。通常有两种参数共享方法：共享模型(Sharing models)和共享状态(Sharing states)。
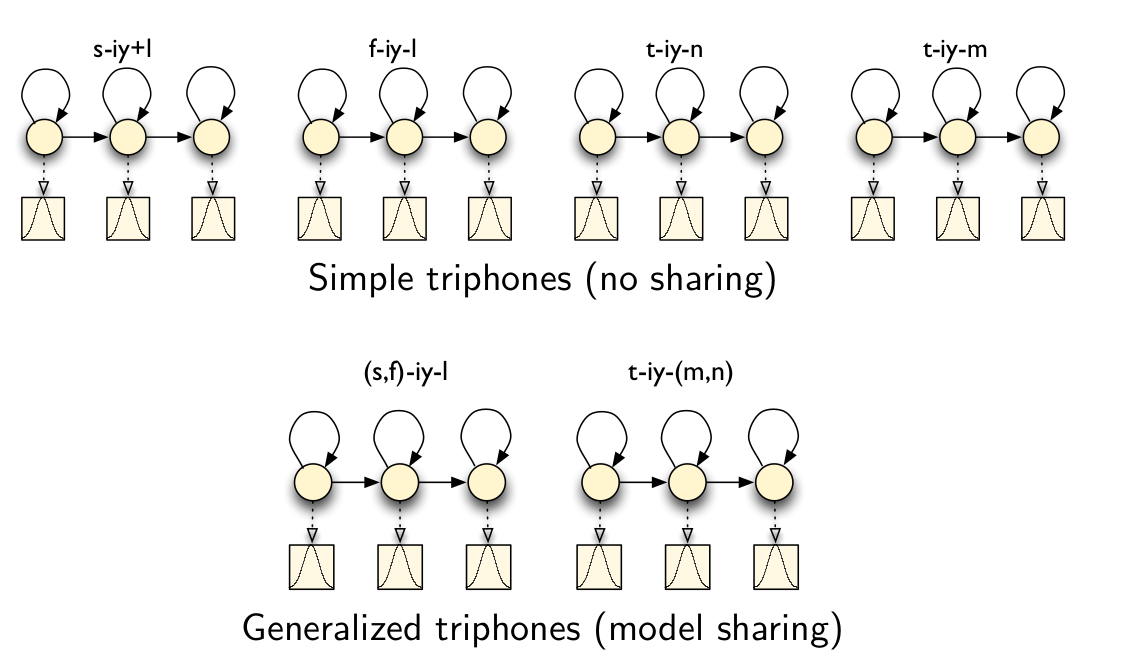
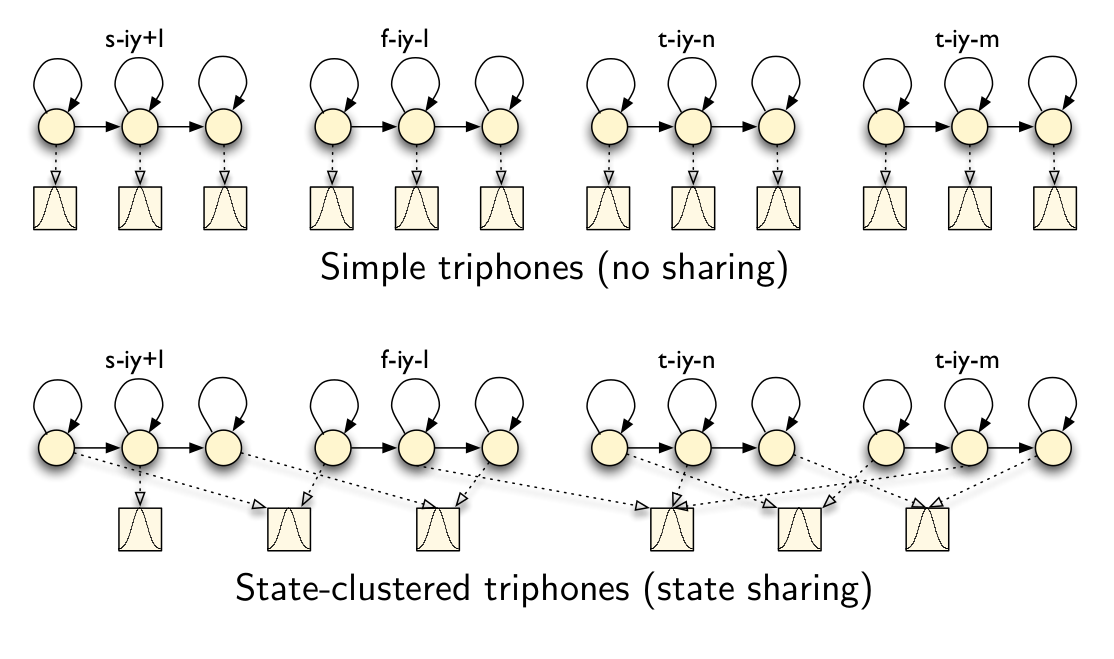
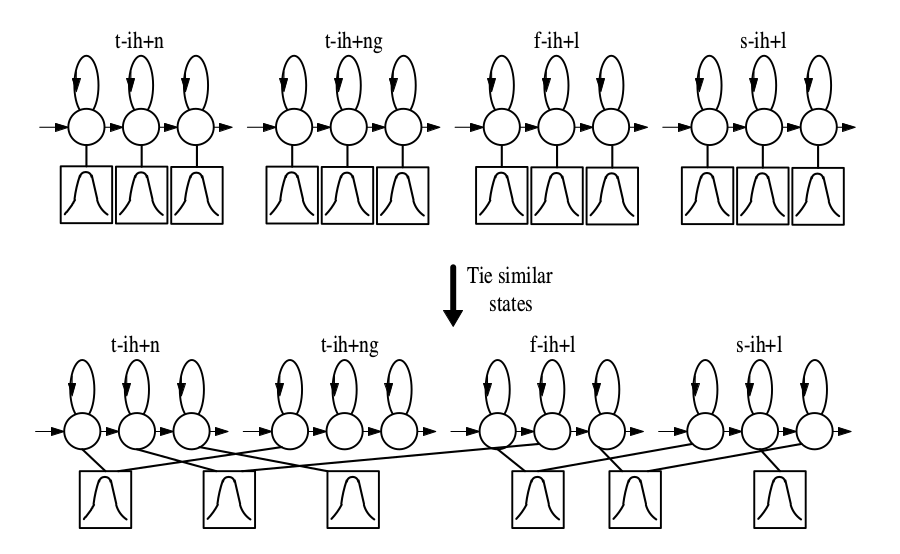
共享模型就是把比较类似的triphone聚类在一起，得到的triphone通常叫做Generalized triphone，如下图所示。
图：共享模型
共享状态就是更加细粒度的共享，它是把每个triphone的每个状态进行聚类，如下图所示。
图：共享状态
聚类通常使用语音决策树(Phonetic Decision Tree)算法，这是一种自顶向下(分裂)的方法。刚开始同一个音素的所有triphone都在根节点，然后每个节点都会根据问题进行分类，常见的问题类似于：
- 左边是不是一个鼻音？
- 右边是不是摩擦音？
下图是语音决策树的一个示例。
图：语音决策树示例
决策树可以一直分裂下去直到每个节点只包含一个triphone，这显然没有意义。我们需要有一个停止分裂的标准，一种标准就是分裂之后要比分裂前得到的模型要好？什么叫好呢？那就是新模型在训练数据上的似然概率要比分裂前好，而且增量$\Delta$越大越好，如果没有增量那么就停止分裂。另外就是问这些问题的顺序，我们会选择似然增量最大的那个问题。
HMM模型在语音识别系统中的应用
前面HMM模型原理的部分介绍了它在语音识别系统中的应用，下面我们从系统实现的架构来了解HMM在语音识别系统中的应用。HMM模型通常用于声学模型的建模，而除了声学模型，语音识别系统还包括语言模型以及更加关注工程实现的解码器。
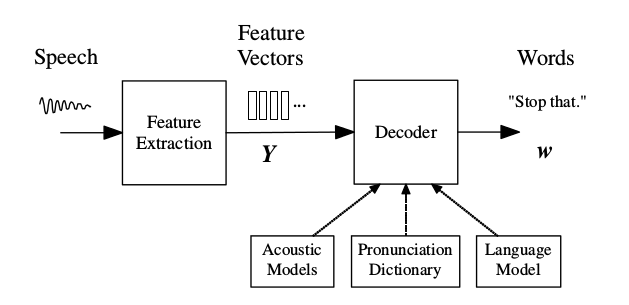
基于HMM的语音识别系统架构如下图所示。来自麦克风的音频波形被转换成固定大小(比如39维的MFCC)的声学特征向量的序列$Y_{1:T}=y_1…y_T$，这个过程叫做特征提取。然后解码器(decoder)试图找到最优的词序列$w_{1:L}=w_1…w_L$使得后验概率最大：
\[\hat{w}=\underset{w}{\operatorname{argmax}}{P(w|Y)}\]因为$P(w|Y)$比较难于直接建模，因此我们使用贝叶斯公式，因为分母与w无关，因此可以得到：
\[\hat{w}=\underset{w}{\operatorname{argmax}}{P(Y|w)P(w)}\]
图：基于HMM的语音识别系统架构
$P(Y|w)$通过声学模型(Acoustic Model)来确定，而$P(w)$由语言模型来确定。声学模型的基本单元是音子(phone)，比如单词”bat”的音子是/b/ae/t/。
每个音子都会有一个声学模型(HMM)，那么一个单词的模型是由它的音子的模型拼接起来，比如上面的单词”bat”就由/b/ae/t/三个音子的HMM拼接而成。而单词与音子的对应关系就是发音词典(Pronunciation Dictionary)，有的单词会有多种发音。每个音子的HMM通过训练数据学习出来。而语言模型通常使用N-gram模型，当然也可以使用神经网络语言模型，通常声学模型和语言模型是独立训练的。预测的时候，解码器理论上会尝试所有可能的词序列，然后找到后验概率最大的词序列。当然实际由于搜索空间太大，一般会在搜索中进行剪枝(prune)，去掉当前看来概率比较低的路径。
HMM声学(Acoustic)模型
前面提到过，每个词$w$可以分解为$K_w$个基本因子(base phone)的发音单位，比如前面的bat可以分解成/b/ae/t/3个基本单元的序列。这个序列叫作这个词的发音$q_{1:K_w}^{(w)}=q_1,…,q_{K_w}$。因为有的词有多个发音，因此我们在计算$P(Y|w)$的时候需要遍历词的每一种发音：
\[P(Y|w)=\sum_Q P(Y|Q) P(Q|w)\]上式中，Q是一条可能的词序列的发音序列：
\[P(Q|w)=\prod_{l=1}^{L} P(q^{(w_l)}|w_l)\]上式中，$q^{(w_l)}$是词$w_l$的一种合法的发音，通常情况下一个词只有一种发音，但是有些词会有多种发音，因此$P(Y|w)$会遍历词序列w的所有可能发音序列Q。
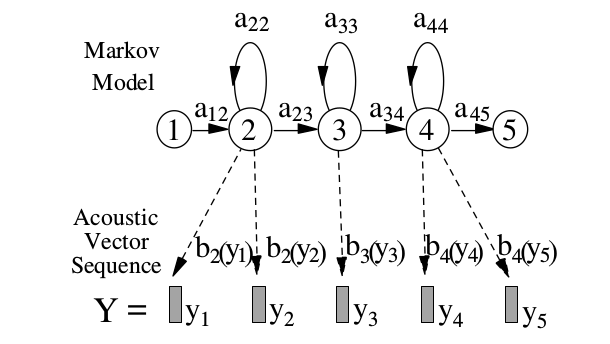
每个基本因子q由一个连续输出的HMM来表示，如下图所示。图中有一个进入状态和退出状态，它是没有输出的，这两个状态是为了方便把不同词的HMM串联起来。每个因子q的HMM由两个状态$a_{ij}$和$b_j(y)$来表示，其中$a_{ij}$表示由状态i跳转到j的概率；$b_j$表示在这个状态j下输出$y$的概率(分布/密度)。HMM的基于如下两个独立性的假设：
- 给定前一个时刻的状态，当前状态不依赖更早之前的状态(一阶马尔科夫)
- 给定当前时刻的状态，当前时刻的输出跟其它时刻的无关
图：基于HMM的因子模型
这里我们可以看出，通过状态的自跳转，HMM可以(一定程度的)解决说话人语速的问题。对于发射概率$b_j(y)$，我们先假设它是最简单的多变量单高斯的模型，后面我们会扩展到高斯混合模型(GMM)，这就是最常见的HMM-GMM模型。它用HMM来建模状态的跳转，用GMM来建模一个状态的输出概率分布。
\[b_j(y)=\mathcal{N}(y;\mu^j,\Sigma^j)=\frac{1}{\sqrt{(2\pi)^n|\Sigma_j|}} e^{-\frac{1}{2} (y_t-\mu_j)^T \Sigma_j^{-1}(y_t-\mu_j)}\]其中$\mu^j$是状态j的高斯分布的均值，而$\Sigma^j$是协方差矩阵。因为y的维度通常比较高（比如39），我们通常假设$\Sigma^j$是对角矩阵(Diagonal Matrix)。之前我们在介绍特征提取的时候，MFCC的一个步骤就是DCT去除不同维度的相关性，从而使得这个假设能够成立。
给定词的发音序列Q，我们可以计算输出Y的概率：
\[P(Y|Q)=\sum_{\theta}p(\theta, Y|Q)\]其中$\theta$是给定发音序列Q时合理的状态序列。
举个例子，假设词序列是两个词”a cat”，它的一种发音序列是/a/k/ae/t/，假设Y的长度是T=18，那么两种$\theta$可能是
\[\begin{split} \theta_1 & =a_0 a_1 a_2 a_2 a_3 a_4/k_0 k_1 k_2 k_3 k_4/ae_0 ae_1 ae_2 ae_3 ae_4/t_0 t_1 t_2 t_3 t_4 \\ \theta_2 & =a_0 a_1 a_2 a_3 a_4/k_0 k_1 k_2 k_3 k_4/ae_0 ae_1 ae_2 ae_2 ae_3 ae_4/t_0 t_1 t_2 t_3 t_4 \end{split}\]$\theta_1$中音素a的中间状态($a_2$)持续了两个时刻，而ae的中间状态$ae_2$只持续了一个时刻；而$\theta_2$正好相反。当然上面我们只列举了两条路径，实际的计算过程中，我们需要变量所有可能的$\theta$，而任意一个状态序列(路径)$\theta_0,\theta_1,…,\theta_{T+1}$(0时刻和T+1时刻是我们增加的进入和退出状态，$\theta_0$跳到$\theta_1$是没有输出的)的概率计算如下：
\[p(\theta, Y|Q)=a_{\theta_0 \theta_1}\prod_{t=1}^{T}b_{\theta_t}(y_t)a_{\theta_t \theta_{t+1}}\]在上式中$\theta_0$和$\theta_{T+1}$是进入(entry)和退出(exit)状态，它们是没有输出的。它们的目的是为了方便把不同词的HMM串联起来。后面为了简单，我们可以暂不考虑它们，而只关注$\theta_1, …, \theta_T$。
声学模型的参数$\lambda=[(a_{ij}),(b_j(y))]$可以使用前向后向(forward-backward)算法了估计，这是EM算法的一个例子。假设第r个训练数据的特征序列$Y^r$的长度是$T^r$。因为我们有它对应的词序列，那么根据发音词典(我们先假设一个词只有一种发音)我们可以得到发音序列，从而可以把每个音素的HMM拼接成一个大的HMM。
比如上图中的例子，我们把a cat的发音/a/k/ae/t/的HMM拼接起来。如果我们知道每一个时刻对应哪个因子的哪个状态，那么我们很容易最大似然估计出$a_{ij}和b_j(y)$来。
当然我们可以用人来标注每个时刻对应哪个状态，但是要人来标注这种对齐是非常困难而且容易出错的。因为很多音素的边界是很难区分，比如下图，让非专业的人通过看波形或者频谱是很难准确的区分其边界的。
图：语音识别
假设我们知道t时刻对应的状态的概率(当然如果认为一个时刻只能“属于”某一个状态，那么它就是类似one-hot的——一个1其余的是0）$\gamma_t^{(rj)}$，这个概率表示(第r个训练数据)t时刻的状态是j的概率，我们通常把它叫作(状态)占用(occupation)概率。那么我们很容易用如下公式最大似然估计$a_{ij}和b_j(y)$：
\[\begin{split} & \hat{\mu}^{(j)}=\frac{\sum_{r=1}^{R} \sum_{t=1}^{T^r} \gamma_t^{(rj)} y_t^{(r)}}{\sum_{r=1}^{R} \sum_{t=1}^{T^r} \gamma_t^{(rj)}} \\ & \hat{\Sigma}^{(j)} = \frac{\sum_{r=1}^{R} \sum_{t=1}^{T^r} \gamma_t^{(rj)} (y_t^{(r)}-\hat{\mu}^{(j)}) (y_t^{(r)}-\hat{\mu}^{(j)})^T}{\sum_{r=1}^{R} \sum_{t=1}^{T^r} \gamma_t^{(rj)}} \end{split}\]上面的公式看起来很复杂，其实它表达的意思很简单：我们要估计状态j对应的高斯分布的均值，那么我们找到所有属于这个状态的时刻t($\gamma_t^{(rj)}$)，然后把它们平均起来就行，不过这里因为我们认为某个时刻可能有一定的概率属于状态j，所以我们需要加权上概率$\gamma_t^{(rj)}$。如果我们考虑特殊情况——一个时刻t只属于一个状态j，那么上面的公式会更加明显。$\hat{\Sigma}^{(j)}$的估计公式其实也是类似的。
类似的我们可以估计状态的跳转：
\[\label{eq:forward-backward2} \hat{a}_{ij} = \frac{\sum_{r=1}^{R} \frac{1}{P^{(r)}} \sum_{t=1}^{T^r} \alpha_t^{(rj)} a_{ij} b_j(y_{t+1}^r) \beta_{t+1}^{(rj)} b_i(y_t^r) }{\sum_{r=1}^{R} \sum_{t=1}^{T^r} \gamma_t^{(rj)}}\]这个公式可以这样来读：分母是变量所有的时刻，找到状态为i的(概率)，然后加起来；而分子表示t时刻是状态i并且t+1时刻是j的概率，两者一除就是跳转概率。关于分子的计算——也就是t时刻是状态i并且t+1时刻是状态j的概率，需要理解后面要介绍的前向概率($\alpha$)和后向概率($\beta$)，请读者熟悉这两个概率之后再来阅读这个公式。
前面介绍了如果我们知道$\gamma_t^{(rj)}$（其实是前向和后向概率）时，我们可以最大似然估计模型的参数$\mu, \Sigma, a_{ij}$。现在的问题是我们怎么前向和后向概率呢？下面我们会介绍：如果知道了模型参数$\mu, \Sigma, a_{ij}$，那么我们可以估计出这两个概率。这样就很有趣：我们如果知道a，那么就可以估计b；同样我们知道b就可以估计a。这很像鸡生蛋和蛋生鸡的问题。我们可以用所谓的EM算法来估计它们：首先随机的初始化参数$\mu, \Sigma, a_{ij}$，然后用它们来估计前向后向概率，然后再用前向后向概率估计新的参数$\mu, \Sigma, a_{ij}$，然后用新的参数$\mu, \Sigma, a_{ij}$估计前向后向概率，直到模型收敛。
那么接下来的问题就是：如果我们知道了模型的参数$\lambda=(\mu, \Sigma, a_{ij})$，我们怎么估计前向后向概率并且怎么用前向后向概率来就是状态占用概率(State Occupation Probability)？
在介绍前向后向概率前我们先来看一下如果不使用动态规划算法，我们应该怎么计算t时刻属于状态i的概率？假设有3个状态1、2和3。这个序列的长度是T，那么总共有$3^T$种可能的状态序列(路径)（当然有些状态之间的跳转是不可能的，另外我们的状态序列要受发音序列约束，而发音序列又由词序列约束）。 我们把t时刻固定为状态i，那么总共还有$3^{T-1}$中可能的路径，如果模型的参数已知，那么每一条状态序列输出y的概率都可以简单的计算出来，我们把所有这些概率加起来就得到t时刻状态为i的概率。但是这样计算的实际复杂度是指数级的，实际根本无法使用。如果我们仔细观察，会发现里面很多的计算是重复的，因此我们可以使用动态规划来减少重复计算。这就是下面我们要介绍的前向-后向算法。
我们首先定义前向概率$\alpha_t^{rj}=P(Y_{1:t}^r, \theta_t=s_j;\lambda)$，它的意思是t时刻的状态为j并且1到t时刻输出为$Y_{1:t}^r$的联合概率。而后向概率$\beta_t^{ri}=P(Y_{t+1:T^{(r)}}^{(r)} | \theta_t=s_i;\lambda)$，它的意思是t时刻状态为i的条件下t+1到T时刻的输出为$Y_{t+1:T}^r$的条件概率。注意这两个概率的区别，一个是联合概率一个是条件概率。
这两个概率都可以用递推公式计算：
\[\begin{split} & \alpha_t^{(rj)} = [\sum_i \alpha_{t-1}^{(ri)} a_{ij}b_j(y_t^{(r)})] \\ & \beta_t^{(ri)} = [\sum_j a_{ij} b_j(y_{t+1}^{(r)}) \beta_{t+1}^{(rj)} ] \end{split}\]我们可以这样“读”第一个公式：t时刻处于状态j，那么可以是t-1时刻属于状态i，然后从状态i跳到j($a_{ij}$)，并且t时刻从状态j输出(发射)$y_t^{(rj)}$($b_j(y_t^{(r)})$)。第二个公式也是类似的，不过它是从后往前的。
另外我们需要递推公式的初始化条件$\alpha_1^{(rj)}$和$\beta_T^{(ri)}$。对于经典的HMM文献，除了状态之间的跳转概率之外还有一个初始状态概率——也就是在第一个时刻时处于这个状态的概率。但是我们这里介绍的HMM没有这个初始状态概率，而是新增加了两个特殊状态$s_0$和$s_{N+1}$。前者只能跳转到状态$s_1,…,s_N$，而后者只能有状态$s_1,…,s_N$跳入，并且它们都没有输出。这两个特殊状态与$s_1,…, s_N$的跳转概率可以等价的实现初始状态概率的作用。
\[\alpha_1^{(rj)}=a_{0j}b_j(y_1^{(r)})\]类似的我们有：
\[\beta_T^{(ri)}=a_{i,N+1}\]有了初始条件和递推公式，我们就可以很容易的计算前向概率和后向概率了，它的时间复杂度是$O(N^2T)$。但是等等！我们的目的似乎不是求这样两个有些奇怪的概率，我们的目的是想知道状态占用概率$\gamma_t^{(rj)}$，也就是t时刻属于状态j的概率。我们可以这样用前向和后向概率来计算这个概率：
\[\gamma_t^{(rj)} = P(\theta_t=s_j|Y^{(r)}; \lambda) = \frac{1}{P^{(r)}} \alpha_t^{(rj)} \beta_t^{(rj)}\]这里不详细推导这个公式，我们可以这样来“理解”：t时刻处于状态j的概率是所有1到t时刻的输出是$Y_{1:t}$并且t时刻状态是j的联合概率($\alpha_t^{(rj)}$)和在t时刻状态为j的条件下t+1到T时刻的输出是$Y_{t+1:T}$的条件概率($\beta_t^{(rj)}$)的乘积，而$P^{(r)}$是一个归一化的因子，使得$\gamma_t^{(rj)}$是一个概率，也就是$\sum_j \gamma_t^{(rj)}=1$，因此：
\[P^{(r)}=\sum_j \gamma_t^{(rj)}=\sum_j \alpha_t^{(rj)} \beta_t^{(rj)}\]其中我们可以把上式的t换成1到T中的任何一个时刻，它们算出来都是$P^{(r)}$，它也是输出的概率$P(Y;\lambda)$。
回顾一下，有了$\gamma_t^{(rj)}$之后，我们就可以用公式来估计高斯分布的参数$\mu_j \text{和} \Sigma_j$。但是我们还需要用公式来估计跳转概率$a_{ij}$，当时因为没有介绍前向和后向概率，所以没有详细介绍这个公式。现在我们再来回顾一下这个公式。
这个公式看起来有些复杂，其实它的意思很简单：我们要计算从状态i跳转到状态j的概率，那么分母就是所有处于状态i的加起来，因为一个时刻不是属于一个状态，而是概率的属于，因此分母是把所有的$\gamma_t^{(rj)}$加起来；而分子是两个求和，首先是下标r，遍历所有训练数据，然后是下标t，遍历一个训练数据的所有时刻，然后找到t时刻属于状态i($\alpha_t^{(ri)}$)并且t+1时刻属于状态j($\beta_{t+1}^{(rj)}$)，当然还要乘以两个发射概率$b_j(y_t^{(r)})$和$b_j(y_{t+1}{(r)})$。
我们再来回顾一下怎么用一个训练数据训练HMM模型的过程。假设训练数据w=”a cat”，Y是对应的输出序列，假设长度是20帧，那么每一个时刻t的$Y_t$是一个39维的(MFCC特征)向量。根据发音词典，词序列w可以转换成发音序列/a/k/ae/t/，然后每个因子(a/k等)都对应一个HMM，我们把这4个因子的HMM拼接起来就得到了这个训练数据的HMM，然后我们随机初始化（通常均值和方差用全局的均值和方差来初始化）这些HMM的参数$\lambda=(\mu, \Sigma, a_{ij})$，根据这些参数计算前向后向概率，然后用前向后向概率更新参数，不断的迭代直到收敛（模型的参数变化很小）。
这种方法不需要更细粒度的标注，因此也通常叫作flat start。这个方法主要的问题在于假设同一个因子(phone)在所有的上下文的发音都是一样的，但是在语音中，很多因子的发音是依赖与它的上下文的。比如wood和cool这两个词，oo的发音是相同的元音，但是由于其前后的因子不同，它们的发音差别是很大的。之前我们假设的与上下文无关的因子我们通常把它叫作monophone。
为了加入上下文的信息，我们通常使用triphone，也就是把这个因子的前后的因子也考虑进来组合成一个triphone。假设基本的因子有N个，那么理论上的triphone个数是$N^3$个（当然实际某些组合是在训练数据中没有出现过的）。因为triphone很多，这会导致数据稀疏的问题，因此我们通常类似的triphone聚类在一起。
图：考虑上下文的因子建模
如图上图所示，W代表词序列，Q代表发音序列，L代表triphone序列，而P代表HMM模型的序列。这里的triphone我们用x-q+y的形式来表示，比如s-t+oh，表示中心的因子是t，它的左边是s右边是oh。注意stop that的p，在图中是oh-p+th，p所在的词是stop，而它的右方上下文是that的th，这种跨越词边界的triphone叫crossword triphone。也有triphone的建模是不跨越词边界的。
前面我们说到为了避免数据稀疏，我们通常会对triphone进行聚类，一种最简单的聚类是直接对所有的triphone进行聚类。但是通常triphone的每个因子都有3个状态，分别表示这个音的开始部分、中间部分和结尾部分。我们也可以更加细粒度的对状态进行聚类，这样的效果会更好。聚类的结果如下图所示，属于不同的triphone的类似状态会聚类在一起，这些状态是绑定(tie)在一起的，我们在参数更新是修改任何一个的时候也会等价于修改其它的（实际实现的时候就是一个共享的状态）。
图：状态聚类(tied-state)的因子建模
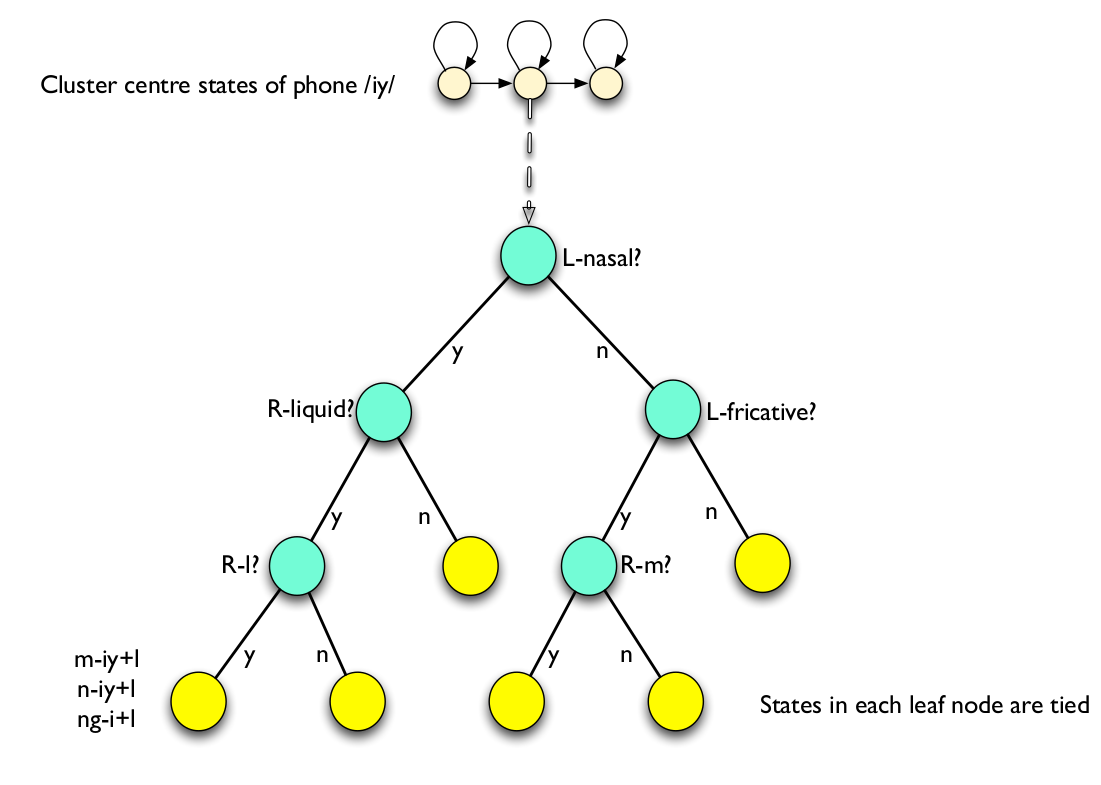
那具体怎么把这些状态聚类(tie)起来呢？通常会使用决策树聚类的方法。如图所示，aw为中心因子的所有triphone比如s-aw+n、t-aw+n等等都放到一棵树的根节点上。我们的示例是聚类这些triphone的第2个状态（如前所述，通常triphone有3个状态），它会通过问一些问题来分裂决策树，树的叶子节点对于一个物理的状态，同一个叶子节点的状态是tie在一起的。问题通常是人来提供的，后面介绍的Kaldi也提供了自动构建问题的方法。这些问题一般都是语音学相关的问题，比如一个问题是“它的左边是否是鼻音？”。
我们最后总结一些使用训练HMM-GMM声学模型的过程：
- 首先初始化一个flat-start的monophone的单高斯模型
- 用EM(前向后向)算法估计参数
- 把训练数据的monophone扩展到triphone，把单高斯的monophone模型的参数作为triphone参数的初始值
- 用EM算法重新估计triphone模型的参数
- 使用决策树对triphone的状态进行聚类，然后再用EM算法对聚类后的状态再进行参数重估计
所谓的GMM就是用多个高斯模型的线性组合来建模更加复杂的发射概率分布($b_j(y_t)$)，理论上GMM可以拟合任何概率密度函数。我们这里不详细介绍GMM以及它的参数估计，有兴趣的读者可以参考相关资料。
通过上述的步骤，最终我们就得到了许多tie-state的triphone模型。
语言模型
给定词序列$w_1,…,w_K$，语言模型会计算这个序列的概率，根据条件概率的定义，我们可以它联合概率分解为如下的条件概率：
\[P(w)=\prod_{k=1}^{K}P(w_k|w_{k-1}, ..., w_1)\]实际的语言模型很难考虑特别长的历史，通常我们会限定当前词的概率值依赖与之前的N-1个词，这就是所谓的N-Gram语言模型：
\[P(w)=\prod_{k=1}^{K}P(w_k|w_{k-1},...,w_{k-N+1})\]在实际的应用中N的取值通常是2-5。我们通常用困惑度(Perplexity)来衡量语言模型的好坏：
\[\begin{split} H & = - \underset{lim}{K \to \infty} \frac{1}{K} log_2 P(w_1,...,w_K) \\ & \approx \frac{1}{K} \sum_{k=1}^{K} log_2 (P(w_k|w_{k-1},...,w_{k-N+1})) \end{split}\]N-Gram语言模型可以通过最大似然方法来估计参数，假设$C(w_{k−2} w_{k−1} w_k)$表示3个词$(w_{k−2} w_{k−1} w_k$连续出现在一起的次数，类似的$C(w_{k−2} w_{k−1}$表示两个词$w_{k−2} w_{k−1}$连续出现在一起的次数。那么：
\[P(w_k|w_{k-1}w_{k-2})=\frac{C(w_{k−2} w_{k−1} w_k)}{C(w_{k−2} w_{k−1})}\]最大似然估计的最大问题是数据的稀疏性，如果3个词没有在训练数据中一起出现过，那么概率就是0，但不在训练数据里出现不代表它不是合理的句子。实际一般会使用打折(Discount)和回退(Backoff)等平滑方法来改进最大似然估计。打折的意思就是把一些高频N-Gram的概率分配给从没有出现过的N-Gram，回退就是如果N-Gram没有出现过，我们就用(N-1)-Gram来估计。比如Katz平滑方法的公式如下：
\[P(w_k|w_{k-1}, w_{k-2}) = \begin{cases} d \frac{C(w_{k−2} w_{k−1} w_k)}{C(w_{k−2} w_{k−1})} & if 0 < C(w_{k−2} w_{k−1} w_k) \le C' \\ \frac{C(w_{k−2} w_{k−1} w_k)}{C(w_{k−2} w_{k−1})} & if C(w_{k−2} w_{k−1} w_k) > C' \\ \alpha(w_{k-2}, w_{k-1})P(w_k|w_{k-1}) & \text{其它情况} \end{cases}\]上式中C’是一个阈值，频次高于它的概率和最大似然估计一样，但是对于低于它（但是至少出现一次）的概率做一些打折，然后把这些概率分配给没有出现的3-Gram，怎么分配呢？通过回退到2-Gram的概率$P(w_k \vert w_{k-1})$来按比例分配。
当然语言模型是一个很大的话题，在后面的章节我们会更深入的讨论，这里就简单的介绍到这。
解码器(Decoder)
训练好模型之后，我们就可以使用解码器来搜索所有可能的状态空间（如果没有语言模型的约束，理论上任何因子的组合都是可能的），然后找到最可能的状态序列，使得输出的概率(这个概率包括声学和概率和语言模型概率)最大。搜索过程可以使用Vertebi算法。但是在实际的识别过程中，由于搜索空间太大，我们通常在搜索的过程中就需要进行剪枝(pruning)，把不太可能的路径提前去掉，除了声学模型得分，也会在搜索的过程中把语言模型考虑进来。我们一般把这个搜索过程叫作解码(decoding)，完成解码过程的模块叫作解码器(decoder)。一个好的解码器既要速度快，又要保证较优的路径不被剪枝掉。后面也会介绍基于加权有限状态转录机(WFST)的解码器。
解码器除了输出最优路径（以及对于概率）之外也可以输出N-best的结果，N通常是100-1000。这样我们可以用一个较小的语言模型来进行第一遍的搜索，找到N-best结果，然后使用更加复杂的语言模型来进行第二遍解码。为了在第二遍解码时不重复计算，我们会在N-best结果中保留更多的一些信息，我们会使用更加高效和紧凑的数据结构来存储搜索路径，我们一般把它叫作word lattice。word lattice有一些点和边表示，点按照时间排列，边表示两个点(时间)对应的词。下图a是一个示例，除了词(ID)之外，边上也可以存储一些其它信息，比如声学模型得分和语言模型得分等。有了这些信息之后，我们就可以用更加复杂的语言模型来对N-best结果进行重新算分(rescoring)，从而跳出更好的路径。
我们也可以把word lattice表示成更加紧凑的confusion network，如下图b所示。图中”-“表示空跳转。在confusion network中，点并不严格表示时间顺序，因此平行的边(起点和终点都相同的边)不代表它们的开始时间或结束时间相同。但是大多数时候，我们可以认为平行的边代表它们对应的词是一种竞争关系，比如图中的HAVE和MOVE。confusion network保证：对于lattice中的每一条路径，在confusion network中都有一条对应的路径。confusion network中的边上一般会有一个与边上词相关的一个后验概率，它是通过在word lattice中使用前向后向算法计算出来概率，然后把平行边的概率归一化了。
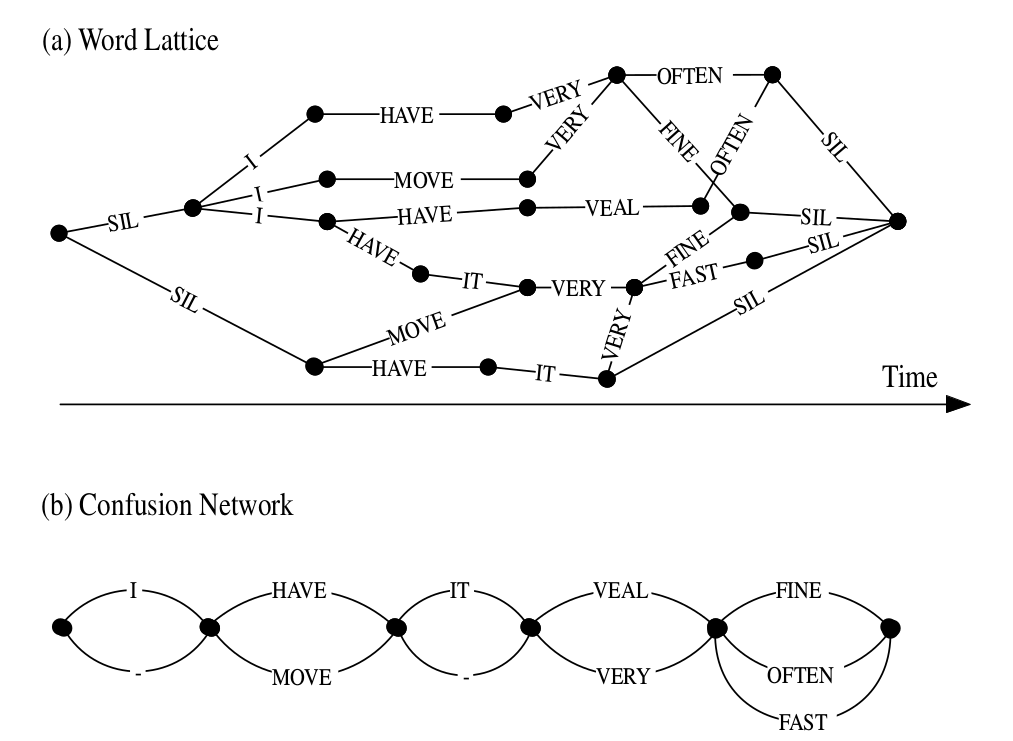图：word lattice和confusion network
- 显示Disqus评论(需要科学上网)