本文介绍自动微分。更多文章请点击深度学习理论与实战:提高篇。
引言
前面我们学习了全连接的多层神经网络,并且详细的推导了反向传播算法并且用numpy(而不是Tensorflow这些框架)从头开始实现算法。以后我们会学习更复杂的网络结构,我们仍然可以自己来求损失函数对参数的梯度,然后自己实现这些模型。但是这么做会非常麻烦,而且每个人自己造一个轮子也不高效,比如我们之前的代码没有办法利用GPU来加速。因此在深度学习领域涌现出了很多框架和工具,我们后面会介绍一些最常用的框架。本章会介绍自动微分技术和一些常见的优化技巧,前者是大多数框架能够自由扩展的基础,而后者很多框架都提供了。
在介绍自动微分(Automatic Differentiation)之前,我们先介绍其它两种计算微分的方法,从而说明自动微分的好处在哪里,为什么它会成为大部分深度学习框架的基础。
数值微分
数值微分使用了导数/梯度的定义: \(f'(x)=\frac{df}{dx}=\lim_{\Delta x \to 0}\frac{f(x+ \Delta x) - f(x)}{\Delta x}\) 当然极限的定义里$\Delta x$是趋于0的,我们实际数值计算的时候可以找一个很小的数h:
\[f'(x)=D_+(h)=\frac{f(x+h) - f(x)}{h}\]或者使用:
\[f'(x)=D_-(h)=\frac{f(x) - f(x-h)}{h}\]或者对称的版本:
\[f'(x)=D_0(h)=\frac{f(x+h) - f(x-h)}{2h}\]也可以使用更加复杂的理查德森外推法(Richardson ‘s extrapolation):
\[f'(x)=\frac{4D_0(h) - D_0(2h)}{3}\]前两种方法的误差是$O(h)$,第三种方法是$O(h^2)$,第四种是$O(h^4)$。
数值微分主要有两个问题:计算量和数值不稳定。前者在第二章的最后也提到了,如果有n个变量,那么求梯度的时候需要forward计算n次。和反向传播算法(等价于自动微分)的一次forward和一次backward比要慢n倍。如果神经网络有一百万参数,那就会慢一百万倍!!!而数值计算的不稳定是由于浮点数的表示精度有限而造成的舍入误差。由于这些原因,数值微分很少在实际中使用,一般我们在自己实现反向传播算法是用它来check我们的算法是否正确,我们可以计算数值微分的结果和我们自己计算的结果的相对误差,一般要求相对误差是个很小的数(比如$10^{-7}$)。如果差距比较大,很有可能(但也不绝对)我们的实现有bug。
符号微分
符号微分就是我们在大学微积分里学的方法,通过符号(包括分部积分法这种trick)计算直接求出微分的“解析”形式。前面的数值微分只能求函数在某个点的微分,如果换一个点就需要重新计算,而符号微分是求出一个闭式(closed form)的“解析解”(简单的函数),我们求一个点的微分时直接代入这个“解析解”即可。但是我们知道,并不是所有的微分都可以求出闭式来,而且符号计算库求出的解析解也不一定是“最简化”的形式。此外,如果一下神经网络是if-else逻辑或者更复杂的包含while循环的话,很难用符号微分求出来。
自动微分
计算图
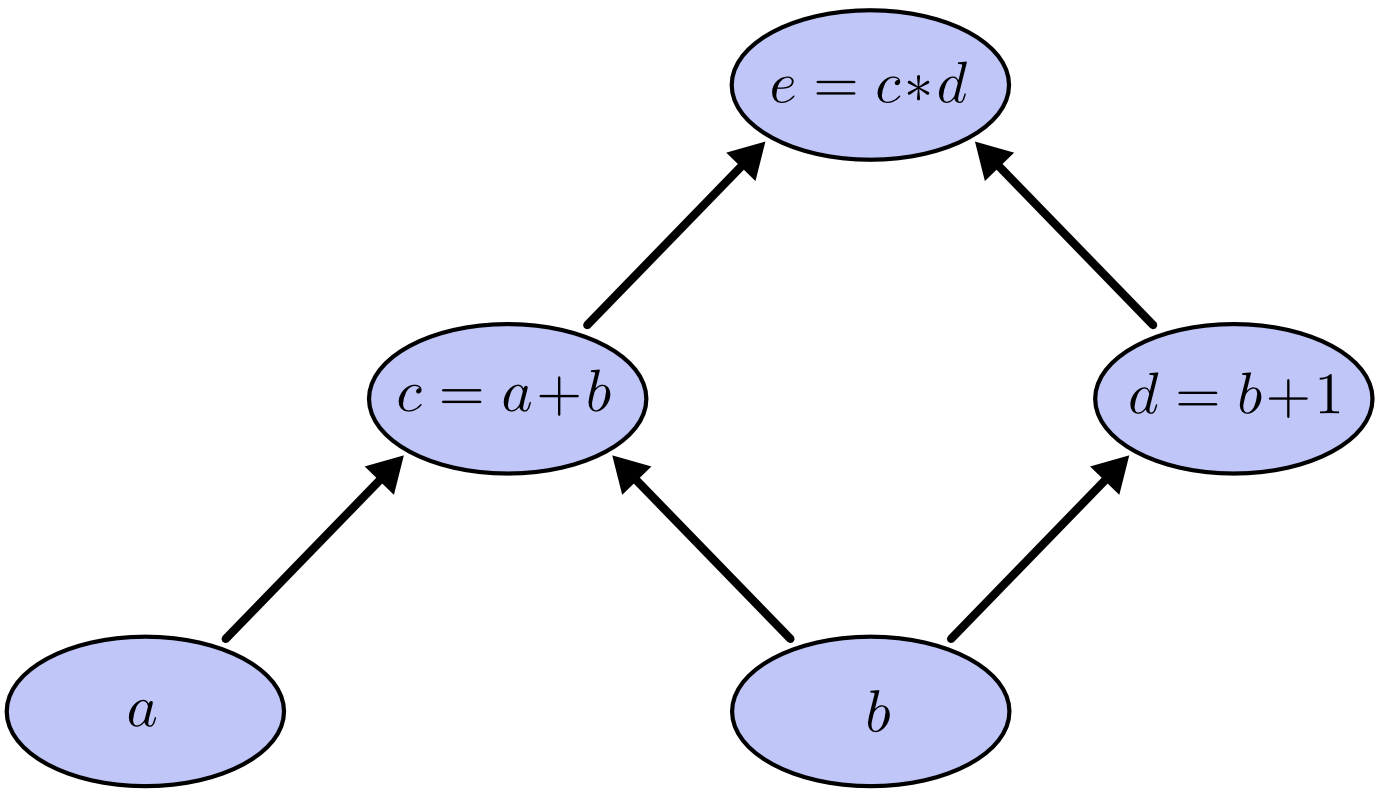
任何一个表达式(函数的求值而不是符号运算)都可以用一个计算图(Computational Graphs)来表示。比如一个简单的表达式$e=(a+b)*(b+1)$,我们可以把它分解成“原子”的表达式的组合:
\[c=a+b\] \[d=b+1\] \[e=c*d\]我们可以把它用下图来表示。
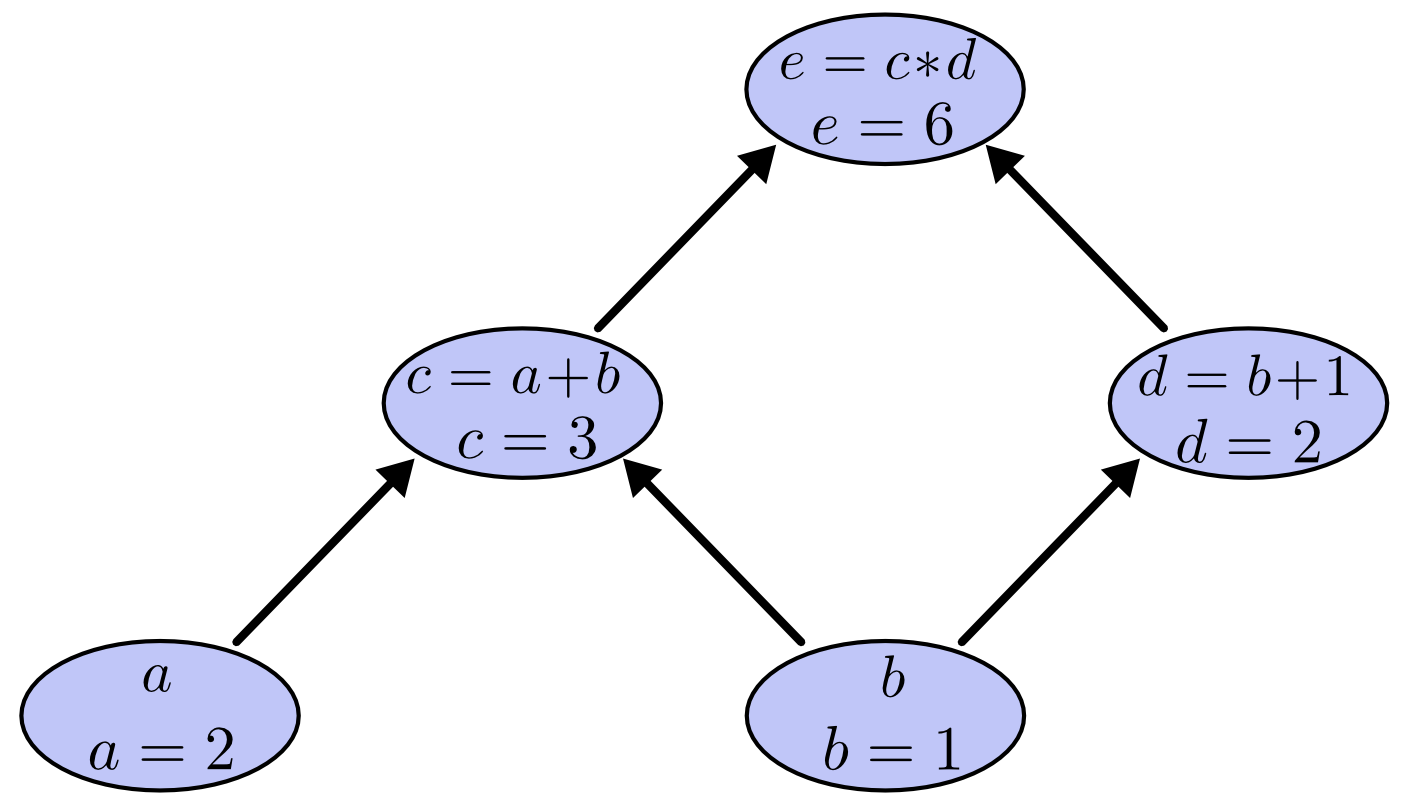
在计算图里,每个中间节点代表一个操作(运算/函数),叶子节点是最原子的“自变量”,边代表依赖关系,在计算机的编译器领域被叫做表达式树。如果我们知道了输入变量的值,那么我们就可以计算出最终的表达式值,比如当$a=2, b=1$时,求值的过程如下图所示。
我们先求中间节点c和d的值,最终求出e=6。
基于计算图的微分方法
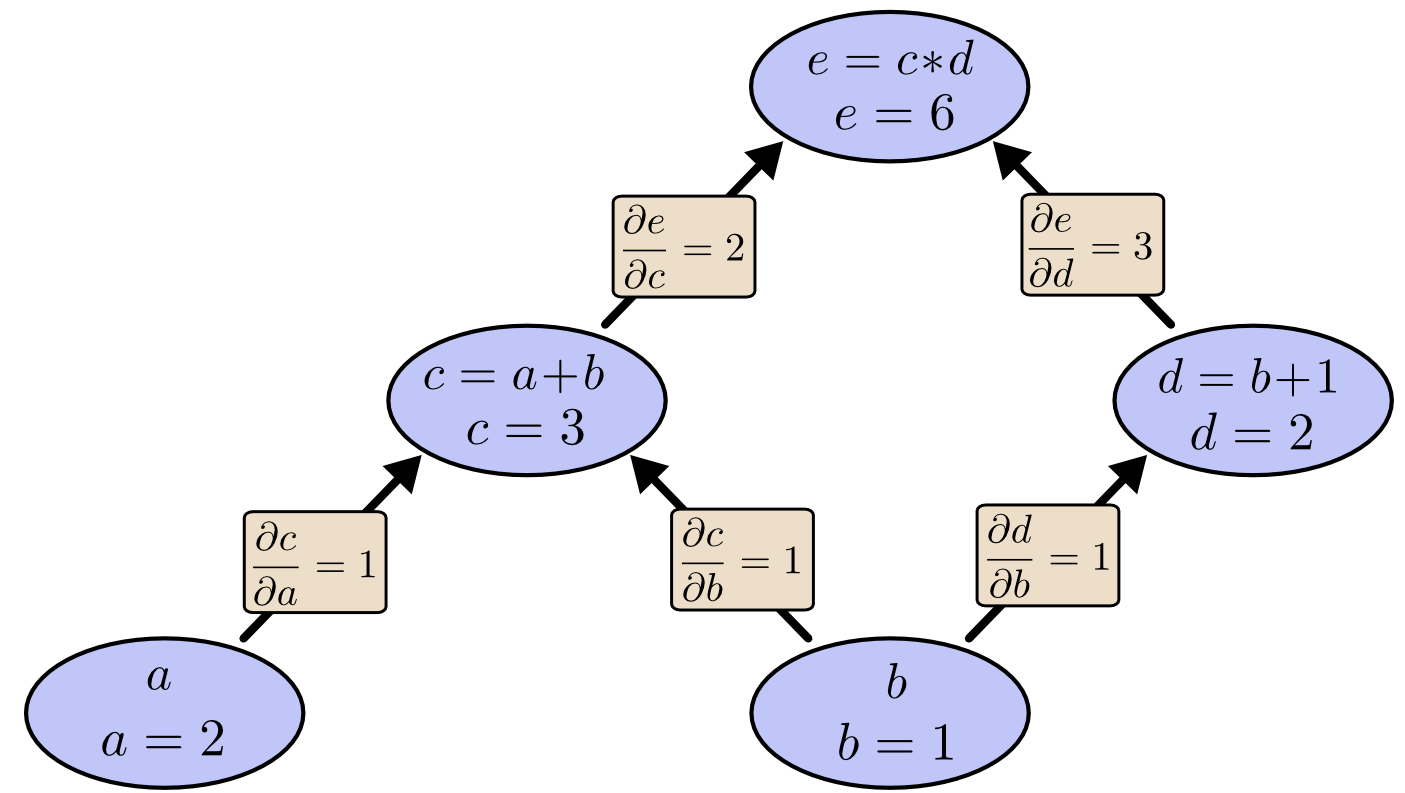
因为图中的每条边代表变量之间的直接依赖关系,因此我们可以求出导数的值来。如下图所示。
如果我们把e当成损失,a和b当成参数,那么我们需要求$\frac{\partial e}{\partial a}$和$\frac{\partial e}{\partial b}$。这是我们有两种方法:前向模式微分(forward-mode differentiation)和反向模式微分(backward-mode differentiation),后者就是我们常说的自动微分。
前向模式微分
为了求$\frac{\partial e}{\partial b}$,我们从自底向上求所有变量对b的偏导数,计算过程如下图所示。
计算过程如下:叶子节点a和b对b的偏导数分别是0和1。然后往上每个节点的值都是孩子(入边)节点的值乘以边的值然后再加起来(其实就是链式法则),最终求得$\frac{\partial e}{\partial b}$。注意前向模式一次计算所有变量对b的偏导数,但是我们关心的是e对所有变量(a,b)的偏导数,因此对于a,我还得再来一次。一般对于神经网络来说,我们的损失函数只有一个,但是参数非常多,因此前向模式微分计算量非常大,我们可以发现在前向模式里我们计算了一些没用的值,比如$\frac{\partial a}{\partial b}$。
反向模式微分
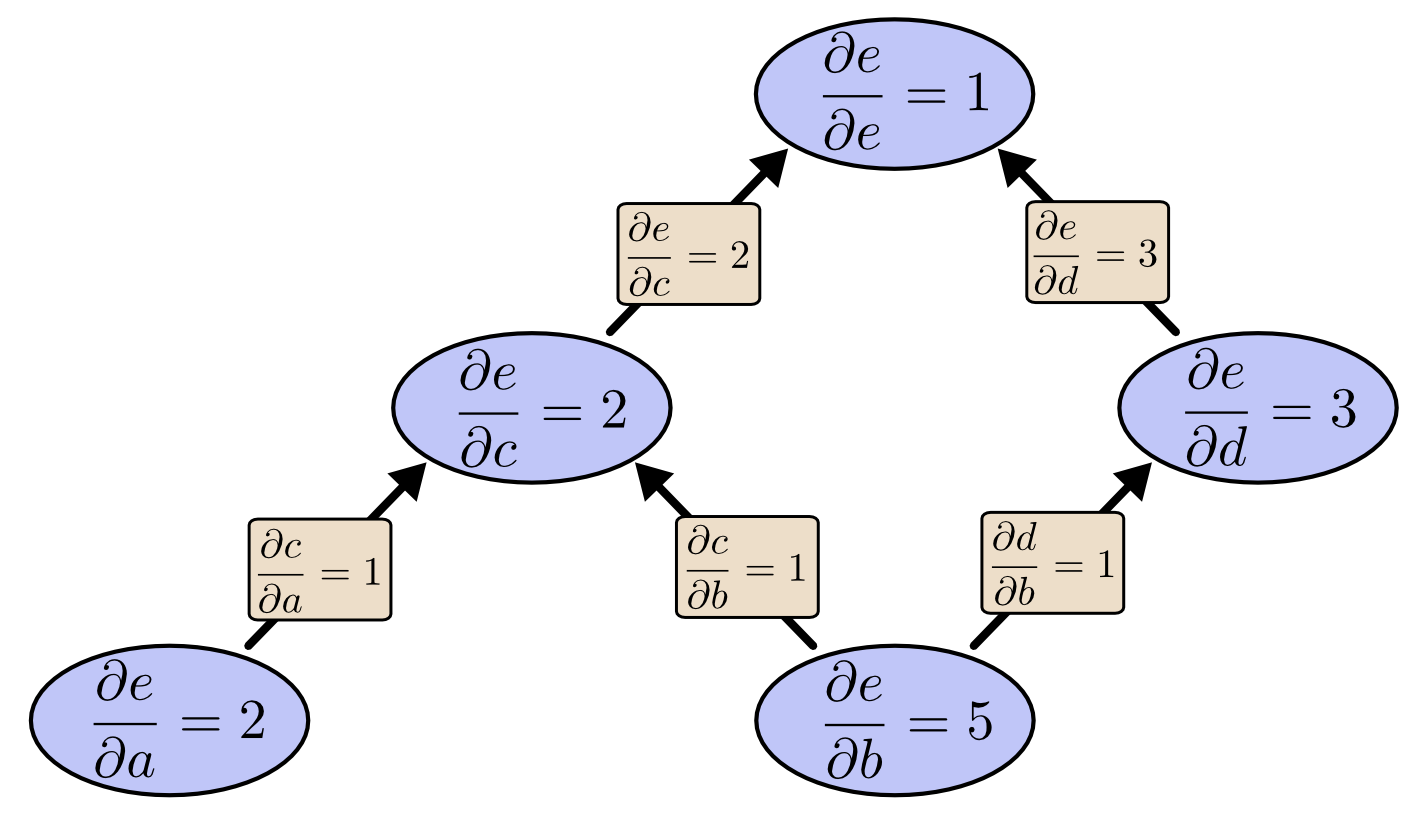
逆向模式和前向相反,是从上往下求e对每个变量的偏导数,如下图所示。
它的计算过程如下:首先是e对自己的偏导数=1,接着是$\frac{\partial e}{\partial c}$和$\frac{\partial e}{\partial d}$,最后是$\frac{\partial e}{\partial a}$和$\frac{\partial e}{\partial b}$。计算的时候把父亲(出边)节点和边的值乘起来然后加起来。
最终我们发现在叶子节点,我们求出了损失e对所有变量a和b的偏导数。和前向模式相比,我们一次就求出了损失对所有参数的偏导数,这非常高效!接下来我们通过代码来更加细致的了解其中的细节。
基本表达式的梯度
加法表达式
\[f(x,y) = x + y \hspace{0.5in} \rightarrow \hspace{0.5in} \frac{\partial f}{\partial x} = 1 \hspace{0.5in} \frac{\partial f}{\partial y} = 1\]乘法表达式
\[f(x,y) = x y \hspace{0.5in} \rightarrow \hspace{0.5in} \frac{\partial f}{\partial x} = y \hspace{0.5in} \frac{\partial f}{\partial y} = x\]max函数
\[f(x,y) = \max(x, y) \hspace{0.5in} \rightarrow \hspace{0.5in} \frac{\partial f}{\partial x} = \mathbb{1}(x \geq y) \hspace{0.5in} \frac{\partial f}{\partial y} = \mathbb{1}(y \geq x)\]复杂表达式的链式法则
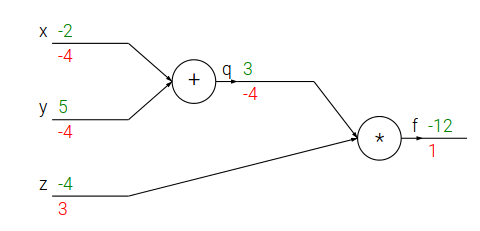
接下来看个稍微复杂点的函数 $f(x,y,z)=(x+y)z$。我们引入一个中间变量q,f=qz,q=x+y,我们可以使用链式法则求f对x和y的导数。 \(\frac{\partial f}{\partial x} = \frac{\partial f}{\partial q} \frac{\partial q}{\partial x} =z \times 1=(x+y)\)
对y的求导也是类似的。下面是用python代码来求f对x和y的导数在某一个点的值。
# 设置自变量的值
x = -2; y = 5; z = -4
# “前向”计算f
q = x + y # q becomes 3
f = q * z # f becomes -12
# 从“后”往前“反向”计算
# 首先是 f = q * z
dfdz = q # 因为df/dz = q, 所以f对z的梯度是 3
dfdq = z # 因为df/dq = z, 所以f对q的梯度是 -4
# 然后 q = x + y
dfdx = 1.0 * dfdq # 因为dq/dx = 1,所以使用链式法则计算dfdx=-4
dfdy = 1.0 * dfdq # 因为dq/dy = 1,所以使用链式法则计算dfdy=-4
我们也可以用下图来表示和计算。
反向传播算法的直觉解释
我们如果把计算图的每一个点看成一个“门”(或者一个模块),或者说一个函数。它有一个输入(向量),也有一个输出(标量)。对于一个门来说有两个计算,首先是根据输入,计算输出,这个一般很容易。还有一种计算就是求输出对每一个输入的偏导数,或者说输出对输入向量的”局部“梯度(local gradient)。一个复杂计算图(神经网络)的计算首先就是前向计算,然后反向计算,反向计算公式可能看起来很复杂,但是如果在计算图上其实就是简单的用local gradient乘以从后面传过来的gradient,然后加起来。
Sigmoid模块的例子
接下来我们看一个更复杂的例子:
\[f(w,x) = \frac{1}{1+e^{-(w_0x_0 + w_1x_1 + w_2)}}\]这个函数是一个比较复杂的复合函数,但是构成它的基本函数是如下4个简单函数:
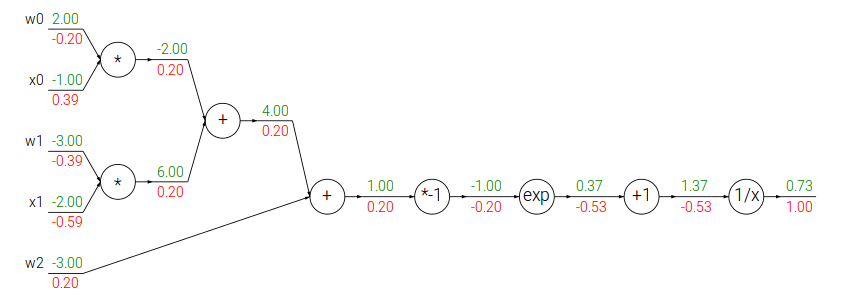
\[\begin{split} f(x) = \frac{1}{x} \hspace{1in} & \rightarrow \hspace{1in} \frac{df}{dx} = -1/x^2 \\ f_c(x) = c + x \hspace{1in} & \rightarrow \hspace{1in} \frac{df}{dx} = 1 \\ f(x) = e^x \hspace{1in} & \rightarrow \hspace{1in} \frac{df}{dx} = e^x \\ f_a(x) = ax \hspace{1in} & \rightarrow \hspace{1in} \frac{df}{dx} = a \end{split}\]我们可以把这个计算过程用下图来表示。
上面我们看到把$f(w,x) = \frac{1}{1+e^{-(w_0x_0 + w_1x_1 + w_2)}}$分解成最基本的加法、乘法、导数和指数函数,但是我们也可以不分解这么细。之前我们也学习过了sigmoid函数,那么我们可以这样分解:
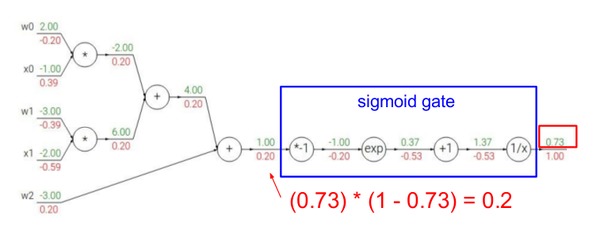
\[\begin{split} z & =w_0x_0 + w_1x_1 + w_2 \\ f & =\sigma(z) \end{split}\]这样我们就可以利用$\sigma’(x)=\sigma(x)(1-\sigma(x))$可以把后面一长串的gate“压缩”成一个gate,如下图所示。
我们来比较一下,之前前向计算$\sigma(x)$ 需要一次乘法,一次exp,一次加法导数;而反向计算需要分别计算这4个gate的导数。而压缩后前向计算是一样的,但是反向计算可以“利用”前向计算的结果$\sigma’(x)=\sigma(x)(1-\sigma(x))$。这只需要一次减法和一次乘法!当然如果不能利用前向的结果,我们如果需要重新计算$\sigma(x)$ ,那么压缩其实没有什么用处。能压缩的原因在于$\sigma$函数导数的特殊形式。而神经网络的关键问题是在训练,训练性能就取决于这些细节。如果是我们自己来实现反向传播算法,我们就需要利用这样的特性。而如果是使用工具,那么就依赖于工具的优化水平了。
下面我们用代码来实现:
w = [2,-3,-3] # 随机初始化weight
x = [-1, -2]
# forward计算
dot = w[0]*x[0] + w[1]*x[1] + w[2]
f = 1.0 / (1 + math.exp(-dot)) # sigmoid function
# 反向计算
ddot = (1 - f) * f # 对dot的梯度
dx = [w[0] * ddot, w[1] * ddot] # 计算dx
dw = [x[0] * ddot, x[1] * ddot, 1.0 * ddot] # 计算dw
上面的例子用了一个小技巧,就是所谓的staged backpropagation,说白了就是给中间的计算节点起一个名字。比如dot。为了让大家熟悉这种技巧,下面有一个例子。
分阶段(staged)计算的练习题
\[f(x,y) = \frac{x + \sigma(y)}{\sigma(x) + (x+y)^2}\]我们用代码来计算这个函数对x和y的梯度在某一点的值。前向计算:
x = 3 # example values
y = -4
# forward pass
sigy = 1.0 / (1 + math.exp(-y)) # 分子上的sigmoid #(1)
num = x + sigy # 分子 #(2)
sigx = 1.0 / (1 + math.exp(-x)) # 分母上的sigmoid #(3)
xpy = x + y #(4)
xpysqr = xpy**2 #(5)
den = sigx + xpysqr # 分母 #(6)
invden = 1.0 / den #(7)
f = num * invden # done! #(8)
反向计算:
# backprop f = num * invden
dnum = invden # gradient on numerator #(8)
dinvden = num #(8)
# backprop invden = 1.0 / den
dden = (-1.0 / (den**2)) * dinvden #(7)
# backprop den = sigx + xpysqr
dsigx = (1) * dden #(6)
dxpysqr = (1) * dden #(6)
# backprop xpysqr = xpy**2
dxpy = (2 * xpy) * dxpysqr #(5)
# backprop xpy = x + y
dx = (1) * dxpy #(4)
dy = (1) * dxpy #(4)
# backprop sigx = 1.0 / (1 + math.exp(-x))
dx += ((1 - sigx) * sigx) * dsigx # Notice += !! See notes below #(3)
# backprop num = x + sigy
dx += (1) * dnum #(2)
dsigy = (1) * dnum #(2)
# backprop sigy = 1.0 / (1 + math.exp(-y))
dy += ((1 - sigy) * sigy) * dsigy #(1)
# done! phew
需要注意的两点:1. 前向的结果都要保存下来,反向的时候要用的。2. 如果某个变量有多个出去的边,第一次是等于,第二次就是+=,因为我们要把不同出去点的梯度加起来。
下面我们来逐行分析反向计算。
(8) f = num * invden 因为local gradient$\frac{df}{dnum}=invden$,而上面传过来的梯度是1,所以 dnum=1∗invden。注意变量的命名规则, df/dnum就命名为dnum(省略了df,因为默认我们是求f对所有变量的偏导数)。同理: dinvden=num。
(7) invden = 1.0 / den local gradient是 $(−1.0/(den^2))$ ,然后乘以上面来的dinvden
(6) den = sigx + xpysqr 这个函数有两个变量sigx和xpysqr,所以需要计算两个local梯度,然后乘以dden。加法的local梯度是1,所以就是(1)*dden。
(5) xpysqr = xpy*2 local gradient是2xpy,再乘以dxpysqr。
(4) xpy = x + y 还是一个加法,local gradient是1,所以dx和dy都是dxpy乘1。
(3) sigx = 1.0 / (1 + math.exp(-x)) 这是sigmoid函数,local gradient是 (1-sigx)*sigx,再乘以dsigx。不过需要注意的是这是dx的第二次出现,所以是+=,表示来自不同路径反向传播过来给x的梯度值
(2) num = x + sigy 还是个很简单的加法,local gradient是1。需要注意的是dx是+=,理由同上。
(1) sigy = 1.0 / (1 + math.exp(-y))
最后是sigmoid(y)和前面(3)一样的。
梯度的矩阵运算
前面都是对一个标量的计算,在实际实现时用矩阵运算一次计算一层的所有梯度会更加高效。因为矩阵乘以向量和向量乘以向量都可以看出矩阵乘以矩阵的特殊形式,所以下面我们介绍矩阵乘法怎么求梯度。
假设 $f:R^{m \times n} \to R$是一个函数,输入是一个$m \times n$的实数值矩阵,输出是一个实数。那么f对A的梯度是如下定义的:
\[\nabla_Af(A)= \ \begin{bmatrix} \frac{\partial f(A)}{\partial A_{11}} & \frac{\partial f(A)}{\partial A_{12}} & \dots & \frac{\partial f(A)}{\partial A_{1n}}\\ \frac{\partial f(A)}{\partial A_{21}} & \frac{\partial f(A)}{\partial A_{22}} & \dots & \frac{\partial f(A)}{\partial A_{2n}}\\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f(A)}{\partial A_{m1}} & \frac{\partial f(A)}{\partial A_{m2}} & \dots & \frac{\partial f(A)}{\partial A_{mn}} \end{bmatrix}\]看起来定义很复杂?其实很简单,我们把f看成一个$m \times n$个自变量的函数,因此我们可以求f对这$m \times n$个自变量的偏导数,然后把它们排列成m*n的矩阵就行了。为什么要多此一举把变量排成矩阵把他们的偏导数也排成矩阵?想想我们之前的神经网络的weights矩阵,这是很自然的定义,同时我们需要计算loss对weights矩阵的每一个变量的偏导数,写出这样的形式计算起来比较方便。
那么什么是矩阵对矩阵的梯度呢?我们先看实际神经网络的一个计算情况。对于全连接的神经网络,我们有一个矩阵乘以向量 $D=Wx$ (我们这里把向量x看成矩阵)。现在我们需要计算loss对某一个 $W_{ij}$ 的偏导数,根据我们之前的计算图, $W_{ij}$ 有多少条出边,那么就有多少个要累加的梯度乘以local梯度。假设W是$m \times n$的矩阵,x是$n \times p$的矩阵,则D是$m \times p$的矩阵
\[\frac {\partial Loss}{\partial W_{ij}} = \sum_{k=1}^{m} \sum_{l=1}^{p} \frac {\partial D_{kl}}{\partial W_{ij}} \frac{\partial Loss}{\partial D_{kl}}\]根据矩阵乘法的定义 $D_{kl}=\sum_{s=1}^{n}W_{ks}x_{sl}$ ,我们可以计算:
\[\frac {\partial D_{kl}}{\partial W_{ij}} = \ \begin{cases} 0, \; k \neq i \\ x_{jl}, \; k=i \end{cases}\]请仔细理解上面这一步,如果 $k \ne i$ ,则不论s是什么, $W_{ks}$ 跟 $W_{ij}$ 不是同一个变量,所以导数就是0;如果 $k=i$ , $\sum_s{W_{is}}x_{sl}=x_{jl}$ ,也就是当求和的下标s取j的时候有 $W_{ij}$ 。因此:
\[\begin{split} \frac {\partial Loss}{\partial W_{ij}} & = \sum_{k=1}^{m} \sum_{l=1}^{p} \frac {\partial D_{kl}}{\partial W_{ij}} \frac{\partial Loss}{\partial D_{kl}} \\ & =\sum_{l=1}^{p} \frac{\partial D_{il}}{\partial W_{ij}} \frac{\partial Loss}{\partial D_{il}} \text{ ,k必须等于0,否则是0} \\ & =\sum_{l=1}^{p} x_{jl} \frac{\partial Loss}{\partial D_{il}} \text{ ,代入上式} \end{split}\]上面计算了loss对一个 $W_{ij}$ 的偏导数,如果把它写成矩阵形式就是$\frac{\partial Loss}{\partial W}$。
前面我们推导出了对 $W_{ij}$的偏导数的计算公式,下面我们把它写成矩阵乘法的形式($\frac{\partial Loss}{\partial W}=\frac{\partial Loss}{\partial D} x^T$)并验证它。
\[(\frac{\partial Loss}{\partial D} x^T)_{ij} \\\\ =\sum_{l=1}^{p} (\frac{\partial Loss}{\partial D} )_{il} (x^T)_{lj} \\\\ =\sum_{l=1}^{p} (\frac{\partial Loss}{\partial D})_{il} (x)_{jl} \\\\ =\sum_{l=1}^{p} \frac{\partial Loss}{\partial D_{il}} (x)_{jl}\]上面的推导似乎很复杂,但是我们只要能记住就行,记法也很简单——把矩阵都变成最特殊的$1 \times 1$的矩阵(也就是标量,一个实数)。$D=w x$,这个导数很容易吧,对w求导就是local gradient x,然后乘以得到$dW=dD x$;同理$dx=dD W$。 但是等等,刚才那个公式里还有矩阵的转置,这个怎么记?这里有一个小技巧,就是矩阵乘法的条件,两个矩阵能相乘他们的大小必须匹配,比如$D=Wx$,W是$m \times n$,x是$n \times p$,也就是第二个矩阵的行数等于第一个的列数。
现在我们已经知道dW是dD“乘以”x了,dW的大小和W一样是$m \times n$,而dD和D一样是$m \times p$,而x是$n \times p$,那么为了得到一个$m \times n$的矩阵,唯一的办法就是 $dDx^T$ 同理dx是$n \times p$,dD是$m \times p$,W是$m \times n$,唯一的乘法就是 $W^TdD$ 下面是用python代码来演示,numpy的dot就是矩阵乘法,可以用numpy.dot(A,B),也可以直接调用ndarray的dot函数——A.dot(B):
# 前向计算
W = np.random.randn(5, 10)
X = np.random.randn(10, 3)
D = W.dot(X)
# 反向计算
dD = np.random.randn(*D.shape) # 和D一样的shape
dW = dD.dot(X.T) #.T gives the transpose of the matrix
dX = W.T.dot(dD)
- 显示Disqus评论(需要科学上网)