DeepSpeech理论与实战

本文介绍基于CTC的End-to-End语音识别系统——DeepSpecch，包括简单的原理介绍和代码介绍。阅读本文之前需要了解CTC的基本原理。更多文章请点击深度学习理论与实战：提高篇。

转载请联系作者(fancyerii at gmail dot com)！

DeepSpeech简介
DeepSpeech代码

DeepSpeech简介

之前介绍的传统的HMM-GMM的语音识别系统非常复杂，有声学模型，语言模型，发音词典(模型)，其中声学模型的训练又需要从flat-start到训练单因子再到三因子的模型。而HMM-DNN的模型只是把GMM替换成了一个DNN，其它的部分并没有变化。接下来我们介绍完全End-to-end的语音识别系统，这个系统甚至没有音素的概念，它的输入是语音的特征(MFCC),输出就是字母。这里的关键技术就是前面介绍的CTC算法，前面也介绍了，CTC不能学到语言的上下文，因此我们也需要一个单独的语言模型。

网络结构

这个系统的核心是一个RNN，它的输入是语音的频谱，输出是英文字符串。训练数据集是$\mathcal{X}=\{(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), …\}$。每个输入$x^{(i)}$，它的长度是$T^{(i)}$，每个时刻就是第t帧的特征向量$x_t^{(i)}, t=1,2,..,T^{(i)}$。RNN的输入是x，输出是每个时刻输出不同字符的概率分布$p(c_t \vert x)$，这里$c_t \in \{a,b,…,z,space, apostrophe, blank\}$，也就是每个时刻RNN输出的是一个概率分布，表示这个时刻输出某个字符的概率。字符集包括a-z这26个字母和空格，‘(what’s里的’) 和空字符(CTC里的$\epsilon$)。

DeepSpeech的模型5个隐层组成。对于输入x，我们用$h^l$表示第l层，$h^0$表示输入。前3层是全连接层，对于第1层，在t时刻的输入不只是t时刻的特征$x_t$，而且还包括它的前后C帧特征，共计2C+1帧。前3层通过如下公式计算：

\[h_t^l=g(W^l h_t^{l-1} + b^l)\]

其中$g(z)=min(max(z,0))$，在ReLU的基础上限制它的最大值，因此也叫Clipped ReLU。第四层是一个双向RNN：

\[\begin{split} h_t^f = g(W^4 h_t^3 + W_r^f h_{t-1}^f + b^4) \\ h_t^b = g(W^4 h_t^3 + W_r^b h_{t+1}^b + b^4) \end{split}\]

这里使用了最普通的RNN而不是LSTM/GRU，原因是为了使得网络结构简单一致，便于计算速度的优化。在这个双向RNN中，输入到隐单元的参数是共享的（包括bias），每个方向的RNN有自己的隐单元-隐单元参数。$h^f$是时刻1开始一直计算到T，而$h^b$是反过来从T时刻开始计算。第5层会把第4层双向RNN的两个输出加起来作为它的输入：

\[\begin{split} h_t^4=h_t^f+f_t^b \\ h_t^5=g(W^5 h_t^4 +b^5) \end{split}\]

最后一层是一个全连接层(无激活函数)，它使用softmax把输出变成对应每个字符的概率：

\[h_{t,k}^6 = \hat{y}_{t,k} \equiv P(c_t=k|x)= \frac{exp(W_k^6 h_t^5 + b_k^6)}{\sum_{j} exp(W_j^6 h_t^5 + b_j^6)}\]

有了$P(c_t=k \vert x)$之后，我们就可以用CTC计算$\mathcal{L}(\hat{y}, y)$，并且求L对参数的梯度。

DeepSpeech网络结构如下图所示。

图：DeepSpeech网络结构

因为CTC不能学到语言上下文的特征，因此我们在用Beam Search的时候会加入语言模型：

\[Q(c)=logP(c|x) + \alpha logP_{lm}(c) + \beta word\_count(c)\]

前面在CTC的章节也介绍过，引入word_count的目的是避免语言模型选择短文本的倾向（因为语言模型的概率一般是越长值越小）。

优化

数据并行

为了利用GPU的计算能力，一次训练会计算较大的batch（通常上千）。此外DeepSpeech会同时用多个GPU计算一个batch的梯度，然后平均这些梯度来更新参数。因为序列的长度是变长的，DeepSpeech会把长度类似的训练数据分成组，然后padding成一样的长度。

模型并行

数据并行可以通过更多GPU来计算梯度，但是因为都是基于当前的参数的梯度，所以相对于一个GPU它的区别只是batch更大，梯度计算的更准（理论上一次计算所有数据的梯度就不是随机梯度下降而是梯度下降）。但是当batch足够大之后，梯度方向已经很准确了，那么再增加batch大小就没有用处了，因此我们如果还想提速的话就需要使用更多的计算资源来计算一个固定大小的batch的梯度，比如有些GPU计算第一层，有些计算第二层，这就是模型并行。相对于数据并行，模型并行更加困难，因为forward时，第二层的结果要依赖第一层，第三层要依赖第二层。这种依赖关系使得模型并行很难实现线性的加速比。怎么在保证依赖关系的情况下利用计算资源，这其实是深度学习框架最核心的差异。除次之外，由于双向RNN的存在，问题更加复杂——虽然两个方向的RNN可以独立计算，但是最终需要加起来，这会带来大量的通信。DeepSpeech采用了一些技巧来提高并行效率，因为我们后面的实现都是使用深度学习框架，所以这里就不介绍了，感兴趣的读者可以参考原始论文。

数据增强

在图像的任务中，我们通常通过变换图像来获得更多训练数据，DeepSpeech也使用了数据增强的技术。包括给干净语音增加噪声来获得更多数据以及提高模型在噪声环境下的性能。另外在录音的时候也考虑了Lombard效应——如果背景噪音较大的时候，说话人会不自觉的提高声强和音调，因此DeepSpeech在录制数据的时候就让录音者听到一些背景噪音。

实验结果

通过海量的训练数据(5000+小时 vs 传统的几百小时的录音)和End-to-End的模型，DeepSpeech得到了解决甚至超过传统的Pipeline的识别结果。

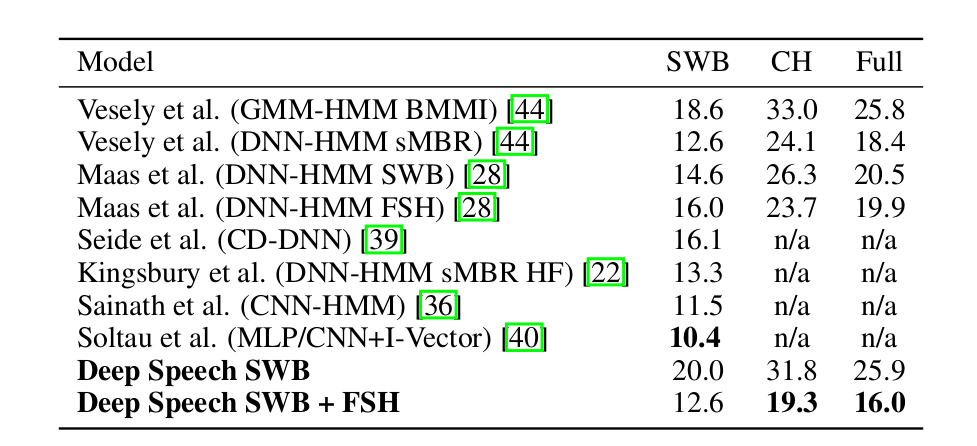
如下图所示，在Switchboard的标准任务上，DeepSpeech的词错误率(WER)是12.6，解决最好的10.4；而在Switchboard的困难任务上，DeepSpeech得到了(当时)最好的结果19.3。

图：DeepSpeech实验结果

DeepSpeech代码

网上有很多DeepSpeech的实现，我们这里使用Mozilla的实现，它是基于Tensorflow的实现，并且使用了warpctc。读者可以从这里 clone代码。

核心的代码在DeepSpeech.py文件，代码接近2000行，这里我们只是阅读网络结构定义相关的部分代码，另外很多代码都是为了支持多GPU训练的，有兴趣的读者可以自己阅读。

def BiRNN(batch_x, seq_length, dropout):
  
  # 输入 shape: [batch_size, n_steps, n_input + 2*n_input*n_context]
  batch_x_shape = tf.shape(batch_x)
  
  # 把 `batch_x` Reshape成 `[n_steps*batch_size, n_input + 2*n_input*n_context]`.
  # 因为第一层期望的输入的rank是2
  
  # 时间主序，这是warpCTC的要求。
  batch_x = tf.transpose(batch_x, [1, 0, 2])
  # 第一层期望的输入rank是2
        # (n_steps*batch_size, n_input + 2*n_input*n_context)
  batch_x = tf.reshape(batch_x, [-1, n_input + 2*n_input*n_context])
  
  # 输入首先经过3个隐层，激活函数是clipped的ReLU，并且使用dropout
  
  # 第一层
  b1 = variable_on_worker_level('b1', [n_hidden_1], 
				tf.random_normal_initializer(stddev=FLAGS.b1_stddev))
  h1 = variable_on_worker_level('h1', [n_input + 2*n_input*n_context, n_hidden_1], 
          tf.contrib.layers.xavier_initializer(uniform=False))
  layer_1 = tf.minimum(tf.nn.relu(tf.add(tf.matmul(batch_x, h1), b1)), FLAGS.relu_clip)
  layer_1 = tf.nn.dropout(layer_1, (1.0 - dropout[0]))
  
  # 第二层
  b2 = variable_on_worker_level('b2', [n_hidden_2], 
				tf.random_normal_initializer(stddev=FLAGS.b2_stddev))
  h2 = variable_on_worker_level('h2', [n_hidden_1, n_hidden_2], 
          			tf.random_normal_initializer(stddev=FLAGS.h2_stddev))
  layer_2 = tf.minimum(tf.nn.relu(tf.add(tf.matmul(layer_1, h2), b2)), FLAGS.relu_clip)
  layer_2 = tf.nn.dropout(layer_2, (1.0 - dropout[1]))
  
  # 第三层
  b3 = variable_on_worker_level('b3', [n_hidden_3], 
				tf.random_normal_initializer(stddev=FLAGS.b3_stddev))
  h3 = variable_on_worker_level('h3', [n_hidden_2, n_hidden_3], 
          			tf.random_normal_initializer(stddev=FLAGS.h3_stddev))
  layer_3 = tf.minimum(tf.nn.relu(tf.add(tf.matmul(layer_2, h3), b3)), FLAGS.relu_clip)
  layer_3 = tf.nn.dropout(layer_3, (1.0 - dropout[2]))
  
  # LSTM，隐单元是n_cell_dim，遗忘门的bias是1.0

  # 前向LSTM:
  lstm_fw_cell = tf.contrib.rnn.BasicLSTMCell(n_cell_dim, forget_bias=1.0, state_is_tuple=True,
    						reuse=tf.get_variable_scope().reuse)
  lstm_fw_cell = tf.contrib.rnn.DropoutWrapper(lstm_fw_cell,
    input_keep_prob=1.0 - dropout[3],
    output_keep_prob=1.0 - dropout[3],
    seed=FLAGS.random_seed)
  # 反向LSTM:
  lstm_bw_cell = tf.contrib.rnn.BasicLSTMCell(n_cell_dim, forget_bias=1.0, state_is_tuple=True, 
    						reuse=tf.get_variable_scope().reuse)
  lstm_bw_cell = tf.contrib.rnn.DropoutWrapper(lstm_bw_cell,
    input_keep_prob=1.0 - dropout[4],
    output_keep_prob=1.0 - dropout[4],
    seed=FLAGS.random_seed)
  
  # 第三层的输出`layer_3` reshape成`[n_steps, batch_size, 2*n_cell_dim]`,
  # 因为后面期望的输入是`[max_time, batch_size, input_size]`.
  layer_3 = tf.reshape(layer_3, [-1, batch_x_shape[0], n_hidden_3])
  
  # 把第三层的输出传入双向LSTM 
  outputs, output_states = tf.nn.bidirectional_dynamic_rnn(cell_fw=lstm_fw_cell,
    cell_bw=lstm_bw_cell,
    inputs=layer_3,
    dtype=tf.float32,
    time_major=True,
    sequence_length=seq_length)
  
  # LSTM的输出包括双向的结果，每一个方向的输出是[n_steps, batch_size, n_cell_dim]，
        # 我们把它拼接起来最后一个时刻的隐状态和最后reshape成[n_steps*batch_size, 2*n_cell_dim]
  outputs = tf.concat(outputs, 2)
  outputs = tf.reshape(outputs, [-1, 2*n_cell_dim])
  
  # 第五个隐层
  b5 = variable_on_worker_level('b5', [n_hidden_5], 
				tf.random_normal_initializer(stddev=FLAGS.b5_stddev))
  h5 = variable_on_worker_level('h5', [(2 * n_cell_dim), n_hidden_5], 
     				tf.random_normal_initializer(stddev=FLAGS.h5_stddev))
  layer_5 = tf.minimum(tf.nn.relu(tf.add(tf.matmul(outputs, h5), b5)), FLAGS.relu_clip)
  layer_5 = tf.nn.dropout(layer_5, (1.0 - dropout[5]))
  
  # 第六层，没有激活函数，输出是logits
  b6 = variable_on_worker_level('b6', [n_hidden_6], 
				tf.random_normal_initializer(stddev=FLAGS.b6_stddev))
  h6 = variable_on_worker_level('h6', [n_hidden_5, n_hidden_6], 
        tf.contrib.layers.xavier_initializer(uniform=False))
  layer_6 = tf.add(tf.matmul(layer_5, h6), b6)
  
  # 把logits 从 [n_steps*batch_size, n_hidden_6]
  # reshape [n_steps, batch_size, n_hidden_6].
  # 注意，它和输入是不同的，因为它是时间主序(而输入是batch主序)
  layer_6 = tf.reshape(layer_6, [-1, batch_x_shape[0], n_hidden_6], name="logits")
  
  # Output shape: [n_steps, batch_size, n_hidden_6]
  return layer_6

代码看起来有点长，其实比较简单，读者只需要根据注释理解Tensor的shape的变化就能理解了。