本文介绍Deep Q-Learning的原理并且通过Mountain Car和Atari Breakout两个例子详细介绍DQN的代码。阅读本文前需要先了解强化学习尤其是Q-Learning的基本概念，读者可以参考本书的相关章节内容。更多文章请点击深度学习理论与实战：提高篇。
目录
- 简介
- 普通的函数近似存在的问题
- Experience Replay
- Target Network
- 状态表示
- DQN算法
- DQN解决Mountain Car问题
- 用DQN来玩Atari Breakout
简介
Deep Q-Networks来自于Google Deepmind发表在Nature上的文章《Human-level control through Deep Reinforcement Learning》，这是深度学习第一次大规模的应用于强化学习。在Atari 2600的49个游戏中的29个中的得分达到了人类的75%以上，而在其中23个游戏中的得分超过了人类选手，如下图所示。
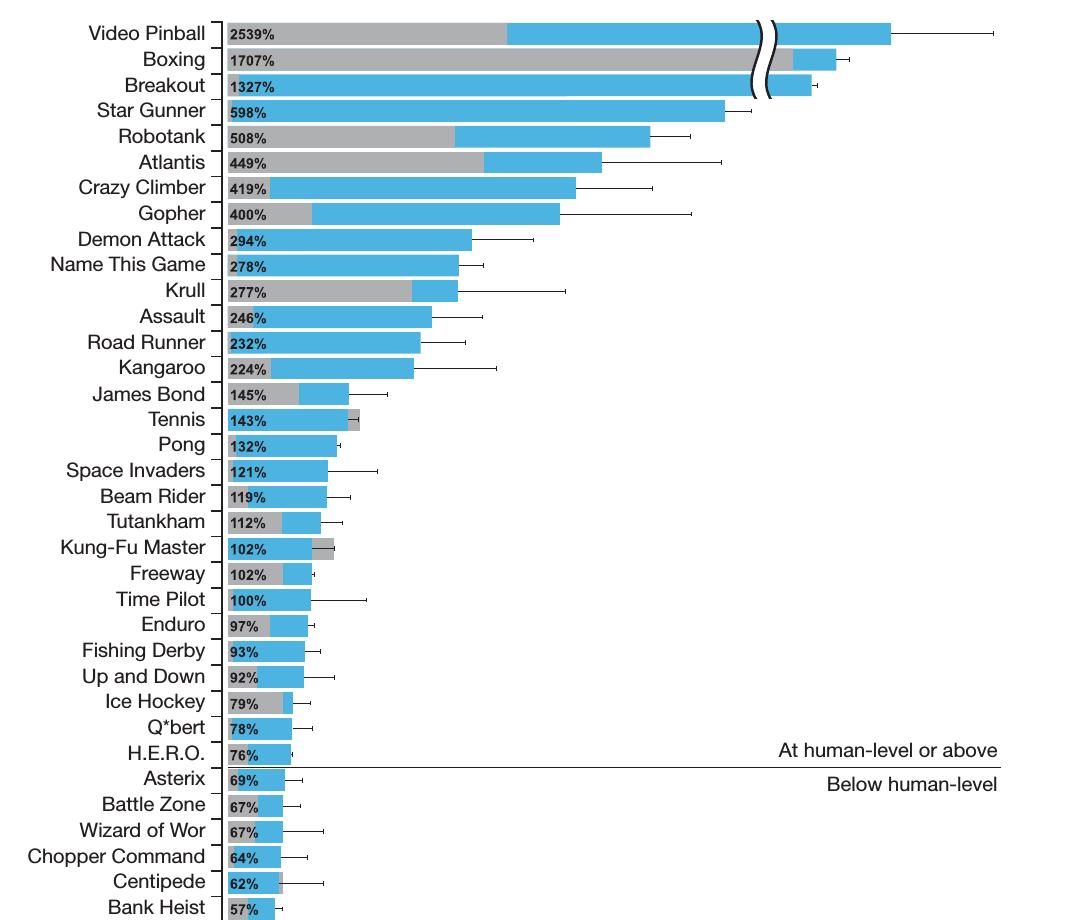图：Deep Q-Networks在Atari2600平台上的得分
在前面我们介绍过Q-Learning，它通过评估Q(s,a)和基于Q的策略提升来学习更好的策略。这是一个off-policy的算法，行为策略通常是ε-贪婪的，以便Explore，而目标策略是贪婪的。Q(s,a)的更新公式如下：
\[\begin{split} & Q(s,a) \leftarrow Q(s,a)+\alpha(R+\gamma max_{a'}Q(s',a')-Q(s,a)) \\ & = (1-\alpha)Q(s, a) + \alpha[R + \gamma max_{a'}Q(s',a')] \end{split}\]普通的函数近似存在的问题
前面介绍的是基于表格的方法，而在Deep Q-Networks里我们用一个神经网络来近似Q(s,a)，这样我们得到如下的算法：
但是上面的算法有两个问题：target不稳定和同一个trajectory的数据相关性。
回顾一下，我们的目标是为了让$Q_\theta(s,a)$拟合真实的$Q(s,a)$，但是我们并不知道真实的$Q(s,a)$，我们使用的是$target=r +\gamma max_{a’} Q_{\theta_k}(s’, a’)$，这个target又是依赖于$Q_\theta(s,a)$的。为了更好的拟合我们调整了$\theta$，但是也改变了$Q_\theta(s,a)$，从而使得target不稳定。
第二个问题就是数据相关性的问题。表格的方法在更新时只会修改某一个Q(s,a)，但是在函数近似的方法里，我们修改的是参数$\theta$，因为函数通常是连续的，所以为了调整参数使得Q(s,a)更加接近target的时候也会修改s附件的其它状态。比如我们调整参数之后Q(s,a)变大了，那么如果s’很接近s，那么Q(s’,a)也会变大。比如在Atari视频游戏中状态s可以表示为连续4帧的图像，同一个trajectory中的两个连续状态肯定很像(可能就是几个像素的区别)，而我们更新的target又依赖于$max_{a’}Q(s’,a)$，因此这会起到一种放大作用，使得这个trajectory的所有估计都偏大，这就很容易造成训练的不稳定。
而这两个问题中第二个问题更为严重，这是通过DQN的实验验证的。DQN提出了Experience replay来解决第二个问题；提出了Target Network来解决第一个问题，实验结果发现Experience replay对于性能的提高起到的作用更大。
Experience Replay
为了避免同一个trajectory数据的相关性，DQN提出了Experience Replay的方法。它会有一个replay buffer，用来存储近期的一些(s,a,r,s’)。训练的时候随机的从replay buffer里均匀的采样一个minibatch的(s,a,r,s’)来调整参数$\theta$。因为是随机挑选的，所以这些数据不太可能有前后相关性。
当然能支持Experience Replay是因为Q-Learning很好的特性——off-policy。在计算target的时候只需要(s,a,r,s’)，如果是MC方法那就不行了，因为它需要整个trajectory的数据。同样on-policy的SARSA也是不能使用Experience Replay的，因为它要求的(s,a,r,s’,a’)，而a’必须是由当前policy产生，但是replay buffer里的都是很久以前的policy产生的a’。而Q-Learning就没有这个问题，因为它只需要(s,a,r,s’)。
Target Network
为了解决target不稳定的问题，DQN引入了一个Target Network $Q_{\theta’}$，这个神经网络和之前的完全一样，只不过它的参数$\theta’$不会更新那么频繁，通常是经过一定时间才从$\theta$里复制过来一次，这样可以保证target的稳定性。
状态表示
DQN是End-to-End的方法，输入是视频游戏的画面的原始像素。而在这之前的方法都是先提取特征，然后使用强化学习来学习策略。这需要人来手工提取特征，通常特征很难表示，而且即使表示出来也很难获取标注的训练数据。
比下图的游戏，我们左右移动木板通过反弹来控制小球碰撞上面的砖块来获取更多得分。如果我们手工来提取特征，应该提取什么样的特征呢？首先我们可能要识别小球的位置、速度和加速度。识别位置需要图像识别，这并不困难，但是我们没有标注数据，当然在这个游戏中求和砖块还是比较容易区分的，因此也许我们可以用更简单的不需要大量标注的方法来识别小球的位置。根据连续几帧的图像我们就可以计算小球的速度和加速度。此外比较重要的特征还包括木板当前的位置，这也需要一个对象检测算法来定位。然后需要考虑的特征还包括当前所有砖块的情况——哪些地方有砖块，哪些没有，从而选择更好的策略(比如把某个区域打穿，然后让小球跑到上面去，参考Youtube视频)。
而使用DQN之后我们的输入就是视频(连续播放的图片)，DQN的$Q_\theta(s,a)$是一个深层神经网络，前面几层是CNN，它能够在加强化学习Reward的驱动下自动的用CNN提取需要的信息，可能它也会提取上面我们描述的各种特征(但是它的里面是个黑盒，实际是否这样还需要分析，好像没有论文分析过在深度强化学习里，CNN到底学习到了哪些特征，这其实是个有趣的方向）。
那么在DQN里我们怎么表示当前的状态呢？最简单的想法是用当前帧的图片来表示当前的状态，但是这种方法无法表示物体的运动信息。如果只有一帧图片的话，我们无法知道小球速度(包括大小和方向)和加速度，这个信息显然是非常重要的，否则我们无法预判小球下一步会移动到什么位置，也就无法把木板提前移动到合适的位置。
为了解决这个问题，DQN在表示当前状态的时候会使用最近的4帧图像作为当前的输入，连续的两帧图像就可以计算出小球运动速度的大小和方向了；而计算加速度则需要连续的三帧图像。DQN的论文对原始输入还做了一些简单预处理，最终把当前状态$s_t$变成输入$\phi(s_t)$。
图：Atari breakout游戏
DQN算法
理解了上面的内容之后，DQN的算法就很简单了。DQN算法的伪代码如下：
DQN解决Mountain Car问题
问题简介
我们首先介绍使用DQN解决Mountain Car问题，这是一个连续状态空间的问题，但是问题相比Atari的更加简单。因此我们的DQN不需要复杂的网络结构，我们通过它先来熟悉DQN的代码。
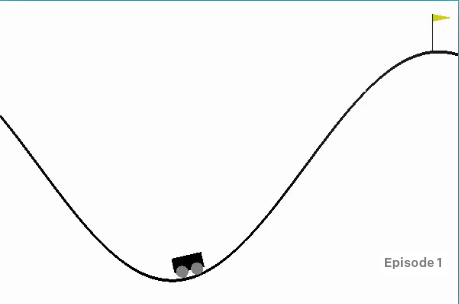
Mountain Car是OpenAI Gym里的一个问题，如下图所示。我们的目标是把小车开到红旗的地方，我们的action有3个——向左加速、向右加速和不加速。但是由于车子的动力不足，如果我们一直向右加速的话车子上到一定坡度就会掉下来。因此正确的操作是让车子先向右走到能走的最高位置，然后向左加速走到最左的位置，然后再向右加速走到最右，…，如此的震荡来积累更大的速度从而可以冲上去。
图：Mountain Car
Q-Learning算法
我们先用普通的Q-Learning来看看怎么解决连续的状态空间问题。
首先我们通过代码来更加深入的了解Mountain Car这个问题。
# 探索Mountain Car环境
env_name = 'MountainCar-v0'
env = gym.make(env_name)
# action空间是离散的空间
# 包括left,neutral,right三种action
print("Action Set size :", env.action_space)
# 状态空间是二维的连续空间
# Velocity=(-0.07,0.07)
# Position=(-1.2,0.6)
print("Observation set shape :", env.observation_space)
print("Highest state feature value :", env.observation_space.high)
print("Lowest state feature value:", env.observation_space.low)
print(env.observation_space.shape)
# 输出为：
Action Set size : Discrete(3)
Observation set shape : Box(2,)
Highest state feature value : [0.6 0.07]
Lowest state feature value: [-1.2 -0.07]
(2,)
此外初始状态position=-0.5, velocity=0，而终止状态position >=0.6。终止状态的reward是1，而其余状态是-1。接下来我们看一些Q-Learning算法的一些超参数：
n_states = 40
episodes = 10 # episode的数量
initial_lr = 1.0 # 初始Learning rate
min_lr = 0.005 # 最小的Learning rate
gamma = 0.99 # discount factor
max_steps = 300
epsilon = 0.05
我们这里使用表格的方法，但是状态空间是二维的连续空间，为了能够使用表格的方法，需要对状态空间进行离散化处理：
def discretization(env, obs):
env_low = env.observation_space.low
env_high = env.observation_space.high
env_den = (env_high - env_low) / n_states
pos_den = env_den[0]
vel_den = env_den[1]
pos_high = env_high[0]
pos_low = env_low[0]
vel_high = env_high[1]
vel_low = env_low[1]
pos_scaled = int((obs[0] - pos_low) / pos_den)
vel_scaled = int((obs[1] - vel_low) / vel_den)
return pos_scaled, vel_scaled
代码很直观，就是把速度范围(-0.07,0.07)切分为40个区间，位置范围(-1.2,0.6)也切分为40个区间，因此总的状态个数为40*40=1600。下面是Q-Learning的主要代码：
# q_table就是存储表格的数据结构
# 这里定义3d的数组，第一维表示位置，第二维表示速度，第三维表示action
q_table = np.zeros((n_states, n_states, env.action_space.n))
total_steps = 0
for episode in range(episodes):
obs = env.reset()
total_reward = 0
# 随着时间的增加逐渐减少learning rate
alpha = max(min_lr, initial_lr * (gamma ** (episode // 100)))
steps = 0
while True:
env.render()
pos, vel = discretization(env, obs)
# epsilon的概率随机探索
if np.random.uniform(low=0, high=1) < epsilon:
a = np.random.choice(env.action_space.n)
# 否则选取q值最大的action
else:
a = np.argmax(q_table[pos][vel])
# 执行a，得到reward和新的状态(观察)obs
obs, reward, terminate, _ = env.step(a)
# q-table更新
pos_, vel_ = discretization(env, obs)
q_table[pos][vel][a] = (1 - alpha) * q_table[pos][vel][a] + alpha * (
reward + gamma * np.max(q_table[pos_][vel_]))
steps += 1
if terminate:
break
print("Episode {} completed with total reward {} in {} steps"
.format(episode + 1, total_reward, steps))
while True: # to hold the render at the last step when Car passes the flag
env.render()
上面的代码非常简单，和前面的伪代码几乎一样，但是有一个细微的差别。那就是target的计算，伪代码为：
if s' 是终止状态:
target = r
s'=随机初始状态
else:
(*$target = r +\gamma max_{a'} Q(s', a')$*)
如果下一个状态是终止(terminal)状态，那么target=r；否则$target = r +\gamma max_{a’} Q(s’, a’)$。代码把$Q_{\theta_k}(terminal, a’)$初始化成了零，而且永远不会更新，因此$\gamma max_{a’} Q(terminal, a’)=0$，所以可以不区分这两种情况。完整代码在这里。运行结果为：
Episode 1 completed with total reward 0 in 25282 steps
Episode 2 completed with total reward 0 in 24729 steps
Episode 3 completed with total reward 0 in 4660 steps
Episode 4 completed with total reward 0 in 2035 steps
Episode 5 completed with total reward 0 in 1574 steps
Episode 6 completed with total reward 0 in 6564 steps
Episode 7 completed with total reward 0 in 4626 steps
Episode 8 completed with total reward 0 in 7693 steps
Episode 9 completed with total reward 0 in 1055 steps
Episode 10 completed with total reward 0 in 2014 steps
我们可以发现它最终是学习到了一定的策略，但是这个策略并不是特别好，需要花很长时间才能成功，下面我们介绍的DQN学习的策略能更快的成功。
DQN算法
接下来我们介绍怎么用DQN来解决这个问题，这有点用牛刀杀鸡的感觉，但是目的是为了通过简单的问题让读者了解DQN的代码。我们可以发现DQN不需要对状态空间进行离散化，使用起来更加简单。当然对于这个简单问题，我们的神经网络是只有一个隐层的全连接网络，最后一层的logits通过softmax输出3个action的概率。我们首先来看训练的主干代码：
if __name__ == "__main__":
env = gym.make('MountainCar-v0')
env = env.unwrapped
dqn = DQN(learning_rate=0.001, gamma=0.9, n_features=env.observation_space.shape[0],
n_actions=env.action_space.n, epsilon=0.0,
parameter_changing_pointer=500, memory_size=5000)
episodes = 10
total_steps = 0
for episode in range(episodes):
steps = 0
obs = env.reset()
episode_reward = 0
while True:
env.render()
# epsilon贪婪的行为策略
action = dqn.epsilon_greedy(obs)
obs_, reward, terminate, _ = env.step(action)
# 保存到buffer里
dqn.store_experience(obs, action, reward, obs_)
# 训练
if total_steps > 1000:
dqn.fit()
episode_reward += reward
if terminate:
break
obs = obs_
total_steps += 1
steps += 1
print("Episode {} with Reward : {} at epsilon {} in steps {}"
.format(episode + 1, episode_reward, dqn.epsilon, steps))
while True: # to hold the render at the last step when Car passes the flag
env.render()
这里先暂时把DQN类看成一个黑盒子，我们这里会发现这里的代码和前面基本相同。接下来我们来打开这个黑盒子，看看DQN的实现。首先是DQN的构造函数：
class DQN:
def __init__(self, learning_rate, gamma, n_features, n_actions, epsilon,
parameter_changing_pointer, memory_size):
self.learning_rate = learning_rate
self.gamma = gamma
self.n_features = n_features
self.n_actions = n_actions
self.epsilon = epsilon
self.batch_size = 100
self.experience_counter = 0
self.experience_limit = memory_size
self.replace_target_pointer = parameter_changing_pointer
self.learning_counter = 0
self.memory = np.zeros([self.experience_limit, self.n_features * 2 + 2])
self.build_networks()
p_params = tf.get_collection('primary_network_parameters')
t_params = tf.get_collection('target_network_parameters')
self.replacing_target_parameters = [tf.assign(t, p) for t, p in zip(t_params, p_params)]
self.sess = tf.Session()
self.sess.run(tf.global_variables_initializer())
参数parameter_changing_pointer是更新Target Network的频率，也就是每过parameter_changing_pointer此学习就把当前网络参数复制到Target Network一次。memory是replay buffer，它的大小是[self.experience_limit, self.n_features * 2 + 2]，每一行需要存储一个experience，也就是(s,s’,a,reward)，一个状态需要2个浮点数来存储，因此总共需要6个浮点数，a本来是整数，但是为了统一放到ndarray里就转换成浮点数了，用的时候需要转成整数。
memory是一个循环数组，老的数据会被新的覆盖，而experience_counter表示总计放入的数据量，可以用来计算下一个写入位置。build_networks函数会构造DQN的神经网络，下面我们会详细介绍，最后是定义一个复制操作replacing_target_parameters，把当前网络参数复制到Target Network。build_networks的代码如下：
def build_networks(self):
# primary network
hidden_units = 10
self.s = tf.placeholder(tf.float32, [None, self.n_features])
self.qtarget = tf.placeholder(tf.float32, [None, self.n_actions])
with tf.variable_scope('primary_network'):
c = ['primary_network_parameters', tf.GraphKeys.GLOBAL_VARIABLES]
# 第一层
with tf.variable_scope('layer1'):
w1 = tf.get_variable('w1', [self.n_features, hidden_units],
initializer=tf.contrib.layers.xavier_initializer(),
dtype=tf.float32, collections=c)
b1 = tf.get_variable('b1', [1, hidden_units],
initializer=tf.contrib.layers.xavier_initializer(),
dtype=tf.float32, collections=c)
l1 = tf.nn.relu(tf.matmul(self.s, w1) + b1)
# 第二层
with tf.variable_scope('layer2'):
w2 = tf.get_variable('w2', [hidden_units, self.n_actions],
initializer=tf.contrib.layers.xavier_initializer(),
dtype=tf.float32, collections=c)
b2 = tf.get_variable('b2', [1, self.n_actions],
initializer=tf.contrib.layers.xavier_initializer(),
dtype=tf.float32, collections=c)
self.qeval = tf.matmul(l1, w2) + b2
with tf.variable_scope('loss'):
self.loss = tf.reduce_mean(tf.squared_difference(self.qtarget, self.qeval))
with tf.variable_scope('optimiser'):
self.train = tf.train.AdamOptimizer(self.learning_rate).minimize(self.loss)
# target network
self.st = tf.placeholder(tf.float32, [None, self.n_features])
with tf.variable_scope('target_network'):
c = ['target_network_parameters', tf.GraphKeys.GLOBAL_VARIABLES]
# 第一层
with tf.variable_scope('layer1'):
w1 = tf.get_variable('w1', [self.n_features, hidden_units],
initializer=tf.contrib.layers.xavier_initializer(),
dtype=tf.float32, collections=c)
b1 = tf.get_variable('b1', [1, hidden_units],
initializer=tf.contrib.layers.xavier_initializer(),
dtype=tf.float32, collections=c)
l1 = tf.nn.relu(tf.matmul(self.st, w1) + b1)
# 第二层
with tf.variable_scope('layer2'):
w2 = tf.get_variable('w2', [hidden_units, self.n_actions],
initializer=tf.contrib.layers.xavier_initializer(),
dtype=tf.float32, collections=c)
b2 = tf.get_variable('b2', [1, self.n_actions],
initializer=tf.contrib.layers.xavier_initializer(),
dtype=tf.float32, collections=c)
self.qt = tf.matmul(l1, w2) + b2
代码会构造两个结构完全一样的神经网络，primary网络会定义loss，而target网络的作用是在就是target的时候用它来计算Q(s,a)的值，因此它的参数不会在训练中更改，只是定期同步primary的参数(使用前面的replacing_target_parameters)。loss的定义如下：
with tf.variable_scope('loss'):
self.loss = tf.reduce_mean(tf.squared_difference(self.qtarget, self.qeval))
这里qtarget是placeholder，训练的时候传入，而qeval就是primary网络的输出(3个值，分别表示Q(s,a1),Q(s,a2),Q(s,a3))。注意：通常对于一个状态s，我们只会更新某一个action a的Q(s,a)，另外两个是不变的，所以placehodler传入的3个值中有一个是修改过的，而另外两个的值就是primary网络(而不是target网络的，因为target网络会滞后)预测的结果，因此是不变的。函数target_params_replaced运行replacing_target_parameters操作来实现target网络的参数更新。
def target_params_replaced(self):
self.sess.run(self.replacing_target_parameters)
函数store_experience用来把新的experience放到replay buffer里。
def store_experience(self, obs, a, r, obs_):
index = self.experience_counter % self.experience_limit
self.memory[index, :] = np.hstack((obs, [a, r], obs_))
self.experience_counter += 1
它首先通过self.experience_counter \% self.experience_limit计算下一个写入位置。然后存入(obs, [a, r], obs_)，表示当前状态，action a，reward r和下一个状态。函数epsilon_greedy用来$\epsilon$-贪婪的行为策略：
def epsilon_greedy(self, obs):
# epsilon贪婪的选择action
if np.random.uniform(low=0, high=1) < self.epsilon:
return np.argmax(self.sess.run(self.qeval, feed_dict={self.s: obs[np.newaxis, :]}))
else:
return np.random.choice(self.n_actions)
注意epsilon以开始是0，也就是完全随机选择action，然后会慢慢的变大(参考fit代码)直到0.9。下面是fit的代码，请仔细阅读代码和注释：
def fit(self):
# 从memory里采样
# 如果buffer没有满
if self.experience_counter < self.experience_limit:
indices = np.random.choice(self.experience_counter, size=self.batch_size)
# buffer已满
else:
indices = np.random.choice(self.experience_limit, size=self.batch_size)
# 一个batch的数据
batch = self.memory[indices, :]
# 使用primary计算Q(s, a)，使用target网络计算Q(s',a)
qt, qeval = self.sess.run([self.qt, self.qeval],
feed_dict={self.st: batch[:, -self.n_features:],
self.s: batch[:, :self.n_features]})
# qtarget是需要更新的Q(s,a1),Q(s,a2),Q(s,a3)
# 我们先复制qeval的值，假设实际的action是a1，那么根据r+gamma max_a' Q(s,a')更新Q(s,a1)
# Q(s,a1) primary预测的值和期望的值有差距(loss)，需要调整参数。
# 而Q(s,a2),Q(s,a3)仍然是primary网络预测的结果，这样它们的损失就是零。
# 因此不需要为了他们调整参数
qtarget = qeval.copy()
batch_indices = np.arange(self.batch_size, dtype=np.int32)
# actions是这batch个数据选择的action
actions = self.memory[indices, self.n_features].astype(int)
# 这batch个数据的reward
rewards = self.memory[indices, self.n_features + 1]
# Q(s, a1)对应的target需要更新
qtarget[batch_indices, actions] = rewards + self.gamma * np.max(qt, axis=1)
# 进行训练，传入当前状态s和target
_ = self.sess.run(self.train, feed_dict={self.s: batch[:, :self.n_features],
self.qtarget: qtarget})
# 逐渐增加epsilon
if self.epsilon < 0.9:
self.epsilon += 0.0002
# 定期更新target网络的参数
if self.learning_counter % self.replace_target_pointer == 0:
self.target_params_replaced()
print("target parameters changed")
self.learning_counter += 1
Episode 1 with Reward : -2860.0 at epsilon 0.3717999999999917 in steps 2859
Episode 2 with Reward : -516.0 at epsilon 0.4749999999999803 in steps 515
Episode 3 with Reward : -539.0 at epsilon 0.5827999999999685 in steps 538
Episode 4 with Reward : -344.0 at epsilon 0.6515999999999609 in steps 343
Episode 5 with Reward : -408.0 at epsilon 0.7331999999999519 in steps 407
Episode 6 with Reward : -519.0 at epsilon 0.8369999999999405 in steps 518
Episode 7 with Reward : -1098.0 at epsilon 0.9001999999999335 in steps 1097
Episode 8 with Reward : -667.0 at epsilon 0.9001999999999335 in steps 666
Episode 9 with Reward : -300.0 at epsilon 0.9001999999999335 in steps 299
Episode 10 with Reward : -500.0 at epsilon 0.9001999999999335 in steps 499
我们可以看到使用DQN学到的策略更优一些。
用DQN来玩Atari Breakout
接下来我们用DQN来解决一个复杂一点的问题——Atari Breakout。这个游戏前面我们也介绍过了，它的输入是视频，我们会提取最近4帧的作为当前的状态，一帧的图片是(210, 160, 3)的，因此是个非常高维的连续问题。
我们这里DQN和之前的基本结构是类似的，只不过把一个隐层的DNN变成了更多层的CNN网络，因为对于图像来说，CNN更加适合。完整代码在这里，代码和前的DQN类似，我们这里只介绍和上面不同的代码。最大的差异就是网络的结构，这主要在函数build_networks里：
def build_networks(self):
# primary network
shape = [None] + self.n_features
self.s = tf.placeholder(tf.float32, shape)
self.qtarget = tf.placeholder(tf.float32, [None, self.n_actions])
with tf.variable_scope('primary_network'):
c = ['primary_network_parameters', tf.GraphKeys.GLOBAL_VARIABLES]
# 第一个卷积层
with tf.variable_scope('convlayer1'):
l1 = self.add_layer(self.s, w_shape=[5, 5, 4, 32], b_shape=[32], layer='convL1',
activation_fn=tf.nn.relu, c=c, isconv=True)
# 第二个卷积层
with tf.variable_scope('convlayer2'):
l2 = self.add_layer(l1, w_shape=[5, 5, 32, 64], b_shape=[64], layer='convL2',
activation_fn=tf.nn.relu, c=c, isconv=True)
# 第一个全连接层
l2 = tf.reshape(l2, [-1, 80 * 80 * 64])
with tf.variable_scope('FClayer1'):
l3 = self.add_layer(l2, w_shape=[80 * 80 * 64, 128], b_shape=[128],
layer='fclayer1', activation_fn=tf.nn.relu, c=c)
# 第二个全连接层
with tf.variable_scope('FClayer2'):
self.qeval = self.add_layer(l3, w_shape=[128, self.n_actions],
b_shape=[self.n_actions], layer='fclayer2', c=c)
with tf.variable_scope('loss'):
self.loss = tf.reduce_mean(tf.squared_difference(self.qtarget, self.qeval))
with tf.variable_scope('optimiser'):
self.train = tf.train.AdamOptimizer(self.learning_rate).minimize(self.loss)
# target network
self.st = tf.placeholder(tf.float32, shape)
with tf.variable_scope('target_network'):
c = ['target_network_parameters', tf.GraphKeys.GLOBAL_VARIABLES]
# 第一个卷积层
with tf.variable_scope('convlayer1'):
l1 = self.add_layer(self.st, w_shape=[5, 5, 4, 32], b_shape=[32],
layer='convL1', activation_fn=tf.nn.relu, c=c, isconv=True)
# 第二个卷积层
with tf.variable_scope('convlayer2'):
l2 = self.add_layer(l1, w_shape=[5, 5, 32, 64], b_shape=[64], layer='convL2',
activation_fn=tf.nn.relu, c=c, isconv=True)
# 第一个全连接层
l2 = tf.reshape(l2, [-1, 80 * 80 * 64])
with tf.variable_scope('FClayer1'):
l3 = self.add_layer(l2, w_shape=[80 * 80 * 64, 128], b_shape=[128],
layer='fclayer1', activation_fn=tf.nn.relu, c=c)
# 第二个全连接层
with tf.variable_scope('FClayer2'):
self.qt = self.add_layer(l3, w_shape=[128, self.n_actions],
b_shape=[self.n_actions], layer='fclayer2', c=c)
这里的网络结构是两个卷积层在加上两个全连接层，第二个全连接层没有激活，只计算logits。构造卷积层和全连接层的代码封装为函数add_layer：
def add_layer(self, inputs, w_shape=None, b_shape=None, layer=None,
activation_fn=None, c=None, isconv=False):
w = self.weight_variable(w_shape, layer, c)
b = self.bias_variable(b_shape, layer, c)
eps = tf.constant(value=0.000001, shape=b.shape)
if isconv:
if activation_fn is None:
return self.conv(inputs, w) + b + eps
else:
h_conv = activation_fn(self.conv(inputs, w) + b + eps)
return h_conv
if activation_fn is None:
return tf.matmul(inputs, w) + b + eps
outputs = activation_fn(tf.matmul(inputs, w) + b + eps)
return outputs
前面的Mountain Car输入是两个连续的值，不需要做什么特殊处理，而Breakout的输入图像需要做如下处理：
def preprocessing_image(s):
s = s[31:195]
s = s.mean(axis=2)
s = imresize(s, size=(80, 80), interp='nearest')
s = s / 255.0
return s
这里首先只保留图像的31-195行，因为之外的那些像素都是背景，球不可能去的位置，而且也没有砖块。接着用s.mean求RGB3个通道的平均值，然后resize成(80,80)，最后把取值范围从0-255变成(0, 1)。最后我们看一下main函数，看怎么把连续4帧的图片变成输入特征：
if __name__ == "__main__":
env = gym.make('Breakout-v0')
env = env.unwrapped
epsilon_rate_change = 0.9 / 500000.0
dqn = DQN(learning_rate=0.0001,
gamma=0.9,
n_features=[80, 80, 4],
n_actions=env.action_space.n,
epsilon=0.0,
parameter_changing_pointer=100,
memory_size=50000,
epsilon_incrementer=epsilon_rate_change)
episodes = 100000
total_steps = 0
for episode in range(episodes):
steps = 0
obs = preprocessing_image(env.reset())
s_rec = np.stack([obs] * 4, axis=0)
s = np.stack([obs] * 4, axis=0)
s = s.transpose([1, 2, 0])
episode_reward = 0
while True:
env.render()
action = dqn.epsilon_greedy(s)
obs_, reward, terminate, _ = env.step(action)
obs_ = preprocessing_image(obs_)
a = s_rec[1:]
a = a.tolist()
a.append(obs_)
s_rec = np.array(a)
s_ = s_rec.transpose([1, 2, 0])
dqn.store_experience(s, action, reward, s_)
if total_steps > 1999 and total_steps % 500 == 0:
dqn.fit()
episode_reward += reward
if terminate:
break
s = s_
total_steps += 1
steps += 1
print("Episode {} with Reward : {} at epsilon {} in steps {}"
.format(episode + 1, episode_reward, dqn.epsilon, steps))
while True:
env.render()
首先我们把初始第一帧图片复制4份得到第一个状态s：
obs = preprocessing_image(env.reset())
s_rec = np.stack([obs] * 4, axis=0)
s = np.stack([obs] * 4, axis=0)
s = s.transpose([1, 2, 0])
obs经过preprocessing_image输出的大小是(80,80)，接着把它复制4次然后stack起来得到(4,80,80)的s_rec，同时复制得到s，然后把s transponse成(80, 80, 4)。因为卷积网络需要的输入是(width, height, channel)，所有要变成(80, 80, 4)，而replay buffer要求的却是(4, 80, 80)，这样便于在新的一帧加入的时候弹出老的一帧构造新的输入。
接着在episode的for循环里：
obs_ = preprocessing_image(obs_)
a = s_rec[1:]
a = a.tolist()
a.append(obs_)
s_rec = np.array(a)
s_ = s_rec.transpose([1, 2, 0])
首先是把当前的新一帧的图片obs_变成(80,80)，然后从s_rec里得到2-4帧，把obs加到最后得到新的s_rec(4, 80, 80)，最后把它transpose成(80, 80, 4)输入到神经网络里。其余的代码基本和原来一样，这里就不介绍了。
- 显示Disqus评论(需要科学上网)