人脸识别简介

本文介绍人脸识别的基本概念和FaceNet算法及其代码。更多文章请点击深度学习理论与实战：提高篇。

转载请联系作者(fancyerii at gmail dot com)！

简介
FaceNet
FaceNet代码

简介

人脸识别是计算机视觉最重要的应用之一，它是基于人的脸部特征信息进行身份识别的一种生物识别技术。广泛用于政府、军队、银行、、电子商务、安防等领域。比如我们上班的门禁系统，就是人脸识别的典型应用场景之一。

在介绍人脸识别算法之前，我们首先澄清几个容易混淆概念。

人脸检测(Face Detection)
人脸验证(Face Verification)
人脸鉴别(Face Identification)
人脸识别(Face Recognition)

人脸检测是一种特殊的目标检测，它只检测人脸。它的任务是从一张图片中找到人脸的Bounding Box。人脸验证的任务是判断两张人脸图片是否是同一个人，这是一个两分类问题，通常用于基于人脸的登录控制、访问控制、身份确认等方面，比如基于人脸的手机解锁，操作系统登录。而人脸鉴别任务是判断一个人脸是属于哪一个人，确定其身份，属于多分类问题。人脸鉴别又分为开放的(open)和封闭的(closed)两种，后者假设输入的人脸照片一定属于预先定义的人群中的一个；而前者有可能输入的是任何人的照片。封闭的人脸鉴别通常用于人脸搜索，比如警察用照片搜索犯罪嫌疑人。它不要求搜索出来的一定就是正确的，因为后面还会有人来确认，算法只是进行初筛，提供可能的候选。而后者除了要找到最相似的候选人之外还需要确认这两个人是同一个人(也就是人脸验证)，比如前面介绍的门禁系统，我们肯定不能假设输入就一定是公司的某一个员工的照片。人脸识别是人脸验证和人脸鉴别的合称，有的时候人脸鉴别也被称为人脸识别。人脸识别是计算机视觉的一个经典任务，有很多的算法，我们这里只介绍基于深度学习的FaceNet。

FaceNet

基本原理

人脸识别虽然看起来是一个分类任务，但是在很多实际应用中很难用普通的分类器来处理，原因之一是每个类(人)的训练样本很少。比如我们做一个门禁系统，每个员工可能只能提供几张照片，不可能让每个人提供几百几千张照片，而且员工总数可能也很少，小型企业一般只有几十或者几百人。当然我们可以把非公司的其他人的照片也拿过来作为训练数据和分类，如果分类为其他人，那么就不能通过门禁。

这样似乎可以解决数据不够的问题，但是还有一个更难处理的问题——重新训练。通常公司的人员是经常变动的，每次人员变动都要重新训练模型，这样的门禁系统估计没人会买。

那怎么办呢？有没有不需要训练的分类器？KNN这是排上用场了。KNN是不需要训练的分类器，或者说训练的过程这是把训练数据存储下来，这显然很适合人脸识别的这类应用。之前KNN被诟病的一个问题就是需要存储所有的训练数据，因此速度很慢而且需要大量空间。而在这个场景下都不是问题，门禁系统的训练数据是非常少的，因此两两计算距离(相似度)不是问题。

比如1-NN算法：来了一个人的照片，我们计算这张照片和库里的所有照片一一计算距离，选择最相似的照片作为它的分类。但是我们还要寻找一个距离阈值，如果小于这个阈值，我们就判断它们是同一个人，否则就认为是其他人。

因此问题的关键是计算两张人脸照片的距离(相似度)。一种方法是学习一个神经网络，输入是两张照片，输出是它们的距离或者相似度。这就是所谓Siamese Network——它的输入是两个物体，而不是分类器的一个物体；输出是它们的距离(区别)，而不是分类概率。

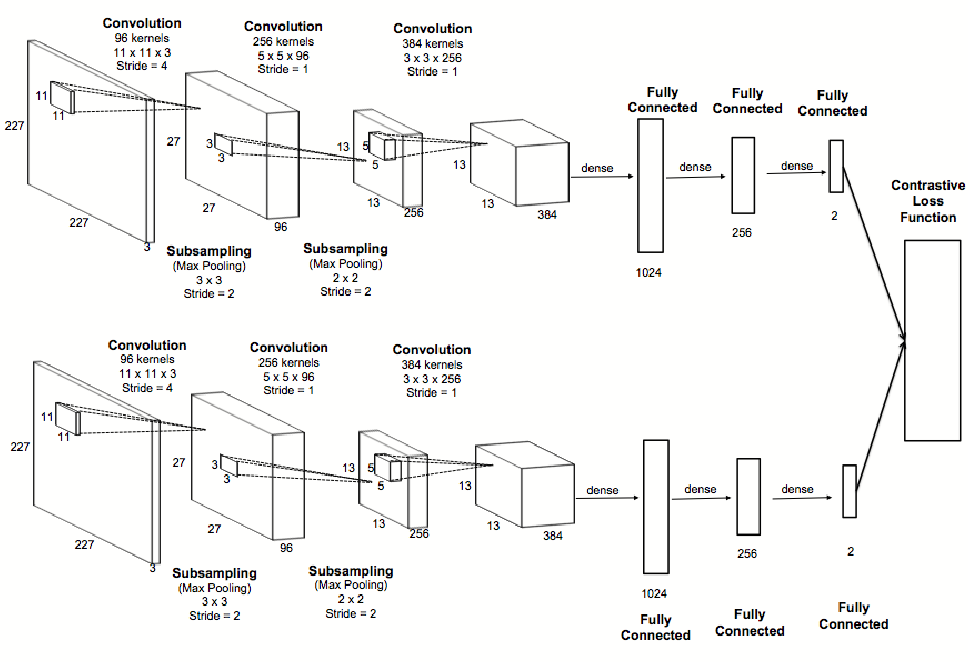
Siamese是连体人的意思，那为什么叫Siamese网络呢？比如下图是一种Siamese网络。第一张图片经过一个深度神经网络最后变成一个特征向量，而第二张照片也经过一个完全一样的网络变成另外一个特征向量，最后把它们组合起来用另外一些网络层来判断它们是否同一个物体。因为问题的对称性，dist(x, y)==dist(y, x)，所以我们通常要求这两个提取特征的网络是完全一样的，包括参数。因此这种网络结构是对称的，很像一个连体人(Siamese)，故名为Siamese网络。

图：Siamese Network示例

使用Siamese实现的学习算法是一种One-Shot Learning(当然还有其它的One-Shot Learning算法)。增加一个新的类别只需要提供一个训练数据就行了（当然多几个没有坏处，不过要改个名字叫Few-Shot Learning，当然不能太多，否则就是普通的Learning了）。一个训练样本，似乎不能再少了，但是还有Zero-Shot Learning。这似乎有点不可能，我没见过一个物体，怎么能认识它呢？

不见过不代表不认识，比如下图中的动物，大家都没有见过。但是我们是“认识”的，我们知道它不是马，也不是犀牛，这是一个新的我们每见过的动物。也许有人会反驳，我都不知道它的名字，怎么算”认识“它了？其实认识不认识和知不知道它的名字是两回事，名字只是一个符号而已，中国人叫它”独角兽”，美国人叫它”Unicorn”，泰国人叫它”ตัวยูนิคอน”。符号本身没有什么意义，只是作为语言用于交流才有意义。猴子不能用语言给物体起名字，不代表它们不能识别物体。

图：不存在的动物

我们还是回到人脸识别的问题上来。前面介绍的Siamese网络是一种解决增加新类的方法。但是它有一个缺点——不能提前计算(或者说索引)。对于门禁系统，上面的方法问题不大。但是比如我们的摄像头拍摄到了小偷的人脸照片，我们需要从几百万甚至几千万张照片中搜索可能的嫌疑人，用神经网络两两计算是不可能的。如果有十张小偷的照片，我们的计算就需要十倍的时间。

另外一种我们即将介绍的方法——Face Embedding就能解决这个问题。Face Embedding指的是输入一张人脸照片，我们用一个深度神经网络提取特征，把它表示成一个d维空间的向量。而计算两张照片的距离就变成这两个向量的运算，比如最简单的计算欧式距离。

对于前面的嫌疑人搜索，我们利用提前把人类库中的所有照片都变成一个d维向量，然后搜索的时候就只需要计算欧式距离就行了，这样会快得多。而且欧式空间的点我们可以通过一些空间索引或者近似索引的方法来找近似的(approximate)近邻，从而实现Approximate KNN算法。

那怎么把一张人脸照片表示成一个向量呢？最常见的做法是用大量的人脸数据库(不只是你们公司员工的那一点点照片)训练一个人脸分类器，这通常是一个深度的神经网络。然后我们把softmax之前的某一个全连接隐层作为人脸的特征向量。这个向量可以认为是这张人脸照片最本质的特征。给定两张照片，我们可以分别计算它们的特征向量，然后简单的计算欧式距离(或者训练一个相似度模型，当然不能太复杂)。这里其实也是一种Transfer Learning，我们用其它人脸的数据学到了区分人脸的有效特征，然后把它用于区分公司员工的人脸。当然Transfer Learning要求两个数据集的Domain是匹配的，用欧洲的人脸数据库来Transfer到亚洲可能并不好用。

但是前面提到的方法有一个问题——全连接层的隐单元通常比较多(通常上千，太少了效果不好)。因此这个特征向量的维度太大，后续的计算很慢（当然和Siamese比是快的)。本文使用了Triple-based损失函数直接学习出一个128维向量，这里的神经网络的输出就是这个128维向量。和前面的方法不同，前面的方法的神经网络的输出是一个分类概率，表示这张照片属于某个人的可能性。而本文的输出就是一个128维的向量，并且这个向量使得同一个人的两张照片得到的向量的欧式距离很近；而不同人的两种照片的欧式距离很远。

模型结构

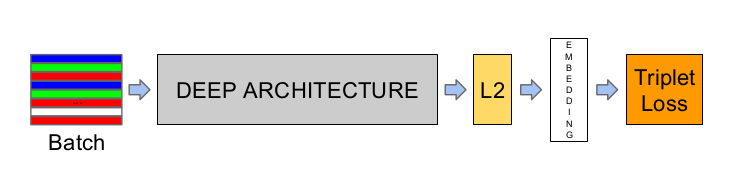
FaceNet模型结构如下图所示。输入是一个Batch的数据(Batch的寻找后面会讲到)，然后经过一个深度的卷积网络后变成一个向量(face embedding)，最后使用Triple Loss进行训练，调整参数。

图：FaceNet模型结构

前面的方法是通过一个人脸分类的任务，然后“间接”的学习到一个人脸向量(face Embedding)，这个向量可能适用于分类，但是不见得适用于距离计算。而FaceNet是直接通过Triple Loss“直接”学习用于距离计算的人脸向量。更具体一点，我们期望学习到一个人脸向量映射函数f(x)，它的输入是人脸照片，输出是$f(x)=R^d$空间里的向量。它有如下的性质：同一个人的人脸照片的欧式距离比较近，而不同人的照片距离比较远。

Triplet Loss

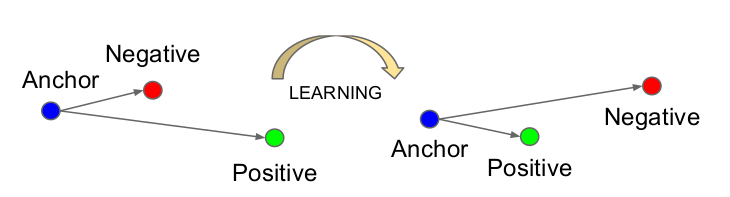
Face　Embedding可以表示为$f(x) \in R^d$，它把输入图像x映射为d维欧式空间里的一个点。此外，我们增加一个约束，要求$\left \lVert f(x) \right \lVert _2=1$，也就是要求所有的点都在半径为1的超球面上。Triplet Loss如下图所示，它的目标是使得同一个人的照片距离近，而不同的人的照片距离远。

图：Triplet Loss

第i个Triplet里有3个图片：$x_i^a, x_i^p, x_i^n$，其中$x_i^a$表示anchor，$x_i^p$是和anchor同一个人的另一张图片，而$x_i^n$是其他人的图片。我们期望它满足如下条件：

\[\left \lVert f(x_i^a) - f(x_i^p) \right \lvert_2^2 + \alpha < \left \lVert f(x_i^a) - f(x_i^n) \right \lvert_2^2\]

用自然语言来描述就是：同一个人的图片的距离加上一个margin($\alpha$)仍然要小于不同人图片的距离。当然上面只是我们的“期望”，模型能不能做到是不知道的。但是我们可以通过Loss函数告诉模型我们的期望：

\[L= \sum_i [ \left \lVert f(x_i^a) - f(x_i^p) \right \lvert_2^2 + \alpha - \left \lVert f(x_i^a) - f(x_i^n) \right \lvert_2^2 ]_+\]

函数$[x]_+=max(0, x)$其实就是ReLU函数，它的意思是如果x大于零，函数值就是x，否则就是零。因此这个Loss函数的意思是：如果相同人的图片的Embedding的距离加上$\alpha$小于不同人，那么就没有loss(零)，否则loss就是它们的差值，并且差值越大损失也越大。因此这样的损失函数迫使模型让相同人的照片尽量聚集在一起，而不同人的照片尽量远离彼此。

Triplet选择

因为Triplet只要求有两个图片是同一个人的，而另外一种照片是另外一个人的，因此这样的组合是非常多的，比如假设有10000个人，每个人10张照片，那么根据排列组合，我们知道总共有$C_{10000}^1 C_{10}^2 C_{9999}^1 C_{10}^1$，大约450亿。要遍历所有的组合是不可能的，因此我们只能挑选其中的一部分Triplet来训练。那怎么挑选呢？这就是本节的主题。

最简单的是随机挑选，但这并不好，更好的办法是挑选”难”的问题。给定$x_i^a$，最难的正(positive)样本是$argmax_{x_p} \left \lVert f(x_i^a) - f(x_i^p) \right \lVert_2^2 $，也就是和anchor距离最远的正样本，它很容易被误判为其他人；类似的最难的负(negative)样本是$argmin_{x_n}\left \lVert f(x_i^a) - f(x_i^n) \right \lVert_2^2 $，也就是距离anchor最近的其他人的照片，它很容易被判断为和anchor同一个人。

但是上面的argmax和argmin要遍历所有的图片，这在计算上是不可行的。而且即使我们找到了它，每次用最难的样本来训练也是会有问题的。这些难的样本很可能根本无法分对，因此即使一个较好的函数也无法把它映射到$R^d$中的一个合适位置。所以都用难的问题来训练，很快你导致分类器学习不到合理的参数——怎么调整loss都很大，那么它就可能不知道怎么做。这和人类学习有类似的地方，如果一上来就是特别困难的问题，那么人类大脑困难也无法训练，只能让人放弃。我们必须从易到难，先用一些容易的问题引导参数向大致正确的方向发展，把容易的问题先解决，之后再用困难的问题让人学习到细微和tricky的细节。这就是所谓的curriculum Learning。

通常我们有两种办法来解决上面的两个问题——计算可行性和从易到难样本：

离线的在某个子集(subset)上使用最新保持的模型选择argmin和argmax
在线的在一个大的mini-batch里使用当前最新的模型寻找argmin和argmax

第一种方法是把argmin和argmax局限与一个子集(这个子集是可以动态采样的)，这样可以避免计算不可行的问题，同时随着模型越来越准确，它挑选的问题也越来越难（刚开始的模型很不准，因此即使它认为难的问题也可能是容易的问题）。

本论文使用第二种方法，它的实现更简单一点。但是它要求mini-batch比较大，否则如果里面都是容易的问题或者都是太难的问题就不好了。

为了保证正样本的数量(负样本很容易活动)，我们要求每个mini-batch里至少有40张照片是同一个人的，剩下的随机选择就行了。对于一个给定的anchor，我们会使用所有的正样本(而不是最难的正样本)，但是负样本我们是选择整个minibatch里最困难的那一个，这样来得到一个Triplet。具体的步骤为：

随机的选择40张的一张作为anchor
随机选择40张的另外一张作为正样本
使用当前的模型参数，在所有(mini-batch)负样本中选择距离anchor最近的作为负样本

前面说了，如果一上来就选择最难的问题，模型也可能无法学习，因此我们除了选择最难的负样本，也会寻找一些semi-hard的负样本。所谓的semi-hard负样本是指有loss的负样本。

举例来说，比如有一个$x_i^a$和一个$x_i^p$，假设它们的距离是$\left \lVert f(x_i^a) - f(x_i^p) \right \lVert_2^2=0.4$，假设margin $\alpha=0.2$，最难的负样本可能是$\left \lVert f(x_i^a) - f(x_i^n) \right \lVert_2^2=0.3$，即使不加$\alpha$，$\left \lVert f(x_i^a) - f(x_i^p) \right \lVert_2^2$也大于0.3了。而semi-hard的负样本的距离可能是0.5，它比正样本要远，但是它和正样本的差距是小于margin的，因此还是属于有一定难度的问题。

神经网络结构

因为这篇论文发表与2015年，因此使用了当时最主流的类似VGG的网络结构和GoogLeNet(Inception)。这里就不详细介绍网络结构了，有兴趣的读者可以参考原论文，也可以尝试用最新的网络结构替代它们。

FaceNet代码

FaceNet有很多开源实现，包括OpenFace，它基于基于Torch。另外也有Tensorflow版本的实现。

这里介绍这篇博客的代码，完整代码在这里。它是基于Keras的实现FaceNet，使用了Dlib实现人脸检测和人脸对齐(或者说Landmarks Dectection)。

简介

人脸识别从图片或者视频里确认人的身份。简单来说，一个人脸识别系统从输入人脸图片中提取特征然后和人脸库中的图片进行比较。如果它和库里最接近照片的相似度大于一定阈值，我们就判断这张照片是人脸库里此人的照片，否则就认为这是一个”未知”的人脸。比较两个人脸照片并且判断它们是否属于同一个人，这就是人脸验证(Face Verification)。

这里的代码会使用Keras来实现CNN提取特征，使用Dlib来对齐人脸。为了演示方便，这里会使用LFW数据集的一部分来训练模型，读者也可以使用自己的数据集来训练。在经过基本的流程之后，本代码会介绍：

在图片中检测人脸，对人脸进行变换(transform)和裁剪(crop)，在输入CNN之前会对人脸进行对齐。这些预处理步骤非常重要，它会影响整体的准确率
使用CNN提取128维的特征表示，或者说Emebedding。
把Embedding和人脸库的照片(的Embedding)进行比较。这里会训练KNN和SVM分类器。

准备工作

为了运行本notebook，需要Python3，然后还需要用pip安装requirments.txt里的依赖，建议读者使用virtualenv。为了使用Dlib库的人脸对齐算法，我们还需要下载Dlib的人脸landmark库文件(后面会简单介绍Face Landmark Detection)。我们可以使用如下的代码下载：

import bz2
import os

from urllib.request import urlopen

def download_landmarks(dst_file):
	url = 'http://dlib.net/files/shape_predictor_68_face_landmarks.dat.bz2'
	decompressor = bz2.BZ2Decompressor()
	
	with urlopen(url) as src, open(dst_file, 'wb') as dst:
		data = src.read(1024)
		while len(data) > 0:
			dst.write(decompressor.decompress(data))
			data = src.read(1024)

dst_dir = 'models'
dst_file = os.path.join(dst_dir, 'landmarks.dat')

if not os.path.exists(dst_file):
	os.makedirs(dst_dir)
	download_landmarks(dst_file)

上面的代码很简单如果landmarks.dat不存在，就从这里下载并且解压得到landmarks.dat，这个文件大概96MB，因此第一次运行时需要一定的下载时间。

CNN结构和训练

这里使用的CNN是Inception结构的变种，在FaceNet的论文里被叫做NN4，在OpenFace项目里被叫做nn4.small2。本notebook使用的是Keras-OpenFace(复制过来进行简单修改)。我们并不关心网络结构的细节，我们只需要知道输入是一张人脸图片，输出是一个128维的向量。完整的代码在model.py文件里，这里只列举部分代码：

def create_model():
	myInput = Input(shape=(96, 96, 3))
	
	x = ZeroPadding2D(padding=(3, 3), input_shape=(96, 96, 3))(myInput)
	x = Conv2D(64, (7, 7), strides=(2, 2), name='conv1')(x)
	x = BatchNormalization(axis=3, epsilon=0.00001, name='bn1')(x)
	x = Activation('relu')(x)
	x = ZeroPadding2D(padding=(1, 1))(x)
	...
	av_pool = AveragePooling2D(pool_size=(3, 3), strides=(1, 1))(inception_5b)
	reshape_layer = Flatten()(av_pool)
	dense_layer = Dense(128, name='dense_layer')(reshape_layer)
	norm_layer = Lambda(lambda  x: K.l2_normalize(x, axis=1), name='norm_layer')(dense_layer)
	 
	return Model(inputs=[myInput], outputs=norm_layer)

create_model()会返回一个Keras的Model，它的输入是(96,96,3)的人脸图片，输出是128维的向量(并且经过l2_normalize使得它的模是1)。使用它的代码为：

from model import create_model
nn4_small2 = create_model()

模型训练的目的是学习出函数f(x)，使得同一个人的照片的L2距离尽量近，而不同人的尽量远。我们可以训练输入下的Triple Loss：

\[L = \sum^{m}_{i=1} \large[ \small {\mid \mid f(x_{i}^{a}) - f(x_{i}^{p})) \mid \mid_2^2} - {\mid \mid f(x_{i}^{a}) - f(x_{i}^{n})) \mid \mid_2^2} + \alpha \large ] \small_+\]

Keras没有提供这个损失函数，我们可以通过一个自定义的Layer来实现Triple Loss。代码如下：

from keras import backend as K
from keras.models import Model
from keras.layers import Input, Layer

# 输入的anchor, positive和negative图片
in_a = Input(shape=(96, 96, 3))
in_p = Input(shape=(96, 96, 3))
in_n = Input(shape=(96, 96, 3))

# 输出 
emb_a = nn4_small2(in_a)
emb_p = nn4_small2(in_p)
emb_n = nn4_small2(in_n)

class TripletLossLayer(Layer):
	def __init__(self, alpha, **kwargs):
		self.alpha = alpha
		super(TripletLossLayer, self).__init__(**kwargs)
	
	def triplet_loss(self, inputs):
		a, p, n = inputs
		p_dist = K.sum(K.square(a-p), axis=-1)
		n_dist = K.sum(K.square(a-n), axis=-1)
		return K.sum(K.maximum(p_dist - n_dist + self.alpha, 0), axis=0)
	
	def call(self, inputs):
		loss = self.triplet_loss(inputs)
		self.add_loss(loss)
		return loss

# 使用之前定义的TripletLossLayer
triplet_loss_layer = TripletLossLayer(alpha=0.2, name='triplet_loss_layer')
				([emb_a, emb_p, emb_n])

# Model定义
nn4_small2_train = Model([in_a, in_p, in_n], triplet_loss_layer)

上面的代码定义了TripletLossLayer，它继承了Layer类来实现Keras的自定义Layer。最重要的是实现call方法，它调用triplet_loss来计算loss，然后调用self.add_loss把loss加入进去，这样Keras知道这一层会产生Loss，从而可以在梯度下降时用到。另外TripletLossLayer有一个参数alpha，这是用于计算loss的margin。

为了训练模型，我们需要选择Triplet，使得正样本$(x^a_i, x^p_i)$和负样本$(x^a_i, x^p_n)$比较难分。我们假设函数triplet_generator()它能生成Triplet，那么训练的代码为：

from data import triplet_generator

generator = triplet_generator() 

nn4_small2_train.compile(loss=None, optimizer='adam')
nn4_small2_train.fit_generator(generator, epochs=10, steps_per_epoch=100)

我们这里使用的triplet_generator是fake的假数据，只是为了演示训练的过程，后面会介绍使用LFW的少量数据的训练：

import numpy as np

def triplet_generator():
	''' Dummy triplet generator for API usage demo only.
	
	Will be replaced by a version that uses real image data later.
	
	:return: a batch of (anchor, positive, negative) triplets
	'''
	while True:
		a_batch = np.random.rand(4, 96, 96, 3)
		p_batch = np.random.rand(4, 96, 96, 3)
		n_batch = np.random.rand(4, 96, 96, 3)
		yield [a_batch , p_batch, n_batch], None

这里triplet_generator返回的X是一个数组[a_batch , p_batch, n_batch]，而Y是None。普通的模型的训练数据一般是输入X和输出Y，模型输出f(X)，然后通过f(X)和Y计算loss。一般在model.compile提供loss函数：

model = Sequential()
model.add(Dense(units=64, activation='relu', input_dim=100))
model.add(Dense(units=10, activation='softmax'))

model.compile(loss='categorical_crossentropy',
	optimizer='sgd',
	metrics=['accuracy'])
model.fit(x_train, y_train, epochs=5, batch_size=32)

而FaceNet的输入是Triplet (a, p, n)，没有输出，Loss是用TripletLossLayer调用add_loss加进去的。我们运行上面的Cell，就可以在fake的数据上进行训练，从而验证我们的代码是work的。

通常我们没有必要自己训练模型，OpenFace提供了很多版本训练好的模型，Keras-OpenFace把它们转换成了hdf5的格式，我们可以使用Keras的load_weights函数直接加载训练好的参数。

nn4_small2_pretrained = create_model()
nn4_small2_pretrained.load_weights('weights/nn4.small2.v1.h5')

自定义数据

接下来我们用LFW的一小部分数据来训练模型，数据在images目录下，共有10个子目录，每个子目录是一个人，下面有10张照片，共计100张照片。

$ tree images/
images/
|-- Ariel_Sharon
|   |-- Ariel_Sharon_0001.jpg
|   |-- Ariel_Sharon_0002.jpg
|   |-- Ariel_Sharon_0003.jpg
|   |-- Ariel_Sharon_0004.jpg
|   |-- Ariel_Sharon_0005.jpg
|   |-- Ariel_Sharon_0006.jpg
|   |-- Ariel_Sharon_0007.jpg
|   |-- Ariel_Sharon_0008.jpg
|   |-- Ariel_Sharon_0009.jpg
|   `-- Ariel_Sharon_0010.jpg
|-- Arnold_Schwarzenegger
|   |-- Arnold_Schwarzenegger_0001.jpg
|   |-- Arnold_Schwarzenegger_0002.jpg
|   |-- Arnold_Schwarzenegger_0003.jpg
|   |-- Arnold_Schwarzenegger_0004.jpg
|   |-- Arnold_Schwarzenegger_0005.jpg
|   |-- Arnold_Schwarzenegger_0006.jpg
|   |-- Arnold_Schwarzenegger_0007.jpg
...................

下面的代码会遍历这个目录结构，把照片的MetaData存储起来，方便后面使用：

import numpy as np
import os.path

class IdentityMetadata():
	def __init__(self, base, name, file):
		# dataset base directory
		self.base = base
		# identity name
		self.name = name
		# image file name
		self.file = file
	
	def __repr__(self):
		return self.image_path()
	
	def image_path(self):
		return os.path.join(self.base, self.name, self.file) 
	
def load_metadata(path):
	metadata = []
	for i in os.listdir(path):
		for f in os.listdir(os.path.join(path, i)):
			# Check file extension. Allow only jpg/jpeg' files.
			ext = os.path.splitext(f)[1]
			if ext == '.jpg' or ext == '.jpeg':
				metadata.append(IdentityMetadata(path, i, f))
	return np.array(metadata)

metadata = load_metadata('images')

IdentityMetadata类用于存放一张照片，它共有3个属性：base,name和file，分别代表根目录，子目录和文件名。而load_metadata(path)函数遍历根目录path，构造出100个IdentityMetadata对象来。

人脸检测和对齐

人脸识别的第一步是人脸检测，其实就是特殊的目标检测。我们当然可以训练一个最先进的Faster R-CNN或者Mask R-CNN模型，有兴趣的读者可以参考这个项目，它直接用我们之前介绍的PyTorch版本的Faster R-CNN来训练人脸检测模型。不过这有点用牛刀杀鸡的感觉，在实际的应用中，我们使用最简单的HoG特征的分类器(比如SVM)就足够准确了，而且速度更快，有兴趣的读者可以参考这篇博客。

因为输入的人脸会有各种角度，虽然理论上FaceNet能够处理不同角度的输入，但是为了得到更好的效果，一般需要将人脸进行对齐(也就是landmarks detection)，然后通过仿射变换尽量把人脸变成标准的中心对称的图片。

对于人脸，我们定义68个特殊点，称为Landmarks，如下图。给定一张人脸照片，我们需要一个机器学习模型来输出这68个点的位置，这就是Face Landmarks Estimation。

图：face-landmarks

下图展示了Landmark检测的结果。有了这个结果，我们可以参考标准的人脸Landmarks，把这种人脸照片做仿射变换，使得检测出来的Landmark点的位置尽量接近标准。这个过程如下图所示，这就是Face Align。这个步骤相当于人脸的归一化过程。

图：Landmark Detection结果

图：Face Align

我们这里使用Dlib实现人脸检测，使用OpenCV实现人脸对齐。具体代码为align.py。

import cv2
import matplotlib.pyplot as plt
import matplotlib.patches as patches

from align import AlignDlib

%matplotlib inline

def load_image(path):
	img = cv2.imread(path, 1)
	# OpenCV的图片是BGR顺序的，我们要把它变成RGB
	return img[...,::-1]

# 构造AlignDlib对象，需要传入前面下载的landmarks.dat文件
alignment = AlignDlib('models/landmarks.dat')

# 加载Jacques Chirac的一张照片
jc_orig = load_image(metadata[2].image_path())

# 进行人脸检测，返回bounding box 
bb = alignment.getLargestFaceBoundingBox(jc_orig)

# 对齐，然后进行仿射变换，最后crop成96x96
jc_aligned = alignment.align(96, jc_orig, bb, landmarkIndices=AlignDlib.OUTER_EYES_AND_NOSE)

# 显示原始图像
plt.subplot(131)
plt.imshow(jc_orig)

# 显示Bounding Box
plt.subplot(132)
plt.imshow(jc_orig)
plt.gca().add_patch(patches.Rectangle((bb.left(), bb.top()), bb.width(), bb.height(), 
			fill=False, color='red'))

#显示对齐后的图像 
plt.subplot(133)
plt.imshow(jc_aligned);

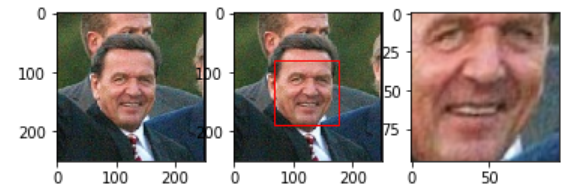
代码运行结果如下图所示。这里使用AlignDlib.getLargestFaceBoundingBox进行人脸检测，找到最大的Bounding Box。

def getAllFaceBoundingBoxes(self, rgbImg):
    """
    找到输入图片的所有人脸的bounding boxes
    :参数 rgbImg: RGB。Shape: (height, width, 3)
    :类型 rgbImg: numpy.ndarray
    :返回: 所有的人脸的Bouding Box 
    :返回类型: dlib.rectangles
    """
    assert rgbImg is not None
    
    try:
	    return self.detector(rgbImg, 1)
    except Exception as e:
	    print("Warning: {}".format(e))
	    # In rare cases, exceptions are thrown.
	    return []

def getLargestFaceBoundingBox(self, rgbImg, skipMulti=False):
    assert rgbImg is not None
    
    faces = self.getAllFaceBoundingBoxes(rgbImg)
    if (not skipMulti and len(faces) > 0) or len(faces) == 1:
	    return max(faces, key=lambda rect: rect.width() * rect.height())
    else:
	    return None

getLargestFaceBoundingBox首先调用getAllFaceBoundingBoxes得到所有的人脸BoundingBox，然后寻找面积最大的那一个。getAllFaceBoundingBoxes调用self.detector来检测所有人脸。self.detector在构造函数里初始化：

def __init__(self, facePredictor):
    self.detector = dlib.get_frontal_face_detector()
    self.predictor = dlib.shape_predictor(facePredictor)

构造函数里还构造了self.predictor，它用于landmark detection，后面用到。

图：人脸检测和对齐结果

人脸对齐使用这里使用AlignDlib.align函数来实现，它的代码为：

def align(self, imgDim, rgbImg, bb=None,
		    landmarks=None, landmarkIndices=INNER_EYES_AND_BOTTOM_LIP,
		    skipMulti=False):

        
        if bb is None:
	        bb = self.getLargestFaceBoundingBox(rgbImg, skipMulti)
        if bb is None:
	        return
        
        if landmarks is None:
	        landmarks = self.findLandmarks(rgbImg, bb)
        
        npLandmarks = np.float32(landmarks)
        npLandmarkIndices = np.array(landmarkIndices)
        
        H = cv2.getAffineTransform(npLandmarks[npLandmarkIndices],
	        imgDim * MINMAX_TEMPLATE[npLandmarkIndices])
        thumbnail = cv2.warpAffine(rgbImg, H, (imgDim, imgDim))
        
        return thumbnail

核心代码是使用 self.findLandmarks(rgbImg, bb)来检测landmark，然后用cv2.getAffineTransform来做仿射变换，最后用cv2.warpAffine来做crop。findLandmarks函数为：

def findLandmarks(self, rgbImg, bb):
    points = self.predictor(rgbImg, bb)
    return list(map(lambda p: (p.x, p.y), points.parts()))

对于模型nn4.small2.v1，因为训练的时候使用了AlignDlib.OUTER_EYES_AND_NOSE，因此我们也需要用它来对所有的图片做预处理，我们把它封装成一个函数方便后续使用：

def align_image(img):
	return alignment.align(96, img, alignment.getLargestFaceBoundingBox(img), 
				  landmarkIndices=AlignDlib.OUTER_EYES_AND_NOSE)

Emebedding向量

经过预处理之后，我们就可以用预训练(或者自己从头训练)的模型来生成Embedding向量了，因为数据量很小，我们直接把这100张图片的Embedding放到一个ndarray里：

embedded = np.zeros((metadata.shape[0], 128))

for i, m in enumerate(metadata):
	img = load_image(m.image_path())
	img = align_image(img)
	# 把0-255的RGB缩放到区间[0,1]
	img = (img / 255.).astype(np.float32)
	# Keras要求第一维度是batch，所以要expand_dim把img从(96,96,3)变成(1,96,96,3)
	embedded[i] = nn4_small2_pretrained.predict(np.expand_dims(img, axis=0))[0]

接下来我们定义距离函数，并且找同一个几张照片来验证是否距离结果是合理的——同一个人的距离小，不同人的距离大。

def distance(emb1, emb2):
	return np.sum(np.square(emb1 - emb2))

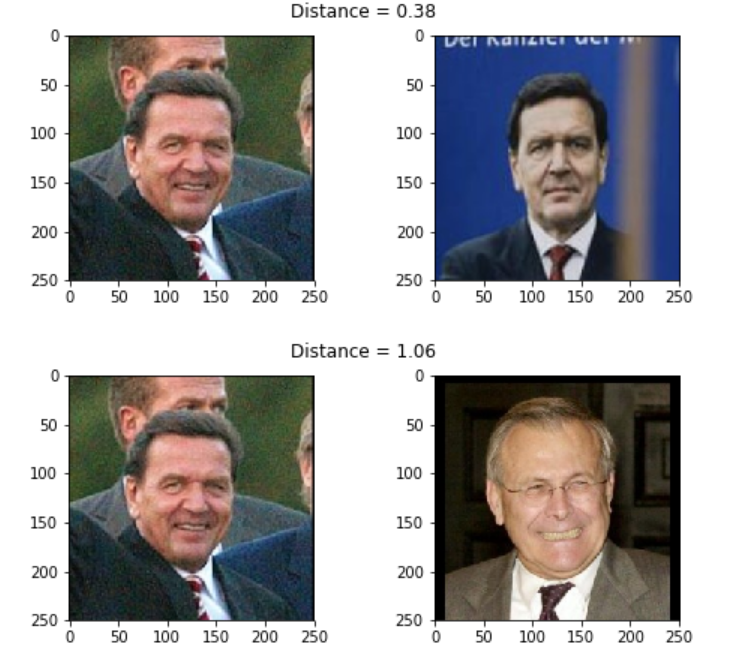
def show_pair(idx1, idx2):
	plt.figure(figsize=(8,3))
	plt.suptitle(f'Distance = {distance(embedded[idx1], embedded[idx2]):.2f}')
	plt.subplot(121)
	plt.imshow(load_image(metadata[idx1].image_path()))
	plt.subplot(122)
	plt.imshow(load_image(metadata[idx2].image_path()));

show_pair(2, 3)
show_pair(2, 12)

结果如下图所示。我们发现Jacques Chirac的两张照片的距离(0.38)确实比他和Gerhard Schröder的(1.06)小。

图：距离计算示例

最佳距离阈值

为了寻找最佳的距离阈值，我们需要有一个数据集，然后尝试不同的阈值，计算不同阈值的效果，最后寻找一个最优的阈值。评价阈值的效果有很多指标，这里我们使用F1值。

from sklearn.metrics import f1_score, accuracy_score

distances = [] # squared L2 distance between pairs
identical = [] # 1 if same identity, 0 otherwise

num = len(metadata)

for i in range(num - 1):
	for j in range(1, num):
		distances.append(distance(embedded[i], embedded[j]))
		identical.append(1 if metadata[i].name == metadata[j].name else 0)

distances = np.array(distances)
identical = np.array(identical)

thresholds = np.arange(0.3, 1.0, 0.01)

f1_scores = [f1_score(identical, distances < t) for t in thresholds]
acc_scores = [accuracy_score(identical, distances < t) for t in thresholds]

opt_idx = np.argmax(f1_scores) 
opt_tau = thresholds[opt_idx] 
opt_acc = accuracy_score(identical, distances < opt_tau)
 
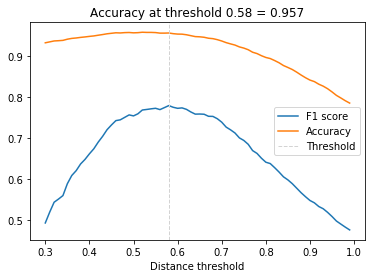
plt.plot(thresholds, f1_scores, label='F1 score');
plt.plot(thresholds, acc_scores, label='Accuracy');
plt.axvline(x=opt_tau, linestyle='--', lw=1, c='lightgrey', label='Threshold')
plt.title(f'Accuracy at threshold {opt_tau:.2f} = {opt_acc:.3f}');
plt.xlabel('Distance threshold')
plt.legend();

上面的代码很简单，就是尝试不同的thresholds值，选择F1最大的那个。里面为了避免重复的距离计算，提取把100张图片的两两距离存储下来了。结果如下图所示，最优的阈值是0.58，对应的分类准确率是95.7%。当然这不是一个很高的准确率，因为我们使用的是一个很小的模型。

图：寻找最优阈值

分类

有了Face Embedding向量之后，我们就可以用KNN来进行分类，找到最可能的分类，之后再把最接近的距离和阈值比较，如果小于阈值就判断为是这个人，否则就判断为人脸库之外的人。KNN的好处是增加新类(人)不需要训练，但是缺点是准确率不高，还有就是人脸库大的时候速度会很慢。为了解决这个问题，我们可以学习一个SVM(或者其他的)分类器，分类器的输入就是Embedding向量。使用分类器的好处是预测速度只取决于模型的结构和参数，而与训练数据大小无关，但是缺点就是每增加一个新人就得重新训练。当然SVM分类之后也需要判断输入图片和这个类的所有图片的最近距离，然后再和阈值比较。这里忽略了这个步骤，简单的假设输入图片一定是人脸库中的某个人。下面的代码使用sklearn实现KNN和SVM分类器。

from sklearn.preprocessing import LabelEncoder
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import LinearSVC

targets = np.array([m.name for m in metadata])

encoder = LabelEncoder()
encoder.fit(targets)

y = encoder.transform(targets)

train_idx = np.arange(metadata.shape[0]) % 2 != 0
test_idx = np.arange(metadata.shape[0]) % 2 == 0

# 每人5张用于训练，总共10*5=50个训练样本
X_train = embedded[train_idx]
# 每人5张用于测试，总共10*5=50个测试样本
X_test = embedded[test_idx]

y_train = y[train_idx]
y_test = y[test_idx]

knn = KNeighborsClassifier(n_neighbors=1, metric='euclidean')
svc = LinearSVC()

knn.fit(X_train, y_train)
svc.fit(X_train, y_train)

acc_knn = accuracy_score(y_test, knn.predict(X_test))
acc_svc = accuracy_score(y_test, svc.predict(X_test))

print(f'KNN accuracy = {acc_knn}, SVM accuracy = {acc_svc}')

最终KNN和SVM得到的准确率都是0.98：

KNN accuracy = 0.98, SVM accuracy = 0.98

我们用SVM来做预测：

import warnings
# Suppress LabelEncoder warning
warnings.filterwarnings('ignore')

example_idx = 29

example_image = load_image(metadata[test_idx][example_idx].image_path())
example_prediction = svc.predict([embedded[test_idx][example_idx]])
example_identity = encoder.inverse_transform(example_prediction)[0]

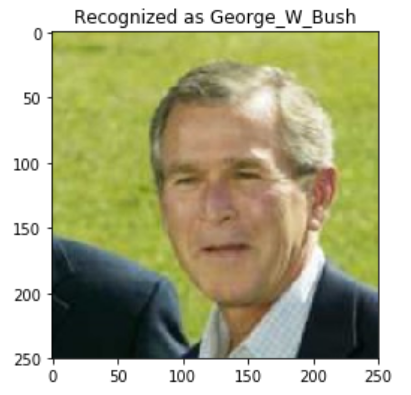
plt.imshow(example_image)
plt.title(f'Recognized as {example_identity}');

结果如下图所示，它确实识别对了George W. Bush。

图：SVM分类测试

数据可视化

为了展示Face Emebedding确实是把同一个人的照片映射到Embedding空间相近的点，我们使用TSNE来进行降维。TSNE可以把高维空间的点降维到2维空间，从而可以可视化。而且它可以使得高维空间接近的点在二维空间仍然接近，具体原理本书不介绍，有兴趣的读者可以参考相关资料。sklearn.manifold提供方便的工具使用TSNE：

from sklearn.manifold import TSNE

# 对embedded进行TSNE降维
X_embedded = TSNE(n_components=2).fit_transform(embedded)

# 遍历10个类别(人)
for i, t in enumerate(set(targets)):
	# 找到这个人的照片(下标)
	idx = targets == t
	# 绘制散点图
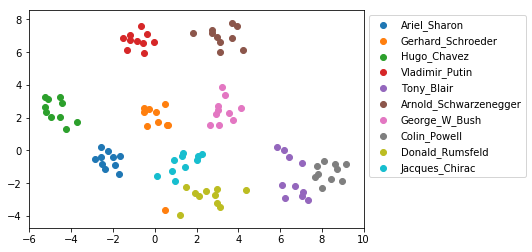
	plt.scatter(X_embedded[idx, 0], X_embedded[idx, 1], label=t)

plt.legend(bbox_to_anchor=(1, 1));

结果如下图所示，我们发现确实Embedding实现了把同一个人的照片映射到了接近的点上。

图：Face Embedding的可视化

简介