本文是《深度学习理论与实战》草稿中的一章,主要参考了Reinforcement Learning: An Introduction Second Edition。编辑认为书太厚,定价太高没人买,所以删除了很多内容。这些内容会放到网上,取了一个tag《深度学习理论与实战》拾遗。 更多本系列文章请点击强化学习简介系列文章。更多内容请点击深度学习理论与实战:提高篇。
目录
引言
前面我们介绍了监督学习,监督学习的特点是有一个“老师”来“监督”我们,告诉我们正确的结果是什么。在我们在小的时候,会有老师来教我们,本质上监督学习是一种知识的传递,但不能发现新的知识。对于人类整体而言,真正(甚至唯一)的知识来源是实践——也就是强化学习。比如神农尝百草,最早人类并不知道哪些草能治病,但是通过尝试,就能学到新的知识。学到的这些知识通过语言文字记录下来,一代一代的流传下来,从而人类社会作为整体能够不断的进步。和监督学习不同,没有一个“老师”会“监督“我们。比如下围棋,不会有人告诉我们当前局面最好的走法是什么,只有到游戏结束的时候我们才知道最终的胜负,我们需要自己复盘(学习)哪一步是好棋哪一步是臭棋。自然界也是一样,它不会告诉我们是否应该和别人合作,但是通过优胜劣汰,最终”告诉”我们互相协助的社会会更有竞争力。和前面的监督非监督学习相比有一个很大的不同点:在强化学习的Agent是可以通过Action影响环境的——我们的每走一步棋都会改变局面,有可能变好也有可能变坏。
它要解决的核心问题是给定一个状态,我们需要判断它的价值(Value)。价值和奖励(Reward)是强化学习最基本的两个概念。对于一个Agent(强化学习的主体)来说,Reward是立刻获得的,内在的甚至与生俱来的。比如处于饥饿状态下,吃饭会有Reward。而Value是延迟的,需要计算和慎重考虑的。比如饥饿状态下去偷东西吃可以有Reward,但是从Value(价值观)的角度这(可能)并不是一个好的Action。为什么不好?虽然我们可以求助于监督学习,比如先贤告诉我们这是不符合道德规范的,不是好的行为。但是我们之前说了,人类最终的知识来源是强化学习,先贤是从哪里知道的呢?有人认为来自上帝或者就是来自人的天性,比如“人之初性本善”,我们会在最后一章讨论哲学的问题。如果从进化论的角度来解释,人类其实在玩一场”生存”游戏,有遵循道德的人群和有不遵循的人群,大自然会通过优胜劣汰”告诉”我们最终的结果,最终我们的先贤“学到”了(其实是被选择了)这些道德规范,并且把这些规范通过教育(监督学习)一代代流传下来。
马尔科夫决策过程(MDP)
马尔科夫决策过程(Markov Decision Process)是强化学习最常见的模型。我们通过这个模型来介绍强化学习的一些基本概念。
和环境的互动
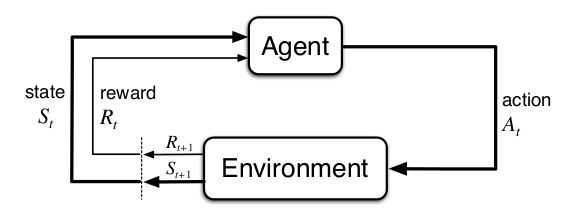
强化学习的本质就是通过与环境的互动来学习怎么达成一个目标。这个学习和做决策的主体就叫Agent。Agent交互的对象就是环境(Environment),环境可大可小,对于坐井观天的青蛙来说,它的环境就是那口小井;而对于人类来说,整个地球甚至太阳系都是我们研究的对象。Agent会持续的和环境交互,根据当前的状态选择行为(Action),而环境会给Agent新的状态和Reward。整个交互过程如下图所示。
Agent和环境的交互假设是时刻t=0,1,…。在t时刻,Agent处于某个状态$S_t \in \mathcal{S}$,这里$\mathcal{S}$表示所有可能状态的集合,也就是状态空间。它可以选择一个行为$A_t \in \mathcal{A}(S_t)$,其中$\mathcal{A}(S_t)$是状态$S_t$时可以选择的所有行为的集合。选择了行为 $A_t$之后,环境会在下一个(t+1)时刻给Agent一个新的状态$S_{t+1}$和Reward $R_{t+1} \in \mathcal{R} \subseteq R$。
一个实数值的Reward是否足够?拿人来说,是有很多方面的追求,比如同时要考虑工作和家庭。当然最简单的方法是把两个目标(goal)进行加权求和,而且这个权重似乎会变化,因此人类是否有一个单一的目标,而其他目标都是它的一种外在表现?我们这里不讨论这个问题,但是对于实际的Task来说,一般是足够了。比如下围棋,就是胜负;玩Atari游戏就是获得最高的得分。
在每个时刻t,Agent根据当前的状态$S_t$会选取不同的行为 $A_t$,选择的方法叫做策略(Policy),一般假设是它一个概率分布(确定的策略是它的特殊情况)$\pi_t(A_t|S_t)$,如果这个随机过程是平稳的(Stationary),那么我们的策略也一般与时间无关的,即$\pi_t(A_t|S_t)=\pi(A_t|S_t)$。策略有好有坏,Agent的目标是学习到最好的策略(是否存在也是强化学习的一个理论问题,不过我们一般认为存在,也有一些理论可以证明如果系统满足一些假设,最优策略是存在的)。
目标和奖励
每个时刻t,环境都会给Agent一个Reward$R_t$,而Agent的目标(Goal)是最大化最终得到的所有Reward的和。这里隐含的意思是:我们的目标不是短期的Reward,而是长期Reward的累加。在学校的时候平时努力学习最终会有回报的,如果短期来看,学习可能会饥饿会疲惫,而出去玩可能会愉快。这就是所谓的“Reward假设”:我们所说的目标(Goal)或者目的(Purpose)最终可以被看成最大化一个Reward信号的累加值。
就像前文说过,用一个数值来描述Agent所有的目标(尤其是人这样复杂的生物)似乎有些不够,我们暂且把Agent放到一些具体的任务(Task)上来看看似乎足够。比如我们让一个老鼠逃离迷宫(Maze),如果它没有找到出口我们给它-1的Reward,这样它学习的目标就是尽快的逃离迷宫。比如下象棋,如果获胜,我们给它+1的Reward,如果输棋则是-1,和棋则是0。又比如扫地机器人,如果它收集到垃圾,那么给它+1的Reward,那么它的目标就是尽可能多的收集垃圾。
注意:我们定义的目标是要告诉Agent我们期望它做的是什么(What),而不是告诉它怎么做(How)。比如下棋时吃掉对方的棋子是一种获胜的策略(怎么做),我们不能给吃子Reward,否则它就可能学到的策略是为了吃子,因为我们知道有的时候为了获胜必须牺牲己方的棋子。
回报(Return)
Agent的目标是最大化长期的Reward累加值,下面我们来形式化的定义这个累加值——回报。假设t时刻之后的Reward是$R_t, R_{t+1}, …$,我们期望这些Reward的和最大。由于环境(可能)是随机的,而且Agent的策略也(可能)是随机的,因此Agent的目标是最大化Reward累加和的期望值。回报$G_t$定义如下:
\[G_t=R_{t+1} + R_{t+2} + R_{t+3} + ... + R_T\]其中T是最后的时刻。有些任务会有一些结束的状态,从任务的初始状态到结束状态,我们称之为一个episode。比如下象棋,从开始下棋到最终分出胜负(或者和棋)一局游戏结束就叫一个episode。如果我们开始一个新的episode,比如下棋重新开始一局,那么Agent的状态会重置到初始化状态,而且新的一局和上一局是没有关系的。除了episode的任务之外,还有一种任务没有结束状态,会一直继续下去,也就是$T=\infty$。
由于未来的不确定性,我们一般会对未来的Reward进行打折(Discount)。这很好理解,眼前的Reward的是确定的,拿到手再说,未来的Reward不确定因素太多,所以要打折。因此我们可以定义打折后的回报(Discounted Return)如下:
\[G_t=R_{t+1} + \gamma R_{t+2} + \gamma ^2 R_{t+3} + ... =\sum_{k=0}^{\infty }\gamma ^kR_{t+k+1}\]其中$\gamma$是一个参数,$0 \leq \gamma \leq 1$,叫做打折率(Discount Ratio)。如果$\gamma < 1$并且Reward是有界的,那么无穷项的和是收敛的。如果$\gamma = 0 $,则Agent只考虑当前t时刻的Reward,而随着$\gamma$趋近于1,则未来的Reward越来越重要,当$\gamma = 1 $时,未来的Reward和当前的一样重要。回报$G_t$有如下的递归公式:
\[\begin{split} G_t & =R_{t+1} + \gamma R_{t+2} + \gamma ^2 R_{t+3} + ... \\ & =R_{t+1}+\gamma(R_{t+2}+\gamma R_{t+3} + ...) \\ & =R_{t+1}+\gamma G_{t+1} \end{split}\]马尔科夫属性
在强化学习里,Agent根据状态来决定采取什么样的行为,而状态是来自环境的一个信号(Signal)。状态可以来自Agent的传感器的测量(Sensory Measurements),也可以是这些原始测量的复杂处理。可以是当前时刻的传感器信号,也可以包含以前的信号。理想的,我们期望状态信号能够紧凑的压缩过去所有的信息,它能够保留所有相关的信息而尽量丢弃无关的信息。这通常要求状态不仅包含当前时刻的信号,还可能包含之前的一些信息,当然通常不需要所有过去的信息。如果一个状态信号包含了所有相关的信息,那么就叫它具有马尔科夫属性(Markov Property)。比如下象棋,当前的局面(包括所有棋子的位置和谁走下一步棋)包含了所有的信息。不管是先走车再走马还是先走马再走车,总之它们到达了相同的局面。因此通常马尔科夫属性通常与具体的“路径”无关。下面我们来形式化的定义马尔科夫属性。
我们假设环境的动力系统(dynamics)是如下的随机过程:
\[Pr\{S_{t+1}=s', R_{t+1}=r|S_0, A_0, R_1,..., S_{t-1}, A_{t-1}, R_t, S_t, A_t\}\]也就是在过去所有的历史信息的情况下($S_0, A_0, R_1,…, S_{t-1}, A_{t-1}, R_t$),Agent处于状态$S_t$下采取$A_t$后环境反馈的新状态是s’并且rewward是r的联合概率分布。如果系统满足马尔科夫属性,那么所有的过去历史信息都压缩在$S_t$里了,因此给定$S_t$的条件下与过去的历史无关,因此满足马尔科夫属性的系统的动力系统可以简化为如下公式:
\[p(s',r|s,a) \equiv Pr\{S_{t+1}=s', R_{t+1}=r|S_t=s, A_t=a\}\]如果环境具有马尔科夫属性,那么在给定当前状态和行为的条件下我们可以使用上式预测下一个状态和Reward(的概率)。通过不断迭代的使用这个公式,我们可以(精确的)计算当前状态的期望回报。
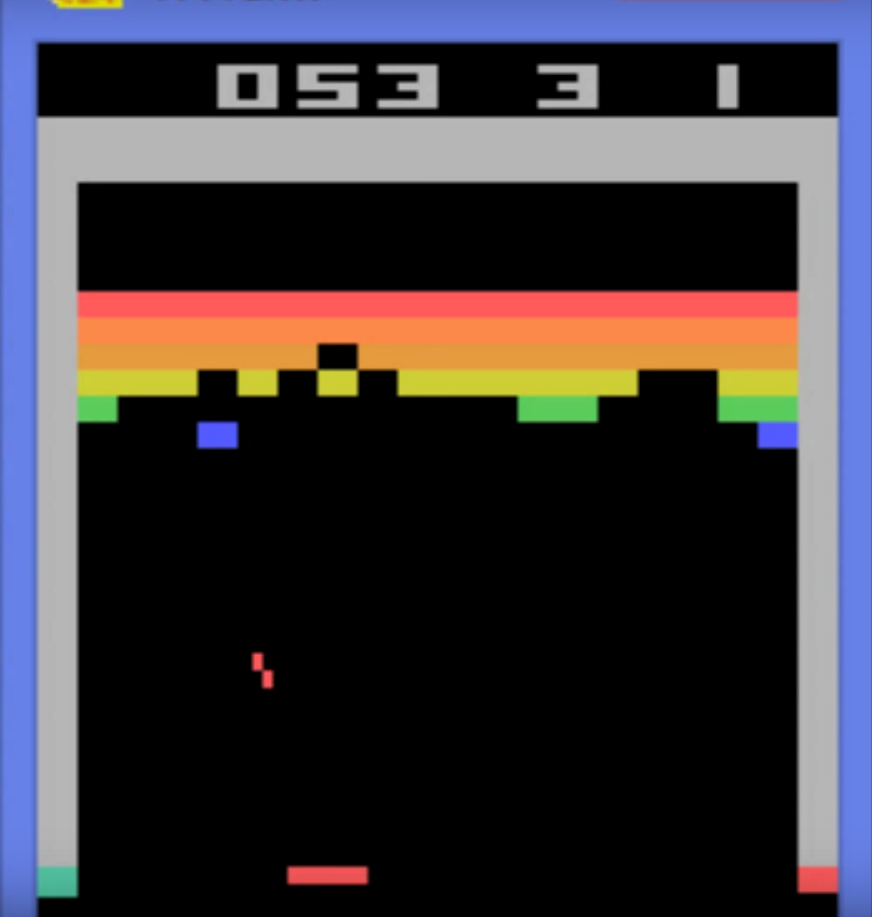
比如上图Atari Broke游戏,玩法就是用下面的挡板把球反弹回去,然后碰掉上方的格子,每碰掉一个格子就会有加分(Reward),如果所有格子都碰掉了或者挡板没有接到球让它落入屏幕下方就算游戏结束。玩家的目标就是获得更多的得分。
如果我们分析这个游戏的环境,假如我们把当前帧的图像作为当前的状态,那么它是否是马尔科夫的呢?似乎不行,因为一幅图像只有今天的信息,可能有两个状态图像相同但是球速可能不同。我们可以把当前帧和前一帧图像作为当前的状态,假设球是匀速直线运动的(在没有碰撞的时候是这样的),那么根据两帧的球的位置可以计算出其速度来。这样就可以大致认为它是具有马尔科夫属性的了。
马尔科夫决策过程(Markov Decision Processes)
满足马尔科夫属性的强化学习叫做马尔科夫决策过程,如果状态空间和行为空间是有限的,那么它就叫有限马尔科夫决策过程。一个马尔科夫决策过程完全由环境的当前状态决定,我们再次重复一下这个重要公式:
\[p(s',r|s,a)\equiv Pr\{S_{t+1}=s', R_{t+1}=r|S_t=s, A_t=a\}\]有了上面的公式,我们可以计算关于环境的任何信息(也就是说环境完全由这个公式确定)。比如我们可以计算某个特点状态s和行为a的期望reward如下:
\[r(s,a)\equiv \mathbb{E}[R_{t+1}|S_t=s, A_t=a]=\sum_{r \in \mathcal{R}}r\sum_{s' \in \mathcal{S}}p(s',r|s,a)\]上面的公式直接根据期望的定义推导出来,我们这里简单的推导一下,后面类似的地方就略过了。
\[\begin{gather*} \text{根据期望的定义:} EX=\sum xP(X=x) \\ \mathbb{E}[R_{t+1}|S_t=s, A_t=a]= \sum_{r \in \mathcal{R}}rP(R_{t+1}=r|S_t=s, A_t=a) \\ \text{再根据边缘分布是联合分布的求和/积分} P(X)=\sum_YP(X,Y) \\ =\sum_{r \in \mathcal{R}}r\sum_{s' \in \mathcal{S}}p(s',r|s,a) \end{gather*}\]同样我们可以得到状态转移概率:
\[p(s'|s,a) \equiv Pr(S_{t+1}=s'|S_t=s, A_t=a)=\sum_{r \in \mathcal{R}}p(s',r|s,a)\]以及给定当前s、当前a和下一个s’条件时期望的Reward:
\[r(s,a,s') \equiv \mathbb{E}\{R_{t+1}|S_t=s,A_t=a,S_{t+1}=s'\} \ =\frac{\sum_{r \in \mathcal{R}}rp(s',r|s,a)}{p(s'|s,a)}\]价值函数(Value Function)
很多强化学习方法会涉及求状态的价值函数(或者State-Action对的价值函数)。这个函数计算Agent处于这个状态(或者Agent处于状态s并且采取xingw行为a)到底有多好。比如下棋的时候我们会思考如果我们处于某个局面(Position)到底是好是坏,从而采取Action引导局面向这个好的局面发展或者避开不好的局面。这里的“好”指的是在这个状态下Agent获得回报的期望值,当然这个期望值是与Agent的策略(Policy)紧密相关的,因此价值函数指的是在某个策略下的价值函数。
回忆一下,策略$\pi$是一个从状态$s \in \mathcal{S}$, Action $a \in \mathcal{A}(s)$到概率$\pi(a | s)$的映射。我们把状态s时策略$\pi$的价值,也就是Agent处于状态s,并且使用策略$\pi$,它所能得到的回报的期望值,定义为$v_{\pi}(s)$。它的形式化定义是:
\[v_\pi(s) \equiv \mathbb{E}[G_t|S_t=s]=\mathbb{E}_\pi[\sum_{k=0}^\infty \gamma^kR_{t+k+1}|S_t=s]\]这里\(\mathbb{E}_\pi[·]\)代表Agent使用策略$\pi$来采取行为时随机变量的期望值。如果有终止状态,我们定义其价值函数为零。我们把函数$v_{\pi}$叫做策略$\pi$的状态价值函数(State Value Function)。
类似的我们可以定义$q_\pi(s,a)$,在状态s下采取Action a的价值,其形式化定义为:
\[q_\pi(s,a) \equiv \mathbb{E}[G_t|S_t=s,A_t=a]=\mathbb{E}_\pi[\sum_{k=0}^\infty \gamma^kR_{t+k+1}|S_t=s,A_t=a]\]我们把$q_\pi$叫做策略$\pi$的行为价值函数(Action Value Function)。
值函数$v_\pi$和$q_\pi$可以从经验(Experience)中估计出来。比如我们可以这样来估计:如果一个Agent使用策略$\pi$模拟很多次,通过平均可以估计出一个值来,如果模拟次数趋于无穷大,那么这种方法得到的估计值\(\hat{v}_\pi(s)\)会收敛到真正的$v_\pi(s)$。这就是蒙特卡罗(Monte Carlo)方法,这个方法也可以用于$q_\pi(s,a)$的估计。如果状态空间非常大,我们也可以假设$v_\pi(s)$或者$q_\pi(s,a)$是参数化的函数(模型)$v_\pi(s;w)$或者\(q_\pi(s,a;w)\),这就是近似的方法。我们可以用深度神经网络来实现$v_\pi(s;w)$或者$q_\pi(s,a;w)$,这就是所谓的深度强化学习(Deep Reinforcement Learning)。
值函数一个非常重要的特效是它满足某种递归性,这在强化学习和动态规划会经常用到。这个递归公式就是贝尔曼方程(Bellman Equation),希望读者能够理解并推导下面的公式(如果有些步骤不能推导,也至少读懂它在说什么并能够“认可”这个等式,书读百遍其义自见,实在不理解多抄两遍也会有帮助)。
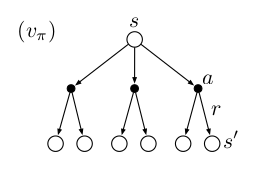
\[\begin{split} v_\pi(s) & \equiv \mathbb{E}_\pi[G_t|S_t=s] \\ & =\mathbb{E}_\pi[R_{t+1}+\gamma G_{t+1}|S_t=s] \;\; \text{ 根据前面的式子} \\ & =\sum_a\pi(a|s)\sum_{s'}\sum_rp(s',r|s,a)[r+\gamma\mathbb{E}[G_{t+1}|S_{t+1}=s']] \\ & =\sum_a\pi(a|s)\sum_{s',r}p(s',r|s,a)[r+\gamma v_\pi(s')]] \end{split}\]我们再来看一下Bellman公式,它是递归定义的——$v_{\pi}(s)$是由$v_{\pi}(s’)$来定义的,对于有些简单问题,我们可以根据这个公式把$v_{\pi}$通过解方程解出来。
我们结合上图来分析上面公式的。当前状态是s,根据策略$\pi$,我们采取行为a的概率是$\pi(a | s)$,而我们在状态a和行为s的条件下,环境反馈r和s’的概率是$p(r,s’|s,a)$,所有可能的(a,r,s’)组合我们都要求和,所以就得到$\sum_a\pi(a|s)\sum_{s’,r}p(s’,r|s,a)$,在每一条路径(每一种s,r,s’的组合)下$R_{t+1}$就是r,因此可以得到$\sum_a\pi(a|s)\sum_{s’,r}p(s’,r|s,a)[r]$。而在给定路径的情况下,$s,r,s’$都固定了,因此s’也是固定的了,而根据马尔科夫属性,$G_{t+1}$只与t+1时刻的状态$S_{t+1}=s’$有关,因此第二项变成了$\sum_a\pi(a|s)\sum_{s’,r}p(s’,r|s,a)[\gamma\mathbb{E}[G_{t+1}|S_{t+1}=s’]$。
最优价值函数(Optimal Value Functions)
解决强化学习任务,粗略来说,就是找到一个策略,使得长期的reward尽可能多。首先我们定义什么是一个策略$\pi$比另外一个策略$\pi ‘$好(或者一样好),记作$\pi \ge \pi’$。形式化的定义是$\pi \ge \pi’ \leftrightarrow \forall s \in \mathcal{S}, v_\pi(s) \ge v_{\pi’}(s)$。 可以证明(这里略过)存在一个(可能有多个)最优的\(\pi_*\),它比所有其它策略都“好”。最优策略对于的价值函数叫做最优价值函数,记作\(v_*(s)\):
\[v_*(s)=\max_\pi v_\pi(s) ,\, \forall s \in \mathcal{S}\]同理对于行为也有一个最优的行为价值函数:
\[q_*(s,a)=\max_\pi q_\pi(s,a) ,\, \forall s \in \mathcal{S}, a \in \mathcal{A}(s)\]\(q_*(s,a)\)和\(v_*(s)\)有如下关系:
\[q_*(s,a)=\mathbb{E}[R_{t+1}+\gamma v_*(S_{t+1})|S_t=s, A_t=a]\]我们可以这样解读这个公式:s和a确定后,它会进入$S_{t+1}$状态并得到Reward $R_{t+1}$,这是过程是有概率的,因此前面有一个期望$\mathbb{E}$。但是这和Agent无关,和Agent有关的是在t+1时刻的行为,如果要得到最优的$q(s,a)$,那么它必须在t+1时刻根据最优策略\(\pi_*\)来计算$v_(S_{t+1})$,因此就是\(v_*(S_{t+1})\)。
需要注意:上面公式的随机变量只是$R_{t+1}$和$S_{t+1}$,它由环境$p(r,s’|s,a)$确定,而\(v_*(s)\)和\(q_*(s,a)\)是两个常量(给定s,a的情况下)。
OpenAI Gym简介
OpenAI Gym是一个用来开发和比较强化学习算法的工具。它对Agent的实现没有任何约束,因此你可以用TensorFlow或者其它任何工具来实现Agent。它提供统一的Environment的接口,你可以用这个接口来定义一个具体的强化学习任务,此外它也提供很多常见的任务,比如很多Atari的游戏。
运行Environment
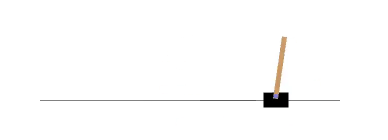
首先我们介绍一个很简单的游戏CartPole-v0,如下图所示。
这个游戏有一个小车,可以对车子施加+1或者-1的力(加速度),车上有一个杆子,我们的目标是要求车子的位置在-2.4到2.4之间,并且杆子相对于垂直的角度在-15°和15°之间。如果从物理的角度来分析,它有4个状态变量,车子的位置,车子的速度,杆的角度,杆的角速度。而我们施加的力会改变车子的速度,从而间接改变车子的位置。我们可以用几行代码运行CartPole-v0这个游戏:
import gym
env = gym.make('CartPole-v0')
env.reset()
for _ in range(1000):
env.render()
env.step(env.action_space.sample()) # take a random action
代码很简单,首先创建一个CartPole-v0 Environment对象env,重置(reset)使环境进入初始状态。接着循环1000次,每次首先把当前的游戏状态绘制出来(render),然后随机的选择一个Action env.action_space.sample(),接着调用env.step函数真正的“执行”这个Action。
观察(Observations)
观察就是MDP里的状态(State),Environment的step有4个返回值:
- observation 一个对象,代表观察,不同的环境返回的对象是不同的。
- reward float类型 表示Reward。
- done bool类型 表示任务是否结束。对于Episode类任务会有结束状态,进入结束状态后再调用step是没有意义的,必须要先调用reset
- info 调试用的一些信息
我们可以用如下代码打印出其中的一些信息:
import gym
env = gym.make('CartPole-v0')
for i_episode in range(20):
observation = env.reset()
for t in range(100):
env.render()
print(observation)
action = env.action_space.sample()
observation, reward, done, info = env.step(action)
if done:
print("Episode finished after {} timesteps".format(t+1))
break
Spaces
Environment对象里有两个空间(Space):状态空间(State Space)和行为空间(Action Space),它们定义了所有可能的状态和行为。我们可以查看一些CartPole-v0的Space:
import gym
env = gym.make('CartPole-v0')
print(env.action_space)
#> Discrete(2)
print(env.observation_space)
#> Box(4,)
从输出可以看出,Discrete(2)表示这个任务有两个选的Action(分布表示向左和向右移动),Box(4,)表示状态由4维向量表示,物理意义分别是车子相对原点的位置和速度,杆相对于垂直方向的角度和角速度。我们可以用如下的代码检查其取值范围:
print(env.observation_space.high)
#> array([ 2.4 , inf, 0.20943951, inf])
print(env.observation_space.low)
#> array([-2.4 , -inf, -0.20943951, -inf])
- 显示Disqus评论(需要科学上网)