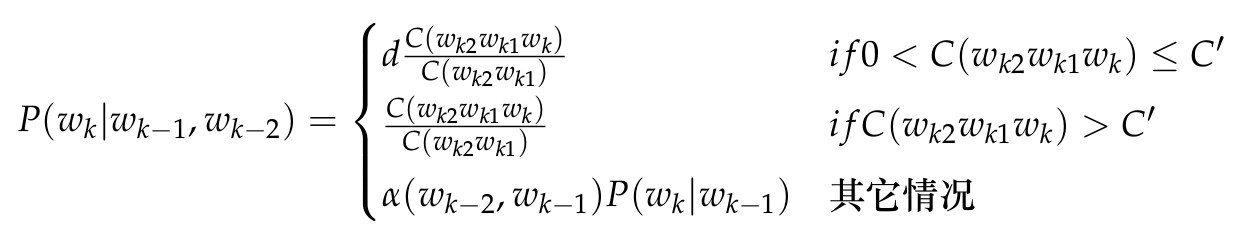本文介绍Word Embedding的基本概念以及常见的无监督训练方法,主要Word2Vec。
目录
词的表示方法
不同于更底层的图像和声音信号,语言是高度抽象的离散符号系统。为了能够使用神经网络来解决NLP任务,几乎所有的深度学习模型都要在第一步把离散的符号变成向量。我们希望把一个词映射到”语义”空间中的一个点,使得相似的词的距离较近而不相似的较远。我们可以用向量来表示一个点,因此我们通常把这个向量叫做词向量。
one-hot向量
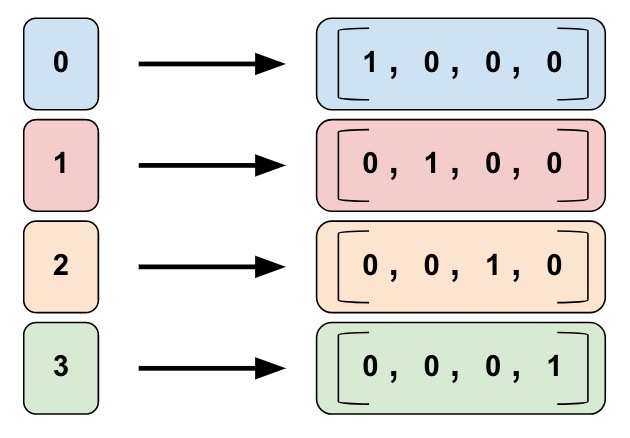
最简单的方法就是one-hot表示。假设我们的词典大小是4(当然实际通常是很多,至少几万),如下图所示,每个词对应一个下标。每个词都用长度为4的向量表示,只有对应的下标为1,其余都是零。比如上面的例子,第一个词是[1, 0, 0, 0],而第三个词是[0, 0, 1, 0]。
one-hot的问题是不满足我们前面的期望——相似的词的距离较近而不相似的较远。对于one-hot向量来说,相同的词距离是0,而不同的词距离是1。这显然是有问题的,因为cat和dog的距离肯定要比cat和apple要远。但是在one-hot的表示里,cat和其它任何词的距离都是1。
one-hot的问题在于它是一个高维(通常几万甚至几十万)的稀疏(只有一个1)向量。我们希望用一个低维的稠密的向量来表示一个词,我们期望每一维都是表示某种语义。比如第一维代表动物(当然这只是假设),那么cat和dog在这一维的值都比较大,而apple在这一维的值比较小。这样cat和dog的距离就比cat和apple要近。
神经网络语言模型
那么我们怎么学习到比较好的词向量呢?最早的词向量其实可以追溯到神经网络语言模型。但是首先我们来了解一下语言模型的概念和传统的基于统计的N-Gram语言模型。
给定词序列$w_1,…,w_K$,语言模型会计算这个序列的概率,根据条件概率的定义,我们可以把联合概率分解为如下的条件概率:
\[P(w)=\prod_{k=1}^{K}P(w_k|w_{k-1}, ..., w_1)\]实际的语言模型很难考虑特别长的历史,通常我们会限定当前词的概率值依赖与之前的N-1个词,这就是所谓的N-Gram语言模型:
\(P(w)=\prod_{k=1}^{K}P(w_k|w_{k-1},...,w_{k-N+1})\) 在实际的应用中N的取值通常是2-5。我们通常用困惑度(Perplexity)来衡量语言模型的好坏: \(\begin{split} H & = - \underset{K \to \infty} {lim}\frac{1}{K} log_2 P(w_1,...,w_K) \\ & \approx \frac{1}{K} \sum_{k=1}^{K} log_2 (P(w_k|w_{k-1},...,w_{k-N+1})) \end{split}\)
N-Gram语言模型可以通过最大似然方法来估计参数,假设$C(w_{k−2} w_{k−1} w_k)$表示3个词$(w_{k−2} w_{k−1} w_k$连续出现在一起的次数,类似的$C(w_{k−2} w_{k−1}$表示两个词$w_{k−2} w_{k−1}$连续出现在一起的次数。那么:
\[P(w_k|w_{k-1}w_{k-2})=\frac{C(w_{k−2} w_{k−1} w_k)}{C(w_{k−2} w_{k−1})}\]最大似然估计的最大问题是数据的稀疏性,如果3个词没有在训练数据中一起出现过,那么概率就是0,但不在训练数据里出现不代表它不是合理的句子。实际一般会使用打折(Discount)和回退(Backoff)等平滑方法来改进最大似然估计。打折的意思就是把一些高频N-Gram的概率分配给从没有出现过的N-Gram,回退就是如果N-Gram没有出现过,我们就用(N-1)-Gram来估计。比如Katz平滑方法的公式如下:
上式中C’是一个阈值,频次高于它的概率和最大似然估计一样,但是对于低于它(但是至少出现一次)的概率做一些打折,然后把这些概率分配给没有出现的3-Gram,怎么分配呢?通过回退到2-Gram的概率$P(w_k|w_{k-1})$来按比例分配。
N-Gram语言模型有两个比较大的问题。第一个就是N不能太大,否则需要存储的N-gram太多,因此它无法考虑长距离的依赖。比如”I grew up in France… I speak fluent _.”,我们想猜测fluent后面哪个词的可能性大。如果只看”speak fluent”,那么French、English和Chinese的概率都是一样大,但是通过前面的”I grew up in France”,我们可以知道French的概率要大的多。这个问题可以通过后面介绍的RNN/LSTM/GRU等模型来一定程度的解决,我们这里暂时忽略。
另外一个问题就是它的泛化能力差,因为它完全基于词的共现。比如训练数据中有”我 在 北京”,但是没有”我 在 上海”,那么$p(上海|在)$的概率就会比$p(北京|在)$小很多。但是我们人能知道”上海”和”北京”有很多相似的地方,作为一个地名,都可以出现在”在”的后面。这个其实和前面的one-hot问题是一样的,原因是我们把北京和上海当成完全两个不同的东西,但是我们希望它能知道北京和上海是两个很类似的东西。
通过把一个词表示成一个低维稠密的向量就能解决这个问题,通过上下文,模型能够知道北京和上海经常出现在相似的上下文里,因此模型能用相似的向量来表示这两个不同的词。
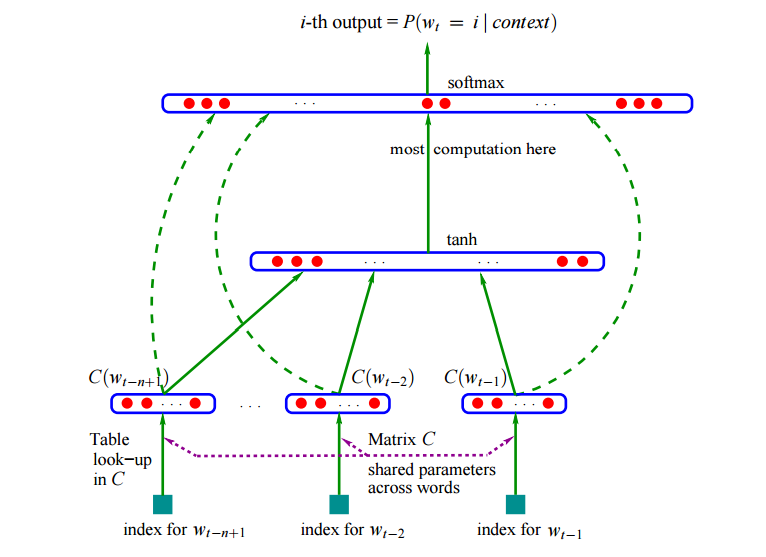
神经网络如下图所示。
这个模型的输入是当前要预测的词,比如用前两个词预测当前词。模型首先用lookup table把一个词变成一个向量,然后把这两个词的向量拼接成一个大的向量,输入神经网络,最后使用softmax输出预测每个词的概率。
Lookup table等价于one-hot向量乘以Embedding矩阵。假设我们有3个词,词向量的维度是5维,那么Embedding矩阵就是(3, 5)的矩阵,比如:
\[\begin{bmatrix} 1.5 & 2.3 & -3.2 & 4.8 & 5.1 \\ 8.3 & 3.3 & 4.1 & -5.3 & 6.8 \\ 3.2 & -4.8 & 5.5 & 16 & -0.7 \end{bmatrix}\]这个矩阵的每一行表示一个词的词向量,那么我们要获得第二个词的词向量,就可以用如下的向量矩阵乘法来提取:
\[\begin{bmatrix} 0 & 1 & 0 \\ \end{bmatrix} \begin{bmatrix} 1.5 & 2.3 & -3.2 & 4.8 & 5.1 \\ 8.3 & 3.3 & 4.1 & -5.3 & 6.8 \\ 3.2 & -4.8 & 5.5 & 16 & -0.7 \end{bmatrix} = \begin{bmatrix} 8.3 & 3.3 & 4.1 & -5.3 & 6.8 \end{bmatrix}\]但是这样的实现并不高效,我们只需要”复制”第二行就可以了,因此大部分深度学习框架都提供了Lookup table的操作,用于从一个矩阵中提取某一行或者某一列。
这个Embedding矩阵不是固定的,它也是神经网络的参数之一。通过语言模型的学习,我们就可以得到这个Embedding矩阵,从而得到词向量。
Word2Vec
我们可以使用语言模型(甚至其它的任务比如机器翻译)来获得词向量,但是语言模型的训练非常慢(机器翻译就更慢了,而且还需要监督的标注数据)。可以说词向量是这些任务的一个副产品,而Mikolov等人提出Word2Vec直接就是用于训练词向量,这个模型的速度更快。
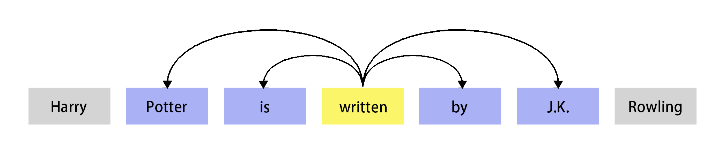
Word2Vec的基本思想就是Distributional假设(hypothesis):如果两个词的上下文相似,那么这两个词的语义就相似。上下文有很多粒度,比如文档的粒度,也就是一个词的上下文是所有与它出现在同一个文档中的词。也可以是较细的粒度,比如当前词前后固定大小的窗口。比如下图所示,written的上下文是前后个两个词,也就是”Portter is by J.K.”这4个词。
除了我们即将介绍的Word2Vec,还有很多其它方法也可以利用上述假设学习词向量。所有通过Distributional假设学习到的(向量)表示都叫做Distributional表示(Representation)。
注意,还有一个很像的术语叫Distributed表示(Representation)。它其实就是指的是用稠密的低维向量来表示一个词的语义,也就是把语义”分散”到不同的维度上。与之相对的通常是one-hot表示,它的语义集中在高维的稀疏的某一维上。
我们再来回顾一下word2vec的基本思想是:一个词的语义可以由它的上下文确定。word2vec有两个模型:CBOW(Continuous Bag-of-Word)和SG(Skip-Gram)模型。我们首先来介绍CBOW模型,它的基本思想就是用一个词的上下文来预测这个词。这有点像英语的完形填空题——一个完整的句子,我们从中“抠掉”一个单词,然后让我们从4个选项中选择一个最合适的词。和真正完形填空不同的是,这里我们不是做四选一的选择题,而是从所有的词中选择。有很多词是合适的,我们可以计算每一个词的可能性(概率)。
它的思路其实是比较简单的,我们下面详细分析它的实现,这里首先介绍上下文是一个词的情况,之后我们再把上下文推广的多个词的情况。读者可能会问上下文只有一个词是什么意思,其实我们把它理解成bi-gram的语言模型就好了,根据前一个词来预测当前词。
上下文(context)是一个词
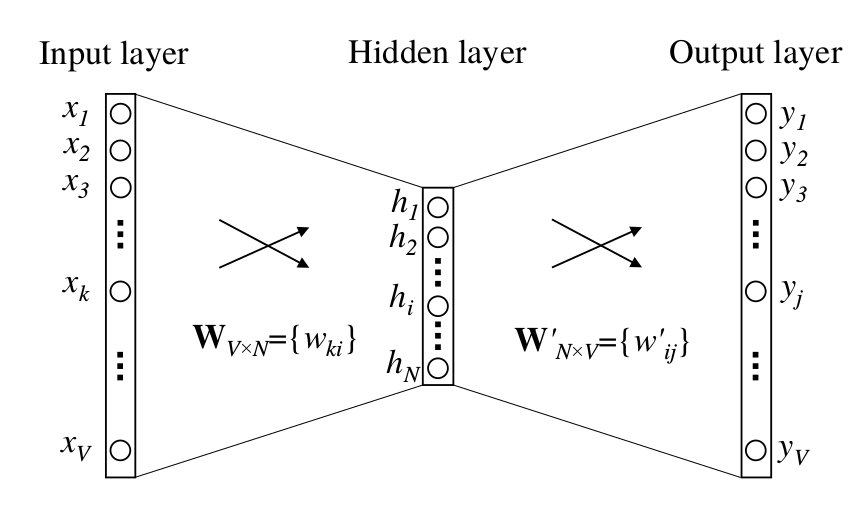
上下文是一个词的CBOW模型如下图所示。这里,词典(Vocabulary)的大小是V(词的个数),隐层的隐单元个数是N。输入层-隐层以及隐层-输出层都是全连接的网络层。输入向量是one-hot的表示,也就是$x_1, x_2, …, x_V$里只有一个1,其余全是0。输入层和隐层的参数是一个$V \times N$的矩阵$W$,$W$的每一行是一个D维的向量$v_w$,这个向量对应输入的词w。更形式化一点,假设输入的词(上下文)是$w$,它对应的下标是k,那么它的one-hot表示x只有第k维是1,其余都是0。因此有:
\[\label{eq:w2v-1} h=W^Tx=W^T_{(k,.)} \equiv W^T_{w_I} \;\;\; \text{(公式1)}\]因此隐层的输出h其实就是输入词$w_I$对应的第k行这个向量,由于x的one-hot特性,我们计算h的时候并不需要真的进行矩阵向量乘法,只需要找到x对应的那一行就好了。在word2vec的隐层,我们一般不使用激活函数。
隐层到输出层的参数矩阵是一个$N \times V$的矩阵$W’$(注意这里W’不是转置的意思,只是表示和W不同第一个矩阵而已),使用它我们可以计算输出第j个词的得分$u_j$为:
\[\label{eq:w2v-2} u_j=v'^T_{w_j}h \;\;\; \text{(公式2)}\]上式中$v’_{w_j}$是$W’$的第j列。为了输出概率,我们对所有的$u_j$进行softmax:
\[\label{eq:w2v-3} p(w_j|w_I)=y_j=\frac{exp(u_j)}{\sum_{j'=1}^{V}exp(u_{j'})} \;\;\; \text{(公式3)}\]把公式1和2代入公式3得到:
\[\label{eq:w2v-4} p(w_j|w_I)=\frac{exp(v'^T_{w_j}v_{w_I})}{\sum_{j'=1}^{V}exp(v'^T_{w_j'}v_{w_I)}} \;\;\; \text{(公式4)}\]在上式中,$v_w$和$v’_w$是词w的两种向量表示,其中$v_w$来自矩阵$W$的某一行,我们把它叫作输入向量;而$v’_w$来自矩阵$W’$的某一列,我们把它叫作输出向量。我们可以发现:如果输入词$w_I$和输出词$w_j$的词向量的内积比较大,说明它们比较相似,则$p(w_j|w_I)$就较大。
前面介绍了一个词的上下文的CBOW模型的forward计算过程,接下来介绍怎么反向计算梯度。读者可能会有疑惑,这其实是一个很简单的三层全连接网络,梯度的推导前面已经介绍过了,为什么还要再来一次呢?原因有两个:首先是因为这个模型的输入x是one-hot的表示,参数W的梯度有更加简洁的形式;其次是我们需要分析参数W’的梯度涉及到的softmax计算,分析计算量最大的地方在哪里,从而了解为什么要用后面的hierachical softmax或者negative sampling了加速。
首先我们来计算隐层到输出层参数W的梯度。我们的损失函数就是交叉熵损失函数,给定输入$w_I$,输出是$w_O$,假设$w_O$对应的下标是$j^*$,那么损失E的计算公式如下:
\[E=-logy_{j^*}=-u_{j^*}+log\sum_{j'=1}^{V}exp(u_{j'})\]E是$u_j$的函数,我们求E对它的偏导数如下:
\[\frac{\partial E}{\partial u_j}=-t_j+\frac{exp(u_j)}{\sum_{j'=1}^Vexp(u_{j'})}=y_j-t_j \equiv e_j\]上式的推导中,\(u_{j^*}\)对$u_j$求偏导数时,如果\(j=j^*\),那么偏导数是1,否则是0,因此最终的结果可以写出\(\mathbb{1}_{j=j^*}\),我们把它记作$t_j$。而第二项的偏导数log的导数是先把它放到分母里,然后再对它求导,而求和的V项中只有当$j’=j$时才有$u_j$,而指数的导数是它本身,因此分子最后就剩下$exp(u_j)$,最后我们对比一下就能发现,第二项就是$y_j$。最后我们用一个记号$e_j$来表示这个值,e的意思是error,可以发现,$\frac{\partial E}{\partial u_j}$等于模型预测的值$y_j$和实际值(下标为$w_O$对应的\(j^*\)的时候$t_j$值是1,否则是0)的差值。如果这个差值很大,说明我们的模型预测的不好,错误就越大,参数需要做更大的调整;反之说明错误小,不需要调整参数。根据链式法则,我们可以求E对参数$w’_{ij}$的导数:
\[\frac{\partial E}{\partial w'_{ij}}=\frac{\partial E}{\partial u_j} \frac{\partial u_j}{\partial w'_{ij}}=e_j \cdot h_i\]求出之后我们可以用梯度下降算法更新参数$w’_{ij}$:
\[w_{ij}^{\prime (new)} \leftarrow w_{ij}^{\prime (old)} - \eta \cdot e_j \cdot h_i\]其中$\eta$是学习率,$e_j=y_j-t_j$。因为词$w_j$对应的$W’$的第j列,因此我们把它写出向量形式:
\[v_{w_j}^{\prime (new)} \leftarrow v_{w_j}^{\prime (old)} - \eta \cdot e_j \cdot h \;,\;for \; j=1,2,...,V\]上面两式说明,对于每一个训练数据(输入$w_I$和输出$w_O$),我们都要更新所有V个词对应的输出词向量$w’_{w_j}$,这个计算量是非常大的。接下来我们求E对隐层的输出$h_i$的梯度:
\[\frac{\partial E}{\partial h_i}=\sum_{j=1}^{V}\frac{\partial E}{\partial u_j} \frac{\partial u_j}{\partial h_i} \ =\sum_{j=1}^V e_j \cdot w'_{ij} \equiv EH_i\]因为$h_i$会输入给所有的$u_j$,所以根据链式法则对$h_i$的导数是从$h_i$到E的所有路径的求和。E对$h_i$的导数求出来后,我们就可以求E对$w_{ij}$的导数了。在这之前,我们把$h_i$和$w_{ij}$的关系写出来:
\[h_i=\sum_{k=1}^{V}x_k \cdot w_{ki}\]因此我们可以求出:
\[\frac{\partial E}{\partial w_{ki}}=\frac{\partial E}{\partial h_i} \cdot \frac{\partial h_i}{\partial w_{ki}} \ =EH_i \cdot x_k\]我们可以把它写成向量的形式:
\[\frac{\partial E}{\partial W}=x \bigotimes EH^T\]这是一个$V \times N$的矩阵,但是x只有一个元素是非零的,因此$\frac{\partial E}{\partial W}$只有那一行是非零的。因此我们的梯度下降算法对于W只需要更新输入$w_I$对应的那一个(行)向量:
\[v_{w_I}^{(new)} \leftarrow v_{w_I}^{(old)} - \eta EH^T\]多个词的上下文
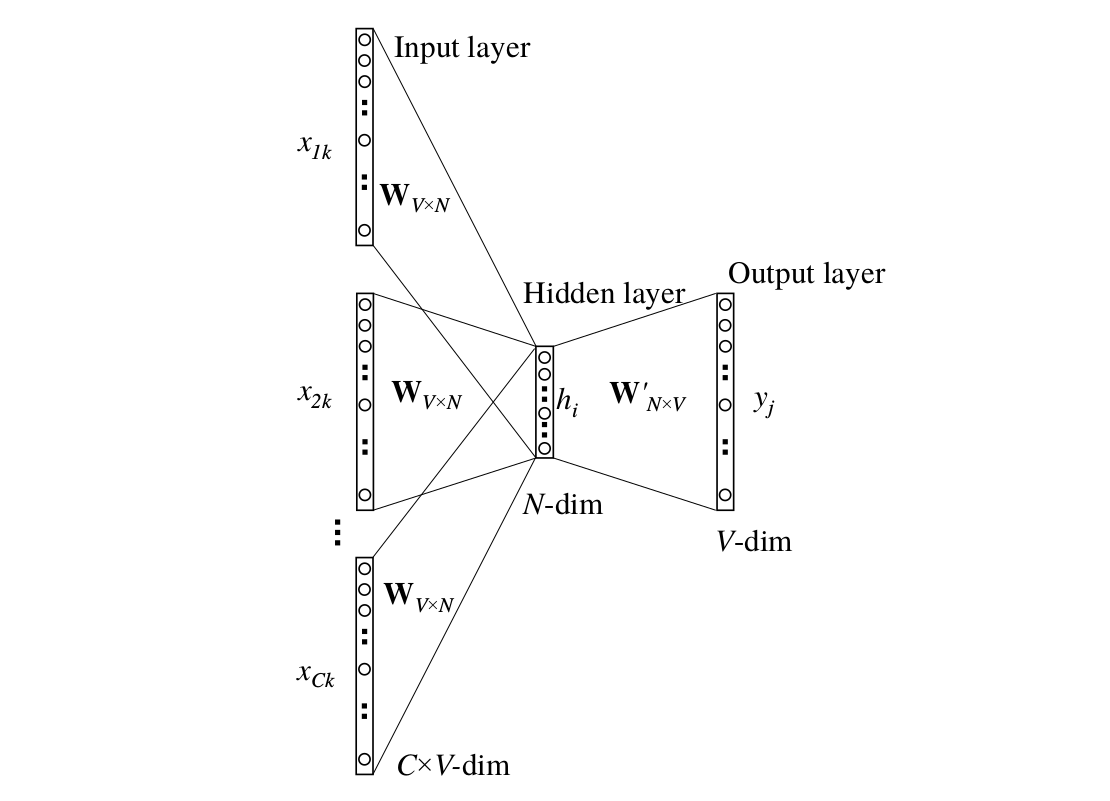
接下来我们把上下文扩展到多个词的情况。模型如下图所示,输入是多个词,我们用一个词周围的多个词来预测这个词。
和前面类似,我们用one-hot的方式来表示每一个词,那怎么把多个向量输入到CBOW模型中呢?这里使用了最简单的平均:
\[h=\frac{}{C}W^T(x_1+x_2+...+x_C)=\frac{1}{C}(v_{w_1}+v_{w_2}+...+v_{w_C})^T\]我们发现一旦h计算出来之后,后面的计算和一个词的完全相同,因此我们可以计算损失:
\[E=-logy_{j^*}=-u_{j^*}+log\sum_{j'=1}^{V}exp(u_{j'})=-v_{w_O}^{\prime T} \cdot h + log\sum_{j'=1}^{V}exp(v_{w_j}^{\prime T}\cdot h)\]这和上式是完全一样的,唯一不同的是h的计算方法不同。因此输出向量的梯度更新公式是完全一样的:
\[w_{ij}^{\prime (new)} \leftarrow w_{ij}^{\prime (old)} - \eta \cdot e_j \cdot h_i\]输入向量的梯度更新稍微有点区别,之前值更新$w_I$输入向量,这里需要更新输入的所有上下文$w_{I,c}$的输入向量,当然还要乘以一个$\frac{1}{C}$: \(v_{w_{I,c}}^{(new)} \leftarrow v_{w_{I,c}}^{(old)} - \frac{1}{C} \cdot \eta \cdot EH^T, \;for \; c=1,2,...,C\) 在上式中,$v_{w_{I,c}}$是要预测的词的第c个上下文词。比如句子是”it is a good day”,假设context窗口是2,单词”a”的context是”it”、”is”、”good”、”day”。而$EH_i=\frac{\partial E}{\partial h_i}$,计算公式为上式。
Skip-Gram模型
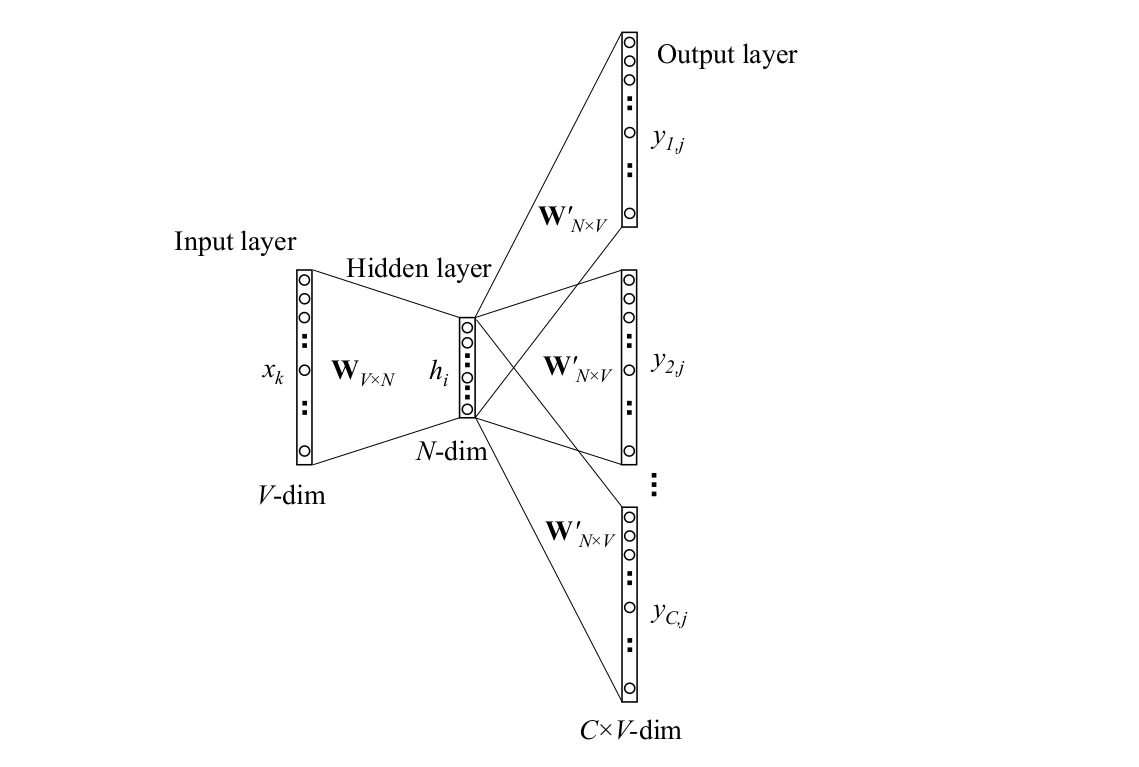
Skip-Gram模型如下图所示,它用一个词来预测它的上下文。比如前面”it is a good day”的例子,比如当前词是”a”,我们会预测它周围4个词的概率。
这个模型看起来比较复杂,但是实际上它非常简单,和前面介绍过的一个词的CBOW很类似。读者可能会奇怪怎么用一个词预测多(C)个词呢?其实我们可以简化一下,一次预测一个词,然后预测C次。虽然我们预测了C次,但是预测的公式都是一个:
\[p(w_{c,j}=W_{O,c}|w_I)=y_{c,j}=\frac{exp(u_{c,j})}{\sum_{j'=1}^{V} exp(u_{c,j'})}\]上式中,$w_I$是输入词,$w_{O,c}$是需要预测的第c个输出。而$u_{c,j}$是预测第c个词的为j的概率,它的公式为:
\[u_{c,j}=u_j=v_{w_j}^{\prime T} \cdot h, for c=1,2,...,C\]从上式可以看出,$u_{c,j}$的计算其实与下标c是无关的。接着我们可以计算损失:
\[\begin{split} E & =-log p(w_{O,1}, w_{O,2}, ..., w_{O,C}|W_I) \\ & =-log \prod_{c=1}^{C}\frac{exp(u_{c,j_c^*})}{\sum_{j'=1}^{V}exp(u_{j'})} \\ & =\sum_{c=1}^{C}u_{j_c^*}+C \cdot log \sum_{j'=1}^{V}exp(u_{j'}) \end{split}\]上式中\(j_c^*\)是要预测的第c个词的下标。到这里我们可以发现Skip-Gram和前面一个词的CBOW非常类似,只不过E是多个词的损失的求和而已。具体的偏导数求导我们就不赘述了。在实际计算中,我们可以把一次预测C个词分解成一次预测一个词然后预测C词。这两者有一点细微的区别——前者的C个词的forward是一次计算出来的,然后用C个词的损失去计算梯度;而后者会计算C次forward,然后backward也会计算C词,而且在这C词的过程中参数W和W’已经发生了细微的变化。当然后者的计算效率较低,但是可以让我们更好的一个词的CBOW对比。
计算的效率
以一个上下文的CBOW为例,对于每一个训练数据,我们计算损失的时候需要对所有V个词都计算它的输出向量和h的内积。而反向更新参数时,我们需要更新输入词对应的输入向量一次,参考上式。而对于输出向量,我们需要更新所有V个词的输出向量,如上式所示,这个计算量是很大的,在实际的数据中,V通常都是几万甚至几十万。下面我们介绍加速计算的一些技术。
Hierarchical Softmax
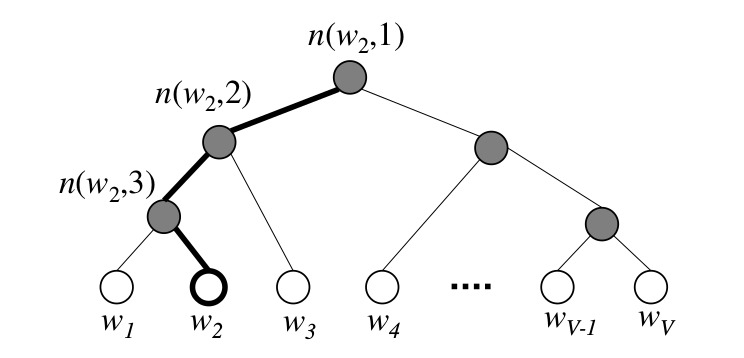
Hierarchical Softmax用一棵二叉树(为了效率通常使用Huffman树)来表示词典里的所有词。这棵树有V个叶子节点,分别对应V个词,它是二叉树,因此有V-1个中间节点。每一个叶子节点都有从树根到它的唯一路径,而输出的概率可以根据这条路径计算出来。我们以下图为例来解释一些术语。比如词$w_2$,$L(w_2)=4$表示这个词对应的叶子节点的路径上的节点的个数。$n(w,j)$表示这条路径第j个节点,比如图中$n(w_2,1)$是根节点,$n(w_2,2)$是第二层最左边的节点,…。
在Hierarchical Softmax里,只有V-1个中间节点对应一个词向量$v’_{n(w,j)}$(普通的Softmax是V个词)。叶子节点(真正的词)根据这个路径来计算概率,计算公式为:
\[p(w)=\prod_{j=1}^{L(w)-1}\sigma([\![ n(w,j+1)=ch(n(w,j)) ]\!] \cdot v_{n(w,j)}^{\prime T} \cdot h)\]上面这个式子有一些复杂,我们仔细来阅读一下。首先$ch(n(w,j))$是节点$n(w,j)$的左孩子,因此$n(w,j+1)=ch(n(w,j))$表示路径上的第j+1个节点是第j个节点的左孩子。$[![ x ]!]$定义如下:
\[[\![ x ]\!] = \begin{cases} 1 & \text{如果}x\text{为true} \\ -1 & \text{否则} \end{cases}\]我们用上图所示的$w_2$为例来展开上面的公式:
\[p(w_2) = \sigma(v_{n(w_2,1)}^{\prime T} \cdot h) \cdot \sigma(v_{n(w_2,2)}^{\prime T} \cdot h) \cdot \sigma(-v_{n(w_3,1)}^{\prime T} \cdot h)\]用自然语言来描述上面的公式其实比较简单:从路径的第二层开始,如果这个节点是父亲的左孩子,那么把它父亲节点的向量乘以h然后用$\sigma$激活($\sigma(v_{parent}^T \cdot h)$);否则如果是父亲的右孩子,则把它父亲节点的向量乘以h后再乘以-1再激活($\sigma(-v_{parent}^T \cdot h)$)。然后把这些值全部乘起来就是概率。
为了使得公式看起来简单,在没有歧义的地方我们用$[![ ]!]\text{表示}[![ n(w,j+1)=ch(n(w,j)) ]!]$,用\(v'_j\)表示\(v_{n(w,j)}^{\prime}\)。
这里我们不证明,读者可以验证一下所有叶子节点的概率加起来是1。根据这个概率我们可以计算损失:
\[E=-log p(w=w_O|w_I) \prod_{j=1}^{L(w)-1} \sigma([\![ ]\!] v_j^{\prime T} \cdot h)\]我们可以来分析一下计算E的复杂度的变化。根据上式计算E需要遍历V个词,它的复杂度是O(V),而现在我们只需要变量L(w)个词,L(w)通常是O(logV)的复杂度。接下来我们简单的推导一下梯度,验证梯度的更新的复杂度也是下降到O(logV)的。
\[\begin{split} \frac{\partial E}{\partial (v'_j)^Th} & = (\sigma([\![ ]\!] (v'_j)^Th )-1) [\![ ]\!] \\ & = \begin{cases} \sigma((v'_j)^Th )-1 & ([\![ ]\!]=1) \\ \sigma((v'_j)^Th ) & ([\![ ]\!]=-1) \end{cases} \\ & = \sigma((v'_j)^Th ) - t_j \end{split}\]接下来我们求E对n(w,j)对应的向量的梯度:
\[\frac{\partial E}{\partial v'_j}=\frac{\partial E}{\partial (v'_j)^Th} \frac{\partial (v'_j)^Th}{\partial v'_j} \\ =(\sigma((v'_j)^Th ) - t_j) \cdot h\]我们可以用梯度下降来更新参数:
\[v_j^{\prime (new)} \leftarrow v_j^{\prime (old)} -\eta (\sigma((v'_j)^Th ) - t_j) \cdot h, j=1,2,...,L(w)\]从上面的参数更新公式可以看出,对于一个训练数据,我们只需要更新路径上的节点对应的v,因此时间复杂度变为O(logV)。最后我们计算E对h的梯度:
\[\begin{split} \frac{\partial E}{\partial h} & = \sum_{j=1}^{L(w)-1} \frac{\partial E}{\partial (v'_j)^Th} \frac{\partial (v'_j)^Th}{\partial h} \\ & = \sum_{j=1}^{L(w)-1} (\sigma((v'_j)^Th ) - t_j) \cdot v'_j \equiv EH \end{split}\]计算EH的复杂度也是O(logV),有了EH之后,输入向量的参数更新就和之前一样了,它只涉及输入词对应的那个向量。
Negative Sampling
在实际应用中,我们通常使用这个算法。它的思路比Hierarchical Softmax更加简单直接——既然计算所有词的softmax太慢,那么我们就只采样一部分来计算!
很显然,需要预测的(Positive)词肯定需要计算,我们还需要采样一些Negative的词(也就是错误预测的词),这就是Negative Sampling的名字由来。这个采样的概率分布我们把它叫作噪音分布$P_n(w)$,在Mikolov的word2vec实现里使用的$P_n(w)=(p(w))^{3/4}$,其中$p(w)$是unigram的概率(基本上就是词频)。有了采样的Negative词,我们就可以和之前一样计算softmax了(认为其它的词的softmax很小,趋近于0)。不过在word2vec的实现里,作者使用了一种更加简单的损失函数。这虽然和softmax不完全等价,但是也能学到不错的word embedding,这个新的损失函数定义为:
\[E=-log \sigma((v'_{w_O})^Th)-\sum_{w_j \in \mathcal{W}_{neg}} \sigma(-(v'_{w_j})^Th)\]其中,$w_O$是输出的词,$v’_{w_O}$是它对于的输出词向量。h是隐层的输出。\(\mathcal{W}_{neg} = \{ w_{j} \vert j=1,2,...,K \}\)是K个negative样本。
我们来简单分析一下这个损失函数:对于正样本$w_O$,$(v’_{w_O})^Th$越大,则E越小;而对于负样本正好相反。这和之前的softmax是一致的。接下来我们推导一下Negative Sampling时的梯度。
\[\begin{split} \frac{\partial E}{\partial (v'_{w_j})^Th} & = \begin{cases} \sigma((v'_{w_j})^Th )-1 & \text{如果}w_j=w_O \\ \sigma((v'_{w_j})^Th ) & w_j \in \mathcal{W}_{neg} \end{cases} \\ & = \sigma((v'_{w_j})^Th ) - t_j \end{split}\]在上式中,如果$w_j$是输出的词,那么$t_j$就是1,否则就是0。接着我们计算E对$v’_{w_j}$的梯度:
\[\frac{\partial E}{\partial (v'_{w_j})} = \frac{\partial E}{\partial (v'_{w_j})^Th} \frac{ \partial (v'_{w_j})^Th }{\partial v'_{w_j} } \\ =(\sigma((v'_{w_j})^Th ) - t_j) h\]接着我们就可以用梯度下降更新参数:
\[v_{w_j}^{\prime (new)} \leftarrow v_{w_j}^{\prime (old)} -\eta (\sigma((v'_{w_j})^Th ) - t_j) \cdot h\]上式我们只需要更新采样的词对应的v就可以了,因此比原来的softmax的复杂度要低得多。同样我们可以计算E对h的梯度:
\[\begin{split} \frac{\partial E}{\partial h} & = \sum_{w_j \in \{w_O\} \cup \mathcal{W}_{neg}} \frac{\partial E}{\partial (v'_{w_j})^Th} \frac{ {\partial (v'_{w_j})^Th} }{\partial h} \\ & = \sum_{w_j \in \{w_O\} \cup \mathcal{W}_{neg}} (\sigma((v'_{w_j})^Th ) - t_j) v'_{w_j} \equiv EH \end{split}\]计算EH也同样只需要计算${w_O} \cup \mathcal{W}_{neg}$里的词对应的向量。而有了EH之后,参数W的更新和之前完全一样。
代码
原始的实现
Mikolov最早的实现在google code,不过google code已经死掉了,读者可以在这里下载到导出的版本。
安装:
$cd src
$make
安装后的二进制程序在bin目录下。
训练
我们需要准备数据,作者使用的是自己抓取的百科网页,由于版权原因不能提供,读者可以这里下载他人提供的数据。我们需要对文本进行预处理,主要是分词,词之间用空格分开。
./bin/word2vec -train baike.txt -output baike.bin -size 200 -window 3 -negative 10 -sample 1e-4 -threads 20 -binary 1 -iter 30
我们需要提供文件baike.txt。训练的模型存放在baike.bin里。读者可以不带参数的运行,默认会打出所有的选项,这里介绍经常需要修改的选项。
- size 词向量的维度,默认100,这里设置为200。
- window 窗口的大小,默认是5,这里设置为3。
- negative 10 使用Negative Sample算法,设置负样本的个数为10
- sample 对高频词进行下采样。这里是1e-4
- threads 线程数,根据机器进行设置
- binary 输出二进制格式的模型
- iter 迭代次数
测试
训练好了我们来测试一下类比实验:
$ ./bin/word-analogy baike.bin
Enter three words (EXIT to break): 湖南 长沙 河北
Word: 湖南 Position in vocabulary: 2720
Word: 长沙 Position in vocabulary: 2394
Word: 河北 Position in vocabulary: 2859
Word Distance
------------------------------------------------------------------------
石家庄 0.900409
保定 0.888418
邯郸 0.857933
廊坊 0.851938
邢台 0.851816
唐山 0.843865
我们看到确实它学到了长沙和湖南的关系等于石家庄与河北的关系,用向量来说就是:
湖南-长沙=河北-石家庄
接下来找一个词最近的词:
$ ./bin/distance baike.bin
Enter word or sentence (EXIT to break): 北京
Word: 北京 Position in vocabulary: 373
Word Cosine distance
------------------------------------------------------------------------
上海 0.827013
天津 0.781236
广州 0.737348
沈阳 0.721798
成都 0.711291
南京 0.706751
深圳 0.706011
ngram2vec
除了作者最原始的实现,网上也有许多其它实现。如果读者想使用现成的词向量,可以参考Chinese-Word-Vectors。 里面预训练好了很多词向量(包括N-Gram的向量),训练工具在这里。
- 显示Disqus评论(需要科学上网)