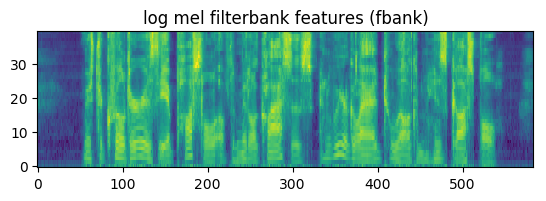
这个模块介绍语音信号的处理，也就是把输入的wav文件变成特征向量的序列。完全不熟悉的读者可以先阅读MFCC特征提取。更多本系列文章请点击微软Edx语音识别课程。
目录
Introduction
视频——模块2内容简介
欢迎来学习模块2，这里我们会介绍信号处理和特征提取。或者说，计算机怎么把声音变成一个个的小块，以便于计算机处理。因此这里我们会学习语音的信号处理。
因此这个模块里，我们会看看语音的传输和录制。语音是怎么从嘴里发出，然后通过空气传播，最后被麦克风录制。我们会看看语音信号被计算机录制，我们也会学习到语音是时变的信号，也就是说我们在发不同的音时，信号的特征会发生很大的变化。我们会使用短时频谱分析的方法来分析语音信号。
Background
语音信号是一种波，它通过空气传播然后被麦克风捕获，麦克风把波的声压转换成电信号。通过对电信号进行采样就可以得到一个离散时间的波形文件。音乐的采样率通常是44,100Hz(或者说每秒钟44,100个采样点)。根据Nyquist定理，频率低于22,050Hz的部分都可以从样本中恢复。语音信号的频率范围通常更窄(低于8000Hz)因此通常使用16,000Hz的采样率。因为电话和手机的带宽限制在3400Hz，因此对于电话语音我们通常使用8000Hz的采样率。
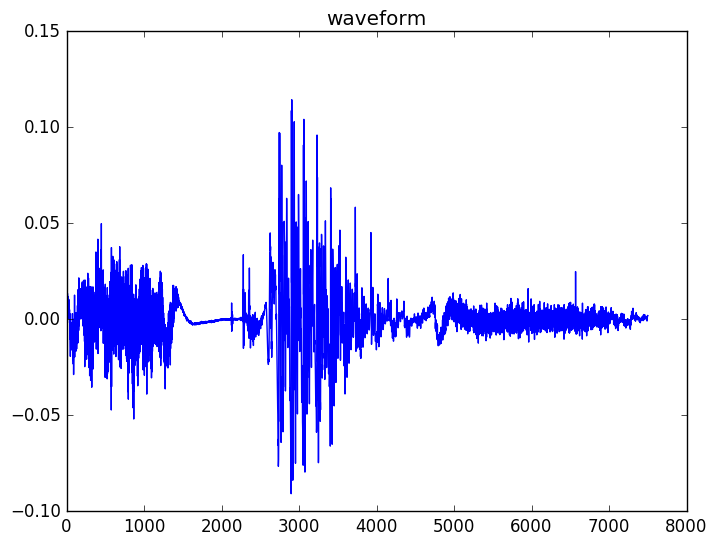
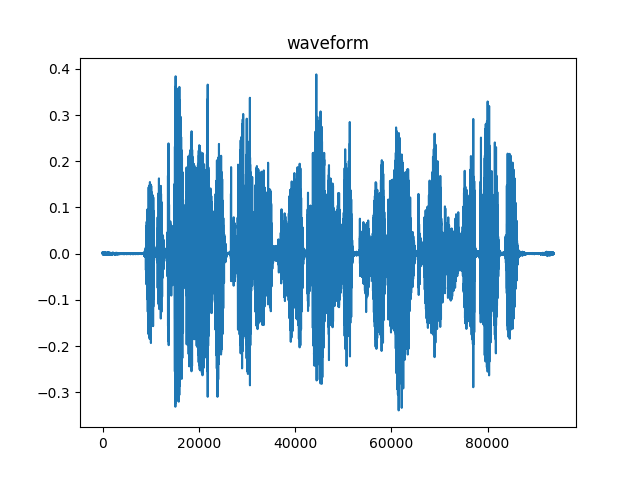
一个典型的波形如下所示，这是句子”speech recognition is cool stuff”的波形。
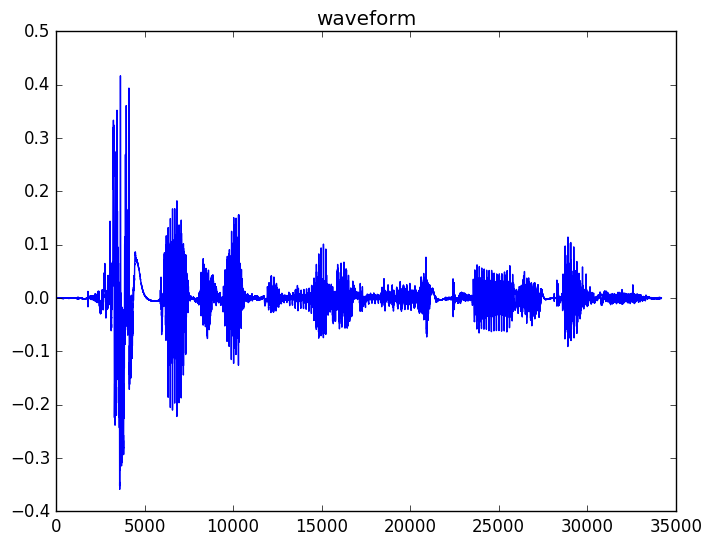图：句子”speech recognition is cool stuff”的波形
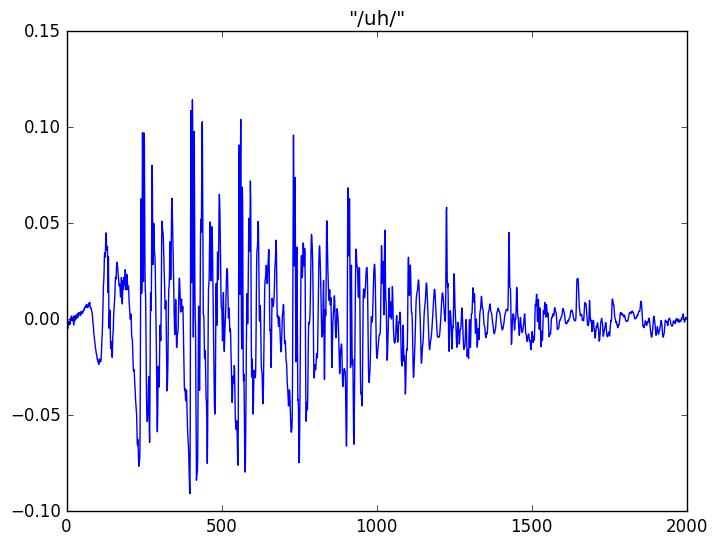
回忆一下模块1，那里我们讨论了浊音音素和清音音素。如果我们观察最后一个词”stuff”，我们会发现它有3个部分组成，首先是开始的清音”st”，中间是浊的元音”uh”，最后是清音”f”。你可以看到清音更像随机的噪声，而浊音因为有声带周期性的振动可以看到明显的周期特性。
图：stuff的波形
如果我们把浊的元音”uh”放大了来看，则它的周期特性更加清晰。它的周期特性来源于声带的周期性振动。
图：uh的波形
通过观察波形，我们发现有两个因素会影响波形的特征。1) 声带的激励引起通过声道和口腔的气流 2)声道(包括喉、口腔和鼻腔等)在发不同声音时的不同形状。
比如，我们可以发现”st”和”f”都很像噪声因为它不像浊音那样有从肺部呼出经过声带的周期性激励。而”uh”由于有声带的周期性激励而表现出明显的周期特征。因此，对于同一个说话人，不同的元音的周期性是相似的(因为同一个人的声带的振动的周期基本是不变的)，但是声道的不同形状导致了不同的声音，从而他人可以分辨出他实在发不同的声音。类似的，两个不同的人在发同一个元音的时候，虽然他们的周期性不同，但是他们在发同一个音的声道(包括喉、口腔、舌头、牙齿等等)的形状是类似的，所以听的人知道他们发的是同一个音。
因此语音的产生过程通常使用信号处理中的source-filter模型。source就是声带产生的周期性信号，它在经过声道时被声带这个filter过滤，最终形成我们听到的声音。这个filter是线性时变系统，因为不同的音素对于不同的声道形状，也就是不同的滤波器。source-filter模型在语音识别、语音合成、分析和编码等很多地方都有应用。有很多方法来估计source信号和filter的参数，比如著名的线性预测编码(LPC)方法。
对于语音识别来说，source并不重要，音素分类主要依赖与声道的形状，也就是source-filter模型的filter部分。因此source信号的部分会被忽略或者丢弃掉。因此语音识别的特征提取过程主要用于提取发不同音时不同filter形状的这些特征。
特征提取——短时傅里叶分析
从波形文件可以发现语音信号是不平稳(non-stationary)的信号。这意味着它的统计特性是会随着时间变化的。因此，为了更好的分析语音信号，我们需要分析很小的一个时间窗口的信号，对于这样小的一个时间范围可以认为它是平稳的信号。这样，我们会分析一系列很短的一帧信号，相邻的帧还会有重合。在语音识别中，我们通常的一帧信号为25ms，帧移是10ms。因此一秒的信号会有10帧。
因为我们是抽取一个很长的连续信号的一小块，因此需要小心的处理窗口的边界。通常我们会使用Hamming窗。假设m是帧的下标，n是样本的下标，L是帧的大小(样本个数)，N是帧移(样本数)，那么每一帧的数据和原始信号的关系如下：
\[x_m[n] = w[n] x[mN+n], n=0, 1, \ldots, L-1\]这里𝑤[𝑛]是窗函数。
然后我们可以使用离散傅里叶变换(DFT)把每一帧信号变换到时域。
\[X_m[k]=\sum_{n=0}^{N-1}x_m[n]e^{-j 2 \pi k n/N}\]不熟悉信号处理的读者可以这样的简单理解，上面的公式把一个离散的时域信号$x_m[0],…x_m[N-1]$变换成频域的信号$X_m[0],…$。读者可能会问频域的信号有多少个点呢？我们可以简单的计算一下：
\[\begin{split} X_m[k+N] & =\sum_{n=0}^{N-1}x_m[n]e^{-j 2 \pi (k+N)n/N} \\ & =\sum_{n=0}^{N-1}x_m[n]e^{-j 2 \pi kn/N}e^{-j2\pi n} \\ & =\sum_{n=0}^{N-1}x_m[n]e^{-j 2 \pi kn/N}=X_m[k] \end{split}\]这里的需要知道欧拉公式： \(e^{jx}=cosx+jsinx\) 这里的j是虚数单位。
从上式可以发现$X_m[k+N]=X_m[k]$，因此我们最多需要频域的N个点就足够了，再多就是重复的了。而如果时域信号x是实数的话，我们还有：
\[\begin{split} X_m[N-k] & = \sum_{n=0}^{N-1}x_m[n]e^{-j 2 \pi (N-k)n/N} \\ & = \sum_{n=0}^{N-1}x_m[n] (cos(2\pi (N-k)n/N)-jsin(2\pi (N-k)n/N)) \\ & = \sum_{n=0}^{N-1}x_m[n] (cos(2\pi kn/N) +j sin(2\pi kn/N) ) \end{split}\]而
\[\begin{split} X_m[k] & = \sum_{n=0}^{N-1}x_m[n]e^{-j 2 \pi kn/N} \\ & = \sum_{n=0}^{N-1}x_m[n] (cos(2\pi kn/N) -j sin(2\pi kn/N) ) \end{split}\]因为$x_m[n]$是实数，所以$X_m[N-k]$和$X_m[k]$是共轭对称的(实部相同，虚部相差一个符号)，所以它们的模是相同的。对于语音信号来说，$x_m[n]$是实数，而且我们后续的分析只关注复数的模，因此我们只需要知道变换的前N/2+1个点就行。比如N=512，那么我们只需要0,1,…,256这257个点就行。后面的代码部分我们会发现这一点。
另外一点：如果输入是N个点，那么做DFT时我们通常只需要做N点DFT就行，但是为了使用更快的快速傅里叶变换(FFT)算法，它要求变换的点是2的幂，因此我们需要找到大于等于N的最小的2的幂。这说起来有点绕，其实很简单，比如输入的一帧为432个点，那么我们需要做512点的DFT而不能是256点的。
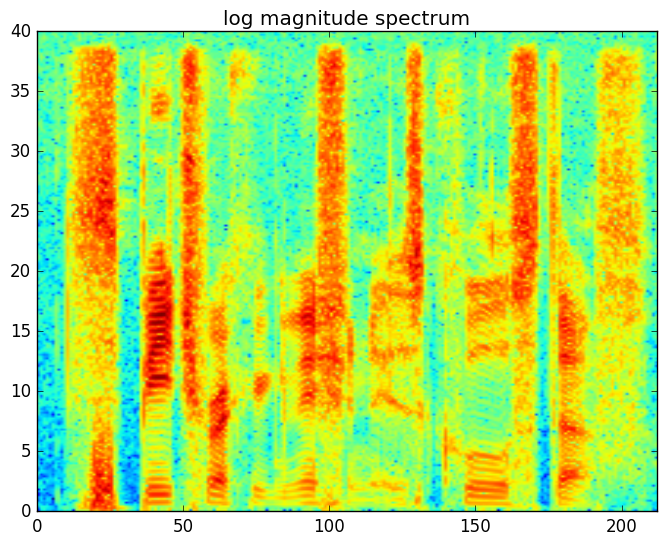
语谱图(spectrogram)是一个二维的图，它的横坐标是帧下标，纵坐标是不同频率的log幅度(复数的模)或者叫能量，频率的范围是从0Hz到Nyquist频率(也就是采样频率的一半)。下图是”speech recognition is cool stuff”这句话的语谱图。在语谱图中颜色越深(比如红色)，对应频率的能量越大。
图：语谱图
Mel filtering
从语谱图可以看出清辅音在高频部分有较多能量(所谓高频能量多也就是有很多剧烈的变化)，而元音(都是浊音)在低频部分有较多的能量。另外我们发现不同的元音会有不同的水平的线，这是浊音的和弦结构(harmonic structure)，它是区分不同元音的重要特征。
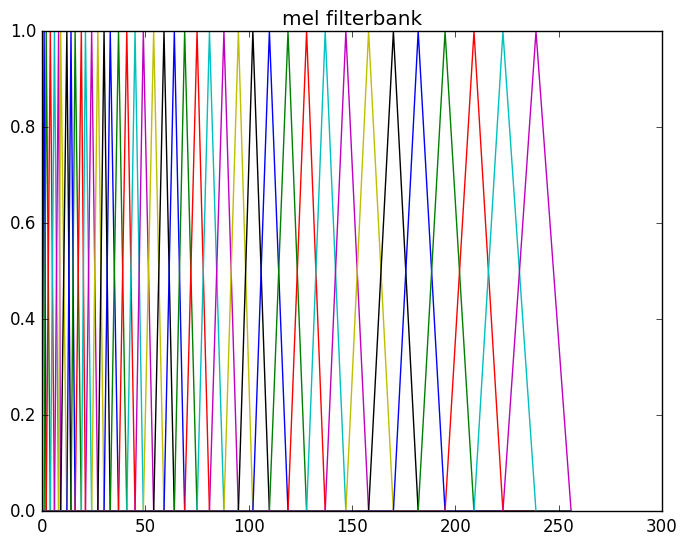
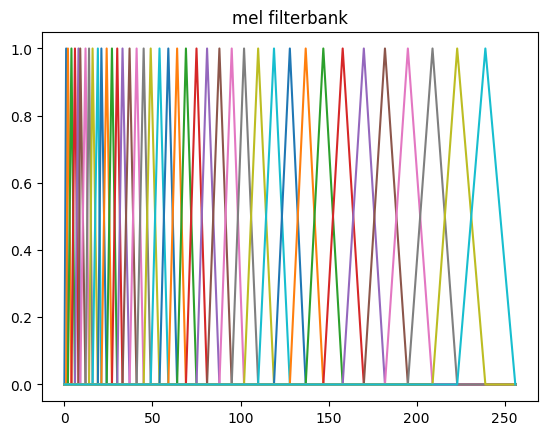
浊音的弦结构和轻音的随机噪声都会引擎语谱图的变化，为了消除这些变化(而保留主要的信息)，我们需要对频谱做平滑。我们会对它使用filterbank，这是受了听觉系统的启发。人类的听觉系统对于低频的声音的区分度比较大而高频的区分度较小，比如400Hz和450Hz相差50Hz，1000Hz和1050Hz也是相差50Hz，但是我们听起来前两者的差别比较大而后两者的差别比较小。为了模拟这种效果，我们会使用滤波器组，每一个滤波器会提取某一个区间内的能量。而且提取高频部分的滤波器会比较”宽”而低频部分比较”窄”。那么具体每个滤波器多宽呢？最常见的是美尔(mel)滤波器组，也就是让它在美尔尺度上是线性的，也就是滤波器在美尔尺度上是等宽的，但是在频率尺度上则是高频的宽低频的窄。
图：美尔滤波器组
比如上图所示，我们的美尔滤波器组通常有40个滤波器，每个都是一个三角形的滤波器，它提取某一个区间的频谱的能量。而且区间的频率越高，滤波器就越宽(但是如果把它变换到美尔尺度则是一样宽的)。为了计算方便，我们通常把40个滤波器用一个矩阵来表示，这个矩阵有40行，列数就是傅里叶变换的点数。通常每一行只有一个区间是一个三角形(一半上升的直线，一半下降的直线)，其余的值都是零。有了这个矩阵，则我们可以计算美尔滤波器输出的第p(共40)个系数：
\[X_{\tt{mel}}[p] = \sum_k M[p,k] \left|X_m[k]\right|\]通常的美尔滤波器组有40个滤波器，但是个数也可以是其它值。
Log压缩
特征提取的最后一步是对每个美尔滤波器的特征(系数)取对数。这也是模拟人类听觉系统对信号的动态范围进行压缩的过程。最终得到的特征一般叫做滤波器组(filterbank)系数/特征。
对于传统的HMM-GMM系统，我们还会对滤波器组系数进行DCT来提取包络和去掉相关性。但是对于DNN的声学模型，直接使用滤波器组的特征效果更好，因此这里我们只提取滤波器组系数。
图：取log后的美尔滤波器特征
其它处理
在上面的步骤之前还有一些常见的预处理步骤，包括：
- Dithering
- 增加很小的随机噪声，这样可以防止特征计算的数学问题(比如对零取log)，因为加了随机噪声后频率的每一个部分都有值。
- DC-removal
- 去除直流分量(也就是使得信号的均值为零)
- Pre-emphasis
- 提升原始信号的高频部分。因为语音在低频部分的能量较大和高频较小，这样高低频的能量差别太多，通过下面的公式可以实现提升高频部分的能量。
feature normalization
通常通信的信道会有一些固定的噪声，比如麦克风的频域响应可能不是均匀的。这些信道的噪声的效果一般是对于频域的信号做一个乘法(放大或者缩小某些频率的信号)，对应到时域就是信号的卷积。
因此我们可以把通道的效应(effects)建模成常量的滤波器：
\[X_{t,{\tt obs}}[k] = H[k] X_t[k]\]对上式取模得到：
\[\left|X_{t,{\tt obs}}[k]\right| = \left|H[k]\right|\left|X_t[k]\right|\]然后我们可以对两边取对数就得到第k个系数，然后对时间t进行累加，得到第k个系数的平均值：
\[\begin{split} \mu_{\tt obs} & =\frac{1}{T}\sum_t \log\left(\left|X_{t,{\tt obs}}[k]\right|\right) \\ & =\frac{1}{T}\sum_t \log\left(\left|H[k]\right|\left|X_t[k]\right|\right) \\ & =\frac{1}{T}\sum_t \log\left(\left|H[k]\right|\right)+\frac{1}{T}\sum_t \log\left(\left|X_t[k]\right|\right) \end{split}\]如果我们假设信道的频率响应是常量，而且语音信号是均值为零。则上式可以简化为：
\[\mu_{tt obs}=\log\left(\left|H[k]\right|\right)\]也就是信道的频率响应等于观察log系数的平均值，因此对于每个信号，我们减去它就可以得到原始信号的log系数。
图：进行均值归一化之后的fbank特征
lab2
Instructions
在这个实验里，我们会编写一些核心的函数来实现音频波形文件的特征提取。我们的程序会把一个录音文件变成取log的FBANK特征向量的序列。
基本的特征提取步骤包括：
- Pre-emphasis
- 把语音信号切分成有重叠部分的帧
- 对于每一帧：
- 加窗
- 就是这一帧的幅度谱(magnitude spectrum)
- 对幅度谱使用美尔滤波器组滤波得到FBANK系数
- 对FBANK系数取log
在这个实验里，你需要修改speech_sigproc.py。这个文件包含了一个只完成部分的FrontEnd类，这个类用于实现特征提取。上面的第二步(把信号分帧)的代码已经实现了，此外构造美尔滤波器组的函数也已经实现了，其余的代码需要你自己完成。
有两个可以运行的python脚本。第一个是M2_Wav2Feat_Single.py，这个脚本读入一个预先指定的音频文件，提取特征，然后输出成HTK的格式。
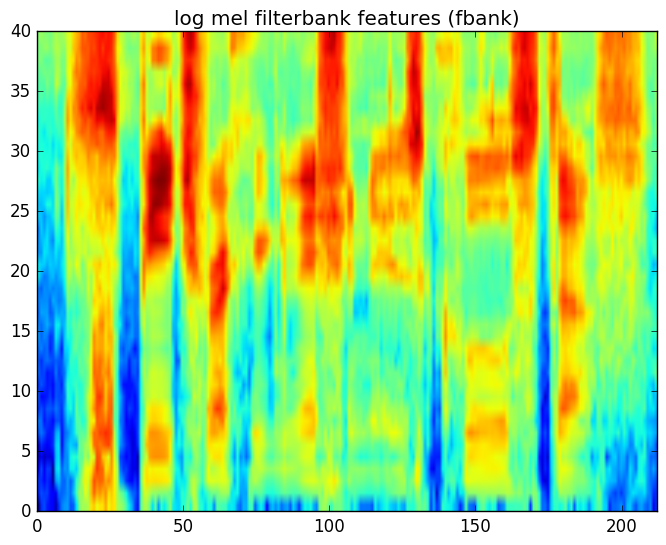
在实验的第一部分，你需要完成FrontEnd类中缺失的代码并且修改M2_Wav2Feat_Single.py来绘制三个图：
- 波形图
- 美尔滤波器组
- Log的FBANK系数
我们也提供了正确程序生成的三个图，因此通过对比这三个图我们可以验证程序是否正确。
图：波形图
图：美尔滤波器组
图：Log的FBANK系数
如果你的代码没有问题了，那么就可以使用M2_Wav2Feat_Batch.py来给librispeech的训练、开发和测试数据提取特征，这些特征会在后面的实验中用到。
$ python M2_Wav2Feat_Batch.py –set train
$ python M2_Wav2Feat_Batch.py –set dev
$ python M2_Wav2Feat_Batch.py –set test
对于训练集，除了提取特征之外还会生成feat_mean.ascii和feat_invstddev.ascii，分别表示训练数据的特征的均值和方差(方差的逆)，这些值在后面的声学模型训练时需要用到。
代码阅读和参考实现
请读者一定要自己想办法实现上面的代码，如果实在完成不了再参考本节内容，否则如果直接就看参考代码不会有太大收获。完整代码在这里。
__init__函数
def __init__(self, samp_rate=16000, frame_duration=0.025, frame_shift=0.010,
preemphasis=0.97, num_mel=40, lo_freq=0, hi_freq=None,
mean_norm_feat=True, mean_norm_wav=True, compute_stats=False):
self.samp_rate = samp_rate
self.win_size = int(np.floor(frame_duration * samp_rate))
self.win_shift = int(np.floor(frame_shift * samp_rate))
self.lo_freq = lo_freq
if (hi_freq == None):
self.hi_freq = samp_rate//2
else:
self.hi_freq = hi_freq
self.preemphasis = preemphasis
self.num_mel = num_mel
self.fft_size = 2
while (self.fft_size<self.win_size):
self.fft_size *= 2
self.hamwin = np.hamming(self.win_size)
self.make_mel_filterbank()
self.mean_normalize = mean_norm_feat
self.zero_mean_wav = mean_norm_wav
self.global_mean = np.zeros([num_mel])
self.global_var = np.zeros([num_mel])
self.global_frames = 0
self.compute_global_stats = compute_stats
这个函数是FrontEnd类的构造函数，主要传入提取特征的一些参数：
- samp_rate 采样率，默认16000
- frame_duration 帧长，默认0.025s，也就是25ms
- frame_shift 帧移，默认0.010s，也就是10ms
- preemphasis preemphasis系数，默认0.97
- num_mel FBANK滤波器组的滤波器个数，默认40
- lo_freq 频率的最小值，默认0
- hi_freq 频率的最大值，默认None，如果None则使用Nyquist频率(sample_rate的一半)
- mean_norm_feat 是否对特征进行均值归一化，默认True
- mean_norm_wav 是否对特征进行方差归一化，默认True
- compute_stats 是否统计所有数据的均值和方程，默认False
代码比较简单，大部分都是把参数保存到self里，下面的代码是计算合适的FFT的点数：
self.fft_size = 2
while (self.fft_size<self.win_size):
self.fft_size *= 2
而比较复杂的是make_mel_filterbank()函数，它用来构造滤波器组的，我们来看一下。
def make_mel_filterbank(self):
# 把lo_freq和hi_freq从频率变成mel
lo_mel = self.lin2mel(self.lo_freq)
# 8000->2840
hi_mel = self.lin2mel(self.hi_freq)
# uniform spacing on mel scale
# 第一个三角形滤波器需要3个点，以后每增加一个滤波器增加一个点
# 因此需要num_mel+2个点，这些点在mel尺度上均匀分布
mel_freqs = np.linspace(lo_mel, hi_mel,self.num_mel+2)
# convert mel freqs to hertz and then to fft bins
# 采样率是16000，而FFT的点数是512，那么每个点对应的带宽是16000/512=31.25
# typically 31.25 Hz, bin[0]=0 Hz, bin[1]=31.25 Hz,..., bin[256]=8000 Hz
bin_width = self.samp_rate/self.fft_size
# 把均匀分布的mel_freqs再变成频率，则它们就不均匀了，高频的宽
# 然后除以bin_width则变成fft的id
mel_bins = np.floor(self.mel2lin(mel_freqs)/bin_width)
num_bins = self.fft_size//2 + 1
self.mel_filterbank = np.zeros([self.num_mel,num_bins])
for i in range(0,self.num_mel):
# 三角形滤波器的第一个点的fft的idx
left_bin = int(mel_bins[i])
# 第二个点的idx
center_bin = int(mel_bins[i+1])
# 第三个点的idx
right_bin = int(mel_bins[i+2])
# 第一个点和第二个点形成往上走的直线
up_slope = 1/(center_bin-left_bin)
for j in range(left_bin,center_bin):
self.mel_filterbank[i,j] = (j - left_bin)*up_slope
# 第二个点和第三个点是往下走的直线
down_slope = -1/(right_bin-center_bin)
for j in range(center_bin,right_bin):
self.mel_filterbank[i,j] = (j-right_bin)*down_slope
频率变成mel和mel变成频率的函数为：
# linear-scale frequency (Hz) to mel-scale frequency
def lin2mel(self,freq):
return 2595*np.log10(1+freq/700)
# mel-scale frequency to linear-scale frequency
def mel2lin(self,mel):
return (10**(mel/2595)-1)*700
process_utterance
这个函数的输入utterance是一个一维的numpy数组，每一个值都是浮点数。
def process_utterance(self, utterance):
wav = self.dither(utterance)
wav = self.pre_emphasize(wav)
frames = self.wav_to_frames(wav)
magspec = self.frames_to_magspec(frames)
fbank = self.magspec_to_fbank(magspec)
if (self.mean_normalize):
fbank = self.mean_norm_fbank(fbank)
if (self.compute_global_stats):
self.accumulate_stats(fbank)
return fbank
它会对utterance进行如下的处理：
- dither函数增加随机的噪声
- pre_emphasize
- wav_to_frames实现分帧
- frames_to_magspec FFT并且计算幅度谱
- magspec_to_fbank 计算log的FBANK系数
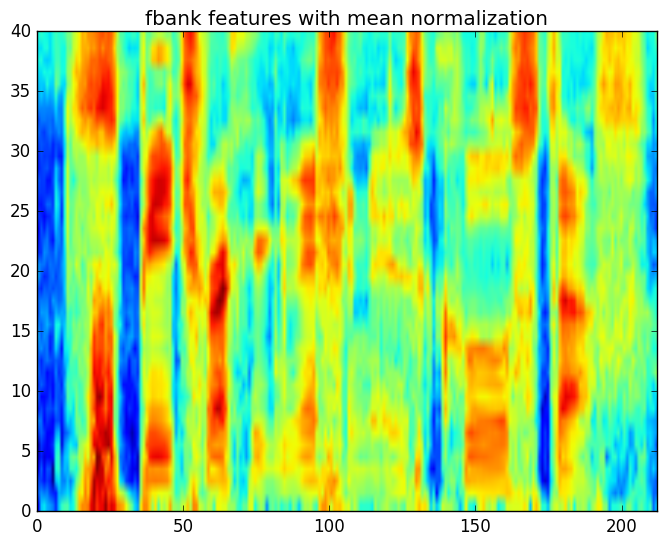
- mean_norm_fbank 对log的FBANK系数进行归一化
- accumulate_stats 计算全局的统计信息
dither
def dither(self, wav):
n = 2*np.random.rand(wav.shape[0])-1
n *= 1/(2**15)
return wav + n
增加很小的随机噪声。
pre_emphasize
def pre_emphasize(self, wav):
# apply pre-emphasis filtering on waveform
preemph_wav = []
preemph_wav.append(wav[0])
for i in range(1, len(wav)):
preemph_wav.append(wav[i] - self.preemphasis * wav[i - 1])
return np.asarray(preemph_wav)
使用前面的公式$y[n] = x[n] - \alpha x[n-1]$计算。
wav_to_frames
def wav_to_frames(self, wav):
# only process whole frames
num_frames = int(np.floor((wav.shape[0] - self.win_size) / self.win_shift) + 1)
frames = np.zeros([self.win_size, num_frames])
for t in range(0, num_frames):
frame = wav[t * self.win_shift:t * self.win_shift + self.win_size]
if (self.zero_mean_wav):
frame = frame - np.mean(frame)
frames[:, t] = self.hamwin * frame
return frames
wav_to_frames实现分帧，首先计算帧数：帧数=(wav样本数-帧长)/帧移+1。然后就是简单的从wav中截取对于的数据，最后乘以窗函数self.hamwin。
frames_to_magspec
def frames_to_magspec(self, frames):
complex_spec = np.fft.rfft(frames, self.fft_size, 0)
magspec = np.absolute(complex_spec)
return magspec
使用np.fft.rfft计算FFT，这里使用rfft表示是对实数进行FFT，它返回的点数为self.fft_size/2+1。然后用np.absolute对复数求其幅度(模)。
magspec_to_fbank
def magspec_to_fbank(self, magspec):
fbank = np.dot(self.mel_filterbank, magspec)
return np.log(fbank)
计算fbank系数，就是把mel_filterbank和magspec相乘。最后把系数取log。
mean_norm_fbank
def mean_norm_fbank(self, fbank):
# compute mean fbank vector of all frames
# subtract it from each frame
mean=np.mean(fbank, axis=1).reshape(-1,1)
return fbank-mean
对fbank的系数的每一维进行均值归一化(使得均值为零)
accumulate_stats
def accumulate_stats(self, fbank):
self.global_mean += np.sum(fbank,axis=1)
self.global_var += np.sum(fbank**2,axis=1)
self.global_frames += fbank.shape[1]
统计全局的均值、方差，用于生成feat_mean.ascii和feat_invstddev.ascii。
M2_Wav2Feat_Single.py
我们简单的来看一下这个脚本，它的作用是提取训练、开发和测试集的特征。
下面以训练集为例。它的输入是Experiments/lists/wav_train.list，我们来看一下：
$ head wav_train.list
LibriSpeech/dev-clean/1272/128104/1272-128104-0000.flac
LibriSpeech/dev-clean/1272/128104/1272-128104-0001.flac
LibriSpeech/dev-clean/1272/128104/1272-128104-0002.flac
LibriSpeech/dev-clean/1272/128104/1272-128104-0003.flac
LibriSpeech/dev-clean/1272/128104/1272-128104-0005.flac
LibriSpeech/dev-clean/1272/128104/1272-128104-0006.flac
LibriSpeech/dev-clean/1272/128104/1272-128104-0007.flac
LibriSpeech/dev-clean/1272/128104/1272-128104-0008.flac
LibriSpeech/dev-clean/1272/128104/1272-128104-0009.flac
LibriSpeech/dev-clean/1272/128104/1272-128104-0010.flac
每一行列举一个录音文件的路径。
对于每一行，都会提取特征保存在feat/下，并且在feat_train.rscp里记录这个id对应的特征的路径。
$ head feat_train.rscp
1272-128104-0000.feat=.../../feat/1272-128104-0000.feat[0,583]
1272-128104-0001.feat=.../../feat/1272-128104-0001.feat[0,479]
1272-128104-0002.feat=.../../feat/1272-128104-0002.feat[0,1246]
1272-128104-0003.feat=.../../feat/1272-128104-0003.feat[0,987]
1272-128104-0005.feat=.../../feat/1272-128104-0005.feat[0,898]
1272-128104-0006.feat=.../../feat/1272-128104-0006.feat[0,561]
1272-128104-0007.feat=.../../feat/1272-128104-0007.feat[0,921]
1272-128104-0008.feat=.../../feat/1272-128104-0008.feat[0,509]
1272-128104-0009.feat=.../../feat/1272-128104-0009.feat[0,1826]
1272-128104-0010.feat=.../../feat/1272-128104-0010.feat[0,557]
上面我们可以知道1272-128104-0000提取的特征存放在feat/1272-128104-0000.feat下。此外还会在am下输出feat_mean.ascii和feat_invstddev.ascii。
下面是我抽取出来的主要代码：
samp_rate = 16000
fe = sp.FrontEnd(samp_rate=samp_rate, mean_norm_feat=True, compute_stats=compute_stats)
for line in wav_files:
x, s = sf.read(wav_file)
feat = fe.process_utterance(x)
# 输出特征文件
htk.write_htk_user_feat(feat, feat_file)
feat_rscp_line = os.path.join(rscp_dir, '..', 'feat', feat_name)
# 在rscp里输出一行，类似1272-128104-0000.feat=.../../feat/1272-128104-0000.feat[0,583]
out_list.write("%s=%s[0,%d]\n" % (feat_name, feat_rscp_line,feat.shape[1]-1))
count += 1
if (compute_stats):
m, p = fe.compute_stats() # m=mean, p=precision (inverse standard deviation)
htk.write_ascii_stats(m, mean_file)
print("Wrote global mean to", mean_file)
htk.write_ascii_stats(p, invstddev_file)
print("Word global inv stddev to ", invstddev_file)
- 显示Disqus评论(需要科学上网)