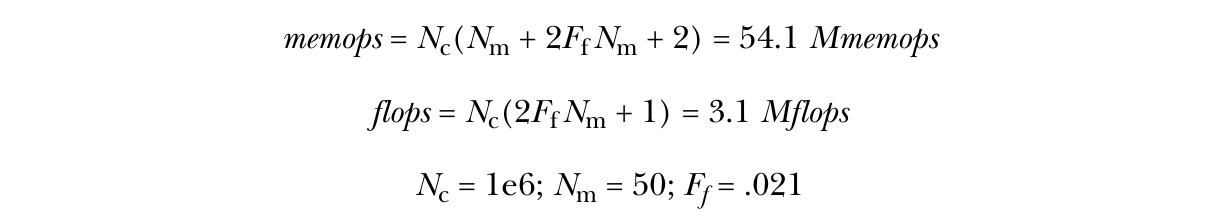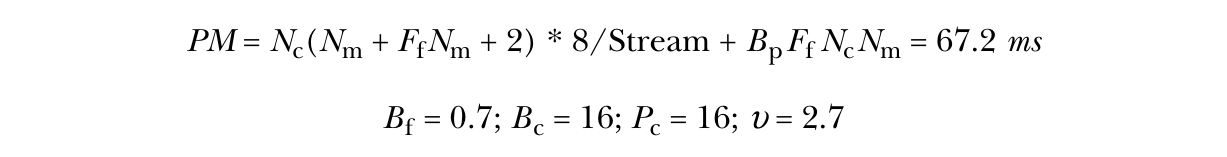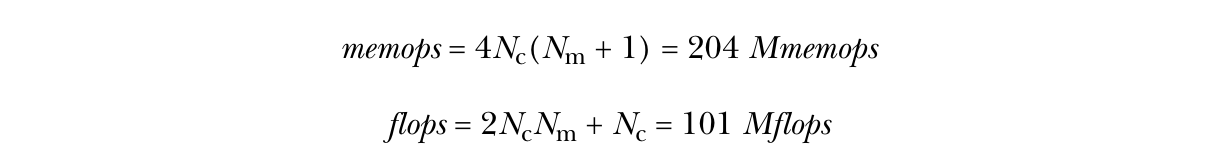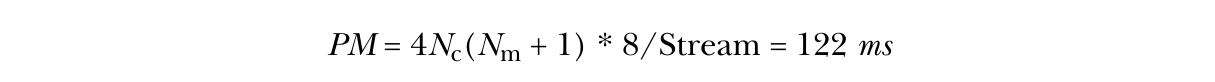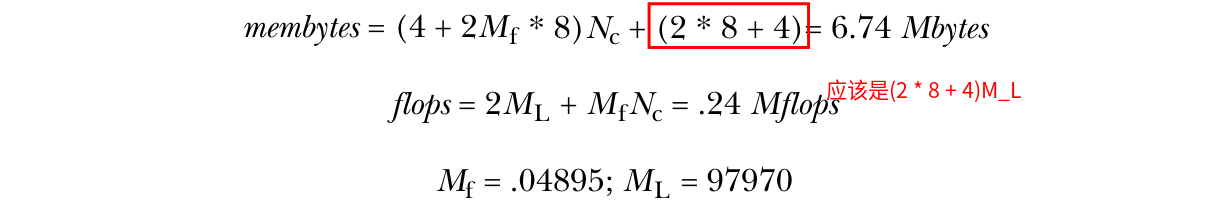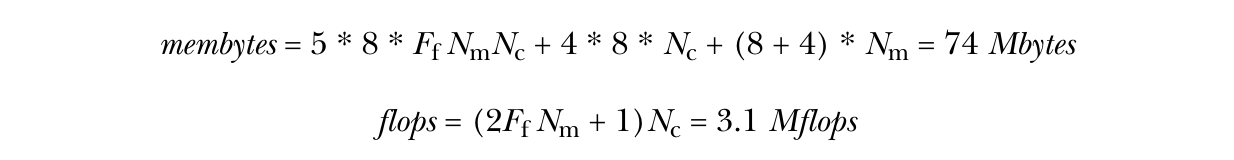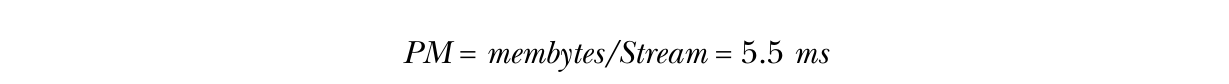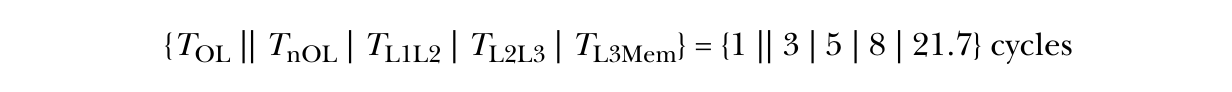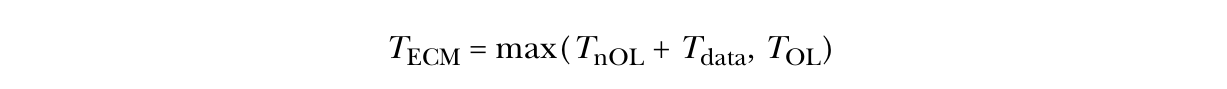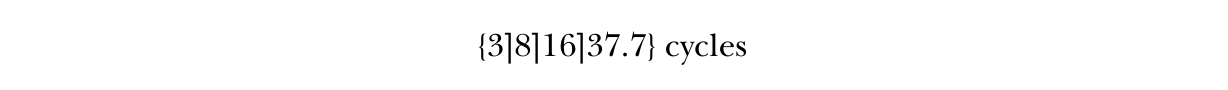第四章：数据设计与性能模型

4.1 高性能数据结构：数据导向设计
4.2 缓存未命中的三种类型：强制性、容量性、冲突性
4.3 简单性能模型：案例研究
- 4.3.1 全矩阵数据表示
- 4.3.2 压缩稀疏存储表示
4.4 高级性能模型
4.5 网络消息

本章内容包括：

为什么实际应用难以实现高性能
解决显著性能不足的内核和循环
为应用选择数据结构
在编写代码之前评估不同的编程方法
理解缓存层级如何将数据传递给处理器

本章涉及两个密切相关的主题：(1) 介绍日益以数据移动为主导的性能模型，因此，必然涉及 (2) 数据的底层设计和结构。尽管它似乎次于性能，但数据结构及其设计至关重要。必须提前确定，因为它决定了整个算法、代码形式以及后来的并行实现。

数据结构和数据布局的选择通常决定了你能实现的性能，并且在设计决策做出时，这些影响并不总是显而易见。考虑数据布局及其性能影响是新兴的编程方法——数据导向设计的核心。该方法考虑了程序中数据的使用模式，并围绕它进行主动设计。数据导向设计为我们提供了一个以数据为中心的世界观，这也与我们关注内存带宽而非浮点运算（flops）相一致。总结起来，为了性能，我们的方法是思考：

数据而非代码
内存带宽而非flops
缓存行而不是单个数据元素
优先考虑已在缓存中的数据的操作

基于数据结构和自然衍生的算法的简单性能模型可以大致预测性能。性能模型(performance model)是计算机系统如何执行代码内核操作的简化表示。我们使用简化模型是因为推理计算机操作的全部复杂性很困难，并且会掩盖我们需要考虑的关键性能方面。这些简化模型应该捕捉到对性能最重要的计算机操作方面。每个计算机系统在操作细节上都不同。因为我们希望我们的应用程序能在广泛的系统上运行，所以我们需要一个抽象出所有系统共有操作的一般性视图的模型。

模型帮助我们理解当前内核性能的运行情况。它有助于建立对性能的期望，以及代码更改可能带来的性能改进。代码更改可能需要大量工作，我们希望在进行工作前了解结果应该是什么。它还帮助我们关注应用性能的关键因素和资源。

性能模型不限于flops，实际上，我们将重点放在数据和内存方面。除了flops和内存操作，整数操作、指令和指令类型也可能很重要，并且应该被计数。但是，与这些额外考虑相关的限制通常与内存性能一致，可以视为从该限制中略微减少的性能。

本章的第一部分讨论简单数据结构及其对性能的影响。接下来，我们将介绍用于快速进行设计决策的性能模型。这些性能模型将用于一个案例研究，以评估复杂数据结构（如压缩的稀疏多材料数组）可能表现良好的数据结构类型。这些决策对数据结构的影响通常在项目后期表现出来，那时更改将更加困难。本章的最后部分专注于高级编程模型，介绍适合深入探讨性能问题或理解计算机硬件及其设计如何影响性能的更复杂模型。让我们深入探讨这些内容，看它们在你的代码和性能问题上意味着什么。

注意：我们鼓励你通过https://github.com/EssentialsofParallelComputing/Chapter4上的示例跟随本章内容进行学习。

4.1 高性能数据结构：数据导向设计

我们的目标是设计能够带来良好性能的数据结构。我们将从多维数组的分配方式开始，然后转向更复杂的数据结构。实现这一目标需要：

理解数据在计算机中的布局
数据如何加载到缓存行然后再到CPU
数据布局如何影响性能
数据移动对当今计算机性能日益重要

在大多数现代编程语言中，数据以一种或另一种形式被分组。例如，在C语言中使用数据结构或在面向对象编程（也称为OOP）中使用类，将相关项目聚集在一起，以方便组织源代码。类的成员与操作它的方法一起收集。虽然面向对象编程的哲学从程序员的角度提供了很多价值，但它完全忽略了CPU的操作方式。面向对象编程导致频繁的方法调用，中间只有几行代码（图4.1）。

图4.1 面向对象语言有深层调用栈和大量的方法调用（如左图所示），而过程式语言在调用栈的一个层次上有长序列的操作。

为了调用方法，必须先将类加载到缓存中。接着，数据被加载到缓存中，然后是类的相邻元素。当操作一个对象时，这很方便。但对于计算密集型应用，有大量的每种项目。在这些情况下，我们不希望每次调用都在一个项目上调用一个方法，每次调用都需要遍历深层调用栈。这会导致指令缓存未命中、数据缓存使用不佳、分支和大量函数调用开销。

C++方法使编写简洁代码变得更容易，但几乎每一行都是一个方法调用，如图4.1所示。在数值模拟代码中，Draw_Line调用很可能是一个复杂的数学表达式。但即使在这里，如果将Draw_Line函数内联到源代码中，C代码中将没有函数跳转。内联是指编译器将子例程的源代码复制到使用它的位置，而不是调用它。然而，编译器只能内联简单、短小的例程。但面向对象代码有无法内联的方法调用，因为其复杂性和深层调用栈。这会导致指令缓存未命中和其他性能问题。如果我们只绘制一个窗口，性能损失可以通过更简单的编程来抵消。如果我们要绘制一百万个窗口，我们无法承受性能损失。

所以，让我们翻转这一点，为性能而不是编程便利性设计我们的数据结构。面向对象编程和其他现代编程风格很强大，但引入了许多性能陷阱。2014年CppCon上，Mike Acton的演讲“数据导向设计与C++”总结了游戏行业的工作，指出了现代编程风格为何阻碍性能。数据导向设计编程风格的倡导者通过创建一种专注于性能的编程风格来解决这一问题。这种方法被称为数据导向设计，它专注于为CPU和缓存设计最佳数据布局。这种风格与高性能计算（HPC）开发者长期使用的技术有很多共同之处。在HPC中，数据导向设计是常态；它自然地继承了人们用Fortran编写程序的方式。那么，数据导向设计是什么样的呢？它：

操作数组而不是单个数据项，避免调用开销和指令及数据缓存未命中
更喜欢数组而不是结构体，以便在更多情况下更好地利用缓存
内联子例程，而不是遍历深层调用层次
控制内存分配，避免幕后无方向的重新分配
使用连续的基于数组的链表，避免C和C++中使用的标准链表实现，这些实现遍布内存，数据局部性和缓存使用不佳

在接下来的章节中，当我们进入并行化时，我们会注意到我们的经验表明，大型数据结构或类也会导致共享内存并行化和向量化的问题。在共享内存编程中，我们需要能够将变量标记为线程私有或跨所有线程全局的。但目前，数据结构中的所有项目都有相同的属性。在逐步引入OpenMP并行化时，这个问题尤其严重。在实现向量化时，我们需要长数组的同质数据，而类通常将异质数据分组。这使事情变得复杂。

4.1.1 多维数组

在本节中，我们将讨论在科学计算中无处不在的多维数组数据结构。我们的目标是了解：

如何在内存中布局多维数组
如何访问数组以避免性能问题
如何从C程序中调用Fortran的数值库

处理多维数组是与性能相关的最常见问题。图4.2的前两个子图展示了传统的C和Fortran数据布局。

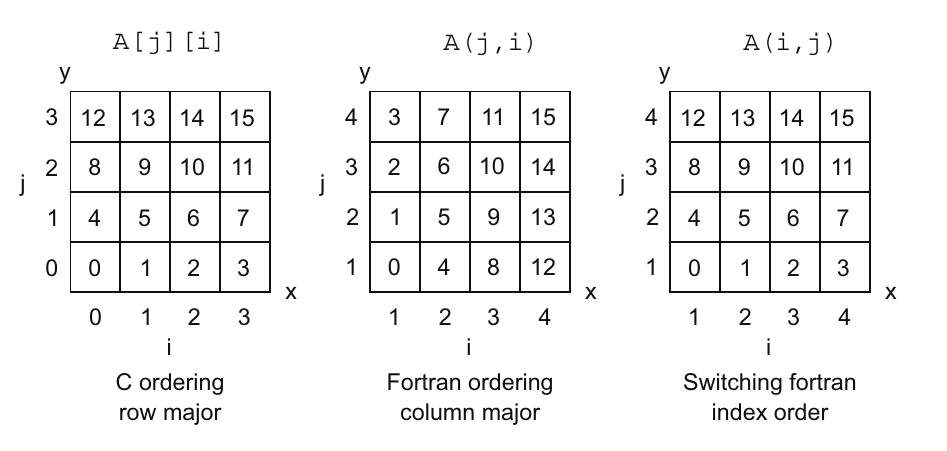图4.2 传统的C排序是行优先，而Fortran排序是列优先。切换Fortran或C的索引顺序可以使它们兼容。注意，Fortran数组索引从1开始，而C从0开始。此外，C的习惯是从0到15对元素进行连续编号。

C的数据顺序被称为行优先（row major），即行中的数据变化比列中的数据更快。这意味着行数据在内存中是连续的。相比之下，Fortran的数据布局是列优先（column major），即列数据变化最快。实际上，作为程序员，我们必须记住在每种情况下应该在内循环中使用哪个索引，以利用连续内存（图4.3）。

图4.3 对于C来说，重要的是要记住最后一个索引变化最快，应该是嵌套循环的内循环。对于Fortran来说，第一个索引变化最快，应该是嵌套循环的内循环。

除了语言之间的数据顺序差异之外，还有一个必须考虑的问题。整个二维数组的内存是否连续？Fortran并不保证内存是连续的，除非你在数组上使用CONTIGUOUS属性，如下例所示：

real, allocatable, contiguous :: x(:,:)

实际上，使用连续属性并不像看起来那么关键。所有流行的Fortran编译器都会为数组分配连续的内存，无论是否有此属性。可能的例外情况是为了缓存性能而进行填充，或者通过子程序接口使用切片操作符传递数组。切片操作符是Fortran中的一个构造，允许你将数组的子集引用为一个例子，比如将二维数组的一行复制到一维数组中的语法：y(:) = x(1,:)。切片操作符也可以在子程序调用中使用，例如：

call write_data_row(x(1,:))

一些研究编译器通过简单地修改数组元数据中的数据元素之间的步长来处理这个问题。在Fortran中，元数据包含数组的起始位置、数组的长度以及每个维度中元素之间的步长。在这个上下文中，dope来源于“给我信息（info）”的意思（在这种情况下是指数组）。图4.4展示了元数据、切片操作符和步长的概念。其思路是通过将元数据中的步长从1修改为4，数据就按行而不是按列遍历了。

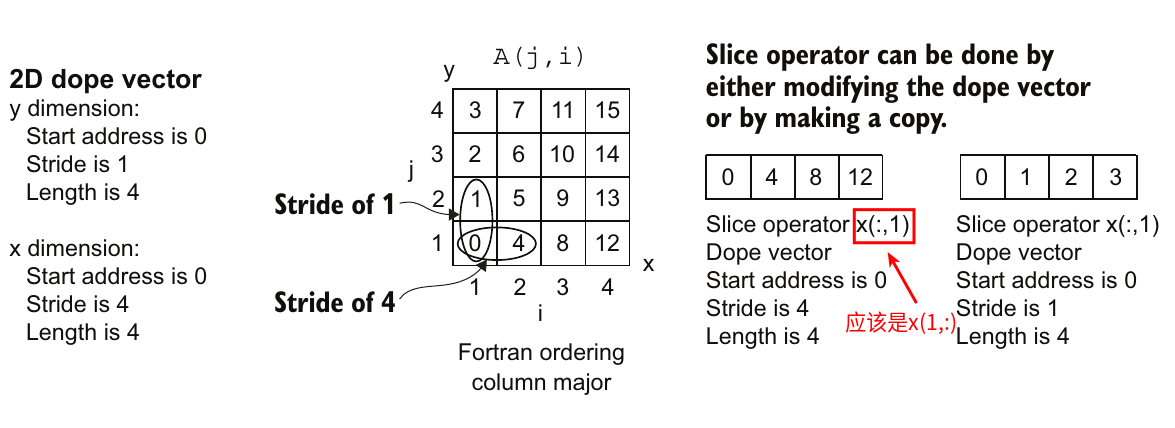图4.4 通过修改元数据向量来创建Fortran数组的不同视图，这组元数据描述了每个维度的起始位置、步长和长度。切片操作符返回Fortran数组的一个部分，维度内的所有元素用冒号（:）表示。可以创建更复杂的部分，如A(1:2,1:2)中的下四个元素，其中上下界用冒号指定。

但实际上，生产环境中的Fortran编译器通常会复制数据并将其传递到子程序中，以避免破坏期望连续数据的代码。这也意味着在调用Fortran子程序时应避免使用切片操作符，因为隐式复制会带来性能成本。

在C中，为二维数组分配连续内存也有其自身的问题。这是由于C中动态分配二维数组的传统方式，如下面的清单所示。

  // first allocate a column of pointers of type pointer to double
  double **x = (double **)malloc(jmax * sizeof(double *));

  // now allocate each row of data
  for (j=0; j<jmax; j++){
     x[j] = (double *)malloc(imax * sizeof(double));
  }

  // computation

  for (j=0; j<jmax; j++){
     free(x[j]);
  }
  free(x);

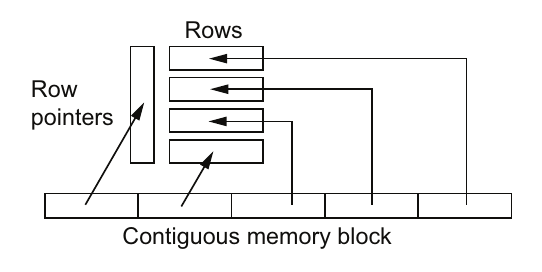
这个清单使用了1+jmax次分配，每次分配可能来自堆中的不同位置。对于较大的二维数组来说，数据在内存中的布局对缓存效率的影响很小。更大的问题是使用非连续数组的情况严重受限；无法将它们传递给Fortran，将其块写入文件，然后传递给GPU或另一个处理器。相反，每一个操作都需要逐行进行。幸运的是，有一种简单的方法可以为C数组分配一个连续的内存块。为什么这不是标准做法？这是因为每个人都学会了清单4.1中的传统方法，而没有深入思考。以下清单展示了如何为二维数组分配一个连续的内存块。

   // first allocate a block of memory for the row pointers
   double **x = (double **)malloc(jmax*sizeof(double *));

   // Now allocate a block of memory for the 2D array
   x[0] = (void *)malloc(jmax*imax*sizeof(double));

   // Last, assign the memory location to point to in the block of data for each row pointer
   for (int j = 1; j < jmax; j++) {
      x[j] = x[j-1] + imax;
   }

   // Computation

   // Deallocate memory
   free(x[0]);
   free(x);

这种方法不仅为你提供了一个连续的内存块，而且只需要两次内存分配！我们可以通过将行指针打包到连续内存分配的开始位置（清单4.2的第11行），从而进一步优化，合并两次内存分配为一次（图4.5）。

图4.5 一个连续的内存块在C中成为一个二维数组。

以下清单展示了在malloc2D.c中单个连续内存分配二维数组的实现。

malloc2D.c

double **malloc2D(int jmax, int imax)
{
   // first allocate a block of memory for the row pointers and the 2D array
   double **x = (double **)malloc(jmax*sizeof(double *) + jmax*imax*sizeof(double));

   // Now assign the start of the block of memory for the 2D array after the row pointers
   x[0] = (double *)(x + jmax);

   // Last, assign the memory location to point to for each row pointer
   for (int j = 1; j < jmax; j++) {
      x[j] = x[j-1] + imax;
   }

   return(x);
}

malloc2D.h
#ifndef _MALLOC2D_H
#define _MALLOC2D_H
double **malloc2D(int jmax, int imax);
#endif

【译注：原书为x[0] = (double *)x + jmax。这是不对的！因为把x转换成(double *)之后在加jmax，就是把x当成double指针进行运算了。这样每次加1移动一个double的长度(8)个字节，而实际我们需要移动的是double *的长度。对于32位的系统来说它是4个字节。本书的源代码是对的。请参考这里。】

现在我们只有一个内存块，包括行指针数组。这应该会改善内存分配和缓存效率。该数组还可以作为一维数组或二维数组进行索引，如清单4.4所示。一维数组减少了整数地址计算，并且更容易向量化或线程化（我们将在第6和第7章中讨论）。该清单还展示了手动将二维索引计算为一维数组。

int main(int argc, char *argv[])
{
   int i, j;
   int imax=100, jmax=100;

   double **x = (double **)malloc2D(jmax,imax);

   // 1D access of the contiguous 2D array
   double *x1d=x[0];
   for (i = 0; i< imax*jmax; i++){
      x1d[i] = 0.0;
   }

   // 2D access of the contiguous 2D array
   for (j = 0; j< jmax; j++){
      for (i = 0; i< imax; i++){
         x[j][i] = 0.0;
      }
   }

   // Manual 2D index calculation into 1D array
   for (j = 0; j< jmax; j++){
      for (i = 0; i< imax; i++){
         x1d[i + imax * j] = 0.0;
      }
   }
}

Fortran程序员理所当然地认为语言中对多维数组的高级处理。尽管C和C++已经存在了几十年，但这些语言仍然没有内置的多维数组。C++标准中有提案要在2023年修订版中添加原生多维数组支持（参见附录A中的Hollman等人的参考文献）。在此之前，清单4.4中介绍的多维数组内存分配是必不可少的。

4.1.2 结构数组（AoS）与数组结构（SoA）

在本节中，我们将讨论结构和类对数据布局的影响。我们的目标是了解：

不同方式的结构在内存中的布局
如何访问数组以避免性能问题

有两种不同的方式将相关数据组织成数据集合：一种是结构数组（AoS），即在最低层级将数据集合成一个单元，然后将这个结构组成数组；另一种是数组结构（SoA），即在最低层级将每个数据数组分别处理，然后将这些数组组成一个结构。第三种方式是这两种数据结构的混合体，称为结构数组的数组（AoSoA）。我们将在4.1.3节中讨论这种混合数据结构。

AoS的一个常见例子是用于绘制图形对象的颜色值。下面的代码清单显示了C语言中的红、绿、蓝（RGB）颜色系统结构。

   struct RGB {
      int R;
      int G;
      int B;
   };
   struct RGB polygon_color[1000];

清单4.5展示了内存中布局的AoS（图4.6）。在图中注意到字节12、28和44处的空白空间，这些是编译器插入的填充，以在64位边界（128位或16字节）上对齐内存。一个64字节的缓存行包含了结构的四个值。然后在第6行中，我们创建了由1000个RGB数据结构类型组成的polygon_color数组。这种数据布局是合理的，因为通常情况下，RGB值一起使用以绘制每个多边形。

图4.6 结构数组（AoS）中RGB颜色模型的内存布局。

SoA是另一种数据布局。下面的代码清单展示了C语言的实现。

   struct RGB {
      int *R;
      int *G;
      int *B;
   };
   struct RGB polygon_color;

   polygon_color.R = (int *)malloc(1000*sizeof(int));
   polygon_color.G = (int *)malloc(1000*sizeof(int));
   polygon_color.B = (int *)malloc(1000*sizeof(int));

   free(polygon_color.R);
   free(polygon_color.G);
   free(polygon_color.B);

内存布局中所有1000个R值都在连续的内存中。G和B颜色值可以紧接在内存中的R值之后，但也可以在堆内存的其他地方，这取决于内存分配器找到空间的位置。堆内存是一个用于动态内存分配的单独区域，使用malloc例程或new运算符进行分配。我们还可以使用连续内存分配器（清单4.3）来强制内存位于一起。

我们关注的是性能。从程序员的角度来看，这些数据结构中的每一个都是合理的，但重要的问题是，这些数据结构在CPU中如何呈现，以及它们如何影响性能。让我们在几个不同的场景中看看这些数据结构的性能。

结构数组（AoS）的性能评估 在我们的颜色示例中，假设在读取数据时，一个点的所有三个组件都被访问，而不是单个R、G或B值，因此AoS表示效果良好。在图形操作中，这种数据布局是常用的。

注意： 如果编译器增加了填充，对于AoS表示来说，内存加载次数会增加25%，但并非所有编译器都会插入这种填充。不过，对于那些会插入填充的编译器来说，这点还是值得考虑的。

如果在一个循环中只访问RGB值中的一个，缓存使用会很差，因为循环会跳过不需要的值。当编译器对这种访问模式进行向量化时，需要使用效率较低的收集/散布(gather/scatter)操作。

数组结构（SoA）的性能评估 对于SoA布局，RGB值有独立的缓存行（图4.7）。因此，对于需要所有三个RGB值的小数据规模来说，缓存使用良好。但随着数组变大并且出现更多数组时，缓存系统会变得难以应对，导致性能下降。在这些情况下，数据与缓存的相互作用变得过于复杂，无法完全预测性能。

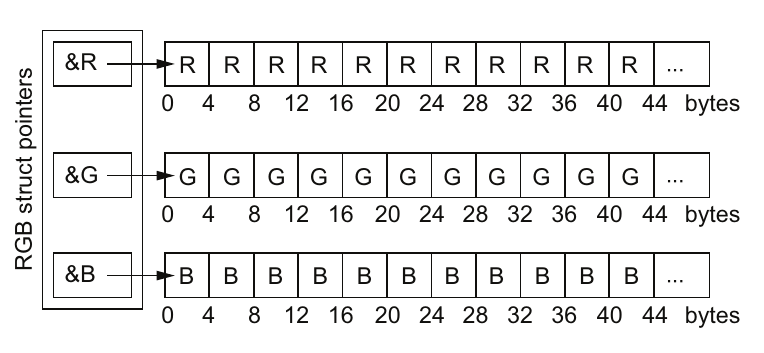图4.7 在数组结构（SoA）的数据布局中，指针在内存中是相邻的，分别指向每种颜色的单独连续数组。

另一个经常遇到的数据布局和访问模式是在计算应用中将变量用作三维空间坐标。以下代码显示了这种情况下的典型C结构定义。

   struct point {
      double x, y, z;
   };
   struct point cell[1000];
   double radius[1000];
   double density[1000];
   double density_gradient[1000];

这种数据结构的一个用途是计算从原点到距离（半径），方法如下：

   for (int i=0; i < 1000; i++){
      radius[i] = sqrt(cell[i].x*cell[i].x + cell[i].y*cell[i].y + cell[i].z*cell[i].z);
   }

将x、y和z的值一起存储在一个缓存行中，并将它们写入到第二个缓存行的radius变量中。这种情况下的缓存使用是合理的。

但是在第二种可能的情况下，计算循环可能使用x位置来计算x方向的密度梯度，方法如下：

   for (int i=1; i < 1000; i++){
      density_gradient[i] = (density[i] - density[i-1])/(cell[i].x - cell[i-1].x);
   }

现在，对x的缓存访问会跳过y和z的数据，因此缓存中只使用了三分之一（甚至四分之一，如果有填充的话）的数据。因此，最佳的数据布局完全取决于使用情况和特定的数据访问模式。

在混合使用的情况下，通常会出现在实际应用程序中，有时结构变量是一起使用的，有时则不是。总体上，AoS布局在CPU上表现更好，而SoA布局在GPU上表现更好。在报告的结果中，存在足够的变异性，值得针对特定的使用模式进行测试。在密度梯度的情况下，以下显示了SoA代码。

   struct point{
      double *x, *y, *z;
   };
   struct point cell;
   cell.x = (double *)malloc(1000*sizeof(double));
   cell.y = (double *)malloc(1000*sizeof(double));
   cell.z = (double *)malloc(1000*sizeof(double));
   double *radius = (double *)malloc(1000*sizeof(double));
   double *density = (double *)malloc(1000*sizeof(double));
   double *density_gradient = (double *)malloc(1000*sizeof(double));

   for (int i=0; i < 1000; i++){
      radius[i] = sqrt(cell.x[i]*cell.x[i] + cell.y[i]*cell.y[i] + cell.z[i]*cell.z[i]);
   }

   for (int i=1; i < 1000; i++){
      density_gradient[i] = (density[i] - density[i-1])/(cell.x[i] - cell.x[i-1]);
   }

   free(cell.x);
   free(cell.y);
   free(cell.z);
   free(radius);
   free(density);
   free(density_gradient);

通过这种数据布局，每个变量都被存储在一个独立的缓存行中，对于这两个内核来说，缓存使用效率都很好。但是当所需的数据成员数量足够大时，缓存很难有效处理大量的内存流。在C++面向对象的实现中，您应该注意其他的缺陷。下一个列表显示了一个cell类，其中包含cell空间坐标和半径作为其数据组件，并且有一个从x、y和z计算半径的方法。

class Cell{
      double x;
      double y;
      double z;
      double radius;
   public:
      void calc_radius() { radius = sqrt(x*x + y*y + z*z); }
      void big_calc();
};

void Cell::big_calc(){
   radius = sqrt(x*x + y*y + z*z);
   // ... lots more code, preventing in-lining
}

运行此代码会导致每个单元格出现几次指令缓存未命中以及子例程调用的开销。指令缓存未命中发生在指令跳转时，下一个指令不在指令缓存中。有两个级别1的缓存：一个用于程序数据，第二个用于处理器的指令。子例程调用需要额外的开销来在调用之前将参数推入堆栈，并进行指令跳转。一旦进入例程，参数需要从堆栈中弹出，然后在例程结束时，还需要进行另一个指令跳转。在这种情况下，代码足够简单，编译器可以内联例程以避免这些成本。但是在更复杂的情况下，比如big_calc例程，它不能这样做。此外，缓存行拉取了x、y、z和radius。缓存有助于加速实际需要读取的位置坐标的加载。但是需要写入的radius也在缓存行中。如果不同的处理器正在写入radius的值，这可能会使缓存行无效，并要求其他处理器重新加载数据到它们的缓存中。

C++有许多使编程更加简单的特性。这些通常应该在代码的较高层次上使用，使用C和Fortran的简单过程式风格，因为性能很重要。在前面的代码中，可以将半径计算作为数组而不是作为单个标量元素来进行。类指针可以在例程开始时解引用一次，以避免重复的解引用和可能的指令缓存未命中。解引用是一种操作，通过该操作从指针引用中获取内存地址，从而使缓存行专用于内存数据而不是指针。简单的哈希表也可以使用一个结构将键和值组合在一起，如下一个列表所示。

struct hash_type {
   int key;
   int value;
};
struct hash_type hash[1000];

这段代码的问题在于它读取多个键，直到找到与之匹配的键，然后读取该键的值。但是键和值被带入单个缓存行，直到匹配发生之前值都被忽略。更好的方法是将键作为一个数组，将值作为另一个数组，以便更快地搜索键。

   struct hash_type {
      int *key;
      int *value;
   } hash;
   hash.key   = (int *)malloc(1000*sizeof(int));
   hash.value = (int *)malloc(1000*sizeof(int));

接下来的列表显示了一个包含密度、三维动量和总能量的物理状态结构体。

struct phys_state {
   double density;
   double momentum[3];
   double TotEnergy;
};

当仅处理密度时，缓存中的下四个值将被未使用。同样，将其作为SoA更为合适。

4.1.3 数组的结构的数组（AoSoA）

有些情况下，混合结构和数组的组合是有效的。数组的结构的数组（AoSoA）可以用来将数据“切片”成矢量长度。我们引入符号 A[len/4]S[3]A[4] 来表示这种布局。A[4] 是包含四个数据元素的数组，是内部连续的数据块。S[3] 表示三个字段的数据结构的下一级。S[3]A[4] 的组合给出了图4.8所示的数据布局。

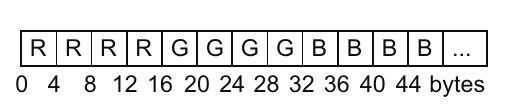Figure 4.8 展示了一个数组的结构的数组（AoSoA），其中最后一个数组长度与硬件的矢量长度匹配，矢量长度为4

我们需要将长度为12的数据块重复 A[len/4] 次才能获取所有数据。如果我们用一个变量替换4，我们就得到了

A[len/V]S[3]A[V]，其中 V=4。

在C或Fortran中，对应的数组可以定义为

var[len/V][3][V], var(1:V,1:3,1:len/V)

在C++中，这可以自然地实现如下代码所示。

const int V=4;
struct SoA_type{
   int R[V], G[V], B[V];
}; 

int main(int argc, char *argv[])
{
   int len=1000;
   struct SoA_type AoSoA[len/V];

   for (int j=0; j<len/V; j++){
      for (int i=0; i<V; i++){
         AoSoA[j].R[i] = 0;
         AoSoA[j].G[i] = 0;
         AoSoA[j].B[i] = 0;
      }
   }
}

通过调整 V 以匹配硬件矢量长度或GPU工作组大小，我们创建了一个可移植的数据抽象。此外，通过定义 V=1 或 V=len，我们可以恢复到 AoS 或 SoA 数据结构。这种数据布局因此成为适应硬件和程序数据使用模式的一种方式。

对于这种数据结构的实现有许多细节需要考虑，以最小化索引成本，并决定是否填充数组以提高性能。AoSoA 数据布局具有 AoS 和 SoA 数据结构的一些特性，因此性能通常接近这两种结构中较好的那种，正如洛斯阿拉莫斯国家实验室的罗伯特·伯德的一项研究所示（图4.9）。

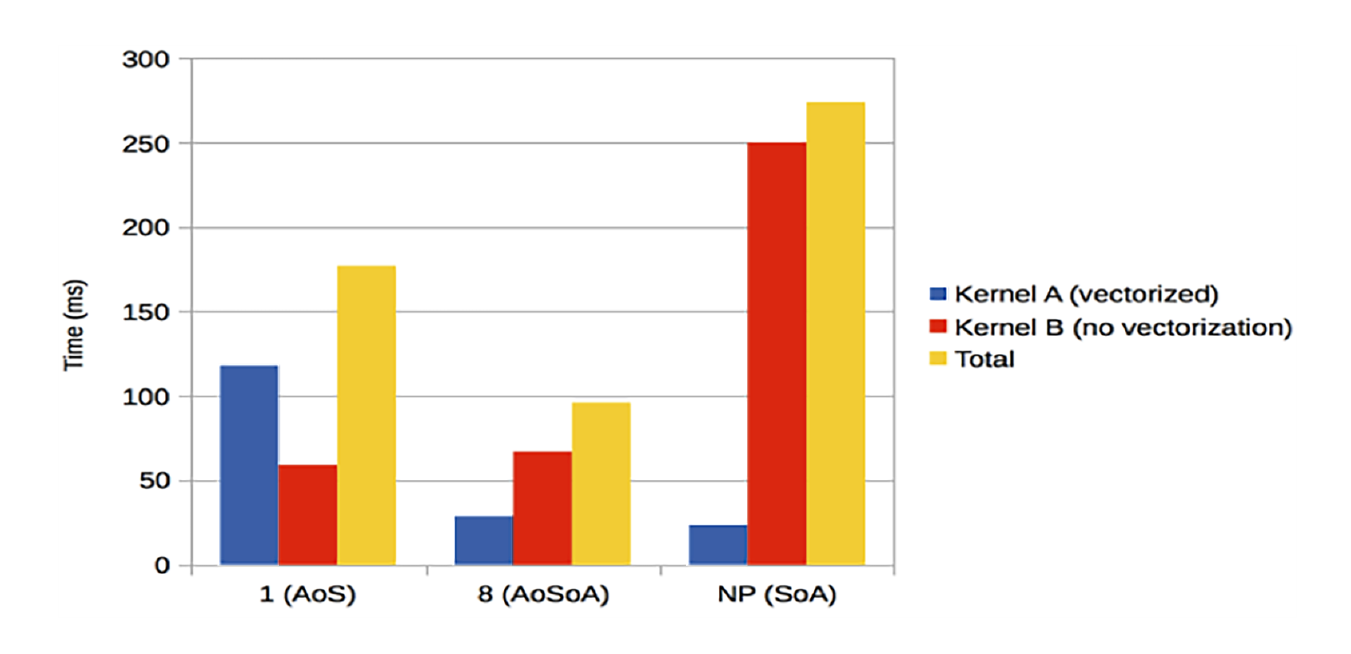Figure 4.9 数组的结构的数组（AoSoA）性能通常与AoSoA和SoA性能中最好的相匹配。x轴图例中的1、8和NP数组长度值代表AoSoA中最后一个数组的值。这些值意味着第一个设置变成了AOS，最后一个设置变成了SoA，而中间设置的第二个数组长度为8，以匹配处理器的矢量长度。

4.2 缓存未命中的三种类型：强制性、容量性、冲突性

缓存效率在密集计算的性能中占主导地位。只要数据在缓存中，计算就会快速进行。当数据不在缓存中时，就会发生缓存未命中。处理器此时必须暂停并等待数据加载。缓存未命中的代价约为100到400个周期；在同一时间内可以完成数百个浮点运算！为了提高性能，我们必须尽量减少缓存未命中。然而，减少缓存未命中需要了解数据从主存到CPU的移动方式。这可以通过一个简单的性能模型来完成，该模型将缓存未命中分为三种类型：强制性、容量性和冲突性。首先，我们必须了解缓存的工作原理。

当数据被加载时，它是以块的形式加载的，这些块被称为缓存行(cache lines)，通常是64字节长。然后，这些块根据其在内存中的地址被插入到缓存位置中。在直接映射缓存(direct-mapped cache)中，只有一个位置可以加载数据到缓存中。这在两个数组映射到同一位置时很重要。使用直接映射缓存时，一次只能缓存一个数组。为避免这种情况，大多数处理器具有N路组相连缓存(N-way set associative cache)，提供N个位置来加载数据。对于大型数组的规则、可预测的内存访问，可以预取数据。也就是说，你可以发出指令在需要数据之前预加载(prefetch)数据，以便它已经在缓存中。这可以通过硬件或由编译器在软件中完成。

逐出(Eviction)是指从一个或多个缓存级别中移除缓存行。这可能是由在同一位置加载缓存行（缓存冲突）或缓存大小有限（容量未命中）引起的。循环中的赋值操作会在缓存中导致写分配，其中创建并修改一个新的缓存行。该缓存行会被逐出（存储）到主存，尽管可能不会立即发生。各种写策略影响写操作的细节。缓存的三种类型是理解密集计算中主导运行时性能的缓存未命中来源的一种简单方法。

强制性——为了首次加载数据所必需的缓存未命中。
容量性——由于缓存大小有限，导致将数据从缓存中逐出以腾出空间用于新的缓存行加载的缓存未命中。
冲突性——当数据加载到缓存中的同一位置时。如果需要同时使用两个或多个数据项，但它们映射到同一缓存行，则每次数据元素访问时都必须重复加载这些数据项。

当由于容量或冲突逐出而导致的缓存未命中随后需要重新加载缓存行时，有时称为缓存抖动(thrashing)，这可能导致性能下降。通过这些定义，我们可以轻松计算出内核的一些特性，并至少了解预期的性能。为此，我们将使用图1.10中的模糊运算内核。

清单4.14显示了stencil.c内核。我们还使用了4.1.1节中的malloc2D.c中的二维连续内存分配例程。这里没有显示计时器代码，但可以在在线源码中找到。包含计时器和likwid（“像我知道我在做什么”）分析器的调用。在迭代之间，对大数组进行写操作以刷新缓存，以确保其中没有相关数据影响结果。

#include <stdio.h>
#include <stdlib.h>
#include <sys/time.h>

#include "malloc2D.h"
#include "timer.h"

#include "likwid.h"

#define SWAP_PTR(xnew,xold,xtmp) (xtmp=xnew, xnew=xold, xold=xtmp)

int main(int argc, char *argv[])
{
   LIKWID_MARKER_INIT;
   LIKWID_MARKER_REGISTER("STENCIL");
   struct timespec tstart_cpu, tstop_cpu;
   double cpu_time;
   int imax=2002, jmax = 2002;

   double **xtmp, *xnew1d, *x1d;
   double **x = malloc2D(jmax, imax);
   double **xnew = malloc2D(jmax, imax);
   int *flush = (int *)malloc(jmax*imax*sizeof(int)*10);

   xnew1d = xnew[0]; x1d = x[0];
   for (int i = 0; i < imax*jmax; i++){
      xnew1d[i] = 0.0; x1d[i] = 5.0;
   }   
   for (int j = jmax/2 - 5; j < jmax/2 + 5; j++){
      for (int i = imax/2 - 5; i < imax/2 -1; i++){
         x[j][i] = 400.0;
      }   
   }   

   for (int iter = 0; iter < 10000; iter++){
      for (int l = 1; l < jmax*imax*10; l++){
          flush[l] = 1.0;
      }   
      cpu_timer_start(&tstart_cpu);
      LIKWID_MARKER_START("STENCIL");
      for (int j = 1; j < jmax-1; j++){
         for (int i = 1; i < imax-1; i++){
            xnew[j][i] = ( x[j][i] + x[j][i-1] + x[j][i+1] + x[j-1][i] + x[j+1][i] )/5.0;
         }   
      }   
      LIKWID_MARKER_STOP("STENCIL");
      cpu_time += cpu_timer_stop(tstart_cpu);

      SWAP_PTR(xnew, x, xtmp);
      if (iter%100 == 0) printf("Iter %d\n",iter);
   }   

   printf("Timing is %f\n",cpu_time);

   free(x);
   free(xnew);
   free(flush);

   LIKWID_MARKER_CLOSE;
}

如果我们有一个完全有效的缓存，一旦数据加载到内存中，它就会被保留在那里。当然，在大多数情况下，这与现实相去甚远。但通过这个模型，我们可以计算出以下内容：

总内存使用量 = 2000 × 2000 ×（5次引用 + 1次存储）× 8字节 = 192 MB
强制性内存加载和存储 = 2002 × 2002 × 8字节 × 2个数组 = 64.1 MB
算术强度 = 5个浮点运算 × 2000 × 2000 / 64.1 MB = 0.312 浮点运算/字节或2.5 浮点运算/字

然后使用likwid库编译程序，并在Skylake 6152处理器上运行以下命令：

likwid-perfctr -C 0 -g MEM_DP -m ./stencil

我们需要的结果在运行结束时打印的性能表的末尾：

通过使用Python脚本（在线材料中提供）显示的屋顶线图展示了stencil内核的性能数据，如图4.10所示。屋顶线图如3.2.4节中所介绍的那样，显示了最大浮点运算和最大带宽在算术强度函数上的硬件限制。

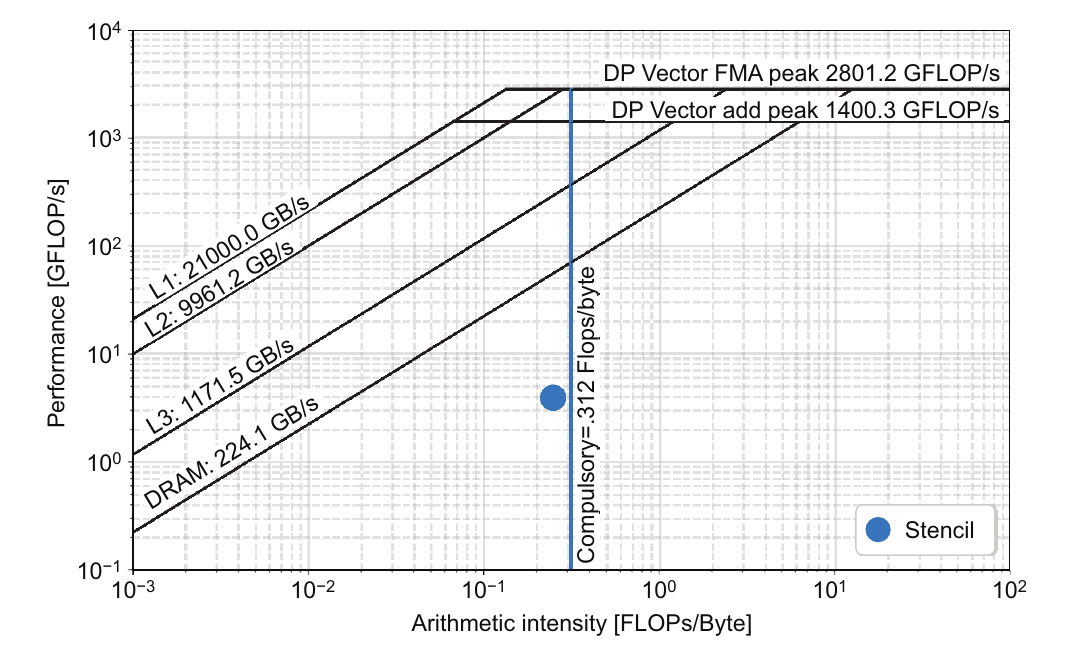图4.10：第1章Krakatau示例中的stencil内核的屋顶线图显示了测量性能右侧的强制上限。

此屋顶线图显示了右侧测量的0.247算术强度（图4.10中的大点）对应的强制数据限制。如果有冷缓存，内核不能优于强制限制。冷缓存是指进入内核之前没有任何相关数据在其中。大点与强制限制之间的距离让我们了解此内核的缓存效率。在这种情况下，内核很简单，容量和冲突缓存加载仅比强制缓存加载多约15%。因此，内核性能没有太多改进空间。大点与DRAM屋顶线之间的距离是因为这是一个带有向量化的串行内核，而屋顶线是并行的，使用OpenMP。因此，通过添加并行性有潜力提高性能。

由于这是一个对数对数图，差异比表面上看起来更大。仔细观察，通过并行化可能提高的性能几乎是一个数量级。通过在缓存行中使用其他值或在缓存中多次重用数据，可以提高缓存使用率。这是两种不同的情况，分别称为空间局部性或时间局部性：

空间局部性(spatial locality)指内存中位置相邻的数据通常被近距离引用。
时间局部性(temporal locality)指最近引用的数据可能在不久的将来再次被引用。

对于stencil内核（清单4.14），当x[1][1]的值被加载到缓存时，x[1][2]也被加载到缓存。这是空间局部性。在循环的下一次迭代中计算x[1][2]时，需要x[1][1]。它应该仍在缓存中并作为时间局部性的一个案例被重用。

通常会将第四个C添加到前面提到的三个C中，这在后面的章节中将变得重要。这称为一致性。

定义：一致性(coherency)适用于在多处理器之间同步缓存所需的那些缓存更新，即当一个处理器的缓存中写入的数据也保存在另一个处理器的缓存中时。

保持一致性所需的缓存更新有时会导致内存总线上的大量流量，有时称为缓存更新风暴。当在并行作业中增加额外的处理器时，这些缓存更新风暴可能导致性能下降而不是提升。

4.3 简单性能模型：案例研究

本节讨论了使用简单性能模型为物理应用中的多材料(multi-material)计算选择数据结构的一个实例。通过一个真实的案例研究展示了以下内容的效果：

真实编程设计问题中的简单性能模型
使用压缩稀疏(compressed sparse)数据结构来延展计算资源

计算科学的一些领域长期以来使用压缩稀疏矩阵表示法，最著名的是自20世纪60年代以来用于稀疏矩阵的压缩稀疏行(Compressed Sparse Row)（CSR）格式，取得了很好的效果。在本案例研究中评估的压缩稀疏数据结构，节省的内存超过95%，运行时间比简单的二维数组设计快90%左右。所使用的简单性能模型预测的性能误差在实际测量性能的20-30%范围内（参见本章后续阅读部分中的Fogerty、Mattineau等人的研究）。但是，使用这种压缩方案是有代价的——需要程序员的努力。我们希望在压缩稀疏数据结构的收益大于成本时使用它。做出这个决策正是简单性能模型显示其用处的地方。

示例：建模喀拉喀托火山灰羽流

你的团队正在考虑建模第1章中的火山灰羽流示例。他们意识到羽流中的灰材料最终可能达到数十甚至上百种，但这些材料不需要在每个单元格中都存在。压缩稀疏表示法在这种情况下是否有用呢？

在解决比二维数组上的双重嵌套循环更复杂的编程问题时，简单性能模型对应用开发者很有帮助。这些模型的目标是通过对特征核中操作次数的简单计数，粗略评估性能，从而为编程选择做出决策。简单性能模型比“三个C”的模型稍微复杂一些。基本过程是计数并记录以下内容：

内存加载和存储（memops）
浮点操作（flops）
连续与非连续内存加载
分支的存在
小循环

我们将计数内存加载和存储（统称为memops）和flops，但也会注意内存加载是否连续以及是否存在可能影响性能的分支。我们还将使用诸如流带宽和通用操作计数等经验数据将计数转化为性能估计。如果内存加载不连续，缓存行中的每8个值中只有1个被使用，因此在这些情况下我们将流带宽除以8。

在本研究的串行部分中，我们将使用具有6 MB L3缓存的MacBook Pro的硬件性能。处理器频率（v）为2.7 GHz。使用第3.2.4节中介绍的流基准代码测得的流带宽为13,375 MB/s。

在有分支的算法中，如果我们几乎总是采取分支，则分支成本很低。当分支不经常采取时，我们会添加分支预测成本（Bc）和可能的预取丢失成本（Pc）。分支预测器的简单模型使用最近几次迭代中最频繁的情况作为可能的路径。如果由于数据局部性而导致分支路径中存在某些聚类，这会降低成本。分支惩罚（Bp）变为NbB f(Bc + Pc)/v。对于典型的体系结构，分支预测成本（Bc）约为16个周期，而缺失预取成本（Pc）经验上约为112个周期。Nb是遇到分支的次数，Bf是分支未命中频率。对于未知长度的小循环的循环开销也会被分配一个成本（Lc）以考虑分支和控制。循环成本估计约为每次退出20个周期。循环惩罚（Lp）变为Lc /v。

我们将在设计研究中使用简单性能模型，研究用于物理模拟的可能的多材料数据结构。该设计研究的目的是在编写任何代码之前确定哪些数据结构将提供最佳性能。过去，这个选择是基于主观判断而不是客观基础。我们研究的特定情况是稀疏情况，即计算网格中有许多材料，但在任何计算单元中只有一种或少数几种材料。我们将在讨论可能的数据布局时参考图4.11中的四种材料的小样本网格。三个单元只有一种材料，而第7个单元有四种材料。

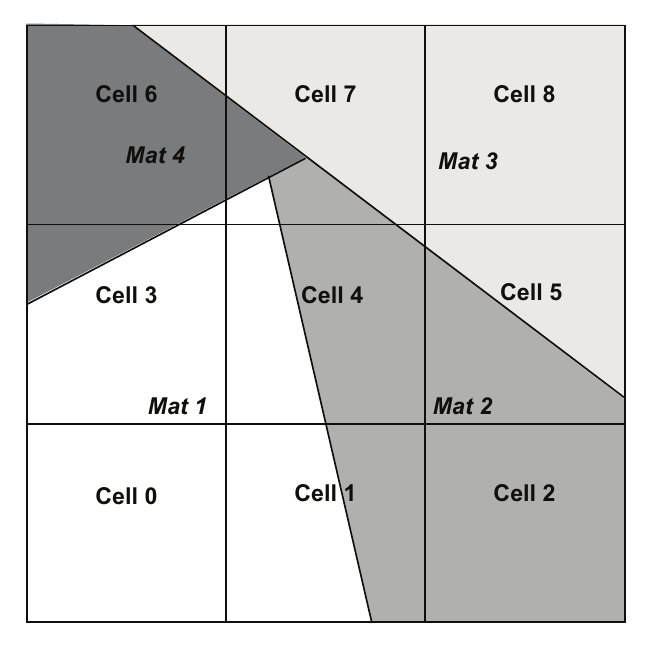图4.11 显示了一个3×3的计算网格，其中单元格7包含四种材料。

数据结构只是故事的一半。我们还需要通过几个具有代表性的核心来评估数据布局：

计算pavg[C]，即网格中单元格的材料平均密度。
使用理想气体定律评估p[C][m]，即每个单元格中每种材料的压力：p(p,t) = nrt/v。

这两种计算的算术强度均为每个字1 flop或更低。我们还预计这些核心将受到带宽限制。我们将使用两个大数据集来测试这些核心的性能。两个数据集均为50种材料（Nm）、100万个单元格问题（Nc），并包含四个状态数组（Nv）。状态数组分别是密度（p）、温度（t）、压力（p）和体积分数（Vf）。这两个数据集是：

几何形状问题：从嵌套矩形材料初始化的网格（图4.12）。该网格是规则的矩形网格。材料位于分开的矩形中而不是散布的，大多数单元格只有一到两种材料。因此，95%的单元格是纯单元格（Pf），5%是混合单元格（Mf）。由于该网格具有一定的数据局部性，因此分支预测失误（Bp）估计约为0.7。
随机初始化问题：一个随机初始化的网格，其中80%的单元格是纯单元格，20%是混合单元格。由于几乎没有数据局部性，分支预测失误（Bp）估计为1.0。

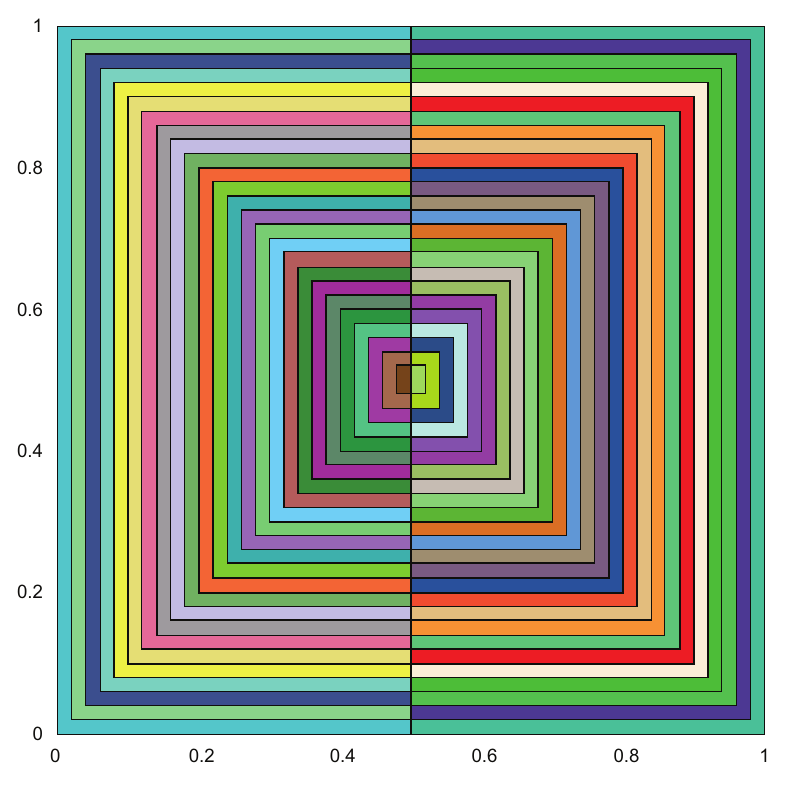图4.12 用于几何形状测试用例初始化网格的五十个嵌套半矩形

在第4.3.1和4.3.2节的性能分析中，有两个主要的设计考虑因素：数据布局和循环顺序。我们将数据布局称为以单元格或材料为中心，具体取决于数据中的较大组织因素。数据布局因子决定了数据顺序中的大步长。我们将循环访问模式称为以单元格或材料为主，以指示哪个是外循环。当数据布局与循环访问模式一致时，情况最好。然而，没有完美的解决方案；一个核心偏好一种布局，而第二个核心偏好另一种布局。

4.3.1 全矩阵数据表示

最简单的数据结构是全矩阵存储表示。这种表示假设每个单元格中都有每种材料。这些全矩阵表示类似于上一节讨论的二维数组。

全矩阵单元格为中心的(CELL-CENTRIC)存储

对于图4.11中的小问题（3x3计算网格），图4.13显示了单元格为中心的数据布局。数据顺序遵循C语言的惯例，每个单元格的材料是连续存储的。换句话说，编程表示是variable[C][m]，其中m变化最快。在图中，阴影元素表示单元格中的混合材料。纯单元格只有一个1.0条目。带有破折号的元素表示该单元格中没有该材料，因此在此表示中给出零。在这个简单示例中，大约一半的条目为零，但在更大问题中，零条目的数量将超过95%。非零条目的数量称为填充分数(filled fraction)（$F_f$），对于我们的设计场景，通常小于5%。因此，如果使用压缩稀疏存储方案，即使考虑到更复杂数据结构的额外存储开销，内存节省也将超过95%。

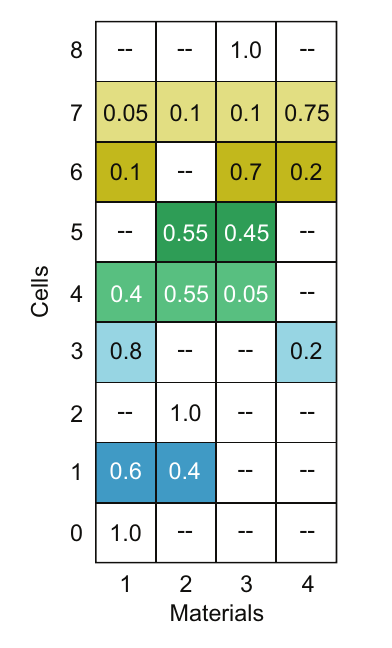图4.13 单元格为中心的全矩阵数据结构，每个单元格的材料连续存储。

全矩阵数据方法的优点是：它更简单，因此更容易并行化和优化。内存节省足够显著，因此可能值得使用压缩稀疏数据结构。但是，这种方法的性能影响是什么？我们可以猜测，把更多的内存用于数据可能会增加内存带宽，从而使全矩阵表示变慢。但是，如果我们测试体积分数，并在其为零时跳过混合材料访问呢？图4.14展示了我们测试这种方法的过程，其中显示了单元格主导循环的伪代码，并在代码行左侧列出了每个操作的计数。单元格主导循环结构在外循环中使用单元格索引，这与单元格为中心的数据结构中的第一个索引一致。

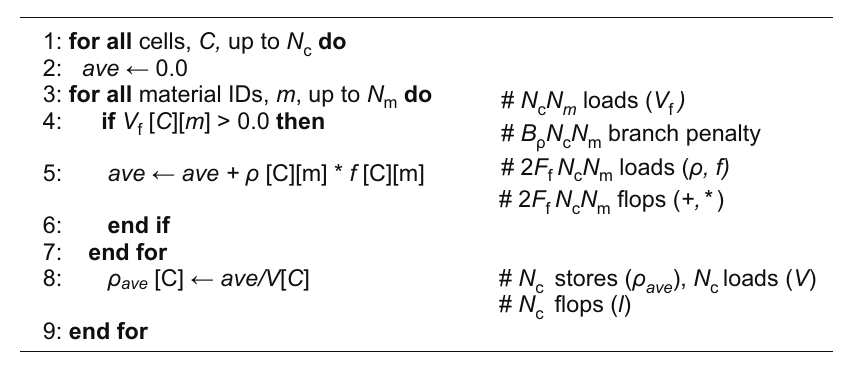图4.14 修改后的单元格主导算法，使用全矩阵存储计算单元格的平均密度。

汇总自图4.14中的行注释（以 # 开头）的计数如下：

如果我们仅考虑浮点运算（flops），我们会认为我们已经很高效，性能将会很出色。但显然，这种算法将主要受内存带宽限制。为了估算内存带宽性能，我们需要考虑分支预测失误。由于分支很少被采用，分支预测失误的概率很高。几何形状问题具有一定的局部性，因此预测失误率估计为0.7。综合这些因素，我们得到如下性能模型（PM）：

【译注：计算过程为， 1e6(50+0.02150+2)8/(133751e6) + 0.7(16+112)/(2.71e9) * 0.021 * 50 * 1e6 = 66.5ms，好像跟67.2ms差了一点。】

分支预测失误的成本使运行时间变长；甚至比我们直接跳过条件并添加零还要高。较长的循环可以摊薄罚成本，但显然，罕见的条件分支并不是最佳的性能方案。我们还可以在条件之前插入预取操作，以在分支被采用的情况下强制加载数据。但这会增加内存操作（memops），因此实际性能提升会很小。它还会增加内存总线上的流量，引发其他问题，特别是在增加线程并行度时导致拥塞。

全矩阵材料为中心的(MATERIAL-CENTRIC)存储

现在让我们看看材料为中心的数据结构（图4.15）。其C语言表示法为variable[m][C]，其中右侧索引C（即单元格）变化最快。在图中，破折号表示填充为零的元素。这种数据结构的许多特性与单元格为中心的全矩阵数据表示相似，但存储索引是反转的。

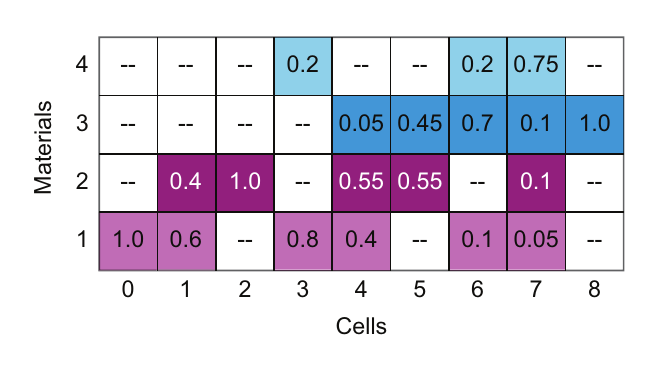图4.15 材料为中心的全矩阵数据结构为每种材料连续存储单元格。C语言中的数组索引表示为density[m][C]，其中单元格索引是连续的。带有破折号的单元格填充为零。

计算每个单元格平均密度的算法可以通过连续的内存加载和一些思考来完成。实现此算法的自然方法是让外循环遍历单元格，在那里将其初始化为零，并在最后除以体积。但这会以非连续的方式遍历数据。我们希望在内循环中遍历单元格，这需要在主循环之前和之后分别进行循环。图4.16展示了该算法，并附有内存操作（memops）和浮点运算（flops）的注释。

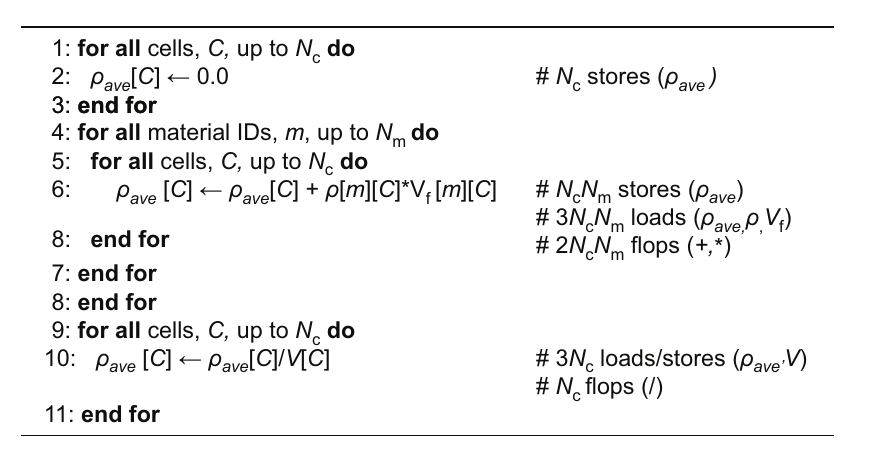图4.16 材料主导算法，使用全矩阵存储计算单元格的平均密度。

收集所有操作的注释，我们得到：

这个内核受限于带宽，因此其性能模型为：

这个内核的性能是单元格为中心数据结构的一半。但这个计算内核偏向于单元格为中心的数据布局，而在压力计算中情况则相反。

4.3.2 压缩稀疏存储表示

现在我们将讨论几种压缩存储表示的优缺点。压缩稀疏存储数据布局显然节省了内存，但设计单元格为中心和材料为中心的布局都需要一些思考。

单元格为中心的压缩稀疏存储

标准方法是为每个单元格建立一个材料的链表。但链表通常很短，并且在内存中跳来跳去。解决方案是将链表放入一个连续的数组中，链接指向材料条目的起始位置。下一个单元格的材料紧接在其后。因此，在正常遍历单元格和材料时，这些将以连续顺序访问。图4.17显示了单元格为中心的数据存储方案。纯单元格的值保存在单元格状态数组中。在图中，1.0表示纯单元格的体积分数，但它也可以是纯单元格的密度、温度和压力值。第二个数组是混合单元格中的材料数量。-1表示这是一个纯单元格。然后材料链表索引imaterial在第三个数组中。如果它小于1，则条目的绝对值是混合数据存储数组的索引。如果它是1或更大，则它是压缩纯单元格数组的索引。

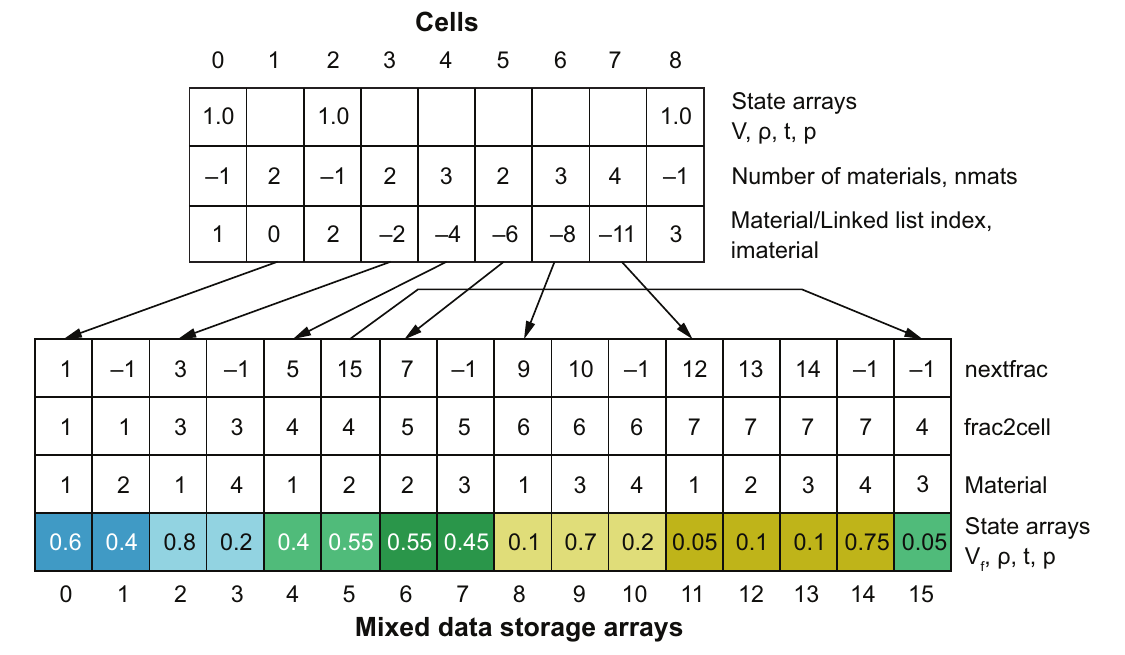图4.17 单元格为中心数据结构的混合材料数组使用在连续数组中实现的链表。底部不同的阴影表示属于特定单元格的材料，并与图4.13中使用的阴影相匹配。

混合数据存储数组基本上是一个在标准数组中实现的链表，以便数据是连续的，从而具有良好的缓存性能。混合数据从一个叫做nextfrac的数组开始，该数组指向该单元格的下一个材料。这使得可以通过将这些材料添加到数组末尾来在单元格中添加新材料。图4.17显示了单元格4的混合材料列表，其中箭头显示第三个材料添加在末尾。frac2cell数组是指向包含该材料的单元格的反向映射。第三个数组，material，包含条目的材料编号。这些数组提供了在压缩稀疏数据结构中导航的方式。第四个数组是每个单元格中每个材料的状态数组集，包括体积分数（Vf）、密度（ρ）、温度（t）和压力（p）。

混合材料数组在数组末尾保留额外内存，以便快速添加新的材料条目。删除数据链接并将其设置为零来删除材料。为了获得更好的缓存性能，这些数组会定期重新排序到连续的内存中。

图4.18显示了计算压缩稀疏数据布局的每个单元格平均密度的算法。我们首先获取材料索引imaterial，看看它是否为零或更小以判断这是一个混合材料单元格。如果是纯单元格，我们不做任何处理，因为我们已经在单元格数组中有了密度。如果是一个混合材料单元格，我们进入循环，求和每个材料的密度乘以体积分数。我们测试索引变为负数的结束条件，并使用nextfrac数组获取下一个条目。一旦我们到达列表的末尾，我们计算单元格的密度（ρ）。在代码行的右侧是操作成本的注释。

图4.18 使用紧凑存储计算平均单元格密度的单元格为主算法

代码行右侧是操作成本的注释。在本分析中，我们将有4字节的整数加载，因此我们将memops转换为membytes。收集计数后，我们得到如下结果：

【译注，原文有错误，漏乘了$M_L$，也就是元素的个数(循环的总次数)。 (4 + 2 * .04895 * 8) + 20 * 97970/1e6 = 6.74 】

同样，这个算法受限于内存带宽。性能模型估算的运行时间比全单元格为中心的矩阵减少了98%。

以材料为中心的压缩稀疏存储结构

以材料为的压缩稀疏存储结构将所有内容细分为单独的材料。回到图4.9中的小测试问题，我们看到材料1有六个单元：0, 1, 3, 4, 6和7（如图4.19中的子集1所示）。子集中有两个映射：一个从网格到子集，即mesh2subset，另一个从子集回到网格，即subset2mesh。子集到网格的列表包含这六个单元的索引。网格数组中对于每个没有该材料的单元标记为-1，而对于有该材料的单元则按顺序编号以映射到子集。图4.19顶部的nmats数组包含每个单元包含的材料数量。图右侧的体积分数（Vf）和密度（ρ）数组则记录了该材料中每个单元的数值。在C语言中，这些可以表示为Vf[imat][icell]和p[imat][icell]。由于材料相对较少且单元列表较长，我们可以使用常规的二维数组分配，而不必强制将它们变为连续的。要操作这种数据结构，我们大多依次处理每个材料子集。

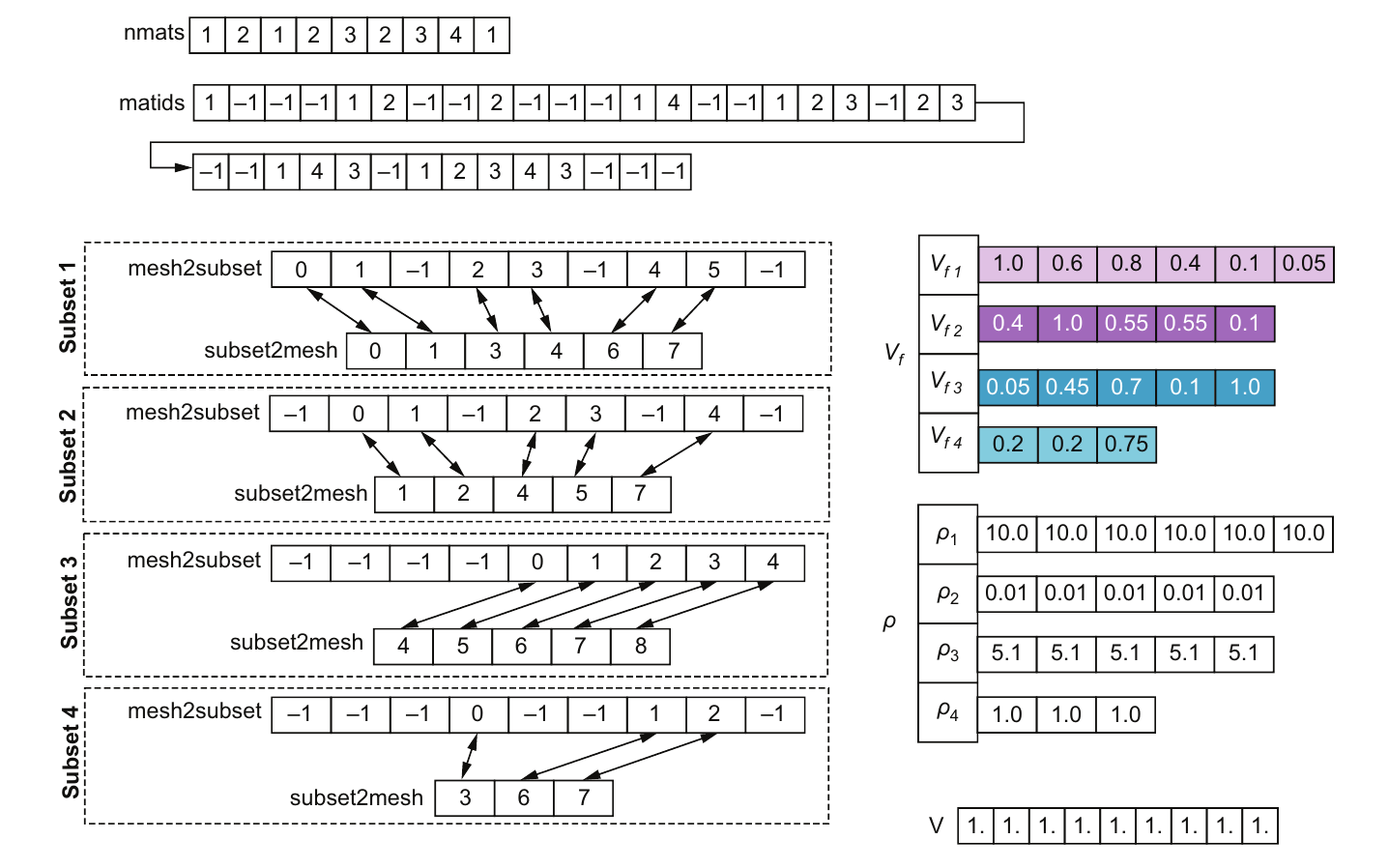图4.19 材料中心的压缩稀疏数据布局是围绕材料组织的。对于每种材料，都有一个包含该材料的单元列表的可变长度数组。阴影部分与图4.15中的阴影部分相对应。该图展示了在全网格和子集之间的映射关系，以及每个子集的体积分数和密度变量。

图4.20 材料主导算法使用材料中心的紧凑存储方案计算单元的平均密度。

图4.20中的材料中心压缩稀疏算法与图4.13中的算法相似，增加了第5、6和8行中的指针检索。但内循环中的加载和浮点运算仅针对网格的材料子集，而不是整个网格。这大大节省了浮点运算和内存操作。收集所有计数后，我们得到如下结果：

【 5 * 8 * 0.021 * 50 + 32 + 很小可以忽略 = 74M bytes 】

性能模型显示，与材料中心的全矩阵数据结构相比，预计运行时间减少了95%以上：

表4.1总结了这四种数据结构的结果。估计的运行时间和测量的运行时间之间的差异非常小。这表明，即使是粗略的内存加载计数也可以很好地预测性能。

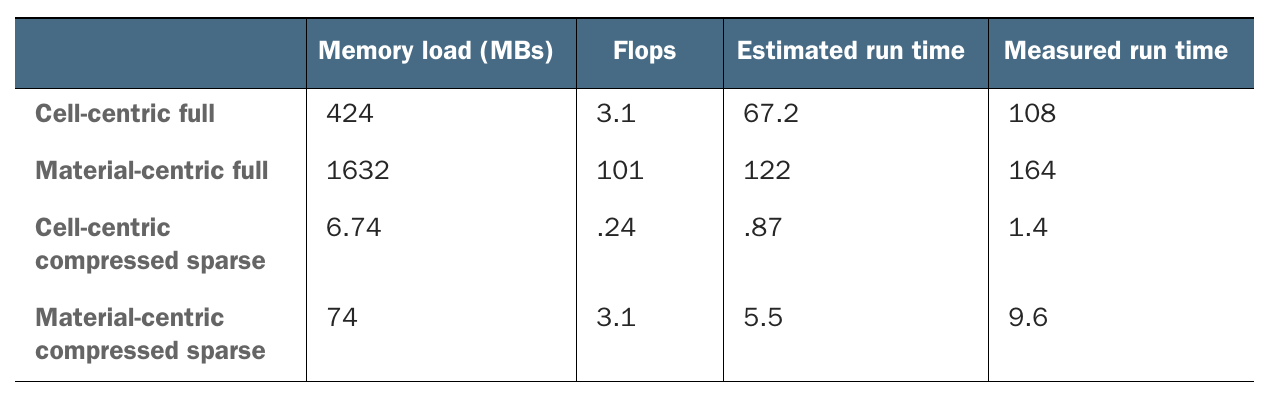表4.1 稀疏数据结构比完整的二维矩阵更快且占用更少的内存。

压缩稀疏表示法的优势显著，既节省了内存又提高了性能。因为我们分析的内核更适合单元中心的数据结构，所以单元中心的压缩稀疏数据结构在内存和运行时间方面都是最佳的。如果我们看一下显示材料中心数据布局的其他内核，结果稍微有利于材料中心的数据结构。但重要的是，任一压缩稀疏表示法都比全矩阵表示法有很大的改进。

虽然此案例研究集中在多材料数据表示上，但许多具有稀疏数据的应用可以从添加压缩稀疏数据结构中受益。类似于本节中所做的快速性能分析可以确定这些应用中是否值得付出额外的努力。

4.4 高级性能模型

还有一些更先进的性能模型可以更好地捕捉计算机硬件的各个方面。我们将简要介绍这些高级模型，以理解它们提供了什么以及可能的经验教训。性能分析的细节并不像得到的结论那么重要。

在本章中，我们主要关注带宽受限的内核，因为这些代表了大多数应用程序的性能限制。我们计算了内核加载和存储的字节数，并根据流基准测试或屋顶线模型（第3章）估算了这些数据移动所需的时间。到现在为止，你应该意识到计算机硬件的操作单位实际上并不是字节或字，而是缓存行，我们可以通过计算需要加载和存储的缓存行来改进性能模型。同时，我们可以估算使用了多少缓存行。

流基准测试实际上由四个独立的内核组成：复制、缩放、加法和三元运算(triad)内核。那么，为什么这些内核的带宽（16156.6–22086.5 MB/s）会有所不同，如3.2.4节的STREAM基准测试中所见？当时暗示其原因是内核之间算术强度的差异，如3.2.4节的表格所示。这只是一部分原因。只要我们处于带宽受限的状态，算术操作的微小差异实际上是相当次要的影响。与算术操作的相关性也不高。为什么缩放操作的带宽最低？真正的问题在于系统的缓存层次结构细节。缓存系统不像流基准测试所暗示的那样像水管中稳步流动的水。它更像是一种水桶接力，将数据通过不同的缓存层级传递，如图4.21所示。这正是Treibig和Hager开发的执行缓存内存（ECM）模型试图捕捉的内容。虽然它需要了解硬件架构，但它可以非常准确地预测流内核的性能。不同层级之间的移动可能受到单个周期内可以执行的操作（μops，称为微操作）数量的限制。ECM模型以缓存行和周期为单位，模拟不同缓存层级之间的移动。

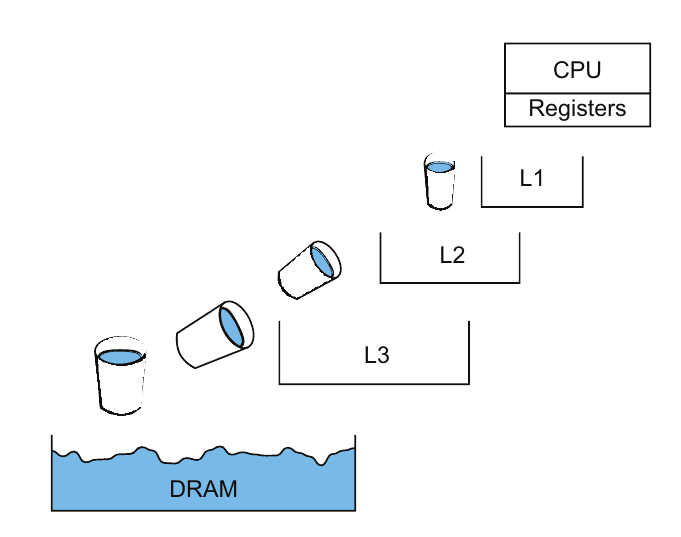图4.21 缓存层级之间的数据移动是一系列离散操作，更像是水桶接力而不是通过管道的流动。硬件的细节以及每个层级和每个方向上可以发出的加载数量在很大程度上影响了通过缓存层次加载数据的效率。

让我们快速看一下流三元运算的ECM模型（A[i] = B[i] + s*C[i]），看看这个模型是如何工作的（图4.22）。这个计算必须针对特定的内核和硬件来完成。我们将使用Haswell EP系统作为本次分析的硬件。我们从计算核心开始，方程为Tcore = max(TnOL ,TOL)，其中T表示周期时间。TOL通常是与数据传输时间重叠的算术操作，TnOL是非重叠的数据传输时间。

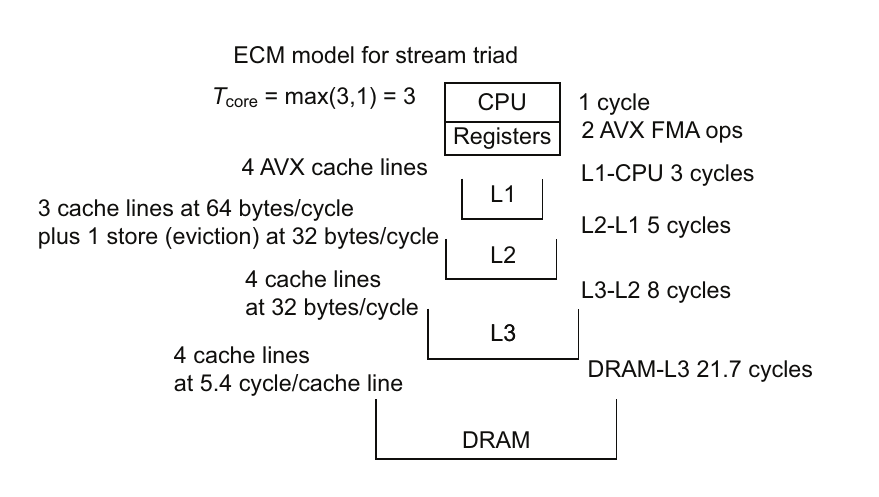图 4.22 针对 Haswell 处理器的执行缓存内存 (ECM) 模型提供了流三重计算在缓存层级之间的数据传输详细时间。如果数据位于主存储器中，将数据传输到 CPU 所需的时间是每个缓存层级之间传输时间的总和，即 21.7 + 8 + 5 + 3 = 37.7 个周期。浮点运算只需要 3 个周期，因此内存加载是流三重计算的限制因素。

对于流三元运算，我们有一个乘加操作的缓存行。如果这是通过标量操作完成的，需要8个周期。但我们可以使用新的高级矢量扩展（AVX）指令来完成。Haswell芯片有两个融合乘加（FMA）AVX 256位矢量单元。每个单元处理四个双精度值。缓存行中有八个值，因此两个FMA AVX矢量单元可以在一个周期内处理完这些值。TnOL是数据传输时间。我们需要加载B和C的缓存行，并且需要加载和存储A的缓存行。由于地址生成单元（AGUs）的限制，这对于Haswell芯片来说需要3个周期。

将四个缓存行从L2移动到L1，以64字节/周期的速度需要4个周期。但使用A[i]是一个存储操作。存储通常需要一个特殊的加载，称为写分配（write-allocate），即在虚拟数据管理器中分配内存空间，并在必要的缓存层级创建缓存行。然后数据被修改并从缓存中逐出（存储）。在这个缓存层级，这只能以32字节/周期的速度操作，导致额外的一个周期，总共5个周期。从L3到L2，数据传输速度为32字节/周期，因此需要8个周期。最后，使用测得的27.1 GB/s带宽，从主存储器移动缓存行需要大约21.7个周期。ECM使用这种特殊的表示法来总结这些数字：

Tcore 由表示的 TOL || TnOL 显示。这些基本上是移动到每个层级所需的时间（以周期为单位），Tcore 是一个特例，因为计算核心上的一些操作可以与从 L1 到寄存器的数据传输操作重叠。然后，该模型通过总结数据传输时间（包括从 L1 到寄存器的非重叠数据传输）来预测从缓存的每个层级加载所需的周期数。然后，使用 TOL 和数据传输时间的最大值作为预测时间：

这种特殊的 ECM 表示法显示了每个缓存层级的预测结果：

这种表示法表明，当内核从 L1 缓存中运行时需要 3 个周期，从 L2 缓存中运行时需要 8 个周期，从 L3 缓存中运行时需要 16 个周期，而当数据必须从主存储器中检索时需要 37.7 个周期。

从这个例子中可以了解到的是，在特定芯片上运行特定内核时碰到的离散硬件限制可能会在缓存层级之间的某次传输中多出一个或两个周期，导致性能变慢。稍微不同版本的处理器可能没有同样的问题。例如，英特尔芯片的后续版本增加了另一个 AGU，这将 L1-寄存器周期从 3 改为 2。

这个例子还表明，矢量单元对算术操作和数据移动都有价值。矢量加载，也称为四倍加载操作，并不是新概念。关于矢量处理器的讨论大多集中在算术操作上。但对于带宽受限的内核，矢量内存操作可能更为重要。Stengel 等人通过 ECM 模型的分析表明，AVX 矢量指令可以比编译器天真地安排的循环性能提高两倍。这可能是因为编译器没有足够的信息。更新的矢量单元还实现了 gather/scatter 内存加载操作，其中加载到矢量单元的数据不必在连续的内存位置（gather），从矢量存储到内存的位置也不必是连续的（scatter）。

注意这种新的 gather/scatter 内存加载功能受到欢迎，因为许多实际的数值模拟代码需要它来获得良好的性能。但目前的 gather/scatter 实现仍然存在性能问题，需要进一步改进。

我们还可以分析缓存层次结构与流存储的性能。流存储绕过缓存系统并直接写入主存储器。大多数编译器都有使用流存储的选项，一些编译器会将其作为优化自行调用。它的作用是减少在缓存层次结构之间移动的缓存行数量，减少拥塞和层级之间较慢的驱逐操作。现在你已经看到了缓存行移动的影响，应该能够理解其价值。

ECM 模型用于评估和优化由几位研究人员提出的模板内核。模板内核是流操作，可以使用这些技术进行分析。要跟踪所有缓存行和硬件特性而不出错有点乱，所以性能计数工具可以帮助我们。我们会在附录 A 中列出一些参考资料以获取更多信息。

高级模型非常适合理解相对简单的流内核的性能。流内核是那些以接近最佳的方式加载数据以有效利用缓存层次结构的内核。但科学和 HPC 应用中的内核通常复杂，带有条件语句、不完美嵌套的循环、归约和循环携带依赖关系。此外，编译器可以以意想不到的方式将高级语言转换为汇编操作，这使得分析更加复杂。通常还有很多内核和循环需要处理。没有专门的工具，分析这些复杂的内核是不可行的，因此我们尝试从简单内核中开发出可以应用于更复杂内核的一般思路。

4.5 网络消息

我们可以扩展我们的数据传输模型，用于分析计算机网络。一个简单的集群或高性能计算系统节点之间的网络性能模型是注意，这是网络带宽，而不是我们一直使用的内存带宽。有一个关于延迟和带宽的高性能计算基准网站，网址为 http://icl.cs.utk.edu/hpcc/hpcc_results_lat_band.cgi

我们可以使用来自高性能计算基准网站的网络微基准来获取典型的延迟和带宽数据。我们将使用 5 微秒的延迟和 1 GB/s 的带宽。这给出了图 4.23 中显示的图表。对于更大的消息，我们可以估计每传输 1 MB 大约需要 1 秒。但绝大多数消息都很小。我们分别看两个不同的通信示例，一个是较大的消息，另一个是较小的消息，以了解每种情况下延迟和带宽的重要性。

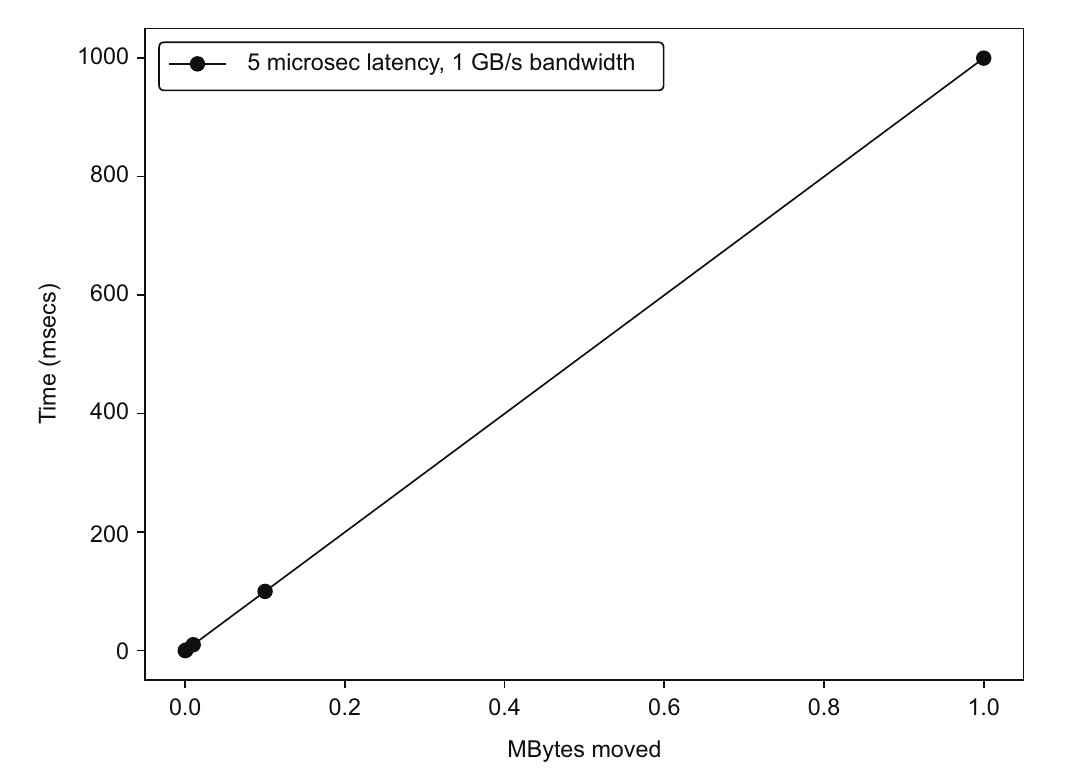图 4.23 典型网络传输时间与消息大小的关系，给出了一个经验法则：1 MB 需要 1 秒，1 KB 需要 1 毫秒，或者 1 字节需要 1 微秒。

示例：Ghost 单元通信

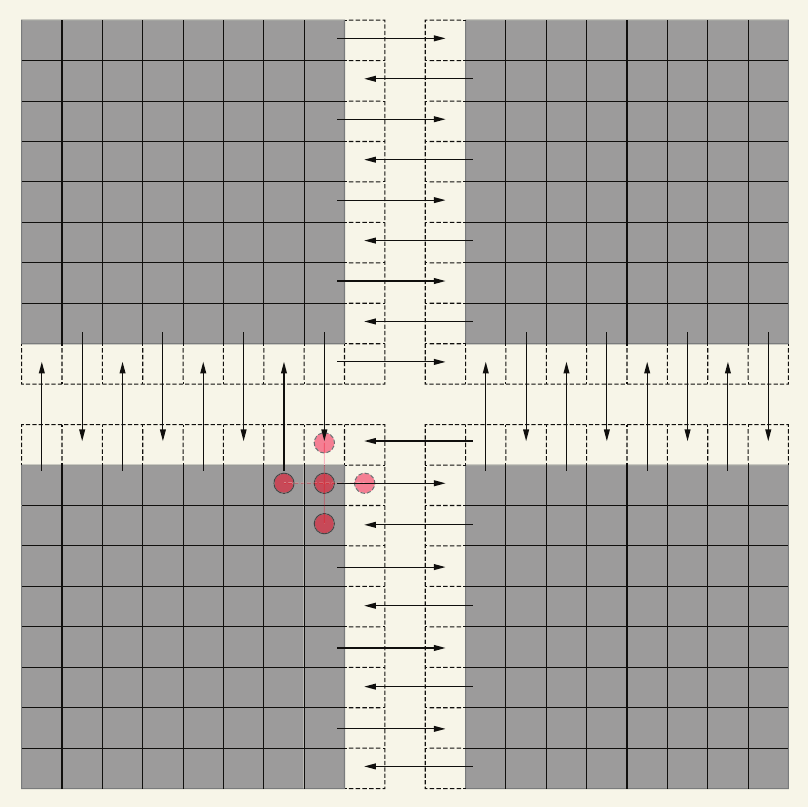
我们采用一个 1000×1000 的网格。我们需要将处理器外部的单元（如下图所示）与相邻的处理器进行通信，以便它可以完成其计算。放置在网格外部的额外单元被称为 Ghost 单元。

1000 个单元在外部 * 8 字节 = 8 KB

通信时间 = 5 微秒 + 8 毫秒

外部单元数据与相邻处理器交换，以便在当前值上进行标量计算。虚线单元称为 Ghost 单元，因为这些单元保存了来自另一个处理器的重复数据。箭头仅显示每个单元之间的数据交换，以便更清楚地看到。

示例：跨处理器求单元数总和

我们需要将单元数传输给相邻的处理器进行求和，然后返回总和。这是两次传输 4 字节整数。

通信时间 = (5 微秒 + 4 微秒) * 2 = 18 微秒

在这种情况下，延迟对于消息传输的整体时间起到了重要作用。

最后一个求和示例是计算机科学术语中的减少操作。处理器之间的单元计数数组被减少为一个值。更一般地说，减少操作是指将从 1 到 N 维度的多维数组减少至少一维，通常是减少到标量值。这些是并行计算中常见的操作，涉及处理器之间的合作以完成。此外，最后一个示例中的减少求和可以以树状模式进行成对方式执行，通信跳数为 $\log_2N$，其中 N 是排名（处理器）的数量。当处理器数量增加到数千个时，操作的时间变得更长。也更重要的是，所有处理器都必须在操作时进行同步，导致许多处理器等待其他处理器到达减少调用的位置。

网络消息还有更复杂的模型可能对于特定的网络硬件有用。但是，网络硬件的细节差异很大，这些模型可能无法对所有可能的硬件的一般行为提供太多见解。