第十章：规约

目录

• 10.1 背景
• 10.2 规约 trees
• 10.3 一个简单的规约内核
• 10.4 最小化控制分歧
• 10.5 最小化内存分歧
• 10.6 减少全局内存访问
• 适合任意输入长度的层次化规约
• 10.6 线程粗化以减少开销
• 10.9 总结

规约 从一个值数组中得出一个单一值。这个单一值可以是总和、最大值、最小值等所有元素中的某一个。这个值也可以是各种类型的：整数、单精度浮点数、双精度浮点数、半精度浮点数、字符等。所有这些类型的 规约 都有相同的计算结构。就像直方图一样，规约 是一种重要的计算模式，因为它从大量数据中生成摘要。并行 规约 是一种重要的并行模式，它需要并行线程彼此协调以获得正确的结果。这种协调必须小心进行，以避免在并行计算系统中常见的性能瓶颈。因此，并行 规约 是一个很好的工具，可以说明这些性能瓶颈，并介绍减轻它们的技术。

10.1 背景

从数学上讲，如果运算符具有明确定义的单位值，就可以基于二元运算符定义一组项的 规约。例如，浮点加法运算符具有单位值 0.0；也就是说，任何浮点值 v 和值 0.0 的加法结果是 v 本身。因此，可以基于加法运算符为一组浮点数定义 规约，该运算符产生集合中所有浮点数的总和。例如，对于集合 {7.0, 2.1, 5.3, 9.0, 11.2}，总和 规约 将产生 7.0+2.1+5.3+9.0+11.2 = 34.6。

通过顺序遍历数组的每个元素，可以执行 规约。图 10.1 显示了在 C 中的顺序总和 规约 代码。该代码将结果变量 sum 初始化为单位值 0.0。然后，它使用 for 循环来迭代保存值集合的输入数组。在第 i 次迭代期间，代码对 sum 的当前值和输入数组的第 i 个元素执行加法运算。在我们的示例中，在第 0 次迭代之后，sum 变量包含 0.0+7.0 = 7.0。在第 1 次迭代之后，sum 变量包含 7.0+2.1 = 9.1。因此，每次迭代之后，输入数组的另一个值将被添加（累积）到 sum 变量中。在第 5 次迭代之后，sum 变量包含 34.6，这是 规约 结果。

图10.1 一个简单的总和 规约 顺序代码。

可以为许多其他运算符定义 规约。可以为浮点乘法运算符定义一个乘积 规约，其单位值为 1.0。一组浮点数的乘积 规约 是所有这些数的乘积。可以为最小（min）比较运算符定义一个最小（min）规约，该运算符返回两个输入中较小的值。对于实数，最小运算符的单位值为正无穷大。可以为最大（max）比较运算符定义一个最大（max）规约，该运算符返回两个输入中较大的值。对于实数，最大运算符的单位值为负无穷大。

图10.2 一个 规约 顺序代码的一般形式。

图 10.2 显示了运算符的 规约 的一般形式，该形式被定义为接受两个输入并返回一个值的函数。在 for 循环的迭代期间访问元素时，所采取的操作取决于正在执行的 规约 类型。例如，对于最大（max）规约，Operator 函数执行两个输入之间的比较，并返回两者中的较大值。对于最小（min）规约，operator 函数比较两个输入的值，并返回较小的值。当 for 循环访问所有元素时，顺序算法结束。对于一组 N 个元素，for 循环迭代 N 次，并在循环退出时生成 规约 结果。

10.2 规约 trees

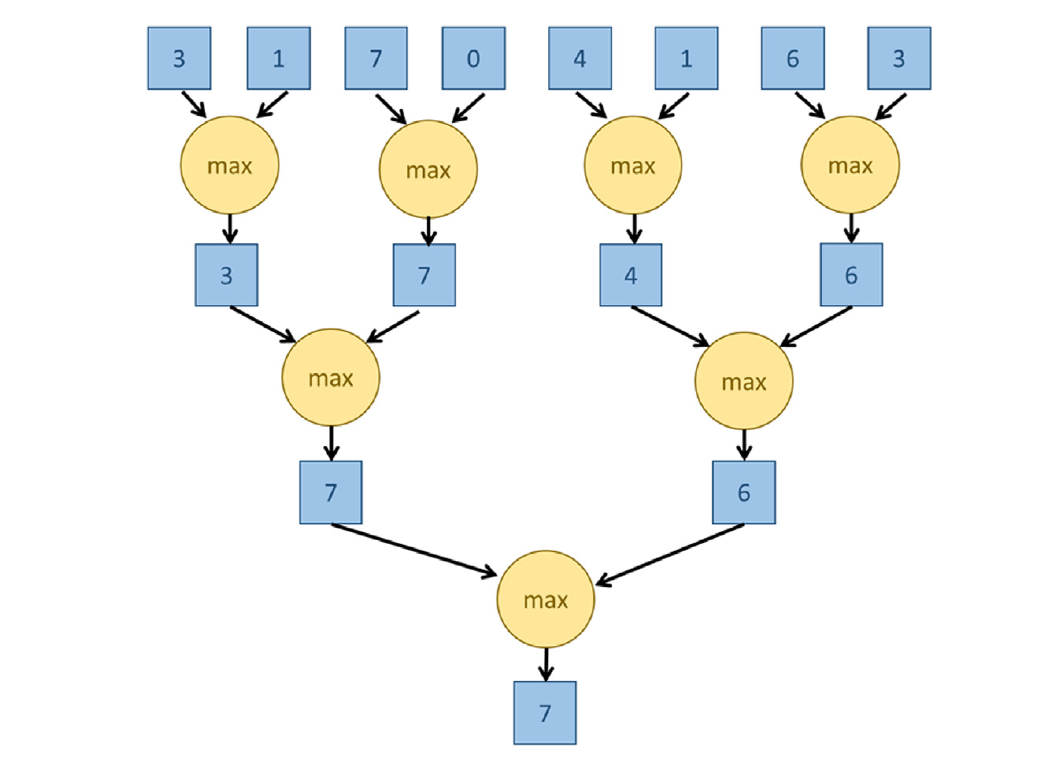
并行 规约 算法在文献中已经得到了广泛的研究。并行 规约 的基本概念如图 10.3 所示，在竖直方向上时间向下推移，线程在每个时间步骤中并行执行的活动在水平方向上显示出来。

图10.3 一个并行max recution树

在第一轮（时间步骤）中，对原始元素的四对进行了四次 max 操作。这四个操作产生了部分 规约 结果：来自四对原始元素的四个较大值。在第二个时间步骤中，对部分 规约 结果的两对进行了两次 max 操作，并产生了两个更接近最终 规约 结果的部分结果。这两个部分结果分别是第一组四个元素中的最大值和原始输入中第二组四个元素的最大值。在第三和最后的时间步骤中，执行一次 max 操作生成最终结果，即原始输入中的最大值 7。

注意，执行操作的顺序将从顺序 规约 算法变为并行 规约 算法。例如，对于图 10.3 顶部的输入，顺序 max 规约 类似于图 10.2 中的顺序 max 规约，首先将单位值（2N）与输入值 3 进行比较，并用获胜者更新单位值，即 3。然后，它将输入值 1 与单位值 (3) 进行比较，并用获胜者 3 更新单位值。接下来，将输入值 7 与单位值 (3) 进行比较，并用获胜者 7 更新单位值。然而，在图 10.3 的并行 规约 中，首先将输入值 7 与输入值 0 进行比较，然后再与 3 和 1 的最大值进行比较。

正如我们所见，并行 规约 假定应用运算符到输入值的顺序无关紧要。在 max 规约 中，无论应用运算符到输入值的顺序如何，结果都将是相同的。如果运算符是结合的，这种性质在数学上是保证的。如果运算符 Θ 是结合的，则（a Θ b）Θ c = a Θ（b Θ c）。例如，整数加法是结合的 ((1+2)+3 = 1+(2+3) = 6)，而整数减法不是结合的 ((1-2)-2) ≠ (1-(2-2))。也就是说，如果运算符是结合的，可以在涉及运算符的表达式的任意位置插入括号，结果都是相同的。通过这种等价关系，可以将任何运算符应用顺序转换为任何其他顺序，同时保持结果的等价性。严格来说，浮点加法不是结合的，因为引入括号的不同方式可能会产生舍入结果。然而，大多数应用程序接受浮点运算结果如果它们彼此之间的差异在可容忍范围内，则视为相同。这样的定义允许开发人员和编译器编写者将浮点加法视为结合运算符。感兴趣的读者可参考附录 A 进行详细处理。

从图 10.2 的顺序 规约 转换为图 10.3 的 规约 tree 需要运算符是结合的。我们可以将 规约 视为操作列表。图 10.2 和图 10.3 之间的操作顺序的差异只是在同一个列表的不同位置插入括号。对于图 10.2，括号是：

((((((3 max 1) max 7) max 0) max 4) max 1) max 6) max 3

而图 10.3 的括号是：

((3 max 1) max (7 max 0)) max ((4 max 1) max (6 max 3))

我们将在第 10.4 节应用一种优化，不仅重新排列应用运算符的顺序，还重新排列操作数的顺序。要重新排列操作数的顺序，此优化进一步要求运算符是可交换的。如果 a Θ b = b Θ a，则运算符 Θ 是可交换的。也就是说，可以在表达式中重新排列操作数的位置，结果都是相同的。请注意，max 运算符也是可交换的，许多其他运算符如 min、sum 和 product 也是可交换的。显然，并非所有运算符都是可交换的。例如，加法是可交换的 (1+2 = 2+1)，而整数减法不是 (1-2 ≠ 2-1)。

图 10.3 中的并行 规约 模式被称为 规约 tree，因为它看起来像一棵树，其叶子是原始输入元素，根节点是最终结果。术语 规约 tree 不应与树数据结构混淆，在树数据结构中，节点要么显式与指针链接，要么隐式与分配的位置链接。在 规约 tree 中，边是概念上的，反映了从一个时间步骤中执行的操作到下一个时间步骤中执行的操作的信息流。

并行操作在产生最终结果所需的时间步骤数量方面显著改进了顺序代码。在图 10.3 的示例中，顺序代码中的 for 循环迭代八次，或者说花费八个时间步骤来访问所有输入元素并生成最终结果。另一方面，在图 10.3 中的并行操作中，并行 规约 tree 方法仅需要三个时间步骤：第一个时间步骤中进行四次 max 操作，第二个时间步骤中进行两次操作，第三个时间步骤中进行一次操作。这是时间步骤数量减少了 5/8 即 62.5%，或者说加速了 8/3 即 2.67 倍。当然，并行方法也有成本：必须有足够的硬件比较器来在同一时间步骤中执行最多四次 max 操作。对于 N 个输入值，规约 tree 在第一轮中执行 1/2 N 次操作，在第二轮中执行 1/4 N 次操作，依此类推。因此，执行的总操作数由几何级数 1/2 N + 1/4 N + 1/8 N + … + 1/N N 确定，这与顺序算法类似。

就时间步骤而言，规约 tree 需要 $\log_2 N$ 步来完成 N 个输入值的 规约 过程。因此，它可以在只需十个步骤的情况下将 N = 1024 个输入值减少为一个结果，前提是有足够的执行资源。在第一步，我们需要 1/2 N = 512 个执行资源！请注意，随着时间步骤的推进，所需资源数量迅速减少。在最后一个时间步骤中，我们只需要一个执行资源。每个时间步骤的并行性水平与所需的执行单元数量相同。计算所有时间步骤的平均并行性是有趣的。平均并行性是执行的总操作数除以时间步骤的数量，即 $(N - 1) / log_2 N$。对于 N = 1024，在十个时间步骤中的平均并行性为 102.3，而峰值并行性为 512（在第一个时间步骤中）。在时间步骤之间并行性和资源消耗水平的变化使得 规约 trees 对于并行计算系统来说是一个具有挑战性的并行模式。

图10.5 一个并行sum recution树

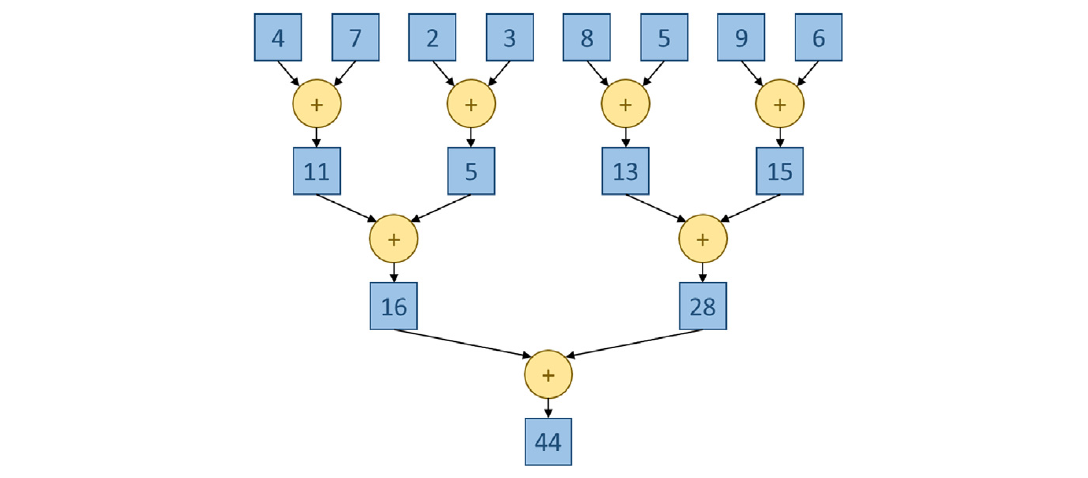
图 10.5 展示了一个包含八个输入值的总和 规约 tree 示例。到目前为止，关于 max 规约 tree 所需的时间步骤数量和资源消耗的一切，也适用于总和 规约 tree。完成这种 规约 需要 $log_2 8 = 3$ 个时间步骤，最多使用四个加法器。我们将使用这个示例来说明总和 规约 kernels 的设计。

并行规约在体育和竞赛中的应用

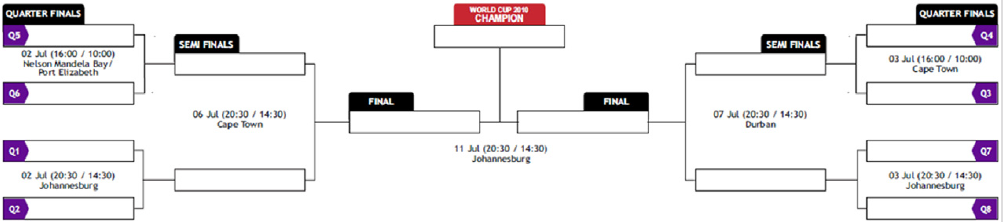
并行 规约 在体育比赛中早在计算机时代之前就被广泛应用。图 10.4 显示了2010年世界杯在南非的四分之一决赛、半决赛和决赛的赛程安排。很明显，这只是一个重新排列的 规约 tree。世界杯的淘汰过程是一个最大值 规约，在这个过程中，最大值运算符返回“击败”另一支球队的球队。锦标赛的“规约”过程分为多个回合进行。球队被分成一对对。在第一轮中，所有的对都同时进行比赛。第一轮的获胜者晋级到第二轮，第二轮的获胜者晋级到第三轮，依此类推。在一个锦标赛中有八支球队参赛时，第一轮（图 10.4 中的四分之一决赛）将产生四个获胜者，第二轮（图 10.4 中的半决赛）将产生两个获胜者，第三轮（图 10.4 中的决赛）将产生一个最终获胜者（冠军）。每个回合都是 规约 过程的一个时间步骤。

图10.4 2010年世界杯的recution树

很容易看出，即使有1024支球队参赛，也只需要10轮比赛就能确定最终获胜者。关键在于要有足够的资源来在第一轮比赛中并行进行512场比赛，在第二轮进行256场比赛，在第三轮进行128场比赛，依此类推。有足够的资源，即使有6万支球队，我们也可以在仅16轮比赛中确定最终获胜者。值得注意的是，虽然 规约 tree 可以极大地加快 规约 过程，但也会消耗大量资源。以世界杯为例，一场比赛需要一个大型足球场、裁判和工作人员，以及酒店和餐厅来容纳庞大的观众人数。图 10.4 中的四分之一决赛在三个城市（尼尔森·曼德拉湾/伊丽莎白港、开普敦和约翰内斯堡）进行，这些城市共同提供了足够的资源来举办四场比赛。请注意，约翰内斯堡的两场比赛是在两天不同的时间进行的。因此，在两场比赛之间共享资源使得 规约 过程需要更长的时间。在计算 规约 tree 中，我们也会看到类似的权衡考虑。

10.3 一个简单的规约内核

我们现在准备开发一个简单的核函数来执行图 10.5 中展示的并行总和 规约 tree。由于 规约 tree 需要所有线程之间的协作，而整个网格无法实现这种协作，因此我们将从实现一个在单个块内执行总和 规约 tree 的核函数开始。也就是说，对于一个包含 N 个元素的输入数组，我们将调用这个简单的核函数并启动一个由 1/2N 个线程组成的块的网格。由于一个块最多可以有 1024 个线程，我们可以处理最多 2048 个输入元素。我们将在第 10.8 节中消除这种限制。在第一个时间步骤中，所有的 1/2N 个线程将参与，每个线程将添加两个元素来生成 1/2N 个部分和。在下一个时间步骤中，一半的线程将退出，只剩下 1/4N 个线程继续参与生成 1/4N 个部分和。这个过程将持续到最后一个时间步骤，在这个时间步骤中，只剩下一个线程将产生总和。

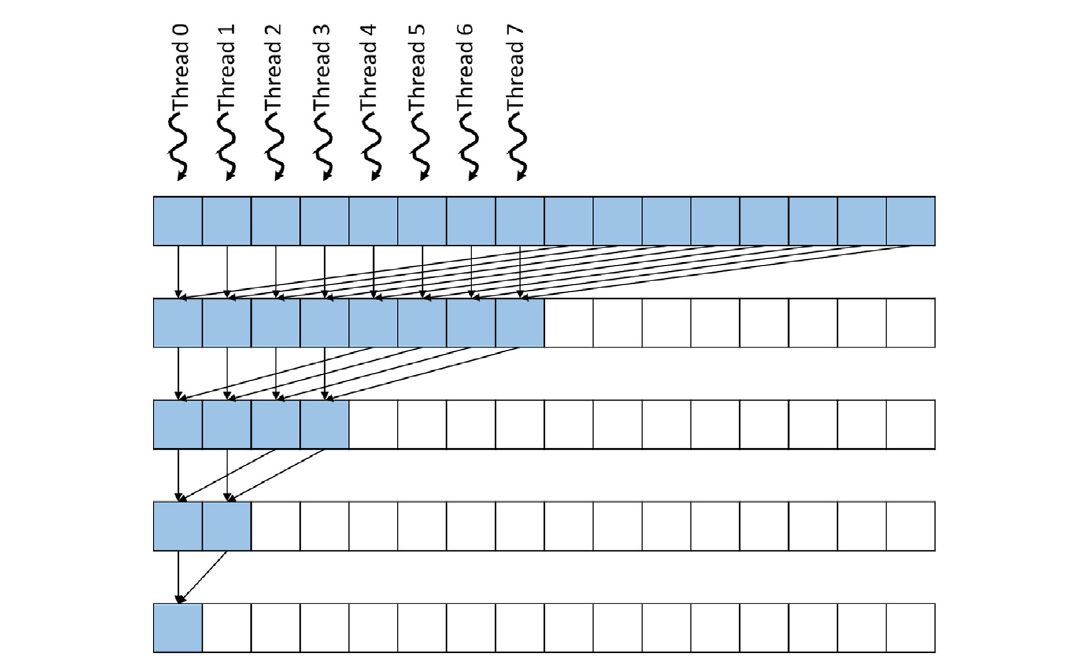
图 10.6 显示了简单总和核函数的代码，图 10.7 展示了由该代码实现的 规约 tree 的执行过程。请注意，在图 10.7 中，时间从上到下逐步进行。我们假设输入数组位于全局内存中，并且在调用核函数时作为参数传递了一个指向数组的指针。每个线程被分配到一个数据位置，即 2 * threadIdx.x（第 02 行）。也就是说，线程被分配到输入数组中的偶数位置：线程 0 被分配到 input[0]，线程 1 被分配到 input[2]，线程 2 被分配到 input[4]，依此类推，如图 10.7 顶部一行所示。每个线程将成为分配给它的位置的“所有者”，并且将是唯一写入该位置的线程。核函数的设计遵循“所有者计算”方法，即每个数据位置都由唯一的线程拥有，并且只能由该所有者线程更新。

图10.6 一个简单的求和规约内核

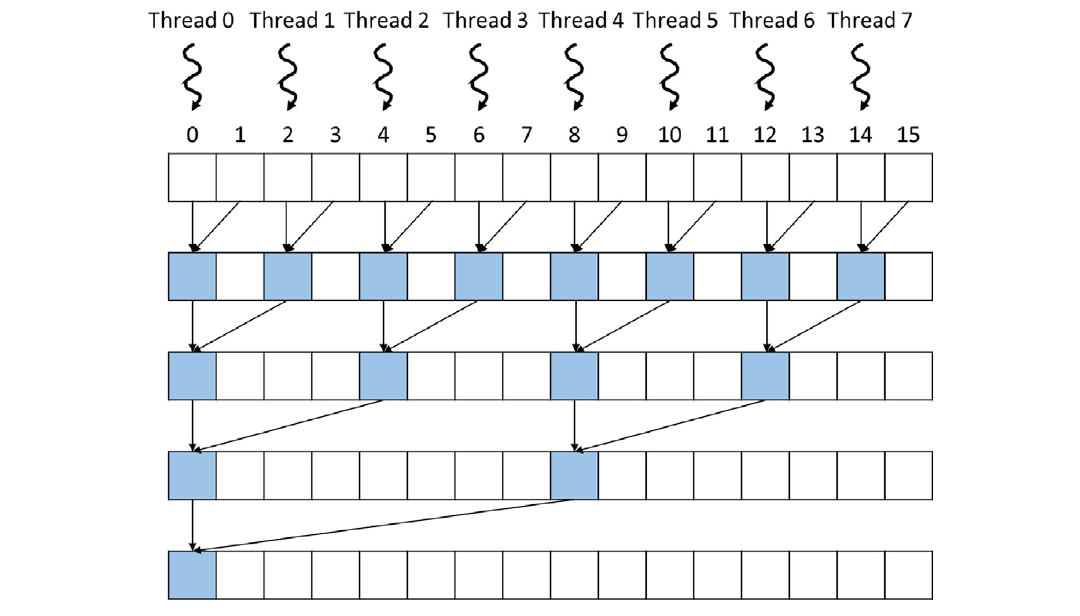图10.7 线程（“所有者”）分配给输入数组位置以及图 10.6 中 SimpleSumReudctionKernel 的执行进度随时间的推移。时间从上到下进行，每个级别对应 for 循环的一次迭代。

图 10.7 的顶行显示了线程分配给输入数组位置的情况，随后的每一行展示了在每个时间步骤中对输入数组位置的写操作，即图 10.6 中 for 循环的迭代（第 03 行）。图 10.7 中标记为填充位置的输入数组位置表示内核在 for 循环的每次迭代中要覆写的位置。例如，在第一次迭代结束时，偶数索引的位置被原始元素对（0-1、2-3、4-5等）的部分和覆写。在第二次迭代结束时，索引为 4 的倍数的位置被相邻四个原始元素（0-3、4-7等）的部分和覆写。

在图 10.6 中，使用一个步幅变量使得线程可以找到合适的部分和以累加到其所属位置。步幅变量在初始化时为 1（第 03 行）。随着每次迭代，步幅变量的值翻倍，因此步幅变量的值为 1、2、4、8等，直到它大于 blockIdx.x，即块中的总线程数。如图 10.7 所示，在每次迭代中的每个活跃线程使用步幅变量将距离为步幅的输入数组元素添加到其所属位置。例如，在第一次迭代中，线程 0 使用步幅值 1 将 input[1] 添加到其所属位置 input[0]。这将 input[0] 更新为输入数组的第一对原始值 input[0] 和 input[1] 的部分和。在第二次迭代中，线程 0 使用步幅值 2 将 input[2] 添加到 input[0]。此时，input[2] 包含输入数组 input[2] 和 input[3] 的和，而 input[0] 包含输入数组的前四个元素的和。因此，第二次迭代后，input[0] 包含输入数组前四个元素的和。在最后一次迭代后，input[0] 包含输入数组的所有原始元素的和，也即求和归约的结果。这个值由线程 0 作为最终输出写入（第 10 行）。

现在我们转向图 10.6 中 if 语句（第 04 行）。if 语句的条件用于选择每次迭代中的活跃线程。如图 10.7 所示，在第 n 次迭代中，线程索引（threadIdx.x）值为 $2^n$ 的倍数的线程执行加法。条件为 threadIdx.x % stride == 0，检查线程索引值是否是步幅变量的倍数。回想一下，步幅的值通过迭代翻倍，因此通过迭代步幅的值为 1、2、4、8等，或者对于第 n 次迭代为 $2^n$。因此，条件实际上测试线程索引值是否为 $2^n$ 的倍数。所有线程执行相同的内核代码。满足 if 条件的线程是执行加法语句的活跃线程（第 05 行）。未满足条件的线程是未活跃的线程，会跳过加法语句。随着迭代的进行，越来越少的线程保持活跃。在最后一次迭代中，只有线程 0 保持活跃并产生求和归约结果。

图 10.6 中的 __syncthreads() 语句（第 07 行）在 for 循环中确保在任何一个线程开始下一次迭代之前，由迭代计算的所有部分和都已经写入到它们在输入数组中的目标位置。这样，进入迭代的所有线程都能正确使用上一次迭代中生成的部分和。例如，第一次迭代后，偶数位置将被成对的部分和替换。__syncthreads() 语句确保了第一次迭代中所有这些部分和确实已经写入到输入数组的偶数位置，并且准备好供第二次迭代中的活跃线程使用。

10.4 最小化控制分歧

图 10.6 中的内核代码实现了图 10.7 中的并行归约树，并产生了预期的求和归约结果。不幸的是，在每次迭代中对活跃和非活跃线程的管理导致了高度的控制分歧。例如，如图 10.7 所示，在第二次迭代期间只有那些 threadIdx.x 值为偶数的线程才会执行加法语句。正如我们在第 4 章《计算架构和调度》中所解释的那样，控制分歧可能会显著降低执行资源利用效率，即用于生成有用结果的资源使用百分比。在这个例子中，一个线程束中的所有 32 个线程都消耗了执行资源，但只有其中一半是活跃的，浪费了一半的执行资源。由于分歧导致的执行资源浪费随着时间的推移而增加。在第三次迭代期间，一个线程束中只有四分之一的线程是活跃的，浪费了四分之三的执行资源。在第 5 次迭代期间，一个线程束中只有一个线程是活跃的，浪费了 31/32 的执行资源。如果输入数组的大小大于 32，整个线程束在第五次迭代后将变为非活跃状态。例如，对于输入大小为 256，会启动 128 个线程或四个线程束。所有四个线程束都具有相同的分歧模式，如我们在前一段中对第 1 到第 5 次迭代的解释。在第六次迭代期间，线程束 1 和线程束 3 将完全变为非活跃状态，因此不会存在控制分歧。另一方面，线程束 0 和线程束 2 将只有一个活跃线程，显示出控制分歧并浪费 31/32 的执行资源。在第七次迭代期间，只有线程束 0 会活跃，显示出控制分歧并浪费 31/32 的执行资源。

通常，对于大小为 N 的输入数组，执行资源利用效率可以计算为活跃线程的总数与消耗的总执行资源数的比率。消耗的总执行资源数与所有迭代中的活跃线程束的总数成正比，因为每个活跃线程束，无论其活跃线程数有多少，都会消耗完整的执行资源。这个数量可以计算如下：

这里，N/64 是启动的总线程束数，因为会启动 N/2 个线程并且每 32 个线程组成一个线程束。N/64 项乘以 5 是因为所有启动的线程束在前五次迭代中都是活跃的。第五次迭代后，每次迭代中的线程束数减半。括号中的表达式给出了所有迭代中所有 N/64 个线程束的活跃线程。第二项反映了每个活跃线程束在所有 32 个线程上消耗完整的执行资源，无论这些线程束中有多少个活跃线程。对于输入数组大小为 256 的情况，消耗的执行资源为 (4 * 5 + 2 + 1) * 32 = 736。

活跃线程提交的执行结果数量是所有迭代中活跃线程的总数：

括号中的项给出了所有 N/64 个线程束在前五次迭代中的活跃线程数。从第六次迭代开始，每次迭代中的线程束数减半，并且每个活跃线程束中只有一个活跃线程。对于输入数组大小为 256 的情况，提交的总结果数为 4 * (32 + 16 + 8 + 4 + 2 + 1) + 2 + 1 = 255。这个结果应该是直观的，因为将 256 个值归约需要的总操作数是 255。

综合前面两个结果，我们发现输入数组大小为 256 时的执行资源利用效率为 255/736 = 0.35。这个比率表示并行执行资源没有充分发挥其加速计算的潜力。平均而言，只有大约 35% 的消耗的资源对求和归约结果有贡献。也就是说，我们只利用了大约 35% 的硬件潜力来加速计算。

通过这种分析，我们可以看到在线程束之间和随时间推移存在广泛的控制分歧。正如读者可能已经想到的那样，可能有一种更好的方法来分配线程到输入数组位置以减少控制分歧并提高资源利用效率。图 10.7 中所示分配的问题在于部分和位置之间的距离逐渐增大，因此拥有这些位置的活跃线程在时间推移中也逐渐远离彼此。这种活跃线程之间的距离增加导致了控制分歧水平的增加。

确实有一种更好的分配策略可以显著减少控制分歧。这个想法是，我们应该安排线程及其拥有的位置，使它们随着时间推移保持彼此接近。换句话说，我们希望随着时间的推移，步长值减小而不是增加。对于一个包含 16 个元素的输入数组，修订后的分配策略如图 10.8 所示。在这里，我们将线程分配给前半部分位置。在第一次迭代期间，每个线程达到输入数组的中间位置，并将一个输入元素添加到其拥有位置。在我们的例子中，线程 0 将输入[8] 添加到其拥有位置 input[0]，线程 1 将输入[9] 添加到其拥有位置 input[1]，依此类推。在每个后续迭代期间，一半的活跃线程将退出，所有剩余的活跃线程将添加一个距离其拥有位置的活跃线程数的输入元素。在我们的例子中，第三次迭代期间仍然有两个剩余的活跃线程：线程 0 将输入[2] 添加到其拥有位置 input[0]，线程 1 将输入[3] 添加到其拥有位置 input[1]。请注意，如果我们将图 10.8 的操作和操作数顺序与图 10.7 进行比较，实际上是对列表中的操作数进行重新排序，而不仅仅是以不同的方式插入括号。为了使结果在这种重新排序中始终保持一致，操作必须是可交换的，同时也必须是可结合的。

图10.8 减少控制分歧的线程分配更好的分配方式。

图10.9 具有较少控制分歧和改善执行资源利用效率的内核。

图 10.9 展示了对图 10.6 中简单内核的一些微妙但关键的更改。拥有位置变量 i 设置为 threadIdx.x 而不是 2 * threadIdx.x（第 02 行）。因此，所有线程的拥有位置现在彼此相邻，如图 10.8 所示。步长值初始化为 blockDim.x，并每次减半直到达到 1（第 03 行）。在每次迭代中，只有线程索引小于步长值的线程保持活跃状态（第 04 行）。因此，所有活跃线程都具有连续的线程索引，如图 10.8 所示。与在第一轮中添加邻居元素不同，它添加距离相互半个区段的元素，而区段大小始终是剩余活跃线程数的两倍。在第一轮中添加的所有配对都彼此相距 blockDim.x。第一次迭代后，所有成对和的结果存储在输入数组的前半部分，如图 10.8 所示。循环在进入下一次迭代之前将步长除以 2。因此，对于第二次迭代，步长变量值是 blockDim.x 值的一半。也就是说，在第二次迭代期间，剩余的活跃线程将添加相互之间相隔一个区段的元素。

图 10.9 中的内核仍然具有一个 if 语句（第 04 行）在循环中。在每次迭代中执行加法操作（第 06 行）的线程数量与图 10.6 中相同。那么为什么两个内核之间会有控制分歧的差异呢？答案在于执行加法操作的线程位置相对于不执行加法操作的线程位置。让我们以一个包含 256 个元素的输入数组为例。在第一次迭代中，所有线程都是活跃的，因此没有控制分歧。在第二次迭代期间，线程 0 到线程 63 执行加法语句（活跃），而线程 64 到线程 127 不执行（非活跃）。在第二次迭代期间，成对和的结果存储在元素 0 到元素 63 中。由于线程束由连续的 threadIdx.x 值组成，线程束 0 到线程束 1 中的所有线程都执行加法语句，而线程束 2 到线程束 3 中的所有线程则变为非活跃。由于每个线程束中的所有线程采用相同的执行路径，因此不存在控制分歧！

然而，图 10.9 中的内核并没有完全消除由 if 语句引起的分歧。读者应该验证，对于 256 元素的例子，从第四次迭代开始，执行加法操作的线程数量将少于 32。也就是说，在这些迭代中，最后五次迭代将只有 16、8、4、2 和 1 个线程执行加法。这意味着内核执行在这些迭代中仍然存在分歧。然而，具有分歧的循环迭代次数从十次减少到了五次。我们可以计算消耗的总执行资源数如下：

括号中的部分反映了每个后续迭代中一半的线程束完全变为非活跃并不再消耗执行资源。这种系列一直持续，直到只有一个完整线程束的活跃线程。最后一项（5 * 1）反映了最后五次迭代中只有一个活跃线程束，其 32 个线程都消耗执行资源，即使只有一小部分线程处于活跃状态。因此，括号中的和给出了所有迭代中的线程束执行总数，当乘以 32 时，就得到了消耗的总执行资源数。

对于我们 256 元素的例子，消耗的执行资源是（4 + 2 + 1 + 5 * 1） * 32 = 384，几乎是图 10.6 中内核消耗的 736 的一半。由于每次迭代中活跃线程的数量从图 10.7 到图 10.8 没有变化，因此新内核图 10.9 的效率是 255/384 = 66%，几乎是图 10.6 内核的效率的两倍。还要注意，由于线程束被调度以轮流在有限执行资源的流多处理器中执行，因此总的执行时间也会随着资源消耗的减少而改善。

图 10.6 和图 10.9 中的内核之间的差异虽然很小，但可能会产生显著的性能影响。需要对设备的单指令、多数据硬件上的线程执行有清晰的理解，才能自信地进行这样的调整。

10.5 最小化内存分歧

图10.6中的简单内核还有另一个性能问题：内存分歧。正如我们在第5章《内存架构和数据局部性》中所解释的，实现每个warp内的内存协调是很重要的。也就是说，warp内相邻的线程在访问全局内存时应该访问相邻的位置。不幸的是，在图10.7中，相邻的线程并不访问相邻的位置。在每次迭代中，每个线程执行两次全局内存读取和一次全局内存写入。第一次读取是从自己的位置读取，第二次读取是从距离自己的位置一定距离的位置读取，然后写入到自己的位置。由于相邻线程拥有的位置并不相邻，因此相邻线程进行的访问不会完全协调。在每次迭代中，由一个warp访问的内存位置相互之间相差stride。

例如，如图10.7所示，在第一次迭代期间，当warp中的所有线程执行第一次读取时，这些位置相距两个元素。结果，触发了两次全局内存请求，并且有一半的数据不会被线程使用。对于第二次读取和写入也是同样的情况。在第二次迭代期间，每隔一个线程会退出，warp访问的位置相互之间相差四个元素。再次进行两次全局内存请求，并且只有四分之一的数据会被线程使用。这种情况会持续下去，直到每个warp中只有一个保持活跃的线程。只有当warp中只有一个保持活跃的线程时，warp才会执行一次全局内存请求。因此，总的全局内存请求次数如下所示：

第一个项(N/64 * 5 * 2) 对应于前五次迭代，其中所有N/64个warp都有两个或更多的活跃线程，因此每个warp执行两次全局内存请求。剩余的项是指最终的迭代次数，其中每个warp只有一个活跃线程，并且在每个后续迭代中，有一半的warp会退出。乘以3是因为每个活跃线程在每次迭代中都会进行两次读取和一次写入操作。对于256个元素的示例，由内核执行的总全局内存请求次数为(4 * 5 * 2 + 4 + 2 + 1) * 3 = 141。

对于图10.9中的内核，每个warp中的相邻线程总是访问全局内存中的相邻位置，因此访问总是协调的。结果，每个warp在任何读取或写入时只会触发一次全局内存请求。随着迭代的进行，整个warp将退出，因此在这些非活跃warp中不会有任何全局内存访问。每次迭代中有一半的warp会退出，直到最后的五次迭代中只剩下一个warp。因此，内核执行的总全局内存请求次数如下所示：

对于256个元素的示例，内核执行的总全局内存请求次数为((4 + 2 + 1) + 5) * 3 = 36。改进后的内核导致了比原始内核少了141/36 = 3.9倍的全局内存请求。由于DRAM带宽是有限的资源，简单内核的执行时间可能会显著延长。对于2048个元素的示例，内核在图10.6中执行的总全局内存请求次数为(32 * 5 * 2 + 32 + 16 + 8 + 4 + 2 + 1) * 3 = 1149，而内核在图10.9中执行的总全局内存请求次数为(32 + 16 + 8 + 4 + 2 + 1 + 5) * 3 = 204。比率为5.6，甚至比256个元素的示例更高。这是因为图10.6中内核的执行模式不高效，在初始五次迭代期间有更多的活跃warp，并且每个活跃warp触发的全局内存请求次数是收敛内核图10.9的两倍。

总之，收敛(convergent)内核在使用执行资源和DRAM带宽方面提供了更高的效率。这种优势来自于减少了控制分歧和改进了内存协调。

10.6 减少全局内存访问

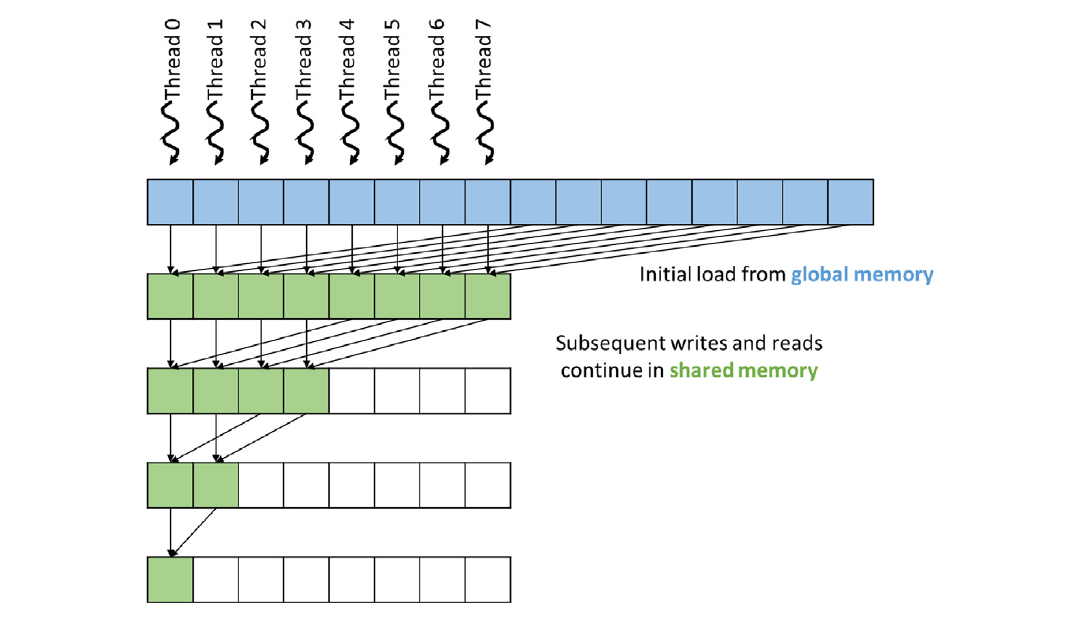
图10.9中的收敛内核可以通过使用共享内存进一步改进。请注意，在每次迭代中，线程将部分求和结果值写入全局内存，并且这些值由相同的线程和下一次迭代中的其他线程重新读取。由于共享内存的延迟时间更短，带宽更高，我们可以通过将部分求和结果保留在共享内存中来进一步提高执行速度。这个想法在图10.10中有所体现。

图10.10 使用共享内存来减少对全局内存的访问。

图10.11 一个使用共享内存来减少全局内存访问的核函数。

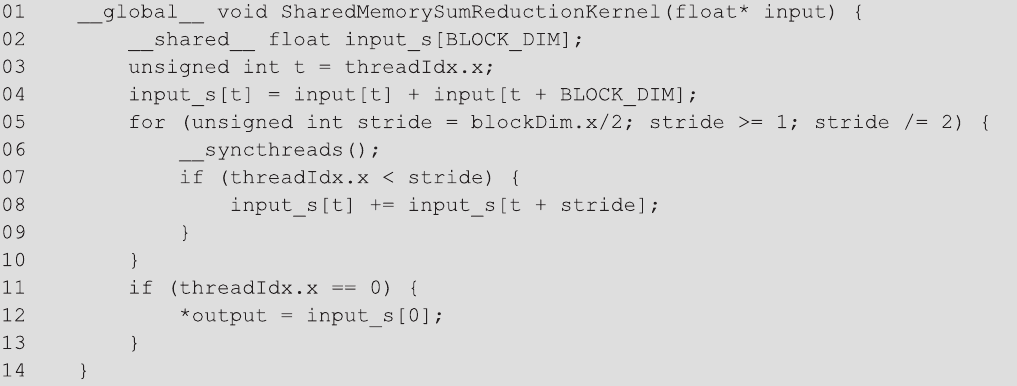
使用共享内存的策略在图10.11所示的内核中实现。其思想是让每个线程在将部分求和结果写入共享内存之前加载和相加两个原始元素（第04行）。由于第一次迭代在循环外访问全局内存位置时已经完成，所以for循环从blockDim.x/2（第04行）开始，而不是blockDim.x。__syncthreads()移到循环的开头，以确保我们在共享内存访问和循环的第一次迭代之间同步。然后线程通过读取和写入共享内存进行剩余的迭代（第08行）。最后，在内核的末尾，线程0将总和写入输出，保持与以前内核相同的行为（第11-13行）。

使用图10.11中的内核，全局内存访问的次数减少到了加载输入数组原始内容和最后写入input[0]的初始次数。因此，对于N个元素的求和，全局内存访问次数仅为N+1。还要注意，图10.11中的两次全局内存读取（第04行）都是协调的。因此，在协调的情况下，全局内存请求只有(N/32)+1次。对于256个元素的示例，触发的全局内存请求总数将从图10.9中的36次减少到图10.10中的8+1 = 9次，改进了4倍。使用共享内存的另一个好处是，除了减少全局内存访问次数外，输入数组不会被修改。这个特性在需要在程序的其他部分进行某些其他计算时需要数组的原始值时非常有用。

适合任意输入长度的层次化规约

到目前为止，我们研究的所有核函数都假设它们将以一个线程块的方式启动。这种假设的主要原因是__syncthreads()用作所有活动线程之间的屏障同步。请记住，__syncthreads()只能在同一块中的线程之间使用。这限制了当前硬件上并行性的级别为1024个线程。对于包含数百万甚至数十亿元素的大型输入数组，我们可以从启动更多线程来进一步加速归约过程中受益。由于我们没有一种良好的方法来在不同块中的线程之间执行屏障同步，因此我们需要允许不同块中的线程独立执行。

图10.12 分段多块归约使用原子操作。

图10.13 分段多块求和归约内核，使用原子操作。

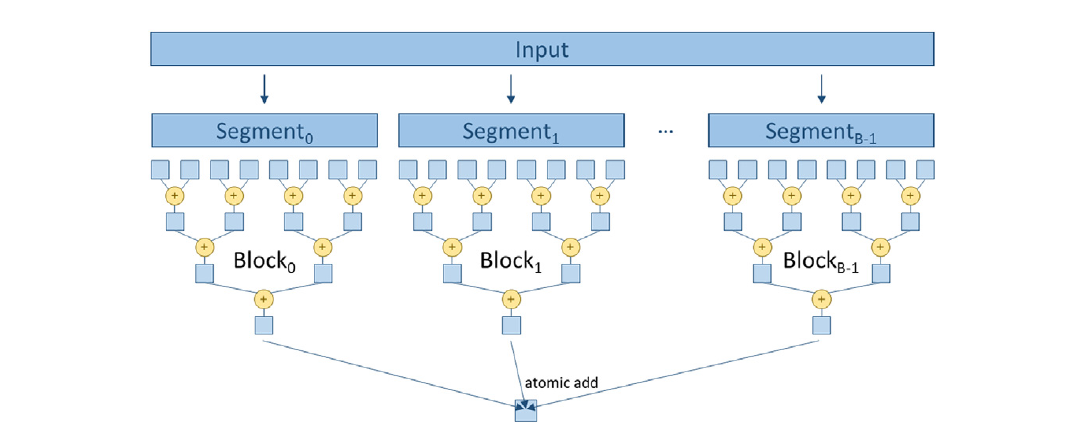
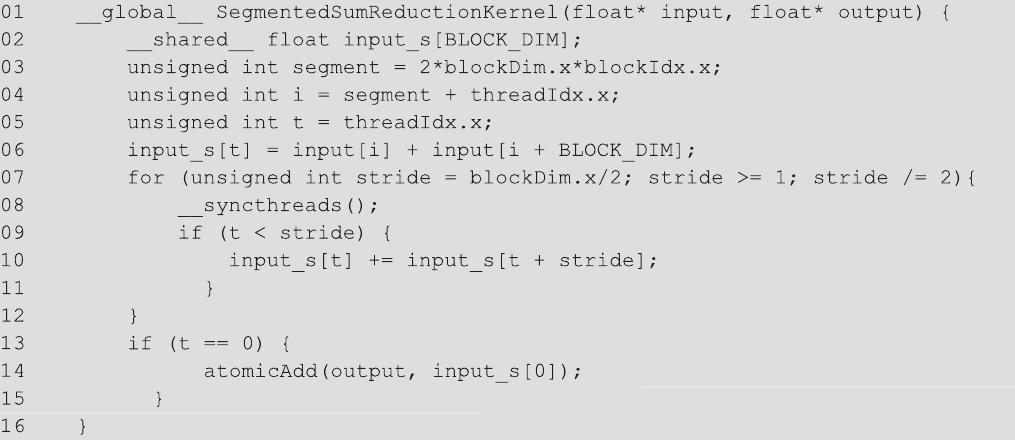
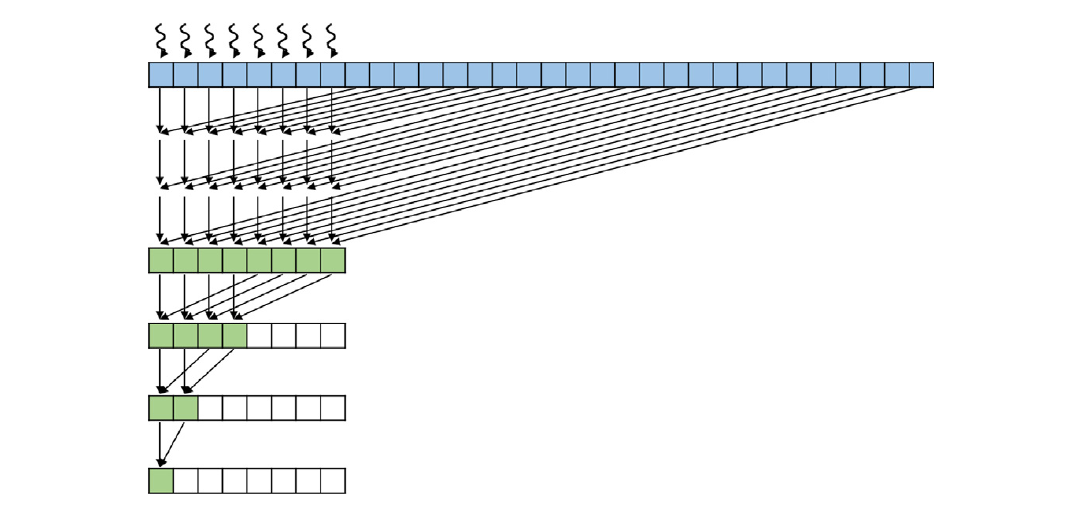
图10.12展示了使用原子操作进行分层分段多块归约的概念，图10.13展示了相应的核函数实现。其思想是将输入数组分割成段，使得每个段的大小适合一个块。然后，所有块都独立执行归约树，并使用原子加操作将它们的结果累积到最终输出。

分割是通过根据线程的块索引为段变量分配不同的值来完成的（第03行）。每个段的大小是2blockDim.x。也就是说，每个块处理2blockDim.x个元素。因此，当我们将每个段的大小乘以块的blockIdx.x时，我们得到块要处理的段的起始位置。例如，如果一个块有1024个线程，段的大小将是2 * 1024=2048。段的起始位置将是0（对于块0）、2048（20481对于块1）、4096（2048 * 2对于块2），依此类推。

一旦我们知道了每个块的起始位置，该块中的所有线程就可以简单地处理分配给它的段，就好像它是整个输入数据一样。在一个块内部，我们通过将threadIdx.x添加到属于该线程所属的块的段起始位置（第04行）来为每个线程分配所属位置。本地变量i保存了线程在全局输入数组中的所属位置，而t保存了线程在共享input_s数组中的所属位置。第06行适应于在访问全局输入数组时使用i而不是t。图10.11中的for循环没有改变。这是因为每个块都有自己的私有input_s，所以它可以使用t=threadIdx.x作为段是整个输入时的索引访问。

归约树的for循环完成后，段的部分和就在input_s[0]中。图10.13中的第16行的if语句选择线程0将input_s[0]的值贡献给output，就像图10.12底部所示。这是通过原子加完成的，如图10.13的第14行所示。

一旦网格的所有块完成执行，核函数将返回，并且总和将位于output指向的内存位置。

10.6 线程粗化以减少开销

到目前为止，我们所使用的归约内核都试图通过尽可能多的线程来最大化并行性。也就是说，对于 N 个元素的归约，会启动 N/2 个线程。在拥有 1024 个线程的线程块大小的情况下，产生的线程块数量为 N/2048。然而，在具有有限执行资源的处理器中，硬件可能仅具有足够的资源来并行执行部分线程块。在这种情况下，硬件会对多余的线程块进行串行化处理，在旧线程块完成后执行新的线程块。

为了并行化归约，我们实际上已经付出了将工作分配到多个线程块中的巨大代价。正如我们在前面的章节中所看到的那样，硬件的空闲利用率会随着归约树的每个连续阶段增加而增加，因为更多的线程束会处于空闲状态，最后一个线程束会经历更多的控制分歧。硬件空闲利用率不足的阶段发生在我们启动的每个线程块中。这是一个不可避免的代价，如果线程块要真正并行运行的话。然而，如果硬件要对这些线程块进行串行化处理，我们最好以一种更有效的方式对它们进行串行化处理。正如我们在第 6 章“性能考虑”中所讨论的那样，线程粗化是一种优化的类别，它将部分工作串行化到更少的线程中，以减少并行化开销。我们首先展示了应用线程粗化的并行归约实现，方法是为每个线程块分配更多的元素。然后，我们进一步阐述了这种实现如何减少硬件空闲利用率。

图10.14 线程粗化在归约中。

图 10.14 展示了如何将线程粗化应用到图 10.10 中的示例中。在图 10.10 中，每个线程块接收 16 个元素，即每个线程接收 2 个元素。每个线程独立地添加它负责的两个元素；然后线程协作执行归约树。在图 10.14 中，我们将线程块粗化了 2 倍。因此，每个线程块接收的元素数量增加了两倍，即 32 个元素，即每个线程接收 4 个元素。在这种情况下，每个线程独立地添加四个元素，然后线程协作执行归约树。添加这四个元素的三个步骤在图 10.14 的前三行箭头中有所说明。请注意，在这三个步骤中，所有线程都是活动的。此外，由于线程独立地添加它们负责的四个元素，它们不需要同步，也不需要在添加完所有四个元素之前将它们的部分和存储到共享内存中。执行归约树的剩余步骤与图 10.10 中的步骤相同。

图10.15 采用线程粗化的求和归约内核。

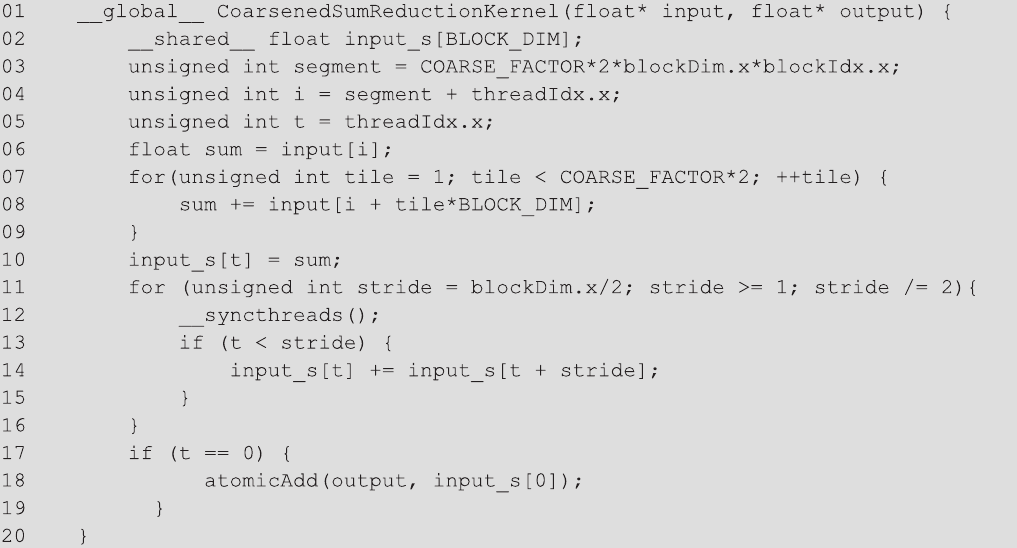
图 10.15 展示了实现使用线程粗化的多块分段归约的内核代码。与图 10.13 相比，内核有两个主要的区别。第一个区别是，在确定块的段的起始位置时，我们乘以 COARSE_FACTOR，以反映块的段的大小是 COARSE_FACTOR 倍大（第 3 行）。第二个区别是，在添加线程负责的元素时，不仅添加了两个元素（图 10.13 中的第 6 行），我们使用了一个粗化循环来遍历元素，并根据 COARSE_FACTOR 添加它们（图 10.15 的第 6-9 行）。请注意，在这个粗化循环中，所有线程都是活动的，部分和累积到本地变量 sum，并且在循环中没有调用 __syncthreads()，因为线程是独立工作的。

图10.16 比较采用线程粗化和不采用线程粗化的并行归约。

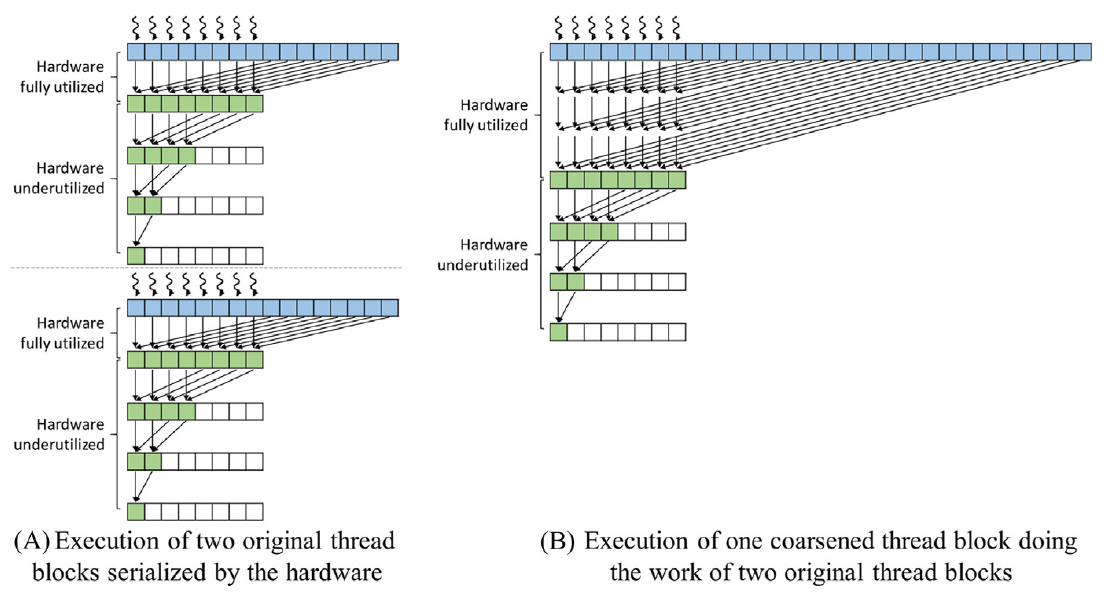
图 10.16 将没有粗化的两个原始线程块的执行与硬件串行化进行了比较，显示在图 10.16A 中，以一个粗化的线程块执行两个线程块的工作，显示在图 10.16B 中。在图 10.16A 中，第一个线程块执行一个步骤，在这个步骤中，每个线程添加它负责的两个元素。在这一步中，所有线程都是活动的，所以硬件被充分利用。剩下的三个步骤执行归约树，每个步骤中一半的线程退出，硬件利用率不足。此外，每个步骤都需要一个屏障同步以及对共享内存的访问。当第一个线程块完成时，硬件会调度第二个线程块，它遵循相同的步骤，但在数据的不同段上执行。总体而言，这两个块共计执行了八个步骤，其中两个步骤充分利用了硬件，六个步骤利用率不足，需要屏障同步和共享内存访问。相比之下，在图 10.16B 中，相同数量的数据只有一个粗化了 2 倍的单个线程块处理。这个线程块最初需要三个步骤，每个线程都添加了它负责的四个元素。在这三个步骤中，所有线程都是活动的，所以硬件被充分利用，没有屏障同步或共享内存访问。剩下的三个步骤执行归约树，每个步骤中一半的线程退出，硬件利用率不足，需要屏障同步和共享内存访问。总体而言，只需要六个步骤（而不是八个），其中三个步骤（而不是两个）充分利用了硬件，三个步骤（而不是六个）利用率不足，需要屏障同步和共享内存访问。因此，线程粗化有效地减少了硬件空闲利用率、同步和共享内存访问方面的开销。

理论上，我们可以将粗化因子增加到超过两倍。然而，必须记住，随着我们对线程进行粗化，可以并行执行的工作量将减少。因此，增加粗化因子将减少硬件利用率。如果我们将粗化因子增加到太大，以至于启动的线程块少于硬件能够执行的线程块，我们将无法充分利用并行硬件执行资源。最佳的粗化因子确保有足够的线程块充分利用硬件，这通常取决于输入的总大小以及特定设备的特性。

10.9 总结

并行归约模式非常重要，在许多数据处理应用中发挥着关键作用。虽然顺序代码很简单，但读者应清楚几种技术是必需的，比如为减少分歧而进行的线程索引分配、为减少全局内存访问而使用的共享内存、带有原子操作的分段归约，以及线程粗化，这些技术需要用于处理大型输入以实现高性能。归约计算也是前缀和模式的重要基础，前缀和模式是许多应用程序并行化的重要算法组件，将在第11章《前缀和 (Scan)》中进行讨论。

• ← Previous Post
• Next Post →