目录
我们的下一个并行模式是稀疏矩阵计算。在稀疏矩阵中，大多数元素都是零。存储和处理这些零元素在内存容量、内存带宽、时间和能量方面都是浪费的。许多重要的现实世界问题涉及稀疏矩阵计算。由于这些问题的重要性，已经提出了几种稀疏矩阵存储格式及其相应的处理方法，并在该领域广泛使用。所有这些方法都采用了某种压缩技术，以避免存储或处理零元素，代价是引入了一定程度的数据表示不规则性。不幸的是，这种不规则性可能导致并行计算中内存带宽的利用不足、控制流发散和负载不平衡。因此，平衡压缩和规范化是很重要的。一些存储格式在高度不规则性的情况下实现了更高水平的压缩。其他格式则在保持表示更规则的同时实现了适度水平的压缩。使用每种存储格式的并行计算的相对性能被认为严重依赖于稀疏矩阵中非零元素的分布。了解稀疏矩阵存储格式及其相应并行算法的丰富工作为并行程序员提供了重要的背景，以面对解决相关问题时的压缩和规范化挑战。
14.1 背景
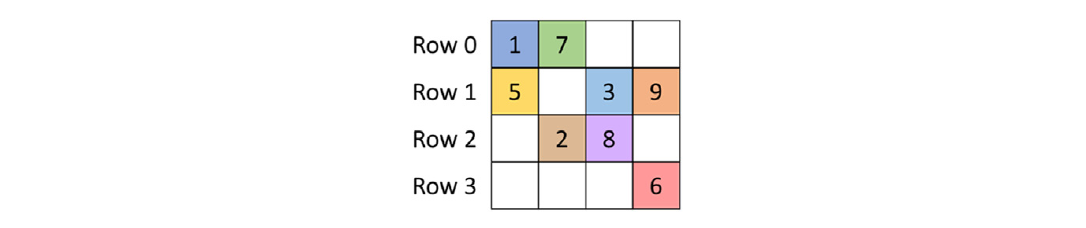
稀疏矩阵是一种矩阵，其中大多数元素都是零。稀疏矩阵出现在许多科学、工程和金融建模问题中。例如，矩阵可以用来表示线性方程组的系数。矩阵的每一行代表线性系统的一个方程。在许多科学与工程问题中，涉及的大量变量和方程是稀疏耦合的。也就是说，每个方程只涉及少量变量。图14.1对此进行了说明，其中矩阵的每一列对应于一个变量的系数：第0列对应于$x_0$，第1列对应于$x_1$，依此类推。例如，第0行在第0列和第1列有非零元素，表明只有变量$x_0$和$x_1$参与了方程0。显然，变量$x_0$、$x_2$和$x_3$出现在方程1中，变量$x_1$和$x_2$出现在方程2中，而只有变量$x_3$出现在方程3中。通常以一种格式或表示形式存储稀疏矩阵，避免存储零元素。
图14.1 一个简单稀疏矩阵的例子
矩阵通常用于解决形式为A * X + Y = 0的N个变量的N个方程的线性系统，其中A是N×N矩阵，X是N个变量的向量，Y是N个常数值的向量。目标是求解满足所有方程的X变量值。直观的方法是将矩阵求逆，以便$X = A^{-1} Y$。对于适度大小的矩阵，可以通过高斯消元等方法实现。虽然从理论上讲可以使用这些方法来解决由稀疏矩阵表示的方程，但许多稀疏矩阵的巨大尺寸可能会压倒这种直观方法。此外，稀疏矩阵的逆矩阵通常比原始矩阵大得多，因为求逆过程倾向于产生许多额外的非零元素，这些元素被称为“填充”。因此，在解决现实世界问题时，通常不切实际去计算和存储逆矩阵。
稀疏矩阵表示的线性方程组可以通过迭代方法更好地解决。当稀疏矩阵A是正定的（即，对于$R^n$中所有非零向量x，$x^T A x > 0$），可以使用共轭梯度方法迭代求解相应的线性系统，并保证收敛到一个解（Hestenes和Stiefel，1952）。共轭梯度方法猜测X的一个解，执行A X + Y，并查看结果是否接近0向量。如果不是，我们可以使用梯度向量公式来细化猜测的X，并执行另一次A X + Y的迭代。这些线性系统的迭代解法与我们在第8章“Stencil”中介绍的微分方程的迭代解法密切相关。
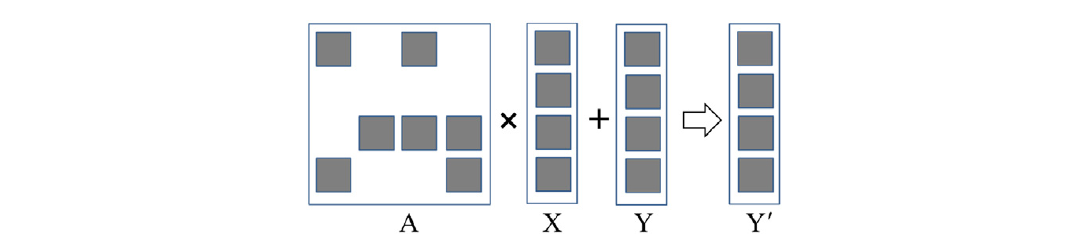
解决线性方程组的迭代方法中最耗时的部分是评估A X + Y，这是一个稀疏矩阵-向量乘法和累加。图14.2显示了一个小型示例，其中A是一个稀疏矩阵的矩阵-向量乘法和累加。A中的深色方块代表非零元素。相比之下，X和Y通常是密集向量。也就是说，X和Y的大多数元素都有非零值。由于其重要性，已经创建了标准化的库函数接口来执行这个操作，名称为SpMV（稀疏矩阵-向量乘法和累加）。我们将使用SpMV来说明并行稀疏矩阵计算中不同存储格式之间的重要权衡。
图14.2 一个矩阵-向量乘法和累加的小示例。
不同稀疏矩阵存储格式的主要目标是从矩阵表示中移除所有零元素。移除所有零元素不仅可以节省存储空间，还可以消除从内存中提取这些零元素并执行无用的乘法或加法操作的需要。这可以显著减少内存带宽和计算资源的消耗。
构建稀疏矩阵存储格式时，会考虑多种设计因素。以下是一些关键考虑因素的列表：
- 空间效率（或压缩）：使用存储格式表示矩阵所需的内存容量
- 灵活性：存储格式在添加或删除非零元素时修改矩阵的容易程度
- 可访问性：存储格式使访问哪些数据变得容易
- 内存访问效率：存储格式为特定计算启用高效内存访问模式的程度（规范化的一个方面）
- 负载平衡：存储格式在特定计算中跨不同线程平衡负载的程度（规范化的另一个方面）
在本章中，我们将介绍不同的存储格式，并检查这些存储格式在这些设计考虑方面如何进行比较。
14.2 使用COO格式的简单SpMV内核
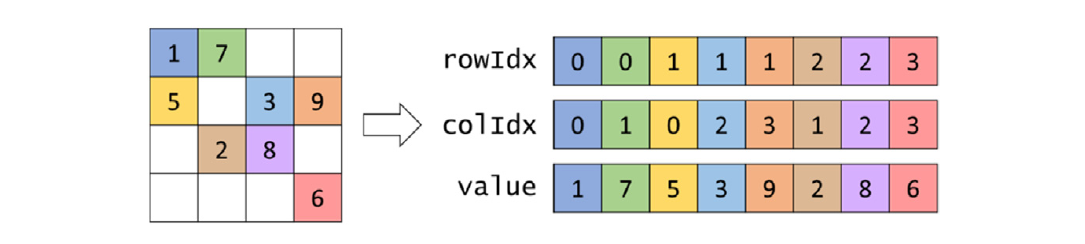
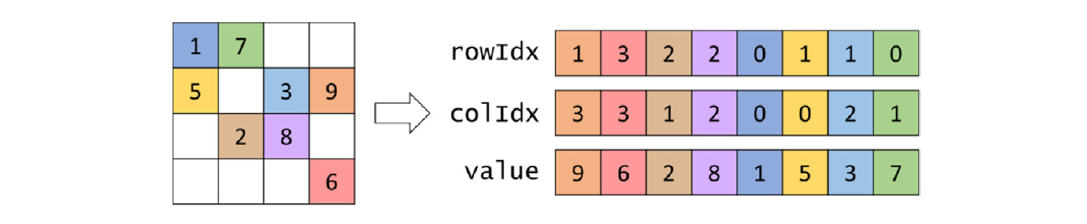
我们将讨论的第一个稀疏矩阵存储格式是坐标列表（COO）格式。COO格式在图14.3中进行了说明。COO在一维数组中存储非零值，显示为值数组。每个非零元素都与其列索引和行索引一起存储。我们有colIdx和rowIdx数组来伴随值数组。例如，我们小示例的A[0,0]存储在值数组的条目中，索引为0（在value[0]中的1），同时它的列索引（在colIdx[0]中的0）和行索引（在rowIdx[0]中的0）也存储在其他数组的同一位置。
图14.3 坐标列表（COO）格式的示例
COO完全从存储中移除了所有零元素。它确实通过引入colIdx和rowIdx数组产生了存储开销。在我们的小示例中，其中零元素的数量并不比非零元素多很多，存储开销实际上超过了通过不存储零元素所节省的空间。然而，应该清楚的是，对于绝大多数元素都是零的稀疏矩阵，引入的开销远远小于通过不存储零元素所节省的空间。例如，在只有1%的元素是非零值的稀疏矩阵中，包括所有开销在内的COO表示的总存储量大约是需要存储零和非零元素的空间的3%。
图14.4 使用COO格式并行化SpMV的示例。
图14.5 一个并行的SpMV/COO内核。
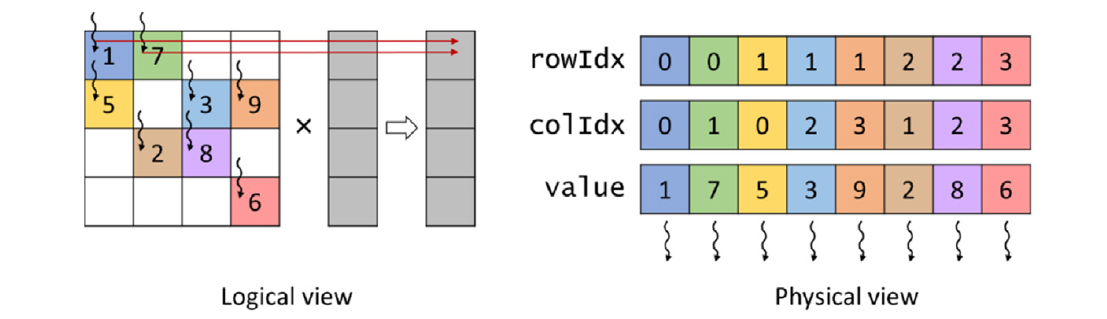
使用COO格式表示的稀疏矩阵并行执行SpMV的一种方法是为矩阵中的每个非零元素分配一个线程。这种并行化方法的示例在图14.4中进行了说明，相应的代码在图14.5中显示。在这种方法中，每个线程确定它负责的非零元素的索引（第02行），并确保它在界限内（第03行）。接下来，线程从rowIdx、colIdx和值数组中分别确定它负责的非零元素的行索引（第04行）、列索引（第05行）和值（第06行）。然后它查找对应于列索引的输入向量值，将其与非零值相乘，然后将结果累加到对应行索引的输出值中（第07行）。由于多个线程可能更新同一个输出元素，因此使用原子操作进行累加，如图14.4中映射到矩阵第0行的前两个线程的情况。显然，任何SpMV计算代码都会反映假定的存储格式。因此我们把存储格式添加到内核名称中以明确使用的组合。我们也把图14.5中的SpMV代码称为SpMV/COO。
现在我们根据第14.1节中列出的设计考虑来检查COO格式：空间效率、灵活性、可访问性、内存访问效率和负载平衡。对于空间效率，我们将讨论推迟到后面，当我们介绍了其他格式之后。对于灵活性，我们观察到我们可以任意重新排序COO格式中的元素，只要我们以相同的方式重新排序rowIdx、colIdx和值数组，就不会丢失任何信息。这通过使用我们在图14.6中的小示例进行了说明，我们重新排序了rowIdx、colIdx和值的元素。现在value[0]实际上包含原始稀疏矩阵中第1行和第3列的元素。因为我们还随着数据值一起移动了行索引和列索引值，我们可以正确地识别这个元素在原始稀疏矩阵中的位置。
图14.6 重新排序坐标列表（COO）格式。
在COO格式中，我们可以以任何我们想要的顺序处理元素。由rowIdx[i]正确识别的y元素将从value[i]和x[colIdx[i]]的乘积中获得正确的贡献。如果我们确保以某种方式对value的所有元素执行此操作，我们将计算出正确的最终答案，而不管我们处理这些元素的顺序如何。
读者可能会问为什么我们要重新排序这些元素。一个原因是数据可能从一个不以特定顺序提供非零元素的文件中读取，我们仍然需要一种一致的方式来表示数据。因此，当矩阵最初被构建时，COO是存储格式的流行选择。另一个原因是不必提供任何顺序可以简单地通过在三个数组的末尾添加条目来向矩阵添加非零元素。因此，当矩阵在计算过程中被修改时，COO是存储格式的流行选择。我们将在第14.5节中看到COO格式灵活性的另一个好处。
接下来我们要检查的设计考虑是可访问性。COO使访问给定非零元素对应的行索引和列索引变得容易。COO的这一特性使得SpMV/COO中跨非零元素的并行化成为可能。另一方面，COO并不使访问给定行或列中的所有非零元素变得容易。因此，如果计算需要矩阵的逐行或逐列遍历，COO不会是格式的好选择。
对于内存访问效率，我们参考图14.4中的物理视图，了解线程如何从内存中访问矩阵数据。访问模式是这样的，连续的线程访问形成COO格式的三个数组中的连续元素。因此，SpMV/COO对矩阵的访问是合并的。
对于负载平衡，我们回顾每个线程负责一个单一的非零值。因此，所有线程负责相同数量的工作，这意味着我们不期望在SpMV/COO中发生任何控制发散，除了边界上的线程。
SpMV/COO的主要缺点是需要使用原子操作。使用原子操作的原因是多个线程被分配到同一行中的非零元素，因此需要更新相同的输出值。如果将同一行中的所有非零元素分配给同一个线程，使得该线程是唯一更新相应输出值的线程，就可以避免原子操作。然而，回想一下，COO格式并没有提供这种可访问性。在COO格式中，访问给定行中的所有非零元素并不容易。在下一节中，我们将看到另一种提供这种可访问性的存储格式。
14.3 使用CSR格式对行非零元素进行分组
在上一节中，我们看到了使用COO格式并行化SpMV由于多个线程更新同一个输出值而使用原子操作的问题。如果同一个线程负责一行的所有非零元素，则可以避免这些原子操作，这需要存储格式能够提供给我们访问给定行的所有非零元素的能力。压缩稀疏行（CSR）存储格式提供了这种可访问性。
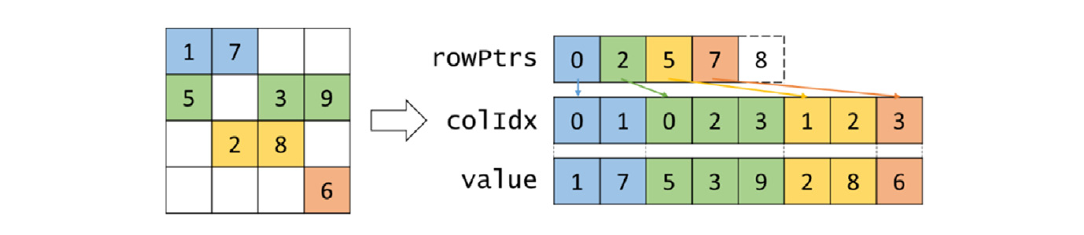
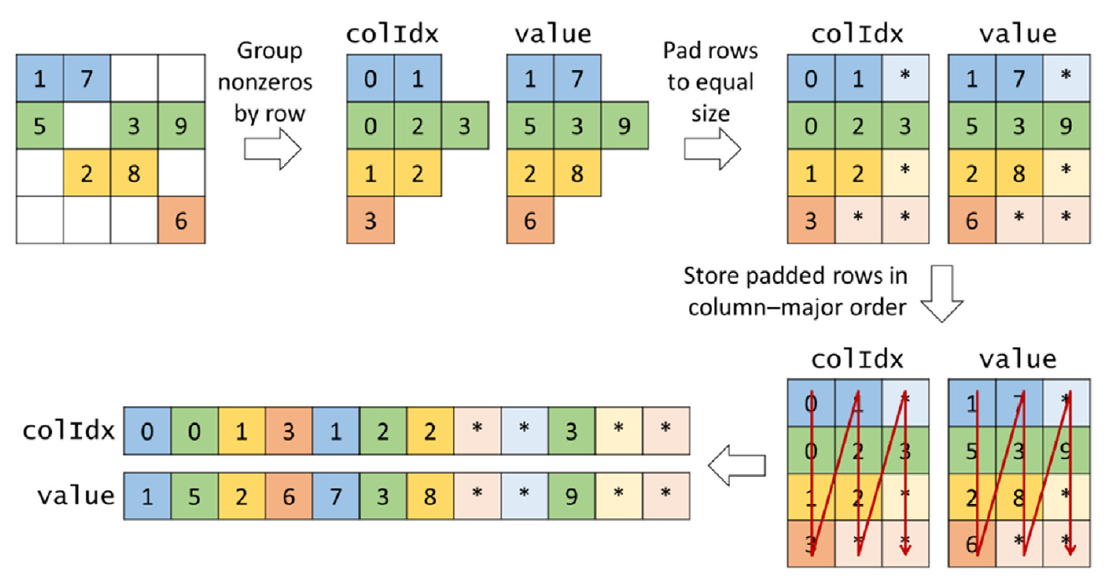
图14.7展示了如何使用CSR格式存储图14.1中的矩阵。像COO格式一样，CSR将非零值存储在一维数组中，如图14.2中显示的值数组。然而，这些非零值按行分组。例如，我们首先存储第0行的非零元素（1和7），然后是第1行的非零元素（5、3和9），接着是第2行的非零元素（2和8），最后是第3行的非零元素（6）。
图14.7 压缩稀疏行（CSR）格式的示例。
与COO格式类似，CSR也为值数组中的每个非零元素在colIdx数组的相同位置存储其列索引。自然地，这些列索引按行分组，就像值一样。在图14.7中，每一行的非零元素按其列索引的递增顺序排序。以这种方式对非零元素进行排序会产生有利的内存访问模式，但这并不是必需的。每一行内的非零元素不一定按其列索引排序，本节介绍的内核仍然可以正确工作。当每一行内的非零元素按其列索引排序时，CSR的值数组（和colIdx数组）的布局可以被视为在消除所有零元素后的矩阵的行主布局。
COO格式和CSR格式的主要区别在于，CSR格式用rowPtrs数组替换了rowIdx数组，该数组存储每一行非零元素在colIdx和值数组中的起始偏移量。在图14.7中，我们展示了一个rowPtrs数组，其元素是每一行的起始位置的索引。也就是说，rowPtrs[0]指示第0行从值数组的位置0开始，rowPtrs[1]指示第1行从位置2开始，依此类推。注意rowPtrs[4]存储了一个不存在的“第4行”的起始位置。这是为了方便起见，因为一些算法需要使用下一行的起始位置来界定当前行的结束。这个额外的标记提供了一种方便的方式来定位第3行的结束位置。
图14.8 使用CSR格式并行化SpMV的示例。
图14.9 一个并行的SpMV/CSR内核。
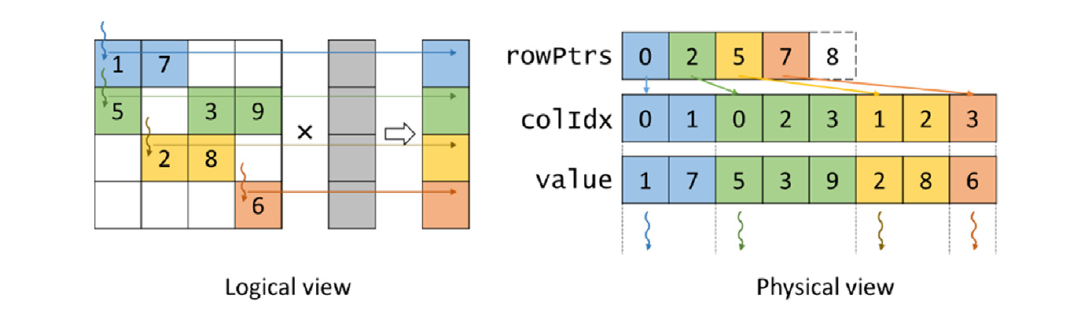
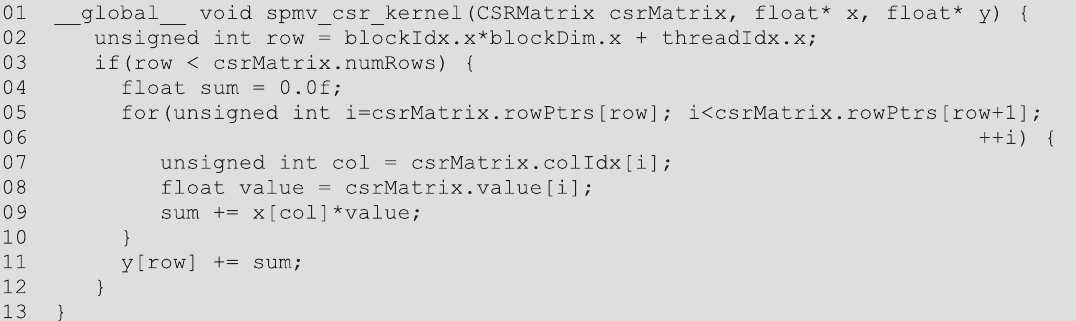
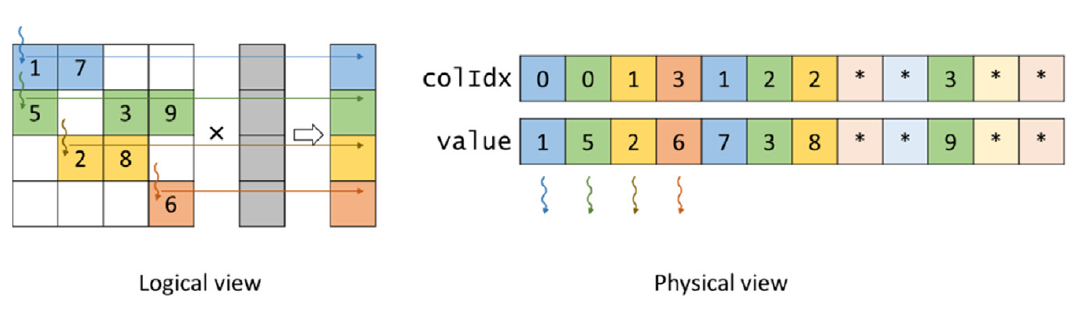
使用CSR格式表示的稀疏矩阵并行执行SpMV，可以为矩阵的每一行分配一个线程。这种并行化方法的示例在图14.8中进行了说明，相应的代码在图14.9中显示。在这种方法中，每个线程确定它负责的行（第02行），并确保它在界限内（第03行）。接下来，线程循环遍历其行的非零元素以执行点积（第05-06行）。为了找到行的非零元素，线程在rowPtrs数组中查找它们的起始索引（rowPtrs[row]）。它还通过查找下一行非零元素的起始索引（rowPtrs[row + 1]）来找到它们的结束位置。对于每个非零元素，线程确定其列索引（第07行）和值（第08行）。然后它查找对应于列索引的输入值，将其与非零值相乘，并将结果累加到局部变量sum中（第09行）。在点积循环开始之前（第04行），sum变量被初始化为0，并在循环结束后累加到输出向量（第11行）。注意，将sum累加到输出向量不需要原子操作。原因是每行由单个线程遍历，因此每个线程将写入一个不同的输出值，如图14.8所示。
现在我们根据第14.1节中列出的设计考虑来检查CSR格式：空间效率、灵活性、可访问性、内存访问效率和负载平衡。对于空间效率，我们观察到CSR比COO更节省空间。COO需要三个数组，rowIdx、colIdx和value，每个数组的元素数量与非零元素的数量相同。相比之下，CSR只需要两个数组，colIdx和value，其元素数量与非零元素的数量相同。第三个数组，rowPtrs，只需要与行数加一的元素数量相同，这使得它比COO中的rowIdx数组小得多。这种差异使CSR比COO更节省空间。
对于灵活性，我们观察到CSR在向矩阵添加非零元素时比COO不够灵活。在COO中，可以通过简单地将其添加到数组的末尾来添加非零元素。在CSR中，要添加的非零元素必须添加到它所属的特定行。这意味着后面的行的所有非零元素都需要移动，后面的行的行指针都需要相应地增加。因此，在CSR矩阵中添加非零元素比在COO矩阵中添加它们要昂贵得多。
对于可访问性，CSR使访问给定行的非零元素变得容易。CSR的这一特性使得SpMV/CSR中可以并行化行，这允许它与SpMV/COO相比避免使用原子操作。在现实世界的稀疏矩阵应用中，通常有数千到数百万个行，每个行包含数十到数百个非零元素。这使得跨行并行化看起来非常合适：有很多线程，每个线程都有大量的工作。另一方面，对于一些应用，稀疏矩阵可能没有足够的行来充分利用所有的GPU线程。在这些类型的应用中，COO格式可以提取更多的并行性，因为非零元素的数量多于行。此外，CSR不便于访问给定列的所有非零元素。因此，如果需要轻松访问列的所有元素，应用程序可能需要维护一个额外的、更面向列的矩阵布局。
对于内存访问效率，我们参考图14.8中的物理视图，了解线程在点积循环的第一次迭代期间如何从内存中访问矩阵数据。访问模式是这样的，连续的线程访问数据元素彼此相距甚远。特别是，线程0、1、2和3将分别访问value[0]、value[2]、value[5]和value[7]，在它们的点积循环的第一次迭代中。然后它们将分别访问value[1]、value[3]、value[6]和没有数据，在第二次迭代中，以此类推。因此，图14.9中的并行SpMV/CSR内核对矩阵的访问不是合并的。内核没有有效地利用内存带宽。
对于负载平衡，我们观察到SpMV/CSR内核可能在所有warp中具有显著的控制流发散。线程在点积循环中所采取的迭代次数取决于分配给线程的行中的非零元素数量。由于非零元素在行之间的分布可能是随机的，相邻的行可以具有非常不同的非零元素数量。因此，在大多数甚至所有warp中可能存在广泛的控制流发散。
总结，我们已经看到CSR相对于COO的优势在于它具有更好的空间效率，并且它允许我们访问一行的所有非零元素，允许我们通过在SpMV/CSR中并行化行计算来避免原子操作。另一方面，CSR相对于COO的缺点是它在向稀疏矩阵添加非零元素时提供较少的灵活性，它表现出不利于合并的内存访问模式，并导致高控制发散。在接下来的部分中，我们将讨论额外的存储格式，这些格式与CSR相比牺牲了一些空间效率，以改善内存合并并减少控制发散。注意，在GPU上从COO转换到CSR是读者使用多个基本并行计算原语（包括直方图和前缀和）的一个很好的练习。
14.4 使用ELL格式改进内存合并
可以通过在稀疏矩阵数据上应用数据填充和平铺来解决非合并内存访问的问题。这些思路被用在了ELL存储格式中，其名字来源于ELLPACK的稀疏矩阵包，ELLPACK是一个用于求解椭圆边界值问题的包（Rice和Boisvert，1984年）。
图14.10 ELL存储格式的示例。
理解ELL格式的一个简单方法是从CSR格式开始，如图14.10所示。从按行分组非零元素的CSR表示，我们确定具有最大非零元素数量的行。然后我们在所有其他行的非零元素之后添加填充元素，使它们的长度与最大行相同。这使矩阵成为一个矩形矩阵。对于我们的小稀疏矩阵示例，我们确定第1行具有最大数量的元素。然后我们向第0行添加一个填充元素，向第2行添加一个填充元素，向第3行添加两个填充元素，使它们的长度相同。这些额外的填充元素在图14.11中显示为带有“填充”字样的方框。现在矩阵已经成为一个矩形矩阵。注意，colIdx数组也需要以相同的方式填充，以保持其与值数组的对应关系。
我们现在可以按列主顺序排列填充矩阵。也就是说，我们将把所有第0列的元素放在连续的内存位置，然后是所有第1列的元素，依此类推。这相当于转置了C语言使用的行主顺序的矩形矩阵。在我们小示例的术语中，转置后，value[0]到value[3]现在包含1、5、2、6，它们是所有行的第0个元素。这在图14.10的左下部分进行了说明。类似地，colIdx[0]到colIdx[3]包含所有行的第0个元素的列位置。注意，我们不再需要rowPtrs，因为行r的开始现在是简单的value[r]。有了填充元素，通过简单地将原始矩阵的行数加到索引上，也很容易从行r的当前元素移动到下一个元素。例如，第2行的第0个元素在value[2]中，下一个元素在value[2+4]中，相当于value[6]，其中4是我们小示例中原始矩阵的行数。
图14.11 使用ELL格式并行化SpMV的示例。
图14.12 一个并行的SpMV/ELL内核。
我们在图14.11中说明了如何使用ELL格式并行化SpMV，并在图14.12中展示了一个并行SpMV/ELL内核。像CSR一样，每个线程被分配到矩阵的不同行（第02行），边界检查确保行在界限内（第03行）。接下来，点积循环遍历每行的非零元素（第05行）。注意，SpMV/ELL内核假设输入矩阵有一个向量ellMatrix.nnzPerRow，记录每行的非零数量，并允许每个线程只遍历其分配行中的非零元素。如果输入矩阵没有这个向量，内核可以简单地遍历所有元素，包括填充元素，并仍然正确执行，因为填充元素的值为零，不会影响输出值。接下来，由于压缩矩阵以列主顺序存储，非零元素在一维数组中的索引i可以通过将迭代次数t乘以行数并加上行索引来找到（第06行）。接下来，线程从ELL矩阵数组中加载列索引（第07行）和非零值（第08行）。注意，对这些数组的访问是合并的，因为索引i以行表示，行本身以threadIdx.x表示，这意味着连续的线程有连续的数组索引。接下来，线程查找输入值，将其与非零值相乘，并将结果累加到局部变量sum中（第09行）。sum变量在点积循环开始之前（第04行）被初始化为0，并在循环结束后累加到输出向量（第11行）。
现在我们根据第14.1节中列出的设计考虑来检查ELL格式：空间效率、灵活性、可访问性、内存访问效率和负载平衡。对于空间效率，我们观察到ELL格式由于填充元素的空间开销，比CSR格式的空间效率低。填充元素的开销高度依赖于矩阵中非零元素的分布。在一行或少数几行具有异常大量的非零元素的情况下，ELL格式将产生过多的填充元素。考虑我们的示例矩阵；在ELL格式中，我们用一个4x3的矩阵替换了一个4x4的矩阵，并且由于列索引的开销，我们存储的数据比原始的4x4矩阵还多。对于一个更现实的例子，如果一个1000x1000的稀疏矩阵有1%的元素是非零值，那么平均每行有十个非零元素。有了开销，CSR表示的大小大约是未压缩总大小的2%。假设一行有200个非零值，而所有其他行少于10个。使用ELL格式，我们将所有其他行填充到200个元素。这使得ELL表示大约是未压缩总大小的40%，比CSR表示大20倍。这就要求我们在从CSR格式转换到ELL格式时控制填充元素的数量，我们将在下一节中介绍。
对于灵活性，我们观察到ELL比CSR在向矩阵添加非零元素时更灵活。在CSR中，向一行添加一个非零元素将需要移动后续行的所有非零元素并增加它们的行指针。然而，在ELL中，只要一行没有矩阵中最大的非零元素数量，就可以通过简单地用实际值替换填充元素来向该行添加非零元素。
对于可访问性，ELL为我们提供了CSR和COO的可访问性。我们在图14.12中看到了ELL如何允许我们访问给定行索引的该行的非零元素。然而，ELL还允许我们访问给定非零元素索引的该元素的行和列索引。列索引很容易找到，因为它可以从同一位置i的colIdx数组中访问。然而，由于填充矩阵的规则性质，行索引也可以访问。回想一下，图14.9中非零元素的索引i是如何计算的：
\[\text{i = t * ellMatrix.numRows + row}\]因此，如果给出的是i，我们想找到行，可以按以下方式找到：
\[\text{row = i % ellMatrix.numRows}\]因为行总是小于ellMatrix.numRows，所以行 row % ellMatrix.numRows就是行本身。这种ELL的可访问性允许跨行以及非零元素并行化。
对于内存访问效率，我们参考图14.11中的物理视图，了解线程在点积循环的第一次迭代期间如何从内存中访问矩阵数据。访问模式是这样的，连续的线程访问连续的数据元素。通过按列主顺序排列元素，所有相邻的线程现在都访问相邻的内存位置，实现内存合并，从而更有效地利用内存带宽。一些GPU架构，特别是旧一代的，对内存合并有更严格的地址对齐规则。可以通过在转置前在矩阵末尾添加几行，强制每个SpMV/ELL内核的迭代完全对齐到架构指定的对齐单位（如64字节）。
对于负载平衡，我们观察到SpMV/ELL仍然表现出与SpMV/CSR相同的负载不平衡，因为每个线程仍然循环遍历它负责的行中的非零元素数量。因此，ELL没有解决控制发散的问题。
总结，ELL格式通过允许用实际值替换填充元素来添加非零元素，提高了灵活性，更好的可访问性，最重要的是，在SpMV/ELL中为内存合并提供了更多的机会。然而，ELL的空间效率比CSR差，SpMV/ELL的控制发散与SpMV/CSR一样糟糕。在下一节中，我们将看到如何改进ELL格式来解决空间效率和控制发散的问题。
14.6 使用JDS格式减少控制发散
我们已经看到ELL格式可以在SpMV中访问稀疏矩阵时实现合并的内存访问模式，并且混合ELL-COO格式可以通过减少填充进一步改善空间效率，也可以减少控制发散。在本节中，我们将看到另一种格式，它可以在SpMV中实现合并的内存访问模式，并且无需进行任何填充即可减少控制发散。这个想法是按照它们的长度对行进行排序，比如说，从最长到最短。由于排序后的矩阵看起来非常像一个三角矩阵，该格式通常被称为锯齿对角线存储（JDS）格式。
图14.14展示了如何使用JDS格式存储矩阵。首先，像CSR和ELL格式一样，非零元素按行分组。接下来，根据每行中非零元素的数量，按递增顺序对行进行排序。在对行进行排序时，我们通常会维护一个额外的行数组，以保留原始行的索引。每当我们在排序过程中交换两行时，我们也会交换行数组的相应元素。因此，我们可以始终追踪所有行的原始位置。行排序完成后，值数组中的非零元素及其在colIdx数组中对应的列索引按列主顺序存储。添加了一个iterPtr数组来跟踪每次迭代的非零元素的开始。
图14.15展示了如何使用JDS格式并行化SpMV。每个线程被分配到矩阵的一行，遍历该行的非零元素，同时执行点积。线程使用iterPtr数组来确定每次迭代的非零元素的开始位置。从图14.15右侧的物理视图可以清楚地看出，该视图描述了每个线程的第一次迭代，线程以合并的方式访问JDS数组中的非零元素和列索引。实现SpMV/JDS的代码留给读者作为练习。
在JDS格式的另一个变体中，排序后的行可以被划分为行的部分。由于行已经排序，一个部分中的所有行可能具有或多或少统一数量的非零元素。然后我们可以为每个部分生成ELL表示。在每个部分内部，我们只需要填充行以匹配该部分中元素数量最多的行。与整个矩阵的一个ELL表示相比，这将大幅减少填充元素的数量。在JDS的这种变体中，不需要iterPtr数组。相反，我们需要一个部分指针数组，它只指向每个ELL部分的开始（而不是每次迭代）。
读者可能会问，对行进行排序是否会导致线性方程组的解不正确。回想一下，我们可以自由地重新排序线性系统的方程，而不会改变解。只要我们随着行一起重新排序y元素，我们就有效地重新排序了方程。因此，我们最终会得到正确的解。唯一的额外步骤是使用行数组将最终解重新排序回原始顺序。另一个问题是，排序是否会产生显著的开销。答案与我们在混合ELL-COO方法中看到的类似。只要SpMV/JDS内核在迭代求解器中使用，人们就可以负担得起执行这样的排序以及最终解的重排序，并将成本分摊到求解器的多次迭代中。
现在我们根据第14.1节中列出的设计考虑来检查JDS格式：空间效率、灵活性、可访问性、内存访问效率和负载平衡。对于空间效率，JDS格式比ELL格式更节省空间，因为它避免了填充。使用每个部分的ELL的JDS变体有填充，但填充的数量少于ELL格式。
对于灵活性，JDS格式并不便于向矩阵的一行添加非零元素。它甚至比CSR格式更不灵活，因为添加非零元素会改变行的大小，可能需要重新对行进行排序。
对于可访问性，JDS格式类似于CSR格式，允许我们给定行索引，访问该行的非零元素。另一方面，它不像COO和ELL格式那样，便于给定一个非零元素，访问该非零元素的行索引和列索引。
对于内存访问效率，JDS格式类似于ELL格式，因为它以列主顺序存储非零元素。因此，JDS格式能够使对稀疏矩阵的访问以合并的方式发生。由于JDS不需要填充，每次迭代中内存访问的起始位置，如图14.15的物理视图所示，可以任意变化。结果，没有简单、经济的方法来强制所有SpMV/JDS内核的迭代从架构指定的对齐边界开始。这种无法强制对齐的选择可能使JDS的内存访问效率低于ELL。
对于负载平衡，JDS的独特特点是它对矩阵的行进行排序，使得同一warp中的线程可能会迭代遍历长度相似的行。因此，JDS在减少控制发散方面非常有效。
14.7 总结
在本章中，我们提出了稀疏矩阵计算作为一个重要的并行模式。稀疏矩阵在许多涉及模拟复杂现象的实际应用中都很重要。此外，稀疏矩阵计算是许多大型实际应用中数据依赖性能行为的一个简单例子。由于零元素的数量很大，使用了压缩技术来减少这些零元素的存储、内存访问和计算量。利用这个模式，我们引入了使用混合方法和排序/分区的规范化概念。这些规范化方法在许多实际应用中都有使用。有趣的是，一些规范化技术将零元素重新引入到压缩表示中。我们使用混合方法来缓解可能引入太多零元素的病态情况。我们引用了Bell和Garland（2009）的工作，并鼓励读者尝试不同的稀疏数据集，以更深入地了解本章介绍的各种SpMV内核的数据依赖性能行为。
应该清楚的是，无论是执行效率还是内存带宽效率，并行SpMV内核都取决于输入数据矩阵的分布。这与我们迄今为止研究的大多数内核有很大的不同。然而，这种数据依赖的性能行为在实际应用中非常普遍。这是并行SpMV这样一个重要的并行模式的原因之一。它简单，但能说明许多复杂并行应用中的重要行为。
我们想就稀疏矩阵计算与密集矩阵计算的性能再做一些额外的评论。通常，无论是CPU还是GPU实现的浮点运算次数（FLOPS）等级，稀疏矩阵计算都远低于密集矩阵计算。对于SpMV来说尤其如此，其中稀疏矩阵中没有数据重用。操作数/周期（OP/B）基本上是0.25，将可实现的FLOPS速率限制在峰值性能的一小部分。各种格式对于CPU和GPU都很重要，因为在执行SpMV时，两者都受到内存带宽的限制。人们经常对过去在CPU和GPU上这种计算类型的低FLOPS等级感到惊讶。阅读完本章后，你将不再对此感到惊讶。
- 显示Disqus评论(需要科学上网)