第十五章：图遍历

15.1 背景
15.2 广度优先搜索
15.3 以顶点为中心的广度优先搜索并行化
15.4 以边为中心的广度优先搜索并行化
15.5 使用边界提高效率
15.6 通过私有化减少竞争
15.7 其他优化
15.8 总结

图是一种数据结构，用于表示实体之间的关系。所涉及的实体以顶点的形式表示，而关系则以边的形式表示。许多重要的现实世界问题都可以自然地表述为大规模图问题，并且可以从大规模并行计算中受益。突出的例子包括社交网络和驾驶导航地图服务。图计算的并行化有多种策略，有些以并行处理顶点为中心，有些则以并行处理边为中心。图与稀疏矩阵有着内在的联系。因此，图计算也可以以稀疏矩阵操作的形式来表述。然而，人们通常可以通过利用特定于正在执行的图计算类型的属性来提高图计算的效率。在本章中，我们将专注于图搜索，这是一种支撑许多现实世界应用的图计算。

15.1 背景

图数据结构表示实体之间的关系。例如，在社交媒体中，实体是用户，关系是用户之间的联系。另一个例子是，在驾驶导航地图服务中，实体是地点，关系是地点之间的道路。有些关系是双向的，如社交网络中的好友联系。其他关系是单向的，如道路网络中的单行道。在本章中，我们将专注于单向关系。双向关系可以通过两个单向关系来表示，每个方向一个。

图15.1 一个有9个顶点和15条方向性边的简单图示例。

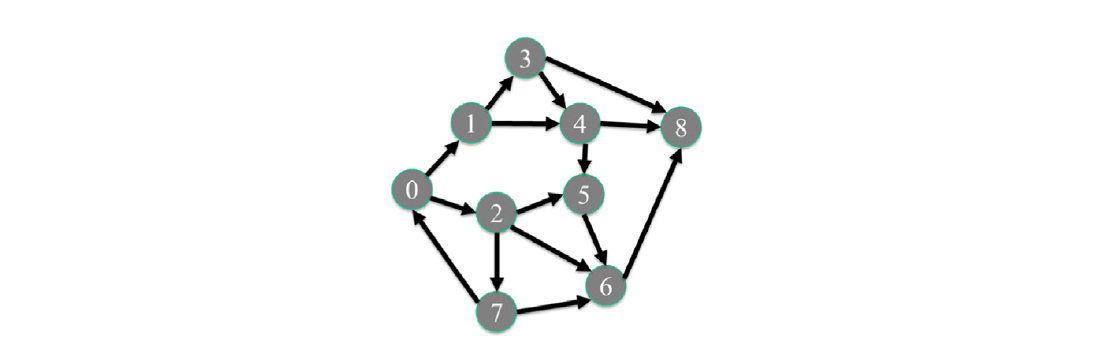
图15.1显示了一个具有方向性边的简单图的示例。一个方向性关系被表示为从源顶点到目标顶点的带箭头的边。我们为每个顶点分配一个独特的编号，也称为顶点ID。从顶点0到顶点1有一条边，从顶点0到顶点2有一条边，以此类推。

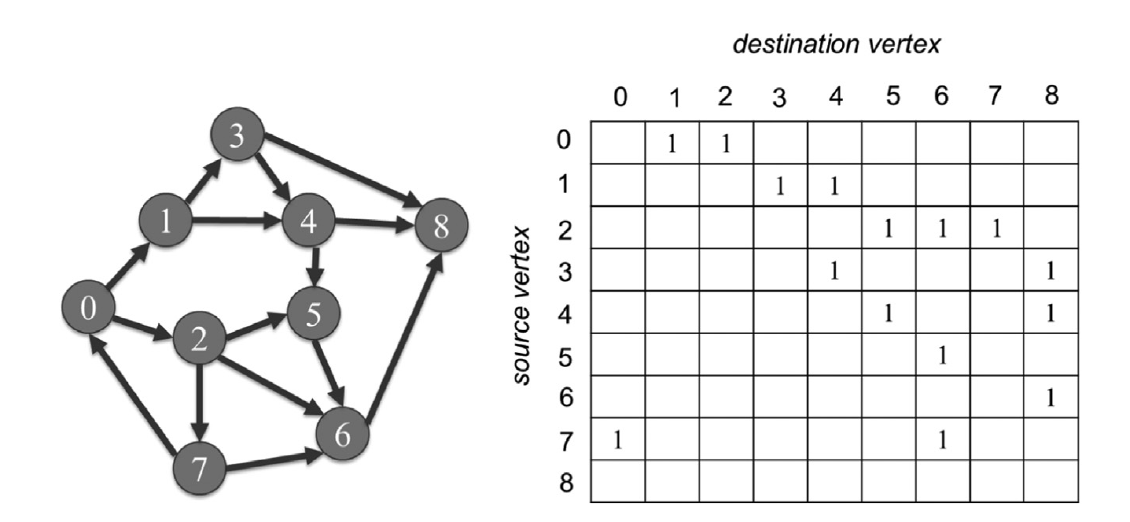
图的一个直观表示是邻接矩阵。如果有一条从源顶点i到目标顶点j的边，邻接矩阵的元素A[i][j]的值就是1。否则，它是0。图15.2显示了图15.1中简单图的邻接矩阵。我们看到A[1][3]和A[4][5]是1，因为有边从顶点1到顶点3。为了清晰起见，我们省略了邻接矩阵中的0值。也就是说，如果一个元素是空的，它的值被理解为0。

图15.2 简单图示例的邻接矩阵表示。

如果一个有N个顶点的图是完全连接的，也就是说，每个顶点都与其他所有顶点相连，每个顶点应该有(N-1)条出去的边。应该有总共N(N-1)条边，因为顶点不会与自身相连。例如，如果我们的九顶点图是完全连接的，每个顶点应该有八条边出去。应该有总共72条边。

显然，我们的图连接度要低得多；每个顶点有三个或更少的出去的边。这样的图被称为稀疏连接。也就是说，每个顶点的平均出去边数远小于N-1。此时，读者很可能已经正确地观察到，稀疏连接的图可能从稀疏矩阵表示中受益。正如我们在第14章“稀疏矩阵计算”中看到的，使用矩阵的压缩表示可以大幅减少所需的存储量和对零元素的浪费操作数量。的确，许多现实世界的图是稀疏连接的。例如，在Facebook、Twitter或LinkedIn等社交网络中，每个用户的平均联系数远小于用户总数。这使得邻接矩阵中的非零元素数量远小于总元素数量。

图15.3 简单图示例的邻接矩阵表示。

图15.3显示了使用三种不同的存储格式表示我们简单图示例的三种表示：压缩稀疏行（CSR）、压缩稀疏列（CSC）和坐标（COO）。我们将行索引和指针数组分别称为src和srcPtrs数组，列索引和指针数组分别称为dst和dstPtrs数组。如果我们以CSR为例，回想一下，在稀疏矩阵的CSR表示中，每行的行指针给出了该行非零元素的起始位置。类似地，在图的CSR表示中，每个源顶点指针（srcPtrs）给出了顶点出去边的起始位置。例如，srcPtrs[3]=7给出了原始邻接矩阵第3行非零元素的起始位置。同样，srcPtrs[4]=9给出了原始矩阵第4行非零元素的起始位置。因此，我们期望在data[7]和data[8]中找到第3行的非零数据，以及这些元素的列索引（目标顶点）在dst[7]和dst[8]中。这些是离开顶点3的两条边的数据和列索引。我们称列索引数组为dst的原因是，邻接矩阵中元素的列索引给出了所表示边的目标顶点。在我们的示例中，我们看到源顶点3的两条边的目标是dst[7]=4和dst[8]=8。我们留给读者作为练习，为CSC和COO表示画出类似的类比。

注意，在这个例子中，数据数组是不必要的。由于所有元素的值都是1，我们不需要存储它。我们可以隐式地使用数据，也就是说，每当存在非零元素时，我们可以假设它是1。例如，CSR表示中目标数组中每个列索引的存在意味着存在一条边。然而，在某些应用中，邻接矩阵可能存储了关于关系的额外信息，如两个地点之间的距离或两个社交网络用户建立联系的日期。在这些应用中，数据数组将需要被明确存储。

稀疏表示可以显著节省存储邻接矩阵所需的空间。对于我们的示例，假设数据数组可以被消除，CSR表示需要存储25个位置，而如果我们存储了整个邻接矩阵，则需要存储81个位置。对于邻接矩阵元素中非常小的一部分是非零的真实问题，节省可以是巨大的。不同的图可能具有截然不同的结构。一种表征这些结构的方法是查看连接到每个顶点的边数（顶点度）的分布。作为图表示的道路网络将具有相对均匀的度分布和每个顶点的低平均度，因为每个道路交叉口（顶点）通常只有少数几条道路连接。另一方面，以图表示的Twitter粉丝，其中每个传入边代表一个“关注”，将具有更广泛的顶点度分布，大度顶点代表一个受欢迎的Twitter用户。图的结构可能影响实现特定图应用的算法选择。

回想一下第14章“稀疏矩阵计算”，每种稀疏矩阵表示为表示的数据提供了不同的可访问性。因此，选择用于图的表示对于使图的哪些信息易于被图遍历算法访问具有影响。CSR表示便于访问给定顶点的出去边。CSC表示便于访问给定顶点的进来边。COO表示便于访问给定边的源和目标顶点。因此，图表示的选择与图遍历算法的选择密切相关。我们通过检查广泛使用的图搜索计算的广度优先搜索的不同并行实现，来演示这个概念。

15.2 广度优先搜索

图计算中的一个重要计算是广度优先搜索（BFS）。BFS通常用于发现从一个顶点到图中另一个顶点需要穿越的最短边数。在图15.1的示例中，我们可能需要找到从由顶点0表示的位置到由顶点5表示的位置的所有替代路线。通过视觉检查，我们可以看到有三条可能的路径：0-1-3-4-5，0-1-4-5和0-2-5，其中0-2-5是最短的。BFS遍历的结果有不同的总结方式。一种方式是，给定一个称为根的顶点，给每个顶点标记上从根到该顶点需要穿越的最小边数。

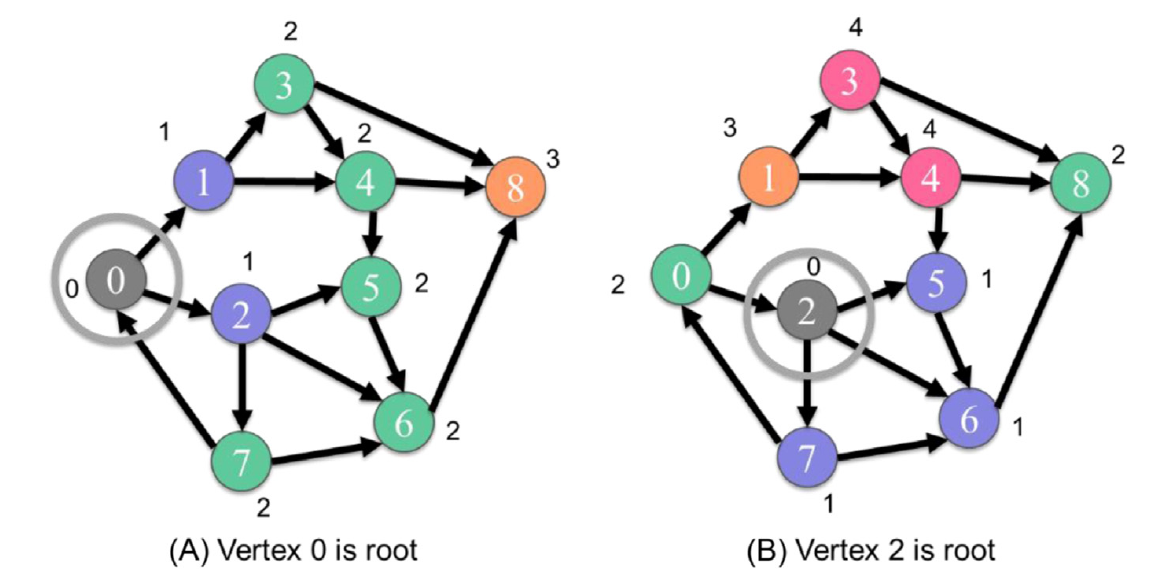图15.4 (A和B) 两个不同根顶点的广度优先搜索结果示例。每个顶点旁边的标签表示从根顶点跳数（深度）。

图15.4(A)显示了以顶点0为根的期望BFS结果。通过一条边，我们可以到达顶点1和2。因此，我们将这些顶点标记为属于第1级。再通过一条边，我们可以到达顶点3（通过顶点1）、4（通过顶点1）、5（通过顶点2）、6（通过顶点2）和7（通过顶点2）。因此，我们将这些顶点标记为属于第2级。最后，再通过一条边，我们可以到达顶点8（通过顶点3、4或6中的任意一个）。BFS的结果如果以另一个顶点为根将会非常不同。

图15.4(B)显示了以顶点2为根的BFS期望结果。第1级的顶点是5、6和7。第2级的顶点是8（通过顶点6）和0（通过顶点7）。只有顶点1在第3级（通过顶点0）。最后，第4级的顶点是3和4（都通过顶点1）。有趣的是，即使我们将根移到距离原根只有一个边的顶点，结果也会非常不同。

人们可以将BFS的标记操作视为构建一个以搜索根节点为根的BFS树。该树由所有标记的顶点组成，并且只有搜索期间穿越的边，从一级顶点到下一级顶点。

一旦我们用它们的级别标记了所有顶点，我们可以很容易地找到从根顶点到任何顶点的路径，所走的边数等同于级别。例如，在图15.4(B)中，我们看到顶点1被标记为第3级，所以我们知道根（顶点2）和顶点1之间的最小边数是3。如果我们需要找到路径，我们可以从目标顶点开始，回溯到根。在每一步，我们选择级别比当前顶点少一级的前驱。如果有多个具有相同级别的前驱，我们可以选择一个。任何这样选择的顶点都会给出一个合理的解决方案。有多个前驱可供选择意味着有多个同样好的解决方案。在我们的示例中，我们可以通过从顶点1开始，选择顶点0，然后顶点7，然后顶点2，找到从顶点2到顶点1的最短路径。因此，一个解决方案路径是2-7-0-1。这当然假设每个顶点都有一个所有进入边的源顶点列表，以便找到给定顶点的前驱。

图15.5显示了BFS在计算机辅助设计（CAD）中的一个重要应用。在设计集成电路芯片时，有许多电子元件需要连接以完成设计。这些元件的连接器称为网络终端。图15.5(A)显示了两个这样的网络终端作为圆点；一个属于左上部分的一个元件，另一个属于芯片右下角的另一个元件。假设设计要求这两个网络终端连接起来。这是通过从第一个网络终端到第二个网络终端运行或布设给定宽度的导线来完成的。

布线软件将芯片表示为布线块的网格，其中每个块都可以作为导线的一部分。导线可以通过水平或垂直方向扩展来形成。例如，芯片下半部分的黑色J形由21个布线块组成，连接了三个网络终端。一旦一个布线块被用作导线的一部分，它就不能再被用作任何其他导线的一部分。此外，它对其周围的布线块形成阻塞。使用过的块的下邻不能将其导线扩展到上邻，左邻不能将其导线扩展到右邻，以此类推。一旦形成了导线，所有其他导线都必须围绕它布线。布线块也可以被电路元件占据，它们施加了与作为导线一部分时相同的阻塞约束。这就是为什么这个问题被称为迷宫布线问题。先前形成的电路元件和导线为尚未形成的导线形成了迷宫。迷宫布线软件在所有先前形成的元件和导线的约束下为每根额外的导线找到一条路线。

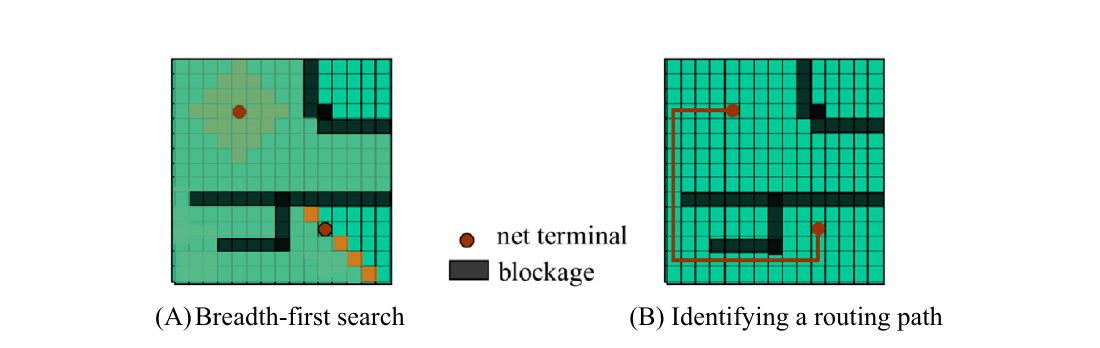集成电路中的迷宫布线——广度优先搜索的应用：(A) 广度优先搜索，(B) 确定布线路径。

迷宫布线应用将芯片表示为图。布线块是顶点。从顶点i到顶点j的边表示可以从块i扩展导线到块j。一旦一个块被导线或元件占据，根据应用的设计，它要么被标记为阻塞顶点，要么从图中移除。图15.5显示应用通过从根网络终端到目标网络终端的BFS来解决迷宫布线问题。这是通过从根顶点开始并按级别标记顶点来完成的。不是阻塞的直接垂直或水平邻居（总共四个）被标记为第1级。我们可以看到，根的所有四个邻居都是可达的，并将被标记为第1级。不是阻塞的也不是当前搜索访问过的第1级顶点的邻居将被标记为第2级。读者应该验证图15.5(A)中有四个第1级顶点，八个第2级顶点，十二个第3级顶点，以此类推。我们可以看到，BFS本质上为每个级别形成了顶点的波阵面。这些波阵面从第1级的开始很小，但在几级内可以迅速变得非常大。

图15.5(B)显示，一旦BFS完成，我们可以通过找到从根到目标的最短路径来形成导线。正如前面解释的，这可以通过从目标顶点开始，回溯到级别比当前顶点低一级的前驱来完成。每当有多个具有等同级别的前驱时，就有多个长度相同的路线。人们可以设计启发式方法来选择前驱，以这种方式最小化尚未形成的导线的约束难度。

15.3 以顶点为中心的广度优先搜索并行化

图算法并行化的自然方式是对不同的顶点或边进行并行操作。实际上，许多图算法的并行实现可以被分类为以顶点为中心或以边为中心。以顶点为中心的并行实现为顶点分配线程，并让每个线程对其顶点执行操作，这通常涉及迭代该顶点的邻居。根据算法的不同，感兴趣的邻居可能是通过出去的边、进来的边或两者都可以到达的。相比之下，以边为中心的并行实现为边分配线程，并让每个线程对其边执行操作，这通常涉及查找该边的源顶点和目标顶点。在本节中，我们将看两种不同的以顶点为中心的BFS并行实现：一种迭代出去的边，另一种迭代进来的边。在下一节中，我们将看BFS的以边为中心的并行实现并进行比较。

我们将要查看的并行实现在迭代层次时遵循相同的策略。在所有实现中，我们首先将根顶点标记为属于第0级。然后我们调用一个核函数将根顶点的所有邻居标记为属于第1级。之后，我们调用一个核函数将第1级顶点的所有未访问邻居标记为属于第2级。然后我们调用一个核函数将第2级顶点的所有未访问邻居标记为属于第3级。这个过程一直持续到没有新的顶点被访问和标记为止。之所以每一层都调用一个单独的核函数，是因为我们需要等待前一层的所有顶点都被标记之后才能继续标记下一层的顶点。否则，我们就有可能错误地标记一个顶点。在本节的其余部分，我们专注于实现每一层被调用的核函数。也就是说，我们将实现一个BFS核函数，该函数给定一个级别，根据前一级顶点的标记，标记所有属于该级别的顶点。

第一个以顶点为中心的并行实现为每个线程分配一个顶点以迭代该顶点的出去的边（Harish和Narayanan，2007）。每个线程首先检查其顶点是否属于前一级。如果是，线程将迭代出去的边，将所有未访问的邻居标记为属于当前级别。这种以顶点为中心的实现通常被称为自顶向下或推实现。由于这种实现需要可访问给定源顶点的出去的边（即邻接矩阵的给定行的非零元素），因此需要CSR表示。

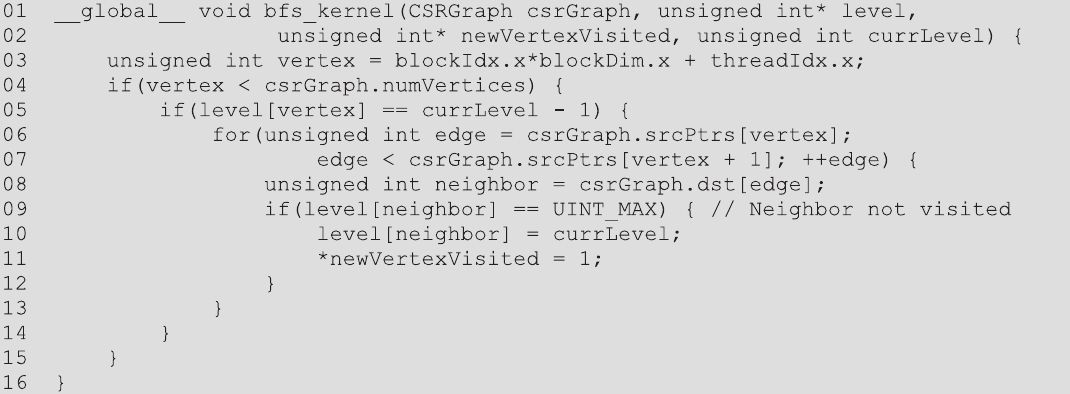图15.6 一个以顶点为中心的推（自顶向下）广度优先搜索（BFS）核函数。BFS，即广度优先搜索。

图15.6显示了以顶点为中心的推实现的核函数代码，图15.7显示了这个核函数如何从第1级（前一级）执行到第2级（当前级别）的遍历示例。核函数首先为每个顶点分配一个线程（第03行），每个线程确保其顶点ID在界限内（第04行）。接下来，每个线程检查其顶点是否属于前一级（第05行）。在图15.7中，只有分配给顶点1和2的线程将通过这个检查。通过这个检查的线程将使用CSR srcPtrs数组定位顶点的出去的边并迭代它们（第06-07行）。对于每个出去的边，线程使用CSR dst数组找到边的目标处的邻居（第08行）。然后线程检查邻居是否未被访问，方法是检查邻居是否已被分配到一个级别（第09行）。

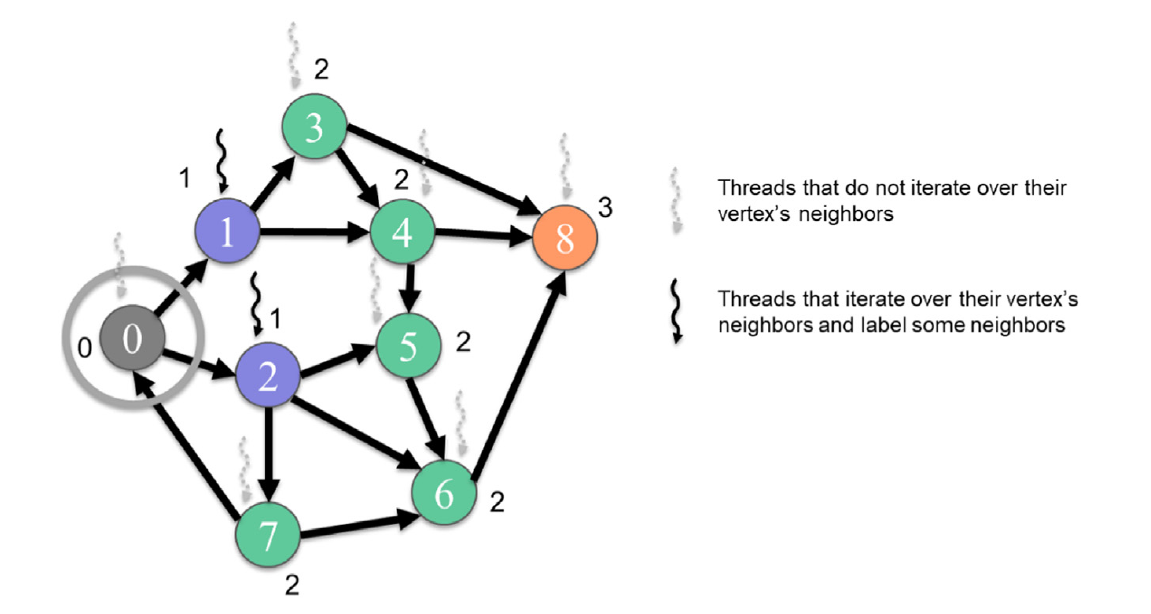图15.7 以顶点为中心的推式BFS遍历示例，从第1级到第2级。BFS，即广度优先搜索。

最初，所有顶点的级别都设置为UINT_MAX，这意味着顶点是不可到达的。因此，如果邻居的级别仍然是UINT_MAX，则邻居尚未被访问。如果邻居尚未被访问，线程将将邻居标记为属于当前级别（第10行）。最后，线程将设置一个标志，表示已访问了一个新的顶点（第11行）。这个标志被启动代码用来决定是否需要启动一个新的网格来处理一个新的级别，或者我们已经到达了终点。注意，多个线程可以给这个标志赋值为1，代码仍然可以正确执行。这个属性被称为幂等性。在像这样的幂等操作中，我们不需要原子操作，因为线程没有执行读-修改-写操作。所有线程写入相同的值，因此不管有多少线程执行写操作，结果都是一样的。

第二个以顶点为中心的并行实现为每个线程分配一个顶点以迭代该顶点的进来的边。每个线程首先检查其顶点是否已被访问。如果没有，线程将迭代进来的边，以找到是否有任何邻居属于前一级。如果线程发现一个属于前一级的邻居，线程将将其顶点标记为属于当前级别。这种以顶点为中心的实现通常被称为自底向上或拉实现。由于这种实现需要可访问给定目标顶点的进来的边（即邻接矩阵的给定列的非零元素），因此需要CSC表示。

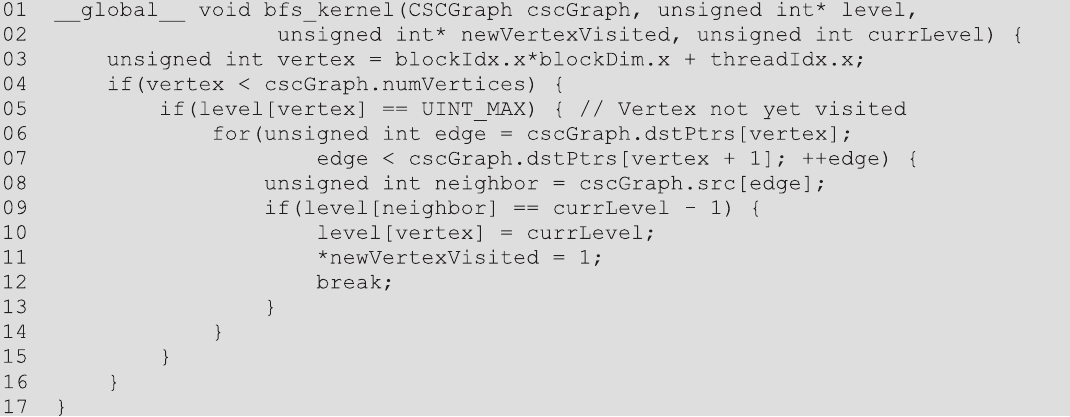图15.8 一个以顶点为中心的拉（自底向上）广度优先搜索（BFS）核函数。BFS，即广度优先搜索。

图15.8显示了以顶点为中心的拉实现的核函数代码，图15.9显示了这个核函数如何从第1级执行到第2级的遍历示例。核函数首先为每个顶点分配一个线程（第03行），每个线程确保其顶点ID在界限内（第04行）。接下来，每个线程检查其顶点是否尚未被访问（第05行）。在图15.9中，被分配到顶点3和8的线程都通过了这个检查。通过这个检查的线程将使用CSC dstPtrs数组定位顶点的进来的边并迭代它们（第06-07行）。对于每个进来的边，线程使用CSC src数组找到边的源处的邻居（第08行）。然后线程检查邻居是否属于前一级（第09行）。如果是，线程将将其顶点标记为属于当前级别（第10行）并设置一个标志，表示已访问了一个新的顶点（第11行）。线程还将跳出循环（第12行）。

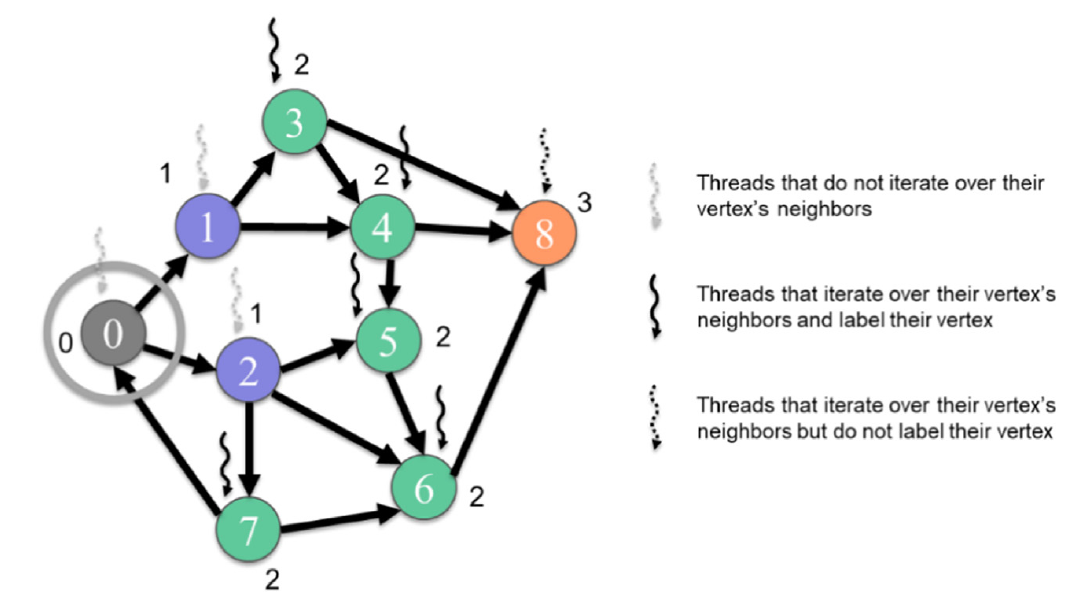图15.9 以顶点为中心的拉（自底向上）遍历示例，从第1级到第2级。

跳出循环的理由如下：对于一个线程来说，要确定其顶点在当前级别，其顶点有一个在前一级的邻居就足够了。因此，线程不需要检查其余的邻居。只有在前一级没有任何邻居的顶点的线程最终会遍历整个邻居列表。在图15.9中，只有被分配到顶点8的线程会在整个邻居列表上循环而不停。

在比较推和拉的以顶点为中心的并行实现时，有两个关键差异需要考虑，它们对性能有重要影响。第一个差异是在推实现中，一个线程循环遍历其顶点的整个邻居列表，而在拉实现中，一个线程可能会提前跳出循环。对于度数低且方差小的图，如道路网络或CAD电路模型，这种差异可能不重要，因为邻居列表小且大小相似。然而，对于度数高且方差大的图，如社交网络，邻居列表很长，大小可能有很大差异，导致线程间的高负载不平衡和控制发散。由于这个原因，提前跳出循环可以通过减少负载不平衡和控制发散来提供显著的性能提升。

两种实现之间的第二个重要差异是，在推实现中，只有被分配到前一级顶点的线程会循环遍历它们的邻居列表，而在拉实现中，所有被分配到任何未访问顶点的线程都会循环遍历它们的邻居列表。对于早期级别，我们期望每级的顶点数量相对较少，图中有大量的未访问顶点。由于这个原因，推实现通常在早期级别表现更好，因为它迭代的邻居列表较少。相比之下，对于后期级别，我们期望每级有更多的顶点和较少的未访问顶点。此外，在拉方法中找到已访问的邻居并提前退出循环的机会更高。由于这个原因，拉实现通常在后期级别表现更好。

基于这一观察，一个常见的优化是使用推实现用于早期级别，然后切换到拉实现用于后期级别。这种方法通常被称为方向优化实现。何时在实现之间切换的选择通常取决于图的类型。度数低的图通常有很多级别，需要一段时间才能达到级别有很多顶点并且已经有大量顶点被访问的点。另一方面，度数高的图通常只有少数级别，级别增长得非常快。只有少数级别就可以从任何顶点到达任何其他顶点的度数高的图通常被称为小世界图。由于这些属性，从推实现切换到拉实现通常对高学位图比对低学位图要早得多。

回想一下，推实现使用图的CSR表示，而拉实现使用图的CSC表示。由于这个原因，如果要使用方向优化实现，就需要同时存储图的CSR和CSC表示。在许多应用中，如社交网络或迷宫布线，图是无向的，这意味着邻接矩阵是对称的。在这种情况下，CSR和CSC表示是等价的，所以只需要存储其中之一，并且可以被两种实现使用。

15.4 以边为中心的广度优先搜索并行化

在本节中，我们将探讨广度优先搜索（BFS）的一种以边为中心的并行实现。在这种实现中，每个线程被分配给一条边。它检查边的源顶点是否属于前一级，以及边的目标顶点是否未被访问。如果是，它将未访问的目标顶点标记为属于当前级别。由于这种实现需要访问给定边的源和目标顶点（即给定非零元素的行和列索引），因此需要一个坐标列表（COO）数据结构。

图15.10 一个以边为中心的BFS核函数。BFS，即广度优先搜索。

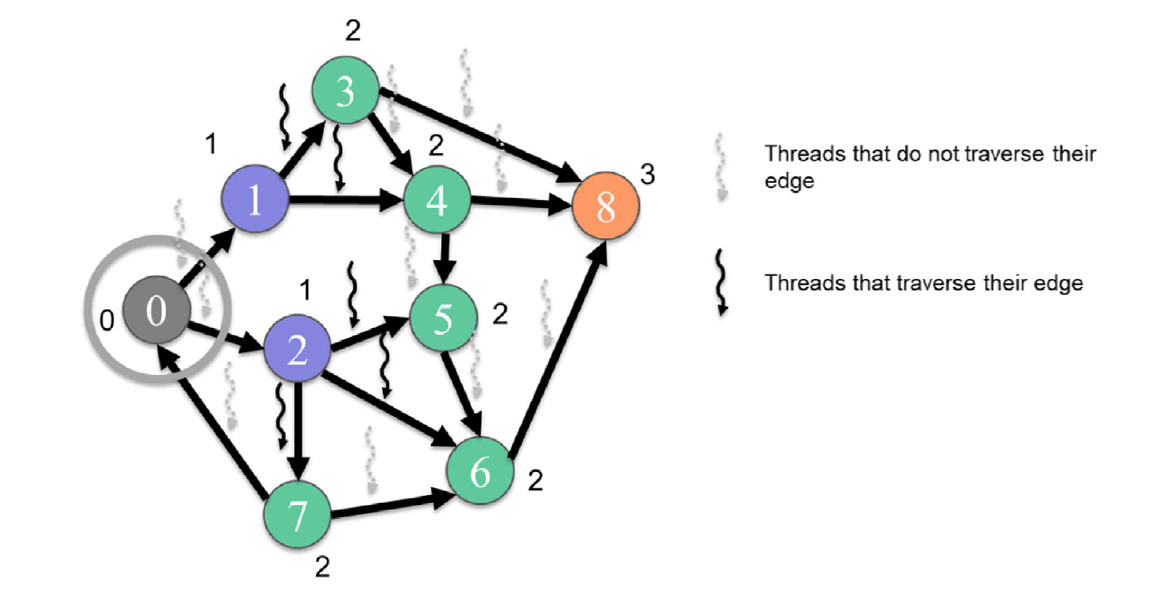
图15.10显示了以边为中心的并行实现的核函数代码，而图15.11展示了这个核函数如何执行从第1级到第2级的遍历。核函数首先为每条边分配一个线程（第03行），每个线程确保其边ID在界限内（第04行）。接下来，每个线程使用COO src数组找到其边的源顶点，并检查该顶点是否属于前一级（第06行）。在图15.11中，只有被分配到顶点1和2的出去边的线程会通过这个检查。通过这个检查的线程将使用COO dst数组定位边的目标处的邻居（第07行），并检查邻居是否未被访问（第08行）。如果没有，线程将将邻居标记为属于当前级别（第09行）。最后，线程将设置一个标志，表示已访问了一个新的顶点（第10行）。

图15.11 以边为中心的遍历示例，从第1级到第2级。

以边为中心的并行实现与以顶点为中心的并行实现相比有两个主要优势。第一个优势是以边为中心的实现暴露了更多的并行性。在以顶点为中心的实现中，如果顶点数量较少，我们可能无法启动足够多的线程来充分利用设备。由于图通常有比顶点多得多的边，以边为中心的实现可以启动更多的线程。因此，以边为中心的实现通常更适合小图。

以边为中心的实现相对于以顶点为中心的实现的第二个优势是，它表现出较少的负载不平衡和控制发散。在以顶点为中心的实现中，每个线程根据其分配的顶点的度数迭代不同数量的边。相比之下，在以边为中心的实现中，每个线程只遍历一条边。与以顶点为中心的实现相比，以边为中心的实现是通过重新排列线程到工作或数据的映射来减少控制发散的一个例子，如第6章性能考虑中所讨论的。以边为中心的实现通常更适合于度数高且顶点度数变化大的图。

以边为中心的实现的缺点是它检查图中的每条边。相比之下，以顶点为中心的实现如果确定某个顶点与某一级别无关，可以跳过整个边列表。例如，考虑某个顶点v有n条边，并且与某个特定级别无关的情况。在以边为中心的实现中，我们的启动包括n个线程，每个边一个，每个线程独立检查v并发现边是不相关的。相比之下，在以顶点为中心的实现中，我们的启动只包括一个线程用于v，该线程在检查一次v后确定其无关，然后跳过所有n条边。以边为中心的实现的另一个缺点是它使用COO，与以顶点为中心的实现使用的CSR和CSC相比，它需要更多的存储空间来存储边。

读者可能已经注意到前一节和这一节的代码示例类似于我们在第14章稀疏矩阵-向量乘法（SpMV）的实现。实际上，通过稍微不同的公式，我们可以将BFS级别迭代完全用SpMV和其他一些向量操作来表示，其中SpMV操作是主要的操作。超出BFS，许多其他图计算也可以用稀疏矩阵计算的术语来表述，使用邻接矩阵（Jeremy和Gilbert，2011）。这种表述通常被称为图问题的线性代数表述，并且是GraphBLAS这样的API规范的焦点。线性代数表述的优势在于它们可以利用成熟和高度优化的稀疏线性代数并行库来执行图计算。线性代数表述的缺点是它们可能错过了利用特定图算法属性的优化。

15.5 使用边界提高效率

在我们前两节讨论的方法中，我们在每次迭代中检查每个顶点或边与所讨论级别的相关性。这种策略的优势在于核函数高度并行，不需要线程间的任何同步。缺点是启动了许多不必要的线程，并执行了大量的无用工作。例如，在以顶点为中心的实现中，我们为图中的每个顶点启动了一个线程，其中许多线程简单地发现顶点不相关并没有执行任何工作。同样，在以边为中心的实现中，我们为图中的每条边启动了一个线程；许多线程简单地发现边不相关并没有执行任何有用的工作。

在本节中，我们的目标是避免启动不必要的线程，并消除它们在每次迭代中执行的冗余检查。我们将重点关注第15.3节中介绍的以顶点为中心的推方法。回想一下，在以顶点为中心的推方法中，对于每个级别，为图中的每个顶点启动一个线程。该线程检查其顶点是否在前一级中，如果是，它将所有未访问的邻居标记为属于当前级别。另一方面，其顶点不在当前级别的线程不执行任何操作。理想情况下，这些线程甚至不应该被启动。为了避免启动这些线程，我们可以在前一级处理顶点的线程之间进行协作，构建它们访问的顶点边界。因此，对于当前级别，只需要为边界中的顶点启动线程（Luo等人，2010）。

图15.12 一个带有边界的以顶点为中心的推（自顶向下）广度优先搜索（BFS）核函数。BFS，即广度优先搜索。

图15.12显示了使用边界的以顶点为中心推实现的核函数代码，图15.13展示了这个核函数如何执行从第1级到第2级的遍历。与以前方法的一个关键区别是，核函数接受额外的参数来表示边界。额外的参数包括数组prevFrontier和currFrontier，分别存储前一个和当前边界中的顶点。它们还包括指向计数器numPrevFrontier和numCurrFrontier的指针，这些计数器存储每个边界中的顶点数量。注意，不再需要表示新顶点已被访问的标志。相反，当当前边界中的顶点数量为0时，主机可以知道已经到达了终点。

我们现在看看图15.12中核函数的主体。核函数首先为前一个边界的每个元素分配一个线程（第05行），每个线程确保其元素ID在界限内（第06行）。在图15.13中，只有顶点1和2在前一个边界中，所以只启动了两个线程。每个线程从前一个边界加载其元素，其中包含它正在处理的顶点的索引（第07行）。线程使用CSR srcPtrs数组定位顶点的出去边，并遍历它们（第08-09行）。对于每个出去边，线程使用CSR dst数组找到边的目标处的邻居（第10行）。然后线程检查邻居是否未被访问；如果没有，它将邻居标记为属于当前级别（第11行）。与以前实现的一个重要区别是，使用了原子操作来执行检查和标记操作。原因将很快解释。如果一个线程成功地标记了邻居，它必须将邻居添加到当前边界。为了做到这一点，线程增加当前边界的大小（第12行）并将邻居添加到相应的位置（第13行）。当前边界的大小需要原子地增加（第12行），因为可能有多个线程同时增加它，所以我们需要确保没有竞争条件发生。

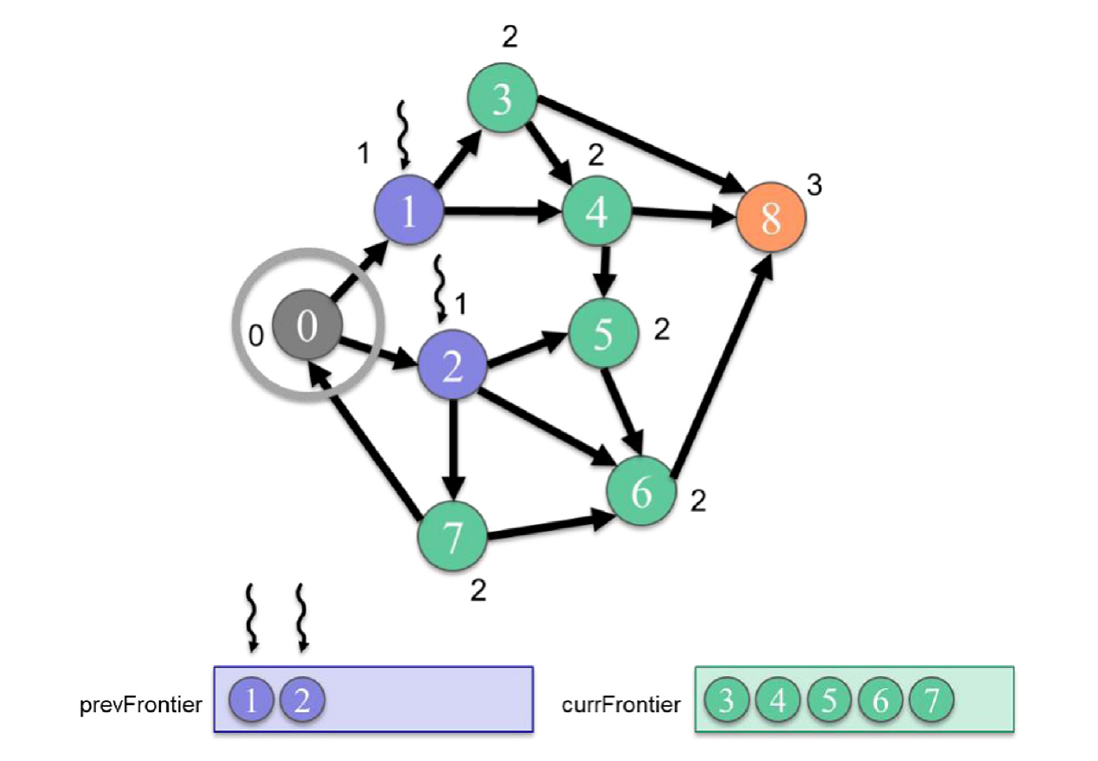图15.13 以顶点为中心的推（自顶向下）BFS遍历示例，从第1级到第2级，使用边界。BFS，即广度优先搜索。

我们现在转向第11行的原子操作。当一个线程遍历其顶点的邻居时，它检查邻居是否已被访问；如果没有，它将邻居标记为属于当前级别。在没有边界的图15.12中的以顶点为中心的推核函数中，检查和标记操作是在没有原子操作的情况下执行的（09-10）。在那个实现中，如果多个线程在任何一个线程能够标记之前检查同一个未访问邻居的旧标签，多个线程可能最终会标记邻居。由于所有线程都使用相同的标签标记邻居（操作是幂等的），允许线程冗余地标记邻居是可以的。相比之下，在图15.12中的基于边界的实现中，每个线程不仅标记未访问的邻居，而且还将其添加到边界。因此，如果多个线程观察到邻居未被访问，它们都会将邻居添加到边界，导致邻居被添加多次。如果邻居被多次添加到边界，它将在下一级中被多次处理，这是冗余和浪费的。为了避免让多个线程观察到邻居未被访问，邻居的标签检查和更新应该原子地执行。换句话说，我们必须检查邻居是否未被访问，如果没有，我们必须将邻居标记为当前级别的一部分，所有这些步骤都应在一个原子操作中完成。可以执行所有这些步骤的原子操作是compare-and-swap，由atomicCAS内联函数提供。这个函数接受三个参数：内存中数据的地址，我们想要比较数据的值，以及如果比较成功，我们想要设置数据的值。在我们的例子中（第11行），我们想要将level[neighbor]与UINT_MAX比较，以检查邻居是否未被访问，如果比较成功，将level[neighbor]设置为currLevel。与其他原子操作一样，atomicCAS返回存储的数据的旧值。因此，我们可以通过将atomicCAS的返回值与atomicCAS比较的值进行比较，来判断compare-and-swap操作是否成功，在这种情况下是UINT_MAX。

如前所述，与上一节中描述的方法相比，这种基于边界的方法的优势在于它通过只启动处理相关顶点的线程来减少冗余工作。基于边界的方法的缺点是长延迟原子操作的开销，特别是当这些操作在同一数据上竞争时。对于atomicCAS操作（第11行），我们期望竞争是适度的，因为只有一些线程，而不是全部，将访问同一个未访问的邻居。然而，对于atomicAdd操作（第12行），我们期望竞争很高，因为所有线程都增加同一个计数器将顶点添加到同一个边界。在下一节中，我们将探讨如何减少这种竞争。

15.6 通过私有化减少竞争

回想第6章“性能考虑”，可以应用一种优化来减少对相同数据的原子操作的竞争，那就是私有化。私有化通过在数据的私有副本上应用部分更新，然后在完成时更新公共副本，从而减少原子操作的竞争。我们在第9章“并行直方图”中的直方图模式看到了私有化的一个例子，同一区块中的线程更新了该区块私有的局部直方图，然后在最后更新了公共直方图。

私有化也可以应用于并发边界更新（对numCurrFrontier的增量）的上下文中，以减少插入边界的竞争。我们可以让每个线程块在整个计算过程中维护自己的局部边界，然后在完成时更新公共边界。因此，线程只与同一区块中的其他线程对相同数据竞争。此外，局部边界及其计数器可以存储在共享内存中，这使得对计数器的低延迟原子操作和对局部边界的存储成为可能。

图15.14 带有边界私有化的以顶点为中心的推（自顶向下）广度优先搜索（BFS）核函数。BFS，即广度优先搜索。

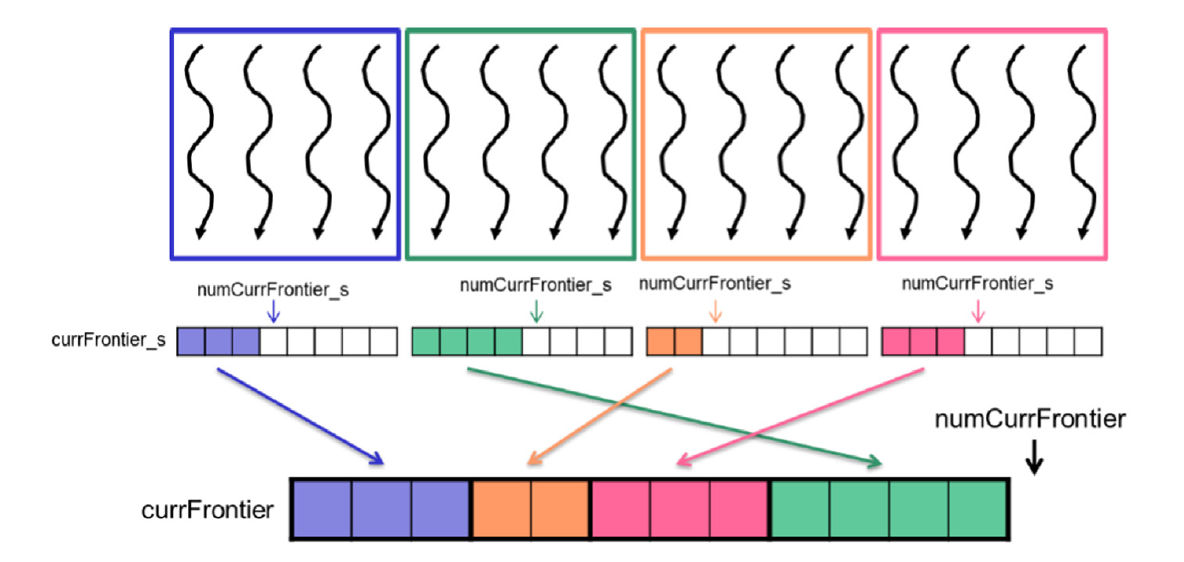
此外，当共享内存中的局部边界被存储到全局内存中的公共边界时，访问可以被合并。图15.14显示了使用私有化边界的以顶点为中心的推实现的核函数代码，而图15.15说明了边界的私有化。核函数首先在共享内存中为每个线程块声明一个私有边界（第07-08行）。区块中的一个线程将边界的计数器初始化为0（第09-11行），所有线程在__syncthreads屏障处等待初始化完成，然后才开始使用计数器（第12行）。代码的下一部分与以前的版本类似：每个线程从边界加载其顶点（第17行），遍历其出去边（第18-19行），找到边的目标处的邻居（第20行），并原子地检查邻居是否未被访问，如果未被访问，则访问它（第21行）。

图15.15 边界私有化的示例。

如果线程成功访问了邻居，即邻居未被访问，它将邻居添加到局部边界。线程首先原子地增加局部边界计数器（第22行）。如果局部边界未满（第23行），线程将邻居添加到局部边界（第24行）。否则，如果局部边界已溢出，线程恢复局部计数器的值（第26行），并通过原子地增加全局计数器（第27行）并将邻居存储在相应的位置（第28行），将邻居添加到全局边界。【恢复局部计时器的目的是为了后面全局拷贝时保持正确的数量】

在区块中的所有线程完成遍历其顶点的邻居后，它们需要将私有化的局部边界存储到全局边界。首先，线程们相互等待完成，确保不再有邻居被添加到局部边界（第33行）。接下来，区块中的一个线程代表其他线程在全局边界为局部边界中的所有元素分配空间（第36-39行），而所有线程等待它（第40行）。最后，线程遍历局部边界中的顶点（第43-44行），并将它们存储在公共边界中（第45-46行）。注意，进入公共边界的索引currFrontierIdx以currFrontierIdx_s表示，后者以threadIdx.x表示。因此，具有连续线程索引值的线程存储到连续的全局内存位置，这意味着存储被合并。

15.7 其他优化

减少启动开销

在大多数图中，BFS初始迭代的边界可能非常小。第一次迭代的边界只有源点的邻居。下一次迭代的边界则有当前边界顶点的所有未访问邻居。在某些情况下，最后几次迭代的边界也可能很小。对于这些迭代，终止一个网格并启动一个新的网格的开销可能超过并行性的益处。处理这些小边界迭代的一种方法是准备另一个核函数，它只使用一个线程块，但可能执行多次连续迭代。该核函数只使用一个局部区块级边界，并使用__syncthreads()在各级之间同步所有线程。这种优化在图15.16中进行了说明。在这个例子中，0级和1级可以每个由单个线程块处理。我们不是为0级和1级启动单独的网格，而是启动一个单区块网格，并使用__syncthreads()在各级之间同步。一旦边界达到溢出区块级边界的大小，区块中的线程将区块级边界的内容复制到全局边界，并返回到主机代码。然后主机代码将在后续的级别迭代中调用常规核函数，直到边界再次变小。

单区块核函数因此消除了小边界迭代的启动开销。我们将其实现留给读者作为练习。

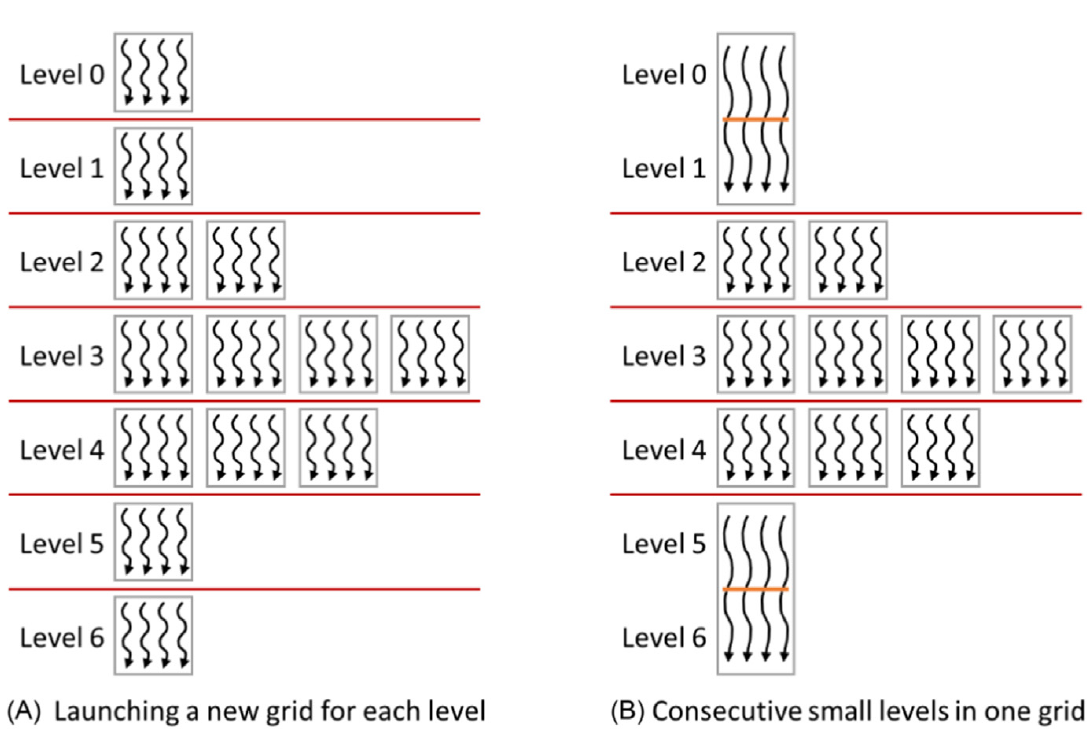图15.16 在一个网格中为具有小边界的级别执行多个级别：(A) 为每个级别启动一个新网格，(B) 一个网格中连续的小级别。

提高负载平衡

回想一下，在以顶点为中心的实现中，每个线程要完成的工作量取决于分配给它的顶点的连接度。在一些图中，如社交网络图，一些顶点（名人）的度数可能比其他顶点高出几个数量级。当这种情况发生时，一个或几个线程可能需要过长的时间，从而减慢整个网格的执行速度。我们已经看到了解决这个问题的一种方法，那就是使用以边为中心的并行实现。另一种可能解决这个问题的方法是通过对边界的顶点根据它们的度数进行排序并将其放入桶中，并在具有适当大小处理器组的单独核函数中处理每个桶。一个值得注意的实现（Merrill和Garland，2012）对度数小、中、大的顶点使用三个不同的桶。处理小桶的核函数为每个顶点分配一个单独的线程；处理中等桶的核函数为每个顶点分配一个单独的warp；处理大桶的核函数为每个顶点分配一个整个线程块。这种技术对于顶点度数变化很大的图特别有用。

15.8 总结

在本章中，我们通过使用广度优先搜索作为示例，看到了与并行化图计算相关的挑战。我们首先对图的表示进行了简要介绍。我们讨论了以顶点为中心和以边为中心的并行实现之间的差异，并观察了它们之间的权衡。我们还看到了如何通过使用边界消除冗余工作，并通过私有化优化了边界的使用。我们还简要讨论了其他高级优化以减少同步开销和改善负载平衡。